奈奎斯特稳定判据ppt课件
合集下载
乃奎斯特稳定判据精品PPT课件
乃奎斯特稳定判据
1
主要内容
幅角定理 乃奎斯特稳定判据 乃氏稳定判据在Ⅰ、Ⅱ 型系统中的应用 在波德图上判别系统稳定性
乃奎斯特稳定判据是用开环频率特性判别闭环系统的稳 定性。不仅能判断系统的绝对稳定性，而且可根据相对稳定 的概念，讨论闭环系统的瞬态性能，指出改善系统性能的途 径。
2
一、幅角定理：
设负反馈系统的开环传递函数为：Gk (s) G(s)H (s) ，其 中：G(s)为前向通道传递函数，H (s)为反馈通道传递函数。
22
射；
③ 以 s = j 代入F(s)，令从－∞→0 ，得第三部分的映射。
得到映射曲线后，就可由柯西幅角定理计算 N = Z－P，式 中Z、P是F(s)在s右半平面的零点数和极点数。
若已知P，并能确定N，可求出Z = N + P 。当Z = 0时，系统 稳定；否则不稳定。
10
第2个问题：辅助方程与开环频率特性的关系。我们所构造的辅 助方程为 F(s) 1 Gk (s)，Gk (s) 为开环频率特性。因此，有以下三 点是明显的：
7
二、乃奎斯特稳定判据： 对于一个控制系统，若其特征根处于s右半平面，则系统是
不稳定的。对于上面讨论的辅助方程 F (s) 1 Gk (s) ，其零点恰 好是闭环系统的极点，因此，只要搞清F(s)的的零点在s右半平 面的个数，就可以给出稳定性结论。如果F(s)的右半零点个数为 零，则闭环系统是稳定的。
6
柯西幅角定理 s平面上不通过F(s)任何奇异点的封闭曲线s包围s平
面上F(s)的z个零点和p个极点。当s以顺时针方向沿封闭 曲线s移动一周时，在F(s)平面上相对应的封闭曲线f 将 以顺时针方向绕原点旋转N圈。N，z，p的关系为：
1
主要内容
幅角定理 乃奎斯特稳定判据 乃氏稳定判据在Ⅰ、Ⅱ 型系统中的应用 在波德图上判别系统稳定性
乃奎斯特稳定判据是用开环频率特性判别闭环系统的稳 定性。不仅能判断系统的绝对稳定性，而且可根据相对稳定 的概念，讨论闭环系统的瞬态性能，指出改善系统性能的途 径。
2
一、幅角定理：
设负反馈系统的开环传递函数为：Gk (s) G(s)H (s) ，其 中：G(s)为前向通道传递函数，H (s)为反馈通道传递函数。
22
射；
③ 以 s = j 代入F(s)，令从－∞→0 ，得第三部分的映射。
得到映射曲线后，就可由柯西幅角定理计算 N = Z－P，式 中Z、P是F(s)在s右半平面的零点数和极点数。
若已知P，并能确定N，可求出Z = N + P 。当Z = 0时，系统 稳定；否则不稳定。
10
第2个问题：辅助方程与开环频率特性的关系。我们所构造的辅 助方程为 F(s) 1 Gk (s)，Gk (s) 为开环频率特性。因此，有以下三 点是明显的：
7
二、乃奎斯特稳定判据： 对于一个控制系统，若其特征根处于s右半平面，则系统是
不稳定的。对于上面讨论的辅助方程 F (s) 1 Gk (s) ，其零点恰 好是闭环系统的极点，因此，只要搞清F(s)的的零点在s右半平 面的个数，就可以给出稳定性结论。如果F(s)的右半零点个数为 零，则闭环系统是稳定的。
6
柯西幅角定理 s平面上不通过F(s)任何奇异点的封闭曲线s包围s平
面上F(s)的z个零点和p个极点。当s以顺时针方向沿封闭 曲线s移动一周时，在F(s)平面上相对应的封闭曲线f 将 以顺时针方向绕原点旋转N圈。N，z，p的关系为：
控制工程基础 (第12讲) 第五章 乃魁斯特(Nyquist)稳定性判据 PPT课件
如果在s平面上曲线包围k个零点和k个极点(k=0,1,2…)，
即包围的零点数与极点数相同，则在 F(s) 平面上，
相应的封闭曲线不包围 F(s) 平面上的原点。
上述讨论是映射定理的图解说明，奈奎斯特稳 定判据正是建立在映射定理的基础上。
相角（幅角）定理：
如果闭合曲线 s 以顺时针方向为正方向，在 s 平
在右半s平面内的零点数和极点数联系起来的判据。这 种方法无须求出闭环极点，得到广泛应用。
奈奎斯特稳定判据是建立在复变函数理论中的图形映 射基础上的 。
相角（幅角）定理：
如果闭合曲线 S 以顺时针方向为正方向，在[S]平
面上包围了Fs 的 Z 个零点和 P 个极点，但不经过
任何一个零点和极点，那么，对应的映射曲线 F 也以
奈魁斯特稳定判据是利用开环频率特性判别闭环系统的稳 定性。不仅能判断系统的绝对稳定性，而且可根据相对稳定的 概念，讨论闭环系统的瞬态性能，指出改善系统性能的途径。 它从代数判据脱颖而出，故可以说是一种几何判据。
06-7-20
控制系统系统的稳定性分析
2
奈魁斯特稳定判据无需求取闭环系统的特征根，而是利用
F(s) 的轨迹将逆时针方向包围 F(s)平面上原点两次
06-7-20
控制系统系统的稳定性分析
9
s平面
B3
2
1
A0
-1
-2
F -3 -3
-2
-1
j
Im
C
2
1.5
F (s)平面
1 B1
0.5
D
E1
0 C1
F1 -0.5
-1
A
-1.5
D1
5-4 奈奎斯特稳定判据
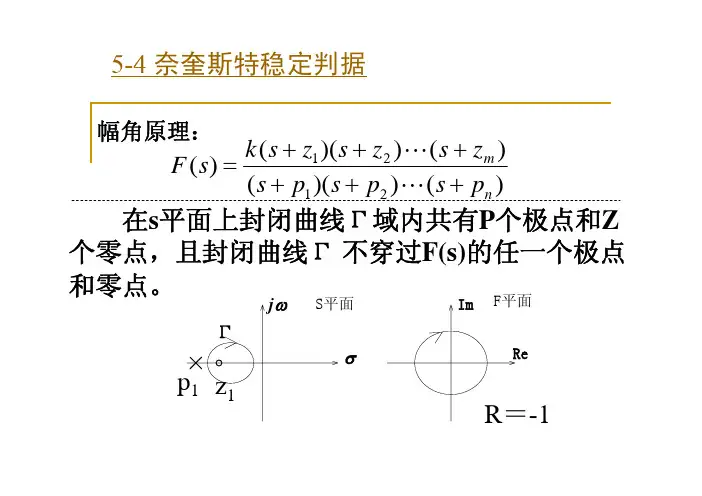
ω 负穿越 相角减小的穿越，N半次穿越 G ( j0+ ) H ( j0+ ) гGH起始或终止于(-1,j0)点左侧负实轴 R=2N=2(N+-N-) N+=0,N-=1 R=2(0-1)=-2
课堂习题
P210 图5-32,计算各小图中,гF包围原点的圈数R
2.Nyquist稳定判据 闭环系统稳定的充分必要条件 1. Nyquist曲线不穿越点(-1,j0) 2. 且逆时针包围(-1,j0)点的圈数R等于开环传 递函数的正实部极点数P 闭合曲线г包围函数F(s)=1+G(s)H(s)的零点数 即闭环控制系统正实部极点数为 Z=P-R=P-2N
εe
jθ
∞e jθ
s = εe
, θ ∈ [0°,+90°]
1 sv G1 ( s )
− jνθ
ε为无穷小
θ
G( s) H ( s) =
1 ν s
G1 ( s ) = K
=
s =εe jθ
1
ε
ν
e
→ ∞e
− jνθ
∏ (τ
j =1 n −ν i =1
m
j
s + 1)
s→0 τ is +1 → 1
∏ (T s + 1)
例5-8 已知单位反馈系统开环幅相曲线(K=10,P=0,v=1),如图 所示，试确定系统闭环稳定时K值的范围 幅相曲线与负实轴交点频率分别ω1,ω2,ω3 解：
G ( jω i ) =
G ( jω1 ) = −2 , G ( jω 2 ) = −1.5 , G ( jω 3 ) = −0.5 10 10 ω = K 若令G(jω1)=-1, 1 K = 若令 G(j ω )=-1, 2 2 2 1 .5 10 −1 同理 K 3 = − 0.5 = 0.5 判断闭环系统稳定性 10
奈奎斯特稳定判据
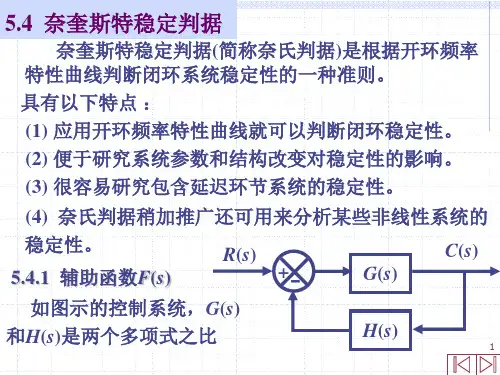
幅角原理：如果封闭曲线内有Z个F(s)的零点， P个
F(s)的极点 ，则s 沿封闭曲线s 顺时针方向转一圈时，在
F(s)平面上，曲线F(s)绕其原点逆时针转过的圈数。
+
5. 4 . 3 奈氏判据
（1）0型系统
0
s为包围虚轴和整个右半平面。
s平面s 映射 F(s)
解：① 由开环传递函数知 P = 1 。 ② 作系统的开环对数频率特性曲线。
() = 90 + arctanT2 (180 arctanT1 )
270
arctan
(T1 1
T2 ) 2T1 T2
当() = 180时，g =(1/T1T2)1/2 ，A(g)=kT2
③ 稳定性判别。 G(s)H(s)有一个积分环节N =1 ，故
开环极坐标图如图
j
01
19
k(0.1s 1) Gk (s) s(s 1)
=0
Im
增补线
1 0.1k
Re 0
(3) 稳定性判别: 因为是1型系统，需作增补线如图
当 0.1k < 1 ，k > 10时， R =1/2，z = p 2R = 0
闭环系统是稳定的。
20
5.4.4 伯德图上的稳定性判据
Im
() 1
(+)
0
由图可知，幅相曲线 不 包 围 (1 ， j0) 点 。 此 结
Re 果也可以根据 增加时幅
相曲线自下向上(幅角减 小)和自上向下(幅角增加) 穿越实轴区间(，1)的 次数决定。
R = N N
自实轴区间（，1）开始向下的穿越称为半次正穿越，自实轴
区间（，1）开始向上的穿越为半次负穿越。
2第3、4、5、6节奈魁斯特稳定判据
2
5.3.1 完整的频率特性极坐标图 R(s) + -
G(s)
H(s)
C(s)
闭环传递函数
C s Gs s Rs 1 Gs H s
KN s 开环传递函数 G s H s s Ds N 0 D0 1, 为串联积分环节个数 K 0 为放大系数
对含有积分环节的开环传递函数，当 s由 j j0 j0 j 变化时，也称 由 0 连续变化。 Tuesday, June 16, 2015
8
Tuesday, June 16, 2015
9
5.3.2 奈奎斯特稳定判据 可用复变函数中的幅角定理证明奈奎斯特稳定判据
Tuesday, June 16, 2015
22
开环频率特性的极坐标图在点(-1,j0)左方正、负穿越 负实轴的次数，对应于伯德图上，在开环对数幅频特性 大于0dB的频段内，相频特性曲线正穿越（相位增加） 和负穿越（相位减少） 180 线的次数。 根据伯德图分析闭环系统稳定性的奈奎斯特稳定判据： 闭环系统稳定的充要条件是，在开环幅频特性大于0dB 的所有频段内，相频特性曲线对 180 线的正、负穿越 次数之差等于P/2，其中P为开环正实部极点个数。 当开环系统含有积分环节时，相频特性应增补 由 0 0 的部分。
● 闭环系统的开环传递函数存在正实部极点的情况
奈奎斯特稳定判据的表述1： 若闭环系统的开环传递函数 Gs H s 有P个正实部极 点，则闭环系统稳定的充要条件是，当s按顺时针方 向沿奈奎斯特围线连续变化一周时， Gs H s 绘出的 封闭曲线应按逆时针方向包围点（－1，j0）P周。
Tuesday, June 16, 2015
奈奎斯特稳定性判据 ppt课件
24
三、例题详解
【解答】 (1)
半奈奎斯特曲线
K (1 j ) 1.1 1 0.1 2 G( j ) H ( j ) K jK 2 j ( j0.1 1) (1 0.01 ) (1 0.01 2 )
幅值变化： A(0 ) , A() 0 相角变化： K : 180
时，可应用对数频率特性稳定性判据，判定系统的 稳定性。基于Bode图和基于Nyquist图的两种稳定性 判据是一致的，只是坐标系不同而已。 负反馈闭环系统，位于右半s平面极点的个数为 (3)
9
二、对数频率特性稳定性判据
式中：P —开环传递函数位于右半s平面极点的个 数； N —相频特性曲线正穿越次数。在 L( ) 0 ( ) 自下而上穿越 对应的频率范围内， (2k 1) 180 线的次数，其中自下而上起 始于或终止于该线的次数，折半计算； N —相频特性曲线负穿越次数。在 L( ) 0 ( ) 自上而下穿越 对应的频率范围内， (2k 1) 180 线的次数，其中自上而下起 始于或终止于该线的次数，折半计算； Z —闭环传递函数，位于右半s平面极点的 个数，即特征方程位于右半s平面根的 10 个数。
18
三、例题详解
【解答】
19
三、例题详解
【解答】
20
三、例题详解
【例3】 某负反馈控制系统，开环传递函数
试：（1）画出幅相特性曲线；（2）判定稳定性。
21
三、例题详解
【解答】 (1)
幅相特性曲线
K (T1 T2 ) 1 2TT 1 2 G( j ) H ( j ) j (1 2T12 )(1 2T22 ) (1 2T12 )(1 2T22 )
54-5 奈奎斯特稳定性判据
P183
曲线Γs包围一个F(s)的极点，当S1沿Γs顺时针连续变化一周，
因为Pi映射到F(s)上是在无穷远，因此ΓF逆时针绕F平面零点一周，
(S+Pi)的相角积累是-2π角度。 幅角原理：设F(s)除平面上的有限个奇点外，为单值解析函
数，若S平面上任选一条封闭曲线Cs以顺时针方向包围F(s)的Z 个零点和P个极点，且使它不通过F(s)的奇点，则其在F(s)平面 上的映射曲线CF将围绕着坐标原点旋转N周，其中N=Z-P。 当N>0，表示曲线CF以顺时针方向旋转；
G( s ) K s(T1 s 1)(T2 s 1)
G( j 0) 0
解：依题有 G( j 0 ) 90
G( j) 0 270
K1 (小)
N 0
(稳定)
K
Z P N 00 0
K 2 (大)
N 2
(不稳定)
Z P N 02 2
2)T1 T2，G( j ) H ( j )曲线穿过 (1, j 0)点，说明闭环系统 有一对虚根，闭环系统 不稳定 ；
3) T1 T2，Z N 说明闭环系统有两个极点 P 2 0 2，
右方，故闭环系统不稳定。 在S平面的
例7：已知单位反馈系统开环传递函数,分析系统稳定性。
zdkzcjlueducn22855频域稳定判据系统稳定的充要条件全部闭环极点均具有负的实部由闭环特征多项式系数不解根判定系统稳定性不能研究如何调整系统结构参数来改善系统稳定性及性能代数稳定判据routh判据由开环频率特性直接判定闭环系统的稳定性可研究如何调整系统结构参数改善系统稳定性及性能问题频域稳定判据nyquist判据对数稳定判据
-j∞
G( jω )
曲线Γs包围一个F(s)的极点，当S1沿Γs顺时针连续变化一周，
因为Pi映射到F(s)上是在无穷远，因此ΓF逆时针绕F平面零点一周，
(S+Pi)的相角积累是-2π角度。 幅角原理：设F(s)除平面上的有限个奇点外，为单值解析函
数，若S平面上任选一条封闭曲线Cs以顺时针方向包围F(s)的Z 个零点和P个极点，且使它不通过F(s)的奇点，则其在F(s)平面 上的映射曲线CF将围绕着坐标原点旋转N周，其中N=Z-P。 当N>0，表示曲线CF以顺时针方向旋转；
G( s ) K s(T1 s 1)(T2 s 1)
G( j 0) 0
解：依题有 G( j 0 ) 90
G( j) 0 270
K1 (小)
N 0
(稳定)
K
Z P N 00 0
K 2 (大)
N 2
(不稳定)
Z P N 02 2
2)T1 T2，G( j ) H ( j )曲线穿过 (1, j 0)点，说明闭环系统 有一对虚根，闭环系统 不稳定 ；
3) T1 T2，Z N 说明闭环系统有两个极点 P 2 0 2，
右方，故闭环系统不稳定。 在S平面的
例7：已知单位反馈系统开环传递函数,分析系统稳定性。
zdkzcjlueducn22855频域稳定判据系统稳定的充要条件全部闭环极点均具有负的实部由闭环特征多项式系数不解根判定系统稳定性不能研究如何调整系统结构参数来改善系统稳定性及性能代数稳定判据routh判据由开环频率特性直接判定闭环系统的稳定性可研究如何调整系统结构参数改善系统稳定性及性能问题频域稳定判据nyquist判据对数稳定判据
-j∞
G( jω )
自动控制理论54-频域奈氏判据精品PPT课件
b. 如果开环系统是不稳定的,且已知有P个开环 极点在s的右半平面，则闭环系统稳定的充要条 件是GH曲线按逆时针绕（-1，j0）点P圈，否则 闭环系统是不稳定系统。
2
3. 公式
Z = N+ P
P——为G(s)H(s)位于s右半平面的极点数。
N —— GH曲线按顺时针绕（-1，j0）点的圈 数。
Z——为闭环系统位于s右半平面的极点数。
根据奈氏判据, 闭环系统在s右半平面极点数 Z=N+P=0 所以系统稳定。
6
例4: 一系统开环传递函数为：
G (s)H (s)s1K Ts(T0,K0)
试判别系统的稳定性。
解：本系统的开环频率特性 G(j)H(j)j1K Tj
0 0 变化时，
系统的奈氏曲线如图所示：
Ⅰ型系统补半圆
因为系统有0个开环极点位于s的右半平面，即：P=0。 图中奈氏曲线是顺时针方向绕（-1，j0）点0圈，即 N=0。
试判断系统的稳定性的K和T值范围。 W=0-
解：本系统的开环频率特性
-2
K
W=0+
1
Im
0
Re
G(j)H(j) K
Tj 1
当 0 0 变化时，
系统的奈氏曲线如图所示。
P根当=据即当1T。奈T<：氏0>P系0判=系统0据。统有, 有闭0一个环个系开开统环环稳极极定点点Z=位位N于于+Pss=的的0右,右N半半=平-平1面,即面，图，即中Im： 奈根氏图0据圈曲中奈，线奈氏是则氏判逆0曲<据时K线针, <闭方是1。环向逆系绕时（统针-稳1方，定向j0Z）绕=点N（+的-K-2P11WW=，圈==000,，+-j0N 1）则=0K点,即>的0 15。 Re
2
3. 公式
Z = N+ P
P——为G(s)H(s)位于s右半平面的极点数。
N —— GH曲线按顺时针绕（-1，j0）点的圈 数。
Z——为闭环系统位于s右半平面的极点数。
根据奈氏判据, 闭环系统在s右半平面极点数 Z=N+P=0 所以系统稳定。
6
例4: 一系统开环传递函数为：
G (s)H (s)s1K Ts(T0,K0)
试判别系统的稳定性。
解：本系统的开环频率特性 G(j)H(j)j1K Tj
0 0 变化时，
系统的奈氏曲线如图所示：
Ⅰ型系统补半圆
因为系统有0个开环极点位于s的右半平面，即：P=0。 图中奈氏曲线是顺时针方向绕（-1，j0）点0圈，即 N=0。
试判断系统的稳定性的K和T值范围。 W=0-
解：本系统的开环频率特性
-2
K
W=0+
1
Im
0
Re
G(j)H(j) K
Tj 1
当 0 0 变化时，
系统的奈氏曲线如图所示。
P根当=据即当1T。奈T<：氏0>P系0判=系统0据。统有, 有闭0一个环个系开开统环环稳极极定点点Z=位位N于于+Pss=的的0右,右N半半=平-平1面,即面，图，即中Im： 奈根氏图0据圈曲中奈，线奈氏是则氏判逆0曲<据时K线针, <闭方是1。环向逆系绕时（统针-稳1方，定向j0Z）绕=点N（+的-K-2P11WW=，圈==000,，+-j0N 1）则=0K点,即>的0 15。 Re
2第3、4、5、6节奈魁斯特稳定判据.
5.3 奈奎斯特稳定判据
Tuesday, June 25, 2019
1
劳思稳定判据分析闭环系统稳定性： 必须知道闭环系统的特征方程；不能指出系统的稳定 程度。
奈奎斯特稳定判据的特点： 利用开环频率特性判定闭环系统的稳定性； 能够指出稳定的程度，揭示改善系统稳定性的方法
Tuesday, June 25, 2019
在画完整的奈奎斯特图时，可只考虑s在整个虚轴和
原点或原点附近的小半圆abc上变化的情况。 Tuesday, June 25, 2019
5
开环传递函数不含积分环节，即 0 时的奈奎斯特图
画出 0 时的 G jH j的极坐标图，再取其关于实 轴对称的图形 G jH j，把它们合在一起就是完
整的奈奎斯特图。
Tuesday, June 25, 2019
6
开环传递函数含有积分环节，即 0 时的奈奎斯特图
s 在原点附近时GsH s的图形： s e j , 0, 0, 2 2
开环传递函数写为： GsH s
K s
K
G jH j 图形的画法与无积分环节时相同。
对含有积分环节的开环传递函数，当
s由 j j0 j0 j 变化时，也称 由
0 Tuesday, June 25, 2019
连续变化。
8
Tuesday, June 25, 2019
9
5.3.2 奈奎斯特稳定判据 可用复变函数中的幅角定理证明奈奎斯特稳定判据
● 闭环系统的开环传递函数存在正实部极点的情况
奈奎斯特稳定判据的表述1：
若闭环系统的开环传递函数 GsH s 有P个正实部极
点，则闭环系统稳定的充要条件是，当s按顺时针方
Tuesday, June 25, 2019
1
劳思稳定判据分析闭环系统稳定性： 必须知道闭环系统的特征方程；不能指出系统的稳定 程度。
奈奎斯特稳定判据的特点： 利用开环频率特性判定闭环系统的稳定性； 能够指出稳定的程度，揭示改善系统稳定性的方法
Tuesday, June 25, 2019
在画完整的奈奎斯特图时，可只考虑s在整个虚轴和
原点或原点附近的小半圆abc上变化的情况。 Tuesday, June 25, 2019
5
开环传递函数不含积分环节，即 0 时的奈奎斯特图
画出 0 时的 G jH j的极坐标图，再取其关于实 轴对称的图形 G jH j，把它们合在一起就是完
整的奈奎斯特图。
Tuesday, June 25, 2019
6
开环传递函数含有积分环节，即 0 时的奈奎斯特图
s 在原点附近时GsH s的图形： s e j , 0, 0, 2 2
开环传递函数写为： GsH s
K s
K
G jH j 图形的画法与无积分环节时相同。
对含有积分环节的开环传递函数，当
s由 j j0 j0 j 变化时，也称 由
0 Tuesday, June 25, 2019
连续变化。
8
Tuesday, June 25, 2019
9
5.3.2 奈奎斯特稳定判据 可用复变函数中的幅角定理证明奈奎斯特稳定判据
● 闭环系统的开环传递函数存在正实部极点的情况
奈奎斯特稳定判据的表述1：
若闭环系统的开环传递函数 GsH s 有P个正实部极
点，则闭环系统稳定的充要条件是，当s按顺时针方
乃奎斯特稳定判据对数稳定判据和稳定裕度-精PPT共64页
25、学习是劳动，是充满思想的劳动。——乌申斯基
谢谢！
乃奎斯特稳定判据对数稳定判据和稳 定裕度-精
16、自己选择的路、跪着也要把它走 完。 17、一般情况下)不想三年以后的向黑暗宣战的人，心里必须 充满光 明。 19、学习的关键--重复。
20、懦弱的人只会裹足不前，莽撞的 人只能 引为烧 身，只 有真正 勇敢的 人才能 所向披 靡。
21、要知道对好事的称颂过于夸大，也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤，荒于嬉；行成于思，毁于随。——韩愈
23、一切节省，归根到底都归结为时间的节省。——马克思 24、意志命运往往背道而驰，决心到最后会全部推倒。——莎士比亚
谢谢！
乃奎斯特稳定判据对数稳定判据和稳 定裕度-精
16、自己选择的路、跪着也要把它走 完。 17、一般情况下)不想三年以后的向黑暗宣战的人，心里必须 充满光 明。 19、学习的关键--重复。
20、懦弱的人只会裹足不前，莽撞的 人只能 引为烧 身，只 有真正 勇敢的 人才能 所向披 靡。
21、要知道对好事的称颂过于夸大，也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤，荒于嬉；行成于思，毁于随。——韩愈
23、一切节省，归根到底都归结为时间的节省。——马克思 24、意志命运往往背道而驰，决心到最后会全部推倒。——莎士比亚
奈奎斯特稳定性判据课件
在多变量系统和非线性系统的 分析中，奈奎斯特稳定性判据 具有重要的应用价值。
03
判据的数学模型
模型建立
01
02
03
确定系统传递函数
首先需要确定控制系统的 传递函数，包括开环和闭 环传递函数。
绘制极坐标图
将传递函数转换为极坐标 形式，以便于分析系统的 频率响应特性。
确定临界频率
根据系统的开环和闭环传 递函数，确定系统的临界 频率。
。
在生物医学工程、环境 工程等领域，利用奈奎 斯特稳定性判据研究复 杂系统的动态行为和稳
定性问题。
TH 据的未来发展
研究方向
深入研究奈奎斯特稳定性判据 的数学原理，探索其在控制系
统中的更广泛应用。
结合现代控制理论和算法， 发展新的稳定性分析方法。
研究奈奎斯特稳定性判据与其 他稳定性判据的关系，完善稳
定性理论体系。
技术发展
1
利用计算机技术和数值计算方法，提高奈奎斯特 稳定性判据的运算效率和精度。
它提供了一种有效的数学方法来分析系统的动态行为，帮助工程师预测系 统的性能和行为。
判据的应用场景
控制系统设计
在控制系统设计中，奈奎斯特稳 定性判据用于分析控制系统的稳 定性和性能。
通信系统分析
在通信系统中，奈奎斯特稳定性 判据用于分析信号传输的稳定性 和可靠性。
信号处理
在信号处理中，奈奎斯特稳定性 判据用于分析信号的频域特征和 系统的稳定性。
2
开发适用于不同控制系统的奈奎斯特稳定性判据 分析工具。
3
探索将奈奎斯特稳定性判据应用于非线性控制系 统的方法。
应用前景
01
02
03
在航空航天、电力、化 工等领域，利用奈奎斯 特稳定性判据优化控制 系统的设计和性能。
03
判据的数学模型
模型建立
01
02
03
确定系统传递函数
首先需要确定控制系统的 传递函数，包括开环和闭 环传递函数。
绘制极坐标图
将传递函数转换为极坐标 形式，以便于分析系统的 频率响应特性。
确定临界频率
根据系统的开环和闭环传 递函数，确定系统的临界 频率。
。
在生物医学工程、环境 工程等领域，利用奈奎 斯特稳定性判据研究复 杂系统的动态行为和稳
定性问题。
TH 据的未来发展
研究方向
深入研究奈奎斯特稳定性判据 的数学原理，探索其在控制系
统中的更广泛应用。
结合现代控制理论和算法， 发展新的稳定性分析方法。
研究奈奎斯特稳定性判据与其 他稳定性判据的关系，完善稳
定性理论体系。
技术发展
1
利用计算机技术和数值计算方法，提高奈奎斯特 稳定性判据的运算效率和精度。
它提供了一种有效的数学方法来分析系统的动态行为，帮助工程师预测系 统的性能和行为。
判据的应用场景
控制系统设计
在控制系统设计中，奈奎斯特稳 定性判据用于分析控制系统的稳 定性和性能。
通信系统分析
在通信系统中，奈奎斯特稳定性 判据用于分析信号传输的稳定性 和可靠性。
信号处理
在信号处理中，奈奎斯特稳定性 判据用于分析信号的频域特征和 系统的稳定性。
2
开发适用于不同控制系统的奈奎斯特稳定性判据 分析工具。
3
探索将奈奎斯特稳定性判据应用于非线性控制系 统的方法。
应用前景
01
02
03
在航空航天、电力、化 工等领域，利用奈奎斯 特稳定性判据优化控制 系统的设计和性能。
奈奎斯特稳定判据PPT共48页
[柯西幅角原理]：S平面上不通过F(s)任何奇异点的封闭曲线CS 包围S平面上F(s)的Z个零点和P个极点。当s以顺时针方向沿封 闭曲线CS移动一周时，在F(s)平面上相对应于封闭曲线CF将以顺
时针方向绕原点旋转N圈。N，Z，P的关系为：N=Z－P。
若N为正，表示CF顺时针运动，包围原点； 若N为0，表示CF顺时针运动，不包围原点； 若N为负，表示CF逆时针运动，包围原点。
F (s) F (s2) F (s1) i m 1 (s2zi) jn 1 (s2pj) i m 1 (s1zi) jn 1 (s1pj)
[例]设：F(s) s2 ，当s平面上的动点沿平行于虚轴的直线，从
s
(-1，j1)到(-1，j0) ，映射到F(s)平面上的点将沿某曲线从(0，-
5.4.2 奈奎斯特稳定判据
奈奎斯特当年就是巧妙地应用了幅角原理得到了奈奎斯特稳 定判据。设系统结构图如图所示
G k(s)G (s)H(s)
(s) G(s) 1G(s)H(s)
令： G(s)M1(s),H(s)M2(s)
N1(s)
N2(s)
R(s)
C(s)
G(s)
H (s)
则开环传递函数为：Gk(s)M N11((ss))M N22((ss)) …………… (a)
s平面
F (s)平面
Cs顺时针
示意图 CF顺时针
s平面
F (s)平面
Cs顺时针
示意图 CF顺时针
在这种映射关系中，有一点是十分重要的，即：不需知道围线
CS的确切形状和位置，只要知道它的内域所包含的零点和极点 的数目，就可以预知围线CF是否包围坐标原点和包围原点多少 次；反过来，根据已给的围线CF是否包围原点和包围原点的次 数，也可以推测出围线CS的内域中有关零、极点数的信息。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
G 1
0.5 0
E D
F
H
C
-0.5
B
-1
A
-1.5
-2
11
-1 -0.5 0 0.5 1 1.5 2 2.5 3
2. 围线CS只包围零点不包围极点
如图所示围线CS包围一个零点z=-2，先考察因子(s+2)辐角a，当 变点s沿CS顺时针绕行一周时，a的变化为-360°。映射到F(S)平 面上对应变点F(S)沿CF绕行一周后的辐角变化也应等于-360°。
围S平面上F(s)的Z个零点和P个极点。当s以顺时针方向沿封闭曲
线CS移动一周时，在F(s)平面上映射的封闭曲线CF将以顺时针方 向绕原点旋转N圈。N，Z，P的关系为：N=Z－P。
s平面
F (s)平面
Cs顺时针
示意图 CF 顺时针
2
若N为正，表示CF顺时针运动，包围原点；
若N为0，表示CF顺时针运动，不包围原点；
p j )
m
n
(s zi ) (s p j )
i 1
j 1
例
F (s) F (s2 ) F (s1)
F(s) s 2 s
(s2 2) (s2 0) (s1 2) (s1 0)
(s2 2) (s1 2) (s2 0) (s1 0)
im1 (s2
zi )
n
(s2
j 1
p
j
)
im1 ( s1
zi )
n
(s1
j 1
p j )
im1 (s2
zi )
m
(s1 i 1
zi
)
n
j 1
(s2
pj)
n
(s1
j 1
4
现考虑S平面上一点s1映射到F(s)平面上的点F(s1)可以用一个向量
来表示，即当
m
K (s1 zi )
F (s1)
i 1 n
(s1 p j )
j 1
m
m
K
F (s1) F (s1) e jF (s1)
i1 n
s1 zi e j(s1zi )
K i1
i1
j1
5
Im S平面
Re
Im
F(s)
(s)
F(s)平面 Re
6
当S平面上动点s从s1经过某曲线CS到达s2，映射到F(s)平面上也 将是一段曲线CF ，该曲线完全由F(s)表达式和s平面上的曲线CS 决定。若只考虑动点s从s1到达s2相角的变化量，则有
F (s) F (s2 ) F (s1)
F (s)平面
df (0, j1)
8
1. 围线CS既不包围零点也不包围极点 如图所示，在S平面上当变点s沿围线 CS按顺时针方向运动一周时，我们 来考察F(S)中各因子项的辐角的变化 规律。 现以图中未被包围的零点-2为例。当 变点s沿CS绕行一周后，因子(s+2)的 辐角a的变化为0°。
值与之对应。
[例]设：
F(s) s 2 s
ds (1, j1)
s平面
2 1
F (s)平面
d f (0, j1)
3
F (s) K (s z1)(s z2 )(s zm ) (s p1)(s p2 )(s pn )
F(s)的值域构成的复平面称为F(s)平面。其中S平面上的全部 零点都映射到F(s)平面上的原点；S平面上的极点映射到F(s)平面 上时都变成了无限远点。除了S平面上的零、极点之外的普通点， 映射到F(s)平面上是除原点之外的有限点。
同理，对未被包围的极点也是一样， 因子项(s+0) 的辐角b在变点s沿CS绕 行一周后的变化也等于0°。
于是，映射到F(S)平面上，当变点 F(s)沿CF绕行一周后的辐角变化也应 等于0°。这表明，围线CF此时不包 围原点。
s平面
◎
A BC
2
1 a
H
1
2
D
3
b
GF E
CS顺时针
2
1.5
F ( s)平面
注意，虽然函数F(s)从S平面到F(s)平面的映射是一一对应的，然 而逆过程往往并非如此。例如已知
ቤተ መጻሕፍቲ ባይዱ
F(s)
K
s(s 1)( s 2)
s(s 1)(s 2) K F (s)
这个函数在有限的S平面上除S=0,－1, － 2以外均解析，除此三 点外，S平面上的每一个S值在F(s)平面只有一个对应点，但是 F(s)平面上的每一个点在S平面上却有三个映射点。最简单的说 明方式就是将方程改写成
2
A BC
s平面
H
D
2 a 1
n
s1 zi
m
n
e j
i
1
(
s1
zi
)
j
1
(
s1
p
j
)
s1 p j e j(s1 p j )
s1 p j
j 1
j 1
向量的幅值为
m
K s1 zi
F(s1)
i 1 n
s1 p j
j1
向量的相角为
m
n
F(s1) (s1 zi ) (s1 p j )
第四节 奈奎斯特稳定判据
1
一、辐角定理： 对于一个复变函数
F (s) K (s z1 )(s z2 )(s zm ) (s p1 )(s p2 )(s pn )
式中-zi(i=1,2,…,m)为F(s)的零点， -pj(j=1,2,…,n)为F(s)的极点。
[柯西辐角原理]：S平面上不通过F(s)任何奇异点的封闭曲线CS包
若N为负，表示CF逆时针运动，包围原点。
对于一个复变函数
F (s) K (s z1 )(s z2 )(s zm ) (s p1 )(s p2 )(s pn )
函数F(s)是复变量s的单值函数，s可以在整个S平面上变化，对
于其上的每一点，除有限(n)个极点外，函数F(s)都有唯一的一个
7
[例]设：F(s) s 2 ，当s平面上的动点沿平行于虚轴的直线，从
s
(-1，j1)到(-1，j0) ，映射到F(s)平面上的点将沿某曲线从(0，-j1)
到(-1，-j0) ，相角的变化为：
s平面
ds(1, j1)
2 1
F (s) F (s2 ) F (s1) 00 1800 (450 1350 ) 900