奈奎斯特判据习题
奈氏判据例题
P 在右半面的个数的极点开环传递函数(s)k G R 0R 00j ,1--(s)k ><+∞→∞=右手式，逆时针，左手式，顺时针，）的次数包围（全闭合曲线开环传递函数R G ωZ在右半面的个数的极点闭环传递函数(s)b G P)(2−+−N N Z在右半面的个数的极点开环传递函数(s)k G -k N -N -1-,-0(s)，负穿越，，正穿越，）次数穿越负实轴（半闭合曲线开环传递函数+→→+∞+∞→=+ωG 在右半面的个数的极点闭环传递函数(s)b G例题1：已知系统开环传递函数)1)(1)(1()(321+++=s T s T s T Ks G k 和其)0[∞+∈，ω时的幅相曲线j1-，试分析该系统的稳定性求解：无积分环节 0=P2)10(2)(2−=−=−=−+N N R 2=−=R P Z 闭环不稳定例题2：已知系统开环传递函数)1)(1(21++=s T s T s KG k 和其)0(∞+∈，ω时的幅相曲线+=0ω，试分析该系统的稳定性求解：有积分环节，且阶次1=v ，需做补线补线为：从0=ω到+=0ω，顺时针补半径为∞，角度为2π×v 的大圆弧 0=P0)00(2)(2=−=−=−+N N R 0=−=R P Z 闭环稳定例题3：已知系统开环传递函数)1(2+=Ts s KG k 和其)0(∞+∈，ω的幅相曲线，试分析该系统的稳定性求解：有积分环节，且阶次2=v ，需做补线补线为：从0=ω到+=0ω，顺时针补半径为∞，角度为2π×v 的大圆弧 0=P2)10(2)(2−=−=−=−+N N R 2=−=R P Z 闭环不稳定例题4：已知)1()1(221++=s T s s T K G k 和ω求解：有积分环节，且阶次2=v ，需做补线补线为：从0=ω到+=0ω，顺时针补半径为∞，角度为2π×v 的大圆弧 0=P0)00(2)(2=−=−=−+N N R 0=−=R P Z 闭环稳定例题5：已知3sK G k =和求解：有积分环节，且阶次3=v ，需做补线补线为：从0=ω到+=0ω，顺时针补半径为∞，角度为2π×v 的大圆弧 0=P2)10(2)(2−=−=−=−+N N R 2=−=R P Z 闭环不稳定例题6：已知321)1)(1(ss T s T K G k ++=和=ω求解：有积分环节，且阶次3=v ，需做补线补线为：从0=ω到+=0ω，顺时针补半径为∞，角度为2π×v 的大圆弧 0=P0)11(2)(2=−=−=−+N N R 0=−=R P Z 闭环稳定例题7：已知)1)(1)(1)(1()1)(1(432165++++++=s T s T s T s T s s T s T K G k 和+=0ω求解：有积分环节，且阶次1=v ，需做补线补线为：从0=ω到+=0ω，顺时针补半径为∞，角度为2π×v 的大圆弧0=P0)11(2)(2=−=−=−+N N R 0=−=R P Z 闭环稳定例题8：已知1−=Ts KG k 和 j1-求解：无积分环节1=P1)021(2)(2=−=−=−+N N R0=−=R P Z 闭环稳定例题9：已知1+−−=Ts KG k 和j1-求解：无积分环节1=P0)00(2)(2=−=−=−+N N R 1=−=R P Z 闭环不稳定例题10：已知)1(+=Ts s K G k 和=0ω求解：有积分环节，且阶次1=v ，需做补线补线为：从0=ω到+=0ω，顺时针补半径为∞，角度为2π×v 的大圆弧 0=P0)00(2)(2=−=−=−+N N R 0=−=R P Z 闭环稳定说明，对积分项作处理，用ε+s 带入积分项)1arctan (arctan222211)(jT )(j )(1)(Ts )(s )s (ωεωωωεωεωωεT j k k eT KK j G KG +−++=++=++=当0=ω时，=∞⇒=0)()(ωθεωK M（4）两图对应关系。
5-4 奈奎斯特稳定判据
ω 负穿越 相角减小的穿越，N半次穿越 G ( j0+ ) H ( j0+ ) гGH起始或终止于(-1,j0)点左侧负实轴 R=2N=2(N+-N-) N+=0,N-=1 R=2(0-1)=-2
课堂习题
P210 图5-32,计算各小图中,гF包围原点的圈数R
2.Nyquist稳定判据 闭环系统稳定的充分必要条件 1. Nyquist曲线不穿越点(-1,j0) 2. 且逆时针包围(-1,j0)点的圈数R等于开环传 递函数的正实部极点数P 闭合曲线г包围函数F(s)=1+G(s)H(s)的零点数 即闭环控制系统正实部极点数为 Z=P-R=P-2N
εe
jθ
∞e jθ
s = εe
, θ ∈ [0°,+90°]
1 sv G1 ( s )
− jνθ
ε为无穷小
θ
G( s) H ( s) =
1 ν s
G1 ( s ) = K
=
s =εe jθ
1
ε
ν
e
→ ∞e
− jνθ
∏ (τ
j =1 n −ν i =1
m
j
s + 1)
s→0 τ is +1 → 1
∏ (T s + 1)
例5-8 已知单位反馈系统开环幅相曲线(K=10,P=0,v=1),如图 所示，试确定系统闭环稳定时K值的范围 幅相曲线与负实轴交点频率分别ω1,ω2,ω3 解：
G ( jω i ) =
G ( jω1 ) = −2 , G ( jω 2 ) = −1.5 , G ( jω 3 ) = −0.5 10 10 ω = K 若令G(jω1)=-1, 1 K = 若令 G(j ω )=-1, 2 2 2 1 .5 10 −1 同理 K 3 = − 0.5 = 0.5 判断闭环系统稳定性 10
自动控制原理5.4 奈奎斯特判据
设Gk s在s右半平面的极点数为p，则闭环系 统稳定的充要条件是：在 Gk s 平面上的
11
★奈氏判据
§5—4 奈奎斯特判据
Gk j 曲线及其镜像当从 时，将逆时
针绕（- 1，j0）点转p周。
(1) 若开环本身稳定,则p 0, 故稳定的充要条件是：
系统稳定，否则系统不稳定。 但Gk F s 1 所以F(s)的Γ曲线绕原点运动相当于 Gk j 的封闭 曲线绕(-1，j0)点运动， 因为F( s)与Gk s只差常数1。
9
★幅角定理（续）
§5—4 奈奎斯特判据
Gk GH的封闭曲线即为 时Gk j 的
1
Mk Nk
Nk Mk Nk
Nb Nk
1
★幅角定理（续）
§5—4 奈奎斯特判据
其中Nk s为开环特征式，Nb s为闭环特征式。
F s的特点：
1、Fs的极点 开环极点， Fs的零点 闭环极点；
2、Fs的零极点个数相等n m；
3、F s与G( s)只差常数1。
§5—4 奈奎斯特判据
[F(s)] 0
5
★幅角定理（续）
§5—4 奈奎斯特判据
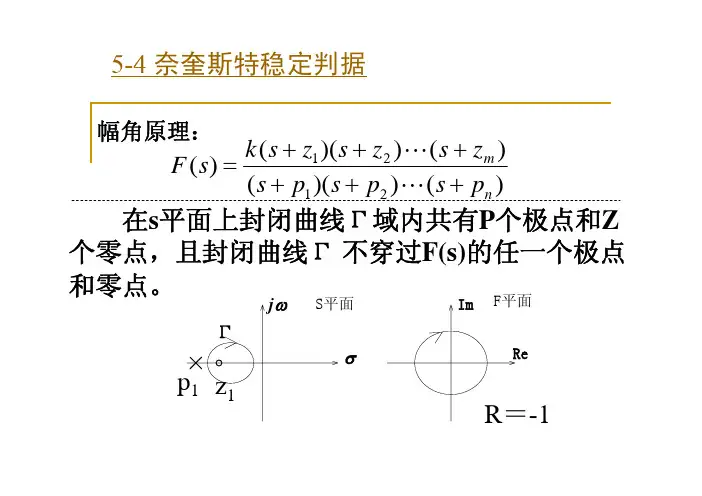
★幅角定理：设s平面上不通过F(s)任何奇点的封 闭曲线Γ包围s平面上F(s)的z个零点和p个极点。 当s以顺时针方向沿着封闭曲线Γ移动一周时， 则在F(s)平面上相对应于封闭曲线Γ的映射函数
j
1'
s
j 2'
F s
曲线。
因为对应于奈氏回线中：
1) 0 ； 3) 0；
只有2)半径R ， Fs 1 Gk s，
而Gk
奈奎斯特定理相关习题
1924年奈奎斯特(Nyquist)就推导出在理想低通信道的最高大码元传输速率的公式:理想低通信道的最高大码元传输速率C= N (其中W是想低通信道的带宽,N是电平强度)1。
带宽为4KHZ,如果有8种不同的物理状态表示数据,信噪比为30dB.那么按奈氏准则和香农定理计算,分别计算其最大限制的数据传输速率.① C=2 F log2N=2*4K*log28=24Kbps② 分贝(dB)的计算是:10lgS/N 即本题为:10lgS/N=30 则:S/N=103C=F log2(1+S/N)= 4K*log21001=40Kbps2。
对于带宽为6MHz的信道，若用4种不同的状态来表示数据，在不考虑热噪声的情况下，该信道的最大数据传输速率是多少答：由无热噪声的奈奎斯特公式: C=2Hlog2N=2*6M*log24=24Mbps，即该信道的最大数据传输速率是24Mbps。
3。
某调制解调器同时使用幅移键控和相移键控,采用0,兀/2,兀和3/2兀四种相位,每种相位又都有两个不同的幅值,问在波特率为1200的情况下数据速率是多少答:log28*1200 = 3600b/s4。
信道带宽为3KHz，信噪比为30db，则每秒能发送的比特数不会超过多bps答：由带热噪声的香农公式:C=Hlog2(1+S/N)=3K*log2(1+1030/10)<3K*log2210=30Kbps，所以每秒能发送的比特数不会超过30Kbps。
5. 采用8种相位、每种相位各有两种幅度的PAM调制方法，问在1200Baud的信号传输率下能达到的数据传输速率为多少我的答案是：S=B·LOG2N =1200xLOG2 16 =4800bps6。
采用每种相位各有两种幅度的带宽为8KHz的无噪信道上传输数字信号，若要达到64Kbps的数据速率，PAM调制方法至少要多少种不同的相位答：由无噪信道的奈奎斯特公式: C=2Hlog2N 得：N=2C/2H=264K/(2*8K)=24=16, 相位数=16/2=8即至少要8种不同的相位。
奈奎斯特稳定判据
二、控制系统的频域稳定性判据
3. n阶系统 n阶系统稳定的充要条件是当ω由0→∞时， 特征矢量D(jω)的相角变化量为 Δ Arg[D(jω)]= n² 90 °
奈奎斯特稳定判据
三、奈奎斯特判据（奈氏判据） 1. 0型系统（开环没有串联积分的系统）
⑴开环是稳定的系统
如果已知开环系统是稳定的，那么当ω由0→∞时， 若矢量F(j ω)的相角变化量为0，也就是F(j ω)的轨迹不包 围原点，那么闭环系统的特征方程式DB(s)的根全部在s 左半平面，系统是稳定的。否则，系统是不稳定的。 这样，系统稳定问题转化为找出ω由0→∞时，矢量 F(j ω)的相角变化量问题。
奈奎斯特稳定判据
四、伯德图上的稳定性判据 奈氏判据除了可以表示在极坐标图上， 还可以表示在伯德图上。
w + w=+ w=0 -1 P=0 w
0
180
-
+
四、伯德图上的稳定性判据
由图可知，幅相曲线不包围（-1，j0）点。 此结果也可以根据ω增加时，幅相曲线自下 向上（幅角减小）和自上向下（幅角增加） 穿越实轴区间（-∞，-1）的次数决定。
如果把自上向下的穿越称为正穿越，正穿越次 数用N+表示。把自下向上的穿越称为负穿越，负 穿越次数用N-表示，则R可以用N+和N-之差确定， 即 R= N+- N-
由图可知， N+=1， N-=1，故R=0。
四、伯德图上的稳定性判据
1.Bode图与Nyquist图的对应关系 a. Nyquist图的单位圆 | G(j )H(j ) | 1 对应 Bode图的横轴 20lg | G(j )H(j ) | 0 b. | G(j )H(j ) | 1 单位圆外 对应 20lg| G(j )H(j ) | 0 横轴以上区域
奈奎斯特稳定判据
次数应为：
N = F(s)的右半零点数－F(s)的右半极点数
= 闭环系统右半极点数－开环系统右半极点数
当已知开环右半极点数时，便可由N判断闭环右极点数。
这里需要解决两个问题：
1、如何构造一个能够包围整个s右半平面的封闭曲线，并且它是
现考虑S平面上一点s1映射到F(s)平面上的点F(s1)可以用一
个向量来表示，即当
m
K (s1 zi )
F (s1)
i 1 n
(s1 p j )
j 1
m
m
F(s1)
K
F (s1) e jF (s1)
i1 n
s1 zi e j(s1zi )
K i1
n
s1 zi
m
n
e j
i
对于一个控制系统，若其特征根处于s右半平面，则系统是 不稳定的。对于上面讨论的复变函数 F(s)＝1＋Gk(s)，其零点恰 好是闭环系统的极点，因此，只要搞清F(s)的零点在s右半平面的 个数，就可以给出稳定性结论。如果F(s)的右半零点个数为零，
则闭环系统是稳定的。
奈奎斯特为了应用柯西幅角原理研究闭环系统的稳定性， 因此设想：
1 GH
1 Gk
……………..(c)
显然，令复变函数等于零即是闭环特征方程。复变函数的 阶数为n阶，且分子分母同阶。则复变函数可写成以下形式：
n
(s zi )
F(s)
i 1 n
。式中， zi , p j 为F(s)的零、极点。
(s pj)
j 1
由 (a)、(b)及(c)式可以看出：
奈奎斯特稳定判据
幅角原理：如果封闭曲线内有Z个F(s)的零点， P个
F(s)的极点 ，则s 沿封闭曲线s 顺时针方向转一圈时，在
F(s)平面上，曲线F(s)绕其原点逆时针转过的圈数。
+
5. 4 . 3 奈氏判据
（1）0型系统
0
s为包围虚轴和整个右半平面。
s平面s 映射 F(s)
解：① 由开环传递函数知 P = 1 。 ② 作系统的开环对数频率特性曲线。
() = 90 + arctanT2 (180 arctanT1 )
270
arctan
(T1 1
T2 ) 2T1 T2
当() = 180时，g =(1/T1T2)1/2 ，A(g)=kT2
③ 稳定性判别。 G(s)H(s)有一个积分环节N =1 ，故
开环极坐标图如图
j
01
19
k(0.1s 1) Gk (s) s(s 1)
=0
Im
增补线
1 0.1k
Re 0
(3) 稳定性判别: 因为是1型系统，需作增补线如图
当 0.1k < 1 ，k > 10时， R =1/2，z = p 2R = 0
闭环系统是稳定的。
20
5.4.4 伯德图上的稳定性判据
Im
() 1
(+)
0
由图可知，幅相曲线 不 包 围 (1 ， j0) 点 。 此 结
Re 果也可以根据 增加时幅
相曲线自下向上(幅角减 小)和自上向下(幅角增加) 穿越实轴区间(，1)的 次数决定。
R = N N
自实轴区间（，1）开始向下的穿越称为半次正穿越，自实轴
区间（，1）开始向上的穿越为半次负穿越。
广义奈奎斯特判据
广义奈奎斯特判据摘要：1.广义奈奎斯特判据的定义和作用2.广义奈奎斯特判据的应用场景3.广义奈奎斯特判据在实际工程中的应用4.广义奈奎斯特判据的局限性及其改进方法5.总结正文：广义奈奎斯特判据是一种在数字信号处理和通信系统中广泛应用的原理，用于判断一个系统是否能够实现无失真传输。
它主要通过分析系统的采样频率和信号频率之间的关系，从而为信号的采样和传输提供理论依据。
广义奈奎斯特判据的核心思想是，当采样频率大于信号频率的两倍时，就可以实现信号的无失真传输。
这一原理在数字信号处理领域具有重要意义，为数字音频、图像和视频的处理和传输提供了理论基础。
在实际应用中，广义奈奎斯特判据帮助我们设计出高效可靠的数字通信系统，确保信号在传输过程中的质量。
然而，在实际工程中，广义奈奎斯特判据并非万能。
有时，尽管满足了奈奎斯特采样定理，但在传输过程中仍然会出现失真。
这是因为在实际系统中，除了采样频率和信号频率之间的关系外，还存在其他因素影响信号的传输质量。
为了解决这个问题，研究人员对广义奈奎斯特判据进行了改进，提出了更符合实际应用的判据方法。
尽管广义奈奎斯特判据在数字信号处理和通信领域具有广泛的应用，但它仍然存在一定的局限性。
首先，广义奈奎斯特判据主要关注的是采样频率和信号频率之间的关系，而对于其他影响信号传输质量的因素，如系统的带宽、噪声等，并没有给予足够的重视。
其次，广义奈奎斯特判据是一种理想化的理论模型，在实际应用中，系统的性能往往受到多种因素的影响，很难完全满足这一判据。
为了解决这些问题，研究人员在广义奈奎斯特判据的基础上，提出了更加完善的判据方法。
这些方法不仅考虑了采样频率和信号频率之间的关系，还将其他影响因素纳入了考虑范围，使得判据更加符合实际应用需求。
总之，广义奈奎斯特判据是数字信号处理和通信领域的重要原理，它在实际工程中具有广泛的应用。
然而，由于其局限性，我们需要在实际应用中不断地对其进行改进，以提高判据的实用性和准确性。
2第3、4、5、6节奈魁斯特稳定判据
系统闭环稳定
Monday, June 15, 2020
系统闭环不稳定 18
[例]系统开环传递函数：G(s)H s K s 1， s并2Ts 1
给出 T 和时T 的 开环极坐标图，判断闭环系统的稳定性。
[解]开环传递函数无正实部极点，P=0。
系统闭环稳定
Monday, June 15, 2020
奈奎斯特稳定判据的表述3： 闭环系统稳定的充要条件是，当 由 0 0时，开环奈 奎斯特图应当按逆时针方向包围点(-1,j0)P/2周，P是 开环传递函数正实部极点的个数。
Monday, June 15, 2020
11
● 开环稳定系统（P=0）的奈奎斯特稳定判据： 若开环稳定，闭环稳定的充要条件是，当 由 变化时，增补完整的开环频率特性极坐标图不包围点 (-1,j0)。
Monday, June 15, 2020
16
GsH起s始 于负实轴上，或终止于负实轴时，穿越次
数定义为1/2次。
若开环极坐标图在点(-1,j0)左方负穿越负实轴的次数 大于正穿越的次数，则闭环系统一定不稳定。
[例]如图所示系统开环极坐标图，系统开环传递函数有 2个正实部极点，闭环系统是否稳定？
Monday, June 15, 2020
在使用奈奎斯特稳定判据时，由 0 0简称为 由0 。
Monday, June 15, 2020
12
[例]开环传递函数为： G(s) ，k 用奈奎斯特
(T1s 1)(T2s 1)
稳定判据判断闭环系统的稳定性。
[解]：开环系统的奈 奎斯特图如右。在s 右半平面的极点数为 0，绕(-1,j0)点的圈 数P=0，故闭环系统 是稳定的。
20
正实部开环极点个数 P=1。由图中看出：
自动控制原理(胥布工)第二版6-7-8章习题及详解
第6章习题及详解6-1 试求图6-93所示电路的频率特性表达式，并指出哪些电路的低频段增益大于高频段增益。
（a ） （b ）R R（c ） （d ）图6-93 习题6-1图解：（a ）1112121212++++ωωCj R R R R Cj R R R R ；（b ）()11212+++ωωCj R R Cj R ；（c ）1155434314368++⎪⎪⎭⎫ ⎝⎛+++ωωCj R Cj R R R R R R R R R R ；（d ） 117767647613++++ωωCj R Cj R R R R R R R R R ；（a ）和（c ）低频段增益小于高频段增益；（b ）和（d ）低频段增益大于高频段增益。
6-2 若系统单位脉冲响应为t t e e t g 35.0)(--+=，试确定系统的频率特性。
解：315.011)(+++=s s s G ，故315.011)(+++=ωωωj j j G 6-3 已知单位反馈系统的开环传递函数为11)(+=s s G 试根据式（6-11）频率特性的定义求闭环系统在输入信号()sin(30)2cos(545)r t t t =+︒--︒作用下的稳态输出。
解：先求得闭环传递函数21)(+=s s T 。
（1）1=ω，447.055211)1(==+=j j T ，︒-=-=∠56.2621arctan )1(j T 。
（2）5=ω，186.02929251)5(==+=j j T ，︒-=-=∠20.6825arctan )5(j T 。
故)2.1135cos(372.0)44.3sin(447.0)(︒--︒+=∞→t t t y t 。
6-4 某对象传递函数为s e Ts s G τ-+=11)( 试求：(1) 该对象在输入()sin()u t t ω=作用下输出的表达式，并指出哪部分是瞬态分量； (2) 分析T 和τ增大对瞬态分量和稳态分量的影响；(3) 很多化工过程对象的T 和τ都很大，通过实验方法测定对象的频率特性需要很长时间，试解释其原因。
奈奎斯特稳定判据
2 幅角定理 幅角定理
非奇异的是指没有突然跳变点，是连续的
s以顺时针方向沿封闭曲线Γ移动一周时，则在F平面上相对应 对于s平面上的任意一条不通过F（s）任何奇异点的封闭曲线Γ, 于Γ’将以顺时针的方向围绕原点旋转 可通过映射关系在F（s）平面上相对应的封闭曲线Γ’
映射
N=-1 不稳定
Z=P-2N=2
例 5-8
系统结构图如图 5-39 所示，试判断系统的稳定性并讨论 K 值对系
统稳定性的影响。
图5-39 例5-8系统结构图
开环传递函数在右半 s 平面上有一个极点， P = 1 。
< 时，曲线不包围（ − 1 , j 0 ）点，即 N = 0 当 K > 1 时，曲线逆时针包围了（ − 1 , j 0 ）点的 1 2 圈，
iii 负虚轴 s = jω ：频率 ω 由 − ∞ 变化到 0。
在 F 平面上绘制与 Γ 相对应的像 Γ' ：当 s 沿虚轴变化时，由式（5-53）则有
F ( jω ) = 1 + G ( jω ) i 和正虚轴对应的是辅助函数的频率特性 F ( jω ) ， 相当于把 G ( jω ) 右移一个单
Z = P − 2 N = 1 − 2 × (1 2) = 0
谢谢大家！ 谢谢大家！ 大家
例 5-7
设系统开环传递函数为
步骤：
52 G ( s) = ( s + 2)( s 2 + 2s + 5)
1、绘出系统的开环幅相特性曲线 试用奈氏判据判定闭环系统的稳定性。 2、右半s平面上，系统的开环极点数
P=0
3、 开环频率特性 G ( jω ) 随着 ω 从 0 变化到 + ∞ 时，顺时针方向围绕（ − 1 , j 0 ）点 的圈数
控制工程奈奎斯特稳定判据
—— 奈奎斯特稳定判据
奈奎斯特稳定判据
一、系统稳定性的定义和条件 二、Nyquist(奈奎斯特）稳定判据的推导 三、结论与举例说明 四、小结
一、什么是稳定性？
➢初所始谓状稳态定恢性复，到就原是来指平扰衡动状消态失的后性，能系。统由
(a)
稳定系统
(b)
不稳定系统
稳定的条件
n
时间响应 y(t) Aiesit B(t) 中：Re( si ) 0 i 1 ✓系统特征方程的所有的根（闭环极点）都 具有负实部(位于s平面的左半部)。
Im
临界稳定
Im
稳
定
Re
区
Re
不稳 定
二、奈氏稳定判据的推导
GB (s)
GK ( j)
1. 函数 F(s)=1+G(s)H(s) 与开环、闭环零 极点的关系。
2. 幅角原理（Cauchy原理） 3. 奈奎斯特判据
小结： [s] [F (s)] [GH ]
闭环极点
闭环传递函 数
GB (s)
系统稳定的 充要条件
LF
F(s) 1 G(s)H(s)
Re
[GH ]
坐标平移一个单位
N p z;且pB右 0;且pB右 zF右 0 N p 0 pF右
[GH]平面上的奈氏轨迹
若系统稳定，则： N p
N pF右 ;且pF右 pK右
Im
LGH
[GH]
N pK右
GH F
Re
(1, j0)
G( j)H ( j) s j
LF
Re
(a)
N p z 1
(b)
N pz 2
(c)
N pz 0
自动控制原理习题与答案解析
1、绘制该系统以根轨迹增益Kr为变量的根轨迹（求出：分离点、与虚轴的交点等）；（8分）
2、求系统稳定且为欠阻尼状态时开环增益K的取值范围。（7分）
六、（共22分）已知反馈系统的开环传递函数为 ，试：
1、用奈奎斯特判据判断系统的稳定性；（10分）
4、 ； ； ；衰减振荡
5、 ；
6、开环极点；开环零点
7、
8、 ； ；稳态性能
二、判断选择题(每题2分，共 20分)
1、D 2、A 3、C 4、A 5、D 6、A 7、B 8、C 9、B 10、B
三、(8分)建立电路的动态微分方程，并求传递函数。
解：1、建立电路的动态微分方程
根据KCL有 (2分)
即 (2分)
3、在经典控制理论中，可采用、根轨迹法或等方法判断线性控制系统稳定性。
4、控制系统的数学模型，取决于系统和, 与外作用及初始条件无关。
依题意： ， （3分）
得 （2分）
故满足稳态误差要求的开环传递函数为
3、满足稳态误差要求系统的相角裕度 ：
令幅频特性： ，得 ， （2分）
， （1分）
相角裕度 ： （2分）
试题三
一、填空题（每空 1 分，共Байду номын сангаас0分）
1、对自动控制系统的基本要求可以概括为三个方面，即：、快速性和。
2、控制系统的称为传递函数。一阶系统传函标准形式是，二阶系统传函标准形式是。
开环相频特性： （1分）
3、求系统的相角裕度 ：
求幅值穿越频率，令 得 （3分）
（2分）
（2分）
对最小相位系统 临界稳定
4、（4分）可以采用以下措施提高系统的稳定裕度：增加串联超前校正装置；增加串联滞后校正装置；增加串联滞后-超前校正装置；增加开环零点；增加PI或PD或PID控制器；在积分环节外加单位负反馈。
自动控制原理习题解答
第三章3－3 已知各系统的脉冲响应，试求系统的闭环传递函数()s Φ：()()1.25(1)()0.0125;(2)()510sin 445;(3)()0.11t t k t e k t t t k t e --==++=-解答： （1） []0.0125()() 1.25s L k t s Φ==+（2）[])222223222()()5sin 4cos 425452442142511616116s L k t L t t t s s s s s s s s ⎡⎤Φ==++⎢⎥⎣⎦⎫=++⎪++⎭⎛⎫+++ ⎪⎝⎭=⎛⎫+ ⎪⎝⎭（3）[]()111()()0.1110313s L k t s s s s ⎡⎤⎢⎥Φ==-=⎢⎥+⎢⎥+⎣⎦ 3-4 已知二阶系统的单位阶跃响应为)6.1sin(5.1210)(1.532.1︒-+-=t t h et试求系统的超调量σ%，峰值时间tp和调节时间ts.解答：因为0<ξ<1，所以系统是欠阻尼状态。
阻尼比ξ=cos(1.53︒)=，自然频率26.0/2.1==w n，阻尼振荡频率wd=6.16.01212=-⨯=-=ξw w n d 1． 峰值时间tp的计算96.16.1===ππwt dp2． 调节时间ts的计算9.226.05.35.3=⨯==w t ns ξ3． 超调量σ%的计算%48.9%1006.0%100%221/6.01/=⨯=⨯=-⨯---eeππξξσ3-5设单位反馈系统的开环传递函数为)6.0(14.0)(++=s s s s G ，试求系统在单位阶跃输入下的动态性能。
解答：方法一：根据比例-微分一节推导出的公式)135(6.014.0)12/()1()(+⨯⨯+=++=s s s s s s K s G w T n d ξ1)5.2(4.0114.0)6.0(14.01)6.0(14.0)2()(1)()(22222+++=+++=+++++=+++=+=s s s s s s s s s s s zs z S G s G s s s w w s w nn dn ξφ)1()](1[12)1sin(1)(222222ξξξξξξξπψξddnddndnn ddn tarctg z arctg z r t w r t h www w zw e n d -+--+-=-+-=ψ+-+=-把z=1/Td=,1=wn,5.0=ξd代入可得)3.8323sin(5.005.11)7.9623sin(5.005.11)( ---=--+=t e t t e t t h峰值时间的计算0472.1)1(2=-=ξξβdddarctg ，-1.6877=ψ158.312=--=ξβψdndpwt超调量得计算%65.21%10011%22=⨯--=-ξξξσddetrpd调节时间得计算29.6)ln(21ln )2ln(2131222=--+-+=-ww w z t ndn n d sd z ξξξ方法二：根据基本定义来求解闭环传递函数为114.0)6.0(14.01)6.0(14.0)(1)()(2+++=+++++=+=s s s s s s s s S G s G s s φ当输入为单位阶跃函数时 )232()21(21.0)232()21(2)21(116.01)1(14.0)(22++-++++-+=++--+=+++=s s s s s s s s s s s C s s 得单位阶跃响应)23sin(1.0)23cos(1)(2121t t t h e et --⨯--=)3.8423sin(121 +-=-t et )0(≥t 1． 峰值时间tp的计算 对h(t)求导并令其等于零得023)23cos()23sin(3.843.842121=⨯+-+︒-︒-t e t epp t t p p 3)23tan(3.84=+︒t p t p = 2. 超调量σ%的计算 %100)()()(%⨯∞∞-=h h h t p σ=%3. 调节时间ts得计算05.0)84.523sin(21≤-⨯-t est s5.33=t s3-6.已知控制系统的单位阶跃响应为6010()10.2 1.2t t h t e e --=+- ，试确定系统的阻尼比ζ和自然频率n ω。
奈奎斯特稳定性判据
一、奈奎斯特稳定性判据 【4 Nyquist相曲线的绘制】
开环幅相曲线的绘制 精确曲线 ——由表达式取点，计算，描点。 概略曲线 ——工程方法。 概略幅相曲线的三要素：
0 1）起点： A( ), ( ) 终点：
2) 与实轴交点及交点处的频率，称为穿越频率ωx； 3) 曲线变化范围：象限，单调性。
三、例题详解
【解答】 首先将各点的坐标改写成
0.05 K 20 K 50 K , , 500 500 500
闭环系统渐近稳定的条件：
K K 20 1 0.05 500 500
或
1 50
K 500
由 20
K K 1 0.05 500 500
得 25 K 10000 得 0 K 10
【解答】 (2)
系统稳定性
Z P 2( N N_ ) 0
P 1, v 1
系统为渐近稳定系统。
三、例题详解
【例5】 某负反馈非最小相位系统，其开环传递函数为
10 G(s) H (s) s(0.2s 2 0.8s 1)
试:（1）画出半奈奎斯特曲线； （2）判定系统的稳定性。
二、对数频率特性稳定性判据
由式（3）可知：系统渐近稳定的充分必要条件是 (4)
由式（3）还可知：渐近稳定的必要条件是 N N； 发散不稳定的充分条件是 N N 。
在 c g 的条件下，当系统参数有微小变化使 c g 时，会使系统由渐近稳定变成不稳定或相反，在这 种条件下，称系统为临界稳定。
三、例题详解
【解答】 (1)
半奈奎斯特曲线
10 G( s) H ( s) s(0.2s 1)( s 1)
奈奎斯特稳定性判据
K 取值范围。
【解答】
三、例题详解
【解答】
三、例题详解
三、例题详解 【例3】 某负反馈控制系统，开环传递函数
试：（1）画出幅相特性曲线；（2）判定稳定性。
三、例题详解
【解答】 (1) 幅相特性曲线
G( j)H ( j)
K(T1 T2 )
(1 )
一、奈奎斯特稳定性判据
【3 奈奎斯特稳定性判据】
式中：P —开环传递函数位于右半s平面极点的个
数； N —半奈式曲线逆时针方向穿越点(1, j0)左
侧实轴的次数。而逆时针起始于或终止 于点 (1, j0)左侧实轴的次数，折半计算 N —半奈式曲线顺时针方向穿越点(1, j0)左 侧实轴的次数。而顺时针起始于或终止 于点(1, j0)左侧实轴的次数，折半计算
j
1 2T1T2
(1 2T12 )(1 2T22 ) (1 2T12 )(1 2T22 )
幅值变化： A(0 ) , A() 0
相角变化： K : 0 0
1 : 90 90
j
1
: 0 45 90
1 jT1
1 : 0 45 90
1 jT2
系统为发散不稳定系统。
三、例题详解
【例8】
某单位负反馈系统，其开环传递函数为 ：
G(s)
2 s2 (s 1)
试：（1）绘制开环频率特性极坐标草图； （2）利用奈奎斯特稳定性判据判定系统的稳定性。
三、例题详解
【解答】 (1) 极坐标草图
1
③ 取 La (0 ) 0 即K / 0 1 0 K
4)ωmin<ω<ωmax： 按转折频率对应的环节绘制
奈奎斯特采样定理例题
奈奎斯特采样定理例题
摘要：
1.奈奎斯特采样定理的概念和原理
2.奈奎斯特采样定理的应用实例
3.实际应用中奈奎斯特采样定理的局限性和解决方法
4.结论
正文：
奈奎斯特采样定理是数字信号处理领域的基本原理之一，它指出为了正确地恢复原始模拟信号，采样频率必须至少是信号带宽的两倍。
这一定理为我们在数字信号处理中如何采样提供了理论依据。
在实际应用中，奈奎斯特采样定理被广泛应用于音频、图像和视频信号的处理中。
例如，当我们需要将一个模拟音频信号转换为数字信号时，我们需要按照奈奎斯特采样定理进行采样，以确保信号的完整性和准确性。
同样，在图像和视频信号的处理中，也需要按照奈奎斯特采样定理进行采样，以确保图像和视频的清晰度和质量。
然而，在实际应用中，奈奎斯特采样定理也存在一些局限性。
例如，当信号带宽很宽时，需要很高的采样频率才能满足奈奎斯特采样定理的要求，这可能会导致数字信号处理的复杂度和成本增加。
此外，当采样频率低于信号带宽的两倍时，会导致信号混叠，从而影响信号的准确性和质量。
为了解决这些问题，实际应用中通常采用一些变通的方法。
例如，可以使用更高频率的采样，以降低信号混叠的影响；也可以使用数字滤波器来滤除混
叠的频率分量，以提高信号的质量。
总的来说，奈奎斯特采样定理是数字信号处理中非常重要的基本原理，它为我们提供了在数字信号处理中如何采样的理论依据。
奈奎斯特定理相关习题
1924年奈奎斯特(Nyquist)就推导出在理想低通信道的最高大码元传输速率的公式:理想低通信道的最高大码元传输速率C=2W.log2 N(其中W是想低通信道的带宽,N是电平强度)1。
带宽为4KHZ,如果有8种不同的物理状态表示数据,信噪比为30dB.那么按奈氏准则和香农定理计算,分别计算其最大限制的数据传输速率.① C=2 F log2N=2*4K*log28=24Kbps②分贝(dB)的计算是:10lgS/N 即本题为:10lgS/N=30 则:S/N=103C=F log2(1+S/N)= 4K*log21001=40Kbps2。
对于带宽为6MHz的信道，若用4种不同的状态来表示数据，在不考虑热噪声的情况下，该信道的最大数据传输速率是多少？答：由无热噪声的奈奎斯特公式: C=2Hlog2N=2*6M*log24=24Mbps，即该信道的最大数据传输速率是24Mbps。
3。
某调制解调器同时使用幅移键控和相移键控,采用0,兀/2,兀和3/2兀四种相位,每种相位又都有两个不同的幅值,问在波特率为1200的情况下数据速率是多少答:log28*1200 = 3600b/s4。
信道带宽为3KHz，信噪比为30db，则每秒能发送的比特数不会超过多bps?答：由带热噪声的香农公式:C=Hlog2(1+S/N)=3K*log2(1+1030/10)<3K*log2210=30Kbps，所以每秒能发送的比特数不会超过30Kbps。
5. 采用8种相位、每种相位各有两种幅度的PAM调制方法，问在1200Baud的信号传输率下能达到的数据传输速率为多少？我的答案是：S=B·LOG2N =1200xLOG2 16 =4800bps6。
采用每种相位各有两种幅度的带宽为8KHz的无噪信道上传输数字信号，若要达到64Kbps的数据速率，PAM调制方法至少要多少种不同的相位？答：由无噪信道的奈奎斯特公式: C=2Hlog2N 得：N=2C/2H=264K/(2*8K)=24=16, 相位数=16/2=8即至少要8种不同的相位。
奈奎斯特曲线例题
奈奎斯特曲线例题
奈奎斯特曲线，也称为奈奎斯特图或频谱分析图，是一种在信号处理和通信领域常用的工具，用于分析信号的频谱特性和采样率的选择。
下面是一个奈奎斯特曲线的例题：
假设有一个连续时间信号x(t)，其频率范围为0 Hz到10 kHz。
我们将该信号进行采样，采样频率为20 kHz。
请问，在频谱上，奈奎斯特曲线的形状如何？并说明它的特点。
解答：
根据采样定理，采样频率必须大于信号频率的两倍才能避免混叠现象。
在这个例子中，信号频率的最高值为10 kHz，则采样频率应大于20 kHz。
由于采样频率为20 kHz，大于信号频率的两倍，因此不会出现混叠现象。
在频谱上，奈奎斯特曲线的形状为一个周期重复的频谱图案。
具体来说，在频谱上会出现多个重复的频谱区域，每个区域的频率范围为0 Hz到10 kHz。
奈奎斯特曲线的特点是，它展示了信号频谱在连续时间和离散时间中的对应关系。
每个重复的频谱区域代表了一个周期，其中包含了信号频率范围内的所有频率成分。
此外，奈奎斯特曲线还反映了采样频率对信号频谱的影响，即采样频率越高，奈奎斯特曲线上出现的重复频谱区域越多，更能准确地还原信号的频域特性。
需要注意的是，奈奎斯特曲线只能展示信号频谱的近似情况，在实际应用中仍需进一步进行信号处理和重建以获得准确的频域信息。