2020年高考备考同步学案二
2020版新高考复习理科数学教学案:解析几何含答案 (2)

A1(-a,0).A2(a,0)
A1(0.-a).A2(0.a)
轴
实轴:线段A1A2.虚轴:B1B2
焦距
|F1F2|=2c
离心率
e= .e∈(1.+∞)
a.b.c的关系
c2=a2+b2
渐近线
y=± x
y=± x
三、离心率e的作用
(1)椭圆:e越大.图形越扁.
(2)双曲线:e越大.开口越小.
四、常见结论
答案:B
7.[20xx·江苏卷]在平面直角坐标系xOy中.P是曲线y=x+ (x>0)上的一个动点.则点P到直线x+y=0的距离的最小值是________.
解析:通解:设P .x>0.则点P到直线x+y=0的距离d= = ≥ =4.当且仅当2x= .即x= 时取等号.故点P到直线x+y=0的距离的最小值是4.
(2)符号语言:||MF1|-|MF2||=2a(2a<|F1F2|).
(3)当|MF1|-|MF2|=2a时.曲线仅表示焦点F2所对应的双曲线的一支;当|MF1|-|MF2|=-2a时.曲线仅表示焦点F1所对应的双曲线的一支;当2a=|F1F2|时.轨迹为分别以F1.F2为端点的两条射线;当2a>|F1F2|时.动点轨迹不存在.
(2)弦长公式:l=2a=2 .
3.切线长公式
圆的方程为f(x.y)=x2+y2+Dx+Ey+F=0.或f(x.y)=(x-a)2+(y-b)2-R2=0.圆外有一点P(x0.y0).由点P向圆引的切线的长为l= .
■自测自评——————————————
1.设a.b.c分别是△ABC中角A.B.C所对的边.则直线sinA·x+ay-c=0与bx-sinB·y+sinC=0的位置关系是( )
2020高考数学二轮复习分层设计(全国I卷)学案:第二层提升篇 专题二数列——第2讲第2讲 数列通项与求和

第2讲 数列通项与求和[全国卷3年考情分析] 年份 全国卷Ⅰ 全国卷Ⅱ 全国卷Ⅲ2019 等比数列的求和·T 14 递推公式的应用·T 19 等差数列的前n 项和·T 142018a n 与S n 关系的应用·T 14等差数列前n 项和的最值问题·T 172017等差数列的基本运算、数列求和·T 17等比数列的通项公式、a n 与S n 的关系·T 17三角形问题交替考查且多出现在第17(或18)题的位置,难度中等,2020年高考此内容难度有可能加大,应引起关注.若以客观题考查,难度中等的题目较多,有时也出现在第12、16题的位置,难度偏大.考点一 a n 与S n 关系的应用[例1] (1)(2019·成都第一次诊断性检测)设S n 为数列{a n }的前n 项和,且a 1=4,a n +1=S n ,n ∈N *,则a 5=________.(2)(2019·武汉市调研测试)已知数列{a n }的前n 项和S n 满足S n =3S n -1+2n -3(n ≥2),a 1=-1,则a 4=________.[解析] (1)法一:由a n +1=S n ,得S n +1-S n =S n ,则S n +1=2S n .又S 1=a 1=4,所以数列{S n }是首项为4,公比为2的等比数列,所以S n =4·2n -1=2n +1,则a 5=S 5-S 4=26-25=32.法二:当n ≥2时,由a n +1=S n ,得a n =S n -1,两式相减,得a n +1-a n =a n ,即a n +1=2a n ,所以数列{a n }是从第2项开始,公比为2的等比数列.又a 2=S 1=4,所以a 5=a 2·23=4×23=32.(2)法一:由S n =3S n -1+2n -3(n ≥2)可得S 2=3S 1+1=3a 1+1,即a 2=2a 1+1=-1.根据S n =3S n -1+2n -3(n ≥2),①知S n +1=3S n +2n +1-3,② ②-①可得,a n +1=3a n +2n (n ≥2). 两边同时除以2n+1可得a n +12n +1=32·a n 2n +12(n ≥2),令b n =a n 2n ,可得b n +1=32·b n+12(n ≥2). ∴b n +1+1=32(b n +1)(n ≥2),数列{b n +1}是以b 2+1=a 222+1=1-14=34为首项,32为公比的等比数列.∴b n +1=⎝⎛⎭⎫32n -2·34(n ≥2),∴b n =12·⎝⎛⎭⎫32n -1-1(n ≥2).又b 1=-12也满足上式, ∴b n =⎝⎛⎭⎫32n -1·12-1(n ∈N *),又b n =a n 2n ,∴a n =2n b n ,即a n =3n -1-2n .∴a 4=33-24=11.法二:由S n =3S n -1+2n -3(n ≥2),a 1=-1,知S 2=3S 1+4-3,∴a 2=-1.S 3=3S 2+8-3,∴a 3=1.S 4=3S 3+16-3,∴a 4=11.[答案] (1)32 (2)11 [解题方略](1)给出S n 与a n 的递推关系求a n 的常用思路:一是利用S n -S n -1=a n (n ≥2)转化为a n的递推关系,再求其通项公式;二是转化为S n 的递推关系,先求出S n 与n 之间的关系,再求a n .(2)形如a n +1=pa n +q (p ≠1,q ≠0),可构造一个新的等比数列.[多练强化]1.已知数列{a n }满足a 1=1,a n +1-2a n =2n (n ∈N *),则数列{a n }的通项公式a n =________.解析:a n +1-2a n =2n 两边同除以2n +1,可得a n +12n +1-a n 2n =12,又a 12=12,所以数列⎩⎨⎧⎭⎬⎫a n 2n 是以12为首项,12为公差的等差数列,所以a n 2n =12+(n -1)×12=n 2,所以a n =n ·2n -1.答案:n ·2n -12.已知数列{a n }中,a 1=1,a 2=2,a n +1=3a n -2a n -1(n ≥2,n ∈N *).设b n =a n +1-a n . (1)证明:数列{b n }是等比数列; (2)设c n =b n(4n 2-1)2n,求数列{c n }的前n 项和S n .解:(1)证明:因为a n +1=3a n -2a n -1(n ≥2,n ∈N *),b n =a n +1-a n , 所以b n +1b n =a n +2-a n +1a n +1-a n =(3a n +1-2a n )-a n +1a n +1-a n =2(a n +1-a n )a n +1-a n =2,又b 1=a 2-a 1=2-1=1,所以数列{b n }是以1为首项,2为公比的等比数列. (2)由(1)知b n =1×2n -1=2n -1, 因为c n =b n(4n 2-1)2n, 所以c n =12(2n +1)(2n -1)=14⎝⎛⎭⎫12n -1-12n +1,所以S n =c 1+c 2+…+c n=14⎣⎡⎦⎤⎝⎛⎭⎫1-13+⎝⎛⎭⎫13-15+…+⎝⎛⎭⎫12n -1-12n +1=14⎝⎛⎭⎫1-12n +1=n 4n +2. 考点二 数列求和 题型一 裂项相消求和[例2] (2019·安徽五校联盟第二次质检)已知数列{a n }的前n 项和为S n ,且S n =2a n -1. (1)求数列{a n }的通项公式; (2)记b n =2a n(a n +1)(a n +1+1),求数列{b n }的前n 项和T n .[解] (1)当n =1时,a 1=S 1=2a 1-1,得a 1=1.当n ≥2时,有S n -1=2a n -1-1, 所以a n =S n -S n -1=2a n -2a n -1,即a n =2a n -1.所以{a n }是公比为2,首项为1的等比数列,故通项公式a n =2n -1.(2)b n =2a n (a n +1)(a n +1+1)=2n (2n -1+1)(2n +1)=2⎝⎛⎭⎫12n -1+1-12n +1, T n =b 1+b 2+b 3+…+b n =2×⎝⎛⎭⎫120+1-121+1+2×⎝⎛⎭⎫121+1-122+1+2×⎝⎛⎭⎫122+1-123+1+…+2×⎝⎛⎭⎫12n -1+1-12n +1=2n-12n +1. [解题方略](1)裂项相消法求和就是将数列中的每一项裂成两项或多项,使这些裂开的项出现有规律的相互抵消,要注意消去了哪些项,保留了哪些项.(2)消项规律:消项后前边剩几项,后边就剩几项,前边剩第几项,后边就剩倒数第几项.题型二 错位相减求和[例3] (2019·福建五校第二次联考)已知数列{a n }的前n 项和S n =3n 2+8n ,{b n }是等差数列,且a n =b n +b n +1.(1)求数列{b n }的通项公式;(2)令c n =(a n +1)n +1(b n +2)n,求数列{c n }的前n 项和T n .[解] (1)因为S n =3n 2+8n ,所以当n ≥2时,a n =S n -S n -1=3n 2+8n -[3(n -1)2+8(n -1)]=6n +5;当n =1时,a 1=S 1=11 所以a n =6n +5,n ∈N * 于是,b n +1+b n =a n =6n +5.因为{b n }是等差数列,所以可设b n =kn +t (k ,t 均为常数),则有k (n +1)+t +kn +t =6n +5,即2kn +k +2t =6n +5对任意的n ∈N *恒成立,所以⎩⎪⎨⎪⎧2k =6,k +2t =5,解得⎩⎪⎨⎪⎧k =3,t =1,故b n =3n +1.(2)因为a n =6n +5,b n =3n +1,所以c n =(a n +1)n +1(b n +2)n =(6n +6)n +1(3n +3)n =2n×(6n +6).于是,T n =12×2+18×22+24×23+…+2n ×(6n +6),①所以2T n =12×22+18×23+24×24+…+2n ×6n +2n +1×(6n +6),②①-②得,-T n =24+6(22+23+…+2n )-2n +1×(6n +6)=24+6×22-2n ×21-2-2n +1×(6n +6)=-2n +1×6n ,故T n =2n +1×6n =2n +2×3n . [解题方略](1)求解此类题需掌握三个技巧:一是巧分拆,即把数列的通项转化为等差数列、等比数列的通项的积,并求出等比数列的公比;二是构差式,求出前n 项和的表达式,然后乘以等比数列的公比,两式作差;三是得结论,即根据差式的特征进行准确求和.(2)运用错位相减法求和时应注意三点:一是判断模型,即判断数列{a n },{b n }一个为等差数列,一个为等比数列;二是错开位置;三是相减时一定要注意最后一项的符号.题型三 分组转化求和[例4] 已知等差数列{a n }的首项为a ,公差为d ,n ∈N *,且不等式ax 2-3x +2<0的解集为(1,d ).(1)求数列{a n }的通项公式a n ;(2)若b n =3a n +a n -1,n ∈N *,求数列{b n }的前n 项和T n .[解](1)易知a ≠0,由题设可知⎩⎨⎧1+d =3a ,1·d =2a ,解得⎩⎪⎨⎪⎧a =1,d =2.故数列{a n }的通项公式为a n =1+(n -1)·2=2n -1. (2)由(1)知b n =32n -1+2n -1-1,则T n =(3+1)+(33+3)+…+(32n -1+2n -1)-n =(31+33+…+32n -1)+(1+3+…+2n -1)-n =31(1-9n )1-9+(1+2n -1)n 2-n=38(9n -1)+n 2-n . [解题方略](1)在处理一般数列求和时,一定要注意运用转化思想.把一般的数列求和转化为等差数列或等比数列进行求和.在利用分组求和法求和时,常常根据需要对项数n 进行讨论.最后再验证是否可以合并为一个表达式.(2)分组求和的策略:①根据等差、等比数列分组;②根据正号、负号分组.[多练强化]1.(2019·福建五校第二次联考)在数列{a n }中,a 1=13,1a n +1=3a n (a n +3),n ∈N *,且b n =13+a n.记P n =b 1×b 2×…×b n ,S n =b 1+b 2+…+b n ,则3n +1P n +S n =________.解析:因为1a n +1=3a n (a n +3)=1a n -1a n +3,所以b n =13+a n =1a n -1a n +1,所以S n =b 1+b 2+…+b n =⎝⎛⎭⎫1a 1-1a 2+⎝⎛⎭⎫1a 2-1a 3+…+⎝⎛⎭⎫1a n -1a n +1=1a 1-1a n +1.因为1a n +1=3a n (a n +3),所以3+a n =3a n +1a n ,所以b n =13+a n =a n 3a n +1,所以P n =b 1×b 2×…×b n =a 13a 2×a 23a 3×…×a n 3a n +1=a 13n a n +1.又a 1=13,故3n +1P n +S n=3a 1a n +1+1a 1-1a n +1=1a 1=3. 答案:32.已知数列{a n }满足:a 1=1,a n +1=n +1n a n +n +12n . (1)设b n =a nn ,求数列{b n }的通项公式;(2)求数列{a n }的前n 项和S n . 解:(1)由a n +1=n +1n a n +n +12n ,可得a n +1n +1=a n n +12n, 又b n =a n n ,所以b n +1-b n =12n ,由a 1=1,得b 1=1,累加可得(b 2-b 1)+(b 3-b 2)+…+(b n -b n -1)=121+122+…+12n -1,即b n -b 1=12⎝⎛⎭⎫1-12n -11-12=1-12n -1,所以b n =2-12n-1.(2)由(1)可知a n =2n -n 2n -1,设数列⎩⎨⎧⎭⎬⎫n 2n -1的前n 项和为T n ,则T n =120+221+322+…+n 2n -1,①12T n =121+222+323+…+n 2n ,② ①-②得12T n =120+121+122+…+12n -1-n 2n =1-12n1-12-n 2n =2-n +22n ,所以T n =4-n +22n -1. 易知数列{2n }的前n 项和为n (n +1), 所以S n =n (n +1)-4+n +22n -1.数学运算——数列的通项公式及求和问题[典例] 设{a n }是公比大于1的等比数列,S n 为其前n 项和,已知S 3=7,a 1+3,3a 2,a 3+4构成等差数列.(1)求数列{a n }的通项公式;(2)令b n =a n +ln a n ,求数列{b n }的前n 项和T n . [解] (1)设数列{a n }的公比为q (q >1). 由已知,得⎩⎪⎨⎪⎧a 1+a 2+a 3=7,(a 1+3)+(a 3+4)2=3a 2,即⎩⎪⎨⎪⎧a 1(1+q +q 2)=7,a 1(1-6q +q 2)=-7.由q >1,解得⎩⎪⎨⎪⎧a 1=1,q =2,故数列{a n }的通项公式为a n =2n -1. (2)由(1)得b n =2n -1+(n -1)ln 2,所以T n=(1+2+22+…+2n-1)+[0+1+2+…+(n-1)]ln 2=1-2n1-2+n(n-1)2ln 2=2n-1+n(n-1)2ln 2.[素养通路]数学运算是指在明晰运算对象的基础上,依据运算法则解决数学问题的素养.主要包括:理解运算对象,掌握运算法则,探究运算思路,选择运算方法,设计运算程序,求得运算结果等.本题通过列出关于首项与公比的方程组,并解此方程组得出首项与公比,从而得出通项公式;通过分组分别根据等比数列求和公式、等差数列求和公式求和.。
2020年高考语文复习第二编古诗文阅读专题二微案五文言句式与翻译学案(含解析)

文言句式与翻译文言文翻译考查的实质是理解文言文,重点是语句中的实词、虚词和句式。
备考时,要坚持以直译为主,尽量将每个单音节词翻译为双音节词。
考试时,要快速理解句子大意,结合语境,对照文意理解,聚焦采分点。
前面微案一里已对文言实词做了详细讲解,文言十八个虚词的系统用法请同学们参看附册《考点知识必背清单》“文言虚词”部分,此处不再赘述,下面我们重点突破文言句式与翻译。
微点突破一文言句式A.今者项庄拔剑舞,其意常在沛公也B.今日往而不反者,竖子也C.且相如素贱人D.尝从人事,皆口腹自役剖析A.“者”用在时间词“今”后,起补足音节的作用;“也”用在句末,表示陈述语气。
可译为:现在项庄拔剑起舞,他的用意总是在沛公身上。
可见句中虽然有“……者……也”,有时也并不表示判断。
B.判断句,“也”表判断语气。
C.通过语意直接表示判断。
D.用“皆”表示判断。
答案 AA .此非孟德之困于周郎者乎B .臣诚恐见欺于王而负赵C .身死人手,为天下笑者,何也D .将军身被坚执锐剖析 A .“于”表被动;B.“见……于”表被动;C.“为”表被动;D.“被”在此处不表被动,通“披”,意思为“穿”。
答案 DA.⎩⎪⎨⎪⎧ ①时人莫之许也②彼且奚适也B.⎩⎪⎨⎪⎧ ①忌不自信,而复问其妾②何为其然也C.⎩⎪⎨⎪⎧ ①沛公安在②古之人不余欺也D.⎩⎪⎨⎪⎧ ①微斯人,吾谁与归②俯察品类之盛剖析 D .①句为宾语前置句,“谁”为介词“与”的前置宾语;②句为定语后置句,“盛”为“品类”的后置定语。
其余三项均为宾语前置句。
A.①“之”,②“奚”前置;B.①“自”,②“何”前置;C.①“安”,②“余”前置。
答案 DA .以其无礼于晋B .君子博学而日参省乎己C .鹤鸣九皋,声闻于天D .州司临门,急于星火剖析 “于”应译为“到”,不能提前。
答案 CA .太子及宾客知其事者B .马之千里者,一食或尽粟一石C .以为凡是州之山水有异态者D .彼童子之师,授之书而习其句读者,非吾所谓传其道解其惑者也剖析 D .为否定判断句,其他三项为定语后置句。
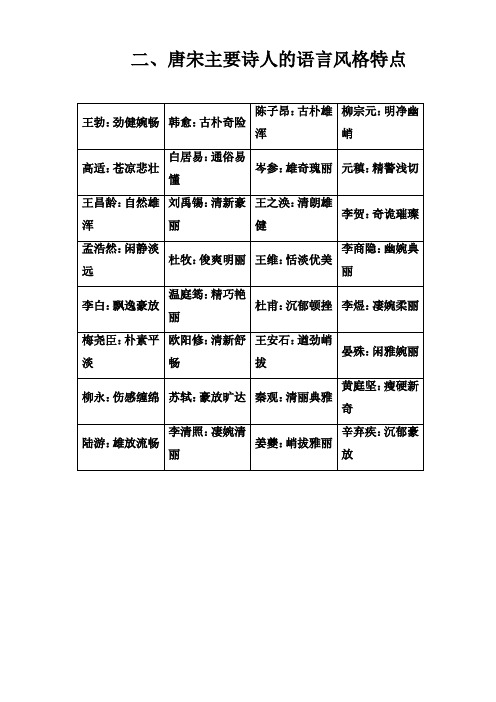
2020届高考语文一轮总复习学案:第二部分 专题二 知识清单 二、唐宋主要诗人的语言风格特点

王勃:劲健婉畅
韩愈:古朴奇险Βιβλιοθήκη 陈子昂:古朴雄浑柳宗元:明净幽峭
高适:苍凉悲壮
白居易:通俗易懂
岑参:雄奇瑰丽
元稹:精警浅切
王昌龄:自然雄浑
刘禹锡:清新豪丽
王之涣:清朗雄健
李贺:奇诡璀璨
孟浩然:闲静淡远
杜牧:俊爽明丽
王维:恬淡优美
李商隐:幽婉典丽
李白:飘逸豪放
温庭筠:精巧艳丽
杜甫:沉郁顿挫
李煜:凄婉柔丽
梅尧臣:朴素平淡
欧阳修:清新舒畅
王安石:遒劲峭拔
晏殊:闲雅婉丽
柳永:伤感缠绵
苏轼:豪放旷达
秦观:清丽典雅
黄庭坚:瘦硬新奇
陆游:雄放流畅
李清照:凄婉清丽
姜夔:峭拔雅丽
辛弃疾:沉郁豪放
2020版新高考复习理科数学教学案:数列含答案 (2)

6.[20xx·惠州调研]已知各项均为正数的等比数列{an}中.a1=1,2a3.a5,3a4成等差数列.则数列{an}的前n项和Sn=( )
A.2n-1B.2n-1-1
C.2n-1D.2n
解析:通解:设{an}的公比为q(q>0).由题意知2a5=2a3+3a4.∴2a3q2=2a3+3a3q.∴2q2=2+3q.∴q=2或q=- (舍去).所以an=2n-1.
■备考工具——————————————
1.求数列的前n项和的方法
(1)公式法
①等差数列的前n项和公式
Sn= =na1+ .
②等比数列的前n项和公式
a.当q=1时.Sn=na1;
b.当q≠1时.Sn= = .
(2)分组求和:把一个数列分成几个可以直接求和的数列.
(3)裂项相消:把一个数列的通项分成两项差的形式.相加过程中消去中间项.只剩有限项再求和.
通项公式的推广
an=a1qn-1
(揭示首末两项的关系)
an=amqn-m
(揭示任意两项之间的关系)
(2)前n项和公式
Sn= 或Sn=
7.等比数列的性质
若{an}为等比数列.则
(1){a }. .{c·an}(c≠0)都是等比数列.
(2)各项及公比都不为0.
8.等比数列项的运算性质
若m+n=p+q(m.n.p.q∈N*).则am·an=ap·aq.
令n=101.则S101+a101=2×101-6+ .所以S101+(S101-S100)=196+ .得2S101-S100=196+ ②.
将①代入②得S100=2× -196- =396+ -196- =200.选B.
答Байду номын сангаас:B
2023年高考小专题复习学案 专题2匀变速直线运动的基本规律

专题2 匀变速直线运动的基本规律【知识梳理】一、匀变速直线运动的基本规律1.匀变速直线运动:沿着一条直线且不变的运动,其v-t图线是一条。
2.四个基本规律(1)速度与时间的关系式:,若是v0=0的匀加速直线运动,则。
(2)位移与时间的关系式:,若是v0=0的匀加速直线运动,则。
(3)速度位移关系式:,若是v0=0的匀加速直线运动,则。
(4)平均速度公式:,则速度位移关系式为。
3.位移的关系式及选用原则(1)不涉及加速度a时,选择。
(2)不涉及运动的时间t时,选择。
二、匀变速直线运动的基本规律解题技巧1.基本思路画过程示意图→判断运动性质→选取→选用公式列方程→解方程并加以讨论2.正方向的选定无论是匀加速直线运动还是匀减速直线运动,通常以的方向为正方向;当v0=0时,一般以的方向为正方向.速度、加速度、位移的方向与正方向相同时取,相反时取。
3.解决匀变速运动的常用方法(1)逆向思维法:对于末速度为零的匀减速运动,采用逆向思维法,可以看成反向的运动。
(2)图像法:借助v-t图像(斜率、面积)分析运动过程。
三、两种匀减速直线运动的比较1.刹车类问题(1)其特点为匀减速到速度为零后运动,加速度a突然消失。
(2)求解时要注意确定实际运动。
(3)如果问题涉及最后阶段(到停止)的运动,可把该阶段看成反向的运动。
2.双向可逆类问题(1)如沿光滑固定斜面上滑的小球,到最高点后仍能以原加速度匀加速下滑,全过程加速度大小、方向均不变。
(2)求解时可分过程列式也可对全过程列式,但必须注意x 、v 、a 等矢量的正负号及物理意义. 【专题练习】 一、单项选择题1.一架战机起飞前从静止做加速度为a 的匀加速直线运动,达到起飞速度v 所需的时间为t ,则战机起飞前运动的距离表达式错误的是( ) A .vtB .2vtC .212atD .22v a2.物体从静止开始做匀加速直线运动,已知第5s 内的位移为x ,则物体运动的加速度为( ) A .49x B .9x C .3x D .29x 3.一物体做匀减速直线运动,在第二秒内的位移为3m ,第三秒内的位移为0.125m ,则物体的加速度大小为( ) A .23m/sB .23.5m/sC .24m/sD .24.25m/s4.一列火车沿直线轨道从静止出发由A 地驶向B 地,火车先做匀加速运动,加速度大小为a ,接着做匀减速运动,加速度大小为2a ,到达B 地时恰好静止。
高三语文“高考作文备考必读”学案2(第五周)(整理精校版)

高三语文“高考作文备考必读”学案2(第五周)作文辅导0528 2136高三语文“高考作文备考必读”学案2(第五周)生命的价值一天,英国著名诗人拜伦在泰晤士河岸上散步时看到了一个落水的富翁在喊救命。
一个穷人冒着生命危险把他拖到了岸上,救了他的命。
但富翁却只拿出一个小小的铜钱作为酬谢。
聚集观看的行人对富翁这种忘恩负义的行为非常气愤,七手八脚把他抬起来,想把他抛回到河里去,但拜伦却阻止了他们,说:“别责怪他,把他放下吧,他自己很清楚他能值多少钱。
”点评:唐朝诗人孟郊有诗曰:“兽中有人性,形异遭人隔。
人中有兽心,几人能真识。
”在我国某地,曾发生过比这个故事更精彩的一幕:有一位先生路过河边,看到一群人在岸上围观一个在河中挣扎呼救的落水女子,就毫不犹豫地拨开人群跳入河中拼死命把女子推上岸来,而自己却因筋疲力尽而沉入河底。
可是,谁也不会想到,在人们的赞叹惊呼惋惜声中,这个被救起的女子却像避瘟疫一样悄悄地逃离了现场。
事后,记者找到了这个女子,问她当时怎么忍心弃自己的救命恩人而不顾?她十分轻松地回答:“我怕他家里人来找我要钱。
”故事中的富翁和这个女子面对救命恩人所表现出的“兽性”,兽类若目睹耳闻,定会自愧弗如。
可是,“兽中有人性”也不乏例子。
在邢台大地震来临之际,一个村庄里的一条狗突然东奔西跑狂吠不停,直至把村民全叫醒。
而当全村人都安全逃离震区时,这条狗却累死了。
上海南汇区农民潘家祥看到一条大毒蛇攻击自家的小花猫,就拿起锄头斩断了大毒蛇的尾巴,毒蛇负伤逃命。
半个月之后的一个夜晚,这条失去尾巴的大毒蛇在养好伤后居然前来报仇。
当它气势汹汹地爬到睡熟的潘家祥的脚边时,小花猫迅速出击,一边大声呼叫,一边护驾斗蛇。
潘家祥被厮杀声惊醒,才得以“蛇口脱险”。
狗和猫本为牲畜,却能知恩图报,实在会让那些忘恩负义者汗颜。
猎户失弓楚国有一个猎户,一天上山打猎回来,发现自己的弓丢了。
家人催促他赶快上山找回来,可猎户却若无其事地说:‚算了,楚人丢了,楚人捡,还去找什么?‛这件事传到了鲁国,孔子说:‚如果去掉一个‘楚’字,成为‘人丢了,人捡’,就更有意义了。
2020届高考语文一轮总复习学案:第二部分_专题二_知识清单_二、唐宋主要诗人的语言风格特点_word版含解析
李煜:凄婉柔丽
梅尧臣:朴素平淡
欧阳修:清新舒畅
王安石:遒劲峭拔
晏殊:闲雅婉丽
柳永:伤感缠绵
苏轼:豪放旷达
秦观:清丽典雅
黄庭坚:瘦硬新奇弃疾:沉郁豪放
二、唐宋主要诗人的语言风格特点
王勃:劲健婉畅
韩愈:古朴奇险
陈子昂:古朴雄浑
柳宗元:明净幽峭
高适:苍凉悲壮
白居易:通俗易懂
岑参:雄奇瑰丽
元稹:精警浅切
王昌龄:自然雄浑
刘禹锡:清新豪丽
王之涣:清朗雄健
李贺:奇诡璀璨
孟浩然:闲静淡远
杜牧:俊爽明丽
王维:恬淡优美
李商隐:幽婉典丽
李白:飘逸豪放
温庭筠:精巧艳丽
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020年高考备考成语学案二学习目标:感知高考高频考查成语课时:两课时一、高频根据下面所给高考真题语境解释成语1、(2017年全国卷I)国家“一带一路”战略的实施,给古丝绸之路的眼线城市带来了活力,很多城市对未来踌躇满志,跃跃欲试。
2、2008年江西卷到半夜,小说终于脱稿了,他地摸着胡子,长长地松了口气踌躇满志”是中性词,形容对自己取得的成就非常得意踌躇满志解释:_______________________________________________________________________。
3、(2017年高考天津卷)大多数人的心目中,真与美并不是一回事,尤其是文艺复兴以后,美成为人文素养中的主要内涵,真与美就南辕北辙了。
4、(2015年山东卷)联合国大会曾经两次召开会议,讨论是否应该废除死刑的问题,但因各方立场南辕北辙,讨论无果而终。
5、(2013年江苏卷)读者欣赏作品清新的故事,却忽略了蕴藏的热情,欣赏文字的朴实,却忽略了作品隐伏的悲痛,实际上近于________。
6、(2007年广东卷)我俩考虑问题时,他习惯从大的方面着眼,我总是从具体方法入手,虽然南辕北辙,但总能殊途同归。
南辕北辙解释:_______________________________________________________________________。
7、(2016年全国卷I)在那几年的工作学习中,杨老师给了我很大的帮助,他的教导在我听来如同空谷足音,给我启示,带我走出困惑。
8、(2014年辽宁卷)在全省经济发展座谈会上,李教授的讲话直击时弊,同时又颇具前瞻性,对于当前经济工作而言,可谓空谷足音。
空谷足音解释:________________________________________________________________________。
9、(2016年全国卷I)第二展厅的文物如同一部浓缩的史书,举重若轻地展示了先民们在恶劣的自然条件下顽强战争、繁衍生息的漫长历史。
10、(2010年江西卷)导演冯小刚把《集结号》中最重要的角色给了谷志鑫,其他演员几乎成了举重若轻的人物。
举重若轻解释:________________________________________________________________________。
11、(2016年全国卷I)这部翻译小说虽然是以家庭生活为题材的,却多侧面、多视角地展现出那个时代光怪陆离的社会生活画卷。
12、(2002年)面对光怪陆离的现代观念,他们能从现实生活的感受出发,汲取西方艺术的精华,积极探索新的艺术语言。
光怪陆离解释:________________________________________________________________________。
13、(2016年全国卷II)这次会谈并没有其他人员参加,他们两个人又都一直讳莫如深,所以会谈内容就成为一个难解之谜。
14、(2010年新课标)开发商们对商品房面积的计算方式一直讳莫如深,由此导致的开发商与业主之间的经济纠纷经常发生。
15、(2005年江苏卷)D.导演对筹拍的这部电视剧主要角色的人选讳莫如深,记者得不到任何信息,大失所望。
讳莫如深解释________________________________________________________________________。
16、(2016年全国卷II)那些航空领域的拓荒者,很多已经离开人世,但他们筚路蓝缕的感人形象一直深深印在人们的记忆中。
17、(2006年山东卷)近年来禽流感在国内时有发生,危害极大,各级政府必须筚路蓝缕,积极作好预防,以免给人民的生命财产带来损失。
筚路蓝缕解释:________________________________________________________________________。
18、(2016年全国卷II)正在悠闲散步的外科主任王教授,突然接到护士电话说有个病人情况危急,他立刻安步当车向医院跑去。
19、(2001年)当时暴雨如注,满路泥泞,汽车已无法行走,抢险队员们只好安步当车,跋涉一个多小时赶到了大坝。
安步当车解释:________________________________________________________________________。
20、(2016年全国卷III)这几幅书法作品笔走龙蛇、流畅飘逸,在本次春季拍卖会甫一亮相,就引起了国内外藏家的极大兴趣。
21、(2009年安徽卷)现在少数媒体放着有重要新闻价值的素材不去挖掘,反倒抓住某些明星的一点逸闻就笔走龙蛇,这种做法真是令人费解。
笔走龙蛇解释________________________________________________________________________。
22、(2016年全国卷III)天寒地冻、滴水成冰的季节终于过去,春天在大家的盼望中姗姗而来,到处都焕然冰释,生机勃勃。
23、(2013年安徽卷)《舌尖上的中国》是国内首次使用高清设备拍摄的美食类纪录片,片中由近距离拍摄呈现出的各类食材的纹理构造,带给观众焕然一新的审美感受。
24、(2008年四川卷)微笑像和煦的春风,微笑像温暖的阳光,它蕴涵着一种神奇的力量,可以使人世间所有的烦恼都焕然冰释。
25、(2003春)由于太平洋暖流的影响,去年春天来得早,春节刚过,北海公园就涣然冰释,让喜欢滑冰的人大失所望。
焕然冰释解释:________________________________________________________________________。
26、(2016年全国卷III)这块神奇的土地上,既有浩如烟海的传统文化典籍,也有丰富多彩的民俗文化和各种流派的现代艺术,这些都深深吸引着前来参现的外国友人。
27、(2013年全国Ⅰ卷)泰山几千年来都是文人墨客们向往的圣地,在浩如烟海的中华典籍中,留下了众多颂扬泰山的诗词文章。
浩如烟海解释________________________________________________________________________。
28、(2016年山东卷)持续多日的强降雨导致部分地区山洪暴发,农田被淹,房屋倒塌,灾情扣人心弦,相关部门正全力以赴组织救灾。
29、(2008年广东卷)眼看两车就要相撞。
在这千钧一发之际,只听“嘎——”的一声,公共汽车司机紧急刹车,避免了一场车祸的发生。
车上乘客目睹了这一扣人心弦的一幕,议论纷纷,怨声载道。
扣人心弦解释:________________________________________________________________________。
30、(2016年浙江卷)他爱好广泛,喜欢安静的棋类运动,对热闹的纸牌游戏也来者不拒;欣赏通俗感性的流行歌曲,对庄重恢宏的交响乐也甘之如饴。
31、(2007年全国卷1).这些战士虽然远离家乡,远离繁华,每天过着艰苦单调的生活,但是他们一个个甘之若饴,毫无怨言。
甘之若饴解释:________________________________________________________________________。
32、(2010年安徽卷)发展低碳经济首当其冲的是要坚持节约资源、保护环境的基本国策,协调资源利用和环境保护的关系,实现可持续发展。
33、(2009年广东卷)四十年来,您培养的莘莘学子,或纵横商海,运筹帷幄,或潜心学界,激扬文字……在各行各业的建设中,总是首当其冲。
34、(2006年北京卷)大英博物馆近来因财力吃紧,裁减工作人员,与中国文物有关的职位首当其冲,这样,中国文物的巡展活动自然难以开展。
35、(2000春)D.据专家测算,•在首都市内的空气污染中,汽车尾气的排放可算首当其冲,竟占了污染总量的45%。
36、(95年)第二次世界大战时,德国展开了潜艇战,于是使用水声设备来寻找潜艇,成了同盟国要解决的首当其冲的问题。
首当其冲解释:________________________________________________________________________。
37、(2008年浙江卷)NBA季后赛中,由于缺少了主力姚明,火箭队内线空虚,在防守上往往顾此失彼,实力明显削弱。
(捉襟见肘)38、(2006年全国卷II )盗挖天山雪莲日益猖獗的主要原因是,违法者众多且分布广泛,而管理部门又人手不足,因此执法时往往捉襟见肘。
39、(2006年湖北卷)随着两个儿子的出世,家庭状况更是捉襟见肘,她不得不去打工赚钱贴补家用,可她一个没有文化的农村妇女,挣的钱少得可怜。
40、(2003年全国卷)滥挖天山雪莲现象日益猖獗的原因之一是,违法者众多且分布广泛,而管理部门人手不足,因此执法时往往捉襟见肘。
捉襟见肘解释:________________________________________________________________________。
41、(2015年广东卷)石钟山上那些错落有致的奇石以及记载着天下兴衰的石刻令人叹为观止。
42、(2014年全国大纲卷)这个剧院的大型话剧、歌剧等演出票价不菲,让许多有艺术爱好而又收入不高的普通人叹为观止,无法亲临现场享受艺术大餐。
43、(2008年安徽卷)有段时间,沪深股市指数波动非常大,有时一天上涨几百点,有时一天下跌几百点,涨跌幅度之大令人叹为观止。
44、(2005年全国3)中国改革开放以来取得的巨大成就,特别是连续十几年经济持续高速增长的表现,让各国经济界人士都叹为观止。
叹为观止解释:________________________________________________________________________。
45、(2013年重庆卷)他的创作风格似乎很难言说,清丽、典雅、豪放、幽默都不足以概括。
在当今文坛上,他的创作可谓独树一帜。
46、(2007年安徽卷)风格鲜明、体系完整、精细雅致的徽州文化,在洋洋洒洒的中华地方文化中独树一帜。
47、(2005年全国3)近年来,在各地蓬勃兴起的旅游热中,以参观革命圣地、踏访英雄足迹为特色的"红色旅游"独树一帜,呈升温之势。
独树一帜解释:________________________________________________________________________。
48、(2014年新课标卷II)消防工作必须立足于_____,从提高公众的防火意识做起。
