时间序列作业
时间序列分析作业

1、某股票连续若干天的收盘价如下表:304 303 307 299 296 293 301 293 301 295 284 286 286 287 284282 278 281 278 277 279 278 270 268 272 273 279 279 280 275271 277 278 279 283 284 282 283 279 280 280 279 278 283 278270 275 273 273 272 275 273 273 272 273 272 273 271 272 271273 277 274 274 272 280 282 292 295 295 294 290 291 288 288290 293 288 289 291 293 293 290 288 287 289 292 288 288 285282 286 286 287 284 283 286 282 287 286 287 292 292 294 291288 289选择适当模型拟合该序列的发展,并估计下一天的收盘价。
解:根据上面的图和SAS软件编辑程序得到时序图,程序如下:data shiyan7_1;input x@@;time=_n_;cards;304 303 307 299 296 293 301 293 301 295 284 286 286 287 284282 278 281 278 277 279 278 270 268 272 273 279 279 280 275271 277 278 279 283 284 282 283 279 280 280 279 278 283 278270 275 273 273 272 275 273 273 272 273 272 273 271 272 271273 277 274 274 272 280 282 292 295 295 294 290 291 288 288290 293 288 289 291 293 293 290288 287 289 292 288 288 285282 286 286 287 284 283 286 282 287 286 287 292 292294 291 288 289;proc print data=shiyan7_1;proc gplot data=shiyan7_1;plot x *time=1;symbol1c=red v=star i=spline;run;通过SAS运行上述程序可得到如下结果:可以看出序列含有长期趋势又含有一定的周期性,故进行差分平稳,又从上述时序图呈现曲线形式,故对原序列作二阶差分,差分程序及时序图如下:data shiyan7_1;input x@@;difx=dif(dif(x));time=_n_;cards;304 303 307 299 296 293 301 293 301 295 284 286 286 287 284282 278 281 278 277 279 278 270 268 272 273 279 279 280 275271 277 278 279 283 284 282 283 279 280 280 279 278 283 278270 275 273 273 272 275 273 273 272 273 272 273 271 272 271273 277 274 274 272 280 282 292 295 295 294 290 291 288 288290 293 288 289 291 293 293 290 288 287 289 292 288 288 285282 286 286 287 284 283 286 282 287 286 287 292 292294 291 288 289;proc print data=shiyan7_1;proc gplot data=shiyan7_1;plot x *time difx*time;symbol1c=red v=star i=join;proc arima;identify var=x(1,1);estimate q=1;forecast lead=5id=time;run;SAS软件运行后可得到差分后的序列时序图,其图形如下:时序图显示差分后序列已无显著趋势或周期,随机波动比较平稳。
时间的序列第五章作业的

第五章SAS作业问题1:1867-1938年英国绵羊数量如下所示:2203 2360 2254 2165 2024 2078 2214 2292 2207 2119 2119 2137 2132 1955 1785 1747 1818 1909 1958 1892 1919 1853 1868 1991 2111 2119 1991 1859 1856 1924 1892 1916 1968 1928 1898 1850 1841 1824 1823 1843 1880 1968 2029 1996 1933 1805 1713 1726 1752 1795 1717 1648 1512 1338 1383 1344 1384 1484 1597 1686 1707 1640 1611 1632 1775 1850 1809 1653 1648 1665 1627 17911、选择恰当模型,拟合该序列的发展;2、利用拟合模型预测1938-1945年英国绵羊的数量;3、按照书本相应例题的格式完成问题,并附上SAS程序。
解:(1)时序图显示,序列具有长期趋势,对序列进行1阶差分▽Xt=Xt-Xt-1,观察差分后序列▽Xt的时序图。
时序图显示长期趋势信息基本被差分运算提取充分,考察差分后序列的自相关图和偏自相关图。
自相关图显示延迟3阶后自相关系数基本在2倍标准差范围内,因此认为该序列为平稳序列。
自相关图表现出拖尾现象,偏自相关图表现出3阶结尾现象,且自相关图中2阶自相关系数在2倍标准差范围内,所以考虑构造疏系数模型AR(1,3)。
残差自相关检验结果显示延迟6期后P值都大于0.05,因此认为残差为白噪声序列,即拟合模型显著有效。
参数估计结果显示两参数P值都小于0.05,都显著有效。
则拟合的AR(1,3)模型为▽Xt=0.32196▽Xt-1 –0.37616▽Xt-3 + εt(2)利用拟合模型对1938-1945年英国绵羊的数量进行预测结果如上图所示,预测图为(3)SAS程序为data a;input x@@;dif1=dif(x);t=1867+_n_-1;format time year4.;cards;2203 2360 2254 2165 2024 2078 2214 2292 2207 2119 211921372132 1955 1785 1747 1818 1909 1958 1892 1919 1853 186819912111 2119 1991 1859 1856 1924 1892 1916 1968 1928 1898 18501841 1824 1823 1843 1880 1968 2029 1996 1933 1805 1713 17261752 1795 1717 1648 1512 1338 1383 1344 1384 1484 1597 16861707 1640 1611 1632 1775 1850 1809 1653 1648 1665 1627 1791;run;proc gplot data=a;plot x*t dif1*t;symbol c=black i=join v=dot;proc arima;identify var=x(1) ;estimate p=(13) noint;forecast lead=7id=t out=out;proc gplot data=out;plot x*t=1 forecast*t=2 l95*t=3 u95*t=3/overlay;symbol1c=black i=none v=star;symbol2 c =red i =join v =none; symbol3 c =green i =join v =none; run ;问题2,使用Auto-Regressive 模型分析例5.9序列。
时间序列大作业

应用时间序列大作业课题:基于ARIMA模型的全国1980-2013年邮电业务函件数量时间序列分析及预测。
姓名:***学号:**********编号:48基于ARIMA 模型全国1980-2013年邮电业务函件数量时间序列分析及预测一.摘要时间序列就是按照时间的顺序记录的一列有序数据。
对时间序列进行观察、研究,找寻它变化发展的规律,预测它将来的走势。
时间序列分析在日常生活中随处可见,有着非常广泛的应用领域。
邮政与我们息息相关,他已经成为社会经济生活不可或缺的通信手段。
在世界上,函各国都以件量来衡量一个国家的邮政发展水平,而我国的函件量增长却不容乐观,这勾起了我研究的兴趣,加上我本人又有集邮的爱好,因此我选用了函件量进行分析研究。
本文用时间序列分析方法,对一段时间序列进行了拟合。
通过对1980至2013年全国邮电业务函件量序列进行观察分析,建立合适的ARIMA 模型,对未来五个月的全国邮电业务函件量序列进行预测。
然后对预测值和真实值进行比较,得出结论,所建立的模型有较好的拟合效果,从而提供了一个行情预测的有效方法。
关键词:时间序列 函件量 ARIMA 时间序列分析 预测二.前言邮政的最初发展史从人们的信函寄送需要开始的,现在邮政的众多业务也是借助经营函件业务而衍生出来的。
目前,函件业务的主要包括为用户传递书面通信、文件资料和书籍等。
他已经成为社会经济和生活不可缺少的通信手段。
如果的函件业务搞不好,邮政其他业务也就失去了赖以生存的基础,这将严重削弱邮政在社会中的地位和作用。
当前,世界各国都以函件量来衡量一个国家邮政发展水平,然而几十年随着经济建设的飞速发展,邮电业务的需求量迅猛增长,唯有函件业务增长不容乐观,与发达国家和甚至一些发展中国家相比还有很大差距。
原因何在?因此,本文就以以我国1980-2013年全国邮电业务函件量的数据为研究对象,做时间序列分析。
首先,对全国33年来全国邮电业务函件量的发展变化规律,运用SAS 软件进行分析其发展趋势。
时序作业

时间序列分析----中国居民民消费价格指数居民价格消费指数价指数(Consumer Price Index),英文缩写为CPI,是反映与居民生活有关的产品及劳务价格统计出来的物价变动指标,通常作为观察通货膨胀水平的重要指标。
在经济学上,是反映与居民生活有关的产品及劳务价格统计出来的物价变动指标,以百分比变化为表达形式。
一般定义超过3%为通货膨胀,超过5%就是比较严重的通货膨胀。
CPI是一个滞后性的数据,但它往往是市场经济活动与政府货币政策的一个重要参考指标。
CPI物价指数指标十分重要,而且具有启示性,必须慎重把握,因为有时公布了该指标上升,货币汇率向好,有时则相反。
因为消费物价指数水平表明消费者的购买能力,也反映经济的景气状况,如果该指数下跌,反映经济衰退,必然对货币汇率走势不利。
但如果消费物价指数上升,汇率是否一定有利好呢?不一定,须看消费物价指数"升幅"如何。
由此可看,正确的把握居民价格指数是极其重要的。
下表是1985年到2007年中国居民消费价格指数的数据:年份居民价格指数年份居民价格指数1985 109.3 1997 102.81986 106.5 1998 99.21987 107.3 1999 98.61988 118.8 2000 100.41989 118 2001 100.71990 103.1 2002 99.21991 103.4 2003 101.21992 106.4 2004 103.91993 114.7 2005 101.81994 124.1 2006 101.51995 117.1 2007 104.81996 108.3根据应用时间序列分析的有关内容,现用EVIEWS软件对1985到2007年的消费价格指数进行分析,并对2008年到2010年的消费价格指数进行预测。
一对原数列的平稳性观察以及纯随机性检验1.平稳性观察用软件对原数列做折线图,如下图:X表示历年的消费价格指数图1历年价格指数折线图根据上图,历年的居民消费价格指数基本在一定的范围内上下波动,因此可以初步认为居民消费价格指数是一个平稳的时间序列。
时间序列分析练习题

17. 在趋势性检验中,进行单位根检验的意义是什么?
单位根检验就是根据已观测到的时间序列,检验产生这个时间序列的随机过程中的一阶 自回归系数是否为一,这个检验实际上就是对时间序列是否为一个趋势平稳过程的检验,如 果检验表明没有单位根,则它是一个趋势平稳过程,否则,它是一个带趋势的单位根过程。
①( 均值为常数 ) ②( 协方差为时间间隔 的函数 )
则称该序列为宽平稳时间序列,也叫广义平稳时间序列。 8. 对于一个纯随机过程来说,若其期望和方差(均为常数),则称之为白噪声过程。白 噪声过程是一个(宽平稳)过程。 9. 时间序列分析方法按其采用的手段不同可概括为数据图法,指标法和(模型法)
19. 线性趋势平稳的特点:当我们将时间序列中的完全确定的线性趋势去掉以后,所形 成的时间序列就是一个平稳的时间序列。
20. 如何以系统的观点看待时间序列的动态性? 系统的动态性就是在某一时刻进入系统的输入对系统后继行为的影响,也就是系统的记 忆性,描述记忆性的函数称为记忆函数。
三、证明题
1. AR(1)模型: X t 1 X t1 at ,其中 at 是白噪声,且 E at2
37. ARMA(n,m) 的逆转形式 X t I j X t j at 。 j 1
38.
模型适应性检验的相关函数法,在显著性水平
0.05 下,若
k
1.96 /
N,
则接受 k 0 的假设,认为 at 是独立的。
39. 模型适应性检验的 2 检验法,在显著性水平 下,若统计量
G12
G22
时间序列分析作业及答案
(3) 5500 4000 (1 x ) 5 5500 x 106.58% 甲厂平均发展速度需 106.58% 4000
a1 a2 a3 a4 a5 1 解 : x x 1 x 1 5 a0 a1 a2 a3 a 4
n
5 (1 5.2%) (1 4.8%) (1 3.8%) (1 3.5%) (1 2.4%) 1
平均每年的降低率: x 96.05% 1 3.95%
lg1.375 0.13830 n 14.32年 15年后可达到乙厂水平 lg1.0225 0.00966
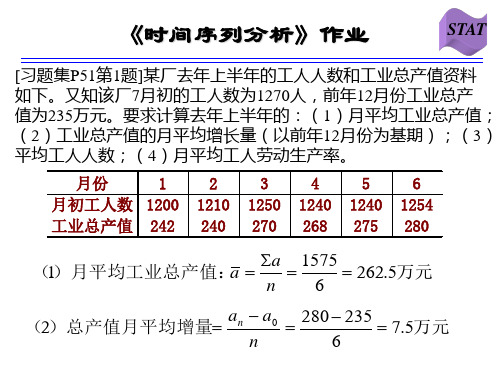
《时间序列分析》作业
STAT
[习题集P53第8题]甲、乙两厂各年产量资料如下。要求:(1) 分别计算两厂的平均发展速度;(2)按现在甲厂平均发展速度, 要几年才能达到乙厂1999年的水平?(3)如要求甲厂从1999年 起,在五年内达到乙厂1999年的水平,则甲厂的平均发展速度 必须达到多少?
a1990 25(1 4%)5 30.42 a2000 30.42(1 4.5%)10 47.24
a2000 25(1 4%)5 (1 4.5%)10 47.24 (万吨)
(2)已知:a2000 3 25 75 75 25(1 4%)5 (1 x )10
5
《时间序列分析》作业
STAT
[习题集P54第10题]某地区1995~2001年财政收入资料如下(单位: 亿元)。根据该资料: (1)用最小平方法的简捷式配合直线趋势方程; (2)根据直线趋势方程预测2002年的财政收入。
时间序列作业 VECM模型

我国FDI与进出口和人民币实际有效汇率——基于协整的VECM分析一、案例分析背景外商直接投资已成为我国经济快速发展的主要推动力之一。
2007年,据联合国《世界投资报告》统计,2006年我国吸引的外国直接投资达694.68亿美元,占当年我国固定资产形成的8%。
影响外商直接投资的因素较多且作用机制比较复杂,本文试图通过对FDI,进口总额,出口总额和人民币实际有效汇率之间的相互关系,发现我国外商直接投资、进出口和人民币汇率等重要宏观变量之间的长期均衡关系及相互作用机制。
二、变量选择和数据来源本实验选取了外商直接投资中实际利用外资金额代表外商直接投资额并记为FDI,以及进口总额,出口总额,人民币实际有效汇率1998年5月至2011年12月月度数据进行分析,由于数据数量较多,具体数据见附录。
三、VECM模型的构建(一)数据处理1.外商直接投资额将外商直接投资额变量记为FDI,FDI经过X12季节性调整后的FDI_SA图形如图1所示。
图1 经季节性调整后FDI走势图为了平滑FDI的变动趋势,对FDI做对数处理记为LFDI。
LFDI的图形如图2所示。
图2 LFDI变动图2、出口总额将出口总额变量记为EX,对EX进行季节性调整,季节性调整后的EX_SA图形如图3所示。
图3 经季节性调整后EX走势图为了平滑EX的变动趋势,对EX做对数处理记为LEX。
LEX的图形如图4所示。
图4 LEX变动图3.进口总额将出口总额变量记为IM,对IM进行季节性调整,季节性调整后的IM_SA图形如图5所示。
图5 经季节性调整后IM走势图为了平滑IM的变动趋势,对IM做对数处理记为LIM。
LIM的图形如图6所示。
图6 Lim变动图4、人民币实际有效汇率将人民币实际有效汇率记为REER,为了减少异方差性,对REER进行取对数处理,并记为LREER,LREER的图形如图5所示。
图7 LREER变动图(二)单位根检验对LFDI,LEX,LIM,LREER四个变量选取相应的形式进行单位根检验。
时间序列分析作业 (2)

应用时间序列分析随堂作业一、单项选择题1.的p 阶差分是( )t X A . B .()t PX B -1t P X B )1(-C . D .t P X B -1Pt BX -12、时间序列中,严平稳与宽平稳的关系是( )A .满足严平稳就满足宽平稳;B .满足宽平稳就满足严平稳;C .二者是相互等价的;D .正态分布时,宽平稳序列也满足严平稳条件3.ARMA(2,1)模型的形式是( )A .112211----++=t t t t t X X X εθεϕϕB .tt t t X εεθεθ+-=--2211C . 21112211------+=t t t t t X X X εθεθϕϕD .tt t t t t X X X εεθεθϕϕ+--+=----211122114.AR (1)模型的逆函数是 ( )A . B.1,0,11>==j I I j ϕjI 1ϕ=C .D .j I 1ϕ-=1ϕ=I 5. AR (1)模型的格林函数是 ( )A . B.j t j t e X -∞=∑=01φjt j j t e X +∞=∑=01φC .D .j t j j t e X -∞=∑=01φt j jt e X ∑∞==01φ6.﹛X t ﹜服从MA (q )过程,则Var (X t )为( )A . ;B .2e σ2221)1(e q σθθ+++ C .D .22121q e θθσ+++ 221e σθ7.下图是某时间序列的自相关和偏自相关图,请根据该图判断该序列是 ()A .MA (1)B .AR (1)C .ARMA (1,1) D.MA (2)8.对时间序列拟合arma (1,1)模型后,对序列残差进行检验发现,LB 统计量拒绝了原假设,这意味着 ( )A .残差序列是独立的B .残差序列存在自相关的;C .残差序列有GARCH 效应D .arma (1,1)模型是恰当的9.ARMA 过程是平稳的,意味着( )A .特征方程的根在单位圆内B .特征方程的根在单位圆外C .系数多项式方程的根在单位圆内D .其中AR 部分每项系数不超过1二、多单项选择题1.关于样本自协方差估计的正确说法有( )A .是样本自协方差的有偏估计量,()()∑-=+--=k N k k t t k y y y y N11ˆγ是样本自协方差的无偏估计量()()∑-=+---=kN k k t t k y y y y k N 1*1ˆγB .利用构造的自协方差矩阵是非负定的()()∑-=+--=k N k k t t k y y y y N 11ˆγC .利用构造的自协方差矩阵是非负定的()()∑-=+---=k N k k t tk y y y y k N 1*1ˆγD .常常用作为样本自协方差统计量k γˆE .是自协方差的无偏估计量;则是自协方差的渐进无偏估计量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3-17解:(1)判断该序列的平稳性与纯随机性。
1)根据题中所列数据,绘制该序列的时序图,如图3-17-1所示。
图3-17-1:某城市过去63年中每年降雪量时序图其中x表示每年降雪量。
时序图显示某城市过去每年降雪量始终围绕在80.3mm附近随机波动,没有明显的趋势或周期性,基本可视为平稳序列。
2)自相关图检验。
如图3-17-2所示。
图3-17-2:样本自相关图样本自相关图显示延迟2阶之后,该序列的自相关系数都落入2倍标准误之内,而且自相关系数在零值附近波动,是典型的短期相关自相关图。
由时序图和样本自相关图的性质,可以认为该序列为平稳序列。
α=,检验结果见表3-17-1。
3)纯随机性检验(0.05)表3-17-1:纯随机性检验结果<,认为该序列为检验结果显示,在6阶延迟下LB检验统计量的P值0.05非白噪声序列。
(2)拟合模型1)模型识别。
根据样本自相关图、偏自相关图对模型进行直接识别。
由(1)可知,该序列在6阶延迟下平稳且非白噪声,已知样本自相关图,即图3-17-2所示,偏自相关图如下图所示。
图3-17-3:样本偏自相关图而该序列的图像并不能直接识别出较为准确的模型,因此进一步利用SAS对模型进行最优模型定阶,结果如图3-17-4所示:图3-17-4:最小信息量结果最后一条信息显示,在自相关延迟系数小于等于5,移动平均延迟系数也小于等于5的所有ARMA(p,q)模型中,BIC信息量相对最小的是ARMA(1,0)模型,即AR(1)模型。
2)参数估计。
先利用SAS输出未知参数估计结果,如下表所示。
表3-17-2:未知参数估计结果3)模型检验。
利用SAS,残差序列白噪声检验结果如下表所示。
表3-17-3:残差自相关检验结果残差白噪声检验显示延迟6阶、12阶、18阶、24阶LB 检验统计量的P 值均显著大于0.05,所以该AR(1)模型显著有效。
参数显著性检验结果(见表3-17-2)显示两个参数t 统计量的P 值均小于0.05,即两个参数均显著。
因此AR(1)模型是该序列的有效拟合模型。
拟合模型的具体形式。
利用SAS ,拟合模型的具体形式如下图所示。
图3-17-5:拟合模型形式该输出形式等价于180.99410.31587.t t t x x ε-=-+(3)预测该城市未来5年的降雪量。
根据观察值数据和(2)中得到的拟合模型,利用SAS 对序列进行短期预测,输出结果如下图所示。
图3-17-6:未来5年的预测结果根据观察值数据和预测结果,利用SAS 绘制拟合预测图,如下图所示。
图3-17-7:拟合预测图【程序】data zuoye3_17;input x@@;time=_n_;cards;126.4 82.4 78.1 51.1 90.9 76.2 104.5 87.4110.5 25 69.3 53.5 39.8 63.6 46.7 72.979.6 83.6 80.7 60.3 79 74.4 49.6 54.771.8 49.1 103.9 51.6 82.4 83.6 77.8 79.389.6 85.5 58 120.7 110.5 65.4 39.9 40.188.7 71.4 83 55.9 89.9 84.8 105.2 113.7124.7 114.5 115.6 102.4 101.4 89.8 71.5 70.998.3 55.5 66.1 78.4 120.5 97 110;proc gplot data=zuoye3_17;plot x*time;symbol i=jion c=black v=star;proc arima data=zuoye3_17;identify var=x nlag=6minic p= (0:5) q= (0:5);estimate p=1;forecast lead=5id=time out=results;proc gplot data=results;plot x*time=1 forecast*time=2 l95*time=3 u95*time=3/overlay; symbol1c=black i=none v=star;symbol2c=red i=jion v=none;symbol3c=green i=jion v=none l=25;run;3-19解:(1)判断该序列的平稳性与纯随机性。
1)根据题中所列数据,绘制该序列的时序图,如图3-19-1所示。
图3-19-1:现有201个连续生产记录时序图其中x表示生产记录数据。
时序图显示现有的201个连续生产记录始终围绕84.1194附近随机波动,没有明显的趋势或周期性,基本可视为平稳序列。
2)自相关图检验。
如图3-19-2所示。
图3-19-2:样本自相关图样本自相关图显示延迟1阶之后,该序列的自相关系数都落入2倍标准误之内,而且自相关系数在零值附近波动,是典型的短期相关自相关图。
由时序图和样本自相关图的性质,可以认为该序列为平稳序列。
α=,检验结果见表3-19-1。
3)纯随机性检验(0.05)表3-19-1:纯随机性检验结果检验结果显示,在6阶、12阶、18阶、24阶延迟下LB检验统计量的P值 ,认为该序列为非白噪声序列。
0.05(2)拟合模型1)模型识别。
根据样本自相关图、偏自相关图对模型进行直接识别。
由(1)可知,该序列在6阶、12阶、18阶、24阶延迟下均平稳且非白噪声,已知样本自相关图,即图3-19-2所示,偏自相关图如下图所示。
图3-19-3:样本偏自相关图由样本自相关图和偏自相关图可知,自相关系数1阶截尾,偏自相关系数拖尾,可以初步确定拟合模型为MA(1)模型。
为了拟合出较为有效的模型,进一步利用SAS对模型进行最优模型定阶,结果如图3-19-4所示:图3-19-4:最小信息量结果最后一条信息显示,在自相关延迟系数小于等于6,移动平均延迟系数也小于等于6的所有ARMA(p,q)模型中,BIC信息量相对最小的是ARMA(0,1)模型,即MA(1)模型。
2)参数估计。
先利用SAS输出未知参数估计结果,如下表所示。
表3-19-2:未知参数估计结果3)模型检验。
利用SAS ,残差序列白噪声检验结果如下表所示。
表3-19-3:残差自相关检验结果残差白噪声检验显示延迟6阶、12阶、18阶、24阶、30阶、36阶LB 检验统计量的P 值均显著大于0.05,所以该MA(1)模型显著有效。
参数显著性检验结果(见表3-19-2)显示两个参数t 统计量的P 值均远小于0.05,即两个参数均显著。
因此MA(1)模型是该序列的有效拟合模型。
4)拟合模型的具体形式。
利用SAS ,拟合模型的具体形式如下图所示。
图3-19-5:拟合模型形式该输出形式等价于184.128890.47959.t t t x εε-=+-(3)预测该序列下一时刻95%的置信区间。
根据观察值数据和(2)中得到的拟合模型,利用SAS 对序列进行预测,输出结果如下图所示。
图3-19-6:下一时刻的预测结果由输出结果可知下一时刻95%的置信区间为(80.4131,90.9580)。
【程序】data zuoye3_19;input x@@;time=_n_;cards;81.9 89.4 79.0 81.4 84.8 85.9 88.0 80.3 82.6 83.5 80.2 85.2 87.2 83.5 84.3 82.9 84.7 82.9 81.5 83.4 87.7 81.8 79.6 85.8 77.9 89.7 85.4 86.3 80.7 83.8 90.5 84.5 82.4 86.7 83.0 81.8 89.3 79.3 82.7 88.0 79.6 87.8 83.6 79.5 83.3 88.4 86.6 84.6 79.7 86.0 84.2 83.0 84.8 83.6 81.8 85.9 88.2 83.5 87.2 83.7 87.3 83.0 90.5 80.7 83.1 86.5 90.0 77.5 84.7 84.6 87.2 80.5 86.1 82.6 85.4 84.7 82.8 81.9 83.6 86.8 84.084.2 82.8 83.0 82.0 84.7 84.4 88.9 82.4 83.085.0 82.2 81.6 86.2 85.4 82.1 81.4 85.0 85.8 84.2 83.5 86.5 85.0 80.4 85.7 86.7 86.7 82.3 86.4 82.5 82.0 79.5 86.7 80.5 91.7 81.6 83.9 85.6 84.8 78.4 89.9 85.0 86.2 83.0 85.4 84.4 84.5 86.2 85.6 83.2 85.7 83.5 80.1 82.2 88.6 82.0 85.0 85.2 85.3 84.3 82.3 89.7 84.8 83.1 80.6 87.4 86.8 83.5 86.2 84.1 82.3 84.8 86.6 83.5 78.1 88.8 81.9 83.3 80.0 87.2 83.3 86.6 79.5 84.1 82.2 90.8 86.5 79.7 81.0 87.2 81.6 84.4 84.4 82.2 88.9 80.9 85.1 87.1 84.0 76.5 82.7 85.1 83.3 90.4 81.0 80.3 79.8 89.0 83.7 80.9 87.3 81.1 85.6 86.6 80.0 86.6 83.3 83.1 82.3 86.7 80.2;proc gplot data=zuoye3_19;plot x*time;symbol i=jion c=black v=star;proc arima data=zuoye3_19;identify var=x minic p= (0:7) q= (0:7);estimate q=1;forecast lead=1id=time out=results;proc gplot data=results;plot x*time=1 forecast*time=2 l95*time=3 u95*time=3/overlay; symbol1c=black i=none v=star;symbol2c=red i=jion v=none;symbol3c=green i=jion v=none l=25;run;。
