函数之平面直角坐标系知识点
平面直角坐标系与函数的概念
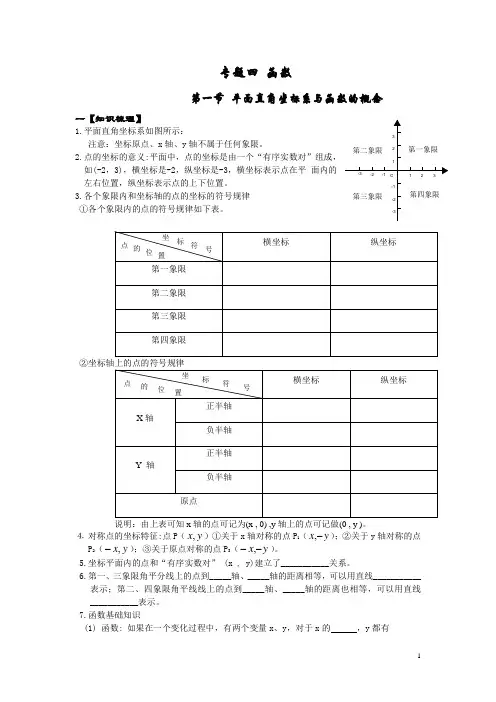
专题四 函数第一节 平面直角坐标系与函数的概念一【知识梳理】1.平面直角坐标系如图所示:注意:坐标原点、x 轴、y 轴不属于任何象限。
2.点的坐标的意义:平面中,点的坐标是由一个“有序实数对”组成,如(-2,3),横坐标是-2,纵坐标是-3,横坐标表示点在平 面内的左右位置,纵坐标表示点的上下位置。
3.各个象限内和坐标轴的点的坐标的符号规律①各个象限内的点的符号规律如下表。
说明:由上表可知x 轴的点可记为(x , 0) ,y 轴上的点可记做(0 , y )。
⒋ 对称点的坐标特征:点P (y x ,)①关于x 轴对称的点P 1(y x -,);②关于y 轴对称的点P 2(y x ,-);③关于原点对称的点P 3(y x --,)。
5.坐标平面内的点和“有序实数对” (x , y)建立了___________关系。
6.第一、三象限角平分线上的点到_____轴、_____轴的距离相等,可以用直线___________表示;第二、四象限角平线线上的点到_____轴、_____轴的距离也相等,可以用直线___________表示。
7.函数基础知识(1) 函数: 如果在一个变化过程中,有两个变量x 、y ,对于x 的 ,y 都有与之对应,此时称y是x的,其中x是自变量,y 是.(2)自变量的取值范围:①使函数关系式有意义;②在实际问题的函数式中,要使实际问题有意义。
(3)常量:在某变化过程中的量。
变量:在某变化过程中的量。
(4) 函数的表示方法:①;②;③。
能力培养:从图像中获取信息的能力;用函数来描述实际问题的数学建模能力。
二【巩固练习】1. 点P(3,-4)关于y轴的对称点坐标为_______,它关于x轴的对称点坐标为_______.它关于原点的对称点坐标为_____.2.龟兔赛跑,它们从同一地点同时出发,不久兔子就把乌龟远远地甩在后面,于是兔子便得意洋洋地躺在一棵大树下睡起觉来.乌龟一直在坚持不懈、持之以恒地向终点跑着,兔子一觉醒来,看见乌龟快接近终点了,这才慌忙追赶上去,但最终输给了乌龟.下列图象中能大致反映龟兔行走的路程S随时间t变化情况的是( ).3.如图,所示的象棋盘上,若○帅位于点(1,-2)上,○相位于点(3,-2)上,则○炮位于点()A.(-1,1)B.(-1,2)C.(-2,1)D.(-2,2)4.如果点M(a+b,ab)在第二象限,那么点N(a,b)在()A.第一象限B.第二象限C.第三象限D.第四象限5.图中的三角形是有规律地从里到外逐层排列的.设y为第n层(n为正整数)三角形的个数,则下列函数关系式中正确的是().A、y=4n-4B、y=4nC、y=4n+4D、y=n26.函数13xyx+=-中自变量x的取值范围是()A.x≥1-B.x≠3 C.x≥1-且x≠3 D.1x<-7.如图,方格纸上一圆经过(2,5),(-2,l),(2,-3),( 6,1)四点,则该圆的圆心的坐标为()A.(2,-1)B.(2,2)C.(2,1) D.(3,l)8.右图是韩老师早晨出门散步时,离家的距离y与时间x的函数图象.若用黑点表示韩老师家的位置,则韩老师散步行走的路线可能是()图3相帅炮9.已知M(3a -9,1-a)在第三象限,且它的坐标都是整数,则a 等于( )A .1B .2C .3D .010.如图, △ABC 绕点C 顺时针旋转90○后得到△A ′B ′C ′, 则A 点的对应点A ′点的坐标是( )A .(-3,-2);B .(2,2);C .(3,0);D .(2,l )11.在平面直角坐标系中,点(34)P -,到x 轴的距离为( )A.3 B.3- C.4 D.4-12.线段CD 是由线段AB 平移得到的。
第9讲 平面直角坐标系与函数

度或函数增减性的变化规律.
[变式5] (2022武汉)匀速地向一个容器内注水,最后把容器注满.在注水过程中,水面高度h随时间t的
变化规律如图所示(图中O-A-B-C为一折线).这个容器的形状可能是(
A
B
C
D
)
A
1
(1)点的对称规律:关于横(或纵)轴对称的点,横(或纵)坐标不变,纵(或横)坐标变号;关于原点对称,
则横、纵坐标都变号.
(2)点的平移规律:左右移,纵不变,横减加;上下移,横不变,纵加减.
(3)有时需要根据点在坐标系中的位置,建立不等式(组)或方程(组),把点的坐标问题转化为不等式
(组)或方程(组)的问题解决.
D.若x-y=0,则点P(x,y)一定在第一、第三象限角平分线上
3.(2022雅安)在平面直角坐标系中,点(a+2,2)关于原点的对称点为(4,-b),则ab的值为(
A.-4
B.4
C.12
D.-12
D)
4.小明从家到学校,先匀速步行到车站,等了几分后坐上了公交车,公交车沿着公路匀速行驶一段时间
后到达学校,小明从家到学校行驶路程s(m)与时间t(min)的大致图象是(
停止.若点 P 的运动速度为 1 cm/s,设点 P 的运动时间为 t(s),AP 的长度为 y(cm),y 与 t 的函数图象
如图②所示.则当 AP 恰好平分∠BAC 时,t 的值为
①
②
2 +2
.
1.(2022常州)在平面直角坐标系xOy中,点A与点A1关于x轴对称,点A与点A2关于y轴对称.已知点
2
A-D-C 向终点 C 运动,设点 Q 的运动时间为 x(s),△APQ 的面积为 y(cm ),若 y 与 x 之间的函数关系的
初三数学函数与平面直角坐标系5大考点总结

初三数学函数与平面直角坐标系5大考点总结考纲要求:1、会画平面直角坐标系,并能根据点的坐标描出点的位置,由点的位置写出点的坐标。
2、掌握坐标平面内点的坐标特征。
3、了解函数的有关概念和函数的表示方法,并能结合图象对实际问题中的函数关系进行分析.4、能确定函数自变量的取值范围,并会求函数值。
一、平面直角坐标系与点的坐标特征1.平面直角坐标系如图,在平面内,两条互相垂直的数轴的交点O称为原点,水平的数轴叫__________,竖直的数轴叫__________,整个坐标平面被x轴、y轴分割成四个象限.二、距离与点的坐标的关系1.点与原点、点与坐标轴的距离点P(x,y)到x轴和y轴的距离分别是|y|和|x|,点P(x,y)到坐标原点的距离为三、函数有关的概念及图像四、函数自变量取值范围的确定确定自变量取值范围的方法:考点一、平面直角坐标系内点的坐标特征方法总结:解这类题的关键是明确各象限内点的坐标特征,总结规律,再结合规律列出不等式(组)求解考点二、图形的变换与坐标方法总结:在平面直角坐标系中,图形的平移、对称、旋转等变换会引起坐标的变化,同样,坐标的变化也会引起图形的变换,两者紧密结合充分体现了数形结合的思想.考点三、函数的概念考点四、函数图像的应用方法总结:利用函数关系和图像分析解决实际问题,要透过问题情境准确地寻找出问题的自变量和函数,要看清横坐标和纵坐标表示的是哪两个变量,探求变量和函数之间的变化趋势,仔细观察图像(直线或曲线)的“走势”特点,合理地分析变化过程,准确地结合图像解决实际问题.考点五、函数自变量取值范围的确定方法总结:自变量的取值必须使含自变量的代数式有意义主要体现在以下几种:含自变量的解析式是整式:自变量的取值范围是全体实数;含自变量的解析式是分式:自变量的取值范围是使得分母不为0的实数;含自变量的解析式是二次根式:自变量的取值范围是使被开方式为非负的实数;含自变量的解析式既是分式又是二次根式时:自变量的取值范围是它们的公共解,一般列不等式组求解;当函数解析式表示实际问题时:自变量的取值必须使实际问题有意义.写在最后:中考数学冲刺阶段的复习,不管的大题还是选择填空这类型的小题,都是非常考验基础的牢固性,只有坚实的基础,加上实用的技巧,拿到高分,冲刺才有实际的意义。
平面直角坐标系与函数

析 已: 知 点 (3 - m , m - 1) 在 第 二 象 限 , 所 以 方法点析 解决此类问题的一般方法是根据点在 , 3-m<0 m>3, 坐标系中的符号特征,建立不等式 (组)或者方 故 ∴m>3,故选择 A. (组)或方程 程 ( 组 ) ,把点的问题转化为不等式 m-1>0, m>1, (组)来解决.
x<0,y<0 点 P(x, y)在第三象限⇔________________ x>0,y<0 点 P(x, y)在第四象限⇔________________
(2)坐标轴上点的坐标的特征
y=0,x为任意实数 点 P(x, y)在 x 轴上⇔__________________
x=0,y为任意实数 点 P(x, y)在 y 轴上⇔__________________
考点聚焦 归类探究 回归教材
作业:
《复习指导用书》
21
[点析] 根据函数图像,结合实际生活意义,对图像 进行分析判断即可得解.
19
考点聚焦
归类探究
回归教材
平面直角坐标系与函数
中考预测:看图说故事.请你编写一个故事,使故事情 境中出现的一对变量 x,y 满足如图所示的函数关系,要求: ①指出变量 x 和 y 的含义;②利用图中的数据说明这对变量 变化过程的实际意义,其中必须涉及“速度”这个量.
3
考点聚焦
归类探究
回归教材
平面直角坐标系与函数
考点3 点到坐标轴或原点的距离
到 x 轴 点 P(a,b)到 x 轴的距离等于点 P 的 b 纵坐标的绝对值 ,即 的距离 ___________________ 到 y 轴 点 P(a,b)到 y 轴的距离等于点 P 的 横坐标的绝对值 ,即 a 的距离 ___________________ 到原点 点 P(a, b)到原点的距离 的距离
初三函数知识点总结

初三函数知识点总结一一、平面直角坐标系1.各象限内点的坐标的特点2.坐标轴上点的坐标的特点3.关于坐标轴、原点对称的点的坐标的特点4.坐标平面内点与有序实数对的对应关系二、函数1.表示方法:⑴解析法;⑵列表法;⑶图象法。
2.确定自变量取值范围的原则:⑴使代数式有意义;⑵使实际问题有意义。
3.画函数图象:⑴列表;⑵描点;⑶连线。
三、几种特殊函数(定义→图象→性质)1. 正比例函数⑴定义:y=kx(k≠0) 或y/x=k。
⑵图象:直线(过原点)⑶性质:①k>0,…②k<0,…2. 一次函数⑴定义:y=kx+b(k≠0)⑵图象:直线过点(0,b)—与y轴的交点和(-b/k,0)—与x轴的交点。
⑶性质:①k>0,…②k<0,…⑷图象的四种情况:3. 二次函数⑴定义:特殊地,都是二次函数。
⑵图象:抛物线(用描点法画出:先确定顶点、对称轴、开口方向,再对称地描点)。
用配方法变为,则顶点为(h,k);对称轴为直线x=h;a>0时,开口向上;a<0时,开口向下。
⑶性质:a>0时,在对称轴左侧…,右侧…;a<0时,在对称轴左侧…,右侧…。
4.反比例函数⑴定义:或xy=k(k≠0)。
⑵图象:双曲线(两支)—用描点法画出。
⑶性质:①k>0时,图象位于…,y随x…;②k<0时,图象位于…,y随x…;③两支曲线无限接近于坐标轴但永远不能到达坐标轴。
四、重要解题方法1. 用待定系数法求解析式(列方程[组]求解)。
对求二次函数的解析式,要合理选用一般式或顶点式,并应充分运用抛物线关于对称轴对称的特点,寻找新的点的坐标。
如下图:2.利用图象一次(正比例)函数、反比例函数、二次函数中的k、b;a、b、c的符号。
初三函数知识点总结二轴对称二次函数图像是轴对称图形。
对称轴为直线对称轴与二次函数图象唯一的交点为二次函数图象的顶点P。
特别地,当b=0时,二次函数图象的对称轴是y轴(即直线x=0)。
中考复习——平面直角坐标系、一次函数、反比例函数及其图象 知识点汇总及典例分析

中考复习——平面直角坐标系、一次函数、反比例函数【知识梳理】一、平面直角坐标系1. 坐标平面上的点与 有序实数对 构成一一对应;2. 各象限点的坐标的符号;3. 坐标轴上的点的坐标特征.4. 点P (a ,b )关于x 轴对称的点的坐标为 ;关于y 轴对称的点的坐标为 ;关于原点对称的点的坐标为5.两点之间的距离二、函数的概念1.概念:在一个变化过程中有两个变量x 与y ,如果对于x 的每一个值,y 都有 的值与它对应,那么就说x 是自变量,y 是x 的函数.2.自变量的取值范围: (1)使解析式 (2)实际问题具有 意义3.函数的表示方法; (1) (2) (3) 三、一次函数的概念、图象、性质1.正比例函数的一般形式是 ( ),一次函数的一般形式是 (k≠0). 2. 一次函数y kx b =+的图象是经过( , )和( , )两点的一条直线.4.若两个一次函数解析式中,k 相等,表示两直线 ;若两直线垂直,则 。
5.的大小决定直线的倾斜程度,越大,直线越 ;四、反比例函数的概念、图象、性质1.反比例函数:一般地,如果两个变量x 、y 之间的关系可以表示成y = 或 或 (k 为常数,k≠0)的形式,那么称y 是x 的反比例函数. 2. 反比例函数的图象和性质k >0,b >0k >0,b <0k <0,b >0k <0,21212211P P )0()0()2(y y y P y P -=, ,,,21212211P P )0()0()1(x x x P x P -=, , ,, 3.k 的几何含义:反比例函数y =k x(k≠0)中比例系数k 的几何意义,即过双曲线y =k x(k≠0)上任意一点P 作x 轴、y 轴垂线,设垂足分别为A 、B ,则所得矩形OAPB 的面积为 。
【例题精讲】 例1.函数22y x =-中自变量x 的取值范围是 ;函数y =x 的取值范围是 .例2.已知点(13)A m -,与点(21)B n +,关于x 轴对称,则m = ,n = . 例3.如图,在平面直角坐标系中,点A 的坐标是(10,0),点B 的 坐标为(8,0),点C 、D 在以OA 为直径的半圆M 上,且四边形OCDB 是平行四边形,点C 的坐标为例4.一次函数y=(3a+2)x -(4-b),求满足下列条件的a 、b 的取值范围。
第1部分 第10讲 平面直角坐标系与函数
孙老师说,杨蕙心学习效率很高,认真执行老师 的复习要求,往往一个小时能完成别人两三个小 时的作业量,而且计划性强,善于自我调节。此 外,学校还有一群与她实力相当的同学,他们经 常在一起切磋、交流,形成一种良性的竞争氛围。
谈起自己的高考心得,杨蕙心说出了“听话” 两个字。她认为在高三冲刺阶段一定要跟随老师 的脚步。“老师介绍的都是多年积累的学习方法, 肯定是最有益的。”高三紧张的学习中,她常做 的事情就是告诫自己要坚持,不能因为一次考试 成绩就否定自己。高三的几次模拟考试中,她的 成绩一直稳定在年级前5名左右。
(1)第一、三象限的角平分线上的点的横坐标与纵
象限角平分线上 坐标⑧___相__等_____;
的点的坐标特征 (2)第二、四象限的角平分线上的点的横坐标与纵
坐标⑨__互__为__相__反__数______
平行于坐标轴的
直线上点的坐标 特征
(1)平行于 x 轴的直线上的点的⑩__纵___坐标相等; (2)平行于 y 轴的直线上的点的⑪_横_____坐标相等
高考总分:711分 毕业学校:北京八中 语文139分 数学140分 英语141分 理综291分 报考高校: 北京大学光华管理学院
北京市理科状元杨蕙心
班主任 孙烨:杨蕙心是一个目标高远 的学生,而且具有很好的学习品质。学 习效率高是杨蕙心的一大特点,一般同 学两三个小时才能完成的作业,她一个 小时就能完成。杨蕙心分析问题的能力 很强,这一点在平常的考试中可以体现。 每当杨蕙心在某科考试中出现了问题, 她能很快找到问题的原因,并马上拿出 解决办法。
第 14 页
②如答图 2,当点 D 在边 PN 上时, ∵∠N=45°,CD=2, ∴CN=CD=2, ∴CM=6-2=4,即此时 x=4. 当 2<x≤4 时,如答图 3,矩形 ABCD 与△PMN 重叠部分是四边形 EMCD,过 点 E 作 EF⊥MN 于点 F, ∴EF=MF=2,∴ED=CF=x-2, ∴y=S 梯形 EMCD=12CD·(DE+CM) =12×2×(x-2+x)=2x-2;
(完整版)初中函数知识点总结
任何一元一次方程到可以转化为ax+b=0(a,b为常数,a≠0)的形式,所以解一元一次方程可以转化为:当某个一次函数的值为0时,求相应的自变量的值. 从图象上看,相当于已知直线y=ax+b确定它与x轴的交点的横坐标的值.
10、一次函数与一元一次不等式的关系
任何一个一元一次不等式都可以转化为ax+b>0或ax+b<0(a,b为常数,a≠0)的形式,所以解一元一次不等式可以看作:当一次函数值大(小)于0时,求自变量的取值范围.
取值范围:① k ≠ 0; ②在一般的情况下 , 自变量 x 的取值范围可以是 不等于0的任意实数 ; ③函数 y 的取值范围也是任意非零实数。
反比例函数的图像属于以原点为对称中心的中心对称的双曲线
反比例函数图像中每一象限的每一支曲线会无限接近X轴Y轴但不会与坐标轴相交(K≠0)。
反比例函数的性质:
注:对于y=kx+b 而言,图象共有以下四种情况:
1、k>0,b>0 2、k>0,b<0 3、k<0,b<0 4、k<0,b>0
4、直线y=kx+b(k≠0)与坐标轴的交点.
(1)直线y=kx与x轴、y轴的交点都是(0,0);
(2)直线y=kx+b与x轴交点坐标为 与 y轴交点坐标为(0,b).
5、用待定系数法确定函数解析式的一般步骤:
(1)根据已知条件写出含有待定系数的函数关系式;
(2)将x、y的几对值或图象上的几个点的坐标代入上述函数关系式中得到以待定系数为未知数的方程;
(3)解方程得出未知系数的值;
(4)将求出的待定系数代回所求的函数关系式中得出所求函数的解析式.
中考总复习数学10-第一部分 第10讲 平面直角坐标系与函数
返回题型清单
返回栏目导航ຫໍສະໝຸດ 3.(2022·石家庄国际学校模拟)如图,直线a⊥b,若以平行于a的直线为x轴,以
平行于b的直线为y轴,建立平面直角坐标系,若A(-3,2),B(2,-3),则坐标系的
原点最有可能是( B )
A.O1
B.O2
C.O3
D.O4
1
2
3
4
第10讲
平面直角坐标系与函数— 题型突破
返回题型清单
和分类讨论思想是解答本题的关键.尤其是实际背景下的
函数问题,如果涉及分段函数,需要根据自变量的不同取值
范围分类进行求解,还需要关注函数与方程(不等式)的联系.
1
2
3
4
5
第10讲
平面直角坐标系与函数— 题型突破
返回题型清单
返回栏目导航
3.(2022·石家庄新华区模拟)用max , 表示a,b两数中较大的数,如
标公式为
x +x y1+y2
,
(如图③).
第10讲
平面直角坐标系与函数— 考点梳理
返回思维导图
返回栏目导航
考点 2 函数及其自变量取值范围
1.函数的相关概念
(1)变量:在某一变化过程中可以取不同数值的量.
(2)常量:在某一变化过程中保持相同数值的量.
(3)函数:一般地,在一个变化过程中如果有两个变量x和y,并且对于x的每一
值范围,根据函数关系式的特点来确定正确的函数图象.
1
2
3
4
5
第10讲
平面直角坐标系与函数— 题型突破
拔高追问
返回题型清单
返回栏目导航
当x等于何值时,函数值y最大?
初二数学函数知识点总结
初二数学《函数》知识点总结(一)平面直角坐标系1、定义:平面上互相垂直且有公共原点的两条数轴构成平面直角坐标系,简称为直角坐标系2、已知点的坐标找出该点的方法:分别以点的横坐标、纵坐标在数轴上表示的点为垂足,作x 轴y 轴的的垂线,两垂线的交点即为要找的点。
3、已知点求出其坐标的方法:由该点分别向x 轴y 轴作垂线,垂足在x 轴上的坐标是改点的横坐标,垂足在y 轴上的坐标是该点的纵坐标。
4、各个象限内点的特征:第一象限:(+,+) 点P (x,y ),则x >0,y >0;第二象限:(-,+) 点P (x,y ),则x <0,y >0;第三象限:(-, -) 点P (x,y ),则x <0,y <0;第四象限:(+,-) 点P (x,y ),则x >0,y <0;5、坐标轴上点的坐标特征:x 轴上的点,纵坐标为零;y 轴上的点,横坐标为零;原点的坐标为(0 , 0)。
两坐标轴的点不属于任何象限。
6、点的对称特征:已知点P(m,n),关于x 轴的对称点坐标是(m,-n), 横坐标相同,纵坐标反号关于y 轴的对称点坐标是(-m,n) 纵坐标相同,横坐标反号关于原点的对称点坐标是(-m,-n) 横,纵坐标都反号7、平行于坐标轴的直线上的点的坐标特征:平行于x 轴的直线上的任意两点:纵坐标相等;平行于y 轴的直线上的任意两点:横坐标相等。
8、各象限角平分线上的点的坐标特征:第一、三象限角平分线上的点横、纵坐标相等。
点P(a,b)关于第一、三象限坐标轴夹角平分线的对称点坐标是(b, a)第二、四象限角平分线上的点横纵坐标互为相反数。
点P(a,b)关于第二、四象限坐标轴夹角平分线的对称点坐标是(-b,-a)9、点P (x,y )的几何意义:点P (x,y )到x 轴的距离为 |y|,点P (x,y )到y 轴的距离为 |x|。
点P (x,y )到坐标原点的距离为22y x10、两点之间的距离:X 轴上两点为A )0,(1x 、B )0,(2x |AB|||12x x -=Y 轴上两点为C ),0(1y 、D ),0(2y |CD|||12y y -=已知A ),(11y x 、B ),(22y x AB|=212212)()(y y x x -+-11、中点坐标公式:已知A ),(11y x 、B ),(22y x M 为AB 的中点则:M=(212x x + , 212y y +) 12、点的平移特征: 在平面直角坐标系中,将点(x,y )向右平移a 个单位长度,可以得到对应点( x-a ,y );将点(x,y )向左平移a 个单位长度,可以得到对应点(x+a ,y );将点(x,y )向上平移b 个单位长度,可以得到对应点(x ,y +b );将点(x,y )向下平移b 个单位长度,可以得到对应点(x ,y -b )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【解析】
【分析】
根据点P(m-3,m+1)在第二象限及第二象限内点的符号特点,可得一个关于m的不等式组,解不等式组即可得m的取值范围.
【详解】
解:∵点P(m-3,m+1)在第二象限,
∴可得到: ,
解得: ,
∴m的取值范围为 ,
故选:C.
【点睛】
本题考查了坐标在象限内的符号,以及不等式组的解法,属于基础题.
∵ ,
∴第2020次相遇地点的坐标为(-1,1);
故选D.
【点睛】
本题主要考查了规律型:点的坐标,掌握甲乙运动相遇时点坐标的规律是解题的关键.
17.已知点P位于y轴右侧,距y轴3个单位长度,位于x轴上方,距离x轴4个单位长度,则点P坐标是( )
A.(3,4)B.(-3,4)C.(-4,3)D.(4,3)
【答案】D
【解析】
【分析】
利用行程问题中的相遇问题,由于长方形的边长为4和2,物体乙是物体甲的速度的2倍,求得每一次相遇的地点,找出规律即可解答;
【详解】
∵A(2,0),四边形BCDE是长方形,
∴B(2,1),C(-2,1),D(-2,-1),E(2,-1),
∴BC=4,CD=2,
∴长方形BCDE的周长为 ,
【答案】A
【解析】
【分析】
根据点到x轴的距离是纵坐标的绝对值,到y轴的距离是横坐标的绝对值,结合第四象限点(+,-),可得答案.
【详解】
解:若点P在第四象限,且点P到x轴的距离为1,到y轴的距离为3,则点的坐标为(3,-1),
故选:A.
【点睛】
本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
【详解】
解:如图,过点C作CE⊥y轴于点E,
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∴∠ABO+∠CBE=90°,
∵∠ABO+∠BAO=90°,
∴∠CBE=∠BAO,
在△ABO和△BCE中,
5.如图,正方形ABCD的边长为4,点A的坐标为(-1,1),AB平行于x轴,则点C的坐标为( )
A.(3,1)B.(-1,1)C.(3,5)D.(-1,5)
【答案】C
【解析】
解:∵正方形ABCD的边长为4,点A的坐标为(﹣1,1),AB平行于x轴,∴点B的横坐标为:﹣1+4=3,纵坐标为:1,∴点B的坐标为(3,1),∴点C的横坐标为:3,纵坐标为:1+4=5,∴点C的坐标为(3,5).故选C.
∵452=2025,45是奇数,
∴第2025个点是(45,0),
第2019个点是(45,6),
所以,第2019个点的纵坐标为6.
故选:B.
【点睛】
本题考查了点的坐标,观察出点个数与横坐标的存在的平方关系是解题的关键.
7.已知直线 与直线 的交点在第四象限,则m的取值范围是( )
A. B. C. D.
8.平面直角坐标系中,P(-2a-6,a-5)在第三象限,则a的取值范围是()
A.a>5B.a<-3C.-3≤a≤5D.-3<a<5
【答案】D
【解析】
【分析】
根据第三象限的点的坐标特点:x<0,y<0,列不等式组,求出a的取值范围即可.
【详解】
∵点P在第三象限,
∴ ,
解得:-3<a<5,
故选D.
【点睛】
∴AB平行于x轴,AB=﹣4﹣(﹣8)=4.
故选A.
2.若点P(x,y)在第三象限,且点P到x轴的距离为3,到y轴的距离为2,则点P的坐标是( )
A.(-2,3) B.(-2,-3) C.(2,-3) D.(2,3)
【答案】B
【解析】【分析】根据点P到x轴的距离为3,则这一点的纵坐标是3或-3,到y轴的距离为2,那么它的横坐标是2或-2,再根据点P所处的象限即可确定点P的坐标.
10.在平面直角坐标系中,以原点为中心,把点 逆时针旋转 ,得到点 ,则点 的坐标为( )
A. B. C. D.
【答案】B
【解析】
【分析】
根据中心对称的性质解决问题即可.
【详解】
由题意A,B关于O中心对称,
∵A(2,3),
∴B(-2,-3),
故选:B.
【点睛】
此题考查中心对称,坐标与图形的变化,解题的关键是熟练掌握基本知识,属于中考常考题型.
16.如图所示,长方形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿长方形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位长度秒匀速运动,物体乙按顺时针方向以2个单位长度秒匀速运动,则两个物体运动后的第2020次相遇点的坐标是( )
A.(2,0)B.(-1,-1)C.( -2,1)D.(-1,1)
A. B. C. D.
【答案】C
【解析】
【分析】
设第n次跳动至点Pn,根据部分点An坐标的变化找出变化规律“P4n(n+1,2n),P4n+1(n+1,2n+1),P4n+2(−n−1,2n+1),P4n+3(−n−1,2n+2)”,依此规律结合2019=504×4+3即可得出点P2019的坐标.
【详解】
【答案】A
【解析】
【分析】
先根据点P(a,b)在第二象限判断出a<0,b>0,据此可得1﹣a>0,从而得出答案.
【详解】
∵若点P(a,b)在第二象限,
∴a<0,b>0,
则1﹣a>0,
∴点Q(b,1-a)所在象限应该是第一象限,
故选:A.
【点睛】
本题是象限的考查,解题关键是判断横、纵坐标的正负
14.在平面直角坐标系中,点P(-3,4)到x轴的距离为( )
本题考查了象限点的坐标的符号特征以及解不等式,该知识点是中考的常考点,常与不等式、方程结合起来求一些字母的取值范围,比如本题中求a的取值范围.
9.如图,在平面直角坐标系上有个点 ,点 第1次向上跳动1个单位至点 ,紧接着第2次向左跳动2个单位至点 ,第3次向上跳动1个单位到达 ,第4次向右跳动3个单位到达 ,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此规律跳动下去,点 的坐标为().
【详解】
解:根据图形,以最外边的矩形边长上的点为准,点的总个数等于x轴上右下角的点的横坐标的平方,
例如:右下角的点的横坐标为1,共有1个,1=12,
右下角的点的横坐标为2时,共有4个,4=22,
右下角的点的横坐标为3时,共有9个,9=32,
右下角的点的横坐标为4时,共有16个,16=42,
…
右下角的点的横坐标为n时,共有n2个,
∵∠C=90°,
∴AC= ,
∵ ,
∴8×6=10CD,
∴CD=4.8,
∴OD= ,
∴ 点的坐标是 .
故选A.
【点睛】
本题考查了图形与坐标的性质,勾股定理,以及面积法求线段的长,根据面积法求出CD的长是解答本题的关键.
13.若点P(a,b)在第二象限,则点Q(b,1﹣a)所在象限应该是()
A.第一象限B.第二象限C.第三象限D.第四象限
设第n次跳动至点Pn,
观察发现:P(1,0),P1(1,1),P2(−1,1),P3(−1,2),P4(2,2),P5(2,3),P6(−2,3),P7(−2,4),P8(3,4),P9(3,5),…,
∴P4n(n+1,2n),P4n+1(n+1,2n+1),P4n+2(−n−1,2n+1),P4n+3(−n−1,2n+2)(n为自然数).
【答案】A
【解析】
【分析】
根据题意,P点应在第一象限,横、纵坐标为正,再根据P点到坐标轴的距离确定点的坐标.
【详解】
解:∵P点位于y轴右侧,x轴上方,
∴P点在第一象限,
又∵P点距y轴3个单位长度,距x轴4个单位长度,
∴P点横坐标为3,纵坐标为4,即点P的坐标为(3,4).
故选A.
【点睛】
本题考查了点的位置判断方法及点的坐标几何意义.
A.a=bB.2a+b=﹣1C.2a﹣b=1D.2a+b=1
【答案】B
【解析】
试题分析:根据作图方法可得点P在第二象限角平分线上,
则P点横纵坐标的和为0,即2a+b+1=0,
∴2a+b=﹣1.故选B.
4.在平面直角坐标系中,若点P(m-3,m+1)在第二象限,则m的取值范围()
A.m<3B.m>−1C.−1<m<3D.m≥0
【详解】∵点P到x轴的距离为3,
∴点的纵坐标是3或-3,
∵点P到y轴的距离为2,
∴点的横坐标是2或-2,
又∵点P在第三象限,
∴点P的坐标为:(-2,-3),
故选B.
【点睛】本题考查了点的坐标的几何意义,横坐标的绝对值就是点到y轴的距离,纵坐标的绝对值就是到x轴的距离.
3.如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于 MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为()
【答案】C
【解析】
【分析】
解方程组求出交点坐标,根据交点在第四象限得到不等式组,即可求出答案.
【详解】
解方程组 ,得 ,
∴直线 与直线 的交点坐标是( , ),
∵交点在第四象限,
∴ ,
得-1<m<1,
故选:C.
【点睛】
此题考查一次函数交点与二元一次方程组的关系:交点的横纵坐标即是方程组的解,直角坐标系中点的坐标的特点,熟记每个象限内点的坐标特点是解题的关键.
