Pushover分析(同济大学翁大根)

合集下载

PUSHOVER分析方法全攻略学习教案

集中型分布型桁架hngji单元轴力内力成分铰特性初始刚度铰位置fx轴力轴力位移相对位移eal单元中心fyfz剪力剪力剪切应变gas单元中心mx扭矩弯矩旋转角gjl单元两端mymz弯矩弯矩旋转铰6eil3eil2eil单元两端内力成分铰特性初始刚度铰位置fx轴力轴力应变ea积分点位置fyfz剪力剪力剪切应变gas积分点位置mx扭矩弯矩曲率gj积分点位置mymz弯矩弯矩曲率ei积分点位置内力成分铰特性初始刚度铰位置fx轴力轴力位移相对位移eal单元中心般连接单元内力成分铰特性初始刚度铰位置fx轴力轴力变形相对位移用户输入eal单元中心fyfz剪力剪力变形相对位移用户输入gasl单元中心mx扭矩弯矩旋转角用户输入gjl单元中心mymz弯矩弯矩旋转铰用户输入eil单元中心44操作流程详解操作流程详解定义分配铰第27页共50页第27页共50页第二十八页共50页
第13页/共50页
抗震分析及设计”
第十四页，共50页。
4、操作流程详解-定义主控数据
定义初始(chū shǐ)荷载
在PUSHOVER 荷载工况中选择(xuǎnzé)考虑初始荷载。考虑轴力变化的影响时需要考虑初始荷载
定义收敛条件
适用于所有(suǒyǒu)PUSHOVER荷载工况
设置刚度折减率默认值
Performance Point Demand Spectrum
Amax
Capacity Spectrum
Dmax
Sd
第6页/共50页
第七页，共50页。
3、pushover分析原理
结构性能(xìngnéng)状况判断
性能点
Pushover分析(fēnxī)工况
设定(shè dìnɡ)需求谱
参考阻尼线（图中红色线）

静力弹塑性分析(Pushover分析)两种方法剖析

静力弹塑性分析(Pushover分析)■简介Pushover分析是考虑构件的材料非线性特点，分析构件进入弹塑性状态直至到达极限状态时结构响应的方法。

Pushover分析是最近在地震研究及耐震设计中经常采用的基于性能的耐震设计(Performance-BasedSeismicDesign,PBSD)方法中最具代表性的分析方法。

所谓基于性能的耐震设计就是由用户及设计人员设定结构的目标性能(targetperformance)，并使结构设计能满足该目标性能的方法。

Pushover分析前要经过一般设计方法先进行耐震设计使结构满足小震不坏、中震可修的规范要求，然后再通过pushover分析评价结构在大震作用下是否能满足预先设定的目标性能。

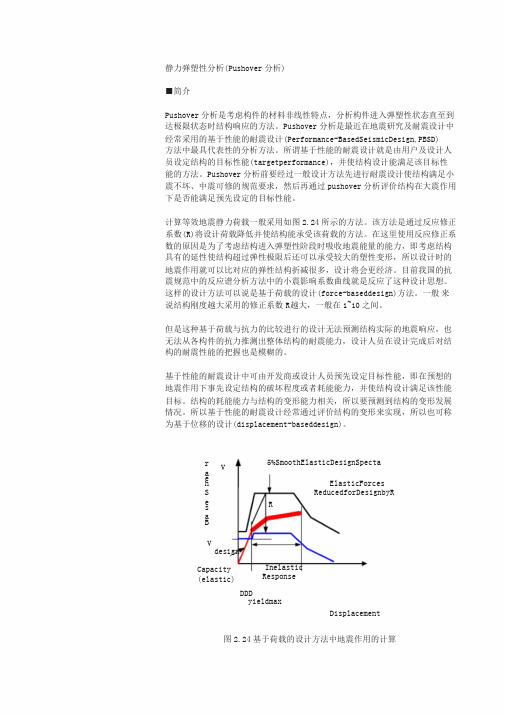
计算等效地震静力荷载一般采用如图2.24所示的方法。

该方法是通过反应修正系数(R)将设计荷载降低并使结构能承受该荷载的方法。

在这里使用反应修正系数的原因是为了考虑结构进入弹塑性阶段时吸收地震能量的能力，即考虑结构具有的延性使结构超过弹性极限后还可以承受较大的塑性变形，所以设计时的地震作用就可以比对应的弹性结构折减很多，设计将会更经济。

目前我国的抗震规范中的反应谱分析方法中的小震影响系数曲线就是反应了这种设计思想。

这样的设计方法可以说是基于荷载的设计(force-baseddesign)方法。

一般来说结构刚度越大采用的修正系数R越大，一般在1~10之间。

但是这种基于荷载与抗力的比较进行的设计无法预测结构实际的地震响应，也无法从各构件的抗力推测出整体结构的耐震能力，设计人员在设计完成后对结构的耐震性能的把握也是模糊的。

基于性能的耐震设计中可由开发商或设计人员预先设定目标性能，即在预想的地震作用下事先设定结构的破坏程度或者耗能能力，并使结构设计满足该性能目标。

结构的耗能能力与结构的变形能力相关，所以要预测到结构的变形发展情况。

所以基于性能的耐震设计经常通过评价结构的变形来实现，所以也可称为基于位移的设计(displacement-baseddesign)。

基于Pushover的双柱墩桥梁抗震延性能力分析

［文章编号】１００２ — ８４１２（２０１５）０５－００７５０－７
Ｄ０Ｉ：１０．１６２２６／ｊ．ｉｓｓｎ．１００２— ８４１２．２０１５．０５．０１３
基于Ｐｕｓｈｏｖｅｒ的双柱墩桥梁抗震延性能力分析
Ａｂｓｔｒａｃｔ：ＴｈｅｍａｉｎｐａｒａｍｅｔｅｒｓｔｈａｔａｆｆｅｃｔｔｈｅｄｕｃｔｉｌｅｃａｐａｃｉｔｙｏｆＲＣｃｏｎｔｉｎｕｏｕｓｇｉｒｄｅｒｂｒｉｄｇｅｌｉｋｅｃｏｎｃｒｅｔｅｓｔｒｅｎｇｔｈ，ｌｏｎｇｉｔｕｄｉｎａｌｒｅｉｎｆｏｒｃｅｍｅｎｔ，ｓｔｉｒｒｕｐｉｓｑｕａｎｔｉｔａｔｉｖｅｒｅｓｅａｒｃｈｅｄｂａｓｅｄＯｆｐｕｓｈｏｖｅｒａｎａｌｙｓｉｓｍｅｔｈｏｄ．Ｗｉｔｈｉｎｔｈｅｓｃｏｐｅｏｆｐａｒａｍｅｔｅｒｓｉｎｔｈｉｓｐａｐｅｒ，ｗｈｅｎｔｈｅｃｏｎｃｒｅｔｅｓｔｒｅｎｇｔｈｃｈａｎｇｅｓｆｒｏｍＣ４５ｔｏＣ６０，ｔｈｅｄｉｓｐｌａｃｅｍｅｎｔｄｕｃｔｉｌｉｔｙｆａｃｔｏｒｒｅｄｕｃｅｓａｌｍｏｓｔ６０％．Ｔｈｅｒｅｆｏｒｅ，ｔｈｅｃｏｎｃｒｅｔｅｓｔｒｅｎｇｔｈ

Pushover分析方法的发展及其在桥梁结构中的应用_盛光祖

文章编号:1003-1375(2008)04-0025-06Pushover 分析方法的发展及其在桥梁结构中的应用盛光祖(同济大学桥梁工程系,上海　200092)摘要:非线性静力分析方法(Pushover 分析方法)可以较好地检验结构的变形能力,找到结构的薄弱环节,控制强烈地震作用下结构破坏程度,对工程设计有很强的指导意义。

但目前Pushover 分析方法的种类很多,各自有着不同的优缺点和适用范围,针对桥梁结构,阐述静力非线性分析方法(Pushover )的原理及其研究发展概况,评述了各种Pushover 方法的优缺点,并分析了Pushover 方法用于桥梁结构的基本原理和评价方法,指出Pushover 方法用于桥梁结构存在的问题。

关键词:Pushov er 分析方法;非线性动力分析;桥梁结构;评价方法中图分类号:P315.9 文献标识码:A0　引言结构在地震作用下的弹塑性分析方法,目前主要向基于性能设计的方向发展,其中尤以非线性动力时程分析及非线性静力分析方法最具代表性。

非线性动力分析可以全过程的了解结构的破坏过程及屈服机制,发现结构的薄弱环节,是对结构进行非线性分析的最有效方法。

但该方法计算非常耗时,输入输出较为繁琐,对于日常工程设计而言不是很合适。

非线性静力分析方法(Pushover 分析方法)是一种将地震荷载等效成侧向荷载,通过对结构施加单调递增水平荷载来进行分析,主要研究结构在地震作用下进入塑性状态时的非线性性能。

Pushover 方法可以较好地检验结构的变形能力,找到结构的薄弱环节,控制强烈地震作用下结构破坏程度,对工程设计有很强的指导意义,并且有重大的社会效益和经济效益,因此在近些年来得到各国学者的推崇[1～3]。

1　Pushover 分析方法的研究发展概况1.1　传统Pushover 分析方法Pushover 分析方法产生于20世纪50年代,它是在基于位移或性能的基础之上发展起来的。

浅谈静力弹塑性分析(Pushover)的理解与应用

浅谈静力弹塑性分析（Pushover ）的理解与应用摘要：本文首先介绍采用静力弹塑性分析（Pushover ）的主要理论基础和分析方法，以Midas/Gen 程序为例，采用计算实例进行具体说明弹塑性分析的步骤和过程，表明Pushover 是罕遇地震作用下结构分析的有效方法。

关键词：静力弹塑性 Pushover Midas/Gen 能力谱需求谱性能点一、基本理论静力弹塑性分析方法，也称Pushover 分析法，是基于性能评估现有结构和设计新结构的一种静力分析方法，在一定精度范围内对结构在罕遇地震作用下进行弹塑性变形分析。

简要地说，在结构计算模型上施加按某种规则分布的水平侧向力或侧向位移，单调加荷载（或位移）并逐级加大；一旦有构件开裂（或屈服）即修改其刚度（或使其退出工作），进而修改结构总刚度矩阵，进行下一步计算，依次循环直到控制点达到目标位移或建筑物倾覆为止，得到结构能力曲线，之后对照确定条件下的需求谱，并判断是否出现性能点，从而评价结构是否能满足目标性能要求。

Pushover 分析的基本要素是能力谱曲线和需求谱曲线，将两条曲线放在同一张图上，得出交会点的位移值，同位移容许值比较，检验是否满足特定地震作用下的弹塑性变形要求。

能力谱曲线由能力曲线（基底剪力-顶点位移曲线）转化而来（图1）。

与地震作用相应的结构基底剪力与结构加速度为正相关关系，顶点位移与谱位移为正相关关系，两种曲线形状一致。

其对应关系为：1/αG V S a =roofroof d X S ,11γ∆=，图1 基底剪力-顶点位移曲线转换为能力谱曲线其中1α、1γ、roof X ,1分别为第一阵型的质量系数，参与系数、顶点位移。

该曲线与主要建筑材料的本构关系曲线具有相似性，其实其物理意义亦有对应，在初始阶段作用力与变形为线性关系，随着作用力的增大，逐渐进入弹塑性阶段，变形显著增长，不论对于构件，还是结构整体，都是这个规律。

需求谱曲线由标准的加速度响应谱曲线转化而来。

不同的侧向荷载加载方式下，框架结构pushover分析

不同的侧向荷载加载方式下，框架结构pushover分析发布时间：2021-06-11T08:50:46.633Z 来源：《基层建设》2021年第5期作者：杨楠[导读] 摘要：Pushover分析方法，常用于结构的静力弹塑性分析，用来分析结构的处于弹塑性变形状态下的位移相应与内力相应。

深圳市和域城建筑设计有限公司广东深圳 518000摘要：Pushover分析方法，常用于结构的静力弹塑性分析，用来分析结构的处于弹塑性变形状态下的位移相应与内力相应。

但是存在不同的侧向荷载输入方式，本文以某实际工程中的框架结构为例，展开探讨。

关键词：框架结构；静力弹塑性；pushover前言：Pushover，中文静力推覆，由Freeman等专家学者于1975年推出。

90年代，学术界和工程界，提出了基于位移（Displacement-based）和基于性能（Performance-based）的设计方法。

Pushover开始在各国工程领域大规模领用于，多用于静力弹塑性分析，罕遇地震的位移分析等。

但是存在不同的加载方法测序荷载的加载方式，即与结构的刚度[K]、质量矩阵[M]有关，又与结构的布置、抗震防线设置、构件的破坏顺序与破坏性能有关,特别是与构件的塑性铰性能相关,塑性铰的变化过程，直接影响阻尼矩阵[C]。

因此，本文就一个实际工程的框架结构，通过加载不同类型的侧向荷载，展开讨论与分析。

1侧向荷载加载方式《结构设计统一技术措施》[3]，弹塑性分析主要用于研究罕遇地震下，结构的变形规律，弹塑性层间位移等。

《高层建筑混凝土结构技术规程》[1] ，高度限制在150m下的高层建筑，结构分析可采用静力弹塑性分析。

对于其他高度建筑，视结构高度复杂程度与高度，选择静力弹塑性分析或弹塑性时程分析方法。

高度超过200m的建筑物，应采用弹塑性时程分析方法。

对于框架、框架等多层或高度较低的高层结构，采用pushover方法进行静力弹塑性分析是适当。

【结构设计】学习静力弹塑性分析方法总结

学习静力弹塑性分析方法总结静力弹塑性分析（Push-over）方法最早是1975年由Freeman等提出的,以后虽有一定发展,但未引起更多的重视.九十年代初美国科学家和工程师提出了基于性能（Performance-based）及基于位移（Displacement-based）的设计方法,引起了日本和欧洲同行的极大兴趣,Push-over方法随之重新激发了广大学者和设计人员的兴趣,纷纷展开各方面的研究.一些国家抗震规范也逐渐接受了这一分析方法并纳入其中,如美国ATC-40、FEMA-273&274、日本、韩国等国规范.我国2001规范提出“弹塑性变形分析,可根据结构特点采用静力非线性分析或动力非线性分析”,这里的静力非线性分析,即主要即是指Push-over分析方法.1、Push-over方法的基本原理和实施步骤（1）基本原理Push-over方法从本质上说是一种静力分析方法,对结构进行静力单调加载下的弹塑性分析.具体地说即是,在结构分析模型上施加按某种方式模拟地震水平惯性力的侧向力,并逐级单调加大,构件如有开裂或屈服,修改其刚度,直到结构达到预定的状态（成为机构、位移超限或达到目标位移）.其优点突出体现在：较底部剪力法和振型分解反应谱法,它考虑了结构的弹塑性特性；较时程分析法,其输入数据简单,工作量较小.（2）实施步骤(a)准备结构数据：包括建立结构模型、构件的物理参数和恢复力模型等；(b)计算结构在竖向荷载作用下的内力（将与水平力作用下的内力叠加,作为某一级水平力作用下构件的内力,以判断构件是否开裂或屈服）；(c)在结构每层的质心处,沿高度施加按某种分布的水平力,确定其大小的原则是：水平力产生的内力与（b）步计算的内力叠加后,恰好使一个或一批件开裂或屈服；(d)对于开裂或屈服的杆件,对其刚度进行修改后,再增加一级荷载,又使得一个或一批杆件开裂或屈服；(e)不断重复（c）、（d）步,直到结构达到某一目标位移（对于普通Push-over方法）、或结构发生破坏（对于能力谱设计方法）.2、Push-over方法研究进展（1）Push-over方法对结构性能评估的准确性许多研究成果表明,Push-over方法能够较为准确（或具有一定的适用范围）反映结构的地震反应特征.Lawson和Krawinkler对6个2~40层的结构（基本周期为0.22~2.05秒）Push-over分析结果与动力时程分析结果比较后,认为对于振动以第一振型为主、基本周期在2秒以内的结构,Push-over方法能够很好地估计结构的整体和局部弹塑性变形,同时也能揭示弹性设计中存在的隐患（包括层屈服机制、过大变形以及强度、刚度突变等）.Fajfar通过7层框剪结构试验结果与Push-over方法分析结果的对比得出结论,Push-over方法能够反映结构的真实强度和整体塑性机制,因此适宜于实际工程的设计和已有结构的抗震鉴定.Peter对9层框剪结构的弹塑性时程分析结果与Push-over方法分析结果进行了对比,认为无论是框架结构还是框剪结构,两种方法计算的结构最大位移和层间位移均很一致.Kelly考察了一幢17层框剪结构和一幢9层框架结构分别在1994年美国Northridge地震和1995年日本神户地震中的震害,并采用Push-over方法对两结构进行分析,发现Push-over方法能够对结构的最大反应和结构损伤进行合理地估计.Lew对一幢7层框架结构进行了非线性静力分析和非线性动力分析,发现非线性静力分析估计的构件的变形与非线性动力分析多条波计算结果的平均值大致相同.笔者曾对6榀框架（层数为3~16,基本周期为0.59~2.22秒）进行了Push-over分析与动力时程分析,发现两种方法计算的结构整体变形（层间位移或顶点位移）及塑性铰分布均较为一致.另外一些研究成果及工程应用也都表明,对于层数不太多或者自振周期不太长的结构,Push-over方法不失为一种可行的弹塑性简化分析方法.(2)水平加载模式水平加载模式指侧向力沿结构高度的分布,如FEMA-274给出的三种模式分别为均匀分布、倒三角形分布和抛物线分布.从理论上讲,加载模式应能代表在设计地震作用下结构层惯性力的分布,因此不同的加载模式将影响Push-over方法对结构抗震性能的评估.显然,惯性力的分布随着地震动的强度不同而不同,而且随地震的不同时刻、结构进入非线性程度的不同而不同.大多数工程应用采用倒三角形分布的加载模式,并且认为分布模式在加载过程中恒定不变.Krawinkler认为只有满足以下两个条件,这种加载模式才较为合理：①结构响应受高振型影响不太显著；②结构可能发生的屈服机制仅有一种,并恰好能被这种模式检验出来.因此建议采取至少两种加载模式来评估结构的抗震性能,分别是：①均布加载模式,即侧向力与楼层质量成正比,相对于整体倾覆弯矩,该加载模式更强调结构下部剪力的重要性；②利用现行规范的设计荷载模式（如底部剪力法）,采用考虑高振型影响的加载模式（如通过层剪力SRSS计算得到）.Peter假定了三种加载模式：①与层质量成正比；②与初始第1振型有关；③与加载过程中变化的第一振型有关；比较了Push-over方法和动力时程分析得到的一个9层框剪结构的层间位移,发现第②种模式更为合理.Moghadam研究了3栋7层结构（分别为规则、上部有内收的框架以及框剪）,比较了由规范反应谱求出侧向力分布和倒三角形直线分布两种模式,认为倒三角形加载模式适宜于规则框架,而不适用于上部有内收的框架以及框剪结构.但他认为倒三角形加载模式即是侧向力沿高度呈倒三角形分布,而与层质量无关.笔者认为,倒三角形加载模式应理解为结构变形沿高度呈倒三角形分布,即底部剪力法模式（侧向力沿高度分布与层质量和高度成正比）.由于上部有内收结构使上部质量减小,故侧向力并不一定沿高度呈倒三角形分布,因此上述“倒三角形加载模式不适用上部有内收的框架”的结论有待商榷.我们提出了基于结构瞬时振型、通过SRSS计算的、在加载过程中不断调整的加载模式,通过与动力时程分析得到的结构响应比较,认为这种加载模式能够较好地评判结构的地震反应.总体看来,在加载中随结构动力特征的改变而不断调整的加载模式应该是合理有效的模式.(3)结构目标位移结构目标位移指结构在一次地震动输入下可能达到的最大位移（一般指顶点位移）.Push-over方法确定结构目标位移时,都要将多自由度结构体系等效为单自由度体系.关于等效方法,Saiidi&Sozen早在1981年就提出了Q模型,给出了等效质量、等效阻尼、等效刚度的计算方法,通过8榀10层小比例的框架、框剪模型试验发现,基于Q模型的计算分析能够反映试验结构的响应特征.Kuramoto提出了另一种等效方法,并以不同结构形式、层强度和刚度不均匀的结构为研究对象,比较了Push-over方法推至目标位移（由等效单自由度体系的动力时程分析得到）时,最大层间位移与原结构动力时程分析得到的最大层间位移,得出的结论是：①对于规则RC和钢结构,单自由度体系与多自由度体系得到的结构响应非常一致；②对于不规则结构,单自由度体系与多自由度体系得到的结构响应基本一致；③对于超过10层以上的结构,单自由度体系得到的位移响应较多自由度体系结果有偏小的趋势,主要原因在于高振型影响.上述结论与Lawson和Krawinkler等的结论相同.我们]参照FEMA及Fajfar的等效单自由度体系的方法,对同一地震动输入下多自由度体系的顶点位移与等效单自由度体系的位移时程进行对比发现,这种等效方法使两体系的位移时程频率变化规律几乎一致,只是位移峰值有所不同,主要原因是,由该等效方法得到的单自由度体系的等效周期与原结构基本周期很接近.目前,目标位移的计算方法有两种.一种方法为：假定结构沿高度的变形向量（一般取第一振型）,利用Push-over方法得到的底部剪力––顶点位移曲线,将结构等效为单自由度体系,然后用弹塑性时程分析法或者弹塑性位移谱法求出等效单自由度体系的最大位移,从而计算出结构的目标位移.另一方法更为简化：目标位移通过弹性加速度反应谱和由结构弹性参数等效的单自由度体系求出.应该说第二种方法能够较好地估计结构目标位移,除非结构的周期较短,这种情况下,结构的弹塑性位移可能远大于弹性位移；而对于周期较长结构,结构弹塑性位移与弹性位移之比大致等于1.0.Faella指出,与动力时程分析得到的结果相比,Push-over方法的目标位移取大于设计地震动下动力时程分析得到结构的最大位移时,两种方法获得的层间位移和柱子损伤才较吻合.究其主要原因在于,动力时程分析输入的加速度值有正有负,而Push-over方法采取单调加载,即仅模拟了左（或右）的单向地震作用.(4)能力谱方法能力谱方法可视为Push-over方法的发展,实质上是通过地震反应谱曲线（地震需求谱Demand Spectrum）和结构能力谱的叠加,来评估结构在给定地震作用下的反应特征.计算步骤如下：(a)输入给定的地震记录,得到单自由度弹性体系（阻尼比一般取5%）的最大反应值（位移、速度和加速度）,据此可绘出最大反应绝对加速度––结构自振周期的曲线（即加速度谱）,或者将（最大加速度,最大位移）点按结构自振周期由小到大连成曲线（即需求谱）；(b)对结构进行Push-over分析,单调加载至结构破坏（成为机构或位移超限）,得到结构底部剪力Vbase––顶点位移Dt关系曲线；(c)将（b）得到的曲线,按以下公式]转换为等效单自由度体系的拟加速度––位移关系,即能力谱曲线:(1)式中g–––重力加速度；Wi–––第i层重量；n–––结构总层数；–––结构变形形状向量（=1.0）第i楼层对应的值.(d)将（a）和（c）得到的谱曲线叠加在同一坐标系中,如果两曲线不相交,说明结构尚未未达到设计地震的性能要求时即发生破坏或倒塌；如果相交,则定义交点为特征反应点（performance point）,从而可根据该点对应的结构基底剪力、顶点位移和层间位移等,来评估结构的抗震性能.不难看出,这种方法用于评估结构在给定地震作用下的弹塑性反应,其结果如何取决于特征反应点的确定.传统需求谱通常是按单自由度弹性体系得到的,如叶燎原将结构周期（在加载过程中不断变化）及其对应的地震影响系数（总水平力与结构自重的比值）绘成曲线,并叠加相应场地的各条（对应于不同的设防水准）加速度反应谱曲线,如果结构反应曲线穿过某条反应谱,就说明结构能够抵抗该条反应谱对应的地震烈度.这种方法实质上是由结构底部剪力（或加速度）确定特征反应点,对于短周期结构,可以较好地估计结构性能；对于由速度或位移控制的中、长周期结构,可能误差较大,此时特征反应点由地震作用下可能达到最大位移来确定才更为合理.叶献国认为单自由度弹性体系得到的需求谱通常过高估计了地震反应,据此提出了改进的能力谱方法,即将Push-over方法得到的能力谱曲线简化为二折线,构造一个相应的弹塑性单自由度体系,计算输入地震动下最大位移值,即谱位移值Sd,在能力谱上找到其对应点,定义为特征反应点.这种方法实质上相当于前面论述的第一种计算结构目标位移的方法.从改进的能力谱方法的计算结果来看,其计算准确性虽有提高,但并不明显,对需求谱的计算仍有待改进.有人建议用加大阻尼（等效阻尼）来获得结构弹塑性需求谱.由于阻尼机理的复杂性,合适的阻尼系数难以确定.Reinhorn利用滞回圈能量等效原则得到等效阻尼比公式,如果弹性阻尼比等于5%,最大位移延性系数为5.0时,则等效阻尼比为0.23（其中考虑了构件恢复力捏缩效应影响）.Moehle则提出了计算等效阻尼比的另一公式,如果弹性阻尼比等于5%,位移延性比为5.0,则等效阻尼比为0.16.Peter对9层框剪RC结构能力谱方法与弹塑性时程分析法在地震动输入下的非线性反应发现当能力谱方法的等效阻尼比取10%时,两者结果最一致.由此可见,等效阻尼系数的确定还很不统一.3、Push-over方法的发展前景对于二维Push-over方法,随着加载模式、目标位移以及需求谱等方面的日趋完善,应用于规则结构的抗震性能评估,能够较好地满足工程设计要求.但是,随着建筑造型和结构体型复杂化,大多数结构平面和竖向质量、刚度不均匀对称,因此将结构简化为二维模型分析将低估结构的反应,尤其是对于远离结构刚度中心的边缘构件更是如此.因此,Push-over方法向三维发展是必然趋势,但需解决一系列在二维模型分析中影响并不显著的问题.例如采用楼板刚度在平面内无穷大的假定,虽然可以大大减小求解方程的未知量,提高运算速度,但对于有错层（如变维住宅等）或楼板大开洞（如室内设天井等）的结构,这一假定应谨慎处理.又如在三维分析中,柱存在双向受力,梁承受双向弯曲和扭转,剪力墙及筒体的受力更复杂（弯曲、剪切和轴向变形）,因此构件的开裂或屈服的判断准则必须首先解决.。

Pushover分析(弹塑性分析)

Pushover曲线能力谱加速度Sa 基底剪力Vb
能力谱曲线
V Sa G1
(Sdt,sat)
Sd
top
1 X top ,1
顶点位移Dt
能力谱位移Sd
有效质量比
1
[ (Gi X i1 ) / g ]2
i 1
n
Sd T 2 Sa G
Gi 为结构第i楼层重量
[ Gi / g ][ (Gi X i2 1) / g]
Push-over的基本问题可以概括为三个方面:
如何求得结构的能力曲线? 如何确定结构的目标位移? 如何对计算结果进行评价?
结构能力曲线的计算包括两个方面的主要内容一计算模型的建立二侧向力的分布形式
结构计算模型—纤维模型
基于平截面假定，将梁柱的内力-变形关系转化成混凝土与钢筋的单轴应力-应变关系。
为阻尼修正系数，取0.3~1.0
ED为阻尼所消耗的能量（图中虚线部分平行四边形的面积） EE为最大应变能（图中斜线阴影部分的三角形的面积）
Sa A1 A2 T 能力谱曲线 Sa api ay T 能力谱曲线 P EE
P
dy Sd ED
dpi
Sd
用双线型代替能力谱曲线的条件：A1=A2
Teq
T 1
T 2 Sdp Sd ( ) Sa R R 2
R表示由于结构的非弹性变形对弹性地震力的折减系数
R ( 1) T 1 T T0 T0

R T T0
T0 0.65 0.3Tg Tg
采用Push-over方法对抗震性能进行评估
最简单的方法是直接得到目标位移点（性能点）与结构的能力曲线。得到性能点后，经过转化可以得到能力曲线上相应的点，能力曲线上的每一个点都对应着结构的一个变形状态。根据性能点对应的变形，可以对结构进行以下方面的评价：顶点侧移和层间位移角是否满足抗震规范规定的位移限值；构件的局部变形（指梁、柱等构件的塑性铰变形），检验他是否超过建筑某一性能水平下的允许变形；结构构件的塑性铰分布是否构成倒塌机构。

Pushover分析方法

静力非线性分析方法（Nonlinear Static Procedure），也称Pushover分析法，是基于性能评估现有结构和设计新结构的一种方法。

静力非线性分析是结构分析模型在一个沿结构高度为某种规定分布形式且逐渐增加的侧向力或侧向位移作用下，直至结构模型控制点达到目标位移或结构倾覆为止的过程。

控制点一般指建筑物顶层的形心位置；目标位移为建筑物在设计地震力作用下的最大变形。

Pushover方法的早期形式是“能力谱方法”（Capacity Spectrum Method, CSM），基于能量原理的一些研究成果，试图将实际结构的多自由度体系的弹塑性反应用单自由度体系的反应来表达，初衷是建立一种大震下结构抗震性能的快速评估方法。

从形式上看，这是一种将静力弹塑性分析与反应谱相结合、进行图解的快捷计算方法，它的结果具有直观、信息丰富的特点。

正因为如此，随着90年代以后基于位移的抗震设计（Displacement-Based Seismic Design, DBSD）和基于性能（功能）的抗震设计（Performance-Based Seismic Design, PBSD）等概念的提出和广为接受，使这种方法作为实现DBSD和PBSD的重要工具，得到了重视和发展。

这种方法本身主要包含两方面的内容：计算结构的能力曲线（静力弹塑性分析）、计算结构的目标位移及结果的评价。

第一方面内容的中心问题是静力弹塑性分析中采用的结构模型和加载方式；第二方面内容的中心问题则是如何确定结构在预定水平地震作用下的反应，目前可分为以ATC-40为代表的CSM和以FEMA356为代表的NSP（Nonlinear Static Procedure，非线性静力方法），CSM的表现形式是对弹性反应谱进行修正，而NSP则直接利用各种系数对弹性反应谱的计算位移值进行调整，两者在理论上是一致的。

在一些文献中只将第一方面的内容称为Pushover，不包括计算目标位移和结果评价的内容。

浅谈结构非线性静力分析法之Pushover分析法

浅谈结构非线性静力分析法之Pushover分析法摘要：结构抗震设计方法较多，静力非线性分析法是比较成熟的一种，我国已普遍采用，本人对Pushover分析法进行了详细的剖析。

关键字：抗震设计、静力非线性分析法、Pushover分析法Abstract: the seismic design method of structure is more, static nonlinear analysis method is a more mature, has been commonly used in our country, I for the Pushover method were analyzed in detail.Keywords: seismic design, non-linear static analysis method, Pushover analysis methodPushover 分析法在国外应用较早，上世纪80年代初期在一些重要的刊物上就有论文采用过这种方法。

进入90年代以后，国际抗震工程界提出了基于性能的抗震设计（PBSD）的新概念，这个概念的提出成为了工程抗震发展史上的一个重要的里程碑。

Pushover 分析法作为实现基于性能的抗震设计的重要方法，其研究逐渐深入，应用也逐渐得到推广。

该方法引入我国后，很快得到了大家的普遍重视与应用。

在我国《建筑抗震设计规范》的修订过程中，有些专家就提出了将Pushover 分析法引入规范的想法，只是最后在提法上明确没有采用这个词。

Pushover分析法的早期形式是“能力谱方法”(Capacity Spectrum Method CSM)，基于能量原理的一些研究成果，试图将实际结构的多自由度体系的弹塑性反应用单自由度体系的反应来表达，初衷是建立一种大震下结构抗震性能的快速评估方法。

从形式上看，这是一种将静力弹塑性分析与反应谱相结合、进行图解的快捷计算方法，它的结果具有直观、信息丰富的特点。

采用Pushover分析方法的抗震评估

文章编号:1009 6825(2009)08 0093 02采用Pushover 分析方法的抗震评估收稿日期:2008 10 20作者简介:杨益波(1983 ),男,助理工程师,中交一公局第三工程有限公司,北京 101102黄杰(1981 ),男,兰州交通大学土木工程学院硕士研究生,甘肃兰州 730070杨益波黄杰摘要:指出静力弹塑性(Pushover)分析方法目前已经成为对已有和新结构进行抗震性能评估常用的方法,对Pushover 分析方法的分析目的,目标位移以及横向荷载的确定进行了简单的介绍,以进一步推广该分析方法的应用。

关键词:Pusho ver ,地震,性能评估,目标位移中图分类号:T U 352.1文献标识码:A在最简单的情况下,结构抗震设计可以看成是一个两步走的过程。

第一步通常也是最重要的一步,是要建立一个有效结构体系的概念,即要设定所有重要的抗震性能目标,从适用性的角度考虑到生命安全以及防止倒塌。

设计过程的第二个步骤应该包括所有重要性能水准需求和能力的评估,这就要求确定重要的能力参数和规定这些参数的接受值以及采用地震动进行的需求预测。

合适的能力参数及其可接受值,还有需求预测所采用的合适方法都将依赖于有待评估的性能水准。

1 Pushover 分析的目的Pushover 分析的目的是通过采用静力非线性分析的方法来估计结构在设计地震下的强度和变形能力,并评价一个结构体系的期待性能,同时将需求结果同我们所关注的性能水准阶段的有效能力进行对比。

评估是基于一系列重要评估参数基础上的,包括整体位移,层间相对位移,构件的非线性变形,构件之间的相对变形,以及构件和构件之间的连接力。

Pushov er 分析可以看作是一种预测地震力和需求变形的方法,它采用一种近似的方式来说明当结构遭遇惯性力而不能再维持在弹性变形阶段时出现内力重分布的情况。

我们期待Pushover 分析给我们提供静力线性分析和动力分析所不能提供的许多关于响应特性的信息。

静力弹塑性分析方法(Pushover方法)与动力弹塑性分析方法的优缺点比较

静力弹塑性分析方法（Pushover方法）与动力弹塑性分析方法的优缺点比较一、Pushover分析法1、Pushover分析法优点：（1）作为一种简化的非线性分析方法，Pushover方法能够从整体上把握结构的抗侧力性能，可以对结构关键机构及单元进行评估，找到结构的薄弱环节，从而为设计改进提供参考。

（2）非线性静力分析可以获得较为稳定的分析结果，减小分析结果的偶然性，同时花费较少的时间和劳力，较之时程分析方法有较强的实际应用价值。

2、Pushover分析法缺点：（1）它假定所有的多自由度体系均可简化为等效单自由度体系，这一理论假定没有十分严密的理论基础。

（2）对建筑物进行Pushover分析时首先要确定一个合理的目标位移和水平加载方式，其分析结果的精确度很大程度上依赖于这两者的选择。

（3）只能从整体上考察结构的性能，得到的结果较为粗糙。

且在过程中未考虑结构在反复加载过程中损伤的累积及刚度的变化。

不能完全真实反应结构在地震作用下性状。

二、弹塑性时程分析法1、时程分析法优点：（1）采用地震动加速度时程曲线作为输入，进行结构地震反应分析，从而全面考虑了强震三要素，也自然地考虑了地震动丰富的长周期分量对高层建筑的不利影响。

（2）采用结构弹塑性全过程恢复力特性曲线来表征结构的力学性质，从而比较确切地、具体地和细致地给出结构的弹塑性地震反应。

（3）能给出结构中各构件和杆件出现塑性铰的时刻和顺序，从而可以判明结构的屈服机制。

（4）对于非等强结构，能找出结构的薄弱环节，并能计算出柔弱楼层的塑性变形集中效应。

2、时程分析法缺点：（1）时程分析的最大缺点在于时程分析的结果与所选取的地震动输入有关，地震动时称所含频频成分对结构的模态n向应有选择放大作用，所以不同时称输入结果差异很大。

（2）时程分析法采用逐步积分的方法对动力方程进行直接积分，从而求得结构在地震过程中每一瞬时的位移、速度和加速度反应。

所以此法的计算工作十分繁重，必须借助于计算机才能完成。

双柱式桥墩横向抗震能力pushover分析

双柱式桥墩横向抗震能力pushover分析本文以某双柱式圆形桥墩为研究对象，介绍了pushover的分析方法和步骤。

利用有限元分析软件Midas-Civil对其进行在罕遇地震作用下横桥向pushover分析，得出了结构在强震作用下的整体变形和屈服后的响应，同时分析结构局部的塑性变形机制和塑性铰位置发生屈服的先后顺序。

标签：双柱墩；pushover分析；抗震性能；塑性铰；采用Pushover法可以有效地對双柱式桥墩的横向抗震能力进行评估，该方法假定双柱式桥墩由单一振型控制，作用于结构的地震荷载等效为单调递增的侧向力，将桥墩推至一个给定的目标位移，从而掌握双柱式桥墩在大震作用下耗能能力和位移需求。

1、数值算例1.1 基本资料合肥南站站前广场配套工程G3号墩为双柱式桥墩，按地震烈度7度设防，场地为Ⅱ类场地，墩底到盖梁顶的高度H = 4.5 m，墩盖梁的高度h = 1.2 m，两墩柱中心距离为5m，墩柱的横截面为直径1 m的圆形，墩柱墩帽均采用C40钢筋混凝土。

结构模型示意图见图 1.本算例采用有限元软件Midas civil 2010进行分析计算，模型中的墩柱和盖梁均采用梁单元来模拟，墩底固结，塑性铰采用分布塑性铰。

1.2 分析方法结构目标位移的确定和水平荷载模式的选择，是静力弹塑性分析方法的两个关键环节。

本分析模型采用基于目标位移的位移控制法，即指定盖梁端部的横桥向最大位移值。

目前确定结构的目标位移有以下几种方法：一是时程分析法；二是能力谱方法；三是位移系数法。

能力谱法是首先通过pushover分析得到结构的剪力-位移曲线，并将它等效转换成单自由度体系的能力谱曲线。

需求谱曲线是由地震运动的反应谱曲线转换而来，它反应的是地震荷载对结构的需求。

地震需求谱曲线和结构能力谱曲线有交点，则说明结构的抗震能力满足要求。

若无交点则须修改设计直至满足要求，如图2所示。

1.3 塑性铰区域及特性当地震力作用在双柱式桥墩的横桥向时，墩柱的顶部和底部为潜在塑性铰区。

pushover分析

（4）累加各个加载阶段的力和变形，就可以获得所有构件在所有加载阶段的总内力和总变形。不断重复步骤(3)直到结构的侧向位移达到预定的目标位移，或者结构中出现的塑性铰过多成为机构。
(a)倒三角形加载
(b)抛物线加载
均匀加载
Pj

V n
(c)均匀加载
此模式适宜于刚度与质量沿高度分布较均匀，且薄弱层为底层的结构。
(d)变振形加载
(a)倒三角形加载
(b)抛物线加载
(c)均匀加载
(d)变振形加载
倒三角加载（底部剪力法模式）
Pj
Wjhj
n
V
Wi hi
i 1
此模式适宜于高度不大于40米，以剪切变形为主且刚度与质量沿高度分布较均匀的结构。
由Pushover方法基本假定（2）可知，结构的高度变形由结
构的形状向量{Φ}表示，并且在整个加载过程中，结构的形
状向量是固定不变的。
假定结构的相对位移向量可由结构顶点位移xtop 和形状向量
{Φ}表示：
x xtop
[M ] xtop [C] xtop R [M ]I xg (t)
Push-over的基本问题可以概括为三个方面:
如何求得结构的能力曲线? 如何确定结构的目标位移? 如何对计算结果进行评价?
结构能力曲线的计算包括两个方面的主要内容一计算模型的建立二侧向力的分布形式
结构计算模型—纤维模型
基于平截面假定，将梁柱的内力-变形关系转化成混凝土与钢筋的单轴应力-应变关系。
静力弹塑性(Pushover)分析方法
静力推覆分析是结构分析模型在一个沿结构高度为某种规定分布形式且逐渐增加的侧向力或侧向位移作用下，采用荷载控制或位移控制的方式，在加载过程中根据构件屈服程度不断调整结构刚度矩阵，直至结构模型控制点达到目标位移或结构倾覆为止，得到结构的基底剪力—顶点位移能力谱曲线。

PUSHOVER分析方法

■静力弹塑性分析方法（ PUSHOVER 分析方法）简介静力弹塑性分析也称PUSHOVER 分析方法，是指在结构上施加竖向荷载并保持不变，同时施加某种分布的水平荷载，该水平荷载单调增加，构件逐步屈服，从而得到结构在横向静力作用下的弹塑性性能。

主要步骤为：（1）按通常做法建立结构模型，包括几何尺寸、物理参数等；（2）根据单元种类（梁、柱、支撑、剪力墙等）和材料类型（钢、钢筋混凝土），确定各单元塑性铰性质（恢复力模型），根据受力形式可分为轴压、弯曲、剪切、压弯铰。

一般程序将塑性铰集中在杆件两端，并不考虑沿杆长的分布，轴压铰集中在杆件中央；（3）施加全部竖向荷载；（4）确定结构的目标位移；（5）选择合适的水平加载模式，施加在结构上，逐渐增加水平荷载，结构构件相继屈服，随之修改其刚度（程序自动完成），直到达到结构目标位移，对结构性能进行评判。

■静力弹塑性分析的原理MIDAS 程序提供的pushover 的分析方法，主要基于两本手册，一本是由美国应用技术委员会编制的《混凝土建筑抗震评估和修复》（ATC —40），另一本是由美国联邦紧急管理厅出版的《房屋抗震加固指南》（FEMA273／274）。

程序中FEMA 较本构关系和性能指标就来自于（FEMA273／274），而pushover 方法的主干部分，即分析部分采用的是能力谱法CSM ，来自于ATC 一40 (1996)和FEMA-273(1997)。

其主要步骤如下：（1）用单调增加水平荷载作用下的静力弹塑性分析，计算结构的基底剪力b V 一顶点位移n u 曲线（图1（a ））。

（2）建立能力谱曲线：对不很高的建筑结构，地震反应以第一振型为主，可用等效单自由度体系代替原结构。

因此，可以将b V —n u 曲线转换为谱加速度aS 一谱位移d S 曲线，即能力谱曲线（图l （b ））。

图1 pushover 曲线和能力谱之间的转换（3）建立需求谱曲线需求谱曲线分为弹性和弹塑性两种需求谱。

Pushover方法在桥梁结构抗震分析中的应用

Pushover方法在桥梁结构抗震分析中的应用摘要：Pushover分析方法作为简化的抗震性能评估方法之一，近年来受到了广大学者和工程设计人员的关注。

相对于弹塑性时程分析方法，采用Pushover 分析方法计算结构的水平最大位移，过程简单，计算量小，且精度也符合工程需求。

本文以一钢筋混凝土连续刚构桥的例子说明Pushover分析方法在桥梁结构抗震分析中的应用。

关键词：Pushover桥梁结构分析Abstract：As a simplified method to evaluate structural seismic performance, pushover procedure is widely noted by many reseachers and engineers. Compared to nonlinear time-history analysis method, pushover procedure is more simple to computer the maximum displacement of structure, and the accuracy of results obtained by pushover procedure meets the demand of engineering. A reinforced concrete continuous rigid frame bridge is used to illustrate the process of evaluating the maximum displacement of structrue by pushover procedure.Keywords: Pushover analysis of bridge structure0 引言随着基于性能的抗震设计思想的提出和发展，Pushover分析方法越来越受到国内外广大学者的关注。

Pushover分析(同济大学翁大根)

基本安全指标建筑性能水平
小震
地震地面运动
中震
小震
可用（Operational）
立即居住（Immediate Occupation）
生命安全（Life Safety）
√
大震大震
中震
√ √
√
注：基本安全指标如上表所示，是达到3-C（生命安全水准）及5-E（结构稳定水准）的双水准性能指标。
非线性静力分析（1）
速评估方法。
从形式上看，这是一种将静力弹塑性分析与反应谱相结
合、进行图解的快捷计算方法，它的结果具有直观、信息
丰富的特点。
非线性静力分析（3）
（Nonlinear Static Procedure）
Pushover方法是90年代以后出现的基于位移的抗震设计
（Displacement-Based Seismic Design)和基于性能（功能）的抗震设计（Performance-Based Seismic Design, PBSD）方法得于实现的重要工具。
退化；或者是某一构件（或一组构件）的侧向变形达到某一数值时，导致结构失去重力承载能力。
11、精确模拟整体的强度退化。如果结构在第10步达到了侧向变形极
限，便停止加载，此时会有一个或者一组构件已经无法继续承担大部分或所有的荷载，即其强度已明显退化，然后这根（批）构件的刚度会减少，或者消失。从第3步开始再建立新的能力曲线。建立尽可能多的 Pushover曲线，可以更充分地表现强度丧失的全过程。图8.2中以三条不同的能力曲线为例子表现这个过程。
（Nonlinear Static Procedure）
Pushover方法从本质上说是一种静力分析方法，对结构

静力弹塑性分析(Push—over)方法的应用与评价

法。
Ｐｓ－ｖｒ析能采用熟悉的静力和动力非线性分ｕｈｏｅ分析程序。例如ＤＲＮ－平Ｃ这面舞｝，或ＤＲＮ一Ｄ、ＲＡＩ — ＢＬＮＧＳＭ一构ＡＩ３ｘＤＮｕＩＤＩＳ、Ｃ
一
展望。关键词弹塑性静力分析
抗震性能评价１前言在近年来的多次强震灾害影响下，世界各国工程界目前广泛关注基于建筑物位移性能（ｉｐａｅｎ／ＤｓｌｃｍｅｔＰｒｒｎｅＢｓｄＳｉｃＤｓｎ）抗震思想。该思ｅｆｍａｃ－ａｅｅｓｅｉ的ｏｍｉｇ想的核心是：对每一种设防水准，结构的抗震性能针将划分为不同等级，计人员根据物主的要求，用合理设采
的抗震性能目标和合适的结构措施。而Ｐｓ — ｖｒ方法ｕｈｏｅ是将结构推覆至目标位移或形成倒塌机制，从某种意义上说，些都是性能目标。基于这一背景，力弹塑这静性分析（即ｐｓ－ｖｒａａｙｉ）法被重新提出并吸ｕｈｏｅｎｌｓｓ方引了越来越多的研究者。Ｐｓ — ｖｒ析是对结构施加能近似反映结构动力ｕｈｏｅ分特性及其变化的、调增长的水平荷载，步进行弹塑单逐性分析，到结构达到目标位移或形成倒塌机制状态。直该方法简单实用，并可根据分析目的，结合地震反应谱，图形的形式对结构的抗震性能进行评价，此可用因以非常直观地表示结构的能力。在这一过程中可得到结构从弹性、服、直到极限倒塌状态的全过程的内屈＿力、形、考察塑性铰的形成，到结构的薄弱部位。变可找２弹塑性静力分析方法的研究现状Ｐｓ — ｖｒ法早在国外七八十年代便提出来了，ｕｈｏｅ方但当时没有得到应有的关注。近年来在基于结构性能的抗震思想的背景下，世界各国的工程界又重新认识到该方法的应用前景。现在已成为世界上几个主要机构研究的焦点，并致力于在抗震规范中加以推广。例如，美国加州结构工程师协会的ＳＡＯＣＶｉｉｎ００Ｅｓ２０ｏ（９６；用技术委员会的ＡＴ４１９；邦应急１９）应Ｃ一０（９７）联管理厅（Ｅ一７；筑抗震安全委员会（ＳＣ）ＦＭＡ２４）建ＢＳ的ＮＥＨＲＰ（９８；洲模式规范（ｕｏｏｅ８）１９）欧Ｅｒｃｄ一；日本的ＰＳＲＥＳ钢筋混凝土建筑结构设计指南等。我国在这方面的研究稍落后于国外，但近年来也得到大家的关注和应用。新近颁布的《筑抗震设计在建规范》（５０１２０ＧＢ０１ — ０１）关于结构分析方面的条文３６２中规定： “ 规则且具有明显薄弱部位可能导致．．不地震时严重破坏的建筑结构，应按本规范有关规定进行罕遇地震作用下的弹塑性变形分析。此时，根据结可构的特点采用静力弹塑性分析或弹塑性时程分析方法。 ”其中的静力弹塑性分析主要是指ｐｓ — ｖｒ分析ｕｈｏｅ