1.5定积分的概念教学设计教案

合集下载

1.5定积分的概念教学设计教案

教学准备
1. 教学目标
（1）知识与技能：定积分的概念、几何意义及性质
（2）过程与方法：在定积分概念形成的过程中，培养学生的抽象概括能力和探索提升能力。

（3）情感态度与价值观：让学生了解定积分概念形成的背景，培养学生探究数学的兴趣.
2. 教学重点/难点
【教学重点】：
理解定积分的概念及其几何意义，定积分的性质
【教学难点】：
对定积分概念形成过程的理解
3. 教学用具
多媒体
4. 标签
1.5.3定积分的概念
教学过程
课堂小结
定积分的定义，计算定积分的“四步曲”，定积分的几何意义，定积分的性质。

定积分的概念教案

1.5.3定积分的概念教学目标能用定积分的定义求简单的定积分；理解掌握定积分的几何意义；重点定积分的概念、定积分法求简单的定积分、定积分的几何意义难点定积分的概念、定积分的几何意义复习： 1．回忆前面曲边图形面积，变速运动的路程，变力做功等问题的解决方法，解决步骤 2．对这四个步骤再以分析、理解、归纳，找出共同点．新课讲授1．定积分的概念一般地，设函数()f x 在区间[,]a b 上连续，用分点0121i i n a x x x x x x b -=<<<<<<<=将区间[,]a b 等分成n 个小区间，每个小区间长度为x ∆（b ax n-∆=），在每个小区间[]1,i i x x -上取一点()1,2,,i i n ξ=，作和式：11()()nnn i i i i b aS f x f n ξξ==-=∆=∑∑如果x ∆无限接近于0（亦即n →+∞）时，上述和式n S 无限趋近于常数S ，那么称该常数S为函数()f x 在区间[,]a b 上的定积分。

记为：()b aS f x dx =⎰其中()f x 成为被积函数，x 叫做积分变量，[,]a b 为积分区间，b 积分上限，a 积分下限。

说明：（1）定积分()ba f x dx ⎰是一个常数，即n S 无限趋近的常数S（n →+∞时）称为()ba f x dx ⎰，而不是n S ．（2）用定义求定积分的一般方法是：①分割：n 等分区间[],a b ；②近似代替：取点[]1,i i i x x ξ-∈；③求和：1()ni i b a f n ξ=-∑； ④取极限：()1()lim n b i a n i b af x dx f n ξ→∞=-=∑⎰ （3）曲边图形面积：()ba S f x dx =⎰；变速运动路程21()t t S v t dt =⎰；变力做功 ()ba W F r dr =⎰ 2．定积分的几何意义如果在区间[,]a b 上函数连续且恒有()0f x ≥，那么定积分()baf x dx ⎰表示由直线,x a x b ==（a b ≠），0y =和曲线()y f x =所围成的曲边梯形的面积。

1.5定积分的概念教案

二、定积分的几何意义
从几何上看，如果在区间上函数连续且恒有，那么定积分表示由所围成的曲边梯形的面积.这就是定积分的几何意义.
【即时训练1】定积分的值是.
阅读教材完成右框内容
三、定积分的性质
（1） .（2） .
（3） .
【即时训练2】已知，，，，求下列各式的值.
课堂小结
三、巩固诊断
1.已知为偶函数且，则等于（）
A．0B．4C．8D．16
2．若是奇函数，则（）
A．0B． C． D．1
3．如图,阴影部分面积分别为，则定积分 _____.
4．说明下列定积分所表示的几何意义，并根据其几何意义求出定积分的值.
闯关题：求定积分：
.
1.5定积分的概念
一、学习目标：1.理解定积分的概念.
2.理解定积分的几何意义.
3.掌握定积分的基本性质
学习重点：理解定积分的概念及其几何意义，定积分的性质
学习难点：对定积分概念形成过程的理检测及课堂展示
阅读教材完成右框内容
一、定积分的概念
一般地，如果函数在区间上连续，用分点将区间等分成小区间，在每个小区间上任取一点，作和式 .当时，上述和式无限接近某个，这个叫做函数在区间上的定积分，记作，即，这里，分别叫做与，区间叫做，函数叫做，叫做，叫做.

教学：1.5定积分的概念第3课时

§1.5.3定积分的概念【学情分析】：前面两节（曲边梯形的面积和汽车行驶的路程）课程的学习为定积分的概念的引入做好了铺垫。

学生对定积分的思想方法已有了一定的了解。

【教学目标】：（1）知识与技能：定积分的概念、几何意义及性质（2）过程与方法：在定积分概念形成的过程中，培养学生的抽象概括能力和探索提升能力。

（3）情感态度与价值观：让学生了解定积分概念形成的背景，培养学生探究数学的兴趣.【教学重点】：理解定积分的概念及其几何意义，定积分的性质【教学难点】：对定积分概念形成过程的理解练习与测试：（基础题） 1.函数()f x 在[],a b上的定积分是积分和的极限，即()baf x dx =⎰_________________ .答案：01lim()niii f x λξ→=∆∑2.定积分的值只与______及_______有关，而与_________的记法无关 . 答案：被积函数,积分区间,积分变量；3.定积分的几何意义是_______________________ .答案：介于曲线()y f x =,x 轴 ,直线,x a x b ==之间各部分面积的代数和； 4.据定积分的几何意义()a b <，则________;badx =⎰________.baxdx =⎰答案：b a - ， 222b a -（提高题）5.将和式极限表示成定积分(1). 21lim(12)n n n →∞+++L解：12211111lim (12)lim lim nnn n n i i i n i xdx n nn n →∞→∞→∞==+++===∑∑⎰L (2). 21lim()ni i i fx λξ→=∆∑，其中{}0121,[,],n i i i i x a x x x b x x Max x ξλ-=<<<<=∈=L解：2201lim()()()nbbi i aai f x g x dx f x dx λξ→=∆==∑⎰⎰6. 利用定义计算定积分211.dx x⎰解：在[1,2]中插入分点21,,,n q q q -L ,典型小区间为1[,]i iq q -，（1,2,,i n =L ）小区间的长度11(1)i i i i x q q q q --∆=-=-,取1i i q ξ-=，（1,2,,i n =L ）1111111()(1)nnni i i i i i i i i f x x q q q ξξ--===∆=∆=-∑∑∑1(1)(1)ni q n q ==-=-∑取2nq =即12nq =，11()(21),nniii f xn ξ=∆=-∑()i g ξi x ∆i ξ1121lim (21)limln 2,1x xx x x x→+∞→+∞--==Q1lim (21)ln 2,nn n →∞∴-=1210111lim lim (21)ln 2.nn i n i idx x n x λξ→→∞==∆=-=∑⎰以下为赠送文档：选修4_5 不等式选讲课题：第01课时不等式的基本性质目的要求：重点难点：教学过程：一、引入：不等关系是自然界中存在着的基本数学关系。

高中数学专题1.5.3 定积分的概念教案新人教A版选修2

定积分的概念【教学目标】1．了解定积分的概念，会用定义求定积分．2．理解定积分的几何意义．3．掌握定积分的基本性质．【教法指导】本节学习重点：掌握定积分的基本性质．本节学习难点：理解定积分的几何意义．【教学过程】☆复习引入☆任何一个平面图形都有面积，其中矩形、正方形、三角形、平行四边形、梯形等平面多边形的面积，可以利用相关公式进行计算．如图所示的平面图形，是由直线x＝a，x＝b(a≠b)，y＝0和曲线y＝f(x)所围成的，称之为曲边梯形，如何计算这个曲边梯形的面积呢？解析：请同学思考并回顾以前所学知识并积极回答之.☆探索新知☆探究点一定积分的概念思考1 分析求曲边梯形的面积和变速直线运动的路程，找一下它们的共同点．答两个问题均可以通过“分割、近似代替、求和、取极限”解决，都可以归结为一个特定形式和的极限．思考2 怎样正确认识定积分ʃb a f(x)d x?(2)定积分就是和的极限limn→∞∑ni＝1(ξi)·Δx，而ʃb a f(x)d x只是这种极限的一种记号，读作“函数f(x)从a到b 的定积分”．(3)函数f(x)在区间[a，b]上连续这一条件是不能忽视的，它保证了和的极限(定积分)的存在(实际上，函数连续是定积分存在的充分条件，而不是必要条件)．例1 利用定积分的定义，计算ʃ10x3d x的值．解令f(x)＝x3.(1)分割在区间[0,1]上等间隔地插入n －1个分点，把区间[0,1]等分成n 个小区间[i －1n ，in](i ＝1,2，…，n )，每个小区间的长度为Δx ＝i n －i －1n ＝1n.(2)近似代替、求和取ξi ＝in(i ＝1,2，…，n )，则ʃ10x 3d x ≈S n ＝∑ni ＝1f (in)·Δx ＝∑ni ＝1(i n )3·1n＝1n 4∑ni ＝1i 3＝1n 4·14n 2(n ＋1)2＝14(1＋1n)2. (3)取极限ʃ10x 3d x ＝lim n →∞S n ＝lim n →∞ 14(1＋1n )2＝14. 反思与感悟 (1)利用定积分定义求定积分的数值仍然是“分割、近似代替、求和、取极值”这一过程，需要注意的是在本题中将近似代替、求和一起作为步骤(2)，从而省略了解题步骤． (2)从过程来看，当f (x )≥0时，定积分就是区间对应曲边梯形的面积．跟踪训练1 用定义计算ʃ21(1＋x )d x .2＋i －1n ，从而得∑n i ＝1f (ξi )Δx ＝∑ni ＝1(2＋i －1n )·1n ＝∑n i ＝1⎝ ⎛⎭⎪⎫2n ＋i －1n 2 ＝2n ·n ＋1n2[0＋1＋2＋…＋(n －1)]＝2＋1n 2·n n －2＝2＋n －12n. (3)取极限：S ＝lim n →∞ ⎝⎛⎭⎪⎫2＋n －12n ＝2＋12＝52. 因此ʃ21(1＋x )d x ＝52.探究点二定积分的几何意义思考1 从几何上看，如果在区间[a ，b ]上函数f (x )连续且恒有f (x )≥0，那么ʃba f (x )d x 表示什么？答当函数f (x )≥0时，定积分ʃba f (x )d x 在几何上表示由直线x ＝a ，x ＝b (a <b )，y ＝0及曲线y ＝f (x )所围成的曲边梯形的面积．思考2 当f (x )在区间[a ，b ]上连续且恒有f (x )≤0时，ʃba f (x )d x 表示的含义是什么？若f (x )有正有负呢？答如果在区间[a ，b ]上，函数f (x )≤0时，那么曲边梯形位于x 轴的下方(如图①)．由于b －an>0，f (ξi )≤0，故 f (ξi )b －a n≤0.从而定积分ʃb a f (x )d x ≤0，这时它等于如图①所示曲边梯形面积的相反值，即ʃba f (x )d x ＝－S .当f (x )在区间[a ，b ]上有正有负时，定积分ʃba f (x )d x 表示介于x 轴、函数f (x )的图象及直线x ＝a ，x ＝b (a ≠b )之间各部分面积的代数和(在x 轴上方的取正，在x 轴下方的取负)．(如图②)，即ʃba f (x )d x ＝－S 1＋S 2－S 3. 例2 利用几何意义计算下列定积分： (1)ʃ3－39－x 2d x ；(2)ʃ3－1(3x ＋1)d x .(2)由直线x ＝－1，x ＝3，y ＝0，以及y ＝3x ＋1所围成的图形，如图所示：ʃ3－1(3x ＋1)d x 表示由直线x ＝－1，x ＝3，y ＝0以及y ＝3x ＋1所围成的图形在x 轴上方的面积减去在x 轴下方的面积，∴ʃ3－1(3x ＋1)d x ＝12×(3＋13)×(3×3＋1)－12(－13＋1)×2＝503－23＝16. 反思与感悟利用几何意义求定积分，关键是准确确定被积函数的图象，以及积分区间，正确利用相关的几何知识求面积．不规则的图象常用分割法求面积，注意分割点的准确确定．跟踪训练2 根据定积分的几何意义求下列定积分的值： (1)ʃ1－1x d x ；(2)ʃ2π0cos x d x ；(3)ʃ1－1|x |d x . 解 (1)如图(1)，ʃ1－1x d x ＝－A 1＋A 1＝0. (2)如图(2)，ʃ2π0cos x d x ＝A 1－A 2＋A 3＝0.(3)如图(3)，∵A 1＝A 2，∴ʃ1－1|x |d x ＝2A 1＝2×12＝1.(A 1，A 2，A 3分别表示图中相应各处面积)探究点三定积分的性质思考1 定积分的性质可作哪些推广？答定积分的性质的推广①ʃb a [f 1(x )±f 2(x )±…±f n (x )]d x ＝ʃb a f 1(x )d x ±ʃb a f 2(x )d x ±…±ʃba f n (x )d x ； ②ʃba f (x )d x ＝ʃc 1a f (x )d x ＋ʃc 2c 1f (x )d x ＋…＋ʃbc n f (x )d x (其中n ∈N *)．思考2 如果一个函数具有奇偶性，它的定积分有什么性质？例3 计算ʃ3－3(9－x 2－x 3)d x 的值．解如图，由定积分的几何意义得ʃ3－39－x 2d x ＝π×322＝9π2，ʃ3－3x 3d x ＝0，由定积分性质得ʃ3－3(9－x 2－x 3)d x ＝ʃ3－39－x 2d x －ʃ3－3x 3d x ＝9π2. 反思与感悟根据定积分的性质计算定积分，可以先借助于定积分的定义或几何意义求出相关函数的定积分，再利用函数的性质、定积分的性质结合图形进行计算．跟踪训练3 已知ʃ10x 3d x ＝14，ʃ21x 3d x ＝154，ʃ21x 2d x ＝73，ʃ42x 2d x ＝563，求： (1)ʃ203x 3d x ；(2)ʃ416x 2d x ；(3)ʃ21(3x 2－2x 3)d x . 解 (1)ʃ203x 3d x ＝3ʃ20x 3d x ＝3(ʃ10x 3d x ＋ʃ21x 3d x )＝3×(14＋154)＝12；(2)ʃ416x 2d x ＝6ʃ41x 2d x ＝6(ʃ21x 2d x ＋ʃ42x 2d x )＝6×(73＋563)＝126； (3)ʃ21(3x 2－2x 3)d x ＝ʃ213x 2d x －ʃ212x 3d x＝3ʃ21x 2d x －2ʃ21x 3d x ＝3×73－2×154＝7－152＝－12. ☆课堂提高☆1．下列结论中成立的个数是( )①ʃ10x 3d x ＝∑ni ＝1i 3n 3·1n； ②ʃ10x 3d x ＝lim n →∞∑ni ＝1i －13n 3·1n；③ʃ10x 3d x ＝lim n →∞∑ni ＝1i 3n 3·1n. A ．0 B ．1 C ．2 D ．3 【答案】 C2．当n 很大时，函数f (x )＝x 2在区间1,i i n n -⎡⎤⎢⎥⎣⎦ (i ＝1,2，…，n )上的值可以用 ( )近似代替 A.inB ．1f n ⎛⎫⎪⎝⎭ C ．i f n ⎛⎫⎪⎝⎭D ．1n【答案】C【解析】f (x )＝x 2在区间1,i i n n -⎡⎤⎢⎥⎣⎦上的值可以用区间1,i i n n -⎡⎤⎢⎥⎣⎦上每一点对应的函数值近似代替，故选C. 3．下列等式不成立的是( ) A. ()()ba mf x ng x dx ⎡⎤+⎣⎦⎰＝m ()b a f x dx ⎰＋n ()ba g x dx ⎰ B. ()1ba f x dx ⎡⎤+⎣⎦⎰＝()ba f x dx ⎰＋b －aC. ()()baf xg x dx ⎰＝()()bbaaf x dxg x dx ⎰⎰D.2π2πsin xdx -⎰＝02π2πsin sin xdx xdx -+⎰⎰【答案】C【解析】利用定积分的性质进行判断，选项C 不成立．例如112xdx =⎰，12013x dx =⎰，13014x dx =⎰，11132000x dx xdx x dx ≠⋅⎰⎰⎰.故选C.4．已知定积分ʃ60f (x )d x ＝8，且f (x )为偶函数，则ʃ6－6f (x )d x 等于( )． A ．0 B ．16 C ．12 D ．8 【答案】 B【解析】偶函数图象关于y 轴对称，故ʃ6－6f (x )d x ＝2ʃ60f (x )d x ＝16，故选B. 5．已知1e e 1xdx =-⎰，221e e e xdx =-⎰，2283x dx =⎰，2122ln 2dx x =⎰.求：(1)20e xdx ⎰；(2)()220e 3xx dx +⎰；(3)211e x dx x ⎛⎫+ ⎪⎝⎭⎰. 【解析】(1)2122201e e e e 1e e e 1x x x dx dx dx =+=-+-=-⎰⎰⎰.(2)()22e3xx dx +⎰＝2e xdx ⎰＋()223x dx ⎰＝2e xdx ⎰＋2203x dx ⎰＝e 2－1＋8＝e 2＋7.(3)211e x dx x ⎛⎫+ ⎪⎝⎭⎰＝21e xdx ⎰＋21122dx x ⎰＝e 2－e ＋ln2. 6．利用定积分的定义计算ʃ21(－x 2＋2x )d x 的值，并从几何意义上解释这个值表示什么．(2)近似代替、求和取ξi ＝1＋in(i ＝1,2，…，n )，则S n ＝∑ni ＝1f (1＋i n )·Δx ＝∑ni ＝1[－(1＋i n )2＋2(1＋i n )]·1n＝－1n 3[(n ＋1)2＋(n ＋2)2＋(n ＋3)2＋…＋(2n )2]＋2n2[(n ＋1)＋(n ＋2)＋(n ＋3)＋…＋2n ]＝－1n3[2n 2n ＋14n ＋16－n n ＋12n ＋16]＋2n2·n n ＋1＋2n2＝－13(2＋1n )(4＋1n )＋16(1＋1n )(2＋1n )＋3＋1n .(3)取极限ʃ21(－x 2＋2x )d x ＝lim n →∞S n ＝lim n →∞[－13(2＋1n )(4＋1n )＋16(1＋1n )(2＋1n )＋3＋1n ]＝23，2 3的几何意义为由直线x＝1，x＝2，y＝0与曲线f(x)＝－x2＋2x所围成的曲边梯形的面积．ʃ21(－x2＋2x)d x＝。

定积分的概念的教学设计

《1.5.3定积分的概念》教学设计1．教材分析1．1课标要求分析从教材上的要求来看，要求学生认识定积分的知识背景，理解背景中两个典型问题的解决思想，并能概括它们的共同特征从而引入定积分概念，理解定积分的含义和其符号的含义，明白定积分的几何意义和基本性质。

我个人认为由两个实例引入定积分概念这步很重要，能让学生理解定积分这一抽象的概念，并理解定积分的用途。

1．2教学内容分析1．2．1内容背景分析本节内容是人教A版选修2—2的1.5.3的内容，前面两节学习了如何解决“求曲边梯形面积”和“求变速运动路程”两个经典问题，在这两个问题的知识背景下这节课很自然地引入了定积分的概念。

这样能让学生充分理解定积分的由来和用途。

1．2．2教学内容的分析人教版的这节课的内容比较简短，要求掌握的层次也比较低。

主要通过前面两个实例的解决思路进行概括引入定积分的概念，明白积分的概念，积分符号的含义，了解定积分的几何意义和几个基本性质。

通过例1让学生进一步熟悉定积分的定义，熟悉计算定积分的“四步曲”。

2．学情分析我上这堂课的班级是高二（3）班，这个班在高二四个班中属于中等水平，上课思维不大活跃，不分学生接受能力还可以，但后进生比较多，这些学生基础较为薄弱，而且定积分的概念较为抽象，在引入的过程中包含了数列求和，求极限等复杂的知识内容。

作为引入定积分概念的课，推导的计算过程简单带过就好，不宜把知识点挖得太深。

我把这节课的重点放在让学生了解定积分概念的由来，明白定积分符号的含义、定积分的集合意义和一些基本性质，让学生掌握用定义求定积分的步骤。

3．教学目标1.通过求曲边梯形的面积和汽车行驶的路程，了解定积分的背景；2.借助于几何直观定积分的基本思想，了解定积分的概念，能用定积分定义求简单的定积分；3.理解掌握定积分的几何意义．4．教学重点和难点重点：理解定积分的概念、定积分的几何意义及基本性质，能用定义求简单的定积分．难点：定积分的概念、定积分的几何意义．5．教学过程1．创设情景复习：1.回忆前面曲边梯形的面积，汽车行驶的路程等问题的解决思路，解决步骤：求曲边梯形面积: 分割→以直代曲→求和→取极限（逼近）求汽车路程:分割→以不变代变→求和→取极限（逼近）2．思考一下解决前面两个问题的共同特点：2．新课讲授1．定积分的概念一般地，设函数()f x 在区间[,]a b 上连续，用分点0121i i n a x x x x x x b-=<<<<<<<=将区间[,]a b 等分成n 个小区间，每个小区间长度为x ∆（b ax n -∆=），在每个小区间[]1,i i x x -上取一点()1,2,,i i n ξ=，作和式：11()()nnn i i i i b aS f x f n ξξ==-=∆=∑∑如果x ∆无限接近于0（亦即n →+∞）时，上述和式nS 无限趋近于常数S ，那么称该常数S为函数()f x 在区间[,]a b 上的定积分。

高中数学1.5.3定积分的概念教学设计新人教A版选修2_2

§1.5.3定积分的概念教案一、教学目标⒈通过求曲边梯形的面积和变速直线运动的路程，了解定积分的背景； ⒉借助于几何直观定积分的基本思想，了解定积分的概念，能用定积分法求简单的定积分．3．理解掌握定积分的几何意义；教学过程：二、预习导学1．回忆前面曲边图形面积，变速运动的路程，变力做功等问题的解决方法，解决2．对这四个步骤再以分析、理解、归纳，找出共同点．三、问题引领，知识探究1．定积分的概念一般地，设函数()f x 在区间[,]a b 上连续，用分点0121i i n a x x x x x x b -=<<<<<<<=将区间[,]a b 等分成n 个小区间，每个小区间长度为x ∆（b ax n-∆=），在每个小区间[]1,i i x x -上取一点()1,2,,i i n ξ=，作和式：11()()nnn i i i i b aS f x f nξξ==-=∆=∑∑如果x ∆无限接近于0（亦即n →+∞）时，上述和式n S 无限趋近于常数S ，那么称该常数S 为函数()f x 在区间[,]a b 上的定积分。

记为：()baS f x dx =⎰其中()f x 成为被积函数，x 叫做积分变量，[,]a b 为积分区间，b 积分上限，a 积分下限。

说明：（1）定积分()baf x dx ⎰是一个常数，即n S 无限趋近的常数S （n →+∞时）称为()baf x dx ⎰，而不是n S ．（2）用定义求定积分的一般方法是：①分割：n 等分区间[],a b ；②近似代替：取点[]1,i i i x x ξ-∈；③求和：1()ni i b af n ξ=-∑；④取极限：()1()lim nbi an i b a f x dx f nξ→∞=-=∑⎰（3）曲边图形面积：()baS f x dx =⎰；变速运动路程21()t t S v t dt =⎰；变力做功 ()baW F r dr =⎰2．定积分的几何意义说明：一般情况下，定积分()baf x dx ⎰的几何意义是介于x 轴、函数()f x 的图形以及直线,x a x b ==之间各部分面积的代数和，在x 轴上方的面积取正号，在x 轴下方的面积去负号．（可以先不给学生讲）．分析：一般的，设被积函数()y f x =，若()y f x =在[,]a b 上可取负值。

定积分地概念教学案例设计

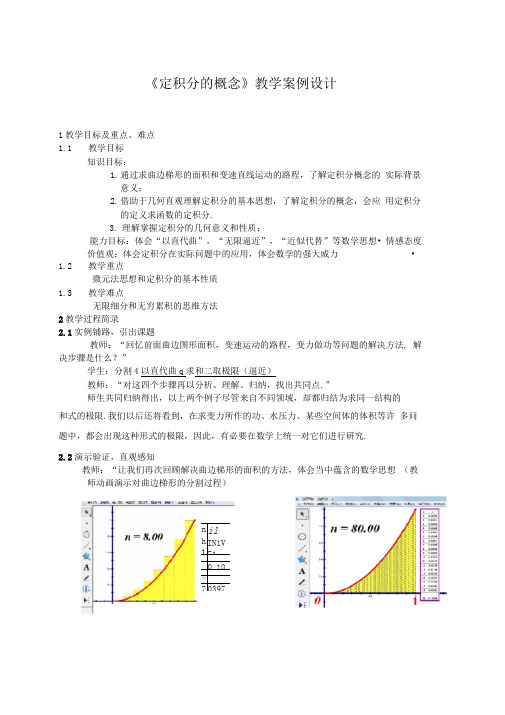
《定积分的概念》教学案例设计1教学目标及重点、难点 1.1 教学目标知识目标：1. 通过求曲边梯形的面积和变速直线运动的路程，了解定积分概念的实际背景意义；2. 借助于几何直观理解定积分的基本思想，了解定积分的概念，会应用定积分的定义求函数的定积分.3. 理解掌握定积分的几何意义和性质；能力目标：体会“以直代曲”，“无限逼近”，“近似代替”等数学思想• 情感态度价值观：体会定积分在实际问题中的应用，体会数学的强大威力 •1.2 教学重点微元法思想和定积分的基本性质1.3 教学难点无限细分和无穷累积的思维方法2教学过程简录2.1实例铺路，引出课题教师：“回忆前面曲边图形面积，变速运动的路程，变力做功等问题的解决方法, 解决步骤是什么？”学生：分割4以直代曲q 求和二取极限（逼近）教师：“对这四个步骤再以分析、理解、归纳，找出共同点.”师生共同归纳得出，以上两个例子尽管来自不同领域，却都归结为求同一结构的和式的极限.我们以后还将看到，在求变力所作的功、水压力、某些空间体的体积等许多问题中，都会出现这种形式的极限，因此，有必要在数学上统一对它们进行研究.2.2演示验证，直观感知教师：“让我们再次回顾解决曲边梯形的面积的方法，体会当中蕴含的数学思想（教师动画演示对曲边梯形的分割过程）n h 1 il IN1V 710.10斥7 0397这是曲边梯形的过剩近似值的拟合效果，请同学们再观察其不足近似值的动画演示教师：体现了哪些数学思想，哪位同学说说？学生1:以上对曲边梯形的无限分割体现了“无限逼近”的思想。

学生2:还有“近似代替”的思想，用不足近似值和过剩近似值代替曲边梯形的面积，以及“以直代曲”的思想.教师：这种求面积的方法具有普遍意义，为此，引入定积分的概念 .2.2.1定积分的概念设函数f(x)在区间［a,b ］上有定义，任意用分点a =x ° ：为：X 2 ：： X n =b将［a,b ］分成n 个小区间，用- X i -表示第i 个小区间的长度，在以亠人］上任取一点i ，作乘积f( ip X i ，i =1,2，…；n .再作和「之刚 F|藝冠口 I 抽週曲至ftE 9U.MI flW ：NE■□Ml H80.00^\o-■<J J.SWW ?dHflh-1J■fJ*1+nP.W?JjJJ riMi ；'•M JJ丨・■ M.-tjJjP几何®• iStfFJj - 1J» HffiKi M ：LI S.T1P9 ItJiQ 曲祈 q EfcAlMI S3S>NI 世團呵 *JiWl Httii .ruras- issi 対 7■龙轉” WL'<丘说吗MXI 3山 ±jfcM> ESN 罡SJ4 童二闻 ■團•■PHLrl-llTrl*ll.l<ll.li 上鼻丄鼻rLIJLd可L*丄 L* ;r.tTNitl »94 ；JZGt B ： uinrr im-ia» = SMI Of)n = 8000.00mlzxzzHEzJ p Ji J- Jn' f( i )厶X i .i 4若当，二max{.%} > 0时，上式的极限存在，则称函数f(x)在区间［a,b ］上可积，并称此1丈切 ™ 极限值为f(x)在［a,b ］上的定积分，记作bf(x)dx.即■ abnf (x)d^ljm^Z f (©)A x i .其中f (x)称为被积函数，f (x)dx 称为被积表达式，x 称为积分变量，［a,b ］称为积许多实际问题都可用定积分表示.例如，若变速直线运动的速度为 v(t)，则在时间区间［a,b ］上，物体经过的路程为bs 「a v(t)dt.⑵同理，图5-1所示的曲边梯形面积可表为bA 二 f (x)dx(3)ab变力做功W 二F(r)dr (4)I • f (x)在［a,b ］可积，是指不管对区间分划的方式怎样，也不管点［Xy,X i ］上如何选取，只要•》0 ,极限值总是唯一确定的.哪些函数是可积的呢？定理在闭区间［a,b ］上连续的函数必在［a,b ］上可积；在区间［a,b ］上有界且只有有限个间断点的函数也必在［a,b ］上可积.II •定积分是一个数，只取决于被积函数与积分区间，而与积分变量的记号无关, 即(1)a, b 分别称为积分下限和上限.i在小区间x图5-1bb baf (x)dx f (u)du f (t)dt.Ill .定义定积分时已假定下限a 小于上限b ，为便于应用，规定当b < a 时,b aaf(x)dx 二- b f(x)dx .af (x)dx 二 0 .a222定积分的几何意义bI .若f(x) _0,则积分a f(x)dx 表示如图所示的曲边梯形的面积，即bf (x)dx = A .ab特别地，当a=b 时，有［f (x)dx=O 。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1.5定积分的概念 教学设计 教案