三角函数与平面向量专题复习
高中二轮复习专题:三角函数与平面向量
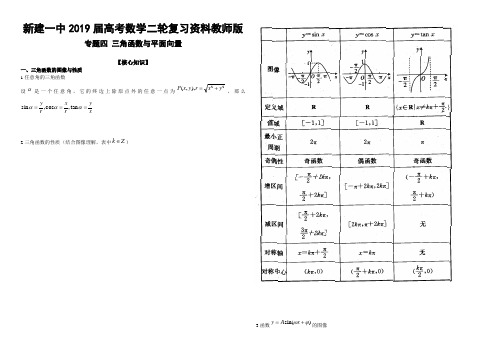
新建一中2019届高考数学二轮复习资料教师版专题四 三角函数与平面向量【核心知识】一、三角函数的图像与性质 1.任意角的三角函数设α是一个任意角,它的终边上除原点外的任意一点为22),,(y x r y x P +=,那么x y r x r y ===αααt a n ,c o s ,s i n .2.三角函数的性质(结合图像理解,表中Z k ∈)3.函数)sin(ϕω+=x A y 的图像(1)“五点法”作图:设ϕω+=x z ,令ππππ2,23,,2,0=z ,求出x 的值与相应的y 的值,描点、连线可得.(2)图像变换 ①xy sin=)sin(ϕ+=xy)sin(ϕω+=xy )0,0)(sin(>>+=ωϕωA x A y ②xy sin=xy ωsin=)sin(ϕω+=xy )0,0)(sin(>>+=ωϕωA x A y .二、三角恒等变换与解三角形1.和、差角公式:(1)βαβαβαsin sin cos cos )cos(=± (2)βαβαβαsin cos cos sin )sin(±=±(3)βαβαβαtan tan 1tan tan )tan( ±=±2.倍角公式:(1)2)2cos 2(sinsin 1;cos sin 22sin αααααα±=±=(2);sin 211cos 2sin cos 2cos 2222ααααα-=-=-=22c o s 1s i n ,22c o s 1c o s 22αααα-=+=(3)ααα2tan 1tan 22tan -=3.辅助角公式:)sin(cos sin 22ϕααα++=+b a b a (其中2222sin ,cos b a b ba a +=+=ϕϕ)4.正、余弦定理及三角形面积公式:(1)正弦定理:R C cB b A a 2sin sin sin ===(R 2为△ABC 外接圆的直径)(2)余弦定理:A bc c b a cos 2222-+=;B ac c a b cos 2222-+=;C ab b a c cos 2222-+=(3)三角形面积公式:Cab B ac A bc S ABC sin 21sin 21sin 21===∆.5.三角形中的常用结论:(1)三角形内角和定理:π=++C B A(2)C B A c b a C B A sin sin sin >>⇔>>⇔>> (3)B c C b a cos cos +=(4)已知两边及其一边的对角,判断三角形解的情况:以已知A b a ,,为例, (i )当A 为直角或钝角时,若b a >,则有一解;若b a ≤,则无解. (ii1.向量的概念(1)零向量模的大小为0,方向是任意的,它与任意非零向量都共线,记为.(2)长度等于1个单位长度的向量叫做单位向量,(3)方向相同或相反的向量叫共线向量(平行向量).(4)如果直线l 的斜率为k ,则),1(k =是直线l 的一个方向向量. (5><,叫做向量b 在向量a 方向上的投影.2.平面向量的运算(1)向量的加法、减法、数乘向量是向量运算的基础,应熟练掌握其运算规律.(2)平面向量数量积的结果是实数,而不是向量.要注意数量积运算与实数运算在运算律方面的差异,平面向量的数量积不满足结合律与消去律.><⋅=⋅b a b a ,cos .3.两非零向量平行、垂直的充要条件:若),(),,(2211y x b y x a ==,则 (1)a ∥⇔b 0)0(1221=-⇔≠=y x y x λλ.(2)a ⊥002121=+⇔=⋅⇔y y x x .(注意a 、为非零向量) 4.利用向量的数量积求线段的长度问题 (1)若),(y x =22y x +==.(2)若),(),,(2211y x B y x A ==212212)()(y y x x -+-==.5.求向量的夹角问题:设θ为a 与b 的夹角,则(1)b a =θcos .(2)若),(),,(2211y x y x ==,则222221212121cos y x y x y y x x +++=θ.(3)夹角大小的判定方法:a b a ⇔>⋅0与的夹角θ为锐角或零角; ⇔<⋅0与的夹角θ为钝角或平角; a b a ⇔=⋅0与的夹角为900. ),(≠≠【考点突破】热点一 三角函数图像与性质从近年高考试题命题情况来看,对三角函数图像与性质的考查是高考命题的热点和重点.试题主要以选择题的形式考查三角函数图像的对称轴、对称中心、单调性、最值等问题,题目难度较小;或以解答题的形式综合考查三角恒等变换、平面向量等知识,综合性较强.此类问题把解析式化为形如)sin(ϕω+=x A y 的一般式是解题的关键.例1.已知函数Rx x x x x x f ∈+-++-=,1cos 2cos sin 6)42sin(2)(2π.(1)求)(x f 的最小正周期;(2)求)(x f 在区间]2,0[π上的最大值和最小值. 【解析】(1)xx x x x f 2cos 2sin 34sin2cos 24cos2sin 2)(-+⋅-⋅-=ππ)42sin(222cos 22sin 2π-=-=x x x .所以)(x f 的最小正周期ππ==22T . (2)因为)(x f 在区间]83,0[π上是增函数,在区间]2,83[ππ上是减函数.又2)2(,22)83(,2)0(==-=ππf f f ,故函数)(x f 在区间]2,0[π的最大值为22,最小值为-2.例2.已知函数R x x A x f ∈+=),sin()(ϕω(其中20,0,0πϕω<<>>A )的图像与x 轴的交点中相邻两个交点之间的距离为2π且图像上一个最低点为)2,32(-πM .(1)求)(x f 的解析式;(2)当]2,12[ππ∈x 时,求)(x f 的值域. 【解析】(1)由已知易得:2=A 且ππωπ=⨯==222T ,得2=ω.)2sin(2)(ϕ+=x x f由232322ππϕπ+=+⨯k .Z k ∈得:62ππϕ+=k .∵20πϕ<<,∴6πϕ=.∴)62sin(2)(π+=x x f 为所求.(2)∵]2,12[ππ∈x ,∴]67,3[62πππ∈+x ,当262ππ=+x 即6π=x 时2)(max =x f . 当6762ππ=+x 即2π=x 时1)(min -=x f . ∴)(x f 值域为]2,1[-.热点二 三角函数图像的变换通过近年各地高考试题可以看出,三角函数图像的变换一直是这些年高考考查的热点,且试题常考常新.高考对三角函数图像变换的考查,常结合三角恒等变换、平面向量等知识进行综合考查. 例3.将函数)(sin cos 3R x x x y ∈+=的图像向左平移)0(>m m 个单位长度后,所得到的的图像关于y 轴对称,则m 的最小值是( )A. 12πB. 6πC. 3πD. 65π【解析】将函数)6cos(2sin cos 3π-=+=x x x y 的图像向左平移m 个单位后,得到函数)6cos(2m x y +-=π的图像,故m 的最小值是6π.【答案】B例4.函数)(x f 图像的横坐标伸长到原来的两倍,再向左平移2π个单位所得到的曲线是xy sin 21=,则函数)(x f =_______________. 【解析】(逆向变换)xy sin 21=)2sin(21π-=xyx x y 2cos 21)22sin(21-=-=π. ∴xx f 2cos 21)(-=为所求. 【答案】x2cos 21-.热点三 三角函数求值从近年高考试题的命题情况来看,高考对三角函数求值的考查题型有三类:①“给角求值”,即在不查表的前提下,通过三角恒等变换求三角函数式的值;②“给值求值”,即给出一些三角函数(或三角函数式)的值,求与之有关的其他三角函数式的值;③“给值求角”,即给出三角函数值,求出符合条件的角.例5.(1)若33)24c o s(,31)4c o s(,02,20=-=+<<-<<βπαπβππα,则)2co s(βα+等于( )A. 33B.33- C. 935 D. 96- 【解析】(1)∵20,31)4cos(πααπ<<=+,∴322)4sin(=+απ. 又∵02,33)24cos(<<-=-βπβπ,∴36)24cos(=-βπ. ∴)]24()4cos[()2cos(βπαπβα--+=+)24sin()4sin()24cos()4cos(βπαπβπαπ-++-+=935363223331=⨯+⨯= 【答案】C(2)设θ为第二象限角,若21)4tan(=+πθ,则θθcos sin +=____________.【解析】(2)∵21t a n 1t a n 1)4t a n (=-+=+θθπθ,∴31t a n -=θ,又θ为第二象限角,∴θθcos sin +510101031010-=-=.【答案】510-例6.(1))45tan 1)(44tan 1()2tan 1)(1tan 1(0000++++ =______________.【解析】(1)∵045=+βα时2)tan 1)(tan 1(=++βα, ∴原式⋅++⋅++=)]43tan 1)(2tan 1[()]44tan 1)(1tan 1[(0000 230002)]45tan 1[()]23tan 1)(22tan 1[(=+⋅++【答案】232(2)设)30cos(cos )(0x xx f -=,则=+++)59()2()1(000f f f __________.【解析】(2)∵)30cos()60cos()30cos(cos )60()(0000--+-=-+x x x x x f x f 3)30cos()30cos(3)30cos(sin 23cos 23000=--=-+=x x x xx∴原式2359)30()]31()29([)]58()2([)]59()1([0000000=+++++++=f f f f f f f【答案】2359热点四 平面向量的运算高考对平面向量的运算的考查常考常新,与平面向量数量积有关的问题(如向量共线、垂直及夹角等问题)是高考考查的重点.此类问题多以选择题、填空题的形式出现,有时也渗透在解答题中与其他知识交汇命题,综合考查学生分析问题、解决问题的能力.例7.已知向量παβββαα<<<==0),sin ,(cos ),sin ,(cos b a . (12=-,求证:a ⊥;(2)设)1,0(=,若c b a =+,求βα,的值. 【解析】(12=-,即22)(222=+⋅-=-b b a a b a .又因为122====,所以222=⋅-,即0=⋅b a ,故⊥b .(2)因为⊥=)1,0()sin sin ,cos (cos =++βαβα,所以⎩⎨⎧=+=+1sin sin 0cos cos βαβα,由此得, )cos(cos βπα-=,由πβ<<0,得πβπ<-<0,又πα<<0,故βπα-=.代入1s i n s i n =+βα得,21sin sin ==βα,而βα>,所以6,65πβπα==.例8.(1)等差数列{}n a 的前n 项和为n S 且36,1042==S S ,则过点),(n a n P 和))(,2(2*+∈+N n a n Q n 的直线的一个方向向量的坐标可以是( )A. )21,1( B. )2,21(-- C. )1,21(-- D.)21,2( 【解析】(1)由已知:⎩⎨⎧=+=+366410211d a d a ,得⎩⎨⎧==431d a ,∴422)2(2===-+-=+d dn n a a K n n PQ .易知:4212=--,∴)2,21(--为该直线的一个方向向量.【答案】B(2)已知)sin 2,cos 2(),2,2(),0,2(αα===,则OA 与OB 夹角范围是( )A.]4,0[πB. ]125,4[ππC. ]125,12[ππD. ]25,125[ππ【解析】由已知点A 为以)2,2(为圆心,2为半径的圆C 上一点,点)0,2(B ,数形结合易得∠AOB最大值为125π,最小值为12π.【答案】C热点五 解三角形“解三角形”不仅反映了三角形边、角间的联系,体现了数与形的结合,且问题易与三角函数图像与性质、简单三角恒等变换、平面向量等知识点联系,符合高考命题“要在知识点的交汇处命题”的要求.故解三角形问题也一直是历年高考热点. 例9.在△ABC 中,62,3==b a ,∠B=2∠A. (1)求cosA 的值; (2)求c 的值.【解析】(1)因为62,3==b a ,∠B=2∠A ,所以在△ABC 中,由正弦定理得A A 2sin 62sin 3=,所以362sin cos sin 2=A A A ,故36cos =A . (2)由(1)已知36cos =A ,所以33cos 1sin 2=-=A A ,又因为∠B=2∠A , 所以311cos 2cos 2=-=A B .所以322cos 1sin 2=-=B B . 在△ABC 中,935sin cos cos sin )sin(sin =+=+=B A B A B A C .所以5sin sin ==A Ca c .例10.若)0(23cos sin cos 3)(2>--=ωωωωx x x x f 的图像与直线)0(>=m m y 相切并且切点横坐标依次成公差为π的等差数列. (1)求ω和m 的值;(2)在△ABC 中a 、b 、c 分别是A 、B 、C 的对边,若)0,2(A是函数)(x f 图像的一个对称中心且4=a ,求△ABC 外接圆面积.【解析】(1)23cos sin cos 3)(2--=x x x x f ωωω)62cos(2sin 212cos 23πωωω+=-=x x x 易知:函数)(x f 周期为π且最大值为m ,∴1,1==m ω.(2)由已知:Z k k A ∈+=+⨯,2622πππ且π<<A 0得3π=A . 在△ABC 中设外接圆半径为R ,则338234sin 2===A a R 得334=R . ∴△ABC 外接圆面积为ππ3162==R S .热点六 解三角形的实际应用利用正、余弦定理解决与测量或几何计算有关的实际问题,也是对正、余弦定理的应用的考查,在近几年的新课标高考中也多有体现,主要是考查分析问题,解决实际问题的能力及计算能力. 例11.如图,游客从某旅游景区的景点A 处下山至C 处有两种路径.一种是从A 沿直线步行到C ,另一种是先从A 沿索道乘缆车到B ,然后从B 沿直线步行到C.现有甲、乙两位游客从A 处下山,甲沿AC 匀速步行,速度为50 m/min.在甲出发2min 后,乙从A 乘缆车到B ,在B 处停留1min 后,再从B 匀速步行到C.假设缆车匀速直线运动的速度为130m/min ,山路AC 长为1260m ,经测量,cosA=12/13,cosC=3/5. (1)求索道AB 的长;(2)问乙出发多少分钟后,乙在缆车上与甲的距离最短?(3)为使两位游客在C 处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?【解析】(1)在△ABC 中,因为53cos ,1312cos ==C A ,所以54sin ,135sin ==C A .从而C A C A C A C A B sin cos cos sin )sin()](sin[sin +=+=+-=π656354131253135=⨯+⨯=由正弦定理B ACC AB sin sin =,得10405465631260sin sin =⨯=⨯=C B AC AB (m).所以索道AB 的长为1040m.(2)假设乙出发t 分钟后,甲、乙两游客距离为d ,此时,甲行走了(100+50t)m ,乙距离A 处130tm ,所以由余弦定理得1312)50100(1302)130()50100(222⨯+⨯⨯-++=t t t t d)507037(2002+-=t t , 因13010400≤≤t ,即80≤≤t ,故当3735=t (min)时,甲、乙两游客距离最短.(3)由正弦定理B ACA BC sin sin =,得50013565631260sin sin =⨯=⨯=A BAC BC (m).乙从B 出发时,甲已走了550)182(50=++⨯(m),还需走710m 才能到达C.设乙步行的速度为v m/min ,由题意得3507105003≤-≤-v ,解得14625431250≤≤v ,所以为使两位游客在C 处互相等待的时间不超过3分钟,乙步行的速度应控制在]14625,431250[(单位:m/min )范围内.例12.(1)一水库大坝的横截面为梯形ABCD ,迎水坡AB 的坡度为1:3=i ,背水坡CD 的坡度为2:1=i .坝高36m ,坡顶宽BC=8m ,则AB=__________,AD=_____________。
-三角函数三角形平面向量高考常考14种题型解题方法

三角函数三角形平面向量高考常考题型解题方法本专题要特别小心: 1.平面向量的几何意义应用 2. 平面向量与三角形的综合 3. 三角形的边角互化4.向量的数量积问题等综合问题5. 向量夹角为锐角、钝角时注意问题6.三角形中角的范围7.正余弦定理综合。
【题型方法】(一)考查平面向量基本定理例1. 设D 为ABC ∆所在平面内一点,若3BC CD =,则下列关系中正确的是( ) A .1433AD AB AC =-+ B .1433AD AB AC =- C .4133AD AB AC =+ D .4133AD AB AC =-【解析】∵3BC CD = ∴AC −−AB =3(AD −−AC ) ∴AD =43AC −−13AB . 选C练习1.设四边形ABCD 为平行四边形,,.若点M ,N 满足,,则( )A .20B .15C .9D .6【解析】不妨设该平行四边形为矩形,以为坐标原点建立平面直角坐标系 则,故练习2. 如图,在ABC 中,D 是BC 的中点,E 在边AB 上,BE =2EA ,AD 与CE 交于点O .若6AB AC AO EC ⋅=⋅,则ABAC的值是_____【解析】如图,过点D 作DF //CE ,交AB 于点F ,由BE =2EA ,D 为BC 中点,知BF =FE =EA ,AO =OD()()()3632AO EC AD AC AE AB AC AC AE =-=+-()223131123233AB AC AC AB AB AC AB AC AB AC ⎛⎫⎛⎫=+-=-+- ⎪ ⎪⎝⎭⎝⎭22223211323322AB AC AB AC AB AC AB AC AB AC ⎛⎫=-+=-+= ⎪⎝⎭得2213,22AB AC =即3,AB AC =故3AB AC=(二)考察数形结合思想(如:向量与圆等图形的结合) 例2. 已知点A ,B ,C 在圆上运动,且ABBC ,若点P 的坐标为(2,0),则的最大值为( )A .6B .7C .8D .9 【解析】由题意,AC 为直径,所以当且仅当点B 为(-1,0)时,取得最大值7选B练习1. 在平面内,定点A ,B ,C ,D 满足==, = = =–2,动点P ,M 满足=1,=,则的最大值是( )A .B .C .D .【解析】甴已知易得以为原点,直线为轴建立平面直角坐标系,如图所示则设由已知,得又,它表示圆上的点与点的距离的平方的,选B练习2. 在矩形ABCD 中,AB =1,AD =2,动点P 在以点C 为圆心且与BD 相切的圆上.若AP =λAB +μAD ,则λ+μ的最大值为( ) A .3 B .22 C .5 D .2 【解析】如图,建立平面直角坐标系设()()()()0,1,0,0,2,1,,A B D P x y 根据等面积公式可得圆的半径是25,即圆的方程是()22425x y -+=()()(),1,0,1,2,0AP x y AB AD =-=-=若满足AP AB AD λμ=+,即21x y μλ=⎧⎨-=-⎩ ,,12x y μλ==- ,所以12xy λμ+=-+设12x z y =-+ ,即102xy z -+-= 点(),P x y 在圆()22425x y -+=上,所以圆心到直线的距离d r ≤,即221514z -≤+ ,解得13z ≤≤ 所以z 的最大值是3,即λμ+的最大值是3,选A(三).考查向量的数量积 例3. 已知向量,则ABC =( )A .30B .45C .60D .120 【解析】由题意,得,所以,选A【小结】(1)平面向量与的数量积为,其中是与的夹角,要注意夹角的定义和它的取值范围:;(2)由向量的数量积的性质知,,,因此,利用平面向量的数量积可以解决与长度、角度、垂直等有关的问题练习1. 已知是边长为4的等边三角形,为平面内一点,则的最小值是A .B .C .D .【解析】以BC 中点为坐标原点,建立如图所示的坐标系则A (0,2),B (﹣2,0),C (2,0),设P (x ,y )则=(﹣x ,2﹣y ),=(﹣2﹣x ,﹣y ),=(2﹣x ,﹣y )所以•(+)=﹣x •(﹣2x )+(2﹣y )•(﹣2y )=2x 2﹣4y +2y 2=2[x 2+(y ﹣)2﹣3]所以当x =0,y =时,•(+)取得最小值为2×(﹣3)=﹣6,选D练习2.在等腰梯形ABCD 中,已知//,2,1,60AB DC AB BC ABC ==∠= ,动点E 和F 分别在线段BC 和DC 上,且,1,,9BE BC DF DC λλ==则AE AF ⋅的最小值为 . 【解析】因为1,9DF DC λ=12DC AB = 119199918CF DF DC DC DC DC AB λλλλλ--=-=-==;AE AB BE AB BC λ=+=+19191818AF AB BC CF AB BC AB AB BC λλλλ-+=++=++=+ ()221919191181818AE AF AB BC AB BC AB BC AB BC λλλλλλλλλ+++⎛⎫⎛⎫⋅=+⋅+=+++⋅⋅ ⎪ ⎪⎝⎭⎝⎭19199421cos1201818λλλλ++=⨯++⨯⨯⨯︒21172117299218921818λλλλ=++≥⋅+= 当且仅当2192λλ=即23λ=时AE AF ⋅的最小值为2918BAD C E(四)考查三角形中的边角互化例 4. 在ABC ∆中,角,,A B C 的对边分别为a , b , c .若ABC ∆为锐角三角形,且满足()sin 12cos 2sin cos cos sin B C A C A C +=+,则下列等式成立的是( )A .2a b =B .2b a =C .2A B =D .2B A = 【解析】()sin 2sin cos 2sin cos cos sin A C B C A C A C ++=+所以2sin cos sin cos 2sin sin 2B C A C B A b a =⇒=⇒=,选A练习1. 在中,角,,所对应的边分别为,,.已知,则()A.一定是直角三角形B.一定是等腰三角形C.一定是等腰直角三角形D.是等腰或直角三角形【解析】由题,已知,由正弦定理可得:即又因为所以即由余弦定理:,即所以所以三角形一定是等腰三角形,选B练习2. 在中,,为边上的一点,且,若为的角平分线,则的取值范围为()A.B.C.D.【解析】因为,为的角平分线,所以在中,,因为,所以在中,,因为,所以,所以则因为,所以所以,则即的取值范围为,选A练习3. 在锐角三角形ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,已知,,,则的面积( ) A .B .C .D .【解析】由题,,所以所以 又因为锐角三角形ABC ,所以 由题,即根据代入可得,,即再根据正弦定理: 面积故选D练习4. 在锐角ABC ∆中,角AB C ,,的对边分别为a b c ,,.且cos cos A B a b +=33Ca,23b =a c +的取值范围为_____.【解析】cos cos 33A B C a b a +=23cos cos sin 3b A a B C ∴+= ∴由正弦定理可得: 23sin cos sin cos sin 3B A A B BC +=,可得:23sin()sin sin A B C B C +==,3sin B ∴=, 又ABC ∆为锐角三角形,3B π∴=,∴可得:sin sin 24(sin sin )4sin 4sin sin sin 3b A b C a c A C A A B B π⎛⎫+=+=+=+- ⎪⎝⎭33A π⎛⎫=- ⎪⎝⎭ 2,3A A π-均为锐角,可得:,62636A A πππππ<<-<-<,(6,43]a c ∴+∈.练习5. 在ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若sin cos cos sin sin sin ab Ca Bb A a A b Bc C+=+-,且3a b +=,则c 的取值范围为________________. 【解析】因为()sin sin sin cos cos sin C A B A B A B =+=+ 所以由正弦定理可得cos cos a B b A c +=, 又因为sin cos cos sin sin sin ab C a B b A a A b B c C+=+-,所以由正弦定理可得222abcc a b c =+- 即222a b c ab +-=,所以222c a b =+-2()3ab a b ab =+-, 因为3a b +=,所以293c ab =-,因为29()24a b ab +≤=, 当且仅当23==b a 时取等号,所以27304ab -≤-<, 所以99394ab ≤-<,即2994c ≤<,所以332c ≤<,故c 的取值范围为3[,3)2(五)三角形与向量综合 例5. 在△中,为边上的中线,为的中点,则( )A .B .C .D .【分析】首先将图画出来,接着应用三角形中线向量的特征,求得,之后应用向量的加法运算法则-------三角形法则,得到,之后将其合并,得到,下一步应用相反向量,求得,从而求得结果.【解析】根据向量的运算法则,可得,所以,故选A .练习1. 已知中,为的重心,则()A.B.C.D.【解析】因为中,为的重心,所以,由余弦定理可得:且所以=练习2. 下列命题中,①在中,若,则为直角三角形;②若,则的最大值为;③在中,若,则;④在中,,若为锐角,则的最大值为.正确的命题的序号是______【解析】①在中,若,可得或,则为直角或钝角三角形,故①错;②若时,即,即垂直,则的最大值为,故②正确;③在中,若,,即,即,,即为,由,可得,故③正确;④在中,,即为,即为,可得,即,可得锐角,可得时,的最大值为,故④正确故答案为:②③④练习3. 在ABC 中, 60A ∠=︒, 3AB =, 2AC =. 若2BD DC =, ()AE AC AB R λλ=-∈,且4AD AE ⋅=-,则λ的值为______________. 【解析】01232cos603,33AB AC AD AB AC ⋅=⨯⨯==+ 则()1221233493433333311AD AE AB AC AC AB λλλλ⎛⎫⋅=+-=⨯+⨯-⨯-⨯=-⇒= ⎪⎝⎭(六)向量与三角函数综合例6. 自平面上一点O 引两条射线OA ,OB ,点P 在OA 上运动,点Q 在OB 上运动且保持PQ 为定值a (点P ,Q 不与点O 重合),已知3AOB π∠=,7a =,则3||||PQ PO QP QOPO QO ⋅⋅+的取值范围为( )A .1,72⎛⎤⎥⎝⎦B .7,72⎛⎤⎥ ⎝⎦C .1,72⎛⎤- ⎥⎝⎦D .7,72⎛⎤- ⎥ ⎝⎦【解析】设OPQ α∠=,则23PQO πα∠=- 322cos 3cos 7cos 3cos 33PQ PO QP QO PQ QP POQO ππαααα⋅⋅⎫⎛⎫⎛⎫+=+-=+- ⎪ ⎪⎪⎝⎭⎝⎭⎭()3331337cos cos 7cos 7sin 22ααααααϕ⎫⎫=-=-+=-⎪⎪⎪⎪⎭⎭其中3tan 9ϕ=,则7sin 14ϕ=20,3πα⎛⎫∈ ⎪⎝⎭,∴当()sin 1αϕ-=时,原式取最大值7 ()()7sin sin 0sin 14αϕϕϕ->-=-=-,∴()77sin 2αϕ->- 37,72PQ PO QP QO PO QO ⎛⎤⋅⋅+∈- ⎥ ⎝⎦∴,选D练习1. 在同一个平面内,向量的模分别为与的夹角为,且与的夹角为,若,则_________.【解析】以为轴,建立直角坐标系,则, 由的模为与与的夹角为,且知,,可得,,由可得 ,(七)三角形中的最值 例7. 在中,内角所对的边分别为.已知,,,设的面积为,,则的最小值为_______. 【解析】在中,由得, 因为利用正弦定理得,再根据,可得,,,由余弦定理得,求得,所以,所以 ,所以,当且仅当,即时取等,所以 的最小值为。
高考数学大二轮复习专题一平面向量、三角函数与解三角形第一讲平面向量课件理

-b)⊥b,则 a 与 b 的夹角为( )
π
π
A.6
B.3
C.23π
D.56π
解析:由(a-b)⊥b,可得(a-b)·b=0,∴a·b=b2.
∵|a|=2|b|,∴cos〈a,b〉=|aa|··|bb|=2bb22=12.
∵0≤〈a,b〉≤π,∴a 与 b 的夹角为π3.故选 B. 答案:B
4.(2019·恩施州模拟)已知向量 a=(1, 3),b=-12, 23,则
3.(2019·河北衡水中学模拟)已知 O 是平面上一定点,A,B,
C
是平面上不共线的三点,动点
P
满
足
→ OP
=
O→B+O→C 2
+
λ
→ AB →
→
+
AC →
,λ∈[0,+∞),则点 P 的轨迹经过△
|AB|cos B |AC|cos C
ABC 的( )
A.外心
B.内心
C.重心
D.垂心
解析:设
答案:A
4.(2018·高考全国卷Ⅲ)已知向量 a=(1,2),b=(2,-2),c= (1,λ).若 c∥(2a+b),则 λ=________.
解析:2a+b=(4,2),因为 c∥(2a+b),所以 4λ=2,得 λ=12. 答案:12
[类题通法] 1.应用平面向量基本定理表示向量的实质是利用 平行四边形法则或三角形法则进行向量的加、减或数乘运 算.一般将向量归结到相关的三角形中,利用三角形法则列出 三个向量之间的关系. 2.用平面向量基本定理解决问题的一般思路:先选择一组基 底,并运用该组基底将条件和结论表示成向量的形式,再通过 向量的运算来解决.注意同一个向量在不同基底下的分解是不 同的,但在每组基底下的分解都是唯一的.
三角向量

三角函数和平面向量专题复习一.高考考试内容及要求:1.三角函数考试要求:(1)了解任意角的概念、弧度的意义,能正确地进行弧度与角度的换算.(2)理解任意角的正弦、余弦、正切的定义.了解余切、正割、余割的定义;掌握同角三角函数的基本关系式,掌握正弦、余弦的诱导公式,了解周期函数与最小正周期的意义;(3)掌握两角和与两角差的正弦、余弦、正切公式;掌握二倍角的正弦、余弦、正切公式; (4)能正确运用三角公式,进行简单三角函数式的化简、求值和恒等式证明;(5)理解正弦函数、余弦函数、正切函数的图像和性质,会用“五点法”画正弦函数、余弦函数和函数y=Asin(ωx+φ)的简图,理解A 、ω、φ的物理意义;(6)会由已知三角函数值求角,并会用符号arcsinx arccosx arctanx 表示;(7)掌握正弦定理、余弦定理,并能初步运用它们解斜三角形。
2. 平面向量考试要求:(1)理解向量的概念,掌握向量的几何表示,了解共线向量的概念; (2)掌握向量的加法和减法;(3)掌握实数与向量的积,理解两个向量共线的充要条件;(4)了解平面向量的基本定理,理解平面向量的坐标的概念,掌握平面向量的坐标运算;(5)掌握平面向量的数量积及其几何意义,了解用平面向量的数量积可以处理有关长度、角度和垂直的问题,掌握向量垂直的条件;(6)掌握平面两点间的距离公式以及线段的定比分点和中点坐标公式,并且能熟练运用.掌握平移公式。
二.走进高考1.(05年1).函数f (x )=|sin x +cos x |的最小正周期是( C )A .4π B .2πC .πD .2π 2.(05年4)已知函数)2,2(tan ππω-=在x y 内是减函数,则( B )A .0<ω≤1B .-1≤ω<0C .ω≥1D .ω≤-13.(05年7)锐角三角形的内角A 、B 满足tanA -A2sin 1=tanB ,则有 ( A )A .sin2A -cosB=0B .sin2A+cosB=0C .sin2A -sinB=0D .sin2A+sinB=04.(05年8)已知点A (3,1),B (0,0)C (3,0).设∠BAC 的平分线AE 与BC 相交于E , 那么有λλ其中,CE BC =等于 ( C )A .2B .21 C .-3D .-315.(06年5)函数()tan f x x π⎛⎫=+⎪4⎝⎭的单调增区间为(C ) A.k k k ππ⎛⎫π-π+∈ ⎪22⎝⎭Z ,,B.()k k π(+1)π,,k ∈ZC.k k k 3ππ⎛⎫π-π+∈ ⎪44⎝⎭Z ,, D.k k k π3π⎛⎫π-π+∈ ⎪44⎝⎭Z,,6.(06年6)ABC △的内角A 、B 、C 的对边分别为a 、b 、c ,若a 、b 、c 成等比数列,且2c a =,则cos B =(B )A .41 B .43 C .42 D .327.(06年文1).已知向量a 、b 满足|a |=1,|b |=4,且a ·b =2,则a 与b 的夹角为( C )A .6π B .4π C .3π D .2π8.(06年理9).设平面向量123,,a a a 的和1230++=a a a .如果平面向量123,,b b b ,满足2=i i b a ,且i a 顺时针旋转30 后与i b 同向,其中123i =,,,则(D ) A.123-++=0b b b B.123-+=0b b b C.123+-=0b b b D.123++=0b b b9.(07年1)α是第四象限角,5tan 12α=-,则sin α=( D )A .15B .15-C .513D .513-10.(07年文10)函数22cos y x =的一个单调增区间是(D )A.ππ44⎛⎫-⎪⎝⎭,B.π02⎛⎫ ⎪⎝⎭, C.π3π44⎛⎫⎪⎝⎭,D.ππ2⎛⎫⎪⎝⎭, 11.(07年理12)函数22()cos 2cos 2x f x x =-的一个单调增区间是(A )A .233ππ⎛⎫ ⎪⎝⎭, B .62ππ⎛⎫ ⎪⎝⎭, C .03π⎛⎫⎪⎝⎭,D .66ππ⎛⎫-⎪⎝⎭, 12.(07年3)已知向量(56)=-,a ,(65)=,b ,则a 与b (A ) A .垂直B .不垂直也不平行C .平行且同向D .平行且反向13.(08年3).在ABC △中,AB = c ,AC = b .若点D 满足2BD D C = ,则AD = ( A )A .2133+b c B .5233-c b C .2133-b c D .1233+b c答: A. 由()2AD AB AC AD -=- ,322AD AB AC c b =+=+ ,1233AD c b =+;14.(08年文6).2(s i n c o s )1y x x =--是( D )A .最小正周期为2π的偶函数B .最小正周期为2π的奇函数C .最小正周期为π的偶函数D .最小正周期为π的奇函数15.(08年8).为得到函数πcos 23y x ⎛⎫=+ ⎪⎝⎭的图像,只需将函数sin 2y x =的图像( A ) A .向左平移5π12个长度单位 B .向右平移5π12个长度单位C .向左平移5π6个长度单位 D .向右平移5π6个长度单位答:A.55cos 2sin 2sin 2,3612y x x x πππ⎛⎫⎛⎫⎛⎫=+=+=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭只需将函数s i n 2y x =的图像向左平移5π12个单位得到函数πcos 23y x ⎛⎫=+⎪⎝⎭的图像.16. (06年理16)设函数())(0)f x ϕϕ=+<<π,若()()f x f x '+是奇函数,则ϕ=π6.17. (06年17)ABC △的三个内角为A B C ,,,求当A 为何值时,cos 2cos 2B C A ++取得最大值,并求出这个最大值.解:由πA B C ++=,得π222B C A +=-,所以有cos sin 22B C A +=.23)212(sin22sin 22sin212sin 2cos 2cos2cos 22+--=+-=+=++A A A A A C B A当1sin22A =,即π3A =时,cos 2cos 2B C A ++取得最大值32.18.(07年文17)(本小题满分10分)设锐角三角形ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,2sin a b A =.(Ⅰ)求B 的大小;(Ⅱ)若a =5c =,求b .解:(Ⅰ)由2sin a b A =,根据正弦定理得sin 2sin sin A B A =,所以1sin 2B =,由ABC △为锐角三角形得π6B =.(Ⅱ)根据余弦定理,得2222cos b a c ac B =+-272545=+-7=.所以,b =19.(07年理17)设锐角三角形ABC 的内角A B C ,,的对边分别为a b c ,,,2sin a b A =. (Ⅰ)求B 的大小;(Ⅱ)求cos sin A C +的取值范围. 解:(Ⅰ)由2sin a b A =,根据正弦定理得sin 2sin sin A B A =,所以1sin 2B =,由ABC △为锐角三角形得π6B =.(Ⅱ)cos sin cos sin A C A A π⎛⎫+=+π-- ⎪6⎝⎭cos sin 6A A π⎛⎫=++ ⎪⎝⎭1cos cos sin 22A A A =++3A π⎛⎫=+ ⎪⎝⎭.由ABC △为锐角三角形知,2B A π>+,A>2263B ππππ-=-=,653A 32π<π+<π,所以23)3A sin(21<π+<,由此有232A π⎛⎫<+< ⎪⎝⎭所以,cos sin A C +的取值范围为322⎛⎫ ⎪ ⎪⎝⎭,.20.(08年文17)设ABC △的内角A B C ,,所对的边长分别为a b c ,,,且cos 3a B =,sin 4b A =. (Ⅰ)求边长a ;(Ⅱ)若ABC △的面积10S =,求ABC △的周长l . 解:(1)由cos 3a B =与sin 4b A =两式相除,有:3cos cos cos cot 4sin sin sin a BaBb B B b A A bBb====又通过cos 3a B =知:cos 0B >, 则3cos 5B =,4sin 5B =,则5a =.(2)由1sin 2S ac B =,得到5c =.由222cos 2a c bB ac+-=,解得:b =10l =+.21.(08年理17).设ABC △的内角A B C ,,所对的边长分别为a b c ,,,且3cos cos 5a Bb Ac -=.(Ⅰ)求tan cot A B 的值;(Ⅱ)求tan()A B -的最大值. 解:(Ⅰ)在ABC △中,由正弦定理及3cos cos 5a B b A c -=可得3333sin cos sin cos sin sin()sin cos cos sin 5555A B B A C A B A B A B -==+=+即sin cos 4cos sin A B A B =,则tan cot 4A B =;(Ⅱ)由tan cot 4A B =得tan 4tan 0A B => 2tan tan 3tan 3tan()1tan tan 14tan cot 4tan A B BA B A BBB B--===+++≤34当且仅当14t a n c o t ,t a n,t a n 22B B B A ===时,等号成立,故当1tan 2,tan 2A B ==时,t a n ()A B -的最大值为34.三.例题精讲例1.(2006年安徽卷).已知310,tan cot 43παπαα<<+=-(Ⅰ)求tan α的值;(Ⅱ)求225sin8sincos11cos822222ααααπα++-⎛⎫- ⎪⎝⎭的值。
2024届高三数学二轮复习专题集训专题3三角函数与平面向量31

2024届高三数学二轮复习专题集训专题3三角函数与平面向量312024届高三数学二轮复习专题集训专题3三角函数与平面向量31三角函数与平面向量是高中数学中的重要内容,也是数学二轮复习中的重点。
学好这一部分知识点,对于提高数学成绩至关重要。
本文将重点介绍2024届高三数学(理)二轮复习专题集训中的专题3三角函数与平面向量的内容,包括三角函数的基本概念、性质和一些重要公式,以及平面向量的基本概念、运算法则和应用等内容。
首先,我们来介绍三角函数的基本概念和性质。
三角函数有正弦函数、余弦函数、正切函数等,它们代表了角度和直角三角形边之间的关系。
正弦函数表示的是一个角的对边与斜边的比值,余弦函数表示的是一个角的邻边与斜边的比值,正切函数表示的是一个角的对边与邻边的比值。
三角函数的周期都是360度或2π弧度,可以通过函数图像的变化规律和一些基本特点进行分析和运用。
在学习三角函数的过程中,我们要掌握一些基本的三角函数公式,例如,和差化积公式、倍角公式、半角公式等。
这些公式可以帮助我们简化复杂的三角函数表达式,转化为更简单的形式,从而更好地解决问题。
接下来,我们介绍平面向量的基本概念和运算法则。
平面向量是具有大小和方向的量,可以用箭头表示。
平面向量有加法和乘法(数量乘法和点乘)两种运算法则。
向量加法满足交换律、结合律和有零向量的存在性质,可以通过平行四边形法则和三角法则进行计算。
向量乘法有数量乘法和点乘法。
数量乘法是将向量与一个实数相乘,使向量的长度发生变化,方向与原来一致(或相反)。
点乘法是将两个向量的对应分量相乘再相加,得到的是一个实数,表示了两个向量之间的夹角关系。
最后,我们要了解平面向量的应用。
平面向量在几何、力学等领域中有着广泛的应用。
例如,可以使用向量来表示平面上的几何图形,计算它们的面积、周长等属性。
还可以使用向量进行力的合成、分解和计算,探究力的平衡、作用和应用等。
此外,还可以利用向量的性质解决一些几何问题,例如直线的垂直、平行关系,点和直线的位置关系等。
专题二三角函数、平面向量

图 5-1
第5讲 │ 要点热点探究
(2)要得到函数
y=cos(2x+π3)的图象,只需将函数
y=12sin2x+
3 2
cos2x 的图象( )
例 3 [2011·安徽卷] 已知函数 f(x)=sin(2x+φ),其中 φ 为实
数,若 f(x)≤f
π6对 x∈R 恒成立,且 f
π2>f(π),则 f(x)的单调
递增区间是( )
A.kπ-π3,kπ+π6(k∈Z)
B.kπ,kπ+π2(k∈Z)
C.kπ+π6,kπ+23π(k∈Z)
D.kπ-π2,kπ(k∈Z)
sinπ4+αsinπ4-β2=13×
33+2 3 2×
36=5
9
3 .
第5讲 │ 要点热点探究
(2)sincoαs-2απ4=
cos2α-sin2α =cosα+sinαcosα-sinα
22sinα-cosα
22sinα-cosα
=- 2(cosα+sinα),
∵sinα=12+cosα,∴cosα-sinα=-12,
专题二 │ 考情分析预测
备考策略
由于该专题内容基础,高考试题的难度不大,经过一轮复习的学生 已经达到了高考的要求,二轮复习就是在此基础上进行的巩固和强化, 在复习中注意如下几点:
(1)该专题具有基础性和工具性,虽然没有什么大的难点问题,但 包含的内容非常广泛,概念、公式、定理很多,不少地方容易混淆, 在复习时要根据知识网络对知识进行梳理,系统掌握其知识体系.
专题复习解三角形与平面向量

1.三角形的有关公式:(1)在△ABC 中:sin(A +B )= ,sinA +B2= (2)正弦定理:(3)余弦定理: _____________________________________________________________________ (4)面积公式:S =12ah a =12ab sin C =12r (a +b +c )(其中r 为三角形内切圆半径).2.平面向量的数量积a ·b = .特别地,a 2=a·a =|a|2,|a|=a 2.当θ为锐角时,a ·b >0,且a·b >0是θ为锐角的必要非充分条件;当θ为钝角时,a·b <0,且a·b <0是θ为钝角的必要非充分条件.3.b 在a 上的射影为|b |cos_θ. 4.平面向量坐标运算设a =(x 1,y 1),b =(x 2,y 2),且a≠0,b≠0,则:(1)a·b = ;(2)|a |= ,a 2=|a |2= ; (3)a ∥b ⇔a =λb ⇔ =0;(4)a ⊥b ⇔a ·b =0⇔|a +b |=|a -b |⇔ =0.(5)若a 、b 的夹角为θ,则cos θ= = . 5.△ABC 中向量常用结论(1)PA →+PB →+PC →=0⇔P 为△ABC 的 ; (2)PA →·PB →=PB →·PC →=PC →·PA →⇔P 为△ABC 的 ;(3)向量λ⎝ ⎛⎭⎪⎪⎫AB →|AB →|+AC →|AC →|(λ≠0)所在直线过△ABC 的 ;(4)|PA →|=|PB →|=|PC →|⇔P 为△ABC 的 . 考点一 解三角形例 1-1设△ABC 的三个内角A ,B ,C 所对的边分别为a ,b ,c ,若b =2,B =π3,C =π4,则△ABC 的面积为( )A .1+33 +1 C .1-33-1 例 1-2△ABC 中,已知3b =23a sin B ,角A ,B ,C 成等差数列,则△ABC 的形状为( ) A .直角三角形 B .等腰三角形 C .等边三角形 D .等腰直角三角形 例 1-3若△ABC 的三个内角满足sin A ∶sin B ∶sin C =5∶11∶13,则△ABC ( ) A .一定是锐角三角形 B .一定是直角三角形C .一定是钝角三角形D .可能是锐角三角形,也可能是钝角三角形变式训练【1-1】设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .若a =2,c =23,cos A =32,且b <c ,则【1-2】设△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,若b cos C +c cos B =a sin A ,则△ABC 的形状为( ) A .直角三角形 B .锐角三角形 C .钝角三角形 D .不确定 【1-3】在锐角△ABC 中,AB =3,AC =4,S △ABC =33,则BC =( ) A .5 或37例 1-4已知A 、B 、C 分别为△ABC 的三边a 、b 、c 所对的角,向量m =(sin A ,sin B ),n =(cos B ,cos A ),且m ·n = sin 2C . (1)求角C 的大小;(2)若sin A ,sin C ,sin B 成等差数列,且CA →·(AB →-AC →)=18,求边c 的长.变式训练 【1-4】 (2015·兰州诊断)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,已知a3cos A=csin C .(1)求A 的大小; (2)若a =6,求b +c 的取值范围.【1-5】 (2014·黄冈模拟)△ABC 的外接圆的直径为1,三个内角A 、B 、C 的对边为a 、b 、c ,m =(a ,cos B ),n =(cos A ,-b ),a ≠b ,已知m ⊥n .(1)求sin A +sin B 的取值范围;(2)若abx =a +b ,试确定实数x 的取值范围.例 1-5如图,渔船甲位于岛屿A 的南偏西60°方向的B 处,且与岛屿A 相距12海里,渔船乙以10海里/时的速度从岛屿A 出发沿正北方向航行,若渔船甲同时从B 处出发沿北偏东α的方向追赶渔船乙,刚好用2小时追上.(1)求渔船甲的速度;(2)求sin α的值.变式训练【1-6】如图,游客从某旅游景区的景点A C 处有两种路径.一种是从A 沿直线步行到C ,另一种是先从A 沿索道乘缆车到B ,然后从B 沿直线步行到C .现有甲、乙两位游客从A 处下山,甲沿AC 匀速步行,速度为50 m/min.在甲出发2 min 后,乙从A 乘缆车到B ,在B 处停留1 min 后,再从B 匀速步行到C .假设缆车匀速直线运行的速度为130 m/min ,山路AC 长为1 260 m ,经测量,cos A =1213,cos C =35.(1)求索道AB 的长;(2)问乙出发多少分钟后,乙在缆车上与甲的距离最短(3)为使两位游客在C 处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内考点二 平面向量例 2-1已知正三角形ABC 的顶点A (3,1),B (33,1),顶点C 在第一象限,若点M (x ,y )在△ABC 的内部或边界,则z =OA →·OM →取最大值时,3x 2+y 2有( )A .定值52B .定值82C .最小值52D .最小值50例 2-2如图所示,在平行四边形ABCD 中,已知AB =8,AD =5,CP →=3PD →,AP →·BP →=2,则AB →·AD →的值是________.例 2-3如图在等腰直角△ABC 中,点O 是斜边BC 的中点,过点O 的直线分别交直线AB 、AC 于不同的两点M 、N ,若AB →=mAM →,AC →=nAN →,则mn 的最大值为( )B .1C .2D .3变式训练【2-1】设a =(a 1,a 2),b =(b 1,b 2),定义一种向量积a ·b =(a 1,a 2)·(b 1,b 2)=(a 1b 1,a 2b 2).已知m =⎝ ⎛⎭⎪⎫2,12,n =⎝ ⎛⎭⎪⎫π3,0,点P (x ,y )在y =sinx 的图象上运动,点Q 在y =f (x )的图象上运动,且满足OQ →=m ·OP →+n (其中O 为坐标原点),则y =f (x )的最大值为________.【2-2】在△ABC 中,∠ACB 为钝角,AC =BC =1,CO →=xCA →+yCB →且x +y =1,函数f (m )=|CA →-mCB →|的最小值为32,则|CO →|的最小值为______.易错题在△ABC 中,sin A +cos A =22,AC =2,AB =3,求tan A 的值和△ABC 的面积.练习题1.向量a =(1,-1),b =(-1,2),则(2a +b )·a =( ) A .-1 B .0 C .1 D .2 2.在△ABC 中,若sin 2A +sin 2B <sin 2C ,则△ABC 的形状是( ) A .锐角三角形 B .直角三角形 C .钝角三角形D .不能确定 3.在△ABC 中,AB =2,AC =3,AB →·BC →=1,则BC =( ) C .2 24.锐角△ABC 中,若A =2B ,则a b的取值范围是( )A .(1,2)B .(1,3)C .(2,2)D .(2,3) 5.如图,在△ABC 中,D 是边AC 上的点,且AB =AD ,2AB =3BD ,BC =2BD ,则sin C 的值为( )6.如图,从气球A 上测得正前方的河流的两岸B 、C 的俯角分别为75°、30°,此时气球的高是60 m ,则河流的宽度BC 等于( )A .240(3-1) mB .180(2-1) mC .120(3-1) mD .30(3+1) m7.记max{x ,y }=⎩⎪⎨⎪⎧x ,x ≥y ,y ,x <y ,min{x ,y }=⎩⎪⎨⎪⎧y ,x ≥y ,x ,x <y ,设a ,b 为平面向量,则( ) A .min{|a +b |,|a -b |}≤min{|a |,|b |} B .min{|a +b |,|a -b |}≥min{|a |,|b |} C .max{|a +b |2,|a -b |2}≤|a |2+|b |2D .max{|a +b |2,|a -b |2}≥|a |2+|b |28.如图为函数f (x )=3sin(ωx +φ)(ω>0)的部分图象,B ,C 分别为图象的最高点和最低点,若AB →·BC →=|AB →|2,则ω=( )9.设△ABC 的内角A 、B 、C 所对的边长分别为a 、b 、c ,且a cos B -b cos A =35c ,则tan Atan B 的值为______.10.在△ABC 中,内角A 、B 、C 所对的边分别为a ,b ,c ,已知△ABC 的面积为315,b -c =2,cos A =-14,则a 的值为________.11.如图,一辆汽车在一条水平的公路上向正西行驶,到A 处时测得公路北侧一山顶D 在西偏北30°的方向上,行驶600 m 后到达B 处,测得此山顶在西偏北75°的方向上,仰角为 30°,则此山的高度CD =________m.12.△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .已知a =3,cos A =63,B =A +π2. (1)求b 的值; (2)求△ABC 的面积.13.△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,向量m =(a ,3b )与n =(cos A ,sin B )平行. (1)求A ; (2)若a =7,b =2,求△ABC 的面积.14.在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .已知tan ⎝⎛⎭⎪⎫π4+A =2. (1)求sin 2A sin 2A +cos 2A 的值; (2)若B =π4,a =3,求△ABC 的面积.15.已知向量m =(cos x ,-1),n =⎝ ⎛⎭⎪⎫sin x ,-32,f (x )=(m -n )·m . (1)求函数f (x )的单调递增区间; (2)锐角△ABC 中角A ,B ,C 的对边分别为a ,b ,c ,其面积S =3,f ⎝⎛⎭⎪⎫A -π8=-24,a =3,求b +c 的值.。
高考数学一轮总复习三角函数、三角形、平面向量专题12平面向量的概念及其线性运算文(含解析)

专题12平面向量的概念及其线性运算一、本专题要特别小心:1.向量加减的几何意义2. 向量共线的问题3. 零向量问题4.向量夹角为锐角和钝角问题5.基本定理的两条路径法表示向量6.向量共线与三点共线的区别与联系7.向量的模与夹角的运算及应用问题8.平行与垂直问题二.【学习目标】1.理解平面向量的概念,理解两个向量相等的含义;理解向量的几何表示.2.掌握向量的加法、减法的运算,并理解其几何意义.3.掌握向量数乘的运算及其几何意义,理解两个向量共线的含义.4.了解向量线性运算的性质及其几何意义.三.【方法总结】1.向量线性运算技巧(1)用已知向量表示与其相关的另外一些向量时,在运用向量的加法、减法、数乘运算的同时,应充分利用平面几何的一些基本定理.(2)在求向量时尽可能转化到某平行四边形或三角形内,以便运用平行四边形法则和三角形法则,涉及到线段比时,一方面考虑平行线定理,另一方面充分运用数乘运算的几何意义.2.向量共线问题(1)向量共线的充要条件中要注意当两向量共线时,通常只有非零向量才能表示与之共线的其他向量,要注意待定系数法和方程思想的运用.(2)证明三点共线问题,可用向量共线来解决,但应注意向量共线与三点共线的区别与联系,当两向量共线且有公共点时,才能得出三点共线. 四.【题型方法】(一)向量共线与三点共线 例1.下列说法正确的是( )A .若||=||a b ,则a 、b 的长度相等且方向相同或相反B .若向量AB 、CD 满足||||AB CD >,且AB 与CD 同向,则AB CD >C .若a b ≠,则a 与b 可能是共线向量D .若非零向量AB 与CD 平行,则A 、B 、C 、D 四点共线 【答案】C【解析】对于A 选项,模相等的向量,方向不一定相同或者相反,也可能垂直,或者成其它的角度,故A 选项错误.对于B 选项,向量不能用大于或者小于号相连,向量的模可以比较大小,故B 选项错误.对于C 选项,不相等的向量可以共线,故C 选项正确.对于D 选项,平行向量不一定是共线的,故B 选项错误.综上所述,本小题选C.练习1.下列说法中正确的是( ) A .单位向量都相等B .平行向量不一定是共线向量C .对于任意向量a ,b ,必有D .若a ,b 满足a b >且a 与b 同向,则a b >【答案】C【解析】对于A,单位向量模都相等,方向不一定相同,故错误,对于B,平行向量就是共线向量,对于C,若a ,b 同向共线,,若a ,b 反向共线,,若a ,b 不共线,根据向量加法的三角形法则及两边之和大于第三边知,综上可知对于任意向量a ,b ,必有正确,对于D,两个向量不能比较大小,故错误.故选C.练习2.设,a b 是非零向量,则“存在实数λ,使得a b λ=”是“”的A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件【答案】B【解析】存在实数λ,使得a b λ=, 说明向量,a b 共线,当,a b 同向时,成立,当,a b 反向时,不成立,所以,充分性不成立.当成立时,有,a b 同向,存在实数λ,使得a b λ=成立,必要性成立,即“存在实数λ,使得a b λ=”是“”的必要而不充分条件.故选:B .练习3.下列命题正确的是( ) A .与共线,与共线,则与也共线B .任意两个相等的非零向量的始点与终点是一平行四边形的四顶点C .向量与不共线,则与都是非零向量D .有相同起点的两个非零向量不平行 【答案】C【解析】由于零向量与任意向量都共线,所以当是零向量时,与不一定共线,故A 不正确; 由于数学中研究的向量是自由向量,所以两个相等的非零向量可以在同一直线上, 而此时不能构成四边形,所以不可能是一个平行四边形的四个顶点,故B 不正确; 零向量与任意向量都共线,故C 正确;向量的平行只要方向相同或相反即可,与起点是否相同无关,故D 不正确. 故选C.练习4.下列说法正确的个数为( ) (1)共线的两个单位向量相等; (2)相等向量的起点相同; (3)若,则一定有直线;(4)若向量,共线,则点A ,B ,C ,D 必在同一直线上.A .0B .1C .2D .3【答案】A【解析】(1)错,共线的两个单位向量的方向可能相反; (2)错,相等向量的起点和终点都可能不相同; (3)错,直线与可能重合;(4)错,与可能平行,则四点不共线.故选A.(二)向量的模 例2. 向量的夹角为,,,则的最大值为( ) A .B .C .D .【答案】C 【解析】又本题正确选项:练习1.对于任意向量a ,b ,下列命题中正确的是( ) A .如果a ,b 满足a b >,且a 与b 同向,则a b > B . C .D .【答案】B【解析】选项A 中,向量不能进行比较大小,所以错误; 选项B 中,两边平方,整理化简得a b a b ⋅≤⋅,即,所以正确;选项C 中,当a 与b 同向时,,所以错误;选项D 中,当a b <时,,不成立,所以错误.故选B 项.练习2. 已知平面向量,则2a b +=( )A .B .3C .12x x D .5【答案】A 【解析】因为,所以,因此.故选A(三)向量加减运算法则的几何意义例3.在四边形ABCD 中,AB AD =且BA CD =,则四边形ABCD 的形状一定是( ) A .正方形 B .矩形C .菱形D .等腰梯形【答案】C【解析】因为BA CD =,所以,四边形是平行四边形,又AB AD =,所以AB AD =, 四边形是菱形,故选C. 练习1.在ABC ∆中,,2AB =,1AC =,E ,F 为AB 的三等分点,则CE CF ⋅=( ) A .89B .109C .179D .259【答案】C 【解析】因为,所以, 化为0AB AC ⋅=,因为2AB =,1AC =,所以,又因为E ,F 为AB 的三等分点,所以,故选C.练习2.在四边形中,,,,那么四边形的形状是( )A .矩形B .平行四边形C .梯形D.以上都不对【答案】C【解析】,,,四边形是梯形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角函数与平面向量专题复习
【课前测试】
1.在边长为2的等边三角形ABC 中,D 是AB 的中点,E 为线段AC 上一动点,则⋅ 的取值范围为 _.
2.在等腰直角三角形ABC 中,AC =BC =1,点M ,N 分别是AB ,BC 的中点,点P 是△ABC (包括边界)内任一点.则AN MP ⋅的取值范围为___ ___.
3.过双曲线22
221(0,0)x y a b a b
-=>>的左顶点A 作斜率为1的直线,该直线与双曲线的两条渐
近线的交点分别为B ,C .若1
2
AB BC =,则双曲线的离心率是___ ___.
4.已知a ,b ,c 分别为△ABC 三个内角A ,B ,C 的对边,cos sin 0a C C b c --=,若a =7,则b +c 的最大值为___ ___.
【例题讲评】
例1.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,cos 2C +22cos C +2=0.
(1)求角C 的大小;
(2)若b =2a ,△ABC 的面积为2
2
sin A sin B ,求sin A 及c 的值.
例2.在ABC ∆中,角A B C 、、的对边分别为a ,b ,c ,已知5
sin 13
B =
,且12BA BC ⋅=. (1)求ABC ∆的面积;
(2)若a ,b ,c 成等差数列,求b 的值.
例3.已知向量,,a b c 满足4,22,a b ==a 与b 的夹角为
4
π
,()()1c a c b -⋅-=-,则c a -的最大值为______.
例4.在△ABC 中,角A ,B ,C 对的边分别为a ,b ,c ,已知a =2..
(1)若3
A π
=
,求b +c 的取值范围;
(2)若1AB AC ⋅=,求△ABC 面积的最大值.
A B
P
C
(第4题)
【课后练习】
1.在△ABC 中,a ,b ,c 分别为角A ,B ,C 所对的边,sin A ,sin B ,sin C 成等差数列,且a =2c ,则cos A =_____.
2.已知a ,b ,c 分别为△ABC 三个内角A ,B ,C 的对边,a =2,且(2+b )(sin A -sin B )=(c -b )sin C ,则△ABC 面积的最大值为________.
3.如图,在直角梯形ABCD 中,AB ∥CD ,90ADC ∠=︒,AB = 3,AD = 2,E 为BC 中点,
若→AB ·→AC = 3,则→AE ·→BC = .
4.如图,o o 19045AB BC APB BPC ==∠=∠=,,,则PA PC ⋅= .
5.△ABC 中,A ,B ,C 的对边分别为a ,b ,c ,面积为S .满足S =34
(a 2+b 2-c 2
). (1)求C 的值;
(2)若a +b =4,求周长的范围与面积S 的最大值.
6.在ABC ∆中,三个内角分别为A,B,C ,已知sin(A )2cosA 6
π
+=.
(1)若cos C =230a c -=.
(2)若(0,)3B π∈,且4
cos()5
A B -=,求sin B .
答案: 【前测】
1.[2316 ,3] 2.[-34 , 3
4] 3. 5 4.21
【例题】
例1.(1)3π4, (2) sin A =1010
,c =1.
例2.答案:(1)由12BA BC ⋅=,则cos 12ac B =.…………………………… 2分
故cos B >0.又5sin 13B =,所以cos B 12
13
=.……………………………… 4分 故13ac =. 所以ABC ∆的面积S 12=
ac sin B 155
132132=⨯⨯=.……………………………… 7分 (2)因为a ,b ,c 成等差数列,所以2b =a +c .
在ABC ∆中,2222cos b a c ac B =+-,即()2
222cos b a c ac ac B =+--.……… 10分 所以()2
2222cos b b ac ac B =--.(*) 由(1)得,13ac =,cos B 1213=,代入(*)得()2
212221321313
b b =-⨯-⨯⨯,… 12分
故b 250
3
=
,b =.……………………………………………………………14分
例3.12+
例4.(1)(2,4] (2) 2
【课后练习】
1.-1
4
2.3 3.-3
4.答案:4
5
-.
【解析】(方法一)2
()PA PC PA PB BC PA BC PA AB PA ⋅=⋅+=⋅=⋅=-, 在△APC 中,设PB x =,知易2PA x =,所以22(2)1x x +=,即21x =,
所以PA PC ⋅=4
5
-;
(方法二)设PB x =,知易2PA x =,同方法一有215
x =,又PC =,
所以PA PC ⋅
=3π4(2))cos 45x ⋅⋅=-;
(方法三)
(方法4)建立如图所示的坐标系, 设(,0)A a ,(,)C b b -,(0,
0)a b >>,
则(0,)b B ,所以b a =且2
214
b a +=,
所以245a =
,即A
,(C ,所以PA PC ⋅=4
5
-.
5.(1)π
3
(2) 3
6.因为sin(A )2cos A 6π+=
1
A cos A 2cos A 2
+=,
即sin A A =,因为()A 0,∈π,且cos A 0≠,
所以tan A =A 3
π
=
. …………4分 (1)因为22sin C cos C 1+=
,cosC =
,()C 0,∈π
,所以sin C = 由正弦定理知a c
sin A sinC =
,即32
a sin A c sinC ===,即230a c -=.…………7分 (2)因为(0,)3B π
∈,所以033A B B ,ππ⎛⎫-=-∈ ⎪⎝⎭
,
因为22sin ()cos ()1A B A B -+-=,所以3sin()5
A B -=, …………10分 所以()(
)sin sin sin cos()cos sin()B A A B A A B A A B =--=---=.……14分。
