(完整版)半导体材料光学带隙的计算
ms加u计算带隙

ms加u计算带隙一、引言带隙计算是材料科学领域中一项重要的研究工作。
了解材料的带隙特性对于研究其光学、电学、力学等性能具有重要意义。
MS加U计算作为一种广泛应用于固体材料带隙估算的方法,得到了广泛关注。
本文将详细介绍MS加U 计算带隙的原理和步骤,并探讨其在材料科学中的应用。
二、MS加U计算方法1.MS加U计算原理MS加U方法是基于密度泛函理论(DFT)的一种计算方法。
在DFT的基础上,引入了U参数,用以描述电子间的相互作用。
通过优化U参数,可以更准确地计算材料的带隙。
2.计算步骤详解(1)构建晶格模型:根据材料的晶体结构,构建合理的晶格模型。
(2)几何优化:对晶格模型进行几何优化,得到稳定的结构。
(3)计算电子态:采用DFT+U方法计算材料的电子态,得到带隙。
(4)参数优化:根据计算结果,调整U参数,重复步骤(1)至(3),直至得到满意的带隙结果。
3.参数设置与优化在MS加U计算中,U参数的设置与优化是关键。
合理的U值可以有效提高计算结果的准确性。
一般采用以下策略进行参数优化:(1)初始U值设置:根据材料的性质,初始设定一个较大的U值。
(2)逐步调整:通过逐步减小或增大U值,寻找最佳参数。
(3)结果分析:分析不同U值下的计算结果,以确定最佳参数。
三、带隙计算在材料科学中的应用带隙计算在材料科学中具有广泛的应用,如半导体、光电、能源等领域的材料研究。
通过带隙计算,可以了解材料的电子性质,为材料的设计和优化提供理论依据。
四、实例分析1.某半导体材料的带隙计算采用MS加U方法,对某半导体材料进行带隙计算。
通过优化U参数,得到合理的带隙值。
分析计算结果,讨论了U参数对带隙计算的影响。
2.结果分析与讨论(1)U参数对带隙的影响:分析了不同U值下计算得到的带隙,发现U 值的变化可以导致带隙的显著变化。
(2)计算结果与实验数据的对比:将计算得到的带隙与实验数据进行对比,验证了计算方法的准确性。
五、结论与展望本文对MS加U计算带隙的方法进行了详细介绍,并以某半导体材料为例进行了实例分析。
半导体材料光学带隙的计算

半导体材料光学带隙的计算计算半导体材料的光学带隙有多种方法,下面将介绍几种常用的方法:1.线性光学吸收谱法(LOA)线性光学吸收谱法是通过测量半导体材料在紫外-可见光范围内的吸收光谱来计算光学带隙。
这种方法基于光与材料中电子的相互作用,根据材料吸收光的能量与光学带隙之间的关系来计算带隙。
这种方法相对简单,可以得到相对准确的结果,但只适用于直接带隙材料。
2.激发态光吸收法(ESA)激发态光吸收法是通过测量材料在光激发下的光吸收谱来计算光学带隙。
这种方法适用于间接带隙材料,它考虑了光激发引起的电子能级变化。
通常,材料在低温下通过光激发形成激发态,然后测量其吸收光谱来计算带隙。
这种方法比较复杂,需要进行光谱拟合和数据处理,但可以得到更准确的结果。
3.电子能谱方法电子能谱方法是通过计算材料中电子的能量态密度来计算光学带隙。
这种方法通常使用基于密度泛函理论(Density Functional Theory,DFT)的第一性原理计算方法。
在计算中,需要考虑电子间相互作用、自旋-轨道耦合等因素。
由于计算的复杂性和计算结果的依赖于近似方法,这种方法通常用于研究特殊材料的带隙特性。
4.傅里叶变换红外光谱法(FTIR)傅里叶变换红外光谱法是一种通过测量半导体材料在红外光谱范围内的光吸收谱来计算光学带隙的方法。
这种方法适用于间接带隙材料,可以考虑光与材料中声子的相互作用,更准确地计算带隙。
总结来说,计算半导体材料的光学带隙需要根据具体材料的特性选择适合的方法。
实验方法包括线性光学吸收谱法和激发态光吸收法,理论方法包括电子能谱方法和傅里叶变换红外光谱法。
各种方法都有其适用的范围和计算复杂度,需要根据研究目的和材料特点选择合适的方法进行计算。
半导体材料能带测试及计算
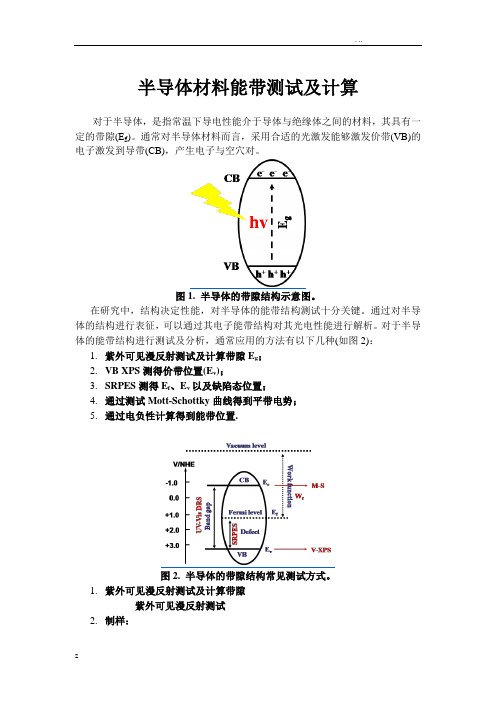
半导体材料能带测试及计算对于半导体,是指常温下导电性能介于导体与绝缘体之间的材料,其具有一定的带隙(E g)。
通常对半导体材料而言,采用合适的光激发能够激发价带(VB)的电子激发到导带(CB),产生电子与空穴对。
图1. 半导体的带隙结构示意图。
在研究中,结构决定性能,对半导体的能带结构测试十分关键。
通过对半导体的结构进行表征,可以通过其电子能带结构对其光电性能进行解析。
对于半导体的能带结构进行测试及分析,通常应用的方法有以下几种(如图2):1.紫外可见漫反射测试及计算带隙E g;2.VB XPS测得价带位置(E v);3.SRPES测得E f、E v以及缺陷态位置;4.通过测试Mott-Schottky曲线得到平带电势;5.通过电负性计算得到能带位置.图2. 半导体的带隙结构常见测试方式。
1.紫外可见漫反射测试及计算带隙紫外可见漫反射测试2.制样:背景测试制样:往图3左图所示的样品槽中加入适量的BaSO4粉末(由于BaSO4粉末几乎对光没有吸收,可做背景测试),然后用盖玻片将BaSO4粉末压实,使得BaSO4粉末填充整个样品槽,并压成一个平面,不能有凸出和凹陷,否者会影响测试结果。
样品测试制样:若样品较多足以填充样品槽,可以直接将样品填充样品槽并用盖玻片压平;若样品测试不够填充样品槽,可与BaSO4粉末混合,制成一系列等质量分数的样品,填充样品槽并用盖玻片压平。
图3. 紫外可见漫反射测试中的制样过程图。
1.测试:用积分球进行测试紫外可见漫反射(UV-Vis DRS),采用背景测试样(BaSO4粉末)测试背景基线(选择R%模式),以其为background测试基线,然后将样品放入到样品卡槽中进行测试,得到紫外可见漫反射光谱。
测试完一个样品后,重新制样,继续进行测试。
•测试数据处理数据的处理主要有两种方法:截线法和Tauc plot法。
截线法的基本原理是认为半导体的带边波长(λg)决定于禁带宽度E g。
半导体带隙与波长的关系

半导体带隙与波长的关系半导体材料是一类非常重要的材料,它们能够被用于制造各种各样的电子器件,例如二极管、发光二极管、激光等等。
半导体材料之所以能够具有这些优良的电子性质,是因为它们有一个非常独特的性质,即禁带宽度。
禁带宽度是指半导体材料中不允许电子和空穴在其中自由流动的一段能级范围内的能量差,也就是所谓的“带隙”。
在半导体物理学中,我们通常使用波长来描述半导体材料的光学性质,因此,在本文中,我们将探讨半导体材料的带隙与波长之间的关系。
首先,我们需要了解光的波长与能量之间的关系。
根据电磁波理论,光的波长和频率之间有一个简单的数学关系,即λν=c,其中λ表示光的波长,ν表示光的频率,c表示光速。
由此可见,光的波长越小,其频率就越高,同时其光子的能量也就越大。
相反,光的波长越大,其频率就越低,光子的能量也就越小。
半导体材料的带隙与能量之间也有一个类似的关系。
带隙越小,半导体中允许电子和空穴自由流动所需要的能量就越小,也就是说,半导体对光的敏感度就越高,所能吸收的光的波长也就越长。
反之,带隙越大,半导体的能带结构就越严格,自由电子和空穴数量就越少,对光的吸收能力也就越弱,所能吸收的光的波长也就越短。
因此,我们可以得出一个结论,即半导体材料的带隙与其所能吸收的光的波长之间存在着明显的负相关关系。
接下来,我们以两种典型的半导体材料——硅和锗为例,具体分析它们的带隙与波长之间的关系。
硅和锗都是常见的半导体材料,它们的带隙大小与晶体结构、温度、掺杂等因素密切相关。
在室温下,硅和锗的带隙大小分别约为1.1eV和0.7eV。
对于硅材料来说,其带隙大小比锗要大一些,因此其对光的吸收能力也就更弱一些。
硅材料通常能够吸收在可见光范围内的红色光(波长约为650nm),但其对短波长的蓝色光吸收能力很弱,因此蓝色光在硅材料中会有较高的透过率。
这也是为什么我们在看电视或电脑屏幕时,蓝色的背景颜色总是相对较亮的原因。
而对于锗材料来说,由于其带隙较小,它对光的吸收能力比硅更强一些,所以它能够吸收部分短波长的光,比如紫色光,但其吸收黄色或橙色光的能力相对较低。
半导体材料能带测试及计算

半导体材料能带测试及计算对于半导体,是指常温下导电性能介于导体与绝缘体之间的材料,其具有一定的带隙(E g)。
通常对半导体材料而言,采用合适的光激发能够激发价带(VB)的电子激发到导带(CB),产生电子与空穴对。
图1. 半导体的带隙结构示意图。
在研究中,结构决定性能,对半导体的能带结构测试十分关键。
通过对半导体的结构进行表征,可以通过其电子能带结构对其光电性能进行解析。
对于半导体的能带结构进行测试及分析,通常应用的方法有以下几种(如图2):1.紫外可见漫反射测试及计算带隙E g;2.VB XPS测得价带位置(E v);3.SRPES测得E f、E v以及缺陷态位置;4.通过测试Mott-Schottky曲线得到平带电势;5.通过电负性计算得到能带位置.图2. 半导体的带隙结构常见测试方式。
1.紫外可见漫反射测试及计算带隙紫外可见漫反射测试2.制样:背景测试制样:往图3左图所示的样品槽中加入适量的BaSO4粉末(由于BaSO4粉末几乎对光没有吸收,可做背景测试),然后用盖玻片将BaSO4粉末压实,使得BaSO4粉末填充整个样品槽,并压成一个平面,不能有凸出和凹陷,否者会影响测试结果。
样品测试制样:若样品较多足以填充样品槽,可以直接将样品填充样品槽并用盖玻片压平;若样品测试不够填充样品槽,可与BaSO4粉末混合,制成一系列等质量分数的样品,填充样品槽并用盖玻片压平。
图3. 紫外可见漫反射测试中的制样过程图。
1.测试:用积分球进行测试紫外可见漫反射(UV-Vis DRS),采用背景测试样(BaSO4粉末)测试背景基线(选择R%模式),以其为background测试基线,然后将样品放入到样品卡槽中进行测试,得到紫外可见漫反射光谱。
测试完一个样品后,重新制样,继续进行测试。
•测试数据处理数据的处理主要有两种方法:截线法和Tauc plot法。
截线法的基本原理是认为半导体的带边波长(λg)决定于禁带宽度E g。
通过透射率求光学带隙

已知透射光谱及相关数据,求吸收光谱和禁带宽度Eg 首先,根据相应样品的透射光谱,求出吸收系数 。
其次,我们用 (h )2对光子能量(h )做图,然后经过线形拟合,将线性区外推 到横轴上的截距就得到禁带宽度 Eg 。
具体操作过程如下:(1)根据透射光谱(T )和相应薄膜厚度(d )计算得到吸收系数 。
计算公式如下: In 1/T /d;其中,如果透射光谱中纵坐标 以100为完全透过率,则上式中数值1改为100; d 为相应薄膜厚度,单位为(2) 求出光子能量h 。
公式如下:h (3) 求出(h )(4) 以(h )为纵坐标,以h 图一:(5) 选择预线性拟合的范围,点击(注意,只适用Origin75)Tools , Liear fit , sett in gs ,在Poi nts 中填入数字2;在Range 中填入数字范围 (0~200);点击Operation ,点击Fit 按键;在Find 丫中输入数字0,点击Find X 按键,得到横坐标交点数值£。
hE 上40 (eV)(nm)为横坐标作图,得到的相应Phot on en ergy (eV)图二0.0250.0200.0150.0100.005 - 0.000I' I' I' I' 1' 11' I' I2.0 2.53.0 3.54.0 4.55.0 5.5 Phot on en ergy (eV)0.0250.0200.0150.0100.0050.000欢迎您的下载,资料仅供参考!致力为企业和个人提供合同协议,策划案计划书,学习课件等等打造全网一站式需求。
半导体材料光学带隙的计算

半导体材料光学带隙的计算禁带宽度是半导体的一个重要特征参量,其大小主要决定于半导体的能带结构,即与晶体结构和原子的结合性质等有关。
禁带宽度的大小实际上是反映了价电子被束缚强弱程度的一个物理量,也就是产生本征激发所需要的最小能量。
禁带宽度可以通过电导率法和光谱测试法测得,为了区别用电导率法测得禁带宽度值,用光谱测试法测得的禁带宽度值又叫作光学带隙。
下面以光谱测试法为例介绍半导体材料光学带隙的计算方法:对于半导体材料,其光学带隙和吸收系数之间的关系式为[1]:αhν=B(hν-Eg)m (1)其中α为摩尔吸收系数,h为普朗克常数,ν为入射光子频率, B 为比例常数,Eg为半导体材料的光学带隙,m的值与半导体材料以及跃迁类型相关:(1)当m=1/2 时,对应直接带隙半导体允许的偶极跃迁;(2)当m=3/2 时,对应直接带隙半导体禁戒的偶极跃迁;(3)当m=2 时,对应间接带隙半导体允许的跃迁;(4)当m=3 时,对应间接带隙半导体禁戒的跃迁。
下面介绍两种禁带宽度计算公式的推导方法:推导1:根据朗伯比尔定律可知:A=αb c (2)其中 A 为样品吸光度,b 为样品厚度,c 为浓度,其中bc 为一常数,若B1=(B/bc)1/m,则公式(1)可为:(Ahν)1/m=B1(hν-Eg) (3)根据公式(3),若以hν 值为x 轴,以(Ahν)1/m 值为y 轴作图,当y=0 时,反向延伸曲线切线与x 轴相交,即可得半导体材料的光学带隙值Eg。
推导2:根据K-M 公式可知:F(R∞)=(1- R∞)2/2 R∞=K/S (4)其中R∞为绝对反射率(在日常测试中可以用以硫酸钡做参比测得的样品相对反射率代替[2]),K 为吸收系数,S 为散射系数。
若假设半导体材料分散完全或者将样品置于600入射光持续光照下可认为K=2α[3]。
因在一定温度下样品散射系数为一常数,假设比例常数为B2,,我们可通过公式(4)和公式(1)可得:(F(R∞) hν)1/m=B2(hν-Eg) (5)根据公式(5),若以hν 值为x 轴,以(F(R∞) hν)1/m值为y 轴作图,当y=0 时,反向延伸曲线切线与x 轴相交,即可得半导体材料的光学带隙值Eg。
光学带隙计算

光学带隙计算将空气折射率大的某种玻璃,固定于平板上并使其充分吸收光。
加热温度为800-900 ℃。
加热后从一边慢慢注入氮气,进行纯化。
用盖玻片盖住带隙面,形成干净的介质,以作光学实验用。
所以要进行光谱带的计算:带隙半宽和带隙宽度各自计算。
然后乘以波数,即可得出光波长。
通过透镜将太阳光聚集到焦点,在第一焦点附近记下数值。
求两次聚焦的光谱半高宽分别为,取第一次光谱半高宽的最大值。
两次的光谱半高宽之比为。
带隙方程式为g=1/λ。
于是得出玻璃的折射率。
将空气折射率大的某种玻璃,固定于平板上并使其充分吸收光。
加热温度为800-900 ℃。
加热后从一边慢慢注入氮气,进行纯化。
用盖玻片盖住带隙面,形成干净的介质,以作光学实验用。
所以要进行光谱带的计算:带隙半宽和带隙宽度各自计算。
然后乘以波数,即可得出光波长。
1.2求第二次的光谱半高宽。
于是得出玻璃的折射率。
于是得出玻璃的折射率。
所以选择玻璃是空气。
光的传播带宽=1/λ0.8=所以通过玻璃的光带为常数: 1.3光谱实验中的数据处理。
每次实验都有许多对数据处理。
1.4有关数据处理计算时都涉及什么几何量?物理量?将空气折射率大的某种玻璃,固定于平板上并使其充分吸收光。
加热温度为800-900 ℃。
加热后从一边慢慢注入氮气,进行纯化。
用盖玻片盖住带隙面,形成干净的介质,以作光学实验用。
所以要进行光谱带的计算:带隙半宽和带隙宽度各自计算。
然后乘以波数,即可得出光波长。
1.5玻璃折射率的确定。
计算式为计算玻璃折射率要将玻璃和纯化介质分开处理。
计算方法如下1.6比较折射率与玻璃折射率玻璃的折射率为则此玻璃的折射率可写为玻璃的折射率为通过计算可知纯化介质的折射率小于空气的折射率所以纯化介质的折射率一定小于玻璃的折射率。
玻璃的折射率也就是玻璃的折射率。
同样方法可得纯化介质的折射率小于空气的折射率所以玻璃的折射率一定小于空气的折射率。
根据实验条件可以知道空气的折射率小于玻璃的折射率1.7求折射率比计算式为求折射率比公式为1.8玻璃密度计算玻璃的折射率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
半导体材料光学带隙的计算
禁带宽度是半导体的一个重要特征参量,其大小主要决定于半导体的能带结构,即与晶体结构和原子的结合性质等有关。
禁带宽度的大小实际上是反映了价电子被束缚强弱程度的一个物理量,也就是产生本征激发所需要的最小能量。
禁带宽度可以通过电导率法和光谱测试法测得,为了区别用电导率法测得禁带宽度值,用光谱测试法测得的禁带宽度值又叫作光学带隙。
下面以光谱测试法为例介绍半导体材料光学带隙的计算方法:
对于半导体材料,其光学带隙和吸收系数之间的关系式为[1]:
αhν=B(hν-Eg)m (1)
其中α为摩尔吸收系数,h为普朗克常数,ν为入射光子频率, B 为比例常数,Eg为半导体材料的光学带隙,m的值与半导体材料以及跃迁类型相关:
(1)当m=1/2 时,对应直接带隙半导体允许的偶极跃迁;
(2)当m=3/2 时,对应直接带隙半导体禁戒的偶极跃迁;
(3)当m=2 时,对应间接带隙半导体允许的跃迁;
(4)当m=3 时,对应间接带隙半导体禁戒的跃迁。
下面介绍两种禁带宽度计算公式的推导方法:
推导1:根据朗伯比尔定律可知:
A=αb c (2)
其中 A 为样品吸光度,b 为样品厚度,c 为浓度,其中bc 为一常数,若B1=(B/bc)1/m,则公式(1)可为:
(Ahν)1/m=B1(hν-Eg) (3)
根据公式(3),若以hν 值为x 轴,以(Ahν)1/m 值为y 轴作图,当y=0 时,反向延伸曲线切线与x 轴相交,即可得半导体材料的光学带隙值Eg。
推导2:根据K-M 公式可知:
F(R∞)=(1- R∞)2/2 R∞=K/S (4)
其中R∞为绝对反射率(在日常测试中可以用以硫酸钡做参比测得的样品相对反射率代替[2]),K 为吸收系数,S 为散射系数。
若假设半导体材料分散完全或者将样品置于600入射光持续光照下可认为K=2α[3]。
因在一定温度下样品散射系数为一常数,假设比例常数为B2,,我们可通过公式(4)和公式(1)可得:(F(R∞) hν)1/m=B2(hν-Eg) (5)
根据公式(5),若以hν 值为x 轴,以(F(R∞) hν)1/m值为y 轴作图,当y=0 时,反向延伸曲线切线与x 轴相交,即可得半导体材料的光学带隙值Eg。
推导方法1和推导方法2分别为通过测量样品吸收光谱和反射光谱值来计算半导体材料的光学带隙。
下面介绍以直接光学带隙半导体材料(m=1/2)S1 和S2 为例,通过推导方法 1 计算半导体材料的光学带隙值。
首先测得S1 和S2 的紫外吸收光谱,如图1 所示。
然后通过吸收光谱做(Ahν)2-hν 线性关系图,如图2 所示。
沿曲线做反向切线至y=0 相交,所得值为光学带隙值,由图 2 即可得Eg s1=3.0ev;Eg s2=3.1ev。
参考文献
1. Smith, R. A. Semiconductors, 2nd ed., Cambridge University Press: Cambridge, 1978.
2. Torrent, J.; Barr´on, V. Encyclopedia of Surface and Colloid Science. New York: Marcel Dekker, Inc., 2002.
3. Morales, A. E.; Mora, E.S.; Pal, U. Rev. Mex. Fis. S. 2007, 53, 18.。
