论文全文ICEMS

合集下载

环境工程专业“学科研究方法论”之教学探讨

环境工程专业“学科研究方法论”之教学探讨［摘要］现今学校鼓励大学生积极参与创新性研究活动，但学生们常对研究方法、论文撰写和学术规范等仍然缺乏系统了解。

修读《学科研究方法论》课程等有助于学生系统全面地了解环境工程专业方向学术研究的方法与规范，这对学生完成本科乃至研究生阶段的研究性学习，撰写毕业及学术论文和深化学术研究具有重要意义。

优化教学内容和教学方式，构建具有学科针对性的《学科研究方法论》课程，使《学科研究方法论》能够成为一门具有前瞻性和指导意义的环境工程专业选修课程，对学科的建设和发展具有重要的意义。

［关键词］环境工程课程；学科；研究；方法论［中图分类号］G642.01前言培养学生富有探索研究能力和创新精神是高水平教育教学极为重要的一环[1-3]。

“钱学森之问”—“为什么我们的学校总是培养不出杰出人才？”，激起了对我国教育制度和方法的反思[4]。

大学是培养创新型人才主要前沿阵地，然而我国高等教育培养人才的研究能力和创新能力仍相对薄弱。

究其原因，与我国高等教育在过去相当长一段时间里，重视对学生科学知识的传授，而一定程度上忽视对其从事研究的一般程序、方法和规范的培养不无关系[5]。

不少高校仍没面向高年级本科生开设“研究方法论”的课程，未能系统指导学生科学规范地从事研究。

然而，在西方发达国家，“研究方法论”则几乎是所有大学的学生都必须完成的一门必修课程[5]。

广州大学注重人才培养，依据党和国家的教育方针政策，结合社会需求、学校办学定位和历史文化，致力于培养德才兼备、家国情怀、视野开阔，爱体育、懂艺术，能力发展性强的高素质创新人才，大力打造拔尖创新实验班、卓越人才培养、交叉复合型人才培养、校企协同育人、国际联合培养等五大类型的本科人才培养模式。

基于学校的教育教学总方针和最新制定的人才培养方案，我校环境科学与工程学院环境工程专业亦开设了“学科研究方法论”专业基础选修课，为学生学习研究方法论知识提供了途径。

国际电力电子相关会议

17
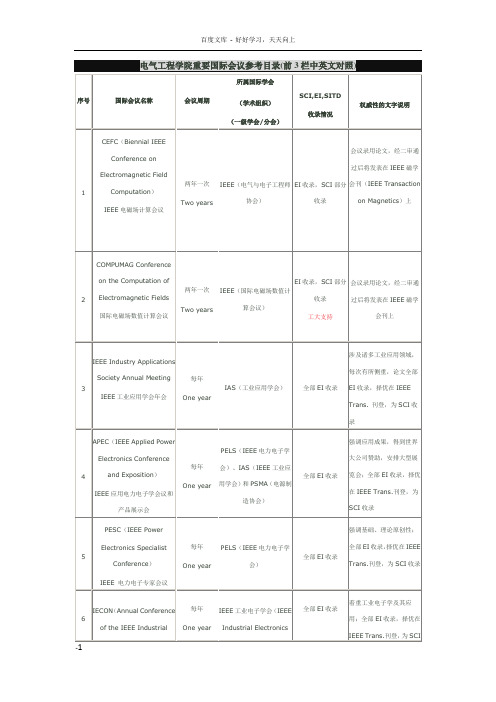
ICEMS（International Conference on Electric Machines and System）
电机和系统国际会议
两年一次
Two years
IEEE IAS
EI目前不收录
国际上针对“电机与驱动”方向最重要的两大会议之一，与IEMDC为“姐妹会议”
18
ICEM（International Conference on Electric Machines）
13
PEMC（EPE：Power Electronics and Motion Control）
欧洲电力电子与运动控制会议
两年一次
Two years
EPE（欧洲电力电子协会）
和EPE会议交叉举行
14
IEEJ International Power Electronics Conference
日本国际电力电子学术会议
IEEE电磁兼容国际研讨会
每年
One year
IEEE电磁兼容学会（IEEE Electromagetic Compatibility Society）
全部ISTP收录
部分EI收录
EMC研究成果，全部ISTP收录，部分EI收录
10
PEDS（IEEE International Conference on Power Electronics and Drive Systems）
IEEE电力电子学与驱动系统国际会议
两年一次
Two years
IEEE下属若干学会
全部ISTP收录
部分EI收录
包含：电机与驱动方向的为数不多的国际会议之一
11
PCIM（Europe：Power Conversion and Intelligent Motion Conference）

国际数学建模竞赛优秀论文英文模板

T eam Control NumberFor office use only38253For office use onlyT1F1 T2 F2 T3 Problem ChosenF3 T4 AF42015 Mathematical Contest in Modeling (MCM) Summary SheetEradicating EbolaAbstractThis paper aim at the problem which is to eradicate or inhibit the spread of Ebola, we start from three sub problem, that is: the demand for drugs, drugs delivery route and the car allocation. And establish the spreading model of Ebola, optimization model of drugs transport system and car allocation model respectively by using the differential equation method and simulated annealing algorithm. Finally, do the model extension and sensitively analysis.The first issue, figure out the demand for drugs in different regions. First, establish Ebola spread SIR model. And in the time of t, using differential equation to find the proportion of infected i (t )=1/Qln(s /s 0), then get the demand for drugs in this region H =kNi (t ).The second issue, how to find the shortest route to deliver drugs. Use Guinea, Liberia and Sierra Leone whose infection is relatively serious as the investigation object. According to the Binary classification to find the rules of iteration, which is useful to find out the nearest city to any other cities, and the result is Bombali. So we put it as the center of distribution. Then use simulated annealing algorithm and put forward two kinds of schemes for shortest path by the different ways in drugs delivery.Schemes one, asynchronous mode: put three countries as a regional countries. Using the TSP method to solve the shortest route is 54.8486, which is start from Bombali to different regions.Schemes two, synchronization method: dividing the whole area into two areas around A and B by use the longitude coordinates of Bombali as a standard. Respectively solve the shortest route is 10.1739 and 29.8075, which is start from Bombali and pass all cities in A and B, and solve the sum of the two route is 39.9814.According to the different drug delivery requirements (such as the shortest distance or transmission synchronization), can choose the asynchronous or synchronous way.The third issue, how to allocate the number of cars reasonable, and obtain the suitable speed of drug production. According to the predict number which obtained in model one, get the vehicles and drug distribution table (the results are shown Table 4.6 and Table 4.7). and obtain the speed V of drugs production is:10(ln ln )ni ii i i i k N V Q T s s =≥-∑At last, the minimum speed of drugs production is 56.14 agent/day to meet the need in three countries by calculating.Finally, use the SIR model which was optimized by using vaccination cycle control. By doing this we can know the number of susceptible and infections in crowd under the condition of the pulse vaccination significantly lower faster than without pulse vaccination. Thus, using pulse vaccination can effectively control the spread of Ebola.Keywords: SIR model; Simulated Annealing Algorithm; Pulse vaccination; EbolaEradicating EbolaContent1 Restatement of the Problem (1)1.1 Introduction (1)1.2 The Problem (1)2 General Assumptions (1)3 Variables and Abbreviations (2)4 Modeling and Solving (2)4.1 Model I (2)4.1.1 Analysis of the Problem (2)4.1.2 Model Design (2)4.2 Model II (6)4.2.1 Analysis of the Problem (6)4.2.2 Model Design (6)4.3 Model Ⅲ (8)4.3.1 Analysis of the Problem (8)4.3.2 Model Design (9)4.4 Extent our models (11)5 Sensitivity Analysis (14)5.1 Effect of Daily Contact Rate (14)5.2 Effect of inoculation rate (14)6 Model Analysis (15)6.1 The Advantages of Model (15)6.2 The Disadvantages of Model (15)7 Non-technical Explanation (16)References (18)1Restatement of the Problem1.1IntroductionEbola virus is a very rare kind of virus. It can cause humans and primates produce Ebola hemorrhagic fever virus, and has a high mortality rate. The largest and most complex Ebola outbreak appeared in the West African country in 2014. This outbreak occurred in guinea first, then through various ways to countries such as Sierra Leone, Liberia, Nigeria and Senegal. The number of cases and deaths, which occurred in this outbreak, is more than the sum of all the other epidemic. And outbreak continued to spread between countries. On August 8, 2014, the general-director of the world health organization announced the outbreak of public health emergency of international concern.In this paper, a realistic and reasonable mathematic model, which considers several aspects such as vaccine manufacturing and drug delivery, has been built.Then optimizing the model to eliminate or suppress the harm done by the Ebola virus.1.2The ProblemEstablishing a model to solve the spread of the disease, amount of drugs needed, possible feasible transportation system, transporting position, the speed of a vaccine or drug manufacturing and any other key factor. Thus, we decompose the problem into three sub-problem, modeling and finding the optimization method to face the Ebola virus.♦Building a model, which can solve the spread of the disease and the demand for drugs.♦Building a model to find the best solution.♦Using the goal programming to solve the problems of production and distribution and optimization of other factors..2General AssumptionsTo simplify the problem, we make the following basic assumptions, each of which is properly justified.♦Our assumptions is reasonable and effective.♦Vehicles only run in the path which we have simulated♦This assumption greatly simplify our model and allow us to focus on the shortest path.♦We consider the model that are enclosed.♦People who recovered, will not infected again, and exit the transmission system3Variables and AbbreviationsThe variables and abbreviations used in this paper are listed in Table 3.1.Table 3.1 Assuming variableSymbol DefinitionS the number of susceptible peopleI the number of infected personsR the number of recoveredT a vaccine or drug production cycleH the amount of drugs needed by RegionA a cycle of a vaccine or drug productionL drug reserve area to the shortest path to all affected areasV speed of vaccine or pharmaceutical productionV’vehicle speedλrate of patient contact per dayμday cure rate per dayαn rights of those infected regions weight4Modeling and Solving4.1Model I4.1.1Analysis of the ProblemAccording to the literature that different types of virus has its own different propagation process characteristics, we do not analyze the spread of viruses from a medical point of view, but from the general to analyze the propagation mechanism. So we have to analyze the spread of the Ebola virus and the requirements of drugs through the SIR[1] model.4.1.2Model DesignIn the dynamics of infectious diseases, the main follow Kermack and McKendrick SIR epidemic model which the dynamics of the established method in 1927. SIR model until now is still widely used and continue to develop. SIR model of the total population is divided into the following three categories: susceptibles, the ratio of the number denoted by s(t), at time t is not likely to be infected, but the number of infectious diseases such proportion of the total; infectives, the ratio of the number denoted by i(t), at time t become a patient has been infected and has the proportion of the total number of contagious; recovered, the ratio of the number denoted by r(t), expressed the number of those infected at time t removed from the total proportion (ie, it has quit infected systems). Assuming a total population of N(t), then there are N(t) = s(t) + i(t) + r(t).SIR model is established based on the following two assumptions:In the investigated region-wide spread of the disease is not considered during the births, deaths, population mobility and other dynamic factors. Total population N(t) remainunchanged, the population remains a constant N.The patients’ contact rate (the average number of effective contacts per patient per day) is constant λ, the cure rate (patients be cured proportion of the total number of patients a day) is a constant μ, clearly the average infectious period of 1/μ, infectious period contact number for Q = λ/μ.In the model based on the assumption that we develop a susceptible person to recover fromthe sick person in the process, such as Figure 4.1:Figure 4.1 SIR the model flowchartSIR basis differential equation model can be expressed as:disi i dt dssi dt dri dt λμλμ⎧=-⎪⎪⎪=-⎨⎪⎪=⎪⎩(5.1)But it can see that s(t), i(t) is more difficult to solve, so we use the numerical calculations to esti mate general variation. Assuming λ = 1, μ = 0.3, i(0) = 0.02, s(0) = 0.98 (at the initial time), then we borrow MATLAB software programming to get results. And according to Table 4.1 analyzed i(t), s(t) of the general variation.Figure4.2 s(t),i(t)The patient scale map Figure 4.3 i ～s Phase track diagramFrom Table 4.1 and Figure4.2, we can see that i(t) increased from the initial value to about t = 7(maximum), and then began to decrease.Based on the calculating the numerical and graphical observation, use of phase trajectories discussed i(t), s(t) in nature. Here i ~ s plane is phase plane , the domain (s, i)∈D in phase plane for:{}(,)0,0,1D s i s i s i =≥≥+≤(5.2)According to equation (5.1) and con tact number of the infectious period Q = λ / μ, we can eliminate dt, get:0011(1)(1)i s i s s sdi ds di ds Q Q =-⋅⇒=-⋅⎰⎰(5.3)Calculated using integral characteristics:0001()()ln si t s i s Q s =+-=(5.4)Curve in the domain of definition, equation(5.3) is a phase trajectory.According to equation(5.1) and equation(5.3), have to analyze the changes. If and only if the patient i(t) for some period of growth, it think that in the spread of infectious diseases , then 1/Q is a threshold. If s 0> 1/Q, infectious diseases will spread , and reduce infectious period the number of contacts with Q, namely raising the threshold 1/Q and will make s 0≤1/Q, then it will not spread diseases.And we note that Q = λ/μ in the formula, the higher the level of people's health, the smaller patients’ contact rate; the higher the level of medical, the cure rate is larger and the smaller Q. Therefore, to improve the level of hygiene and medical help to control the spread of infectious diseases. Of course, can also herd immunity and prevention, to reduce s 0.In the process, we analyzed the spread of the disease, then we are going to discuss the amount of medication needed.According to equation(5.4), you can get i(t) values, we can calculate the number of people infected with the disease who I was:()()I i t N t =⋅(5.5)And the amount of drug required, we can be expressed as: H kI =(k is a constant, w> 0)If k> 0, it indicates that the number of infections is still rising, measures to control the virus also needs to be strengthened, and the amount of drugs is a growing demand mode until fluctuation; if k≤0, it means reducing the number of people infected, the virus the measure is better, and the dose of demand is also gradually reduced.According to the data provided by the WHO, we can get the number of infections various，which areas before January 30, 2015. see Table 4.2:Table 4.2 As the number of infections January 30, 2015Region Number Proportion Region Number ProportionNzerekore 2 0.0045 Koinadugu 1 0.0022Macenta 1 0.0022 Kambia 25 0.0558Kissdougou 1 0.0022 Western Urban 105 0.2344Kankan 1 0.0022 Western Rural 64 0.1429Faranah 4 0.0089 Mali 1 0.0022Kono 28 0.0625 Boffa 4 0.0089Bo 6 0.0134 Dubreka 11 0.0246Kenema 2 0.0045 Kindia 2 0.0045Moyamba 8 0.0179 Coyah 11 0.0246Port Loko 78 0.1741 Forecariah 24 0.0536Tonkolili 18 0.0402 Conakry 20 0.0446Bombal 18 0.0402 Montserrado 13 0.029Based on the latest data Ebola virus infections in January 2015, and the regional population and the associated parameter value Ebola assumptions, the model has been solved to a time t proportion of those infected i(t) = 1/Q ln (s/s0), using MATLAB software, we have predict the number of infections each region in February, then get a weight value of those infected forecast for each region in February 2015, as can be show Table 4.3.Table 4.3 As the number of infections February 28, 2015Region Number Proportion Region Number ProportionNzerekore 1 0.00233 Koinadugu 8 0.01864Macenta 3 0.00700 Kambia 24 0.05594Kissdougou 2 0.00470 Western Urban 69 0.16083Kankan 1 0.00233 Western Rural 78 0.18182Faranah 2 0.00470 Mali 4 0.00932Kono 22 0.05130 Boffa 2 0.00470Bo 5 0.01166 Dubreka 10 0.02331 Kenema 5 0.01166 Kindia 1 0.00233Moyamba 1 0.00233 Coyah 9 0.020979Port Loko 100 0.23310 Forecariah 20 0.046620Tonkolili 12 0.02797 Conakry 18 0.041968Bombal 23 0.05361 Montserrado 9 0.020979From Table 4.2 can be known, According to the number of cases of expression，we made a rough prediction that Ebola outbreak in February. it’s provide a reference for the production of vaccines and drugs. Indeed, it have provide a theoretical basis for the relevant departments which take appropriate precautions.4.2Model II4.2.1Analysis of the ProblemBased on the model I, we obtained the equation expression of disease transmission speed and number of drugs. However, in addition to these two factors, we should also consider how to transport drugs to the demanded area quickly and effectively. Thus, it is very important to develop a good transportation system, which can greatly improve the efficiency of drug transport and reduce the cost.4.2.2Model DesignBy searching on Wikipedia, we obtain cities which have erupted Ebola, and the latitude and longitude coordinates[2]. The results are shown in Table 4.4We get the best point, which is Bombali by programming. So, we assume it as the city which produces drugs.Because these cities are breaking points, both as a place of delivery. In order to find out the optimal path, we make following assumptions:♦The demand for each city is same♦The quantity of vehicles can meet the demand of transport♦Vehicles only run in the path which we have simulated4.2.2.1SA modelSA[3] is a random algorithm which is established by imitating metal annealing principle. It can be implemented in large rough search and local fine search by controlling the changes of temperature.Basic principle of SA:♦First, generated initial solution x0 randomly, and make it as the current best solution xopt. Then calculate the value of objective function f (xopt).♦Second, make a random fluctuation on the current solution. Then calculate the value of the new objective function f (x).♦Calculating and judgingΔf = f(x) - f(xopt).IfΔf >0, accept it as the current best solution;Otherwise, accept it in the form of probability P.The calculation method of P is:10=exp[(()())]0opt i f P f x f x f ≤⎧⎨-->⎩ (5.6)In this chapter, the SA algorithm is extended by selecting Bombali as a starting point to solve the optimal path. In the extended SA algorithm.we exploits the exponential cooling strategies and controls the change of temperature, namely10k i T Apha T -=⨯(5.7)Where T i is current controlled temperature, T 0 is the initial temperature, Apha is temperature reduction coefficient, k is the iterations.Solving the initial temperature 0T by means of random iterative and setting Apha = 0.9, the results are shown in Figure 4.4Longitude coordinates of citiesP a r a l l e l v a l u e o f c i t i e sthe total distance:54.8486Figure 4.4 Path graphThe value of the shortest total distance y is 54.8486 The shortest path is presented as follow:Bombali →Tonkolili →Nzerekore →Moyamba →Kambia →Port Loko →Coyah →Mali →Bo →Kindia →Western Urban →Kono →Dubreka →Faranah →Western Rural →Kenema →Kiss-dou gou →Kankan →Forecariah →Boffa →Macenta →Conakry →Montserrado →Koinadugu → Bombali4.2.2.2 SA model refinementSA model got all the shortest path problem of the city, but transport route is single and the efficiency is not high. So we use the longitude coordinates of Bombali as the basis to divide these cities into two parts. Urban classification is shown inTable 4.5, then simulate respectively.Table 4.5 The divided city distributionClassify CitiesLeft half Conakry, Moyamba, Port Loko, Kambia, Western Urban, Western Rural, Boffa, Dubreka, Kindia, Coyah, Forecariah, Bombali.Right halfMontserrado, Nzerekore, Macenta, Kissdougou, Kankan, Faranah, Kono, Bo, Kenema, Tonkolili, Koinadugu, Mali, Bombali .Bombali appears twice, because it is the starting point.After the algorithm simulation result is shown in Figure4.5 and Figure 4.6:Longitude coordinates of citiesP a r a l l e l v a l u e o f c i t i e sLongitude coordinates of citiesP a r a l l e l v a l u e o f c i t i e sthe total distance:28.2716Figure4.5 Left half Figure 4.6 Right halfThe path of left half ：Bombali →Port Loko →Boffa →Forecariah →Dubreka →Moyamba →Kindia →Coyah →West e-rnRural →Conakry →Kambia →Western Urban →Bombali The path of right half ：Bombali →Kenema →Faranah →Mali →Nzerekore →Bo →Kissdougou →Kankan →Koinadu gu →Kono →Tonkolili →Montserrado →Macenta →Bombali The total distance is:L=10.1739+29.8075=39.9814.It is smaller than the answer before, the transport time is reduced and the efficiency of transportation is improved.4.3 Model Ⅲ4.3.1 Analysis of the ProblemAccording to the above analysis of the first model and the second model, we can learn something about the spreading of Ebola, then finding the shortest path to transport medicines or vaccines. On the basis of the spreading of Ebola, we can know the numbers of illness with Ebola, then, get the quantity demanded of illness. According to the city distribution of infected zone, we find the shortest path to transport medicines, as well as ensure the shortest transporting route.After comprehending the demand for vaccine in infected zones and its the shortest transporting route, the next problem we think about is how to transport the vaccines or drugs from storage zone to infected zone using the maximum efficiency. Besides, we also need to consider whether the production speed can keep up with the demand for drugs and delivery speed. That is to say, the quantity of medicine production must be greater than or equal to the demand for drugs. Only in this method can we give sufficient vaccines or drugs to infected zones by using the fastest speed to control the spread of Ebola. 4.3.2 Model DesignIn the second model, we consider the shortest path and find the shortest path to all infected zones, then get its occurrence of distance. Getting the basic solve of the first model and the second model, the drugs or vaccines transport system can allot cars for infected zones judging by the weight of the numbers of infections in different cities. hypothesis ：♦ All allocation cars are the same vehicle size, moreover, have sufficient cars. That is to say, the quantity of vaccines or drugs in all cars is equal.♦ All delivery routes will not block up, and the cars will not break down. That is to say, all allocation cars can reach the infected area on time.♦ In order to avoid Ebola propagate to other place, this area should be isolated immediately once this area burst Ebola.♦ The car allocation in different regions can match up with the pharmaceutical demand in different regions. That is to say, they are positively related♦ By looking for date, we can get the number of infections in different regions :I1,I2,I3….In, then get the weight of the number of infections in different regions:11,2,3nn nnn I n Iα===∑(5.8)The pharmaceutical demand in different regions is:1,2,3n n H C n α==(5.9)C is the total quantity of car ，αn is the weight of the number of infections in different regions.According to the hypothesis, we can know that the pharmaceutical demand in each infected zone is directly related to the car allocation, so, we allot all cars in the light of weight. That is to say, the bigger weight can get more cars, the smaller weight will get less cars. Thus, we not only can save time, but also cost.According to the above analysis, we can know that the model also should meet the follow conditions:123'n A H H H H L T V ≥++++⎧⎪⎨≤⎪⎩(5.10)H n is the pharmaceutical demand in different regions, V ＇is vehicle speed, T is theproduction cycle of vaccines or drugs. According to the model I solving scheme, we can get the proportion of infected is i(t)=1/Qln(s/s 0)in t time, At the same time the region's demand for drugs is H=kNi(t), Drug production speed need to meet :10(ln ln )ni ii i i i k N V QT s s =≥-∑(5.11)We seek the latest date information from WTO official website [4], and get the new casedistribution graphs of Guinea 、Sierra Leone 、Liberia .You can see on Figure 4.7Figure 4.7 Geographical distribution of new and total confirmed casesWe can get the number of infections about 24 cities in infected zones from the diagram [5], then figure out the weight of infection numbers in different regions and clear up these dates. You can see on the Table 4.1.According to the model I, it have forecast the number of infections in 2015 February, and calculate the number of infections in various regions of the weight, the allocation of all transport vehicles, and have meet the demand for drugs in February at epidemic area. so, according to the predicted values, We can get the drug distribution table show in Table 4.6 and vehicle allocation table show in Table 4.7.the future of the epidemic and how to reasonable distribution of drugs,.According to the above model analysis, after ensuring the demand for vaccines and medicines in different regions and the shortest transport route, and on the double bind of medicine production speed and medicine delivery speed. we have a discussion ,then get the car allocation in different regions to make sure the medicines or vaccines reach the infected zones by using the fastest speed. So, we can remit current epidemic situation of Ebola.4.4 Extent our modelsIn the model I, we have studied the classical SIR epidemic model, then we have an improved in the model I, the improved model is:()()()()()()()()dSN I S t dt dIS t I t I t dt dRI t R t dt λβλβλμμλ⎧=-+⎪⎪⎪=-+⎨⎪⎪=-⎪⎩(5.12)In the infectious disease model, We've added the μto the population birth rate and natural mortality, ‘β’is the coefficient of the spread of the disease, ‘N’ is the number of species number. In this model assumes that there is no population move out and the death due to illness, the number of population is constant.As mentioned above, the ‘I’ is the number of infected patients, if the ‘S’ ‘I’ ‘R’ have given the initialvalue, By solving the differential equations(5.12), can get the value of ‘I(t)’ at a certain moment. For this model, we expect the people infected can stable at a low level, this means that the spread of infectious diseases has been effectively controlled. Analyzed the infectious disease model, if we want to control effectively to ‘I’, should decrease the coefficient of the spread of the disease β, and improve disease recovery rate λ, In terms of emergency rescue, it’s should ensure that there are have adequate relief drug to patients in emergency treatment, and make the probability of recovery to increase, then , it can control effectively to the increase of ‘I’.At the beginning of the outbreak of infectious diseases, when it ’s have a pulse vaccination for the population cycle T, the spread of the corresponding SIR epidemic model [6] is shown in Figure 4.8, Propagation model expressed in equation (4.13).S λI λRλFigure 4.8 The flow chart of pulse SIR1()()()()()()()()()(1)()()()0,1,2()()()nn nn dSN I S t dt dI S t I t I t t tdt dR I t R t t t T dtS t p S t I t I t t t n R t R t pS t λβλβλμμλ+----⎧=-+⎪⎪⎪=-+≠⎪⎪⎨=-=+⎪⎪=-⎪⎪===⎪=+⎩(5.13)P is vaccination rate.Impulsive vaccination is different from traditional large-scale disposable vaccination, it can ensure to make an effective control by using the spread of lower vaccination rate. We can obtain something from the analysis of the first model that i(t) is the function which increase first and then decrease with the time. Thus, the population infected will tend to zero ultimately. If 0dIdt <, then the critical value of c S is:()(1)(1)T c TT p e pTS T p e λλλγλλβλ+--+=>-+ (5.14)Then the critical value of c p is ：()(1)()(1)T c T T e p T e λλλλμβμβλμβ+--=--+- (5.15)We can know that, if the vaccination rate p>p c , system can obtain a stable disease-free periodic solution.When the infectious disease, which is described at model(5.12), burst out at one region, we should firstly know the demand for vaccine in different rescue cycle area before doing vaccinate to the infected populations. On account of epidemical diffusion law that indicated by SIR model(5.13), which possessing the pulse vaccination, we use the following form of demand forecasting that change over time.()k k D pS T -=(5.16)We can know something from the second model that we divide the whole infected zone into two regions. The two regions are assumed to be A and B. There is a stockpile around A and B. Known about the above information, we use the suggested model to do car allocation for A and B.Given the parameters in Ebola spread model(5.13) and its initial value, as shown in the Table 4.8 and Table 4.9. If the pulse vaccination cycle T=50, we use MATLAB programming to figure out the arithmetic solution of Ebola spread model (5.8) and model(5.9), as shown in the follow form:Table 4.8 Infectious disease model parametersParameter λ β μ p T Numerical0.000060.000020.0080.150Table 4.9 A and B area initial values i r Infected area A 830 370 0 Infected area B92278daysn u m b e r sthe SIR model with pulse vaccination in the demand point Adaysn u m b e r sthe SIR model without pulse vaccination in the demand point A(a) (b)daysn u m b e r sthe SIR model with pulse vaccination in the demand point Bdaysn u m b e r sthe SIR model without pulse vaccination in the demand point B(c) (d)Figure 4.9 Numerical solution of diffusion model SIR diseaseCompare Figure 4.9(a) with Figure 4.9(b), we can see that infected people and vulnerable people are going down faster under the circumstance of pulse vaccination. The same circumstance can be seen in the comparison of Figure 4.9(c) and Figure 4.9(d), it indicate that the pulse vaccination can control the spread of Ebola more effective. Because of this, we use the pulse vaccination to make our model solve the spread of Ebola preferably.5 Sensitivity Analysis5.1 Effect of Daily Contact RateIn model Ⅰ, we get the variation of function i (t ) and s (t ) by assuming variable value. So further discuss the value of λ is 2 or 3 whether impact on the result.Based on MATLAB software programming, can get the graphics when λ=2 or λ=3.daysn u m b e r sThe rate of healthy people and patientsdaysn u m b e r sThe rate of healthy people and patientsFigure 5.1 λ=2 or λ=3Conclusion:♦ Through comparing with Figure 4.2 ( λ=1 ) in model Ⅰ, it can be seen that the growth of the I (t) section is slightly reduced.♦ Observe the Figure 5.1, you can see λ=2 or λ=3 graphics haven't changed much5.2 Effect of inoculation rateIn the model Ⅲ, we have introduced the method of pulse vaccination. At the same time drew a conclusion that pulse vaccination can effectively control the spread of the virus.。

英文学术论文范文英文学术论文范文范例(优秀7篇)

英文学术论文范文英文学术论文范文范例（优秀7篇）推荐英文学术论文篇一会议相关事项：1、正式开会时间为：20某某年8月17-19日。

16日下午报到。

2、会议语言为中文和英文。

有同声翻译。

会议日程安排和具体资料请见本会专用网站：3、基金会承担您参加会议期间的午餐。

没有会务费。

其他费用自理(如果需要大会筹备组代订宾馆，请在报名时标明)。

4、诚请您在收到邀请函后即登录会议网站进行网上报名，也可用传真形式通知(参会回执可从网上获取)。

推荐英文学术论文篇二，关于某某大学第三届研究生国际学术会议的通知为了进一步营造科学研究氛围，开拓研究生国际学术视野，搭建研究生展示科研成果的平台，提升研究生研究能力、学术水平和国际交流能力，定于20某某年11月18-20日举办某某大学第三届研究生国际学术会议。

现将有关事项通知如下：本次研究生国际学术会议由某某大学研究生院主办，国际教育学院等相关学院协办。

成立第三届研究生国际学术会议组织委员会负责具体组织工作。

组委会成员如下：组长：江驹副组长：刘丽琳范祥涛王亚彤成员：沈星黄金泉赖际舟刘少斌左敦稳汪涛葛红娟刘友文张卓李栗燕屈雅红刘长江于敏王箭秘书：张廷赟沈楠郑珺子20某某年11月18日-20日中国某某某某大学㈠征稿范围本次国际学术会议征稿对象为某某大学硕、博士研究生（含留学生）、国内其他高校硕、博士研究生（含留学生）、国外研究生。

㈡投稿时间国外研究生投稿时间为20某某年6月10日-8月31日国内研究生（含留学研究生）投稿时间为20某某年6月10日-10月1日。

㈢投稿要求1、本次学术会议论文投稿领域分航空宇航、机械、信息、材料、人文经管、其他共六大类。

论文要求为原创研究成果，论文内容不涉密、不涉及政治与宗教问题。

2、本次学术会议以研究生提交英文论文、大会英文发言交流形式参会。

所有未正式发表的论文均可投稿，长度不限。

㈣评审时间1、会议形式本次会议官方用语为英语，会议分大会交流和分组交流，组委会将选出不超过10篇论文参加大会英文发言交流，其余所有录用论文将在分会场进行交流发言。

永磁同步电机参数辨识研究

华中科技大学硕士学位论文永磁同步电机参数辨识研究姓名：汤斯申请学位级别：硕士专业：控制理论与控制工程指导教师：沈安文20090527华中科技大学硕士学位论文摘要随着伺服技术在家庭生活和工业生产中的应用越来越广泛，具有高性能，高性价比的永磁同步电机伺服系统已经成为伺服控制系统的发展趋势。

由于永磁同步电机定子参数对于电机控制的性能有着极为关键的影响，于是本文针对永磁同步电机定子参数的辨识方法进行了研究。

文章首先对目前流行的永磁同步电机参数辨识方法进行了概述，并对各种方案进行了简单分析。

然后介绍了永磁同步电机的数学模型和空间磁场定向矢量控制方法，并对电机定子参数与电流控制器参数设计之间的关系进行了说明，阐述了电机参数辨识的重要性。

在这个背景下提出了一种基于离线方式下简单有效的永磁同步电机参数辨识方法。

随后在matlab/simulink中建立了仿真模型，对辨识方法的可行性进行了验证，并分析了硬件参数对于辨识结果产生的影响。

最后在硬件平台上对辨识方法进行了实现，并且针对微处理器本身的基本特点，实现了自然对数高精度计算，并利用了矩阵方程，最小二乘法曲线拟合等数据处理方法对参数辨识结果进行了优化处理，减小了实际硬件参数、采样数据偏差等因素产生的辨识误差。

初步的仿真和试验结果验证了所提出辨识方法的可行性和稳定性，说明本文研究的永磁同步电机参数辨识方法具有一定的实用价值。

关键词：交流伺服永磁同步电动机参数辨识最小二乘法曲线拟合华中科技大学硕士学位论文AbstractAs the servo technique servo technology has been applied more and more widely in family life and industry production, the PMSM servo system with both high performance and cost-performance ratio has become the future tendency of the development of servo control system. Since the stator parameters of the PMSM have a significant affect on the performance of motor control, the thesis focuses on the research of the stator parameters identification of the PMSM servo system.Firstly the thesis generally illustrates the popular parameter identification methods of the PMSM in the contemporary world. It also makes a brief analysis of each method. Then the mathematic models of PMSM and the methods of FOC are introduced，what’s more, the thesis states the relationship between motor parameters and the design of current controller parameters, explaining the importance of the motor parameters identification. Under this background an easy and effective PMSM parameters identification method based on the off-line mode is introduced in the thesis, additionally, by making the relevant emulator models in the matlab/simulink platform, the feasibility of the identification method is proved and the influence on the results of identification caused by the hardware parameters is taken into consideration. Finally the identification method is carried out on the hardware platform, based on the fundamental characteristics of the micro processor itself, the test implements the high precision calculation of the natural logarithm, also, by making use of the matrix equation, the curve fitness of the least square modeling and other calculation methods in order to form an optimized process on the outcomes of the parameter identification, the test reduces the identification errors caused by some factors, such as real hardware parameters and sampling data difference.Elementary emulator and the results of the tests have proved the feasibility and stability of the parameter identification which is introduced, indicating that the research on PMSM parameter identification method in this thesis does have practical values.Keywords: AC Servo PMSM Parameter Identification Least Square Modeling Curve Fitness独创性声明本人声明所呈交的学位论文是我个人在导师指导下进行的研究工作及取得的研究成果。

SCI论文模板范文

SCI论文模板范文Research on XXXXAbstractXXXX is an important problem for the research field of XXXXXX, widely studied by scholars in recent years. This paper firstly introduces the basic concepts and research backgrounds of XXXX. It then summarizes the main research progress in this field, and subsequently reviews the challenges and possible solutions for the existing problems in detail. Finally, the prospects and related potential topics are put forward for the further research of XXXX.Keywords: XXXX; XXXXX; XXXXX; XXXXX1. Introduction2. Main research progressXXX is the fundamental problem of XXXX research. In recent years, scholars have made a lot of attempts to solve the XXXX problem. In terms of methods, the research approaches can be roughly divided into two categories: one is the traditional XXXX approach, and the other is the XXXXXX approach. XXXX based on XXXXXX has achieved some encouraging results. XXXX, XXXX, XXXX and other methods are widely used in the Internet of Things (IoT). In terms of research results, XXXXXX has made greatprogress in recent years. XXXX, XXXX and XXXX have been successfully applied in XXXXXX.3. Challenges and solutions4. Prospects and potential topicsReferences[1]XXX.XXX.XXXX[J].XXXXXX,2024,XX(XX):XXX–XXX.[2]XXXX,XXXX.XXXX[J].XXXXXX,2024,XX(XX):XXX–XXX.[3]XXXX,XXXX.XXXX[J].XXXXXX,2024,XX(XX):XXX–XXX.[4]XXXX,XXXX.XXXX[J].XXXXXX,2024,XX(XX):XXX–XXX.。

2013ICM 优秀论文

Team # 23198
Page 2 of 19
Contents
1 Introduction ............................................................................................................................... 3 1.1 Previous Models ............................................................................................................ 3 1.2 Our Models ................................................................................................................... 3 Assumptions .............................................................................................................................. 4 Models....................................................................................................................................... 4 3.1 Basic Model: Impulse-network ..................................................................................... 4 3.1.1 Establishment of the Model............................................................................... 4 3.1.2 Pulse Process ..................................................................................................... 6 3.1 Global-Scale Model ...................................................................................................... 7 3.2.1 Node Determination .......................................................................................... 8 3.2.2 Edge Determination .......................................................................................... 9 3.2.3 Interactions ...................................................................................................... 10 3.2 Nonlinear Dynamic Network Model ........................................................................... 11 3.3.1 Model Establishment ....................................................................................... 11 3.3.2 Example Illustration ........................................................................................ 12 3.3.3 Model Analysis................................................................................................ 14 Model Verification .................................................................................................................. 14 Analysis................................................................................................................................... 16 5.1 How to use our model? ............................................................................................... 16 5.1.1 Establish the topological structure of the global biological network .............. 16 5.1.2 Determine the value of K ................................................................................ 16 5.1.3 Forecast the future health conditions of the earth ........................................... 16 5.2 What can our model do? ............................................................................................. 16 5.2.1 The rationality of parameters, nodes and edges .............................................. 16 5.2.2 Critical nodes and edges.................................................................................. 17 5.2.3 Human elements .............................................................................................. 17 5.2.4 Influence on future decision-making ............................................................... 17 5.3 Strengths and weaknesses ........................................................................................... 18 References ............................................................................................................................... 18

ICEM CFD中文

ICEM CFD 实例教程
目录前言 .........................................................................................................................................................................1 1 ICEM CFD 概述 .........................................................................................................................................................2 1.1 ICEM CFD 简介 ............................................................................................................................................2 1.2 总体工作流程 .............................................................................................................................................2 1.3 ICEM CFD 的用户界面 ...................................................................................................................

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

The Research of parallel structure and composite fuzzy control for linear machine based on MamdanimethodMingfei XuCollege of Electrical Engineering, southeast University,Nanjing, ChinaE-mail:491135410@Haitao YuCollege of Electrical Engineering, southeast University,Nanjing, ChinaE-mail:htyu@Abstract—According to the serious nonlinearity and highly coupling of variables in linear machine, which can contribute to the unsatisfactory control effect, therefore, one kind of parallel structure and composite fuzzy controller is proposed. Firstly, the velocity to voltage mathematical model was established. Secondly, through Ziger-Nichlol method mixed with manual fine-tune method, three parameters of PID controller could be accessed based on the model. Finally, the fuzzy controller was designed: the subordinate function of the input variables adopt gauss form; and fuzzy deduction manner of Mamdani method; the subordinate function of the output variables adopt triangular form. After above work, the MATLAB simulation was performed. The simulation indicates that this parallel structure and composite fuzzy controller has better control effect than the traditional PID controller, and the maximum overshoot decreases from 9.6% to 0%, the regulation time ranges from 1.23 seconds to 0.95 seconds, verifying that this fuzzy controller has positive feasibility.Keywords—linear machine; fuzzy control; PID control; Ziger-Nichlol method; Mamdani methodI.I NTRODUCTIONCompared with the traditional rotary motor, the linear motor mainly has the following characteristics: Firstly, the structure is simple, thus the weight and volume is greatly decreased; Secondly, it has the advantage of high positioning accuracy, if microcomputer control is used, it can also greatly improve the positioning precision of the whole system; Thirdly, it also has the feature of fast reaction rate, high sensitivity; Lastly, it is safe and reliable with long service life while working. The traditional control method can’t balance the steady and dynamic performance requirements due to the variable parameters so that the desired control effect can’t be achieved. In recent years, burgeoning fuzzy control method takes advantage of the control experience of human experts[1], for the control of nonlinear, complex objectives shows good robustness, high control performance, the control method is especially suitable for the linear motor. MATLAB was used for the simulation of established linear machine’s mathematical model, through comparison between the simulation waveform of traditional PID control and composite fuzzy control, it is discovered that the composite fuzzy control has evident advantage over traditional PID control in dynamic performance. This control method is in the guarantee of steady state accuracy. Above all, a kind of effective control method is proposed for the control of linear machine.II.T HE MATHEMATICAL MODEL OF THE LINEAR MOTOR In the power transmission system, linear motor is a kind of machine which can directly convert electrical energy into kinetic linear motion energy and does not need to install any intermediate mechanical transmission mechanism. It has the advantages of simple structure, high energy conversion efficiency, low noise, excellent operating reliability and so forth. When the rotary motor is cut open along the radial, and then along the circumferential flattened, the linear motor canbe obtained, as shown in figure 1.Fig.1. rotary motor transfers to linear motorThe stator is primary while the rotor is secondary, according to the kinematic properties and electromagnetic characteristics of linear motor, the linear motor motion equations, the voltage balance equation and the electromagnetic force equations[2] can be obtained in the time domain format:()()()()dI tU t E t RI t Ldt=++（1）()()mF t k I t=（2）22()()()()d x t dx tm c kx t F tdtdt++=（3） Among the formula,()()(),()Edx t dx tE t k V tdt dt==.U is the loop voltage, E as the counter electromotive force, R for the coil conductor resistance, I as the loop current, L is the coil conductor inductance, k E as the back EMF constant, x is the displacement of the linear motor, F as the electromagneticforce coil, k m as the force constant of the linear motor, m as the coil quality, c is the coefficient of friction viscous state, k is the spring stiffness coefficient, v as the linear motion for the linear motor speed.Apply Laplace transformation to (1),(2),(3) formula ：()()()()E U s k sx s RI s LsI s =++ （4）()()m F s k I s = （5）2()()()()ms x s csx s kx s F s ++= （6）Along with ()()V s sx s =, By formula (4), (5), (6), thetransfer function between the speed and voltage is:2()()()()m E m k s V s U s k k s R Ls ms cs k =++++ （7）III. Z IGER -N ICHLOL METHOD PARAMETER TUNING OF PIDCONTROLLER The output of the PID controller m(t) is proportional to the error signal e(t), and is also proportional to the integral of e(t), and is proportional to the first order derivative of e(t). The controller maintains the advantages of enhancing the system steady state performance based on the PI control rule, and it has more advantages in improving the system dynamic performance. Equations for PID controller in the time domain is:01()()()()t p d i de t m t K e t e t dt T T dt ⎡⎤=++⎢⎥⎣⎦⎰ （8） In the formula(8), m is the output of the PID controller, e is the input of PID controller, K p is the proportion coefficient of controller, T i is the integral time constant for the controller, T d is the differential time constant.After years of development, the Ziger-Nichlol method has become a parameter setting, intermediate methodology between experience and the calculation method. This method can determine the parameters very accurately for the controller, then can also be slightly tuned.The Ziger-Nichlol method consists of two steps: the construction of a close loop control circuit, determination of the stability limit. Controller parameter is calculated according to the formula. Stability limit is determined by the ratio number of element. When the steady state oscillation ouccrs, the limitation will be reached. The critical factor pcrit K and the critical oscillation cycle crit T can be obtained.When the critical factorpcritK and the criticaloscillation cycle crit T are confirmed, other parameters can be obtained based on the formula in table I:of manual fine tuning, we can calculate:5,40,2p I D K K K === IV.T HE DESIGN METHOD OF FUZZY CONTROLLER BASEDON M AMDANI METHODThe block diagram of fuzzy control system is shown in Figure 3:Fig.3. composite linear motor fuzzy control systemThe fuzzy controller in Figure 3 is the two-dimensional fuzzy controller [3], it has two inputs e and e ∙, they are the system error and error change rate (the exact amount); E and EC are the fuzzy set respectively in fuzzy system which reflects language variables of the deviation and deviation change (fuzzy amount); U as output variables; the exact amount of the output of fuzzy controller which has the control action is u ; y as the output of fuzzy control system (the exact amount).A. Fuzzy processing of error and error change rateFor fuzzy processing of deviation and rate of change which are the linguistic variables, we define positive big as PB, positive medium as PM, positive small as PS, zero as O, negative small as NS, negative medium as NM, negative big as NB. 7 linguistic variables [4] are used to describe the system. The membership function of the error and error change rate belong to the Gauss function. Parameters of each language variable values are shown in Table 2 and Table 3.Fig.4. Membership function curve of error and error change rateB. Fuzzy rules and fuzzy reasoningIn this paper, the fuzzy controller has double input and the single output, control rules of it are fuzzy conditional statements as follows:If E and EC then UWhen fuzzy relation of each fuzzy conditional statement R i (i=1,2,... m, where m is the number of sentences)is acquired, due to the "or" relationship between statements, the whole control system of fuzzy relation for fuzzy control rules can be calculated:121mm i i R R R R R ==∨∨⋅⋅⋅∨=∨ （9）If fuzzy subsets of E and EC in the input language variablefor fuzzy controller are given, and the fuzzy relation R i (i=1,2,... m) determined by every fuzzy statement based on the control rule is also given. Then fuzzy subset of U of the output language variable domain can be expressed as12()()()mU E EC R E EC R E EC R =⨯∨⨯∨⋅⋅⋅∨⨯ 1()mi i E EC R ==∨⨯ （10）Among them:“∨”： the maximum of two numbers.“⨯”：direct product, x, y are any two sets, we call {(,)|}X Y x y x X y Y ⨯=∈∈or is the direct product of x and y.“ ”：The synthetic operation of relations, it can be expressed as ==Q R S R S M M M M , if ,,Q R S M M M are expressed as []=,=,=Q ij R ik S kj M q M r M s ⎡⎤⎡⎤⎣⎦⎣⎦, then:=1=()nij ik kj k q r s ∨∧，i=1,2,3,…,m; k=1,2,3,…,n;j=1,2,3,…,p 。