最新微波课后作业地的题目(部分)
(完整版)微波课后作业题(部分)
习题课1.1 设一特性阻抗为50Ω的均匀传输线终端接负载R l =100Ω，求负载反射系数Γl ，在离负载0.2λ、0.25λ及0.5λ处的输入阻抗及反射系数分别为多少？解：根据终端反射系数与终端阻抗的关系10l 10100501100503Z Z Z Z --Γ===++根据传输线上任一点的反射系数与输入阻抗的关系2()j zlz ein 01()1()z Z Z z 得到离负载0.2λ、0.25λ及0.5λ处的输入阻抗及反射系数分别为2πj20.2λj0.8πλ1(0.2λ)3l eeZ (0.2λ)29.4323.79Ωin2πj20.25λλ1(0.25λ)3l e Z (0.25)25Ωin2πj20.5λλ1(0.5λ)3l e（反射系数具有λ/2周期性） Z (0.5)100Ωin （输入阻抗具有λ/2周期性）1.2 求内外导体直径分别为0.25cm 和0.75cm 的空气同轴线的特性阻抗；若在两导体间填充介电常数εr=2.25的介质，求其特性阻抗及300MHz 时的波长。
解：空气同轴线的特性阻抗为0.7560ln60ln65.9Ω0.25b Z a填充相对介电常数εr=2.25的介质后，其特性阻抗为60600.75lnln 43.9Ω0.252.25rb Z af =300Mhz 时的波长/=0.67m rc f1.4 有一特性阻抗Z 0=50Ω的无耗均匀传输线,导体间的媒质参数εr=2.25，μr=1，终端接有R l =1Ω的负载。
当f =100MHz 时，其线长度为λ/4。
试求：① 传输线实际长度； ② 负载终端反射系数； ③ 输入端反射系数； ④ 输入端阻抗。
解：①传输线上的波长为/=2m g rc f所以，传输线的实际长度为=0.5m 4gl②根据终端反射系数与终端阻抗的关系10l 101504915051Z Z Z Z --Γ===-++③根据传输线上任一点的反射系数与终端反射系数的关系220.2524949()5151j j zl z ee ④传输线上任一点的反射系数与输入阻抗的关系in 04911()51502500Ω491()151z Z Z z1.10 特性阻抗为Z 0=150Ω的均匀无耗传输线, 终端接有负载Z l =250+j100Ω，用λ/4阻抗变换器实现阻抗匹配（如图所示），试求λ/4阻抗变换器的特性阻抗Z 01及离终端距离。
微波技术习题解答
微波技术习题解答第1章练习题1.1 无耗传输线的特性阻抗Z0= 100()。
根据给出的已知数据，分别写出传输线上电压、电流的复数和瞬时形式的表达式：(1) R L= 100 ()，I L = e j0(mA)；(2) R L = 50()，V L = 100e j0(mV)；(3) V L = 200e j0 (mV)，I L = 0(mA)。
解：本题应用到下列公式：(1)(2)(3)(1) 根据已知条件，可得：V L = I L R L = 100(mV)，复数表达式为：瞬时表达式为：(2) 根据已知条件，可得：复数表达式为：瞬时表达式为：(3) 根据已知条件，可得：复数表达式为：瞬时表达式为：1.2 无耗传输线的特性阻抗Z0 = 100()，负载电流I L = j(A)，负载阻抗Z L = j100()。
试求：(1) 把传输线上的电压V(z)、电流I(z)写成入射波与反射波之和的形式；(2) 利用欧拉公式改写成纯驻波的形式。
解：根据已知条件，可得：V L = I L Z L = j(j100) = 100(V)，1.3 无耗传输线的特性阻抗Z0 = 75()，传输线上电压、电流分布表达式分别为试求：(1) 利用欧拉公式把电压、电流分布表达式改写成入射波与反射波之和的形式；(2) 计算负载电压V L、电流I L和阻抗Z L；(3) 把(1)的结果改写成瞬时值形式。
解：根据已知条件求负载电压和电流：电压入射波和反射波的复振幅为(1) 入射波与反射波之和形式的电压、电流分布表达式(2) 负载电压、电流和阻抗V L = V(0) = 150j75，I L = I(0) = 2 + j(3) 瞬时值形式的电压、电流分布表达式1.4 无耗传输线特性阻抗Z0 = 50()，已知在距离负载z1= p/8处的反射系数为 (z1)= j0.5。
试求(1) 传输线上任意观察点z处的反射系数(z)和等效阻抗Z(z)；(2) 利用负载反射系数 L计算负载阻抗Z L；(3) 通过等效阻抗Z(z)计算负载阻抗Z L。
廖承恩《微波技术基础》习题解答(最全的版本)
（2） （3）
（4）
sc oc 当 Z in (d ) = j100Ω ， Z in (d ) = − j 25Ω ， Z in (d ) = 75∠30°Ω 时
1562 . 5 +1875 × 75 ×
3 + 62 . 5 j 2
sc oc 2－6 在长度为 d 的无耗线上测得 Z in (d ) = j50Ω ， Z in (d ) = − j 50Ω ，接 实
第二三四六七章习题解答 第二章习题解答
2－1 某双导线的直径为 2mm，间距为 10cm，周围介质为空气，求 其特性阻抗。某同轴线的外导体内直径为 23mm，内导体外直径为 10mm， ，求其特性阻抗；若在内外导体之间填充εr 为 2.25 的 介 质 ， 求其特性阻抗。
解：双导线：因为直径为 d＝2mm＝2×10－3m 间距为 D＝10cm＝10－1m 所以特性阻抗为
ZL = Z0
2 — 12 画出图 2— 1 所示电路沿线电压、电流和阻抗的振幅分布图，
所以 ΓL =
Z L '− Z 02 450 − 450 = =0 Z L '+ Z 02 450 + 450
微波技术基础习题答案华科
微波技术基础习题答案华科微波技术基础习题答案华科微波技术是现代通信领域中的重要一环，它涉及到无线通信、雷达、卫星通信等众多应用。
在学习微波技术的过程中，习题是一个非常重要的辅助工具，通过解答习题可以帮助我们巩固所学的知识，并且提高我们的解决问题的能力。
下面是华中科技大学微波技术基础习题的答案，希望对大家的学习有所帮助。
一、选择题1. 以下哪项不是微波技术的应用领域？A. 无线通信B. 雷达C. 卫星通信D. 电视广播答案：D2. 微波技术中，波长范围一般为：A. 1 mm - 1 cmB. 1 cm - 1 mC. 1 m - 1 kmD. 1 km - 1 m答案：A3. 微波传输线的特点是：A. 传输损耗小B. 传输速度快C. 传输带宽大D. 以上都是答案：D4. 以下哪个是微波技术中常用的天线类型？A. 偶极子天线B. 棱角天线C. 高增益天线D. 以上都是答案：D5. 在微波技术中，常用的传输介质是：A. 真空B. 空气C. 金属D. 介质答案：D二、填空题1. 微波技术中，一般使用的频率范围是______ GHz。
答案：1-3002. 微波传输线的特点之一是传输损耗______。
答案：小3. 微波技术中，常用的天线类型之一是______天线。
答案：偶极子4. 微波技术中，常用的传输介质是______。
答案：介质5. 微波技术中，常用的调制方式之一是______调制。
答案：频率三、简答题1. 请简述微波技术的应用领域。
微波技术广泛应用于无线通信、雷达、卫星通信等领域。
在无线通信中，微波技术被用于移动通信、无线局域网等，可以实现高速、稳定的无线数据传输。
在雷达领域，微波技术可以实现目标的探测、跟踪和定位，广泛应用于军事、航空等领域。
在卫星通信中，微波技术实现了地球与卫星之间的长距离通信，使得人们可以通过卫星实现远距离的通信和数据传输。
2. 请简述微波传输线的特点。
微波传输线具有传输损耗小、传输速度快和传输带宽大的特点。
最新微波技术答案(一二章)
微波技术答案(一二章)题 解第 一 章1-1 微波是频率很高，波长很短的一种无线电波。
微波波段的频率范围为8103⨯Hz~12103⨯Hz ，对应的波长范围为1m~0.1mm 。
关于波段的划分可分为粗分和细分两种。
粗分为米波波段、分米波波段、厘米波波段、毫米波波段、亚毫米波段等。
细分为Ka K Ku X C S L UHF 、、、、、、、…等波段，详见表1-1-2。
1-2 简单地说，微波具有下列特点。
（1） 频率极高，振荡周期极短，必须考虑系统中的电子惯性、高频趋肤效应、辐射效应及延时效应；（2） 波长极短，“反射”是微波领域中最重要的物理现象之一，因此，匹配问题是微波系统中的一个突出问题。
同时，微波波长与实验设备的尺寸可以比拟，因而必须考虑传输系统的分布参数效应；（3） 微波可穿透电离层，成为“宇宙窗口”；（4） 量子特性显现出来，可用来研究物质的精细结构。
1-3 在国防工业方面：雷达、电子对抗、导航、通信、导弹控制、热核反应控制等都直接需要应用微波技术。
在工农业方面，广泛应用微波技术进行加热和测量。
在科学研究方面，微波技术的应用也很广泛。
例如，利用微波直线加速器对原子结构的研究，利用微波质谱仪对分子精细结构进行研究，机载微波折射仪和微波辐射计对大气参数进行测量等等。
第 二 章2-1 解 ∵01011Z Z Z Z +-=Γ ∴)(82.811Ω=Z2-2 解图（a ）的输入阻抗021Z Z ab =； 图（b ）的输入阻抗0Z Z ab =；图（c ）的输入阻抗0Z Z ab =；图（d ）的输入阻抗052Z Z ab =； 其等效电路自绘。
2-3 解 ∵01011Z Z Z Z +-=Γ ∵e j j 4121)1(21π=+=Γ 2-4 解（1） ∵e j Z Z Z Z 40101122π=+-=Γ ∴83.511ρ11=Γ-Γ+=（2） ∵π2 =l β ∴e e j l -j l 4π) β2(11022=Γ=Γϕ 2-5 解 ∵ljZ Z l jZ Z Z Z tg βtg β10010++= ∴)(39.673.8Ω+=j Z in)(24.6009.2201Ω+=j Z)(1005003Ω+=j Z2-6 证明∵)(00ββe e lj l j U U Γ+=-+ )(00ββ0e e l j l j Z U I Γ-=-+ 而I Z E I Z E U g 0-=-=∴e U E l j 0β2-+= 故2EU =+2-7 证明lZ j l j Z l jZ Z l jZ Z Z in tg β1tg βtg βtg β111001++=++= 而 ρ11min =Z ，对应线长为1min l 故 1min 11min 1tg β1tg βρ1l Z j l j Z ++= 整理得 1min 1min 1tg βρρtgβ1l j l j Z --=2-8 解∵38.001011=+-=ΓZ Z Z Z而给定的1Z 是感性复阻抗，故第一个出现的是电压腹点，即λ/4线应接在此处。
微波技术练习题及答案
工作波长分别为 7 cm，6 cm 和 3 cm 时，波导中可能存在的模式；(3) 当工作波长为 7 cm 时， 主模的波导波长 λg。
3-21 空气圆波导，已知工作波长 λ ＝5mm，要求单模传输，试确定圆波导的半径，并
2-20 在阻抗圆图中，为什么 Vmax 线上的归一化 R 值就是驻波比 ρ 的值？
2-21 试说明导纳圆图与阻抗圆图中的特殊的点、线、面的对应关系。 2-22 实用圆图中有哪些标度？怎样利用圆图求得工作状态量？ 2-23 无耗传输线特性阻抗 Zc ，终端负载阻抗 Z0（或负载导纳 Y0），利用圆图求解： （1）Zc = 50 Ω，Z0 = 200 + j75 Ω，求终端电压反射系数、电压驻波比及驻波相位。 （2）Zc = 100 Ω，Z0 = 80 － j120 Ω，求终端电压反射系数、距离终端最近的电压波节 和波腹点的位置。
习题二
2-1 传输线中可能存在的波有哪些？传输线的特性参量有哪些？ 2-2 什么叫行波状态？形成行波状态的负载状态是什么？此时电压和电流的振幅沿线 的分布情况如何？ 2-3 什么叫纯驻波状态？形成纯驻波状态的负载条件是什么？在纯驻波状态下，电压、 电流的振幅沿线的分布情况怎样？ 2-4 什么叫驻波？接什么样的负载可形成驻波状态？驻波状态下电压、电流的振幅值 沿线的分布规律与纯驻波状态有什么相同点和不同点？ 2-5 分析驻波参量与反射系数的关系。 2-6 请总结传输线共有哪些工作状态参量及这些参量之间的关系。 2-7 如图所示的传输系统中，末端所接负载的阻抗值 Z0=200 Ω ，两段传输线的特性阻
西电微波网络-课后题答案
第2讲习题本作业针对微波网络的参量矩阵，介绍了Z 矩阵，Y 矩阵，A 矩阵，S 矩阵和T 矩阵的定义以及各矩阵间的相互转换。
2.1 证明Z 矩阵与A 矩阵的关系式二端口Z 矩阵电压-电流关系为2121111I Z I Z V +=（1）2221212I Z I Z V +=（2）由（2）得2212222111I Z ZV Z I -=（3）将（3）带入（1）得221221111I Z V Z Z V ∆-=证毕2.2 求图2-13所示网络的Z 矩阵cb a bc a I Z Z Z Z Z Z I V Z +++===)(|011112 c b a c b a I Z Z Z Z Z Z I V Z +++===)(|022221c b a c b I Z Z Z Z Z I V Z ++===021121| cb ac b I Z Z Z Z Z I V Z ++===012212| 2.3 求图2-14所示网络的A 矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡++++=⎥⎥⎦⎤⎢⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡βθθβθθβθθβθθβθθθθβsin cos sin sin cos 2sin sin cos 1101cos sin 1sin cos 110102000000Z j Z Z j j jZ Z j Z j jZ j2.4 已知图2-11所示网络的[]⎥⎦⎤⎢⎣⎡=22211211A A A A A ，端口2接阻抗l Z ，求端口1的输入阻抗。
⎩⎨⎧-=-=22222112122111I A V A I I A V A V则 2221121122222121221111A Z A A Z A I A V A I A V A I V Z l lin ++=--==2.5⎩⎨⎧+=+=22222122122111i a u a i i a u a u 利用111b a u +=222b a u += 111b a i -=222b a i -=得⎩⎨⎧--+=---+=+)()()()()()(22222221112212221111b a a b a a b a b a a b a a b a两式相加2222112112222112111)()(2b a a a a a a a a a a ++++-+-=2222112112221121112221121122a a a a a a a a a a a a a a b ++++-+-++++=即 22211211212a a a a s +++=222112112221121122a a a a a a a a s ++++-+-=222112112221121111--a a a a a a a a s ++++=[]2221121112det 2a a a a a s +++=2.6 （a ）[]⎥⎦⎤⎢⎣⎡=101z A根据电路理论，得⎩⎨⎧-=-=22121ZI V V I I 利用01111)(Z b a I -= 02222)(Z b a I -= 01111)(Z b a V += 02222)(Z b a V +=得01220211)()(Z b a Z b a --=-Z b a Z b a Z Z b a )()()(220222020111--+=+于是⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡--=⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡+-210202010102210202010102)(a a Z Z Z Z Z Z b b Z Z Z Z Z Z⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡+-+-++=⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡--⎥⎥⎦⎤⎢⎢⎣⎡-+++=⎥⎦⎤⎢⎣⎡2102020101020102020102020102210202010102020201010202010221)(22)()(1)(1a a Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z a a Z Z Z Z Z Z Z Z Z Z Z Z Z Z Z Zb b即ZZ Z ZZ Z s +++-=020*******ZZ Z ZZ Z s +++-=020*******ZZ Z Z Z s s ++==0201020121122由t 矩阵与s 矩阵的关系得02010*********Z Z ZZ Z s t ++==020102012122122Z Z Z Z Z s s t +--=-=020101022111212Z Z Z Z Z s st +-== )(2)(020102012020122122Z Z Z Z Z Z Z Z s t ++--=∆-= (b)[]⎥⎥⎦⎤⎢⎢⎣⎡=N N A 100根据电路理论，得21nV V = 211I nI -=利用01111)(Z b a I -= 02222)(Z b a I -= 01111)(Z b a V += 02222)(Z b a V +=得02220111)()(Z b a n Z b a +=+ 01220211)()(Z b a Z b a n --=-于是⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡-=⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡-21010202012101020201a a Z Z n Z n Z b b Z Z n Z n Z ⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡-+-+=⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡-⎥⎥⎦⎤⎢⎢⎣⎡-+=⎥⎦⎤⎢⎣⎡210220102010201022010220121010202010102020102201212211a a Z n Z Z Z n Z Z n Z n Z Z n Z a a Z Z n Z n Z Z Z n Z n Z Z n Zb b即022010220111Z n Z Z n Z s ++-= 022010220122Z n Z Z n Z s +-= 02201020121122Z n Z Z Z n s s +== 由t 矩阵与s 矩阵的关系得020102201211121Z Z n Z n Z s t +==02010********122Z Z n Z n Z s s t --=-= 0201022012111212Z Z n Z n Z s s t +-== )(2)(0220102012022012122Z n Z Z Z n Z n Z s t +--=∆-= 2.7 已知一双端口网络的s 矩阵满足21122211,s s s s ==。
微波技术习题答案5.docx
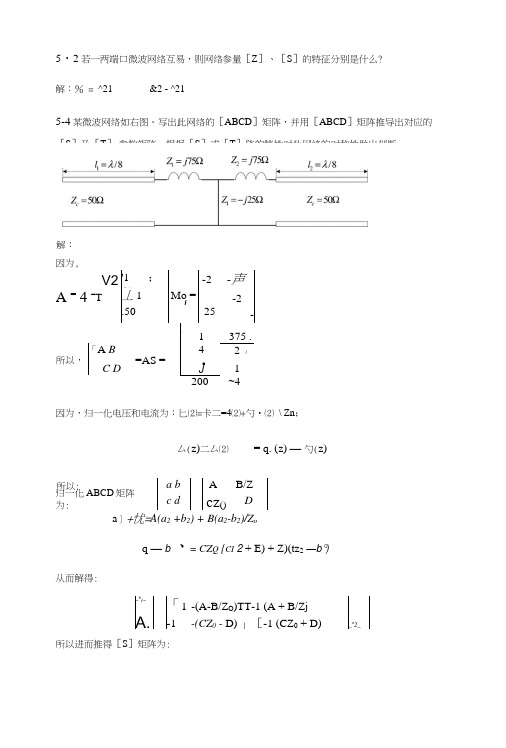
5・2若一两端口微波网络互易，则网络参量［Z ］、［S ］的特征分别是什么?解：％ = ^21&2 - ^21因为,V2 '1 ；50__-2 -声 A = 4 =T 丄1 Mo = J-2.50_25 -一1 375 .「A B4 2」 所以， C D =AS =■J1 200 ~4因为，归一化电压和电流为：匕⑵=卡二=4⑵+勺•⑵ \ Zn ；厶(z)二厶⑵= q. (z) — 勺(z)a 〕+忧=A(a 2 +b 2) + B(a 2-b 2)/Z oq — b、= CZ Q {CI 2 + E) + Z)(tz 2—b°)从而解得:~b i~「1 -(A-B/Z O )TT-1 (A + B/ZjA.-1 -(CZ 0 - D)」［-1 (CZ 0 + D)_a 2_所以进而推得［S ］矩阵为:a b_AB/Z （「c dcz () D 归一化ABCD 矩阵为:所以:5-4某微波网络如右图。
写出此网络的［ABCD ］矩阵，并用［ABCD ］矩阵推导出対应的［S ］及［T ］ 参数矩阵。
根据［S ］或［T ］阵的特性对此网络的对称性做出判断。
解：2（AD-BC ）—A + B / Z （）— CZ （）+ D乙+Zc — K z _7 U 乙+Z 』v[Z][/] = [V]⑸一 A + B/Z （）+CZo + D_ A + B/ Z （）—CZ Q — D2 由(3)式解得[S] -1 1 ~—- + 4/ 27 . 27所以, b\ _ 1~ 2A —B / Z° — CZ （）+DA —B / Z （）+ CZ 1 A + B / Z° — CZ Q — D A — B / Z° — CZ°+ D2 A + B/Zo + CZo + D A-B/Z +CZ -D7 .—/21力• ----- 4 j 2----- 4 j 2 7 . * （9）因为［s ］阵的转置矩阵［sy 二［S ］,所以，该网络是互易的。
北理工微波工程导论课后习题解答第2章
（1）放大器的稳定性如何？ （2）放大器最大增益为多少分贝？ （3）最大功率增益情况的负载阻抗 Z L 为多少？ （4）对 50Ω 系统，输入阻抗 Z in 为多少？
（1）
2 2 2 1 − S11 − S 22 + ∆ = > 1 K 2 S12 S 21 2 K > 1 1 − S11 > S12 S 21 ⇒ ∆ <1 2 1 − S 22 > S12 S 21 = ∆ S11S 22 − S12 S 21
上式中除了“和频”( ωL + ωR ) 与“差频”( ωL − ωR ) 外，还有二次谐波 2ωR 、
= M ωL ± N ωR 。 2ω L 项。 三次和高次项产生较高次谐波， 其混频产物为 ω 式中， M ,N
M、N 是正整数。所要的混频输出一般是中频（IF）成分，以 ωI 表示。 ωI 可以 是较低的下边频 ( ωL − ωR ) 或上边频 ( ωL + ωR ) 。较低的边频通常是我们所感兴趣 的， “混频器”这个名词一般是指这种情形。 （2）技术指标与物理意义 变频损耗 Lc 或变频增益 Gc ：表征混频器频率变换能力的参数。 噪声系数：由于放大器本身有噪声，输出端的信噪比和输入端信噪比是不一
(S
(S
22
∗ − S 11 ∆ 2
)
2
∗
S 22 − ∆
R I = CS + jCS 分别为 输入稳定圆的半径 rS 和圆心 C S
rS =
S12 S 21 , CS = 2 2 S 22 − ∆
11
∗ − S 22 ∆ 2
微波技术习题解答(部分)概要
欲使 A 处无反射，要求有 ZinA Z0 得到
2 Z0 Z01 jZ0 ZL tan l Z01ZL jZ01 tan l
由上式得 又
Z01 100 2
tan l 2
c 3 108 m 0.1m 10cm 9 f 3 10
arc tan 2
微波技术基础课后习题
杜 英
2011.5.1
第二章 传输线理论
2-6 如图所示为一无耗传输线，已知工作频率 f 3GHz ， Z0 100 ，
ZL 150 j50 ，欲使 A 处无反射，试求
l 和
Z 01 。
答案：由输入阻抗定义知
ZinA Z01 Z L jZ01 tan l Z01 jZ L tan l
3 108 答案：当工作频率 f 5GHz ， m 60mm 9 5 10
矩形波导TE、TM波截止波长公式为：
c
2
m a n b
2
2
当矩形波导的尺寸为 a b 109.2mm 54.6mm ，各波型的截止波长c 为
第三章 微波传输线
矩形波导中能传输的波型有 TE10 TE20 TE01 TE11 TM11 TE21 TM 21
2
p
1 c
2
vg v 1 c
2
第三章 微波传输线
3-9 一个空气填充的矩形波导，要求只传输 TE10 模，信号源的频率为 10GHz，试确定波导的尺寸，并求出相速 vp 、群速 vg 及相波长 p 答案： f 10 Hz
10
c 3 108 m 3cm 10 f 10
T T e j S12 e j12 S21 e j21
微波技术期末复习 课后习题
1.微波是频段在3×108Hz~3×1012Hz.2.微波的特点是频率高、波长短、散射性、穿透性、量子特性.3.微波传输的波动方程：一般形式: 022=+∇E Eμεω,022=+∇H Hμεω；真空：0202=+∇E k E,0202=+∇H k H，边界条件: s s n D ρρ=⋅=即,00=⋅=B n B n 即,s s t J H n J H =⨯=即,00=⨯=E n E t 即，导行波的类型:横向波(TEM)、色散波(TE/TM)、表面波.特点:横向波Ez=0，Hz=0、色散波(TE 波Ez=0，Hz ≠0；TM 波Ez ≠0，Hz=0)、表面波Ez ≠0，Hz ≠0.4.微波传输线的类型:导行波为TEM 波传输线、导行波为TE/TM 波传输线.5.矩形波导传输波的导模类型:不能传输TEM 波，TEmn\TMmn ，TE10.6.矩形波导传输波的主模是TE10模，传输波类型是TE/TM 波.场结构P347.矩形波导的壁电流分布是上下宽壁表面壁电流方向相反，左右宽壁表面壁电流方向相同. 辐射缝和无辐射缝的判别标准：切割是辐射缝、不切割是无辐射缝.8.圆柱波导的常用模的类型:TE11、TM01、TE01；应用:TE11:矩圆过渡段、TM01:天线铰链、TE01:远距离传输. 9.同轴线传输波的主模是TEM 模，传输波类型是任意波.场结构P6610.微波长线的传输线方程:0),(),(22=-∂∂t z ZYu z t z u ，0),(),(22=-∂∂t z ZYi z t z i .解:z z e A e A z U γγ21)(+=- ，)(1)(210z z e A e A Z z I γγ-=- . 11.均匀无耗线波的工作状态行波状态、纯驻波状态、行驻波状态. 特点：行波：输入阻抗Z L =Z 0，反射系数为0，功率能量全部被负载吸收、纯驻波：输入阻抗为纯电抗(±jX)，反射系数模为1，功率能量负载不吸收、行驻波：输入阻抗为复数Z L =R+jX ，终端的反射系数在(0,1)之间，功率能量一部分被负载吸收.12.为什么要匹配：①解决如何从微波源中取出最大功率；②解决如何使负载吸收最大功率. 匹配的类型：①微波源的匹配；②负载的匹配.匹配的方法：①并联单支调配；②并联双支和并联三支调配；③λ/4阻抗调配器.13.微波谐振腔的基本特性：多谐性、高Q 值. 参量：谐振频率f0(或谐振波长λ0)、固有品质因数Q0、特性阻抗ζ0. 14.矩形波导谐振器的主模是TE101模，类型是两端短路的λp /2型. 15.矩形波导谐振器的谐振频率为 ，截止频率为 .16.同轴谐振器的类型：两端短路的λ/2型、一端短路一端开路的λ/4型、电容加载型.17.微波电阻性元件的类型:吸收式衰减器、极化衰减器、截止式衰减器. 要求:吸收式衰减器：尖劈型，表面涂金属，斜长度λp /2整数倍、极化衰减器：边1、3平行于宽边，边2可转动，1与2夹角0度时衰减最小，90度时衰减最大. 18.微波移相器的类型：波程式移相器、波长式移相器. 19.微波电抗性元件的类型：膜片、销钉、螺钉.20.微波定向耦合器的类型：微带分支定向耦合器、波导单孔定向耦合器、平行耦合线定向耦合器、波导匹配双T 、波导多孔定向耦合器、微带混合环.21.微波定向耦合器的主要性能指标：耦合度、隔离度、方向性、输入驻波比、频带宽度.1.为什么矩形波导不能传输TEM 波？答：假定矩形波导能传输TEM 波，根据TEM 波的定义可知:Ez=0，Hz=0，电磁场为横向波.由高斯定理可知，磁力线在波导横面是闭合曲线.由安培环路定理可知，要产生这种磁场，必须存在纵向电流.由于矩形波导是单导体，所以不能有传导电流，只能有位移电流，必存在纵向电场Ez ≠0，与假设矛盾，故矩形波不能传输TEM 波.2.矩形波导的尺寸选择依据及尺寸的经验确定.答：选择依据:①必须保证单模传输，有效抑制高次模的干扰.即a<λ<2a;②损耗与衰减尽量小，保证较高的传输效率.即a<λ<1.8a;③功率容量大;④色散尽量小，以免信号失真。
电磁场与微波技术第一二三章课后习题及部分答案
电磁场与微波技术第一二三章课后习题及部分答案第 1 章习题1、求函数()D Cz By Ax u +++=1的等值面方程。
解：根据等值面的定义：标量场中场值相同的空间点组成的曲面称为标量场的等值面，其方程为)( ),,(为常数c c z y x u =。
设常数E ，则，()E D Cz By Ax =+++1，即：()1=+++D Cz By Ax E针对不同的常数E （不为0），对应不同的等值面。
2、已知标量场xy u =，求场中与直线042=-+y x 相切的等值线方程。
解：根据等值线的定义可知：要求解标量场与直线相切的等值线方程，即是求解两个方程存在单解的条件，由直线方程可得：42+-=y x ，代入标量场C xy =，得到： 0422=+-C y y ，满足唯一解的条件：02416=??-=?C ，得到：2=C ，因此，满足条件的等值线方程为：2=xy3、求矢量场z zy y y x xxy A 222++=的矢量线方程。
解：由矢量线的微分方程：zy x A dz A dy A dx ==本题中，2xy A x =，y x A y 2=，2zy A z =，则矢量线为：222zy dzy x dy xy dx ==，由此得到三个联立方程：x dy y dx =，z dz xdx =，zy dzx dy =2，解之，得到： 22y x =，z c x 1=，222x c y =，整理，y x ±=，z c x 1=，x c y 3±=它们代表一簇经过坐标原点的直线。
4、求标量场z y z x u 2322+=在点M (2,0,-1)处沿z z y xy x x t ?3??242+-=方向的方向导数。
解：由标量场方向导数的定义式：直角坐标系下，标量场u 在可微点M 处沿l 方向的方向导数为γβαcos cos cos zuy u x u l u ??+??+??=??α、β、γ分别是l 方向的方向角，即l 方向与z y x、、的夹角。
微波技术习题课 Vol.2 波导共24页PPT
66、节制使快乐增加并使享受加强。 ——德 谟克利 特 67、今天应做的事没有做，明天再早也 是耽误 了。——裴斯 泰洛齐 68、决定一个人的一生，以及整个命运 的，只 是一瞬 之间。 ——歌 德 69、懒人无法享受休息之乐。——拉布 克 70、浪费16、人民应该为法律而战斗，就像为 了城墙 而战斗 一样。 ——赫 拉克利 特 17、人类对于不公正的行为加以指责 ，并非 因为他 们愿意 做出这 种行为 ，而是 惟恐自 己会成 为这种 行为的 牺牲者 。—— 柏拉图 18、制定法律法令，就是为了不让强 者做什 么事都 横行霸 道。— —奥维 德 19、法律是社会的习惯和思想的结晶 。—— 托·伍·威尔逊 20、人们嘴上挂着的法律，其真实含 义是财 富。— —爱献 生
微波部分计算题+填空题整理
1、微波定义：3×10^8 Hz ~ 3×10^12 Hz2、微波特点：①高频特性 ②短波特性 ③散射特性 ④穿透性 ⑤量子特性3、边界条件：（1）两种理想介质分界面处的边界条件：①221n 121E 即n n n E D D εε==②221n 121H 即n n n H B B μμ==③21t t H H = ④21t t E E =(2)理想导体表面的边界条件：①s D n ρ=②0B n = ③s t J H = ④0=t E4、波动方程：①电磁场波动方程002222=+∇=+∇H H E Eμεωμεω②真空中无源区的波动方程为0202220=+∇=+∇H k H E k E5、导行波类型及特点：①横电波（TE 波），0,0≠=zz H E ；②横磁波（TM 波），0,0=≠z z H E ；③横电磁波（TEM 波），0,0==zz H E 6、微波传输线类型：TEM 波传输线、色散波传输线、表面波传输线。
7、矩形波导传输波的导模类型：TE108、圆柱波导的常用模的类型及应用：①TE11波（矩圆过渡段）②TE01波（远距离传输）③TM01波（天线旋转交变） 9、均匀无耗线波的工作状态及特点：①行波状态：0Z Z L =或长线为无限长；②驻波状态：长线终端短路（0=L Z ）、开路（∞=L Z ）或接纯电抗负载jX Z L =；③行驻波状态：jX R Z L +=，R 、X 为任意值。
10、微波传输线的阻抗匹配：（1）为什么要匹配？没有反射，没有干扰，传输最大功率。
（2）匹配类型：支节匹配（单支节；多支节；4λ匹配，变换器） （3）匹配方法：①调配器 ②阻抗变换器。
11、微波谐振腔的基本特性与参量：①谐振频率0f ②品质因数0Q ③特性阻抗0ζ 方法：场解法、相位法、电纳法、集总参数法LCπ210=f12、矩形波导谐振器的谐振频率和截止频率的计算公式，矩形波导谐振器的主模。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
习题课1.1 设一特性阻抗为50Ω的均匀传输线终端接负载R l =100Ω，求负载反射系数Γl ，在离负载0.2λ、0.25λ及0.5λ处的输入阻抗及反射系数分别为多少？解：根据终端反射系数与终端阻抗的关系10l 10100501100503Z Z Z Z --Γ===++根据传输线上任一点的反射系数与输入阻抗的关系2()j zl z e b -G =Gin 01()1()z Z Z z +G =-G得到离负载0.2λ、0.25λ及0.5λ处的输入阻抗及反射系数分别为2πj20.2λj0.8πλ1(0.2λ)3l ee --G =G =Z (0.2λ)29.4323.79Ωin =?2πj20.25λλ1(0.25λ)3l e-G =G =-Z (0.25)25Ωin l =2πj20.5λλ1(0.5λ)3l e-G =G =（反射系数具有λ/2周期性） Z (0.5)100Ωin l =（输入阻抗具有λ/2周期性）1.2 求内外导体直径分别为0.25cm 和0.75cm 的空气同轴线的特性阻抗；若在两导体间填充介电常数εr=2.25的介质，求其特性阻抗及300MHz 时的波长。
解：空气同轴线的特性阻抗为00.7560ln60ln 65.9Ω0.25b Z a === 填充相对介电常数εr=2.25的介质后，其特性阻抗为00.7543.9Ω0.25b Z a=== f =300Mhz 时的波长0.67ml1.4 有一特性阻抗Z0=50Ω的无耗均匀传输线,导体间的媒质参数εr=2.25，μr=1，终端接有R l=1Ω的负载。
当f=100MHz时，其线长度为λ/4。
试求：①传输线实际长度；②负载终端反射系数；③输入端反射系数；④输入端阻抗。
解：①传输线上的波长为2mgl=所以，传输线的实际长度为=0.5m4gll=②根据终端反射系数与终端阻抗的关系10l101504915051Z ZZ Z--Γ===-++③根据传输线上任一点的反射系数与终端反射系数的关系220.2524949()5151jj zlz e eplb l--G=G=-=④传输线上任一点的反射系数与输入阻抗的关系in04911()51502500Ω491()151zZ Zz++G===-G-1.10 特性阻抗为Z0=150Ω的均匀无耗传输线, 终端接有负载Z l=250+j100Ω，用λ/4阻抗变换器实现阻抗匹配（如图所示），试求λ/4阻抗变换器的特性阻抗Z01及离终端距离。
解：先把阻感性负载，通过一段特性阻抗为Z0的传输线，变为纯阻性负载。
由于终端反射系数为250j1001500.3430.54250j100150lllZ ZZ Z-+-G===?+++离波腹点较近。
第一个波腹点离负载的距离为max0.540.04344lll lf lp p===即在距离负载l=0.043λ可以得到一个纯电阻阻抗，电阻值为max0R Z r=1||2.04411||l l r +G ==-G在此处插入一个λ/4阻抗变换器即可实现阻抗匹配，其可特性阻抗为01214.46ΩZ =1.12在特性阻抗为600Ω的无耗双导线上测得|U|max 为200 V ，|U|min 为40V ，第一个电压波节点的位置l min1=0.15λ，求负载Z l 。
今用并联支节进行匹配，求出支节的位置和长度。
解：传输线上驻波比maxmin||5||U U r ==第一组解'10.06692l λπ==2arctan 0.418942l λλλπ=-= l 1=l 1′+l min1=0.2169λl 2=0.4189λ另一组解'1arctan0.06692πl λλ=-=-20.081142πl λλλ=+=l 1=l 1′+l min1= 0.1831λl 2=0.0811λ2.1 试说明规则金属波导内不能传播TEM 波的原因答：空心波导内不能存在TEM 波。
这是因为，如果内部存在TEM 波，则要求磁场应完全在波导的横截面内，而且是闭合回线。
由麦克斯韦方程可知，b 闭合曲线线磁场的环路积分应等于与回路交链的轴向电流。
此处是空心波导，不存在轴向的传导电流，故必要求有轴向的位移电流，由位移电流的定义式d DJ t¶=¶知，这时必有轴向变化的电场存在。
这与TEM 波电场、磁场仅存在于垂直于传播方向的横截面内的命题是完全矛盾的，所以波导内不能存在TEM 波。
2.2矩形波导的横截面尺寸为a=22.86mm, b=10.16mm, 将自由空间波长为20mm 、30mm 和50mm 的信号接入此波导，能否传输？若能，出现哪些模式？解：当λ<λc 时信号能传播，矩形波导中各模式的截止波长为1020011111245.72mm22.86mm220.32mm18.5687mmcTEcTEcTEcTE cTMaabllll l==========因此当λ=50mm时，所有模式都截止；λ=30mm时，只有主模TE10模成为传导模；当λ=20mm 时，TE10、TE20、TE01三种模式为传导模。
2.3 矩形波导截面尺寸为a×b=23mm×10 mm，波导内充满空气，信号源频率为10 GHz，试求：①波导中可以传播的模式；②该模式的截止波长λc、相移常数β、波导波长λg及相速v p。
解：①信号的工作波长λ=c/f=3cm=30mm各模式的截止波长102001246mm23mm220mmcTEcTEcTEaablll======所以当频率为3GHz时，波导内只有TE10模②截止波长λc==2a=46mm相移常数22222158.8 rad/mckm nka a aplp p pb=骣骣骣鼢?珑?=+=鼢?珑?鼢?珑?桫桫桫波导波长239.5mmgplb==相速823.9510m/spfvw pb b===?2.12 什么叫模式简并？矩形波导和圆形波导中模式简并有何异同？答：波导中，场结构不同但传输特性相同的两种模式称为简并模，这里传输特性相同，主要指的是截止波数kc相同。
矩形波导中TEmn模和TMmn模的截止波数c k =m 、n ，TEmn 模和TMmn 构成简并模。
在圆形波导中，TE 0n 和TM 1n 构成E-H 简并，而对于m ≠0的非圆对称模式存在极化简并。
2.13 圆波导中最低次模是什么模式？旋转对称模式中最低阶模是什么模式？损耗最小的模式是什么模式？答：圆波导中最低次模是TE 11模；旋转对称模式中最低阶模是TM 01模；损耗最小的模式是TE 01模。
2.15 在波导激励中常用哪三种激励方式？ 答：电激励、磁激励和电流激励。
3.2一根以聚四氟乙烯(εr=2.1)为填充介质的带状线，已知b=5 mm ，t=0.25 mm ，w=2 mm ，求此带状线的特性阻抗及其不出现高次模式的最高工作频率。
解：各参数的含义如图所示根据p61页3-1-4由下向上进行计算可得：Z 0=69.4Ω。
带状线的主模为TEM 模，但若工作频率过高也会引起高次模，最短工作波长应满足1010min max(,)cTE cTM l l l >根据62页3-1-9式和3-1-10式10102 5.8mm 214.5mmcTE cTM l l ==所以最高工作频率8max 3min31020GHz 14.510c f l -´===´ 3.3 已知某微带的导带宽度为w=2mm ，厚度t →0，介质基片厚度h=1mm ，相对介电常数εr=9，求此微带的有效填充因子q 和有效介电常数εe 及特性阻抗Z 0（设空气微带特性阻抗Z 0a=88Ω）解：根据66页3-1-25式，由于这里w/h=2，因此应使用第二式来计算填充因子12111210.68922h q w -⎛⎫=++= ⎪⎝⎭有效介电常数，根据63页3-1-27r 1(1) 6.5e q =+-=εε特性阻抗034.5Z α==Ω4.5 设某系统如图所示，双端口网络为无耗互易对称网络，在终端参考面T2处接匹配负载，测得距参考面T1距离l 1=0.125 λg 处为电压波节点，驻波系数为1.5，试求该双端口网络的散射矩阵。
解：可以先求S11，它就是T1面的反射系数。
根据驻波比可以求出反射系数的模值。
l 10.21ρρ-Γ==+在smith 圆图上，画驻波比为0.2的圆，与负实轴的交点为波节点，从波节点朝负载（逆时针）走0.125λ，也就是90°，到T1面，可以看出T1面反射系数的相角应为-π/2，所以21110.2j0.2jT S ep -=G ==-由于网络对称：S11=S22；由于网络互易S12=S21，所以只需求出S21即可，由于网络无耗 [S]+[S]=[I]212121212121*21*21221*2121*21210.20.2100.20.2010.20.2100.2010.20.0410.20.20j S j S S j S j j S j S S j S j S j S j S S S +轾轾轾--犏犏犏=犏犏犏--臌臌臌轾轾轾-犏犏犏=犏犏犏-犏臌臌臌+=-=?=可以得出S21=±0.98，所以S 矩阵为0.20.980.980.2j j 轾-犏犏-臌或0.20.980.980.2j j 轾--犏犏--臌4.7求如图所示网络的［S ］矩阵。
解：可以先求出各网络归一化a 矩阵，相乘得到整个网络a ，矩阵，通过S 与a 的关系，得到网络的S 矩阵。
112211221212121212121212cos jsin cos jsin 10[]jsin cos jsin cos 1cos()j sin cos jsin()sin sin cos cos jsin()cos()j cos sin a y y y y y q q q q q q q q q q q q q q q q q q q q q q q q 轾轾轾犏犏犏=犏犏犏臌臌臌轾+++-犏=犏++++臌根据a 矩阵和S 矩阵的关系1121222()()222[]22j j j j y y e e y yS y y e e y y q q q q q q --+-+-轾犏-犏++犏=犏犏-犏++臌4.8 设双端口网络［S ］已知，终端接有负载Z l ，如图所示，求输入端反射系数。
解：终端负载为Z l ，那么终端反射系数l l l Z Z Z Z -G =+那么根据93页4-4-22，输入端反射系数212in 11221llS S S G G =+-G。