正方体截面总结(最全,适用于公务员图形推理)
正方体截面总结(最全-适用于公务员图形推理)

正方体截面的形状tf O结论如下:1、可能出现的:锐角三角型、等边、等腰三角形,正方形、矩形、非矩形的平行四边形、梯形、等腰梯形、五边形、六边形、正六边形2、不可能出现:钝角三角形、直角三角形、直角梯形、正五边形、七边形或更多边形正方体的截面形状一:问题背景在家做饭时,切菜尤其是切豆腐时,发现截面有很多形状。
若用不同的截面去截一个正方体,得到的截面会有哪几种不同的形状?二:研究方法先进行猜想,再利用土豆和萝卜通过切割实验研究。
三:猜想及其他可能的证明:1•正方形:因为该立体几何图形是正方体,所以用从任意位置与该正方体上下底面平行的平面进行截取可以得到,或者和侧面平行进行截取,由下列图示证明:由图示可知,水平方向截取正方体,得到的截面为正方形由图示可知,竖直方向截取正方体,得到的截面为正方形。
2. 矩形:因为正方形也属于矩形,所以对正方形的证明同适用于矩形。
》》》其次,当长宽不等的矩形截面的图示如下:由上图所示可知,按不同角度截取正方体可以得到矩形。
例如,正方体的六个对角面都是矩形。
3. 平行四边形:当平面与正方体的各面都不平行时,所得截面为平行四边形,图示如下:由上图所示可知,当截面不与正方体的各面平行时,所得截面可能为平行四边形。
4. 三角形:根据一定角度过正方体的三条棱进行截取可以得到三角形的截面,图示如下由上图可知,正方体可以截得三角形截面。
但一定是锐角三角形,包括等腰和等边三角形特别的,当截面刚好经过三个面的对角线时,所得的三角形截面为正三角形,图示如下:》得到: 正三棱锥5. 猜想之外的截面形状:(1)菱形:女口下图所示,f A,B为所在棱的中点时,该截面为菱形:当(2)梯形:如图所示,当按一定角度使截面在正方体的上下底面上所存在的线段长短有异时,所得截面可能是梯形:(4 )六边形:如图所示,可以截得六边形截面:==》》》(3 )五边形:如图所示,可以截得五边形截面:通过实践及资料查询可知,无法得到正五边形。
(备考2023年)江苏省淮安市公务员省考行政职业能力测验真题(含答案)

(备考2023年)江苏省淮安市公务员省考行政职业能力测验真题(含答案) 学校:________ 班级:________ 姓名:________ 考号:________一、图形推理(6题)1.左边给出一立体图形,从任意面将其剖开,下面哪一项不可能是该立体图形的截面?A.2.从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性。
3.从所给的四个选项中.选择最合适的一个填入问号处.使之呈现一定的规律性:4. 从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性:5. 从所给的四个选项中,选择最合适的一个填人问号处,使之呈现一定的规律性。
6. 从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性。
()二、定义判断(10题)7.生态足迹也称生态占用,是指特定数量人群按照某一种生活方式所消费的、自然生态系统提供的各种商品和服务功能,以及在这一过程中所产生的废弃物需要环境(生态系统)吸纳,并以生物生产性土地(或水域)面积来表示的一种可操作的定量方法。
通过生态足迹需求与自然生态系统的承载力进行比较即可以定量的判断某一国家或地区目前可持续发展的状态,以便对未来人类生存和社会经济发展做出科学规划和建议。
根据上述定义,下列各项说法错误的是:A.生态足迹是一种衡量对生态环境破坏程度的定性方法B.生态足迹是判断某一国家或地区目前的可持续发展的状态的重要指标C.生态足迹的值越高,人类对生态的破坏就越严重D.日本每人的生态足迹远远超过日本土地、水源所具备的生产能力,所以日本只能利用别国资源8. 土地使用权,是指单位或者个人依法或依约定,对国有土地或集体土地所享有的占有、使用、收益和有限处分的权利。
根据上述定义,以下情况不属于土地使用权的是()。
A.农民在承包土地上种植甘蔗、玉米、花生等农作物B.农村村民住宅用地的使用权C.为了提高居民的身体素质,某市政府在市中心划出一块地建造了一座综合性健身馆D.某老板未经政府批准,在处于城市规划区内的别墅后院挖了一个面积为100平米的游泳池9. 缺陷补偿是指个体在充当社会角色时不可能事事成功,当自我角色目标失败时,常常可能会对相关的社会角色的重要性做重新评价,从而进行自我定义以补偿自己的角色缺陷。
2019-2020年公务员考试备考行测《图形推理》试题精选含答案解析(九十七)[上海]
![2019-2020年公务员考试备考行测《图形推理》试题精选含答案解析(九十七)[上海]](https://img.taocdn.com/s3/m/e660483aa26925c52dc5bf22.png)
2019-2020年公务员考试备考行测《图形推理》试题精选含
答案解析(九十七)[上海]
一、第1题:
下面是一个水平放置的正方体的表面展开图,若图中“快”是正方体的上面,则这个正方体的下面是
A.A
B.B
C.C
D.D
【答案】:B
【来源】:2015年下半年吉林《行测》真题(乙级)
【解析】
【解析】从题干的平面展开图可以判断出“快”与“福”、“幸”与“康”、“乐”与“健”是相对面关系,所以题中所求“快”是正方体的上面,它的下面为其相对面“福”。
故答案选B。
二、第2题:
根据(1)和(2)的变化规律,(3)与图(____)对应。
A.
B.
C.
D.
【答案】:C
【来源】:暂无
【解析】
(1)(2)中均有5个元素组成,未知图形也应该与(3)一样,由4个元素组成,排除D。
(1)(2)中小方块的位置发生了变化,由右上角变为左下角,所以未知图形中的小方块应从右边变到最左边,排除AB。
故正确答案为C。
三、第3题:
从A、B、C、D四个图形中选出最合适的一个,使得它保持左边四个图形所呈现的规律性( )
A.A
B.B
C.C
D.D
【答案】:B
【来源】:2011年917联考
【解析】
各图均包含横向对称轴,排除A、D项。
各图中黑色方块的数量为3、2、3、4,呈奇、偶交替排列,则所求图形黑方块个数应为奇数个,B项正确。
四、第4题:。
2019-2020年公务员考试备考行测《图形推理》精选练习题含答案解析(第七篇)[贵州]
![2019-2020年公务员考试备考行测《图形推理》精选练习题含答案解析(第七篇)[贵州]](https://img.taocdn.com/s3/m/58e140be0242a8956aece411.png)
2019-2020年公务员考试备考行测《图形推理》精选练习题
含答案解析(第七篇)[贵州]
一、第1题:
将左边的图形从任意面剖开,下面哪一项不可能是该图形的截面____(____ )
【答案】:D
【来源】:暂无
【解析】
正方体共有6个面,故其截面不可能为八边形,答案为D。
A、B、C图形的剖开方
式分别如下图所示:
二、第2题:
请从所给的四个选择项中,选择唯一的一项填在问号处,使之呈现一定的规律性。
A.A
B.B
C.C
D.D
【答案】:B
【来源】:2012年江苏C类
【解析】
B。
每一行、每一列的三个图形的对称性如下表:
每一行、每一列均有一个非对称图形和两个对称图形(轴对称或中心对称),因此问号处应该为非对称图形,B项符合。
三、第3题:
根据规律,填入恰当的图形:
A.如图所示
B.如图所示
C.如图所示
D.如图所示
【答案】:C
【来源】:2015年山东公务员考试《行测》真题试卷
【解析】
此题考查样式类。
第一段前两个图形求异得到第三个图形,第二段同样由前两个图形求异,因此选C。
四、第4题:
从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性(____)。
公考截面口诀

公考截面口诀以下是为您生成的十个适用于小学生的公考截面口诀:1. 一观形状二看边,立体图形在眼前。
截面形状要分辨,圆柱切出有椭圆。
圆锥横切是圆面,三棱柱来不一般。
平行底面切三角,上下移动变多边。
正方体呀最简单,平行切出正方形,斜着切出三角形,梯形偶尔也出现。
2. 一瞧立体二想切,图形变幻心不怯。
长方体呀有特点,平行切出长方形,斜着一弄三角形。
圆柱上下一般粗,平行切圆斜着柱。
圆锥尖尖顶上头,横切圆圆侧着锥。
三棱锥呀仔细瞧,切面多样要记牢,三角四边和五边,想象清楚不混淆。
3. 一看图形二思切,截面秘密在里面。
正方体中找截面,平行能把正方现,斜着可能三角见。
圆柱如同大水桶,平行切圆斜柱形。
圆锥好似尖帽子,横切圆来侧三角。
三棱柱呀要小心,平行三角斜四边。
想象动手多尝试,截面不难记心间。
4. 一探图形二定切,截面模样脑海现。
长方体呀长又扁,平行切成长方形,斜切三角或梯形。
圆柱肚子圆滚滚,平行切圆斜变形。
圆锥脑袋尖尖顶,横切圆面侧三角。
四棱柱呀有多种,平行四边斜多边。
多观察来多思考,截面知识掌握好。
5. 一瞅物体二琢磨,截面形状有着落。
正方体呀真方正,平行正方斜三角。
圆柱好似大烟囱,平行切圆斜椭圆。
圆锥就像甜筒样,横切圆来侧锥状。
三棱柱呀有诀窍,平行三角斜四边。
五棱柱呀稍复杂,平行多边斜更多。
认真想呀仔细看,截面不难被发现。
6. 一瞧立体二打算,截面出现不慌乱。
长方体呀块头大,平行长方斜梯形。
圆柱身材很圆润,平行切圆斜着混。
圆锥尖尖站得稳,横切圆面侧三角。
三棱柱呀要留意,平行三角斜四边。
六棱柱呀更多样,平行多边斜变形。
记住规律多练习,截面清晰在眼前。
7. 一看图形二规划,截面形状能拿下。
正方体中做文章,平行正方斜多样。
圆柱如同大柱子,平行切圆斜不直。
圆锥好像尖顶屋,横切圆来侧锥突。
三棱柱呀有乾坤,平行三角斜四边。
四棱锥呀要分辨,平行多边斜更乱。
用心观察多动脑,截面不难找答案。
8. 一观物体二谋算,截面模样心里转。
正方体的几种截面

正方体的几种截面正方体是一种具有六个相等的正方形面的立体图形。
它的截面有多种形式,每一种截面都展现了正方体在不同方向上的特性和特点。
本文将以几种常见的正方体截面为标题,详细介绍它们的特点和应用。
一、正方形截面正方形截面是正方体最基本的截面形式。
它的特点是四条边相等且内角均为90度。
正方形截面在建筑、工程和设计领域中广泛应用。
例如,在建筑结构设计中,正方形截面的柱子能够提供较好的稳定性和承重能力,因此常用于大型建筑物的支撑结构。
二、长方形截面长方形截面是正方体的另一种常见截面形式。
它的特点是两对相等的边,且每一对边长度可以不相等。
长方形截面在工程和建筑领域中有着广泛的应用。
例如,在桥梁设计中,长方形截面的梁能够提供较好的强度和刚度,从而能够承受大量的荷载。
三、三角形截面正方体的三角形截面是指由正方体的三个顶点和与它们相连的三条边所围成的图形。
三角形截面具有较高的稳定性和刚度,因此常用于建筑中的支撑结构或桥梁中的支撑柱。
此外,三角形截面还常用于设计飞机或汽车的支撑杆,以提高结构的强度和稳定性。
四、菱形截面菱形截面是指由正方体的四个角点和与它们相连的四条边所围成的图形。
菱形截面具有较好的强度和稳定性,因此常用于建筑物的支撑结构或桥梁中的支撑柱。
此外,在船舶设计中,菱形截面的船体能够提供较好的抗风浪能力,因此被广泛应用于各类船舶的设计和制造。
五、圆形截面正方体的圆形截面是指由正方体的四个角点围成的圆形。
圆形截面具有较好的强度和稳定性,因此常用于建筑物的支撑结构或桥梁中的支撑柱。
此外,在机械工程领域中,圆形截面的轴能够提供较好的扭转刚度,因此被广泛应用于各类机械设备的设计和制造。
六、椭圆形截面椭圆形截面是指由正方体的四个角点围成的椭圆形。
椭圆形截面具有较好的强度和刚度,因此常用于建筑物的支撑结构或桥梁中的支撑柱。
此外,在电子工程中,椭圆形截面的导线能够提供较好的电流传输能力,因此被广泛应用于各类电子设备的设计和制造。
正方体截面形状小结Word 文档
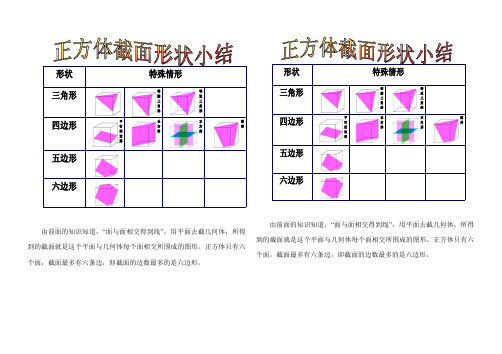
梯形
长方形
平行四边形
等腰三角形
由前面的知识知道,“面与面相交得到线”,用平面去截几何体,所得
到的截面就是这个平面与几何体每个面相交所围成的图形。
正方体只有六个面,截面最多有六条边,即截面的边数最多的是六边形。
梯形
长方形
平行四边形
由前面的知识知道,“面与面相交得到线”,用平面去截几何体,所得
到的截面就是这个平面与几何体每个面相交所围成的图形。
正方体只有六个面,截面最多有六条边,即截面的边数最多的是六边形。
正方体截面总结

结论如下:1、可能出现的:锐角三角型、等边、等腰三角形,正方形、矩形、非矩形的平行四边形、梯形、等腰梯形、五边形、六边形、正六边形2、不可能出现:钝角三角形、直角三角形、直角梯形、正五边形、七边形或更多边形正方体的截面形状一:问题背景在家做饭时,切菜尤其是切豆腐时,发现截面有很多形状。
若用不同的截面去截一个正方体,得到的截面会有哪几种不同的形状?二:研究方法先进行猜想,再利用土豆和萝卜通过切割实验研究。
三:猜想及其他可能的证明:1.正方形:因为该立体几何图形是正方体,所以用从任意位置与该正方体上下底面平行的平面进行截取可以得到,或者和侧面平行进行截取,由下列图示证明:====》》》由图示可知,水平方向截取正方体,得到的截面为正方形。
====》》》由图示可知,竖直方向截取正方体,得到的截面为正方形。
2.矩形:因为正方形也属于矩形,所以对正方形的证明同适用于矩形。
其次,当长宽不等的矩形截面的图示如下:由上图所示可知,按不同角度截取正方体可以得到矩形。
例如,正方体的六个对角面都是矩形。
3.平行四边形:当平面与正方体的各面都不平行时,所得截面为平行四边形,图示如下:==》由上图所示可知,当截面不与正方体的各面平行时,所得截面可能为平行四边形。
4.三角形:根据一定角度过正方体的三条棱进行截取可以得到三角形的截面,图示如下:==》》》由上图可知,正方体可以截得三角形截面。
但一定是锐角三角形,包括等腰和等边三角形特别的,当截面刚好经过三个面的对角线时,所得的三角形截面为正三角形,图示如下:==》得到:正三棱锥5.猜想之外的截面形状:(1)菱形:如下图所示,当A,B为所在棱的中点时,该截面为菱形:(2)梯形:如图所示,当按一定角度使截面在正方体的上下底面上所存在的线段长短有异时,所得截面可能是梯形:==》》》(3)五边形:如图所示,可以截得五边形截面:=》通过实践及资料查询可知,无法得到正五边形。
(4)六边形:如图所示,可以截得六边形截面:=》特别的,当平面与正方体各棱的交点为中点时,截面为正六边形,如图所示:拓展探究:1.正方体最大面积的截面三角形 2.正方体最大面积的截面四边形3.最大面积的截面形状4.截面五边形、六边形性质1.正方体最大面积的截面三角形:如该图所示可证明,由三角面对角线构成的三角形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
结论如下: 1、可能出现的:
锐角三角型、等边、等腰三角形,正方形、矩形、非矩形的平行四边形、梯形、等腰梯形、五边形、六边形、正六边形
2、不可能出现:
钝角三角形、直角三角形、直角梯形、正五边形、七边形或更多边形
正方体的截面形状
一:问题背景
在家做饭时,切菜尤其是切豆腐时,发现截面有很多形状。
若用不同的截面去截一个正方体,得到的截面会有哪几种不同的形状?
二:研究方法
先进行猜想,再利用土豆和萝卜通过切割实验研究。
三:猜想及其他可能的证明:
1.正方形:
因为该立体几何图形是正方体,所以用从任意位置与该正方体上下底面平行的平面进行截取可以得到,或者和侧面平行进行截取,由下列图示证明:
====》》》
由图示可知,水平方向截取正方体,得到的截面为正方形。
====》》》
由图示可知,竖直方向截取正方体,得到的截面为正方形。
2.矩形:
因为正方形也属于矩形,所以对正方形的证明同适用于矩形。
其次,当长宽不等的矩形截面的图示如下:
由上图所示可知,按不同角度截取正方体可以得到矩形。
例如,正方体的六个对角面都是矩形。
3.平行四边形:
当平面与正方体的各面都不平行时,所得截面为平行四边形,图示如下:
==》
由上图所示可知,当截面不与正方体的各面平行时,所得截面可能为平行四边形。
4.三角形:
根据一定角度过正方体的三条棱进行截取可以得到三角形的截面,图示如下:
==》》》
由上图可知,正方体可以截得三角形截面。
但一定是锐角三角形,包括等腰和等边三角形
特别的,当截面刚好经过三个面的对角线时,所得的三角形截面为正三角形,图示如下:
==》得到:正三棱锥
5.猜想之外的截面形状:
(1)菱形:
如下图所示,当A,B为所在棱的中点时,该截面为菱形:
(2)梯形:
如图所示,当按一定角度使截面在正方体的上下底面上所存在的线段长短有异时,所得截面可能是梯形:
==》》》
(3)五边形:
如图所示,可以截得五边形截面:
=》
通过实践及资料查询可知,无法得到正五边形。
(4)六边形:
如图所示,可以截得六边形截面:
=》
特别的,当平面与正方体各棱的交点为中点时,截面为正六边形,如图所示:
拓展探究:1.正方体最大面积的截面三角形2.正方体最大面积的截面四边形3.最大面积的截面形状4.截面五边形、六边形性质
1.正方体最大面积的截面三角形:
如该图所示可证明,由三角面对角线构成的三角形。
2.正方体最大面积的截面四边形:
通过猜想及查询资料可知,正方体截面可能得到的四边形有:正方形、矩形、梯形、平行四边形。
根据四边形的面积公式:面积=长*宽
联系正方体图形:
得到:当由两条平行的面对角线和两对平行棱构成的四边形的长最大,又因为在各个情况下的宽不变。
则由猜想得到:“最大面积的截面四边形:由两条平行的面对角线和两对平行棱构成的四边形。
”
3.最大面积的截面形状:
正方体的截面可以分为:三角形、正方形、梯形、矩形、平行四边形、五边形、六边形、正六边形。
其中三角形还分为锐角三角型、等边、等腰三角形。
梯形分位非等腰梯形和等腰梯形。
首先比较三角形与五边形和六边形,所得这三种截面的情况有一共同特点:不能完整在该截面所在平面在正方体内所截的范围的最大值,有部分空间空出。
因此可以得到:最大面积一定是四边形。
所以最大面积的截面形状:即最大截面四边形(猜想)。
初步推断为如图所示的矩形:
4.截面五边形、六边形性质
通过课本及资料查询知:截面五边形:有两组边互相平行.截面六边形:三组对边平行的六边形.
正方体的截面图
四:结论如下:
1、可能出现的:
锐角三角型、等边、等腰三角形,正方形、矩形、非矩形的平行四边形、非等腰梯形、等腰梯形、五边形、六边形、正六边形
2、不可能出现:
钝角三角形、直角三角形、直角梯形、正五边形、七边形或更多边形。
