第五章 管中流动
合集下载
流体力学龙天渝课后答案第五章孔口管嘴管路流动
解�由题得� � � �
1 � 0.707
l
� d � �� �1
6.如上题�当管嘴外空气压强为当地大气压强时�要求管嘴出流流速为 30m/s。此时静压箱 内应保持多少压强�空气密度为 ρ=1.2kg/m3。
解� v � � 2 �p �得 �p � 1.08kN / m 2 �
7.某恒温室采用多孔板送风�风道中的静压为 200Pa�孔口直径为 20mm�空气温度为 20℃� μ=0.8。要求通过风量为 1m3/s。问需要布置多少孔口�
∴负压值为-2.93m 16.如图水泵抽水系统�管长、管径单位为 m�ζ 给于图中�流量 Q=40×10-3m3/s�λ=0.03。 求�
�1�吸水管及压水管的 S 数。 �2�求水泵所需水头。 �3�绘制总水头线。
5
解��1� S H1
=
� 8�� �
�
L1 d1
�
��1 �
2
d
4 1
g
�
2
� �� �
� 8� l1
解�(1)
S P1 �
d1
�
2
d
4 1
�8� l2
SP2 �
d2
�
2
d
4 2
� 8(� l3 � 1)
SP3 �
d3
�
2
d
4 3
S P � S P1 � S P 2 � S P3
p � SPQ2
解得� p � 2500 Pa
�2�铅直安装不会改变总压�因为同种气体位压等于零 �3� p � S P Q 2 � 2830 Pa 18. 并联管路中各支管的流量分配�遵循什么原理�如果要得到各支管中流量相等�该如何 设计管路�
第五章 管中流动解析

Re≤2320 流型判据: 2320< Re<13800 或为湍流)
Re ≥ 13800
层流 过渡状态(或为层流
湍流
5.1.4 水力直径
过流断面面积A与过流断面上流体与固体 接触周长S之比的4倍来作为特征尺寸。这种尺 寸称为水力直径,用dH表示
dH
4
A S
式中 A ——过流断面面积;
S ——过流断面上流体与固体相润湿的 周界长,称为湿周。
湍流的剪应力: 由分子运动和质 点脉动所引起
e
du
dy
e 涡流粘度,它表征脉动的强弱.
Re为一无因次量,称为雷诺数。
雷诺数的物理意义:
Re
du
u 2 u d
惯性力 粘性力
Re越大,表示惯性越大,湍动程度越剧烈; Re小,表示粘性力占主导地位,湍动程度小。
这就是说,液体流动时的雷诺数若相同,则 它的流动状态也相同。另一方面液流由层流转变 为湍流时的雷诺数和由湍流转变为层流的雷诺数 是不同的,前者称为上临界雷诺数,后者为下临 界雷诺数,后者数值小,所以一般都用后者作为 判别液流状态的依据,简称临界雷诺数,当液流 实际流动时的雷诺数小于临界雷诺数时,液流为 层流,反之液流则为湍流,常见的液流管道的临 界雷诺数可由实验求得。
(2) 湍流 当流体微团间互相掺混作无序地流动,其流速、压力等力学 参数在时间和空间中发生不规则脉动的流体运动,称为湍流,又 称为紊流。湍流是在大雷诺数下发生的,其基本特征是流体微团 运动的随机性。湍流中由于这种随机运动而引起的动量、热量和 质量的传递,其传递率比层流高很多。它一方面强化传递和反应 的效果;另一方面剧增了摩擦阻力和能量损耗。
5.1 流动形态
5.1.1 雷诺实验
流体力学第五章 管中流动-1

解: (1)由表1-6(P28)查此时水的粘度为1.308×10-6
Re vd 1.0 0.1 76453 Rec 2300 6 1.308 10
管中流动为湍流。 (2) Rec vc d
vc
Rec
d
1.308 106 2300 0.03 0.1
2012年12月15日 20
5.2 圆管中的层流
本章所讨论的流体 1. 流体是不可压缩的; 2. 运动是定常的;
主要内容: • 速度分布 • 流量计算 • 切应力分布 • 沿程能量损失
2012年12月15日 21
过流截面上流速分布的两种方法
vd
我们知道当
较小,即速度和管子直径较小而粘度较大时出现层流
哈根-伯肃叶(Hagen-Poiseuille)定律, 它与精密实验的测定结果完全一致。
2012年12月15日 26
粘 度 的 测 定 方 法
利用哈根-伯肃叶(Hagen-Poiseuille)定律可以测定粘度,它是测 定粘度的依据。因为,根据公式可以导出:
pd 4
128qvl
pd 4t
4 A 4 Bh 2h 4cm S 2B vd 要使 Re H 2320 v 0.017 m / s dH
2012年12月15日 18
例题三:某段自来水管,d=100mm,v=1.0m/s,
水温10℃, (1)试判断管中水流流态? (2)若要保持层流,最大流速是多少?
(2)速度分布具有轴对称性,速度分布呈抛物线形。 (3)等径管路中,压强变化均匀。 (4)管中的质量力不影响流动性。
2012年12月15日 22
• 1.第一种方法 • 根据圆管中层流的流动特点,对N-S方程式
Re vd 1.0 0.1 76453 Rec 2300 6 1.308 10
管中流动为湍流。 (2) Rec vc d
vc
Rec
d
1.308 106 2300 0.03 0.1
2012年12月15日 20
5.2 圆管中的层流
本章所讨论的流体 1. 流体是不可压缩的; 2. 运动是定常的;
主要内容: • 速度分布 • 流量计算 • 切应力分布 • 沿程能量损失
2012年12月15日 21
过流截面上流速分布的两种方法
vd
我们知道当
较小,即速度和管子直径较小而粘度较大时出现层流
哈根-伯肃叶(Hagen-Poiseuille)定律, 它与精密实验的测定结果完全一致。
2012年12月15日 26
粘 度 的 测 定 方 法
利用哈根-伯肃叶(Hagen-Poiseuille)定律可以测定粘度,它是测 定粘度的依据。因为,根据公式可以导出:
pd 4
128qvl
pd 4t
4 A 4 Bh 2h 4cm S 2B vd 要使 Re H 2320 v 0.017 m / s dH
2012年12月15日 18
例题三:某段自来水管,d=100mm,v=1.0m/s,
水温10℃, (1)试判断管中水流流态? (2)若要保持层流,最大流速是多少?
(2)速度分布具有轴对称性,速度分布呈抛物线形。 (3)等径管路中,压强变化均匀。 (4)管中的质量力不影响流动性。
2012年12月15日 22
• 1.第一种方法 • 根据圆管中层流的流动特点,对N-S方程式
传热学第五章_对流换热原理-6
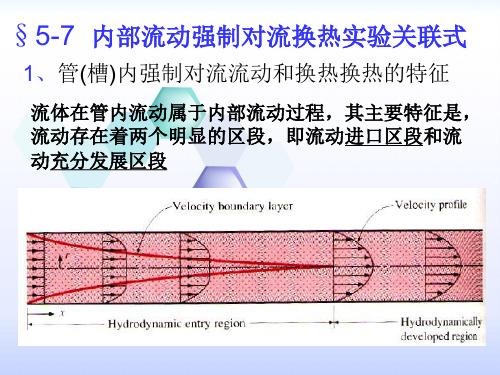
2-2)管内流体平均温度
t f
c p tudf
f
c pudf
2 R 2um
R
turdr
0
f
其中,tf为根据焓值计算的截断面平均温度。
由热平衡方程
dQ hx (tw t f )x * 2R * dx cpumR2dt f
和
dQ q * 2R * dx
可得
dt f 2q 2hx (tw t f ) x
t
( tw t r tw t f
)rR
( r )rR tw t f
const
而同时又有
q
(
t r
)
r
R
h(t w
tf
)
于是,得
(
t r
)
r
R
h
const
tw t f
上式又表明,常物性流体在热充分发展段的一个特点是 换热系数保持不变。
另外,如果边界层在管 中心处汇合时流体流动 仍然保持层流,那么进 入充分发展区后也就继 续保持层流流动状态, 从而构成流体管内层流 流动过程。
若 Pr<1, 则意味着流动进口段长于热进口段; 1-3)管内流动充分发展段的流态判断
Re 2300 2300 Re 10 4 Re 10 4
层流 过渡流 旺盛湍流
2)管内流体平均速度与平均温度
2-1)管内流体运动平均速度
um
f udf 0f
2
R 2
R rudr V
0
f
其中,V-体积流量;f-管的截断面积;u-局部流速
dx c pum R
c pum R
积分上式可得全管长流体的平均温度。
由于热边界存在有均匀壁温和均匀热流两种典型情
第五章 孔口、管嘴出流和有压管路

(2)管嘴长度l=(3~4)d。
5.2.4 其他形式管嘴
工程上为了增加孔口的泄水能力或为了增加(减少)出 口的速度,常采用不同的管嘴形式
(1)圆锥形扩张管嘴 (θ=5~7° ) (2)圆锥形收敛管嘴 (较大的出口流速 ) (3)流线形管嘴 (阻力系数最小 )
孔口、管嘴的水力特性
5.3 有压管路恒定流计算
1
从 1→2 建立伯努利方程,有
v2 H 0 00 n 2g 2g 2g
l (3 ~ 4)d
0v0 2
v 2
H
c
0 d
2
0
1 v n
2 gH0 n 2 gH0
c
2
n 0.5
式中:
1 n n
1
n 为管咀流速系数, n 0.82
pc
0.75H 0
对圆柱形外管嘴:
α=1, ε=0.64, φ=0.82
5.2.3 圆柱形外管嘴的正常工作条件
收缩断面的真空是有限制的,如长江中下游地区, 当真空度达7米水柱以上时,由于液体在低于饱和蒸汽 压时会发生汽化 。 圆柱形外管嘴的正常工作条件是: (1)作用水头H0≤9米;
5.2 管嘴出流
一、圆柱形外伸管嘴的恒定出流
计算特点: 出流特点:
hf 0
在C-C断面形成收缩,然后再扩大,逐步充满 整个断面。 1
l (3 ~ 4)d
H
c
0 d
2
0
c
2
1
在孔口接一段长l=(3~4)d的 短管,液流经过短管并充满出口 断面流出的水力现象成为管嘴出 流。 根据实际需要管嘴可设计成: 1)圆柱形:内管嘴和外管嘴 2)非圆柱形:扩张管嘴和收缩 管嘴。
第5章-圆管流动

e/d
Re
莫迪图λ
结论
0.03 0.1473 0.00102 1.732×106 0.02 用0.02重算
0.02 0.1358 0.0011 1.87×106 0.02
一致
d 0.298 1/5 0.1358m 即设计的最小管径为0.1358m
5.6 圆管湍流的沿程损失
5.6.3 非圆管的湍流沿程损失
——摩擦阻力系数,与
管径d、管中流速u和管 壁的光滑程度有关;
5.4 圆管中流体的湍流运动:
湍流剪应力分布与普朗特混合长度理论
1
2'
du dy
ux'
u
' y
平均值:
脉动值:
Re数较小时,1 占主导地位
Re数很大时, 2 1
牛顿内摩擦力 雷诺应力
y
u(y l')
第五章 圆管流动
内容提纲
5.1 雷诺实验与流态判据 5.2 圆管中流体的层流运动 5.3 椭圆管中流体的层流运动(自学) 5.4 圆管中流体的湍流运动 5.5 流体运动的两种阻力 5.6 圆管湍流的沿程损失 5.7 管路的局部损失 5.8 管路计算(自学)
按流体与固体接触情况来分,流体运动主要有下列四种形式。
1 2 umax
(层流时平均速度为最大速度的1/2)
5.4 圆管中流体的湍流运动:
湍流运动:三维随机运动,脉动性
瞬时速度 = 时均速度 + 脉动速度
u u u'
u 1
T
udt
T0
u' u u, 1 T u'dt 0
第五章 孔口管嘴出流及管路计算

hw 2 s2
1 s2
hw 3 s3
1 s3
Q1 Q2
s2
Q2 ; s1 Q3
s3
Q3 ; s1 Q1
s3 s1
或者:
Q1 : Q2 : Q3 1 s1 : 1 s2 : 1 s3
流量分配规律
第四节 流体通过缝隙液流动 一、平行平板缝隙 图示为在两块平行平板所形成的缝隙间充 满了液体,缝隙高度为h,缝隙宽度和长度 为b和l,且一般恒有b>>h和l>>h。
QA QB QC Q0 Q
管路水力计算
2.阻力损失关系:串联管路系统的总水头损失(压头)损失 等于各管段水头损失之和。
hw hw A hwB hwC
2 2 2 hw S A Q A S B QB S C QC
第三节
三、并联管路计算
由不同直径或粗糙度的 简单管道连接在一起的 管道叫做串联管道 1.流量关系:
管路水力计算
列1-1及2-2断面伯努利方程:
2 pa v12 p a v2 H 0 hw g 2 g g 2 g 2 v2 H hw 2g v2 l 对于短管: hw h f h j d 2g l 8 hw 2 4 Q 2 hw SQ2 d gd
第二节
1、管嘴出流流量
管嘴出流
以管嘴中心线为基准线,列1-1及b-b断面伯努利方程:
αV V2 H ζ 2g 2g 2g
2 1 1
α V2
令
1
H0 H
1v12
2g
管嘴出口速度为
V
αζ
2 gH0 n 2 gH0
管嘴流量 Q VA n A 2gH 0 un A 2gH 0
流体力学课件 第五章 流动阻力

斜直线分布
r hf 1 g grJ 2 l 2
du grh f dr 2l
抛物线分布
2.流速分布 3.流量
Q
r0 0
gh f 2 2 u (r0 r ) 4l
gh f 2 2 gh f 4 (r0 r ) 2 rdr d 4l 128l
(3)粗糙区
莫迪
§5-7 局部损失计算
一、边界层理论
1.边界层:贴近平板存在 较大切应力、粘性影响不能 忽略的这一层液体 。
2.边界层的厚度:当流速达到 边界层的厚度顺流增大,即δ是x的函数。
处时,它
3.转捩点,临界雷诺数 转捩点:在x=xcr处边界层由层流转变为紊流的过渡点。
临界雷诺数: Recr
三、总水头损失
hw h f h j
i 1 i 1 n n
§5-2 流体流动的两种型态
一、雷诺实验
1883年英国物理学家雷诺按图示试验装置对粘性流体进行 实验,提出了流体运动存在两种型态:层流和紊流。
1 4
(a)
hf 5
(b)
2
3
(c)
1.层流 :管中水流呈层状流动,各层的流体质点互不掺混的 流动状态。
四、湍流切应力分布和流速分布
1.切应力分布
du 2 du 2 1 2 L ( ) dy dy
摩擦切应力 普朗特混合长度 : 附加切应力
y L ky 1 r0
k 称为卡门常数
k 0.36 ~ 0.435
2.流速分布 (1)近壁层流层: 管壁切应力
du u 0 dy y
§5-6 湍流的沿程损失
一、湍流沿程损失计算
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
p1 p 2
Δpf
压力降→阻力损失 的直观表现
说明:若管路不为水平或直径不等,则上下游之间的压力 变化 除因阻力损失外,还包括位能或动能变化所引 起的部分。 即:p1-p2≠△pf
直管阻力损失的计算
hf p1 p 2
hf g Δpf
2 p1 u12 p2 u2 z1 z2 Hf g 2 g g 2g
Hf
g
Δ p f h f gH f
阻力损失:△pf ——Pa
hf ——J/kg
Hf ——m
(2) 范宁公式
p1r 2 p2r 2 w 2rl
p f p1 p2 ( 4l ) w d
W
p1 r
W
p2
w l u 2 p f 8 u 2 d 2
e 涡流粘度, 它表征脉动的强弱.
随 Re 及所处的位置而变. 不同于粘度., 难于测定.
5.3.2 边界层概念
为什么引入边界层概念? 实际流体与固体壁面作相对运动时,流体内部 存在剪应力作用,由于速度梯度集中在壁面附近, 故剪应力也集中在壁面附近。而远离壁面处的速度 变化很小,作用于流体层间的剪应力也小到可以忽 略,这部分流体便可以当作理想流体。 也就是说,分析实际流体与固体壁面的相对运 动时,应以壁面附近的流体为主要对象。故普兰德 提出了边界层的概念。
5.4 管内流动的阻力损失
流体流动阻力包括:1· 直管阻力损失(沿程阻力损失)
5.4.1 直管阻力损失
局部阻力损失(管件、阀门等的阻力损失) 2·
1 2
(1) 直管阻力损失的直观表现 2 p1 u12 p 2 u2 z1 g z2 g hf 2 2
u
p1 R p2
hf
C→D:截面继续扩大,p ↑,近壁面处流体在反向压力(逆压强梯 度)作用下被迫倒流,产生大量旋涡,此即边界层分离。
C点:由于阻力损失,流速降为0(若为理想流体,D点流速降为0);
边界层分离演示
边界层分离的后果:〈1〉产生大量的旋涡
〈2〉造成较大能量损失
平板及流线型物体不会发生边界层分离
流体沿壁面流过时的阻力→表皮阻力(或摩擦阻力) 流体的流道发生弯曲、突然扩大或缩小、绕过物体流 动,引起边界层分离→形体阻力。
ur
p r 2 c 2 l 2
因紧贴在管壁上的运动速度为零:即r = R, u= 0,代入上式求c
Δp 2 c R 4l
p ur (R2 r 2 ) 4l
u max Δ p 2 R 4 l
在管中心,r =0, ur 达到最大值umax
2 pR r ur 1 u max 4l R 2
5.1.3 雷诺数
实验表明,液体在圆管中的流动状态不仅 与管内的平均流速v有关,还和管径d、液体的 运动粘度ν 有关,但是真正决定液流运动状态 的是用这三个数所组成的一个称为雷诺数Re的 无量纲数,即
Re
du
=
du
3
du (m)(m / s)(kg / m ) 0 0 0 m kg s Re kg /(m s) Re为一无因次量,称为雷诺数。
本章主要讨论管中不可压缩流体的运动规 律,其中有许多基本概念对于绕流或明渠流动也 是适用的,管中流动所涉及的问题包括流动状态、 速度分布、起始段、流量和压差的计算、能量损 失等等。其中能量损失问题是本章的重点。该问 题在第三章稍有涉及但并未深入讨论,因为它与 流动状态有关。本章首先介绍层流和湍流概念, 讨论层流和湍流能量损失的形成原因和计算方法, 介绍沿程阻力和局部阻力系数的公式和图表,然 后以短管和长管为例说明上述原理的具体应用, 最后再简单介绍管中水击现象。
b
du d
k
q
u
第五章
1 2 3 4
管中流动
按流体与固体接触情况来分,流体运动主要有下列四种形式。
流体在固体内部的管中流动和缝隙中流动; 流体在固体外部的绕流; 流体在固体一侧的明渠流动; 流体与固体不相接触的孔口出流和射流。
除此之外也还有一些更复杂的形式。这些广泛的流体运动形 式与航空、水利等多种学科有关。就机械制造类专业来说,以第 一种形式较为常见,不要说大范围的工厂车间中管道比比皆是, 就是小范围的机床汽车中也往往有错综复杂的润滑、冷却、液压 或燃料管道,甚至叶轮机叶轮及其他许多机械构件的通道也不妨 可以看作是一种疏导流体的异形管道。
p1
p2 r 2
du y dy
5.2.1 层流速度分布
2rl r p1 p 2 2rl 2l
du r dr
y R r , dy dr
du p 即: r r dr 2 l p dur rdr 2 l
r 2 1 R
上式即为管内层流时的速度分布表达式u 随r 按抛物线分布, 在空间的速度分布图形则为一旋转抛物面。
5.2.2 湍流的速度分布 r p1 p 2
2l du 湍流条件下:特征方程=+e 中的e 难测定 dy n
ห้องสมุดไป่ตู้
雷诺数的物理意义:
Re
du
u 惯性力 u d 粘性力
2
Re越大,表示惯性越大,湍动程度越剧烈; Re小,表示粘性力占主导地位,湍动程度小。
这就是说,液体流动时的雷诺数若相同,则 它的流动状态也相同。另一方面液流由层流转变 为湍流时的雷诺数和由湍流转变为层流的雷诺数 是不同的,前者称为上临界雷诺数,后者为下临 界雷诺数,后者数值小,所以一般都用后者作为 判别液流状态的依据,简称临界雷诺数,当液流 实际流动时的雷诺数小于临界雷诺数时,液流为 层流,反之液流则为湍流,常见的液流管道的临 界雷诺数可由实验求得。
将b、q、k表示为a、c、j 的函数,整理得
c+k=2 j=1-k a=-b-k-q
c=2-k
带入Δp的幂函数中: p f Kd bk ql bu 2k 1k k q
p f Kd bk ql bu 2k 1k k q
p f
p f
l K 2 u d
R 2u
2
u
p f 8l
R
2
p f 32l
d2
p f
32 lu d2
此式称为哈根(Hagen)-泊谡叶(Poiseyulle)公式
2 l u 与范宁公式比较 p f d 2
64 64 = du Re
由哈根-泊谡叶公式得层流时阻力损失与速度的一次方 成正比、与管长的一次方成正比、与管径的两次方成反 比。注意该式适用于层流、牛顿流体
w 令=8 u 2
2
l
l u p f d 2
l u hf d 2
2
l u2 Hf d 2g
上三式为计算直管阻力损失的范宁公式,
它适用于层流和湍流。
5.4.2 层流时的摩擦损失
由层流时的最大速度与压力降的关系可得:
u max
p f 4l
n
6
0.791
7
0.817
8
0.837
9
0.852
10
0.865
u/ uc
5.3
圆管中的湍流
5.3.1 湍流的脉动现象和时均化
时均速度和脉动速度 : u
1 T
T
0
udt
瞬时速度 时均速度 脉动速度, 即u u u
湍流的剪应力: du 由分子运动和质 e dy 点脉动所引起
5.4.3 湍流流动的阻力损失
(1)因次分析法
因次……就是量纲 ,如质量[M]、长度[L]、时间[T] 因次论的依据:1· 物理量方程的因次一致性 2·π定理:任何因次一致的物理量方程都 可以表示为准数关联式;准数个数i=n-m 式中:n为物理量个数, m为用于表示所有物理量的基本因次数目 影响直管阻力损失的因数有三个: 1· 物性因数:μ和ρ 2·设备因数:l 、d和管壁粗糙度 ε 3· 流动因数:u
[u]=L T
-1 -1 -1
式中各物理量的因次 为: L
-1
[d]=L [ε]=L
[ρ]=ML-3 [μ ]=ML T 将各物理量的因次代入,整理得:
MT 2 L1 M j k Labc3 j k qT ck
根据因次一致性原则得: j+k=1 a+b+c-3j-k+q=-1
S ——过流断面上流体与固体相润湿的 周界长,称为湿周。
5.2 流体在圆管内的速度分布
流体在管内流动的受力分析
在长度为l的管段内划出半径 为r的圆柱形流体段作分析。
〈1〉压力(取流速方向为正)
2 2 P r p P r p2 1 1, 2
〈2〉重力,垂直于管轴,故投影为0
〈3〉阻力,作用于侧表面2πrl 上的剪力为
qv 1 u u max 平均速度: 2 R 2
(层流时平均速度为最大速度的1/2)
湍流时,有ur= umax(1-r/R) 1/n= umax(1-r/R)1/7 (令n=7)
u 0.817umax
即湍流时平均速度大约等于管中心处最大速度的0.82倍。 Re 越大,则n值越大,求出之ur/ umax便越大。
5.3.3 边界层及其形成
壁面附近速度变化较大、流动阻力集中在此区域→边界层 离壁面较远、速度基本不变的区域,流动阻力可忽略→主流区 边界层的范围:速度0 →99%u主体
5.3.4 边界层分离
边界层的一个重要特点是在某些情况下会脱离壁 面,称为边界层分离。
