典型例题
典型例题(22套)典型例题20

典型例题(22套)典型例题20
把一个装满水的酒瓶倒立在装着水的盘子里,使瓶颈浸没在盘内水面下,如下图,就做成了一个简便自动家禽喂水器.试讲明它的工作原理.
选题目的:通过此题扩展学生知识,提高分析能力.
解答:这一简便自动家禽喂水器是利用大气压强工作的.由于瓶内水柱产生的压强远小于外界大气压强,当瓶口浸入水中时,瓶口外水受大气压强作用,使瓶内外的压强相等,水可不能流出.当家禽饮水使盘子里的水面下降而瓶口刚露出水面时,空气能够从瓶口进人瓶内,使瓶内压强大于不处大气压强,瓶内的水就会流出来,升高盘里的水位.使瓶口重新没入水中.瓶中的水连续流出,使瓶中气体体积增大,压强减小,直至瓶口内外压强相等时,水就停止流出.因此只要瓶内有水,盘里的水就能不断得到补充.实现家禽自动喂水.。
典型例题

第七节 功率典型例题例1一个质量为m 的物体沿倾角a=30°的光滑斜面由静止滑下.当它竖直方向下落h 高时,重力的即时功率为 ( ) A.gh mg 2 B.gh mg 2sin30° C.gh mg 2cos30° D.0[说明]本题用到即时功率的表达式。
例2汽车发动机的额定功率为60kw ,汽车质量为5×103kg ,汽车在水平路面上行驶时,阻力是车重的0.1倍,求:(1)汽车保持额定功率,从静止起动后能达到的最大速度是多少?(2)汽车从静止开始,保持0.5m /s 2的加速度作匀加速直线运动,这一过程能维持多长时间?[说明]要能解好该题,我们首先应知道机车功率的含义,机车功率即为发动机的功率,而发动机是产生牵引力的。
故机车功率P 只能与牵引力F 联系在一起,不能和机车所受的阻力或者机车的合外力联系在一起。
也即 P=F ·v ≠f ·v ≠F 合·v 基础练习1.关于功率,下列说法中正确的是 ( ) A .由P=w/t 可知.P 与W 成正比 B .由P=W/t 可知,P 与t 成反比C .由P=W/t 可知,只要知道W 和t 的值就可以计算出任一时刻的功率D .由P=Fv 可知,汽车的输出功率恒定时,牵引力一定与其速度成反比2.有一水平恒力F 先后两次作用在同一物体上,使物体由静止开始沿着力的方向发生相同的位移s ,第一次是在光滑的平面上运动;第二次是在粗糙的平面上运动。
比较这两次力F 所做的功W 1和W 2以及力F 做功的平均功率P 1和P 2的大小 ( )A. W 1=W 2 ,P 1>P 2B. W 1=W 2,P 1=P 2C. W 1>W 2,P 1>P 2D. W 1<W 2,P 1<P 23.雨滴在空中运动时所受阻力与其速度的平方成正比。
若有两个雨滴从高空中落下,其质量为m 1、m 2,落至地面前均已做匀速直线运动,则其匀速运动时重力的功率之比为 ( )A.21:m mB.21:m mC.12:m mD.3231:m m4.质量为m 的物体沿倾角为θ的斜面滑至底端时的速度大小为v 0,此时重力对物体做功的功率是 ( ) A. mgv B. mgvsin θ C.mgvcos θ D. 05一位高三年级的男生在平直的公路上以最快速度骑自行车,该车所受阻力为车和人总重力的0.05倍,则该男生的功率最接近于 ( )A .40WB .l00WC .250WD .500W6.起重机的钢绳吊着物体由静止开始竖直向上运动,先以加速度a(a<g)加速运动,接着匀速运动,最后减速到静止。
典型例题

若要以带符号 数形式显示, 应如何处理?
9
2、字符串处理
例5
例6
输入小写字母,显示其前导和后继;
输入字符串,显示最后4个字符;
例7 输入字符串,并逆序显示; 例8 输入字符串str1和str2,若str2是str1的子串,则输出Y, 否则输出N; 例9 删除串首尾空格,压缩串内空格;
从str1串首开始,至str1中能够截取与str2相同长度串的字符结束;
str1子串与str2的比较; str1长度范围内,匹配不成功,则继续循环; 匹配成功,则显示Y; 循环次数达到,则显示N;
17
循环体
循环控制
2019年2月2日星期六
开始
例8流程图 (方法2)
Str2是空串? Y
19
串中,则保留一个空格;若是串尾,设置串尾标志0;
2019年2月2日星期六
开始
例9 流程图
串扫描初始化 DI、CX(最大值)、AL(空格)、DF 设置新串指针BX,起始位置同DI 在原串中扫描非空格
Y
最后扫描字符为0?
Y
N
是串首?
在新串中保留 串尾标志0 结束
2019年2月2日星期六
清除串首标志
Y 从当前位置之后开始匹配str1和str2 Y 匹配成功? N str1搜索完毕? 显示Y
2019年2月2日星期六
N
Y
显示N
16
结束
例8(方法2 ) 输入字符串str1和str2,若str2是str1的子串, 则输出Y,否则输出N。
方法2:直接进行str1的子串与str2的比较;
具体的处理方法 从str1不同位置截取长度与str2相同子串,进行比较;
典型例题(有答案)
典型例题
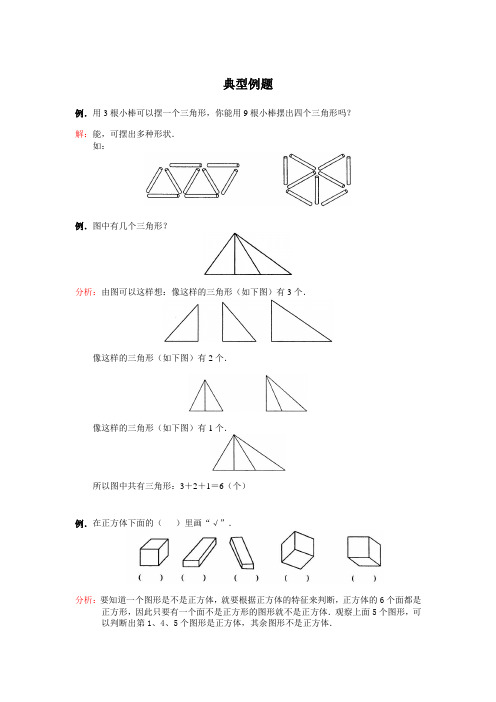
例.用3根小棒可以摆一个三角形,你能用9根小棒摆出四个三角形吗?
解:能,可摆出多种形状.
如:
例.图中有几个三角形?
分析:由图可以这样想:像这样的三角形(如下图)有3个.
像这样的三角形(如下图)有2个.
像这样的三角形(如下图)有1个.
所以图中共有三角形:3+2+1=6(个)
例.在正方体下面的()里画“√”.
分析:要知道一个图形是不是正方体,就要根据正方体的特征来判断,正方体的6个面都是正方形,因此只要有一个面不是正方形的图形就不是正方体.观察上面5个图形,可以判断出第1、4、5个图形是正方体,其余图形不是正方体.
解:
例.数一数下面的图(1)中有多少个三角形?
分析:先观察图,从图中很容易看出上面有1个三角形,中间有1个三角形,下面左、右两边各有一个三角形,合起来共有4个小三角形,如图(2)所示.
假如把中间三角形的三条边去掉,那么图形就变成了一个大三角形,如图(3)所示.因此,图中就有小三角形4个,大三角形1个,合起来是5个三角形.
解:此图形中有5个三角形.
例.仔细观察小松鼠在几个长方形中.
分析:这样想:小松鼠所在的长方形有以下几种形状:
所以:小松鼠在4个长方形中.
解:小松鼠在4个长方形中.
例.先剪三张正方形纸片,如图所示,再用这三张正方形纸片拼出不同的图形.
分析与参考答案:可以拼出的图形很多,下面是其中的几种:。
牛吃草经典例题

牛吃草经典例题
牛吃草问题是著名的趣味数学问题,典型例题有:
例1:牧场上一片青草,每天牧草都匀速生长。
这片牧草可供10头牛吃20天,或者供15头牛吃10天。
问可供25头牛吃几天?
例2:某块草地,假设每天匀速生长出青草正好够10头牛吃,这块草地可以放牧24头牛,则可以放牧多少头牛?
例3:有一片牧场,已知养牛60头,10天可以把草吃完;如果养牛45头,15天可以把草吃完;那么如果养牛20头,多少天可以把草吃完?
例4:有一块牧场,如果养25只羊,8天可以把草吃没,如果养21只羊,12天可以把草吃没,如果养16只羊,几天能把牧场上的一片牧草吃没?。
典型例题(有答案).DOC

典型例题
例 如图1,请你根据格子中的数,从1开始横着数或者竖着数,按照1,2,3,4,5,6,7,8,9,10的顺序数到10,如图2是其中的一种数法,你还有其他的吗?请你试一试.
分析与参考答案:
有以下几种不同的数法:
例.填空.
54)(=- 8)(10=- 分析:解答这组题可以想数的组成与分解.如54)(=-,想4和5组成几,4和5组成9,
所以括号里填9.8)(10=-,想10可以分成几和8,10可以分成2和8,所以括号里填2.根据加减法算式中各数的关系(即整体与部分的关系)来计算未知数也是
可以的,如
5
4
)
(=
-,想4加5等于几,4加5等9,所以括号里填9.8
)
(
10=
-,
想10减8等于几,10减8等于2,所以括号里填2.
答案:
5
4
)9(=
-8
)2(
10=
-
例.连线.
分析:第(1)题的意思是:左边算式的结果是几就应该和右边相应的数连起来.如:左边7+2=9,应该和右边的9连起来.
第(2)题是把左边和右边的结果相同的算式连起来,如:左边7+3=10,右边5+5=10,应该把这两个算式连起来.
例.在□里填上合适的数.
分析:做这道题要对数的组成比较熟悉.另外还要掌握解题技巧,按一定的顺序做,如:可以按从左往右,即10的分解来想.由于10的分解中右边的数又是7的组成中的一部分,因此所填的数必须比7小,即1、2、3、4、5、6,那么在7的组成中,右边的□所填的数相应是6、5、4、3、2、1.也可以按从右往左或从下往上,方法同上.
答案:略.。
函数的图像经典例题

函数的图象一、典型例题例1 设函数2()45f x x x =-- (1)在区间[2,6]-上画出函数()f x 的图像;(2)设集合{}()5,(,2][0,4][6,)A x f x B =≥=-∞-+∞ ,试判断集合A 和B 之间的关系,并给出证明;(3)当2k >时,求证:在区间[1,5]-上,3y kx k =+的图像位于函数()f x 图像的上方。
例2(1)若把函数()y f x =的图像作平移,可以使图像上的点()1,0P 变换成点()2,2Q ,则函数()y f x =的图像经此变换后所得图像对应的函数为 ( )A .(1)2y f x =-+ B.(1)2y f x =--C . (1)2y f x =++D . (1)2y f x =+-(2)己知函数33(),()232x f x x x -=≠-,若(1)y f x =+的图像是1C ,它关于直线y x =对称图像是22,C C 关于原点对称的图像为33,C C 则对应的函数解析式是__________(3)作出下列函数的大致图象: ①()21y x x =-+;② 21x y x -=+; ③ lg 1y x =-④ 11xy x -=-例3 (1)设函数()x f 的定义域为R ,它的图像关于直线1x =对称,且当1≥x 时()13-=x x f 则( ) ⎪⎭⎫ ⎝⎛<⎪⎭⎫ ⎝⎛<⎪⎭⎫ ⎝⎛322331A.f f f ⎪⎭⎫ ⎝⎛<⎪⎭⎫ ⎝⎛<⎪⎭⎫ ⎝⎛312332B.f f f ⎪⎭⎫ ⎝⎛<⎪⎭⎫ ⎝⎛<⎪⎭⎫ ⎝⎛233132C.f f f ⎪⎭⎫ ⎝⎛<⎪⎭⎫ ⎝⎛<⎪⎭⎫ ⎝⎛313223D.f f f (2)已知()f x 是定义域为(-∞,0)∪(0,+∞)的奇函数,在区间(0,+∞)上单调递增, ()f x 的图象如图所示,若[]()()0x f x f x --<,则x 的取值范围是__________________例3 已知函数()()()()1212()211xx f x x x x ⎧⎛⎫-≤-⎪ ⎪=⎝⎭⎨⎪-->-⎩,如果方程()f x a =有四个不同的实根,求实数a 的取值范围。
典型例题

典型例题
例1 下列各式哪些是代数式,哪些不是代数式。
(1);(2);(3);(4);
(5)3;(6);(7);(8)
分析本题目的在于考查对代数式概念的理解。
解:(1),(3) ,(5)3,(6),(8)都是代数式;
(2),(4)(7)都不是代数式。
例2 填空:
(1)汽车每小时行驶60千米,小时行驶_______千米;
(2)哥哥今年岁,比妹妹大岁,妹妹今年
________岁;
(3)行树一共有棵,平均每行树有________棵;
(4)某件商品原价元,春节期间以8折出售,则打折后售价为_______元。
分析本题考查用代数式表示几个比较简单的数量关系,一定要熟悉书写代数式时应注意的几点事项。
解:(1);(2);(3);(4)
点拨(2)(3)(4)小题往往易错,(2)题关键在于分清大数、小数和差。
(3)题在于区分份数、每份数相总量。
(4)题是一道联系实际的题目,首先要弄清
打折的含义,其次要准确找到单位“1”。
例3 说出下列代数式的意义。
(1);(2);(3);
(4);(5);(6)
分析本题考查用语言表达代数式的意义。
解:(1)的意义是的一半与5的差;
(2)的意义是与5的差的一半;
(3)的意义是除以与的和的商;
(4)的意义是除以的商与的和;
(5)的意义是与的差的平方;
(6)的意义是与的平方差。
点拨本例中(1)与(2),(3)与(4),(5)与(6)实质为对比题型,它们的意义易混淆,要注意二者读法的区别。
代数式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
典型例题-G-方差分析-2某企业准备用三种方法组装一种新的产品,为确定哪种方法每小时生产的产品数量最多,随机抽取了30名工人,并指定每个人使用其中的一种方法。
通过对每个工人生产的产品数进行方差分析,得到如下表所示的结果。
每个工人生产产品数量的方差分析表(2)若显著性水平为α=0.05,检验三种方法组装的产品数量之间是否有显著差异。
解:(1)完成方差分析表,以表格中所标的①、②、③、④、⑤、⑥为顺序,来完成表格,具体步骤如下: ①求k -1根据题目中“该企业准备用三种方法组装一种新的产品”可知,因素水平(总体)的个数k =3,所以第一自由度df 1=k -1=3-1=2,即SSA 的自由度。
②求n -k由“随机抽取了30名工人”可知,全部观测值的个数n =30,因此可以推出第二自由度df 2=n -k =30-3=27,即SSE 的自由度。
③求组间平方和SSA已知第一自由度df 1=k -1=3-1=2,MSA =210 根据公式1-==k SSAMSA 自由度组间平方和所以,SSA =MSA ×(k -1)=210×2=420④求总误差平方和SST由上面③中可以知道SSA =420;此外从表格中可以知道:组内平方和SSE =3836,根据公式SST =SSA +SSE 可以得出SST =420+3836=4256,即总误差平方和SST=4256 ⑤求SSE 的均方MSE已知组内平方和SSE =3836,SSE 的自由度n -k =30-3=27 根据公式0741.142273836==-==k n SSE MSE 自由度组内平方和所以组内均方MSE =142.0741⑥求检验统计量F已知MSA =210,MSE =142.0741 根据4781.10741.142210===MSE MSA F所以F=1.4781(2)题目中假设α=0.05,根据第一自由度df 1=k -1=3-1=2和第二自由度df 2=n -k =30-3=27,查F 分布表得到临界值F 0.05(2,27)=3.354131,所以F =1.4781<F α=3.354131,所以接受原假设,即μ1=μ2=μ3成立,表明μ1、μ2、μ3之间没有显著差异,也就是说,用三种方法组装的产品数量之间没有显著差异。
典型例题-G-方差分析-3五个地区每天发生交通事故的次数如表1所示。
由于是随机抽样,有一些地区的样本容量较多,(如南部和西部)而有些地区样本容量较少(如东部)。
试以α=0.01的显著性水平检验各地区平均每天交通事故的次数是否相等。
解:计算原数据的和:以及原数据的平方和:()()∑∑===++++-++++=-=rj nji ij x n x SST 112226538.2006755646657261771539834898831()0167.1186676555645664577715398348988312222221112=⎪⎪⎭⎫⎝⎛++++-++++=-=∑∑∑===jrj nji rj j ijx n x SSE6371.820167.1186538.200=-=-=SSE SST SSA6593.2046371.821,4151==-=∴=-=-r SSA MSA r6198.5210167.118,21526==-=∴=-=-r n SSE MSE r n6762.36198.56593.20===∴MSE MSA F单因素方差分析表假设检验:H 0:μ1=μ2=μ3=μ4=μ5,五个地区平均每天交通事故的次数相等。
H 1:μ1,μ2,μ3,μ4,μ5不全相等,五个地区平均每天交通事故的次数不相等。
查表得:F 0.01(4,21)=4.37>F =3.6762所以接受H 0,即五个地区平均每天交通事故的次数相等。
典型例题-H-相关与回归分析-2设有统计资料如下表所示。
用EXCEL 的回归分析(置信度90%),得到如下结果: SUMMARY OUTPUT 回归统计Multiple R 0.987760119R Square 0.975670053Adjusted R Square 0.972628809标准误差3.545815055观测值10方差分析dfSS MSF Significance F 回归分析14033.5175654033.517565320.81287799.67595E-08残差8100.582435312.57280441总计94134.1Coefficients 标准误差t Stat P-value Lower 95%Upper 95%下限 90.0%上限 90.0%Intercept -0.208871752.879726332-0.0725318060.943959317-6.849532574 6.431789074-5.563861187 5.146117686X Variable 10.7176566730.04006736917.911250049.67595E-080.6252611530.8100521930.6431494750.792163871试通过用公式计算,比较对照,理解所得结果。
解:x -bar =66.2,y -bar =47.3 相关系数为()()()()987760119.01.41346.78314.562022=⨯=----=∑∑∑Y Y X X Y Y X X r iii iXY()1.413412=-=∑=ni i y y SST717656673.066251656104736623693310ˆ212121111=-⨯⨯-⨯=⎪⎭⎫ ⎝⎛-⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛-=∑∑∑∑∑=====n i n i i i n i i ni i ni i i x x n y x y x n β20887175.02.66717656673.03.47ˆˆ0-=⨯-=-=x y ββi i x y717656673.020887175.0ˆ+-= ()517565.4033ˆ12=-=∑=ni i y ySSR()5824353.100ˆ12=-=∑=n i i i yy SSESSR +SSE =4033.517565+100.5824353=4134.1=SST222)(987760119.0975670053.01.4134517565.4033XY r SST SSR r =====对于第一部分:SUMMARY OUTPUT回归统计Multiple R 0.987760119R Square 0.975670053Adjusted R Square 0.972628809标准误差3.545815055观测值10通过以上计算分析,可知:Multiple R 0.987760119 是相关系数; R Square 0.975670053 是判定系数;Adjusted R Square 0.972628809 是根据以下公式来计算的:972628809.01110110)975670053.01(111)1(122=---⨯--=---⨯--=p n n R R标准误差 3.545815055 是根据以下公式来计算的:()545815055.32105824353.10022ˆ12=-=-=--=∑=n SSE n yy s ni iie观测值 10 是原始数据的个数,即n 。
对于第二部分:方差分析df SSMS FSignificance F 回归分析14033.5175654033.517565320.81287799.67595E-08残差8100.582435312.57280441总计94134.1第一列df 是自由度,第1行的1表示是一元线性回归;第二行是残差的自由度n -2=8,第三行是总的自由度1+8=9;第二列SS 是误差平方,第一行是SSR =4033.517565,第二行是SSE =100.5824353,第三行是SST =4134.1,这里有SSR +SSE =SST ;第三列MS 是平均误差平方,第一行是MSR =4033.517565/1=4033.517565,第二行是MSE =100.5824353/8=12.57280441;第四列F 是F =MSR /MSE =4033.517565/12.57280441=320.6128779;最后一列Significance F 是用EXCEL 函数FDIST(320.8128779,1,8)计算出来的。
9.67595E-08是科学计数法,表示9.67595×10-8 对于第三部分:Coefficients 标准误差t Stat P-value Lower 95%Upper 95%下限 90.0%上限 90.0%Intercept -0.208871752.879726332-0.0725318060.943959317-6.8495325746.431789074-5.5638611875.146117686X Variable 10.7176566730.04006736917.911250049.67595E-080.6252611530.8100521930.6431494750.792163871第一列Coefficients 是回归系数,第一行是截距的回归系数,即β0^=-0.20887175,第二行是斜率的回归系数,即β1^=0.717656673;第二列标准误差,第一行是截距的标准误差,是根据以下公式来计算的:()879726332.26.78312.66101545815055.3)(12122ˆ0=+⨯=-+=∑=ni i i ex x x ns s β第二行是斜率的标准误差,是根据以下公式来计算的:()040067369.06.7831545815055.312ˆ1==-=∑=ni i i ex x s s β第三列t Stat ,即t 统计量,由对应的回归系数除以标准误差:-0.20887175/2.879726332=-0.072531806 0.717656673/0.040067369=17.91125004第四列P value ,是用EXCEL 函数TDIST(|t Stat|,n -2,2)计算出来的,第一个参数是t 统计量,第二个参数是自由度,第三个参数2表示双尾。
TDIST(|-0.072531806|,8,2)=TDIST(0.072531806,8,2)=0.943959317 TDIST(|17.91125004|,8,2)=TDIST(17.91125004,8,2)=9.67595E-089.67595E-08是科学计数法,表示9.67595×10-8第五、六列的Lower 95%,Upper 95%是EXCEL 默认的95%置信度下,截距和斜率的置信区间,是根据以下公式来计算的:879726332.230600413.220887175.0)2(ˆ0ˆ0⨯±-=-±βαβs n t即:849532574.6)2(ˆ0ˆ0-=--βαβs n t431789074.6)2(ˆ0ˆ0=-+βαβs n t040067369.030600413.2717656673.0)2(ˆ1ˆ1⨯±=-±βαβs n t即:625261153.0)2(ˆ1ˆ1=--βαβs n t810052193.0)2(ˆ1ˆ1=-+βαβs n t第七、八列的下限90%,上限90%是根据输入的90%置信度下,截距和斜率的置信区间,是根据以下公式来计算的:879726332.285954803.120887175.0)2(ˆ0ˆ0⨯±-=-±βαβs n t即:563861187.5)2(ˆ0ˆ0-=--βαβs n t146117686.5)2(ˆ0ˆ0=--βαβs n t040067369.085954803.1717656673.0)2(ˆ1ˆ1⨯±=-±βαβs n t即:643149475.0)2(ˆ1ˆ1=--βαβs n t792163871.0)2(ˆ1ˆ1=-+βαβs n t典型例题-I-时间序列分析-1某企业某种产品的有关资料如表1所示。
