排队等候问题e(精选)
排队模型——精选推荐
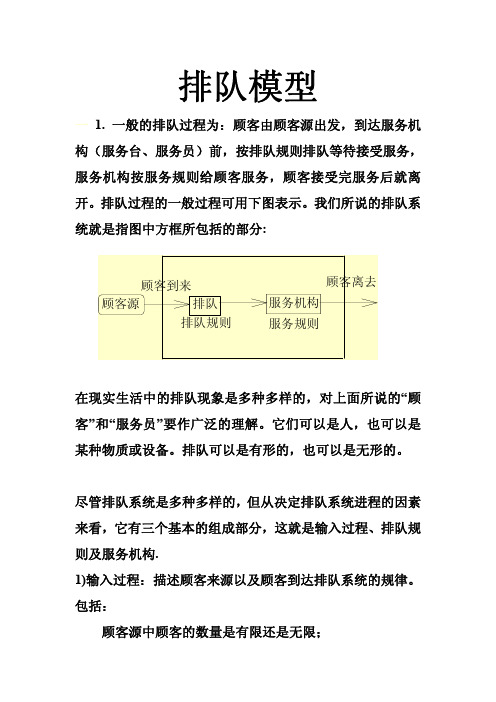
排队模型一 1. 一般的排队过程为:顾客由顾客源出发,到达服务机构(服务台、服务员)前,按排队规则排队等待接受服务,服务机构按服务规则给顾客服务,顾客接受完服务后就离开。
排队过程的一般过程可用下图表示。
我们所说的排队系统就是指图中方框所包括的部分:在现实生活中的排队现象是多种多样的,对上面所说的“顾客”和“服务员”要作广泛的理解。
它们可以是人,也可以是某种物质或设备。
排队可以是有形的,也可以是无形的。
尽管排队系统是多种多样的,但从决定排队系统进程的因素来看,它有三个基本的组成部分,这就是输入过程、排队规则及服务机构.1)输入过程:描述顾客来源以及顾客到达排队系统的规律。
包括:顾客源中顾客的数量是有限还是无限;顾客到达的方式是单个到达还是成批到达;顾客相继到达的间隔时间分布是确定型的还是随机型的,分布参数是什么,是否独立,是否平稳。
2)排队规则:描述顾客排队等待的队列和接受服务的次序。
包括:即时制还是等待制;等待制下队列的情况(是单列还是多列,顾客能不能中途退出,多列时各列间的顾客能不能相互转移);等待制下顾客接受服务的次序(先到先服务,后到先服务,随机服务,有优先权的服务)。
3)服务机构:描述服务台(员)的机构形式和工作情况。
包括:服务台(员)的数目和排列情况;服务台(员)的服务方式;服务时间是确定型的还是随机型的,分布参数是什么,是否独立,是否平稳。
2.到达和服务过程的模型2.1 到达过程的模型用表示第i 个顾客到达的时间,.i t 称为第i 个到达时间间隔.1i i T t t +=−i 我们用的特征来刻画顾客到达过程. 最常见的情况是独立同分布. 用X 表示这样的随机变量.12,,T T 12,,T T 如果X 服从参数为λ的指数分布.这时1()()i E T E X λ==即平均每隔1λ来一个顾客.换句话说,单位时间理平均有λ个顾客到来.称λ为到达速率. 用表示到时刻t 为止到达的顾客总数,则在上面的假设下()N t ()()N t P t λ∼.除了指数分布外,常用的还有爱尔朗分布,其密度函数为1()(), 0.(1)!k RxR Rx e f x x k −−=≥− 这时2(), ()i i k k E T D T R R==. k 叫形状参数, R 叫速率参数.当取λ使得R k λ=, 则爱尔朗分布可以看成是k 个独立的服从参数为λ的指数分布随机变量的和的分布.2.2服务过程的模型一般总是认为不同顾客接受服务占用的时间长短是相互独立的. 用Y表示一个客户接受服务的时间长短, 它是一个随机变量.若Y的分布是参数为μ的指数分布, 意味着一个顾客的服务时间平均为1μ. 单位时间里可以完成的平均顾客数为μ.若Y服从形状参数为k, 速率参数为R kμ=的爱尔朗分布, 则平均服务时间为1μ, 根据爱尔朗分布的性质, 可以将Y看作是k个相继子服务的总时间, 每个子服务都服从参数为1kμ的指数分布且相互独立.在排队论中,我们常用如下字母表示特定的到达时间间隔或服务时间分布:M: i.i.d. 指数分布D: i.i.d. 的确定分布E k: i.i.d. 的形参为k的爱尔朗分布GI: 到达时间间隔是i.i.d. 的某种一般分布G: 服务时间是i.i.d. 的某种一般分布在处理实际排队系统时,需要把有关的原始资料进行统计,确定顾客到达间隔和服务时间的经验分布,然后按照统计学的方法确定符合哪种理论分布。
小学数学二年级排队问题及答案练习题及答案

小学数学二年级排队问题及答案练习题及答案题目一:排队问题练习题一、选择题1. 以下哪个是队伍中的第一个人?A. 张三B. 李四C. 王五D. 赵六2. 以下哪个是队伍中的第二个人?A. 王二B. 张三C. 李四D. 赵六3. 以下哪个是队伍中的第三个人?A. 李四B. 张三C. 王五D. 赵六二、填空题1. 当队伍中只有两个人时,第一个人是____,第二个人是____。
2. 假设有一个排队的队伍,从左到右分别有3个小朋友,他们的名字分别是:李四、王五和赵六。
请你按照顺序填写队伍的排列顺序。
第一个人:____ 第二个人:____ 第三个人:____三、解答题1. 如果有四个小朋友排队,他们的名字分别是:李四、王五、赵六和张三。
请你写出所有可能的排列组合,用数字表示。
答案:________________2. 小明排队时看到队伍的第一个人是李四,他站在了赵六的后面。
请你推断小明在队伍中的位置,写出可能的结果。
答案:________________题目二:排队问题答案一、选择题1. A2. C3. B二、填空题1. 第一个人是张三,第二个人是赵六。
2. 第一个人是李四,第二个人是王五,第三个人是赵六。
三、解答题1. 1234、1243、1324、1342、1423、1432、2134、2143、2314、2341、2413、2431、3124、3142、3214、3241、3412、3421、4123、4132、4213、4231、4312、4321。
2. 小明可能在队伍的第四个位置或第五个位置。
一年级上册数学排队问题及答案练习100题及答案

一年级上册数学排队问题及答案练习100题及答案1. 请画出下列人物按顺序排队的图形。
A ->B ->C ->D -> E)2. 请按从右到左的顺序写出下列字母。
E, D, C, B, A3. 请找出下列排队图形中的错误,并将正确的形状画出来。
A B C DE F G H4. 请按顺序将下列数字从小到大排队: 6, 3, 8, 15. 小明站在队伍的第几个位置?(队伍中有9个人并按照从左到右的顺序依次编号)6. 请将下列人名按照拼音的顺序排列:小明、小红、小李、小张、小王7. 请计算下列数字之和:2 + 5 + 3 + 6 + 18. 若小红站在队伍的第4个位置,小明站在队伍的第8个位置,队伍一共有多少人?9. 请按从大到小的顺序写出下列数字:9, 4, 7, 2, 510. 若小明站在队伍的第3个位置,小红站在队伍的第6个位置,队伍一共有多少人?11. 小明站在队伍的倒数第几个位置?(队伍一共有8个人)12. 请按顺序将下列数字从大到小排队:10, 7, 15, 213. 若小红站在队伍的第5个位置,小明站在队伍的第2个位置,队伍一共有多少人?14. 小红站在队伍的倒数第几个位置?(队伍一共有7个人)15. 请计算下列数字之和:4 + 2 + 6 + 3 + 116. 请找出下列排队图形中的错误,并将正确的形状画出来。
A B C DE F H G17. 请按从左到右的顺序写出下列字母。
A, B, C, D, E18. 请按顺序将下列人名的姓氏排列:王小明、李小红、张小李、赵小王19. 请将下列人物按逆序排队的图形画出来。
A ->B ->C ->D -> E)20. 小红站在队伍的第几个位置?(队伍中有10个人并按照从左到右的顺序依次编号)答案:1. E D C B A2. A B C D E3.A B C DE F G H4. 1, 3, 6, 85. 第7个位置6. 小李、小明、小红、小王、小张7. 178. 8个人9. 9, 7, 5, 4, 210. 10个人11. 倒数第2个位置12. 15, 10, 7, 213. 6个人14. 倒数第3个位置15. 1616.A B C DE F G H17. E D C B A18. 李小红、张小李、王小明、赵小王19. E D C B A20. 第5个位置。
小学数学一年级排队问题及答案练习题及答案

小学数学一年级排队问题及答案练习题及答案一.理论部分:1. 简答题根据你对排队问题的理解,回答以下问题:a. 什么是排队?为什么要排队?b. 排队的原则是什么?请列举几个常见的排队原则。
c. 排队时应遵守的基本行为是什么?请列举几点。
2. 判断题判断下列说法的正误,正确的请写“对”,错误的请写“错”。
a. 每位小朋友都可以随意插队。
()b. 排队时可以争抢前进的位置。
()c. 排队时可以追赶和超过前面的人。
()二.运算练习:1. 填空题请根据题意填写空白处的数字。
a. 如果一共有5个小朋友排队,那么一共有____种不同的排队方式。
b. 如果一共有8个小朋友排队,那么一共有____种不同的排队方式。
2. 计算题请根据实际情况计算。
a. 有6个小朋友排队,小明先排第一位,请计算小明所在的位置。
(结果写成顺序数)b. 有9个小朋友排队,小华排在第4位,请计算小华后面的位置。
(结果写成顺序数)三.应用题:1. 问题解答a. 小明、小华、小强三个小朋友排队,小明在最前面,小强在最后面。
请问,小强排在第几位?b. 有3个小朋友排队,小明和小华之间有1个小朋友,请问,小明和小华分别排在第几位?2. 组合问题a. 有4个小朋友排队,请问,他们一共有几种不同的排队方式?b. 有5个小朋友排队,小明想排在第2位,小华想排在第5位,请问,他们的排队方式有几种?题目答案:一.理论部分:1. 简答题a. 排队是指按照一定的顺序站成一列等待。
排队的目的是为了增加秩序,遵守公平原则,合理安排等候时间。
b. 常见的排队原则包括先到先得原则、老幼病弱优先原则、有序等待原则等。
c. 排队时应遵守的基本行为包括排队不插队、按序前进、不搭讪嬉戏等。
2. 判断题a. 错b. 错c. 错二.运算练习:1. 填空题a. 5b. 82. 计算题a. 第1位b. 第5位三.应用题:1. 问题解答a. 第3位b. 小华排在第2位,小明排在第4位。
小学数学排队问题及答案练习题及答案

小学数学排队问题及答案练习题及答案小学数学练习题及答案:排队问题假设在一次课间操场比赛中,全校所有学生按照身高从低到高排成了一列,刚好有100个学生。
现在要按照下面的要求进行排队。
要求1:将所有学生按照身高从高到低重新排队。
要求2:将所有男生按照身高从低到高排队。
要求3:将所有女生按照身高从高到低排队。
要求4:将身高在1.3米以上的学生按照身高从高到低排队。
要求5:将身高在1.5米以下的学生按照身高从低到高排队。
1. 请你计算:a) 要求1中,排在第30位的学生是第几位?b) 要求2中,排在第60位的男生是第几位?c) 要求3中,排在第70位的女生是第几位?d) 要求4中,有多少个学生在队列中?e) 要求5中,有多少个学生在队列中?2. 现在假设在原有队列的基础上,又加入了新的学生。
a) 如果加入一个身高为1.4米的男生,他在新队列中排在第几位?b) 如果加入一个身高为1.6米的女生,她在新队列中排在第几位?c) 新队列中,身高在1.2米到1.4米之间的学生有多少个?d) 新队列中,身高在1.5米以下的学生有多少个?3. 请你总结并回答下列问题:a) 在要求1中,排在第10位和第90位的学生分别是原队列中的第几位?b) 在要求4中,排在第20位的学生是原队列中的第几位?c) 在要求5中,排在第40位的学生是原队列中的第几位?答案:1.a) 要求1中,排在第30位的学生是原队列中的第71位。
b) 要求2中,排在第60位的男生是原队列中的第33位。
c) 要求3中,排在第70位的女生是原队列中的第37位。
d) 要求4中,队列中有31个学生。
e) 要求5中,队列中有18个学生。
2.a) 加入一个身高为1.4米的男生后,他在新队列中排在第71位。
b) 加入一个身高为1.6米的女生后,她在新队列中排在第19位。
c) 新队列中,身高在1.2米到1.4米之间的学生有50个。
d) 新队列中,身高在1.5米以下的学生有19个。
排队论

泊松输入中的顾客到达间隔时间 T 相互独立且服从同参数 λ 的负指数分 布,其密度函数为
其平均到达间隔时间为
λ 称为到达率。
三. 排队系统的主要特征
1. 输入过程 ⑴ 定长输入( D, Deterministic ) ⑵泊松输入 (最简单流, M ) ⑶ 一般独立输入( G,General Independent ) —— 指顾客到达间隔时间 T 为相互独立且同分布的随机变量。最简单 流是它的一个特例。 此外,在本章所讨论的排队系统中,总假定输入过程是平稳的,或 称对时间是齐次的。 平稳的输入过程 —— 指顾客到达间隔时间的分布与时间无关。否则就称 为非平稳的。
服务台m
服务台 1
⑸
服务台 2
服务台 1 服务台 2
···
···
服务台 m
服务台 m
三. 排队系统的主要特征
1. 输入过程 2. 服务时间 τ 的分布 3. 服务机构(服务台) 4. 服务规则
⑴ 先到先服务(FCFS) ⑵ 后到先服务(LCFS)
如信息处理、仓库中堆积的货物等。 ⑶ 随机服务(SIRO) ⑷ 优先权服务(PR) ⑸ 一般服务规则(GD)
1909年,由丹麦工程师爱尔朗(A.K.Erlang)在研究电话系统时初创的。
§l 排队论的基本概念及研究的问题
一.排队论中有两个基本概念:
顾客:把提出需求的对象称为顾客(或需求); 服务:把实现服务的设施称为服务机构(或服务台)。
顾客和服务机构组成一个排队系统,称为随机服务系统。 因此也称排队论为随机服务系统理论
⑴ 定长输入( D, Deterministic ) —— 每隔一定时间 α 到达一个顾客,顾客到达间隔时间 T 的分布函数为
三. 排队系统的主要特征
人教版四年级上册数学广角《排队等候问题》

最佳方案:
时间短的
时间长的
船3
船2
船1
1小时 (1+4)小时 (1+4+8)小时
共19小时
第7页,共10页。
总ห้องสมุดไป่ตู้:
这节课我们学习了一个关于排队等候 的问题,通过这个例子,我们知道了 应该从需要时间最少的那个开始,最 后才是需要时间最多的那个。这样可 以使总的等候时间最少。
时间短的
时间长的
第8页,共10页。
答:打电话的顺序分别是:小玉、小芳、小云。时间 最少是34分钟。
第10页,共10页。
想一想:可以有哪些卸货的顺序?
船1 船2 船3 船1 船3 船2 船2 船1 船3 船2 船3 船1 船3 船1 船2 船3 船2 船1
第5页,共10页。
船1 船2
8 8+4
船1 船3
8 8+1
船2 船1
4 4+8
船2 船3
4 4+1
船3 船1
1 1+8
船3 船2
1 1+4
船3 共33小时
8+4+1
加油站每次只能给一辆车加油,加满一辆大卡车的油需7分钟, 加满面包车需4分钟,加满小轿车需2分钟。现在有这3种车各 一辆来到加油站加油,怎样安排加油的顺序使三辆车的等候 时间总和最少?最少时间是多少分钟?
答:加油的顺序分别是:小轿车、面包车、大卡车。 最少时间是21分钟。
第9页,共10页。
三个小朋友排队打电话,小玉要打4分钟,小云要打8分 钟,小芳要打7分钟。要使三人等待的时间的总和最少, 应该怎样安排三人打电话的顺序?时间最少是多少?
第3页,共10页。
【精品】三年级下册数学竞赛试题-应用题讲解--第一讲:排队问题 北师大版( 含答案)

第一讲:排队问题内容精要:1. 直线型排队问题学生排队,以其中某一名学生为参照来数人数,知道这名学生的左边、右边的人数或从左、右数他排第几,这类问题就是排队问题。
在排队问题中,作为参照的这名学生既不能遗漏,也不能重复。
2. 在封闭型排队问题中,按照顺时针或逆时针方向报数,在计算总人数的时候要注意不要漏掉某一个部分。
同时,以每次报数开始和结束的同学作为参照,既不能重复,也不能遗漏。
3. 在方阵排队问题中,注意根据题意整理出有多少列,有多少行,行数×列数就得到总人数。
4. 解决涉及逻辑推理的排队问题时,尽可能画出他们的座位图,给能够确定的先安排座位,然后再根据条件来分析其他人的座位。
第一种类型直线型排队问题例1:若干名学生排成一排,旭旭的左边有12名学生,右边有7名学生,那么这一排一共有多少名学生?【解析】旭旭左边12人里面不包含旭旭,右边7人也不包含旭旭,所以12+7+1=20(名)。
答:共有20名学生。
例2:三(1)班全体学生站成一队,正数第5名学生和倒数第6名学生之间有16名学生,那么三(1)班一共有多少名学生?【解析】把整个队伍分为三部分,分别是前5个人,后6个人,以及他们之间的16个人,将三部分的和算出来即是学生的总人数,5+6+16=27(名)。
答:共有27名学生。
过关检测1. 若干名学生排队做操,从前往后数,曼曼排在第8位。
曼曼前面一共有多少名学生?2. 小朋友们排成一排,第7名和第27名同学之间有多少人?3. 22名学生排队,旭旭的前面有9名学生。
旭旭的后面有多少名学生?4. 一个班里的40名学生排成一队去看电影,正数第10名和倒数第8名之间是女生。
这个班里的女生有多少名?过关检测答案1. 8-1=7(人)答:共有7名学生。
2. 第7名与第27名之间是第8名到第26名,26-8+1=19(人)答:共有19人。
3. 旭旭前面有9名同学,旭旭就是第10 名,22-10=12(人)答:共有12人。
