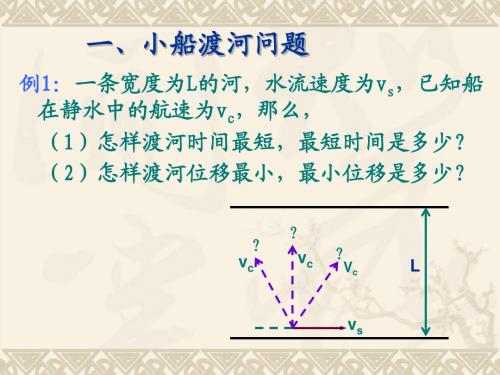
3小船渡河的问题
小船渡河,船绳问题(鲁科版必修1)课件
V2?
d
V2?
V2?
d
V2
V1
v1 解析:为了使割下的玻璃都成规定 cos v2 尺寸的矩形，金刚钻割刀应相对于 v1 玻璃板的边垂直切割。 arccos v2 设金刚钻的割刀速度与玻璃板运动 方向成α角，则v2cosα=v1，故 d 切割一次的时间： t
2 v2 v12
V1
L L L V s （2）此时最小位移为：S m i n sinα cosθ Vc
小船渡河动画演示
练习1：一船准备渡河，已知船在静水中的航速为 v1=2m/s，水流速度为v2=1m/s，求： ①要使船能够垂直地渡过河去，那么应向何方划船？ ②要使船能在最短时间内渡河，应向何方划船？
θ V F
（3）VA=V1=Vsin θ﹤V=VB
B V1
例4：如图所示,重物A､B由刚性绳拴接,跨过定滑轮处于图中 实线位置,此时绳恰好拉紧,重物静止在水平面上,用外力水
平向左推A,当A的水平速度为vA时,如图中虚线所示,求此时B
的速度vB=______.
分析：A､B通过绳子连接,由于绳子是不可伸长的,故A､B沿
【答案】 ①船的航向与上游河岸的夹角为60°； ②船的航向与河岸垂直。
练习2：船在静水中的速度大小V1=3m/s，要横渡宽 d=30m的河，河水流速V2=5m/s，问： （1）船能否垂直于河岸航线抵达对岸？ （2）船渡河最短的时间是多少？ （3）船渡河最小的位移是多少？
解： （1）不能 （2） t min
Vs cosθ Vc Vs θ arccos Vc
若 Vc<Vs, 怎样渡河位移最小？
思考：①若Vc<Vs, 船还能垂直渡河吗？ ②Vc<Vs时，船身与上游河岸的夹角θ等于多少 时渡河位移最小？最小位移是多少?
小船过河问题三种情况及其公式
小船过河问题三种情况及其公式
小船渡河三种情况公式推导是：
1、小船过江时的水流速度与船过江的时间无关，只与船的速度有关。
从船的速度都是用来过河的，而不是作为分速度来说，可以推导出沿河岸垂直过河是最短的过河方式，公式为t=s/v船。
2、当船速大于水速时，当前速度和船速的组合速度可以垂直于河岸。
当船速与流速的夹角为时，即当船向(-90)度方向向上游倾斜时，船可以垂直过河，此时的渡河时间可以表示为T=S/cos(-90)V 船。
3、如果满足流速大于船速的前提，流速和船速的组合速度不能垂直于河岸。
但不要忘了船的位移最短，就是画一个以船速的长度为半径，以速度的箭头末端为圆心的圆。
这时圆上有无数条切线，所以要求出速度初始位置的切线，也就是这条切线与最短位移重合，所以此时的公式是s=河宽*v水/v船。
小船渡河问题归纳总结
小船渡河问题归纳总结小船渡河问题是物理学中的一个经典问题，它涉及到相对运动、速度、时间和距离等多个物理概念。
以下是关于小船渡河问题的归纳总结，详细介绍：一、基本概念1. 小船渡河：指的是一个船只在河流中从一岸行驶到另一岸的过程。
2. 静水速度：船只在静止的水中行驶的速度，通常记为vc。
3. 河流速度：河流的流速，通常记为vs。
4. 合速度：船只在河流中的实际速度，是静水速度和河流速度的矢量和。
5. 渡河时间：船只从一岸出发到达另一岸所需要的时间。
6. 渡河距离：船只在水面上实际行驶的距离。
二、问题分类1. 最短时间渡河：在给定河宽和船只静水速度的条件下，求船只渡河的最短时间。
2. 最短距离渡河：在给定河宽和船只静水速度的条件下，求船只渡河的最短距离。
3. 指定地点渡河：船只需要在河对岸的指定地点登陆，求船只的行驶方向和速度。
三、解题方法1. 最短时间渡河：-当静水速度大于河流速度时，船只应该以静水速度垂直于河岸行驶，这样渡河时间最短。
-当静水速度小于河流速度时，船只无法垂直于河岸行驶，此时渡河时间取决于静水速度与河流速度的比值。
-当静水速度等于河流速度时，船只可以垂直于河岸行驶，渡河时间也是最短的。
2. 最短距离渡河：-当静水速度大于河流速度时，船只应该以静水速度与河流速度的比值确定合速度的方向，使得合速度垂直于河岸，这样渡河距离最短。
-当静水速度小于河流速度时，船只无法垂直于河岸行驶，此时渡河距离取决于静水速度与河流速度的比值。
-当静水速度等于河流速度时，船只可以垂直于河岸行驶，渡河距离也是最短的。
3. 指定地点渡河：-确定船只的合速度方向，使得合速度的方向与指定地点的连线垂直。
-计算合速度的大小，使得船只能够准确到达指定地点。
四、实际应用1. 航海导航：在航海过程中，船只需要在不同的水流速度和方向下，选择合适的行驶方向和速度，以达到目的地。
2. 水上救援：在进行水上救援时，救援船只需要根据河流的流速和救援地点的位置，选择合适的行驶方向和速度，以尽快到达救援地点。
小船渡河问题归纳总结
小船渡河问题归纳总结在生活中，我们常常会遇到各种各样的问题，有些问题看似简单却隐藏着深刻的道理。
其中，小船渡河问题是一种经典的思考题，它涉及到数学逻辑、思维策略以及团队合作等多个方面。
通过对小船渡河问题的分析与总结，不仅可以锻炼我们的思维能力，还能帮助我们理解人际关系和团队合作的重要性。
小船渡河问题是一种经典的思维问题，故事背景一般是有若干人或物需要过河，但是河上只有一艘小船，而且船的载重有限。
最常见的版本是有一只狼、一只绵羊和一根青草需要过河，但狼会吃掉绵羊，绵羊会吃掉青草。
问题是，如何能够让所有的物品都安全地渡过河流？从这个问题中，我们可以看到思维逻辑的重要性。
一般来说，要解决这类问题，我们需要先从整体上思考，并找到解决问题的关键点。
在小船渡河问题中，关键点就是船的载重限制以及物品相互之间的关系。
通过分析这些关键点，我们可以得出一些解题的策略。
首先，我们可以考虑使用逆向思维。
即先让狼和绵羊过河，再让狼回来，最后再让绵羊和青草过河。
这样一来，狼和绵羊的关系和青草和绵羊的关系就不会产生冲突。
通过这种思维方式，我们可以找到一种安全的渡河方案。
其次，小船渡河问题也能帮助我们理解团队合作的重要性。
在现实生活中，我们经常需要与他人合作解决问题，而团队合作能够提高工作效率和解决问题的能力。
在小船渡河问题中，不同的角色代表了团队中的不同成员，互相之间的关系和配合至关重要。
船的载重限制则可以理解为资源的有限性，提醒我们要合理分配和利用资源。
只有通过合作和团队精神，才能成功地让所有的物品都安全地渡过河流。
除了思维逻辑和团队合作，小船渡河问题还可以引申出许多有意思的思考。
例如，我们可以思考如何扩大问题的规模，让更多的物品渡过河流。
我们还可以考虑如何应对不同的情境变化，例如增加船的载重限制或者改变物品之间的关系等等。
通过对这些问题的思考与探讨，我们可以发展出更加复杂和深入的解题策略。
小船渡河问题是一种锻炼思维能力和团队合作意识的好方式。
高中物理小船过河问题含答案讲解
小船过河问题轮船渡河问题：（1）处理方法：轮船渡河是典型的运动的合成与分解问题，小船在有一定流速的水中过河时，实际上参与了两个方向的分运动，即随水流的运动（水冲船的运动）和船相对水的运动（即在静水中的船的运动），船的实际运动是合运动。
1．渡河时间最少：在河宽、船速一定时，在一般情况下，渡河时间sin1船d dt，显然，当90时，即船头的指向与河岸垂直，渡河时间最小为vd ，合运动沿v 的方向进行。
2．位移最小若水船结论船头偏向上游，使得合速度垂直于河岸，位移为河宽，偏离上游的角度为船水cos若水船v v ，则不论船的航向如何，总是被水冲向下游，怎样才能使漂下的距离最短呢？如图所示，设船头v 船与河岸成θ角。
合速度v 与河岸成α角。
可以看出：α角越大，船漂下的距离x 越短，那么，在什么条件下α角最大呢？以v 水的矢尖为圆心，v 船为半径画圆，当v与圆相切时，α角最大，根据水船v v cos船头与河岸的夹角应为v水θv αABEv船v 水v船θvV水v 船θv 2v 1水船v v arccos，船沿河漂下的最短距离为：sin)cos (min 船船水v dv v x 此时渡河的最短位移：船水v dv d scos【例题】河宽d ＝60m ，水流速度v 1＝6m ／s ，小船在静水中的速度v 2=3m ／s ，问：(1)要使它渡河的时间最短，则小船应如何渡河?最短时间是多少? (2)要使它渡河的航程最短，则小船应如何渡河?最短的航程是多少?★解析： (1)要使小船渡河时间最短，则小船船头应垂直河岸渡河，渡河的最短时间ss dt2030602(2)渡河航程最短有两种情况：①船速v 2大于水流速度v 1时，即v 2>v 1时，合速度v 与河岸垂直时，最短航程就是河宽；②船速v 2小于水流速度v l 时，即v 2<v 1时，合速度v 不可能与河岸垂直，只有当合速度v方向越接近垂直河岸方向，航程越短。
(完整版)小船渡河问题练习题大全
小船过河问题I1河宽d = 60m，水流速度v i = 6m/ s,小船在静水中的速度V2=3m / s,问：（1）要使它渡河的时间最短，则小船应如何渡河？最短时间是多少？（2）要使它渡河的航程最短，则小船应如何渡河？最短的航程是多少？2在抗洪抢险中，战士驾驶摩托艇救人，假设江岸是平直的，洪水沿江向下游流去，水流速度为v i，摩托艇在静水中的航速为V2,战士救人的地点A离岸边最近处0的距离为d,如战士想在最短时间内将人送上岸，则摩托艇登陆的地点离0点的距离为（C ）C.速，则船速与水速之比为（）3某人横渡一河流，船划行速度和水流动速度一定，此人过河最短时间为了T i;若此船用最短的位移过河，则需时间为T2，若船速大于水(B) T2(C)T iJ2T22(D)T iT4小河宽为d，河水中各点水流速度大小与各点到较近河岸边的距离成正比,4v nV水kx, k —0, X是各点到近岸的距离，小船船头d垂直河岸渡河，小船划水速度为v0，则下列说法中正确的是（）A、小船渡河的轨迹为曲线C、小船渡河时的轨迹为直线B、小船到达离河岸-处，船渡河的速度为• 2v02D、小船到达离河岸3d/4处，船的渡河速度为.1^05.如图1所示，人用绳子通过定滑轮以不变的速度v0拉水平面上的物体A ,当绳与水平方向成B角时,物体A的速度6如图3所示，某人通过一根跨过定滑轮的轻绳提升一个质量为m的重物，开始时人在滑轮的正下方，绳下端A点离滑轮的距离为H。
人由静止拉着绳向右移动，当绳下端到B点位置时，人的速度为v , 与水平面夹角为B。
问在这个过程中，人对重物做了多少功？7. 一条宽度为L的河，水流速度为v水，已知船在静水中速度为v船，那么:（1）怎样渡河时间最短？（2）若v船v水，怎样渡河位移最小? 3）若v船v水，怎样渡河船漂下的距离最短?绳8河宽60m,小船在静水中的速度为4m/s,水流速度为3m/s。
求小船渡河的最小时间是多少，小船实际渡河的位移为多大？若小船在静水中的速度为5m/s,水流速度为3m/s。
《小船渡河问题》 知识清单
《小船渡河问题》知识清单在物理学中，小船渡河问题是一个经典且有趣的运动学问题，它涉及到速度的合成与分解，对于理解物体的运动规律有着重要的意义。
下面就让我们一起来详细探讨一下小船渡河问题。
一、问题描述通常情况下，小船渡河问题的场景是这样的：小船在宽度一定的河流中渡河，船头的指向可以改变，水流速度恒定。
我们需要研究小船如何以最短的时间渡河、如何以最短的位移渡河，以及在给定条件下小船的实际渡河路径等。
二、基本概念1、合速度小船在水中的实际速度是由小船自身的速度（船头指向的速度）和水流速度合成的，这个合成的速度称为合速度。
2、分速度小船自身的速度和水流速度分别称为分速度。
三、常见类型1、最短时间渡河当船头垂直于河岸时，小船渡河时间最短。
此时，渡河时间 t ＝ d／ v 船（d 为河宽，v 船为小船在静水中的速度）。
因为在垂直河岸的方向上，小船的速度分量最大，所以能在最短时间内到达对岸。
2、最短位移渡河（1）当 v 船＞ v 水时，合速度可以垂直于河岸，此时渡河位移最短，等于河宽 d 。
（2）当 v 船＜ v 水时，无论船头指向如何，合速度都无法垂直于河岸，此时要使渡河位移最短，船头应斜向上游，并且与合速度的方向垂直。
四、速度的合成与分解这是解决小船渡河问题的关键方法。
我们要根据平行四边形定则，将小船的速度和水流的速度进行合成与分解。
例如，假设小船在静水中的速度为 v 1 ，水流速度为 v 2 。
以小船的速度 v 1 的方向为邻边，水流速度 v 2 的方向为对边，作平行四边形，那么平行四边形的对角线就是小船的实际速度。
在分解速度时，通常将速度分解为沿着河岸方向和垂直河岸方向的两个分速度。
沿着河岸方向的速度影响小船在河岸方向上的移动距离，垂直河岸方向的速度影响小船渡河的时间。
五、实例分析假设河宽为 100 米，小船在静水中的速度为 5m/s，水流速度为3m/s。
1、求最短时间渡河船头垂直河岸，t ＝ 100 ／ 5 ＝ 20s 。
小船渡河问题归纳总结
小船渡河问题归纳总结小船渡河问题是一个经典的数学难题，涉及到逻辑思维和数学推理。
在这个问题中，有一条河，河中有一只小船，以及一些不同速度的人。
考虑到小船只能承载一定数量的人，并且在渡河过程中船上的人数不能超过船的承载量，并给出各人的渡河速度，我们需要找到最短的时间完成所有人的过河。
首先，我们可以根据题目给出的条件得出以下结论：1. 渡河速度最慢的人需要始终伴随着船。
2. 若A、B两人渡河时间相同，则可以先让A渡河，再由A返回并让B渡河，而不影响总时间。
3. 若A、B两人渡河时间不同，则应让速度较快的人先行渡河，以减少总时间。
基于以上结论，我们可以提出一种基本的渡河策略：1. 将速度最慢的人与速度第二慢的人配对，让他们一起渡河。
这样可以保证渡河时间的最小值为这两人的时间之和。
2. 速度第二慢的人将船送回，速度最快的人与速度第三快的人一起渡河。
这样可以确保速度最快的人在返航时没有较慢的人在船上拖延时间。
3. 速度第三快的人将船送回，速度最慢的两个人一起渡河。
这样可以确保速度最快的人在返航时没有较慢的人在船上拖延时间。
4. 最后，速度第二快的人与速度最快的人一起渡河。
通过以上策略，我们可以保证总时间最短。
但是，需要注意的是，在实际操作过程中可能会出现一些特殊情况，需要灵活应对。
例如，当最慢的人数为奇数时，我们可能需要调整策略，让最快的两个人先行渡河，从而避免时间的浪费。
除了基本策略外，还有一些变体可以考虑。
在某些情况下，每个人的渡河速度可能是不确定的，我们只知道每个人之间的速度关系。
在这种情况下，我们可以利用排列组合的方法来找到最优解。
通过将不同速度的人进行排列组合，并计算每种组合的总时间，最终选择总时间最小的一种组合。
此外，我们还可以通过编程来解决小船渡河问题。
利用计算机的高速计算能力，我们可以根据题目给出的具体条件，通过编写算法来自动找到最优解，从而节省了人工计算的时间和精力。
这在实际生活中可能会更加便捷和高效。
小船渡河练习题及答案
小船渡河练习题及答案在生活中，我们常常遇到许多需要解决问题的情况，而解决问题的能力和智慧正是我们成长的基石。
小船渡河练习题作为一种常见的逻辑思维训练题，可以帮助我们锻炼思维的灵活性和解决问题的能力。
下面将为大家介绍一些关于小船渡河的练习题以及相应的答案。
题目一：小船渡河问题有一对夫妇和两个小孩需要渡河，河边只有一条只能承载两人的小船。
夫妇需要船带回来，而且小孩之间不能独自在河边，夫妇之间也不能独自在河边。
请考虑一种渡河方案，使得所有人都成功渡河。
解答：首先，夫妻一起渡河，然后丈夫返回，而妻子和其中一个小孩留在对岸。
随后，丈夫从河对岸返回，然后带着另一个小孩一起渡河。
接下来，丈夫留在对岸，而妻子返回河边。
最后，妻子和其中一个小孩一起渡河，完成所有人的渡河任务。
题目二：加入限制条件在之前的小船渡河问题的基础上，加入以下限制条件：1. 大家都需要戴口罩。
2. 大家每次渡河都需要保持安全距离（至少1米）。
解答：在考虑口罩和安全距离的情况下，解决方案如下：夫妻和一个小孩一起上船，丈夫带着这个小孩一起返回。
然后，妻子和另一个小孩一起上船，妻子将第一个小孩送回对岸后返回。
最后，夫妻一起上船，丈夫将妻子送回对岸后返回。
在整个过程中，每个人都要佩戴口罩，并在上下船和接触时保持安全距离，以确保安全。
题目三：时间限制在之前的小船渡河问题中，加入以下时间限制条件：1. 整个渡河过程需要在10分钟内完成。
2. 每次通行船程不能超过5分钟。
解答：这个问题需要考虑每次船行的时间。
解决方案如下：夫妻和一个小孩一起上船，丈夫带着这个小孩一起返回（用时5分钟）。
然后，妻子和另一个小孩一起上船，妻子将第一个小孩送回对岸后返回（用时5分钟）。
最后，夫妻一起上船，丈夫将妻子送回对岸后返回（用时5分钟）。
通过按照这个方案行动，整个渡河任务可以在10分钟内完成。
通过以上的小船渡河练习题，我们可以锻炼自己的逻辑思维和问题解决能力。
无论是在日常生活中还是工作中，这种能力都是非常重要的。
小船渡河问题归纳总结
小船渡河问题归纳总结引言小船渡河问题是一个经典的逻辑问题，通常用于考察人们在限制条件下寻找解决办法的能力。
本文将对小船渡河问题进行归纳总结，包括问题背景、常见解法以及相关思考等内容。
问题背景小船渡河问题通常描述为：有一条河流，一只小船和一些人要从一岸渡到对岸。
然而，根据以下限制条件，需找到一种方法满足所有人的渡河需求。
限制条件： 1. 小船每次只能搭载一至两个人； 2. 如果岸上有若干人，其中有一人在场，则可以使用小船； 3. 在任意一岸，如果岸上有人比待渡人数少，则小船必须离开，并将其他人带往对岸。
基本解法基本解法是指最简单且最直接的小船渡河问题解决方法。
1.初始状态下，将所有人和小船都放在河的一侧。
2.选定一种策略，例如每次渡船都尽量多带人，即每次渡船都将小船上的人数最大化。
3.重复以下步骤，直至所有人和小船都到达对岸：–将小船上的一至两个人带到对岸；–如果岸上有人数少于待渡人数的一侧，则将小船返回，将人带往对岸；–如果岸上没有人数少于待渡人数的一侧，则将小船返回并不带任何人。
4.完成渡河任务。
变体解法除了基本解法外，还有一些变体解法用于增加问题的难度，考察解决问题的灵活性和创造力。
以下是一些常见的变体解法。
1. 增加障碍物在河流中增加障碍物，如岩石、鳄鱼等，限制小船的移动。
解决这个问题需要额外的策略和判断。
2. 不同速度的人员假设不同的人员具有不同的渡河速度，解决这个问题需要合理安排人员的搭乘顺序，以达到最短的总渡河时间。
3. 具有特殊技能的人员假设某些人员具有特殊技能，例如划船或拆除障碍物等，解决这个问题需要合理利用特殊技能，提高渡河效率。
思考与拓展小船渡河问题是一个具有挑战性的逻辑问题，可以引发一些思考和拓展。
1.如何扩展问题规模？如果人员较多、小船的承载能力不同或对应岸上的人数限制不同，如何解决渡河问题？2.如何应用算法解决小船渡河问题？例如，可以使用图论中的最短路径算法来解决渡河问题。
小船过河问题分析与题解
小船过河问题分析与题解【问题概说】（1）船的实际运动是水流的运动和船相对静水的运动的合运动。
（2）三种速度:船相对水的速度为v 船（即船在静水中的速度），水的流速为v 水（即水对地的速度），船的合速度为v （即船对地的速度，船的实际速度，其方向就是船的航向）。
（3）三种情景：①过河时间最短:当船头垂直河岸，渡河时间最短，且渡河时间与水的流速无关。
②过河路径最短：在v 船>v 水的条件下，当船的合速度垂直于河岸时，渡河位移（航程或路径）最小并等于河宽。
在v 船<v 水的条件下，当船头与船的合速度垂直时，渡河位移（航程或路径）最小。
此种情况下，合速度不可能垂直于河岸，无法垂直渡河。
最短航程确定如下:如图所示，以v 水矢量末端为圆心，以v 船矢量的大小为半径画弧，从v 水矢量的始端向圆弧作切线，则合速度沿此切线方向航程最短。
（下图中v 1表船速，v 2表水速）③最小渡河速度：水速和航向一定，船速垂直航向有最小船速。
【典型题例】两河岸平行，河宽d=100m ，水流速度v 1=3m/s ，求：（1）船在静水中的速度是4m/s 时，欲使船渡河时间最短，船应怎样渡河？最短时间是多少？船的位移是多大？（2）船在静水中的速度是6m/s 时，欲使船航行距离最短，船应怎样渡河？渡河时间多长？（3）船在静水中的速度为1.5m/s 时，欲使船渡河距离最短，船应怎样渡河？船的最小航程是多少？[思路分析]（1）当船头垂直于河岸时，渡河时间最短：t min =d/v 2=100/4=25s 合速度v=s m v v /543222221=+=+ 船的位移大小s=v t min =125m（2）欲使船航行距离最短，需船头向上游转过一定角度使合速度方向垂直于河岸，设船的开行速度v 2与岸成θ角，则cosθ=216321==v v ， 所以θ=600，合速度v=v 2sin600=3s m /3 t=s v d 93100=（3）船在静水中速度小于水流的速度，船头垂直于合速度v 时，渡河位移最小， 设船头与河岸夹角为β，如图所示： cosβ=2135.112==v v 所以β=600 最小位移s min =m d 20060cos 100cos 0==β [答案](1) 船头垂直于河岸时，渡河时间最短：t min =25s ，s =125m ；(2) 船头向上游转过一定角度, 与岸成600角航程最短，t=s 93100； (3) 船头垂直于合速度,船头与河岸夹角600时航程最短，s min =m 200。
高考物理计算题复习《小船渡河问题》(解析版)
《小船渡河问题》一、计算题1.河宽d=60m，水流速度v1=3m/s，小船在静水中的速度v2=6m/s，问：(1)要使它渡河的时间最短，则小船应如何渡河？最短时间是多少？(2)要使它渡河的航程最短，则小船应如何渡河？最短的航程是多少？(3)若水流速度变为v3=10m/s，要使它渡河的航程最短，则小船应如何渡河？最短的航程是多少？2.如图所示，一条小船位于d=200m宽的河正中A点处，从这里向下游100√3m处有一危险区，当时水流速度为V1=4m/s，(1)若小船在静水中速度为V2=5m/s，小船到岸的最短时间是多少？(2)若小船在静水中速度为V2=5m/s，小船以最短的位移到岸，小船船头与河岸夹角及所用时间？(3)为了使小船避开危险区沿直线到达对岸，小船在静水中的速度至少是？3.一条河宽100m，水流速度为3m/s，一条小船在静水中的速度为5m/s．(1)若要小船过河的时间最短，则船头应该指向哪里？过河的最短时间是多少⋅来表示)，小船需用多长时间到达对岸？(sin300=0.5,sin370=0.6,sin450=0.707)4.河宽d=100m，水流速度v1=3m/s，船在静水中的速度是v2=4m/s，求：(1)欲使船渡河时间最短，最短时间是多少？(2)欲使船航行距离最短，渡河时间多长？5.一小船从河岸的A点出发渡河，小船船头保持与河岸垂直方向航行，经过10min到达河对岸B点下游120m的C处，如图所示。
如果小船保持原来的速率逆水斜向上游与河岸成α角方向航行，则经过12.5min恰好到达正对岸的B处。
求：(1)水流速度；(2)河的宽度。
6.如图所示，河宽d=120m，设船在静水中的速度为v1，河水的流速为v2，小船从A点出发，在渡河时，若出发时船头指向河正对岸的B点，经过8min小船到达B点下游的C点处；若出发时小船保持原来的速度逆水向上与河岸成α角方向行驶，则小船经过10min恰好到达河正对岸的B点。
高中物理小船渡河问题与关联速度问题(解析版)
小船渡河问题与关联速度问题一、小船过河问题1．船的实际运动是水流的运动和船相对静水的运动的合运动。
2．三种速度：船在静水中的速度v 1、水的流速v 2、船的实际速度v 。
3．三种情况(1)渡河时间最短：船头正对河岸，渡河时间最短，t min ＝dv 1(d 为河宽)。
(2)渡河路径最短(v 2＜v 1时)：合速度垂直于河岸，航程最短，x min ＝d 。
(3)渡河路径最短(v 2＞v 1时)：合速度不可能垂直于河岸，无法垂直河岸渡河。
确定方法如下：如图所示，以v 2矢量末端为圆心，以v 1矢量的大小为半径画弧，从v 2矢量的始端向圆弧作切线，则合速度沿此切线方向航程最短。
由图可知sin θ＝v 1v 2，最短航程x min ＝d sin θ＝v 2v 1d 。
4. 解题思路5. 解题技巧(1)解决小船渡河问题的关键是：正确区分分运动和合运动，船的航行方向也就是船头所指方向的运动，是分运动，船的运动也就是船的实际运动，是合运动，一般情况下与船头指向不共线。
(2)应用运动分解的基本方法，按实际效果分解，一般用平行四边形定则沿水流方向和船头指向分解。
(3)渡河时间只与垂直河岸的船的分速度有关，与水流速度无关。
(4)求最短渡河位移时，根据船速v 船与水流速度v 水的大小情况，用三角形定则求极限的方法处理。
【典例1】一小船渡河，河宽d ＝180 m ，水流速度v 1＝2.5 m/s 。
若船在静水中的速度为v 2＝5 m/s ，则： (1) 欲使船在最短时间内渡河，船头应朝什么方向？用多长时间？位移是多少？(2) 欲使船渡河的航程最短，船头应朝什么方向？用多长时间？位移是多少？【典例2】如图所示，河水由西向东流，河宽为800 m，河中各点的水流速度大小为v水，各点到较近河岸的距离为x，v水与x的关系为v水＝3400x(m/s)(x的单位为m)，让小船船头垂直河岸由南向北渡河，小船划水速度大小恒为v船＝4 m/s，则下列说法正确的是()A．小船渡河的轨迹为直线B．小船在河水中的最大速度是5 m/sC．小船在距南岸200 m处的速度小于在距北岸200 m处的速度D．小船渡河的时间是160 s【答案】B【跟踪短训】1. (多选)下列图中实线为河岸，河水的流动方向如图v的箭头所示，虚线为小船从河岸M驶向对岸N 的实际航线．则其中可能正确的是()．【答案】AB【解析】船头垂直于河岸时，船的实际航向应斜向右上方，A正确，C错误；船头斜向上游时，船的实际航向可能垂直于河岸，B正确；船头斜向下游时，船的实际航向一定斜向下游，D错误．2. 如图所示，甲、乙两同学从河中O点出发，分别沿直线游到A点和B点后，立即沿原路线返回到O 点，OA、OB分别与水流方向平行和垂直，且OA＝OB.若水流速度不变，两人在静水中游速相等，则他们所用时间t甲、t乙的大小关系为()．A．t甲<t乙B．t甲＝t乙C．t甲>t乙D．无法确定【答案】 C【解析】设两人在静水中游速为v0，水速为v，则t甲＝x OAv0＋v＋x OAv0－v＝2v0x OAv20－v2t乙＝2x OBv20－v2＝2x OAv20－v2<2v0x OAv20－v2故A、B、D错，C对．3. 一小船在静水中的速度为3 m/s，它在一条河宽为150 m，水流速度为4 m/s的河流中渡河，则该小船()．A．能到达正对岸B．渡河的时间可能少于50 sC．以最短时间渡河时，它沿水流方向的位移大小为200 mD．以最短位移渡河时，位移大小为150 m【答案】 C4．船在静水中的速度与时间的关系如图甲所示，河水的流速随离一侧河岸的距离的变化关系如图乙所示，经过一段时间该船以最短时间成功渡河，下列对该船渡河的说法错误的是()A．船在河水中的最大速度是5 m/sB．船渡河的时间是150 sC．船在行驶过程中，船头必须始终与河岸垂直D ．船渡河的位移是13×102 m 学-科/网 【答案】B【解析】 由题图乙可知，水流的最大速度为4 m/s ，根据速度的合成可知，船在河水中的最大速度是5 m/s ，选项A 正确；当船头始终与河岸垂直时，渡河时间最短，有t ＝d v ＝3003 s ＝100 s ，因此船渡河的时间不是150 s ，选项B 错误，C 正确；在渡河时间内，船沿水流方向的位移x 在数值上等于水流速度与时间图像所围成的面积大小，根据速度变化的对称性可得x ＝4×1002 m ＝200 m ，再根据运动的合成与分解可得，船渡河的位移为13×102 m ，选项D 正确。
《小船渡河问题》课件
当船速和水速垂直时，实际航线偏离最小，此时渡河时间最短。
03
渡河问题的解决方案
船头垂直于河岸渡河
船头垂直于河岸时，船的合速度方向即为船头指向，与河岸垂直。此时，船渡河时 间最短，但船的位移不是最小。
船渡河时间等于河宽除以船在静水中的速度。
船的位移等于船在静水中的速度与水流速度的合速度在垂直于河岸方向上的投影。
科学实验中的应用
物理实验
在流体力学实验中，渡河问题常常被用来模拟和研究流体动力学现象，如水流的阻力、流速等问题。
生物学实验
在生态学研究中，渡河问题也被用来模拟和研究物种迁移、基因传播等现象，帮助科学家理解生物多 样性的形成和演化。
05
小船渡河问题的思考与启示
小船渡河问题中的哲学思考
自然规律的客观性
水速对渡河的影响
水速越大，实际航线偏离越少
当水速大于船速时，船头斜向下游，实际航线偏离越少。
水速越小，实际航线偏离越多
当水速小于船速时，船头垂直河岸，实际航线偏离越多。
船速与水速的相互作用
船速与水速相等时，船头方向任意
当船速和水速相等时，船头方向可以任意选择，渡河时间不变。
船速与水速垂直时，实际航线偏离最小
战术部署
在军事行动中，渡河点常常成为重要 的战术支点。通过控制渡河点，可以 有效地分割敌军，实现各个击破。
日常生活中的应用
竹筏等水上工具的使 用，使得人们可以方便地渡过河 流。
救援行动
在洪涝灾害等紧急情况下，渡河 成为救援人员和受困群众的重要 通道，及时的救援可以大大降低 灾害损失。
船的渡河位移和时间都介于船 头垂直于河岸和船头斜向下游 之间。
在这种情况下，船的位移和时 间都大于船头垂直于河岸渡河 的情况。
小船渡河问题知识点总结
小船渡河问题知识点总结小船渡河问题通常涉及到数学逻辑、图论和排列组合等方面的知识。
解决这类问题需要玩家具备一定的数学逻辑能力，能够对问题进行分析、归纳和推理。
同时，还需要注意到一些常见的解题技巧和方法，比如状态空间搜索、限制条件推理和剪枝等。
以下是小船渡河问题的一些关键知识点总结：1. 状态空间搜索：小船渡河问题实质上是一个状态空间搜索问题。
在这个问题中，状态空间可以表示为一个状态图，其中每个节点代表一个状态，每条边代表一次渡河操作。
玩家需要通过搜索状态空间，找到一条能够满足所有条件的路径，使得所有的乘客都能够安全地渡河。
2. 限制条件推理：在解决小船渡河问题时，通常会存在一些限制条件，比如小船的容量、乘客之间的矛盾关系等。
玩家需要通过对这些限制条件进行推理和分析，找到一种合理的解决方法。
通常可以利用逻辑推理或者排除法，逐步缩小解空间，从而找到一个满足所有条件的解答。
3. 剪枝技巧：在搜索状态空间时，通常会遇到一些无效操作或者不必要的搜索路径。
玩家可以通过一些剪枝技巧，比如最优先搜索、启发式搜索等，来避免不必要的搜索，从而提高解题效率。
4. 数学逻辑：小船渡河问题还涉及到一些数学逻辑方面的知识，比如组合数学、排列组合等。
通过对乘客的数量、小船的容量等进行数学分析和推理，可以更好地理解和解决这类问题。
5. 图论知识：在某些小船渡河问题中，可以将问题建模为图论问题，通过图论的知识和方法来解决。
比如可以将渡河过程建模为一个图，通过图的遍历和路径搜索来解决问题。
总之，小船渡河问题是一个涉及到数学逻辑、图论和排列组合等知识点的经典问题。
通过掌握这些知识点和解题技巧，可以更好地理解和解决小船渡河问题，提高解题效率。
同时，这类问题也可以培养玩家的逻辑思维能力和解决问题的能力。
小船渡河问题分析及模型求解方法总结
小船渡河问题分析及模型求解方法总结小船渡河问题是著名的“搜索穷举”(searchforenumeration)问题。
在一条由南至北的河流上，有一艘小船，上面有三个乘客，分别是一个牧师、一个撒谎者和一个犯人，这三个乘客的目的地都不同，他们需要利用这艘小船才能跨越河流到达他们的目的地。
根据他们各自的特性，要求三个乘客同时搭乘小船时必须满足两个条件：1.师和犯人不能同时在船上；2.谎者不能和牧师在一起。
在小船渡河问题中，首先要考虑的是如何分析和分类其状态空间，即要建立一套有效的状态空间模型。
对于每一个节点状态，其状态可以通过三个乘客的位置来确定，可以用一个三元组(P,L,S)来代表，其中P表示牧师的位置，L表示犯人的位置，S表示撒谎者的位置。
根据这种状态空间模型，小船渡河问题可以抽象成一棵带有深度限制的有向无环图，其节点表示可能的状态，边表示可能的操作策略，从而将问题转化为深度优先搜索的问题。
深度优先搜索法是小船渡河问题最常用的求解方法。
它是一种搜索穷举策略，即按照状态节点深度的增加顺序，从根节点出发，沿着有向无环图中的路径穷举所有可能的状态结果，最终找到满足要求的解所在的路径，从而解决问题。
具体的操作步骤如下：1.从源节点出发，并将其放入一个“搜索表”中；2.从“搜索表”中取出节点，将其扩展出所有可能的子节点，并将其放入搜索表中；3.重复上述过程，直到搜索表为空；4.根据最终节点是否满足目标条件，通过搜索表中记录的父节点，得到最优解路径。
此外，在解决小船渡河问题时，可以采用一些其他的求解方法，比如蒙特卡洛方法和遗传算法。
蒙特卡洛方法是一种模拟技术，通过仿真模拟大量的实验，最终得到预期的结果，可以有效地求解小船渡河的最优解路径。
而遗传算法则是一种仿生搜索算法，它采用“选择”、“交叉”、“突变”等“进化”过程，将复杂问题转化为数学优化问题，可以有效地求解出最优解路径。
综上所述，小船渡河问题是一个典型的“搜索穷举”问题，可以通过有效构建状态空间模型并采用深度优先搜索法、蒙特卡洛方法和遗传算法等方法求解。
《小船渡河问题》 说课稿
《小船渡河问题》说课稿尊敬的各位评委、老师：大家好！今天我说课的题目是《小船渡河问题》。
下面我将从教材分析、学情分析、教学目标、教学重难点、教法与学法、教学过程、板书设计这几个方面来展开我的说课。
一、教材分析“小船渡河问题”是高中物理运动学中的一个重要模型，它涉及到运动的合成与分解这一重要知识点。
在教材中，这一内容通常安排在运动的合成与分解之后，通过对小船渡河问题的研究，能够帮助学生进一步理解和掌握运动的合成与分解规律，培养学生的物理思维能力和解决实际问题的能力。
这部分内容不仅在高中物理中具有重要地位，也为学生后续学习平抛运动、圆周运动等知识奠定了基础。
二、学情分析学生在学习本节课之前，已经掌握了位移、速度、加速度等基本物理量，以及矢量的合成与分解法则。
但是，对于如何将实际问题转化为物理模型，如何运用运动的合成与分解规律来解决问题，学生还存在一定的困难。
此外，学生在数学运算和逻辑推理方面的能力还有待提高，这可能会影响他们对小船渡河问题的分析和求解。
三、教学目标1、知识与技能目标（1）学生能够理解小船渡河问题中合运动与分运动的关系。
（2）掌握小船渡河的最短时间和最短位移的求解方法。
2、过程与方法目标（1）通过对小船渡河问题的分析和讨论，培养学生的物理建模能力和逻辑推理能力。
（2）让学生经历从实际问题中抽象出物理模型的过程，提高学生运用数学知识解决物理问题的能力。
3、情感态度与价值观目标（1）激发学生学习物理的兴趣，培养学生的科学探索精神。
（2）让学生体会物理知识与实际生活的紧密联系，增强学生学以致用的意识。
四、教学重难点1、教学重点（1）小船渡河问题中合运动与分运动的关系。
（2）小船渡河最短时间和最短位移的求解方法。
2、教学难点（1）如何引导学生正确地将小船的运动分解为沿河岸方向和垂直河岸方向的两个分运动。
（2）当船头方向不同时，小船渡河的位移和时间的变化规律。
五、教法与学法1、教法（1）讲授法：通过讲解和演示，让学生理解小船渡河问题的基本概念和求解方法。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
小船渡河的问题在高中物理教学中，往往遇到小船在水有一定流速的河中渡河的问题。
这类问题一般有小船渡河的时间最小，位移最小，速度最小三种情况：问题一：小船如何渡河时间最小，最小时间为多少？分析及解答：设河宽为d，小船在静水中的速度为V船，水流速度为V水，如图1中的甲。
将船对水的速度沿平行河岸方向和垂直河岸方向正交分解。
沿平行河岸方向的速度不影响渡河的快慢，小船渡过河时时间与垂直河岸方向的速度有关，当小船垂直河岸渡过河时时间最小，即最小时间为t min=d/V船。
[例题1]：河宽60m,小船在静水中的速度为4m/s,水流速度为3m/s。
求小船渡河的最小时间是多少，小船实际渡河的位移为多大？分析及解答：如图1中的乙，当小船垂直河岸渡过河时时间最小，即最小时间为t min=d/V船。
∴t min=d/V船=60/4=15(s)。
小船实际渡河的位移S AB=V合t min=5*15=75(m).问题二：小船如何渡河到达对岸的位移最小，最小位移是多少？分析及解答：在小船渡河过程中，将船对水的速度沿平行河岸方向和垂直河岸方向正交分解，如图2中的甲。
当小船沿平行河岸方向的分速度与水速大小相等，方向相反时，即V1=V水，小船的合速度（V2）就沿垂直河岸方向，这时渡河到达对岸的位移最小，S min=d。
而渡河时间t=d/V2=d/Vsinθ。
[例题2]：河宽60m,小船在静水中的速度为5m/s,水流速度为3m/s。
求小船渡河的最小位移是多少，小船实际渡河的时间为多大？分析及解答：如图2 中的乙，当小船沿平行河岸方向的分速度V1=V水，小船要垂直河岸方向渡河，这时渡河到达对岸的位移最小，Smin=d=60(m)。
而V船与河岸的夹角θ=arc cos(V船/V水)=530。
这时小船实际渡河的时间t=d/V2=d/V船sinθ=60/4=15(s).问题三：小船如何渡河速度最小，最小速度为多少？分析及解答：将小船渡河运动看作水流的运动（水冲船的运动）和小船相对静水的运动（设水流不流动时船的运动）的合运动。
如图3中的甲，要使小船沿直线从A运动到B，小船在静水中的最小速度为多少？根据运动的合成和平行四边形定则，当小船的速度垂直于AB直线时，船速最小，最小船速为V船=V水sinθ，船速与水速方向的夹角为900+arc sin(V船/V水)。
[例题3]：如图3的乙，一条小船位于100m宽的河岸A点处，从这里向下游100√3米处有一危险区，若水流速度为4m/s，为了使小船避开危险区沿直线到达对岸，小船在静水中的速度至少多大？分析及解答：为了使小船避开危险区沿直线AB到达对岸，则小船的合速度方向沿直线AB。
根据运动的合成和平行四边形定则，当小船的速度垂直于AB直线时，船速最小，最小船速为V船=V水sinθ。
由几何关系可知：tgθ=√3/3, θ=300。
∴V船=4*sin300=2(m/s).而船速与水速方向的夹角为900+arc sin(V船/V水)=1200。
方法解二：运动的合成与分解专题中，有一个重要类型题“小船渡河”问题，这类题目主要研究“船怎样行驶，渡河时间、渡河位移最短”。
教学实践中，我观察到许多学生是死记硬背记住结论，有时还混淆，怎样让学生利用运动的合成与分解规律理解渡河问题呢？我经过多届学生试验，摸索出一种浅显易懂的讲解方法。
例题：一条宽为d的河，水流速度为V1，船在静水中的速度为V2，那么（1）怎样渡河时间最短，最短时间为多少？（2）若V1＜V2，怎样渡河位移最小，最小位移为多少？（3）若V1 ＞V2，怎样渡河位移最小，最小位移为多少？（4）若V1 = V2，怎样渡河位移最小，最小位移为多少？一、渡河时间最短问题讲授之前，先复习合运动与分运动的关系，（等时性、独立性、等效性、运算法则为三角形定则），然后画图讲解，小船的运动方向可能有三种情况，一是沿河岸上游开船，如轨迹1、2、3，可能向河正对岸开船如轨迹4，可能向河岸下游开船如轨迹5、6、7，由于渡河时间t=S船/V船= S水/V水= S合/V合，而船渡河的分位移容易求，所以利用t=S船/V船计算简单，从船运动的分位移图中可知，当船头垂直正对岸开动时，船的分位移最短，渡河时间最短。
二、渡河位移最短问题首先分析渡河位移，是指船的实际位移，即合位移。
合位移的方向大致有三种，沿河岸上游、垂直河对岸、沿河岸下游，如图2，显然合位移为河宽时，渡河位移最短，而合位移方向即是合速度方向，假设水速方向向右，由三角形定则可知，船速方向应斜向上游某一角度θ，而且由几何关系知，船速只有大于水速时，合速度才可能指向正对岸，最短位移才可能为河宽。
此时cosθ= V水/ V船,从而求出θ。
当水速大于船速时，由三角形定则可知，两个分速度应该首尾相接，合速度由第一个矢量的始端指向第二个矢量的末端，船速的可能方向如图3，就像以水速末端为圆心，以船速为半径画的圆一样，对应的合速度方向如图4，由合速度的方向即为合位移方向可知，合位移方向如图4虚线，显然从水速始端做圆的切线时，合位移为最短。
此时船速与合速度垂直，船速方向仍应斜向上游某一角度θ，cosθ=V船 / V水，可求出θ，由几何关系可求最短位移Smin=d/ cosθ=d V水/ V船。
讲到这里，学生感觉好象船速大于水速与船速小于水速，求解最短位移的分析方法不同，我们应澄清这一错误认识。
我们再按三角形定则，在水速的末端做出船速的可能方向，找出对应的合速度、合位移方向，如图5，由图可知，当船速方向斜向上游某一角度θ，可以使合速度方向恰好指向河正对岸，渡河位移最短。
由此可见两种情况下的分析方法是完全一致的。
只是当船速大于水速时，采用第一种方法略微简单而已。
采用这种讲解方法，还可以轻松回答最棘手的问题-----船速等于水速时最短的渡河位移。
仍按三角形定则做图6，由图可知，船速方向与河岸上游的夹角越小，渡河位移就越短，最极限的状态为船速方向刚好与水速方向相反，这时最短渡河位移为河宽。
1、一条河宽100米，船在静水中的速度为4m/s ，水流速度是5m/s ，则：（ ）A. 该船可能垂直河岸横渡到对岸B. 当船头垂直河岸横渡时，过河所用的时间最短C. 当船头垂直河岸横渡时，船的位移最小是100米D. 当船横渡时到对岸时，船对岸的最小位移是100米2、在抗洪抢险中，战士驾驶摩托艇救人，假设江岸是平直的，洪水沿江向下游流去，水流速度为v 1，摩托艇在静水中的航速为v 2，战士救人的地点A 离岸边最近处O 的距离为d ，如战士想在最短时间内将人送上岸，则摩托艇登陆的地点离O 点的距离为：（ ） A. 21222v v dv - B. 0 C. 21v dv D. 12v dv 3、如右上图6-2-5所示，河水流速为v 一定，船在静水中的速度为v '，若船从A 点出发船头分别朝AB 、AC 方向划行到达对岸，已知划行方向与河的垂线方向夹角相等，两次的划行时间分别为t AB 、t AC ，则有：（ ）A ．t AB >t AC B ．t AB <t AC C ．t AB =t ACD ．无法确定4.某人以一定的速率垂直河岸将船向对岸划去，当水流匀速时，关于它过河需时间，发生的位移与水速的关系是：（ ）A.水速小时，位移小，时间不变B.水速大时，位移大，时间长C.水速大时，位移大，时间不变D.位移，时间与水速无关5.一条机动船载客渡河,若其在静水中的速度一定,河水的流速也不变,且V 船>V 水,则：（ ）A.船垂直到达对岸,渡河最省时B.使船身方向垂直于河岸, 渡河最省时C.船沿垂直河岸的轨迹, 渡河路程最短D.使船身方向垂直于河岸, 渡河路程最短5．物体受到几个力的作用而做匀速直线运动，如果只撤掉其中的一个力，其它力保持不变，它可能做( )A .匀速直线运动B .匀加速直线运动C .匀减速直线运动D .曲线运动7．关于运动和力，下列说法中正确的是（ ）A ．物体受到恒定合外力作用时，一定做匀变速直线运动B ．物体受到变化的合外力作用时，它的运动速度大小一定变化C ．物体做曲线运动时，合外力方向一定与瞬时速度方向垂直D ．所有曲线运动的物体，所受的合外力一定与瞬时速度方向不在一条直线上8．在向右匀速行驶的火车中，向后水平抛出一物体，在站在地面上的人看来，该物体的运动轨迹可能是图中的（ ） A ．A 、D 、E B ．B 、C 、D C ．C 、D 、E D ．A 、B 、C9．一物体由静止开始下落一段时间后，突然受到一恒定水平风力的影响，但着地前一小段时间风突然停止，则其运动轨迹的情况可能是图中的（ ）10．双人滑运动员在光滑的水平冰面上做表演，甲运动员给乙运动员一个水平恒力F ，乙运动员在冰面上完成了一段优美的曲线MN ，其速度方向v M 与v N 正好成90°角，则此过程中乙运动员受到甲运动员的恒力可能是图中的（ ）A ．F 1B ．F 2C ．F 3D ．F 4此过程中乙运动员的速度将（ ）A ．不断增大B ．不断减小C ．先增大后减小D ．先减小后增大11．（2010年江苏卷）如图所示，一块橡皮用细线悬挂于O 点，用铅笔靠着线的左侧水平向右匀速移动，运动中始终保持悬线竖直，则橡皮运动的速度A ．大小和方向均不变B ．大小不变，方向改变C ．大小改变，方向不变D ．大小和方向均改变12．（2001年全国卷）在抗洪抢险中，战士驾驶摩托艇救人，假设江岸是平直的，江水沿江向下游流去，水流速度为v 1，摩托艇在静水中的航速为v 2，战士救人的地点A离岸边最近处O 的距离为d ，如战士想在最短时间内将人送上岸，则摩托艇登陆的地点离O 点的距离为（ ）A ．22221dv v v -B ．0C ．12dv vD ．21dv v 13．（2009年广东卷）船在静水中的航速为v 1，水流的速度为v 2．为使船行驶到河正对岸的码头，则v 1相对v 2的方向应为（ ）14．如图所示，一条小船位于200m 宽的河正中A 点处，从这里向下游3100m 处有一危险区，当时水流速度为 4 m/s ，为了使小船避开危险区沿直线到达对岸，小船在静水中的速度至少是（ ）A ．334m/sB ．338m/s C ．2 m/s D ．4 m/s 上题中，若小船在静水中的速度为5m/s ，船到达对岸的最短时间为 ；到达对岸时距离危险区 m ，若使船能以最短位移到达对岸，船头与上游所成角度为 ，最短位移为 m ．15．如图所示，汽车以速度v 匀速行驶，当汽车到达P 点时，绳子与水平方向的夹角为θ，则物体M 的速度大小为__________．16．如图所示，水平面上有一物体，小车通过定滑轮用绳子拉它，在图示位置时，若小车的速度为v 1=5m/s ，则物体的瞬时速度v 2为多少？。