第三章题解a
(完整word版)现代控制理论习题解答(第三章)

第三章 线性控制系统的能控性和能观性01010( 1) A10 1B( 2) A 0 0 1 ,B 011024311113 10 1 1( 3) A0 10 1 0 3 0 , B00 ( 4) AB0 0 11 001211【解】:(1)11U c B AB 1 1, rankU c n 2 ,所以系统完全能控。
c 0 1 c(2)10 0 1 2U c B AB A 2B1 1 11 1 17前三列已经可使 rankU c n 3 ,所以系统完全能控(后续列元素不必计算) 。
(3)A 为约旦标准型, 且第一个约旦块对应的B 阵最后一行元素全为零, 所以系统不完全 能控。
(4)A 阵为约旦标准型的特殊结构特征, 所以不能用常规标准型的判别方法判系统的能控 性。
同一特征值对应着多个约旦块,只要是单输入系统,一定是不完全能控的。
可以求一下能控判别阵。
1213 1223B AB A 2B A 3B2 3 U c1 1 12 13 1 11 12 31111rankU c 2 ,所以系统不完全能控。
3 1110 10 0 x0 3 0x 0 0ux0 01x 0u (1)0 0 12(2)61161101yxy10 0x1 10解】:1)311 已知 A 0 30,B0 001220 0 D CB CAB CA 2B 0 0 前两列已经使 rank D CBCAB110 1 0 00 , C ,D1 1 0 0 031112CA B m2, 所以系统输出能控。
(2) 系统为能控标准型,所以状态完全能控。
又因输出矩阵 状态维数 n ,所以状态能控则输出必然能控。
C 满秩,且输出维数 m 小于1 0x0 01xx1 1 (1)2 43 ; (2) 1 x 0;011y1 1xyx12 12 1 0 4 0 0x0 20xx4 0x(3);(4)0 030 1y0 1 1x y11 4x解】:1)已知 A01 00 242-3-3 判断下列系统的能观性。
理论力学课后习题第三章解答

理论力学课后习题第三章解答3.1解 如题3.1.1图。
均质棒受到碗的弹力分别为,棒自身重力为。
棒与水平方向的夹角为。
设棒的长度为。
由于棒处于平衡状态,所以棒沿轴和轴的和外力为零。
沿过点且与轴平行的合力矩为0。
即:①②③ 由①②③式得:④ 又由于即⑤ 将⑤代入④得:图题1.3.11N ,2N G θl x y A z 0sin 2cos 21=-=∑θθN N F x0cos 2sin 21=-+=∑G N N Fyθθ0cos 22=-=∑θlG c N M i ()θθ22cos 1cos 22-=c l ,cos 2c r =θrc 2cos =θ3.2解 如题3.2.1图所示,均质棒分别受到光滑墙的弹力,光滑棱角的弹力,及重力。
由于棒处于平衡状态,所以沿方向的合力矩为零。
即①由①②式得:所以()cr c l 2224-=o图题1.3.21N 2N G y 0cos 2=-=∑G N Fyθ0cos 22cos 2=-=∑θθlG d N M z ld=θ3cos 31arccos ⎪⎭⎫ ⎝⎛=l d θ3.3解 如题3.3.1图所示。
棒受到重力。
棒受到的重力。
设均质棒的线密度为。
由题意可知,整个均质棒沿轴方向的合力矩为零。
3.4解 如题3.4.1图。
轴竖直向下,相同的球、、互切,、切于点。
设球的重力大小图题1.3.32AB i G ag ρ=1i G bgρ=2ρz ()BH BF G OD G M z --⋅=∑21sin θ=0sin cos 2sin 2=⎪⎭⎫ ⎝⎛--θθρθρa b gb a ga aba b 2tan 22+=θ图题1.3.4Ox A B C B C D为,半径为,则对、、三个球构成的系统来说,在轴方向的合力应为零。
即:①对于球,它相对于过点与轴平行的轴的合力矩等于零。
即:②由式得:3.5解 如题3.5.1图。
梯子受到地面和墙的弹力分别为,,受地面和墙的摩擦力分别为,。
大学物理第3章习题解答

第三章 刚体的定轴转动3-1掷铁饼运动员手持铁饼转动1.25圈后松手,此刻铁饼的速度值达到125-⋅=s m v 。
设转动时铁饼沿半径为R=1.0 m 的圆周运动并且均匀加速。
求: (1)铁饼离手时的角速度; (2)铁饼的角加速度;(3)铁饼在手中加速的时间(把铁饼视为质点)。
解:(1)铁饼离手时的角速度为(rad/s)250125===.//R v ω(2)铁饼的角加速度为)(rad/s 83925122252222..=⨯⨯==πθωα(3)铁饼在手中加速的时间为(s)628025251222..=⨯⨯==πωθt3-2一汽车发动机的转速在7.0s 内由2001min -⋅r 均匀地增加到3001min -⋅r 。
(1)求在这段时间内的初角速度和末角速度以及角加速度; (2)求这段时间内转过的角度和圈数;(3)发动机轴上装有一半径为r=0.2m 的飞轮,求它的边缘上一点在第7.0s 末的切向加速度、法向加速度和总加速度。
解:(1)初角速度为(rad/s)9206020020./=⨯=πω末角速度为(rad/s)3146030002=⨯=/πω角加速度为)(rad/s 9410792031420...=-=-=tωωα(2)转过的角度为)186(rad 1017172314920230圈=⨯=⨯+=+=..t ωωθ(3)切向加速度为)(m/s 388209412t ...=⨯==R a α法向加速度为)(m /s 10971203142422n ⨯=⨯==..R a ω总加速度为)(m/s 10971)10971(378242422n 2t ⨯=⨯+=+=...a a a总加速度与切向的夹角为9589378101.97arctan arctan 4t n '︒=⨯==.a a θ3-3 如图所示,在边长为a 的六边形顶点上分别固定有质量都是m 的6个小球(小球的直径a d <<)。
信号与线性系统题解第三章
第三章习题答案da3.1 计算下列各对信号的卷积积分()()()y t x t h t =*:(a) ()()()()t tx t e u t h t e u t αβ==(对αβ≠和αβ=两种情况都做)。
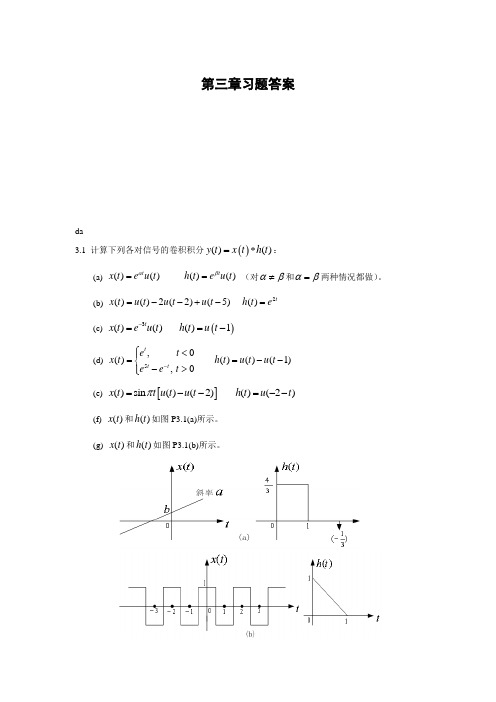
(b) 2()()2(2)(5)()tx t u t u t u t h t e =--+-=(c) ()3()()()1tx t eu t h t u t -==-(d) 5,0()()()(1),0tt t e t x t h t u t u t e e t -⎧<⎪==--⎨->⎪⎩(e) []()sin ()(2)()(2)x t t u t u t h t u t π=--=--(f) ()x t 和()h t 如图P3.1(a)所示。
(g) ()x t 和()h t 如图P3.1(b)所示。
图P3.1 解:(a) ()()0()()()(0)t ttty t x t h t eed eed t βτατβαβτττ------=*==>⎰⎰当αβ≠时,()1()()ttey t e u t αβββα----=-当αβ=时,()()t y t te u t α-=(b) 由图PS3.1(a)知, 当1t ≤时,252()2()22(2)2(5)021()22t t t t t y t ed ed e e e ττττ----⎡⎤=-=-+⎣⎦⎰⎰ 当13t ≤≤时,252()2()22(2)2(5)121()22t t t t t y t ed ed e e e ττττ-----⎡⎤=-=-+⎣⎦⎰⎰ 当36t ≤≤时,52()2(5)211()2t t t y t ed e e ττ---⎡⎤=-=-⎣⎦⎰ 当6t >时,()0y t =(c) 由图PS3.1(b)知,当1t ≤时,()0y t = 当1t >时,133(1)01()13t t y t ed e ττ----⎡⎤==-⎣⎦⎰3(1)1()1(1)3t y t e u t --⎡⎤∴=--⎣⎦(d) 由图PS3.1(d)知: 当0t ≤时,11()tt t t y t e d e eττ--==-⎰当01t <≤时,055(1)1014()(2)255t ttt t y t e d e e d e eeτττττ-----=+-=+--⎰⎰当1t >时,555(1)(1)111()(2)2255t tt tt t y t e ed eeeeτττ------=-=-+-⎰(e) 如下图所示:(f) 令()11()(2)3h t h t t δ⎡⎤=+--⎢⎥⎣⎦,则11()()()(2)3y t x t h t x t =*-- 由图PS3.1(h)知,11424()()()()(21)333t t y t x t h t a b d a t b ττ-=*=+=-+⎰2411()(21)(2)()3333a y t tb a t b a t b x t ∴=-+---=+= (g) ()x t 是周期信号,由此可推知()()()y t x t h t =*也是周期的,且周期也为2。
电工与电子技术之电工技术第三章课后题解

第3章 正弦交流电路的稳态分析本章的主要任务是学习正弦量、正弦交流电路和相量法的基本概念、正弦交流电路的稳态分析与计算、正弦交流电路功率的概念和计算。
在此基础上理解和掌握功率因数提高的意义,和谐振的概念。
本章基本要求(1) 正确理解正弦量和正弦交流电路概念; (2) 正确理解相量法引入的意义;(3) 正确理解有功功率和功率因数的概念; (4) 掌握相量法;(5) 掌握电路定律的相量形式和元件约束方程的相量形式; (6) 分析计算正弦稳态电路; (7) 了解功率因数提高的意义; (8) 了解谐振的概念。
本章习题解析3-1 已知正弦电压和电流的三角函数式,试用有效值相量表示它们,并画出它们的相量图。
(1))20sin(210 +=t i ωA ,)60sin(2150 +=t u ωV (2))20sin(28 -=t i ωA ,)45sin(2120 -=t u ωV (3))30sin(25 +=t i ωA ,)90sin(2100 +=t u ωV解 (1)︒∠=2010IA ,︒∠=60150U V ,相量图如图3-1(a )所示。
(2))20(10︒-∠=IA ,)45(120︒-∠=U V ,相量图如图3-1(b )所示 (3)︒∠=305IA ,︒∠=90100U V ,相量图如图3-1(c )所示3-2 已知电压、电流的相量表示式,试分别用三角函数式、波形图及相量1+j (a )1+(b )1+j(c )图3-1图表示它们。
(1)4030j U+= V ,43j I += A (2)100=UV ,43j I -= A (3)V 10045 j e U=,A 44j I +=解 (1))13.53(504030︒∠=+=j U=︒+︒13.53sin 5013.53cos 50j ,V )13.53(543︒∠=+=j I=︒+︒13.53sin 513.53cos 5j ,A 波形图相量图如图3-2(a )所示。
第三章部分习题解答
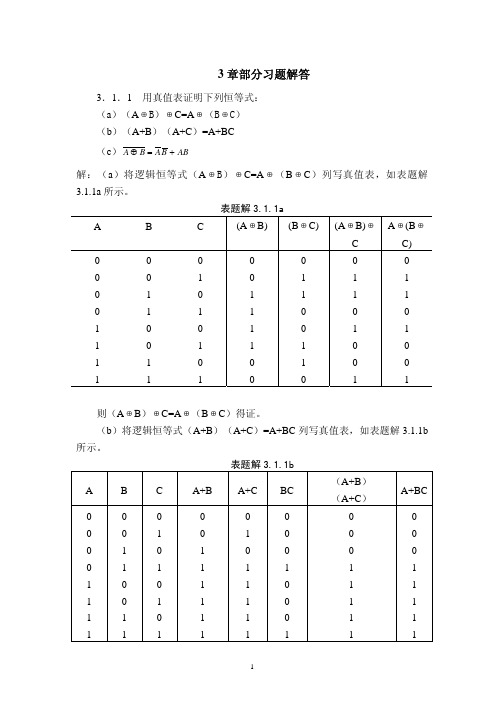
(b) ( A + B)(AB ) = AAB + BAB = AB
(c) ABC(B + C ) = ( A + B + C )(B + C ) = C + B( A + B ) = C + AB
(d) A + ABC + ABC + CB + CB = A(1 + BC + BC) + C(B + B ) = A + C
L3 = A3 ⊕ C
可分别用异或门、三态门设计逻辑电路,如图题解 3.4.4a、b 所示。
图题解 3.4.4
7
3.4.7 某雷达站有 3 部雷达 A、B、C,其中 A 和 B 功率消耗相等,C 的 功率是 A 的两倍。这些雷达由两台发电机 X 和 Y 供电,发电机 X 的最大输出功 率等于雷达 A 的功率消耗,发电机 Y 的最大输出功率是 X 的 3 倍。要求设计一 个逻辑电路,能够根据各雷达的启动和关闭信号,以最节约电能的方式启、停 发电机。
X = ABC + ABC + ABC + ABC = AB ⊕ C + B A ⊕ C
Y =AB+C 由逻辑表达式可设计出最节约电能的发电机启、停方式的逻辑电路,如图 题解 3.4.7b 所示。
表题解 3.4.7
A
B
C
X
Y
0
0
0
0
0
0
0
1
0
1
0
1
0
1
0
0
1
1
0
1
1
0
0
1
0
材料力学习题解答[第三章]
解:危险点在B截面的最上和最下面的两点上。
3-27图3-68为某精密磨床砂轮轴的示意图。已知电动机功率 ,转子转速 ,转子重量 。砂轮直径 ,砂轮重量 。磨削力 ,砂轮轴直径 ,材料为轴承钢。试表示危险点的应力方向,并求出危险点的应力大小。
解:矩形截面扭转
其中b=50mm,h/b=100/50=2,
3-18圆柱形密圈螺旋弹簧,簧丝横截面直径为 ,弹簧平均直径为 。如弹簧所受拉力 ,试求簧丝的最大切应力。
3-19试求图3-60中 杆横截面上的最大正应力。已知
, 。
扭弯组合
3-20矩形截面折杆 ,受图3-61所示的力F作用。已知 , 。试求竖杆内横截面上的最大正应力,并作危险截面上的正应力分布图。
解:(1)约束反力:
(2)各杆轴力
题3-3图
(3)各杆的正应力
3-4钢杆 直径为20mm,用来拉住刚性梁 。已知F=10kN,求钢杆横截面上的正应力。
解:
题3-4图
3-5图示结构中,1、2两杆的横截面直径分别为10mm和20mm,试求两杆内的应力。设结构的横梁为刚体。
解:取BC段分析, 题3-5图
取AB段分析:
题3-21图
所以:
最大压应力在槽底上各点:
(3)如果在左侧也开槽,则为轴心受压:
3-22图示短柱受载荷 和 作用,试求固定端角点A、B、C及D的正应力,并确定其中性轴的位置。
题3-22图
解:在ABCD平面上的内力:
横截面的几何特性:
应力计算:
中性轴方程为:
3-23图3-64所示为一简易悬臂式吊车架。横梁AB由两根10号槽钢组成。电葫芦可在梁上来回移动。设电动葫芦连同起吊重物的重量共重 。材料的 。试求在下列两种情况下,横梁的最大正应力值:(1)、只考虑由重量W所引起的弯矩影响;(2)、考虑弯矩和轴力的共同影响。
工程力学顾晓勤编著习题解答第三章
第三章 平衡方程的应用习题解析3—1静定多跨梁的荷载及尺寸如图3-1所示,长度单位为m ,求支座反力和中间铰处的压力。
图3-1 题3—1图解:a)按照约束的性质画静定多跨梁BC 段受力图(见图3-2),对于BC 梁由平衡条件得到如下方程:图3-2062021660cos ,0)(201=⨯⨯-⨯=∑=NC ni i B F F M ,kN 120=NC F060sin ,001=-=∑=NC Bx ni ix F F F , kN 9.10360sin 0==NC Bx F F060cos kN 620,001=+⨯-=∑=NC By ni iy F F F , kN F By 60=故支座反力C 反力kN 120=NC F ,方向垂直与支撑面;中间铰处B 的压力kN 9.103=Bx F 、kN 60=By F 。
如果同学有兴趣,可以进一步计算固定端A 约束反力,按照约束的性质画AB 段受力图(见图3-3),由作用反作用定律得'Bx F Bx F =kN 9.103=、'By F By F =kN 60=。
对于BC 梁由平衡条件得到如下方程:图3-3'1,0Bx Ax ni ix F F F ==∑=kN 9.103=01=∑=ni iy F , 'By Ay F F =kN 60=0340,0)('1=⨯-⋅-=∑=By A ni i A F m kN M F M ,A M m kN ⋅=220b) 按照约束的性质画静定多跨梁ABC 段、CD 段受力图(见图3-4),对于BC 梁由平衡条件得到如下方程:图3-40m kN 22.521m kN 54,0)(21=⋅⨯⨯-⋅-⨯=∑=ND ni i C F F M , m kN 5.2⋅=ND F0,01==∑=Cx ni ix F F0kN 25.2,01=+⨯-=∑=ND Cy ni iy F F F , kN 5.2=Cy F由作用反作用定律得'Cx F Cx F ==0、'Cy F Cy F =kN 5.2=。
线性代数第三章习题及解答
43
3 5 5
2 2 1 5 2 0 0 0 −1 1 0 0
−1 3 0
1
3
6. 设 α1 , α2 , . . . , αn 是一组 n 维向量,已知 n 维单位坐标向量 e1 , e2 , . . . , en 能由它们线性表示, 证明 α1 , α2 , . . . , αn 线性无关.
4 1 −1 1 −2 −22 1 −2 −1 3 6
−24 −11 3 −2 1 −2 −1 0 11 −→ 10 5 −20 0 0 0
10 0
5 9 1 T T 齐次方程的基础解系为 ξ1 = ( 21 11 , 11 , 1, 0) , ξ2 = (− 11 , 11 , 0, 1)
α4 = 8 α − α2 + 2α3 5 1 1 1 2 2 1 0 2 1 5 −1 (2) 3 2 0 3 −1 1 1 0 4 −1 1 1 2 2 1 1 1 0 2 1 5 −1 0 2 解: 2 0 3 −1 3 −→ 0 0 1 1 0 4 −1 0 0 α1 α2 α3 α4 α5 1 1 0 4 −1 1 0 0 1 0 1 0 3 −1 3 −→ 0 1 0 0 0 1 −1 1 0 0 1 −1 0 0 0 0 0 0 0 0 0 于是最大线性无关向量组之一为 α1 , α2 , α3 α4 = α1 + 3α2 − α3 , α5 = α3 − α2
T
− 20 83
5 83
− 17 83
注册会计师考试《审计》第三章经典题解
注册会计师考试《审计》第三章经典题解注册会计师考试《审计》第三章经典题解导语:参加注册会计师全国统一考试成绩合格,并从事审计业务工作二年以上的,可以向省、自治区、直辖市注册会计师协会申请注册。
下面和店铺来看看注册会计师考试《审计》第三章经典题解。
希望对大家有所帮助。
一、单项选择题1、下列有关审计证据的说法中,正确的是()。
A.外部证据与内部证据矛盾时,注册会计师应当采用外部证据B.审计证据不包括会计师事务所接受与保持客户或业务时实施质量控制程序获取的信息C.注册会计师可以考虑获取审计证据的成本与所获取信息的有用性之间的关系D.注册会计师无需鉴定作为审计证据的文件记录的真伪【答案】C【解析】选项A,如果从不同来源获取的审计证据或获取的不同性质的审计证据不一致,表明某项审计证据可能不可靠,注册会计师应当追加必要的审计程序,而不是直接信任外部证据;选项B,审计证据包括会计师事务所接受与保持客户或业务时实施质量控制程序获取的信息;选项D,审计工作通常不涉及鉴定文件记录的真伪,如果在审计过程中识别出的情况使其认为文件记录可能是伪造的,或文件记录中的某些条款已发生变动,注册会计师应当做出进一步调查。
2、确定审计证据的相关性时,下列表述中错误的是()。
A.特定的审计程序可能只为某些认定提供相关的审计证据,而与其他认定无关B.只与特定认定相关的审计证据并不能替代与其他认定相关的审计证据C.针对某项认定从不同来源获取的审计证据存在矛盾,表明审计证据不存在说服力D.针对同一项认定可以从不同来源获取审计证据或获取不同性质的审计证据【解析】选项C是审计证据的可靠性,而不是审计证据的相关性。
同时,注册会计师从不同来源获取的审计证据或获取的不同性质的审计证据不一致,则表明某项审计证据可能不可靠,注册会计师应当追加必要的审计程序,不能直接认为审计证据不存在说服力。
【答案】C3、下列有关审计证据的表述中,不正确的是()。
A.如果被审计单位财务报表的重大错报风险越高,对审计证据的要求也越高B.注册会计师在获取审计证据时,应当考虑获取审计证据的`成本C.如果注册会计师从不同来源获取的不同审计证据相互矛盾时,注册会计师应当追加必要的审计程序D.如果注册会计师获取的审计证据质量越高,需要的审计证据数量可能越少【答案】B【解析】在获取审计证据时,只有满足了充分、适当的前提下,注册会计师才会考虑获取审计证据的成本。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0
+11.25
0
0
+12.5
+2.5 +9.5 0
+13.125 +24.275 +12.625 +13.75 0 +8.75
+7.5 +20 +2.5 -10
用对角线法评定: 用对角线法评定: 用最小区域法评定: 用最小区域法评定:
200 fBE = ×0.02×(20 +10) = 0.12mm =120µm 1000
形位公差习题答案
试将下列各项形位公差要求标注在图3 3-l 试将下列各项形位公差要求标注在图3-73 上。 圆柱面对φ40H7孔轴线的径向圆跳动公差为0.018mm φ40H7孔轴线的径向圆跳动公差为0.018mm; ①φ100h8 圆柱面对φ40H7孔轴线的径向圆跳动公差为0.018mm; 右两凸台端面对φ40H7孔轴线的端面圆跳动公差均为0.012mm φ40H7孔轴线的端面圆跳动公差均为0.012mm; ②左、右两凸台端面对φ40H7孔轴线的端面圆跳动公差均为0.012mm; 轮毂键槽中心平面对φ40H7孔轴线的对称度公差为0.02mm φ40H7孔轴线的对称度公差为0.02mm。 ③ 轮毂键槽中心平面对φ40H7孔轴线的对称度公差为0.02mm。
形位公差习题答案
试将下列各项形位公差要求标注在图3 75上 3-3 试将下列各项形位公差要求标注在图3-75上。 圆锥面A 的圆度公差为0.006mm 0.006mm; ① 圆锥面A 的圆度公差为0.006mm; 圆锥面A 的素线直线度公差为0.005mm 0.005mm; ② 圆锥面A 的素线直线度公差为0.005mm; 圆锥面A 的轴线对φd圆柱面轴线的同轴度公差为0.01mm φd圆柱面轴线的同轴度公差为0.01mm; ③ 圆锥面A 的轴线对φd圆柱面轴线的同轴度公差为0.01mm; φd圆柱面的圆柱度公差为0.015mm; 圆柱面的圆柱度公差为0.015mm ④φd圆柱面的圆柱度公差为0.015mm; 右端面B对 圆柱面轴线的端面圆跳动公差为 圆柱面轴线的端面圆跳动公差为0.01mm。 ⑤ 右端面 对φd圆柱面轴线的端面圆跳动公差为 。
形位公差习题答案
形位公差习题答案
3-4试将下列各项形位公差要求标注在图3-76 上。 试将下列各项形位公差要求标注在图3 16mm键槽中心平面对 键槽中心平面对φ55k6 圆柱面轴线的对称度公差为0.012mm 0.012mm; ① 16mm键槽中心平面对φ55k6 圆柱面轴线的对称度公差为0.012mm; φ55k6圆柱面 圆柱面、 圆柱面和φ80G7孔分别对φ65k6圆柱面和φ75k6 φ80G7孔分别对φ65k6圆柱面和 ②φ55k6圆柱面、φ60r6 圆柱面和φ80G7孔分别对φ65k6圆柱面和φ75k6 圆柱面的公共轴线的径向圆跳动公差皆为0.025mm 0.025mm; 圆柱面的公共轴线的径向圆跳动公差皆为0.025mm; 平面F的平面度公差为0.02mm 0.02mm; ③平面F的平面度公差为0.02mm; 平面F 圆柱面和φ75k6 φ75k6圆柱面的公共轴线的端面圆跳动公差为 ④平面F对φ65k6 圆柱面和φ75k6圆柱面的公共轴线的端面圆跳动公差为 0.04mm; 0.04mm; 10×20P8孔 均布) φ65k6圆柱面和φ75k6圆柱面的公共轴线 圆柱面和φ75k6圆柱面的公共轴线〔 ⑤10×20P8孔(均布)对φ65k6圆柱面和φ75k6圆柱面的公共轴线〔第一 基准)及平面F 第二基准)的位置度公差为φ0.5mm φ0.5mm。 基准)及平面F(第二基准)的位置度公差为φ0.5mm。
x = −1.25, y = 5.625
fMZ
7.5 + y = −10 + x + 2y = 2.5 + 2x
200 = ×0.02×24.375 = 0.0975mm = 97.5µm 1000
形位公差习题答案
82所示轴套的四种标注方法 所示轴套的四种标注方法, 3-11 图3-82所示轴套的四种标注方法,试分析说明它们所表示的要求有何 不同?填入表3 33内 不同?填入表3-33内。
T形∠t位 形 位
形位公差习题答案
形位公差习题答案
形位公差习题答案
用水平仪按节距法测量有效长度为2000mm 的车床导轨的直线度误差。 3-7 用水平仪按节距法测量有效长度为2000mm 的车床导轨的直线度误差。所用 水平仪的分度值为0.01mm/ 桥板跨距为250mm 测点共九个。 250mm, 水平仪的分度值为0.01mm/ m ,桥板跨)依次为0,+ l , + 1 , O ,-1 , -1.5 ,十1 , +0.5 , + 1.5 。试按 最小条件和用两端点连线法作图求解该导轨的直线度误差值 fMZ 和 fBE 。
图序 a b c d
采用的公差原则 或公差要求 包容要求 最大实体要求 最小实体要求 独立原则
孔为最大实体尺寸 时的形位公差值 0 Φ0.05 Φ0.18 Φ0.05
孔为最小实体尺寸时 允许的形位误差值 Φ0.13 Φ0.18 Φ0.05 Φ0.05
理想边界名称、边界尺寸 最大实体边界Φ20 最大实体实效边界 19.95 最小实体实效边界Φ20.18 无边界
形位公差习题答案
用最小区域法评定: 用最小区域法评定:
fMZ
2.5 − 2 f = 2+ ×3+ 0.5 = 2.75 格 ( ) 6 250 = ×0.01×2.75 = 0.006875mm = 6.875µm 1000
形位公差习题答案
用分度值为0.02mm/m 的水平仪测量一工件表面的平面度误差。 3-9 用分度值为0.02mm/m 的水平仪测量一工件表面的平面度误差。按网 格布线,共测九点,如图3 80( 所示。 方向和y 格布线,共测九点,如图3-80(a)所示。在x 方向和y方向测量所用桥板的 跨距皆为200mm 各测点的读数( 200mm, 见图3 )。 跨距皆为200mm,各测点的读数(格)见图3-80( b )。试按最小条件和对 角线法分别评定该被测表面的平面度误差值。 角线法分别评定该被测表面的平面度误差值。
点序 0 1 +1 +1 2 +1 +2 3 0 +2 4 -1 +1 5 -1.5 -0.5 6 +1 +0.5 7 +0.5 +1 8 +1.5 +2.5 读数 (格) 0 累计(格) 0
用两端点法评定: 用两端点法评定:
2.5 2.5 f = 2 − ×2 + ×5 + 0.5 = 3.4375(格 ) 8 8 250 fBE = ×0.01×3.43750 = 0.00859mm = 8.59µm 1000
试将下列各项形位公差要求标注在图3 74上 3-2 试将下列各项形位公差要求标注在图3-74上。 两个φd孔的轴线分别对它们的公共轴线的同轴度公差均为0.02mm φd孔的轴线分别对它们的公共轴线的同轴度公差均为0.02mm; ①两个φd孔的轴线分别对它们的公共轴线的同轴度公差均为0.02mm; φD孔的轴线对两个φd孔公共轴线的垂直度公差为0.01mm; 孔的轴线对两个φd孔公共轴线的垂直度公差为0.01mm ②φD孔的轴线对两个φd孔公共轴线的垂直度公差为0.01mm; φD孔的轴线对两个φd孔公共轴线的对称度公差为0.03mm。 孔的轴线对两个φd孔公共轴线的对称度公差为0.03mm ③ φD孔的轴线对两个φd孔公共轴线的对称度公差为0.03mm。
形位公差习题答案
题3-4 题3-4
形位公差习题答案
试指出图3 78( )(b)(c 中形位公差标注的错误,并加以改正( 3-6 试指出图3-78(a)(b)(c)中形位公差标注的错误,并加以改正(形位 公差特征项目不允许变更,正确的形位公差标注不要修改)。 公差特征项目不允许变更,正确的形位公差标注不要修改)。
