基于车辆稳态动力学特性的汽车动态轨迹规划_孙浩
基于Attention机制和递归思想的LSTM车辆轨迹预测
基于Attention机制和递归思想的LSTM车辆轨迹预测作者：张恒陈焕明党步伟王继贤来源：《青岛大学学报（工程技术版）》2024年第02期摘要：针对现有车辆轨迹预测模型在长时预测方面准确性不足的问题，基于Attention机制和递归思想的长短时记忆网络（long short-term memory， LSTM）构建了一种新型的车辆轨迹预测模型，即ATT-LSTM（RE）模型，使用编码器–解码器架构更精确地预测车辆未来的行驶轨迹。
研究结果表明，模型意图识别的准确率为91.7％，F1分数、召回率、精确率均在0.872 ～0.977之间；1 s、2 s、3 s、4 s、5 s的终点轨迹预测的均方根误差为0.52 m、1.07 m、1.69 m、2.58 m、3.31 m，优于同类型模型。
关键词：车辆轨迹预测；意图识别；长短时记忆网络； Attention机制；递归思想中圖分类号：TP391.41文献标识码： A文章编号： 10069798（2024）02007409； DOI： 10.13306/j.10069798.2024.02.011收稿日期： 20240402; 修回日期： 20240515基金项目：山东省高等学校科技计划项目（J18KA048）第一作者：张恒（1998 ），男，硕士研究生，主要研究方向为车辆系统动力学仿真与控制。
通信作者：陈焕明（1978 ），男，博士，副教授，主要研究方向为车辆系统动力学仿真与控制。
Email：*************.cn随着科技的进步和人们生活水平的提高，汽车已成为日常生活中不可或缺的交通工具。
为了提升驾驶安全性和稳定性，准确识别驾驶员的驾驶意图及精确预测车辆行驶轨迹变得至关重要。
对车辆轨迹的预测方法有两种：基于模型建模和基于数据驱动。
基于模型建模的轨迹预测方法多通过建立车辆运动学或动力学模型，依托各种参数间的数学关系来预测车辆的行驶轨迹［1］，如利用恒定角速度和加速度模型并结合意图识别的多项式轨迹规划来预测车辆轨迹［2］。
一种二自由度汽车运动微分方程的推导方法
《一种二自由度汽车运动微分方程的推导方法》
一、引言
二自由度汽车运动微分方程是汽车模式的基础，能够准确描述汽车的运动特性，是汽车控制中的重要参数。
本文通过对二自由度汽车运动的基本原理进行推导，探讨二自由度汽车运动微分方程的推导方法。
二、基本原理
二自由度汽车运动模型是汽车模型的基本框架，它考虑了汽车本身的动力学特性和运动轨迹的交互作用。
根据牛顿第二定律，汽车的运动状态可以用方程来描述，即汽车的运动微分方程。
三、推导方法
（1）在汽车运动模型中，首先根据牛顿第二定律推导出汽车的运动方程，即汽车的运动微分方程。
（2）然后，利用经典的Lagrange方程，可以求出汽车的质心速度和质心加速度，以及汽车的速度和角速度：
（3）最后，根据几何关系，可以求出汽车的位置和角度，从而得到汽车的运动微分方程。
四、结论
本文通过对二自由度汽车运动的基本原理进行推导，探讨了一种二自由度汽车运动微分方程的推导方法。
结果表明，在推导汽车运动微分方程时，需要充分考虑汽车的动力学特性、运动轨迹特性以及几何关系。
汽车轨迹跟踪模型预测控制的加速求解方法
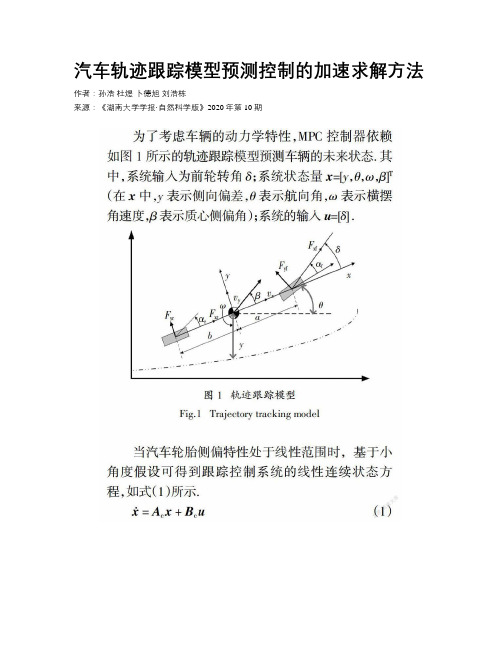
汽车轨迹跟踪模型预测控制的加速求解方法作者：孙浩杜煜卜德旭刘浩栋来源：《湖南大学学报·自然科学版》2020年第10期摘要：针对汽车轨迹跟踪模型预测控制求解中存在的规模较大、求解效率较低的问题，提出一种基于时域分解的加速计算方法提高求解效率. 首先引入全局一致性变量，将模型预测控制中邻接控制周期的时域耦合约束转化为全局一致性约束，实现时域解耦;随后在交叉方向乘子法框架下推导了时域分解后优化问题的分块更新方法，并设计了分块更新数值求解问题的停止准则，从而将大规模优化问题转化为小规模子问题;最后搭建了Simulink-CarSim平台进行了算法的仿真验证. 仿真结果表明，在求解精度不变的情况下，求解耗时下降24.21%，从而实现模型预测控制问题的加速求解.关键词：模型预测控制;自动驾驶汽车;轨迹跟踪;交叉方向乘子法;时域分解中图分类号：U461.99 文献标志码：AAccelerated Solution Method for Vehicle TrajectoryTracking Based on Model Predictive ControlSUN Hao1，2，DU Yu1，2†，BU Dexu3，LIU Haodong1，2（1. Beijing Key Laboratory of Information Service Engineering，Beijing Union University，Beijing 100101，China;2. College of Robotics，Beijing Union University，Beijing 100027，China;3. College of Traffic and Transportation Engineering，Central South University，Changsha 410076，China）Abstract：To solve the problems of large scale and low efficiency in the solution of intelligent vehicle trajectory tracking algorithm based on model predictive control，this paper proposes a time-domain splitting method to accelerate the calculation. First，global consistency variables are introduced to transform the time-domain coupling constraints of the adjacent control cycles into global consistency constraints，thus to achieve time-domain decoupling. Then，under the framework of Alternating Direction Method of Multipliers，the block updating method of optimization problem after time domain splitting is derived，and the stop criterion of block updating numerical solution is designed. Therefore，the large-scale optimization problem is converted into several small-scale sub-problems. Finally，the Simulink-CarSim platform is set up and the algorithm is verified by simulation. The simulation results show that，under the same accuracy of the solution，the efficiency of solution is improved by 24.21% on average with the proposed method，achieving accelerated solution for vehicle trajectory tracking based on model predictive control.Key words：model predictive control; autonomous vehicles; path tracking; alternating direction method of multipliers; time splitting自動驾驶汽车是提高交通系统安全、效率、经济等性能的有效途径，而轨迹跟踪是实现智能驾驶的核心技术之一[1]，其目标是在满足汽车复杂动力学约束、行驶安全性约束前提下，以较小的偏差、较高的舒适性跟踪所规划的轨迹[2]. 模型预测控制（ModelPredictive Control，MPC）最早被应用在成本不敏感的大型工程中（如化工产业），并被认为是当年最具影响力的现代控制算法之一[3]. MPC通过引入参考模型，对约束的处理直接简单，不仅能够有效处理被控模型特性、约束带来影响，还能够通过滚动求解优化问题找到当前的最优控制量[4].基于上述优点，MPC在汽车轨迹跟踪问题的研究中得到国内外研究者的广泛关注.求解MPC问题的主流思路是将其转化为二次规划（Quadratic Programming，QP）问题. 其中，无约束MPC求解相对简单. Xu等以跟踪误差为性能指标实现AGV的轨迹跟踪控制[5]，Shen等则建立了综合考虑跟踪精度和舒适性的目标函数[6]，也有研究将输入量的边界建模为目标函数中代价值，构成“软约束”，但其数学原问题仍是无约束二次规划. 无约束二次规划问题可通过梯度下降等方法直接求解，但其局限在于仅考虑车辆的运动及动力学约束，没有考虑运动过程中所受到的其它约束，局限性较强. 因此，约束MPC更具备实际意义. 如Bo等建立了基于动力学的增量模型，考虑了执行机构的动力学特性约束[7]; Cai等则通过4自由度车辆模型加入车辆运动的侧翻约束，提高车辆跟踪控制的安全性[8]. 约束MPC的数学原问题是约束QP问题（MPC-QP问题），需要通过数值优化方法计算求解. 求解约束二次规划问题主要采用主动集法、内点法等方法，迭代次数较多. Wang和Boyd的研究表明，对于状态维数为m、控制输入维数为n、求解时域为T的MPC问题，状态转移形式及控制输入形式的MPC-QP问题求解的时间复杂度分别为O（[T（n+m）]3）和O（[Tn]3）[9]. 综上，虽然MPC在轨迹跟踪问题研究中得到广泛关注，但MPC-QP问题存在规模大、求解所需的浮点运算多、求解效率低的缺点，制约了MPC的性能. 因此，提高轨迹跟踪MPC问题的求解效率具有重要的意义.针对上述问题，本文提出一种加速求解方法以提高求解效率. 该方法通过交叉方向乘子法（Alternating Direction Method of Multipliers，ADMM）实现汽车轨迹跟踪问题的时域分解，将集中大规模的优化问题转为分块小规模优化问题，从而降低汽车轨迹跟踪MPC问题的时间复杂度，实现求解加速.1 模型预测控制问题的时域分解1.1 问题建模为了考虑车辆的动力学特性，MPC控制器依赖如图1所示的轨迹跟踪模型预测车辆的未来状态. 其中，系统输入为前轮转角δ;系统状态量x=[y，θ，ω，β]T（在x中，y表示侧向偏差，θ表示航向角，ω表示横摆角速度，β表示质心侧偏角）;系统的输入u=[δ] .当汽车轮胎侧偏特性处于线性范围时，基于小角度假设可得到跟踪控制系统的线性连续状态方程，如式（1）所示.式（1）中各矩阵如式（2）所示. 其中，k1、k2分别为二自由度模型中车辆前、后轮等效侧偏刚度;a、b分别为二自由度模型中车辆直线到前、后轴的距离.那么，可得线性离散时间系统的狀态空间模型，如式（3）所示.x（k+1） = Ad x（k） + Bd u（k）（3）且连续与离散系统矩阵转换关系如式（4）所示，其中Ts为离散系统的采样时间.不失一般性，假设当前时刻系统状态为x0，根据离散系统的状态方程（3），在预测时域N内系统的输入与系统状态之间的转移关系如图 2所示，其中x∈Rm，u∈Rn.设离散时刻t下系统的参考状态为rt，那么综合考虑跟踪精度、舒适性的优化目标函数J 可用式（5）表示. 式中Q∈Rm × m、R∈Rn × n分别为状态变量、输入变量的权重对角矩阵.在轨迹跟踪问题中，代价函数越小越好. 对式（5）进行展开，轨迹跟踪的MPC问题可转化为如式（6）所示的约束二次规划问题. 在目标函数中，省略了不影响极值求解的常数项. 在约束条件中，（6a）表示汽车的动力学约束，（6b）表示不同时刻下状态变量及控制变量的可行域约束. 可以看出，虽然目标函数J在时域上解耦，但由于约束条件（6a）的存在（即t周期的终止状态为t+1周期的初始状态），并不能在求解过程中实现问题的分块解耦计算.1.2 时域分解为了实现问题的时域解耦，本文引入全局一致性变量，将汽车动力学带来的时域耦合约束转为全局一致性约束，从而实现问题的分块求解. 图 3为ADMM时域分解示意图.首先，以控制周期为单位对状态变量、控制变量进行分块表达. 对于所关注预测时域内的N个控制周期，按照次序给予编号1到N. 对于每个控制周期，该周期初始状态量、输入状态量和输出状态量可分别用x（t）t表达，其中上角标（t）表示为变量所属的分块编号，且块内变量之间的关系由汽车动力学特性决定，如式（7）所示：而块间关系由时域耦合约束决定，满足式（8）：为解耦式（8）所示的时域耦合约束，引入全局一致性变量[z][～] = （z0，z1，…，zN）T ，并使x与z之间满足如式（9）所示的关系，其中：（9a）表示分块（t）的输入变量与zt-1的一致性约束;（9b）表示分块（t）的输出变量与zt的一致性约束.因此，联合式（7）～式（9），问题（6）可重写为如式（10）所示形式. 此时，邻接块之间不存在直接关系，其耦合约束通过一致性变量间接表达，从而实现控制周期之间时域解耦.2 分块求解方法2.1 问题求解综上所述，本文已经构建了MPC问题的时域分解范式，本节的工作则是基于ADMM求解时域分解后的问题. ADMM的标准构型如式（11）所示.为了方便地将式（10）转换为ADMM标准构型，引入块变量：[x][～]t = （x（t）求解MPC问题的主流思路是将其转化为二次规划（Quadratic Programming，QP）问题.其中，无约束MPC求解相对简单. Xu等以跟踪误差为性能指标实现AGV的轨迹跟踪控制[5]，Shen等则建立了综合考虑跟踪精度和舒适性的目标函数[6]，也有研究将输入量的边界建模为目标函数中代价值，构成“软约束”，但其数学原问题仍是无约束二次规划. 无约束二次规划问题可通过梯度下降等方法直接求解，但其局限在于仅考虑车辆的运动及动力学约束，没有考虑运动过程中所受到的其它约束，局限性较强. 因此，约束MPC更具备实际意义. 如Bo等建立了基于动力学的增量模型，考虑了执行机构的动力学特性约束[7]; Cai等则通过4自由度车辆模型加入车辆运动的侧翻约束，提高车辆跟踪控制的安全性[8]. 约束MPC的数学原问题是约束QP问题（MPC-QP问题），需要通过数值优化方法计算求解. 求解约束二次规划问题主要采用主动集法、内点法等方法，迭代次数较多. Wang和Boyd的研究表明，对于状态维数为m、控制输入维数为n、求解时域为T的MPC问题，状态转移形式及控制输入形式的MPC-QP问题求解的时间复杂度分别为O（[T（n+m）]3）和O（[Tn]3）[9]. 综上，虽然MPC在轨迹跟踪问题研究中得到广泛关注，但MPC-QP问题存在规模大、求解所需的浮点运算多、求解效率低的缺点，制约了MPC的性能. 因此，提高轨迹跟踪MPC问题的求解效率具有重要的意义.针对上述问题，本文提出一种加速求解方法以提高求解效率. 该方法通过交叉方向乘子法（Alternating Direction Method of Multipliers，ADMM）实现汽车轨迹跟踪问题的时域分解，将集中大规模的优化问题转为分块小规模优化问题，从而降低汽车轨迹跟踪MPC问题的时间复杂度，实现求解加速.1 模型预测控制问题的时域分解1.1 问题建模为了考虑车辆的动力学特性，MPC控制器依赖如图1所示的轨迹跟踪模型预测车辆的未来状态. 其中，系统输入为前轮转角δ;系统状态量x=[y，θ，ω，β]T（在x中，y表示侧向偏差，θ表示航向角，ω表示横摆角速度，β表示质心侧偏角）;系统的输入u=[δ] .当汽车轮胎侧偏特性处于线性范围时，基于小角度假设可得到跟踪控制系统的线性连续状态方程，如式（1）所示.式（1）中各矩阵如式（2）所示. 其中，k1、k2分别为二自由度模型中车辆前、后轮等效侧偏刚度;a、b分别为二自由度模型中车辆直线到前、后轴的距离.那么，可得线性离散时间系统的状态空间模型，如式（3）所示.x（k+1） = Ad x（k） + Bd u（k）（3）且连续与离散系统矩阵转换关系如式（4）所示，其中Ts为离散系统的采样时间.不失一般性，假设当前时刻系统状态为x0，根据离散系统的状态方程（3），在预测时域N内系统的输入与系统状态之间的转移关系如图 2所示，其中x∈Rm，u∈Rn.設离散时刻t下系统的参考状态为rt，那么综合考虑跟踪精度、舒适性的优化目标函数J 可用式（5）表示. 式中Q∈Rm × m、R∈Rn × n分别为状态变量、输入变量的权重对角矩阵.在轨迹跟踪问题中，代价函数越小越好. 对式（5）进行展开，轨迹跟踪的MPC问题可转化为如式（6）所示的约束二次规划问题. 在目标函数中，省略了不影响极值求解的常数项. 在约束条件中，（6a）表示汽车的动力学约束，（6b）表示不同时刻下状态变量及控制变量的可行域约束. 可以看出，虽然目标函数J在时域上解耦，但由于约束条件（6a）的存在（即t周期的终止状态为t+1周期的初始状态），并不能在求解过程中实现问题的分块解耦计算.1.2 时域分解为了实现问题的时域解耦，本文引入全局一致性变量，将汽车动力学带来的时域耦合约束转为全局一致性约束，从而实现问题的分块求解. 图 3为ADMM时域分解示意图.首先，以控制周期为单位对状态变量、控制变量进行分块表达. 对于所关注预测时域内的N个控制周期，按照次序给予编号1到N. 对于每个控制周期，该周期初始状态量、输入状态量和输出状态量可分别用x（t）t表达，其中上角标（t）表示为变量所属的分块编号，且块内变量之间的关系由汽车动力学特性决定，如式（7）所示：而块间关系由时域耦合约束决定，满足式（8）：为解耦式（8）所示的时域耦合约束，引入全局一致性变量[z][～] = （z0，z1，…，zN）T ，并使x与z之间满足如式（9）所示的关系，其中：（9a）表示分块（t）的输入变量与zt-1的一致性约束;（9b）表示分块（t）的输出变量与zt的一致性约束.因此，联合式（7）～式（9），问题（6）可重写为如式（10）所示形式. 此时，邻接块之间不存在直接关系，其耦合约束通过一致性变量间接表达，从而实现控制周期之间时域解耦.2 分块求解方法2.1 问题求解综上所述，本文已经构建了MPC问题的时域分解范式，本节的工作则是基于ADMM求解时域分解后的问题. ADMM的标准构型如式（11）所示.为了方便地将式（10）转换为ADMM标准构型，引入块变量：[x][～]t = （x（t）求解MPC问题的主流思路是将其转化为二次规划（Quadratic Programming，QP）问题.其中，无约束MPC求解相对简单. Xu等以跟踪误差为性能指标实现AGV的轨迹跟踪控制[5]，Shen等则建立了综合考虑跟踪精度和舒适性的目标函数[6]，也有研究将输入量的边界建模为目标函数中代价值，构成“软约束”，但其数学原问题仍是无约束二次规划. 无约束二次规划问题可通过梯度下降等方法直接求解，但其局限在于仅考虑车辆的运动及动力学约束，没有考虑运动过程中所受到的其它约束，局限性较强. 因此，约束MPC更具备实际意义. 如Bo等建立了基于动力学的增量模型，考虑了执行机构的动力学特性约束[7]; Cai等则通过4自由度车辆模型加入车辆运动的侧翻约束，提高车辆跟踪控制的安全性[8]. 约束MPC的数学原问题是约束QP问题（MPC-QP问题），需要通过数值优化方法计算求解. 求解约束二次规划问题主要采用主动集法、内点法等方法，迭代次數较多. Wang和Boyd的研究表明，对于状态维数为m、控制输入维数为n、求解时域为T的MPC问题，状态转移形式及控制输入形式的MPC-QP问题求解的时间复杂度分别为O（[T（n+m）]3）和O（[Tn]3）[9]. 综上，虽然MPC在轨迹跟踪问题研究中得到广泛关注，但MPC-QP问题存在规模大、求解所需的浮点运算多、求解效率低的缺点，制约了MPC的性能. 因此，提高轨迹跟踪MPC问题的求解效率具有重要的意义.针对上述问题，本文提出一种加速求解方法以提高求解效率. 该方法通过交叉方向乘子法（Alternating Direction Method of Multipliers，ADMM）实现汽车轨迹跟踪问题的时域分解，将集中大规模的优化问题转为分块小规模优化问题，从而降低汽车轨迹跟踪MPC问题的时间复杂度，实现求解加速.1 模型预测控制问题的时域分解1.1 问题建模为了考虑车辆的动力学特性，MPC控制器依赖如图1所示的轨迹跟踪模型预测车辆的未来状态. 其中，系统输入为前轮转角δ;系统状态量x=[y，θ，ω，β]T（在x中，y表示侧向偏差，θ表示航向角，ω表示横摆角速度，β表示质心侧偏角）;系统的输入u=[δ] .当汽车轮胎侧偏特性处于线性范围时，基于小角度假设可得到跟踪控制系统的线性连续状态方程，如式（1）所示.式（1）中各矩阵如式（2）所示. 其中，k1、k2分别为二自由度模型中车辆前、后轮等效侧偏刚度;a、b分别为二自由度模型中车辆直线到前、后轴的距离.那么，可得线性离散时间系统的状态空间模型，如式（3）所示.x（k+1） = Ad x（k） + Bd u（k）（3）且连续与离散系统矩阵转换关系如式（4）所示，其中Ts为离散系统的采样时间.不失一般性，假设当前时刻系统状态为x0，根据离散系统的状态方程（3），在预测时域N内系统的输入与系统状态之间的转移关系如图 2所示，其中x∈Rm，u∈Rn.设离散时刻t下系统的参考状态为rt，那么综合考虑跟踪精度、舒适性的优化目标函数J 可用式（5）表示. 式中Q∈Rm × m、R∈Rn × n分别为状态变量、输入变量的权重对角矩阵.在轨迹跟踪问题中，代价函数越小越好. 对式（5）进行展开，轨迹跟踪的MPC问题可转化为如式（6）所示的约束二次规划问题. 在目标函数中，省略了不影响极值求解的常数项. 在约束条件中，（6a）表示汽车的动力学约束，（6b）表示不同时刻下状态变量及控制变量的可行域约束. 可以看出，虽然目标函数J在时域上解耦，但由于约束条件（6a）的存在（即t周期的终止状态为t+1周期的初始状态），并不能在求解过程中实现问题的分块解耦计算.1.2 时域分解为了实现问题的时域解耦，本文引入全局一致性变量，将汽车动力学带来的时域耦合约束转为全局一致性约束，从而实现问题的分块求解. 图 3为ADMM时域分解示意图.首先，以控制周期为单位对状态变量、控制变量进行分块表达. 对于所关注预测时域内的N个控制周期，按照次序给予编号1到N. 对于每个控制周期，该周期初始状态量、输入状态量和输出状态量可分别用x（t）t表达，其中上角标（t）表示为变量所属的分块编号，且块内变量之间的关系由汽车动力学特性决定，如式（7）所示：而块间关系由时域耦合约束决定，满足式（8）：为解耦式（8）所示的时域耦合约束，引入全局一致性变量[z][～] = （z0，z1，…，zN）T ，并使x与z之间满足如式（9）所示的关系，其中：（9a）表示分块（t）的输入变量与zt-1的一致性约束;（9b）表示分块（t）的输出变量与zt的一致性约束.因此，联合式（7）～式（9），问题（6）可重写为如式（10）所示形式. 此时，邻接块之间不存在直接关系，其耦合约束通过一致性变量间接表达，从而实现控制周期之间时域解耦.2 分块求解方法2.1 问题求解综上所述，本文已经构建了MPC问题的时域分解范式，本节的工作则是基于ADMM求解时域分解后的问题. ADMM的标准构型如式（11）所示.为了方便地将式（10）转换为ADMM标准构型，引入块变量：[x][～]t = （x（t）。
自动驾驶4WS车辆路径跟踪最优控制算法仿真
第37卷第4期计算机仿真2020年4月文章编号：1006 -9348(2020)04 -0123 -05自动驾驶4W S车辆路径跟踪最优控制算法仿真郭旭东，杨世春(北京航空航天大学交通科学与工程学院，北京H X H91)摘要:针对自动驾驶车辆高速主动转向工况下传统的控制算法的控制效果容易出现较多的超调量和较长调节时间的问题，提出了基于车辆动力学模型的轨迹预测跟踪主动转向控制算法，并基于轮胎侧偏刚度非线性的特性设计了权系数线性最优二次型（L Q R)后轮转角控制算法，通过联合仿真对控制算法效果进行了验证。
仿真结果表明：自动驾驶四轮转向车辆在低、髙速工况下进行自主换道行驶时，算法控制效果满足汽车操纵稳定性要求，且权系数L Q R后轮转向算法比定侧偏刚度的L Q R线性控制算法有更优越的操控性能。
关键词：自动驾驶；四轮转向；模型预测控制;操纵稳定性中图分类号:T P391.9 文献标识码：BSimulation of Optimal Control Algorithmfor Automatic Driving 4WS Vehicle Path TrackingGUO X u-dong,YANG Shi-chu n(S c h o o l of Transportation S c i e n c e a n d E n g i n eering, B e i h a n g University, Beijing 100191 ,C h i n a)A B S T R A C T：A i m i n g at the p r o b l e m that the control effect of the traditional control algorithm in the high -s p e e d a ctive steering condition of the self -driving vehicle is p r o n e to overshoot a n d longer a d j u s t m e n t t i m e,the control algorithm for trajectory prediction a n d tracking active steering b a s e d o n the vehicle d y n a m i c s m o d e l is p roposed. B a s e d o nthe nonlinearity of the tire's cornering stiffness, the linear o ptimal quadratic ( L Q R) rear w h e e l angle control algorithm w a s designede. T h e effect of the control algorithm w a s verified thr o u g h joint simulation. T h e simulation resultss h o w that the algorithm control effect satisfies the req u i r e m e n t s of vehicle steering stability w h e n the self -driving four-w h e e l steering vehicle p e r f o r m s a u t o n o m o u s lane c h a n g e u n d e r l o w a n d hig h s p e e d co n d i t i o n s,a n d the w e i g h t c oefficient L Q R rear w h e e l steering algorithm h a s better m a n e u v e r i n g p e r f o r m a n c e tha n the L Q R linear control algorithmof the fixed side stiffness.K E Y W O R D S：A u t o n o m o u s driving；F o u r-w h e e l steering；M o d e l predictive control；H a n d l i n g stabilityi引言车辆智能化是汽车行业新的发展方向，其中自动驾驶是 为了实现高度智能化的交通系统。
考虑全局最优性的汽车微观动态轨迹规划
万方数据
・
９２０
・
吉林大学学报（工学版）
第４４卷
２基本行驶行为抽象
完成路径需要一系列的行驶行为。常见行驶 行为包括换道、保持车道、减速避让、超车、道路交 叉口、停车等。实际上，在结构化道路上发生的安 全、合法的行车行为，根据该行驶行为与车道的关 系可以分为换道和车道保持两种基本驾驶行为： 换道指换入不同车道；车道保持指保持在当前车 道。 在车道保持命令下，汽车不离开当前所在车 道。该情况下的轨迹规划问题仅针对纵向的速度 进行规划，不涉及横向规划，其横向轨迹由道路线 决定。车辆纵向轨迹规划相对比较简单，现已被 广泛应用，如自适应巡航系统。综上，本文提出将 微观轨迹规划的研究抽象为不同道路条件下的换 道行为研究。 对任意换道行为，终点约束由目标航向角和 目标偏移量两部分组成。理想换道结束时，汽车 应处于车道中心线位置且汽车航向角与目标车道 中心线方向相同。即换道行为结束时目标航向角 与目标偏移量均必须满足相应的约束。 以汽车当前时刻质心为原点，建立以汽车行 驶方向为Ｘ轴的大地坐标系Ｘ０ｙ，如图２所示。
孙
浩，邓伟文，张素民，吴梦勋
（吉林大学汽车仿真与控制国家重点实验室，长春１３００２２）
摘
要：针对智能汽车关键技术之一的自主行驶问题，提出了一种分层决策框架，并重点对框
架中的下层轨迹规划问题进行了研究。本文首先提出了一种将微观轨迹规划问题抽象为不同 终点约束换道行为的方法，并提出了一种能够同时满足行驶安全和全局性能最优的动态轨迹 规划方法。根据全局性能最优指标，提出了一种以三次多项式表达的最优换道轨迹；随后，本 文在交通车轨迹预估的基础上，以简单车辆动力学模型为轨迹发生器建立了汽车行驶的安全 搜索空间；最后以最优换道轨迹为目标决策出汽车行驶的最终轨迹。在Ｓｉｍｕｌｉｎｋ仿真平台中 对本文方法进行了仿真试验并证明了其有效性。 关键词：车辆工程；动态轨迹规划；汽车智能化；无人驾驶 中图分类号：Ｕ４６１．９９ 文献标志码：Ａ 文章编号：１６７１—５４９７（２０１４）０４—０９１８—０７
基于汽车碰撞事故的人体头部有限元模型建立与验证
56
南京工程学院学报（自然科学版）
2020年3月
百分位成年男性的头部几何信息，通过计算机断层 扫描技术（CT）及磁共振技术（MRI）获取头部信息 后导入医学图像处理软件Mimics,运用三维有限 元技术将头部数据信息构建成几何模型•该模型通 过图像分割技术得到一名成年男性头部解剖的几 何数据，包括脑脊液、脑室系统、灰质、白质、脑干和 小脑等，几何模型如图1所示.
-
杨氏模量 0/MPa 2 190 2 190 2 190 2 190 2 190 2 190 30 30 -
2头部有限元模型验证
为了检查有限元模型对头部撞击损伤的预测 情况，利用正面碰撞下的头部压力和应力来验证数 值模型的精确度.应用重5.59 kg的圆柱形冲击器 以9. 94 m/s冲击速度进行头部撞击试验，模型仿 真验证如图3所示.
1头部有限元模型的建立
1.1几何模型 头部模型的构建是基于新加坡华人特征的50
收稿日期：2019 -12-02；修回日期：2019-12-30 基金项目：江苏省自然科学基金项目! BK20161522 ）；江苏省“六大人才高峰”资助项目（JXQC-023 ）；江苏省研究生实践创新计划项目
! SJCX19_0515）；南京工程学院校级科研基金项目! YKJ201841） 作者简介：孙浩,硕士研究生,研究方向为车辆安全与人体损伤. E-mail: 381069572@ 引文格式：孙浩，羊垢，汪煖媛•基于汽车碰撞事故的人体头部有限元模型建立与验证［J］ •南京工程学院学报（自然科学版），2020,18 （1） $55 —59.
投稿网址:http：//xb .元模型建立与验证
孙浩1，羊q2，汪暧媛1
（1.南京工程学院机械工程学院，江苏南京211167； 2.南京工程学院汽车与轨道交通学院，江苏南京211167）
《2024年基于模型预测控制的无人驾驶车辆轨迹跟踪控制算法研究》范文
《基于模型预测控制的无人驾驶车辆轨迹跟踪控制算法研究》篇一一、引言随着科技的飞速发展，无人驾驶车辆已成为现代交通领域的重要研究方向。
无人驾驶车辆的核心技术之一是轨迹跟踪控制算法，其性能直接影响到车辆的行驶安全和稳定性。
模型预测控制（MPC）作为一种先进的控制策略，在无人驾驶车辆的轨迹跟踪控制中具有广泛的应用前景。
本文旨在研究基于模型预测控制的无人驾驶车辆轨迹跟踪控制算法，以提高无人驾驶车辆的行驶性能和安全性。
二、模型预测控制概述模型预测控制（MPC）是一种基于模型的优化控制策略，通过建立车辆动力学模型和预测模型，实现对未来时刻车辆状态的预测和优化。
MPC具有多约束处理能力、对模型不确定性的鲁棒性以及能处理多目标优化问题的特点，使得其在无人驾驶车辆的轨迹跟踪控制中具有显著优势。
三、无人驾驶车辆轨迹跟踪控制算法研究1. 车辆动力学模型建立为了实现精确的轨迹跟踪控制，首先需要建立准确的车辆动力学模型。
本文采用非线性车辆动力学模型，考虑车辆的纵向、横向以及横摆运动，为后续的轨迹跟踪控制提供基础。
2. 预测模型的构建预测模型是MPC的核心部分，通过对未来时刻车辆状态的预测，实现对轨迹的跟踪控制。
本文采用基于滚动时域的预测方法，通过优化目标函数，实现对未来时刻车辆状态的预测和优化。
3. 控制器设计基于建立的车辆动力学模型和预测模型，设计控制器实现轨迹跟踪控制。
控制器采用MPC算法，通过优化目标函数，实现对未来时刻车辆状态的优化和控制。
同时，考虑到实际道路交通环境的复杂性，本文还引入了约束条件，如速度、加速度等限制，以保证车辆行驶的安全性和稳定性。
四、算法仿真与实验验证为了验证基于模型预测控制的无人驾驶车辆轨迹跟踪控制算法的有效性，本文进行了仿真实验和实际道路测试。
仿真实验结果表明，该算法能够实现对期望轨迹的准确跟踪，具有较好的鲁棒性和稳定性。
实际道路测试结果也表明，该算法能够适应不同道路条件和交通环境，实现安全、稳定的行驶。
车辆操纵动力学稳定性分析
车辆操纵动力学摘要：汽车的前轮转角和横摆角速度是衡量汽车稳定性的两个重要指标。
汽车在行驶过程中，由于路况的各种不确定因素，驾驶员可能会采取紧急制动和转向的行为来避免交通事故。
在此过程中汽车的操纵稳定性会起到关键性的作用，因此对于汽车的稳定性的分析必不可少。
本文建立了汽车线性二自由度汽车模型，以前轮转角为输入，运用MATLAB进行时域分析。
对不同车型的在相同行驶速度、相同前轮转角下分析横摆角速度瞬态响应；在相同行驶速度下，在不同前轮转角输入下分析达到相同加速度的横摆角速度瞬态响应；随着车速增加，分析车辆瞬时转向响应与系统特征根之间的关系。
关键词：横摆角速度；前轮转角；特征根引言车辆稳定性控制是汽车主动安全领域研究的热点，已有的研究如以车辆横摆角速度、质心侧偏角、轮胎的滑移率、侧向加速度及这些变量联合作为控制变量的控制策略研究。
本文主要考虑车辆横摆角速度和前轮转角对车辆操纵稳定性的影响，进一步利用MATLAB得出状态空间矩阵的特征根变化趋势，了解车辆瞬时响应与其之间的关系。
1建立汽车数学模型假设汽车的驱动力不大，不考虑地面切向力对轮胎侧偏特性的影响，没有空气动力的作用，忽略左、右车轮轮胎由于载荷的变化而引起轮胎特性的变化以及轮胎回正力矩的作用。
汽车模型即可简化为线性二自由度模型，如图1。
图1 线性二自由度模型根据假设以及图1模型，二自由汽车收到的外力沿y轴方向的合力与绕质心的力矩和为：⎩⎨⎧-=∑+=∑2121cos cos Y Y Z Y Y Y bF aF M F F F δδ (1) 式中，FY1、FY2为地面对前后轮的侧向反作用力；δ为前轮转角；a 、b 分别为汽车前、后轮至质心的距离。
汽车前、后轮侧偏角与其运动参数有关，如图1所示，汽车前、后轴中点的速度u 1、u 2，侧偏角为α1、α2，质心的侧偏角为β，β=v/u 。
ξ是u 1与x 轴的夹角，其值为：uawu aw v r r +=+=βξ (2) 根据坐标系规定，由式（2）得，前、后轮侧偏角为：⎪⎪⎩⎪⎪⎨⎧-=-=-+=--=u bw u bw v uaw r r r βαδβξδα21)( （3） 考虑到δ角较小，前、后轮所受到的侧向力与相应的侧偏角成线性关系，则FY1、FY2为：⎪⎪⎩⎪⎪⎨⎧⋅-=⋅=⋅-+=⋅=cru bw cr a FY cf uaw cf a F r r Y )(2)(211βδβ （4） 将公式（2）、（3）、（4）以及公式β=v/u 带入（1），消去α1、α2，得二自由度汽车运动微分方程为：⎪⎪⎩⎪⎪⎨⎧+----=---+-=+δδr r r f r f r Z f r r f r aC w u C b C a v u bC aC w I C w ubC aC v u cr cf uw v m 22)( （5） 2 MATLAB 系统仿真本文采用MATLAB 对汽车的操纵稳定性进行仿真研究。
基于MPC的无人驾驶拖拉机轨迹跟踪控制
第３８卷第９期重庆交通大学学报（自然科学版）Ｖｏｌ．３８㊀Ｎｏ．９２０１９年９月ＪＯＵＲＮＡＬＯＦＣＨＯＮＧＱＩＮＧＪＩＡＯＴＯＮＧＵＮＩＶＥＲＳＩＴＹ（ＮＡＴＵＲＡＬＳＣＩＥＮＣＥ）Ｓｅｐ．２０１９㊀㊀ＤＯＩ：１０．３９６９／ｊ．ｉｓｓｎ．１６７４⁃０６９６．２０１９．０９．０１基于ＭＰＣ的无人驾驶拖拉机轨迹跟踪控制严国军１，２，３，贲能军１，顾建华１，杨㊀彦１（１．盐城工业职业技术学院江苏盐城２２４０００；２．东南大学，江苏南京２１１１８９；３．南京理工大学，江苏，南京２１００９４）摘要针对无人驾驶拖拉机在给定行驶路径的情况下通过对建立的拖拉机运动学非线性模型进行线性化处理得到线性时变系统运用模型预测控制算法对拖拉机转向进行控制达到轨迹跟踪的目的为了优化控制器运算速度提出自适应控制器该控制器的预测时域能够根据参考轨迹曲率的变化自动调节在确保轨迹跟踪效果的前提下降低控制器的运算时间保证控制系统的实时性研究结果表明基于设计的轨迹跟踪控制器能够使拖拉机在车速为行驶时有效跟踪既定的行驶轨迹距离误差小于航向角误差小于关键词车辆工程轨迹跟踪拖拉机中图分类号文献标志码文章编号０㊀引㊀言农用车辆自动化作业能够使农业劳动者从沉重的体力劳动中解放出来，其中农用车辆自动化行走是实现自动化作业的基础㊂近阶段针对农用车辆自动行走的研究逐渐成为各国研究重点［１⁃２］㊂在早期研究中，一些学者在园艺设施中尝试将一些引导线埋藏在地下，以引导车辆沿着固定的轨道进行作业，但这种方法在实施过程中具有很大的局限性㊂随着科技不断进步，摄像头和卫星定位系统得到广泛应用，促使农用车辆在自由轨迹上行驶的研究越来越多［２⁃６］㊂总的来看，农业机械自动驾驶的研究方向㊀收稿日期：２０１８⁃０３⁃０１；修订日期：２０１９⁃０２⁃２６㊀基金项目：国家重点研发计划重点专项（２０１６ＹＦＤ０７００９０５）；江苏省国内访问学者资助项目（２０１６ＧＲＦＸ０６２）；盐城市２０１５年度农业科技创新专项引导资金（ＹＫＮ２０１５０３０）；盐城市２０１６年度农业科技创新专项引导资金（ＹＫ２０１６＿０６）；盐城工业职业技术学院科研基金项目资助（ＹＧＹ１７０３）㊂㊀第一作者：严国军（１９７３ ），男，江苏盐城人，副教授，主要研究方向为测控与机电设备自动控制㊂Ｅ⁃ｍａｉｌ：ｙｇｊ６９６１＠１６３．ｃｏｍ㊂㊀通信作者：贲能军（１９８５ ），男，江苏东台人，博士研究生，主要研究方向为农业机械设计及智能控制㊂Ｅ⁃ｍａｉｌ：ｂｅｎｅｒｉｃ＠１２６．ｃｏｍ㊂可以分为车辆行驶轨迹规划和车辆轨迹跟踪控制两个方面㊂车辆轨迹跟踪控制的实质是车辆能够根据给定的行驶路径完成自主转向控制，并使跟踪误差最小，即使在行驶过程中遇到一些干扰，也能够保证稳定行驶㊂轨迹跟踪控制是自动驾驶车辆体系中最基础的一环，它的性能好坏直接影响到整个自动驾驶车辆是否能够完成给定的驾驶任务［７］㊂车辆在给定行驶轨迹时，需能稳定且迅速地跟踪给定行驶轨迹，这是对自动驾驶车辆最基本的要求㊂轨迹跟踪的重点就是设计出轨迹跟踪控制器，使智能驾驶车辆能够跟随既定行驶轨迹驾驶，行驶路径可以通过车载ＥＣＵ采集各种探测器信号并经ＥＣＵ计算得出㊂笔者针对无人驾驶拖拉机在给定轨迹情况下的循迹效果开展研究㊂１㊀车辆运动学模型建立动力学模型和运动学模型是车辆模型建立过程中最常用的两种模型，车辆的动力学模型是根据车辆在行驶中的受力情况，利用牛顿第二定律建立的；车辆的运动学模型是从几何学角度来研究车辆的运动规律，包括车辆所位于的位置坐标㊁航向角㊁速度等㊂在车辆的路径跟踪研究中使用运动学模型，可以满足行驶过程中的运动学约束㊂拖拉机速度一般在０．５ ３．０ｍ／ｓ，属于低速行驶的运动车辆，可以不考虑拖拉机在行驶过程中侧滑㊁侧倾等稳定性控制的动力学问题，因此采用运动学模型设计的轨迹跟踪控制器具有可靠的控制性能［８］㊂拖拉机的运动模型如图１，其中，（Ｘｆ，Ｙｆ）㊁（Ｘｒ，Ｙｒ）为拖拉机前轴和拖拉机后轴中心点的位置坐标，Ｘ㊃㊁Ｙ㊃为沿坐标轴Ｘ㊁Ｙ的一阶微分，φ为拖拉机的航向角，δｆ为拖拉机前轮转角，ｖｒ为拖拉机后轴中心速度，ｖｆ为车辆前轴中心速度，ｌ为拖拉机前后轴轴距㊂在拖拉机转向过程中，Ｒ为后轮转向半径，Ｐ为拖拉机的瞬时转动中心，Ｍ为后轴中心，Ｎ为前轴中心㊂在后轴中心（Ｘｒ，Ｙｒ）处，后轴中心速度ｖｒ为：ｖｒ＝Ｘ㊃ｒｃｏｓ（φ）＋Ｙ㊃ｒｓｉｎ（φ）（１）前后轴的运动学约束方程为：Ｘ㊃ｆｓｉｎ（φ＋δｆ）－Ｙ㊃ｆｃｏｓ（φ＋δｆ）＝０Ｘ㊃ｆｓｉｎ（φ）－Ｙ㊃ｆｃｏｓ（φ）＝０{（２）图１㊀拖拉机运动学模型Ｆｉｇ．１㊀Ｔｒａｃｔｏｒｋｉｎｅｍａｔｉｃｓｍｏｄｅｌ由式（１）和（２）可得：Ｘ㊃ｒ＝ｖｒｃｏｓ（φ）Ｙ㊃ｒ＝ｖｒｓｉｎ（φ）{（３）根据前后轮的几何关系可得：Ｘ㊃ｆ＝Ｘ㊃ｒ＋ｌｃｏｓ（φ）Ｙ㊃ｆ＝Ｙ㊃ｒ＋ｌｓｉｎ（φ）{（４）由式（４）可得横摆角速度ω为：ω＝ｖｒｌｔａｎ（δｆ）（５）同时，由ω和车速ｖｒ可得到转向半径Ｒ和前轮偏角δｆ㊂Ｒ＝ｖｒ／ωδｆ＝ａｒｃｔａｎ（ｌ／Ｒ）{（６）由上式可以得到拖拉机的运动学模型为Ｘ㊃ｒＹ㊃ｒφ㊃éëêêêêêùûúúúúú＝ｃｏｓ（φ）ｓｉｎ（φ）ｔａｎ（δｆ）／ｌéëêêêêùûúúúúｖｒ（７）２㊀模型预测控制模型预测控制（ＭｏｄｅｌＰｒｅｄｉｃｔｉｖｅＣｏｎｔｒｏｌＭＰＣ）算法是２０世纪７０年代末，美国㊁法国等工业领域中最早出现的一种计算机优化控制算法，模型预测控制在实现过程中都是基于预测模型㊁滚动优化和反馈矫正的控制策略［９⁃１０］㊂这些方法不仅具有较强的鲁棒性和较好的控制效果，而且对控制系统模型的精确度要求较低㊂基于模型预测控制的优势，其被大量应用到过程控制中，现已经在机械工程和化工生产中得到成熟运用㊂２㊀㊀重庆交通大学学报（自然科学版）㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀第３８卷线性时变模型预测控制算法是基于线性时变的模型控制算法，其与非线性模型预测控制相比，具有计算较为简单㊁计算速度快㊁实时性好的优点［１１⁃１５］㊂对车辆的轨迹跟踪控制而言，实时性是最重要的考虑因素，因此笔者采取线性时变的模型预测控制算法㊂考虑离散系统的线性化模型：ｘ（ｋ＋１）＝Ａｋ，ｔｘ（ｋ）＋Ｂｋ，ｔｕ（ｋ）（８）ｘ（ｋ）和ｕ（ｋ）是在第ｋ采样时刻系统的状态量和控制量，设定：ξ（ｋ｜ｔ）＝ｘ（ｋ｜ｔ）ｕ（ｋ－１｜ｔ）éëêêùûúú（９）可以得到一个新的状态空间表达式：ξ（ｋ＋１｜ｔ）＝Ａｋ，ｔξ（ｋ｜ｔ）＋Ｂｋ，ｔΔｕ（ｋ｜ｔ）η（ｋ｜ｔ）＝Ｃｋ，ｔξ（ｋ｜ｔ）{（１０）假设：Ａｋ，ｔ＝Ａｔ，Ｂｋ，ｔ＝Ｂｔ㊀（ｋ＝１， ｔ＋Ｎ－１）（１１）系统预测时域为Ｎｐ，控制时域为Ｎｃ，则预测时域内的状态量和系统输出量可用下式表示：ξ（ｔ＋Ｎｐ｜ｔ）＝ＡＮｐｔξ（ｔ｜ｔ）＋ＡＮｐ－１ｔＢｔΔｕ（ｔ｜ｔ）＋ ＋ＡＮｐ－Ｎｃ－１ｔＢｔΔｕ（ｔ＋Ｎｃ｜ｔ）η（ｔ＋Ｎｐ｜ｔ）＝ＣｔＡＮｐｔξ（ｔ｜ｔ）＋ＣｔＡＮｐ－１ｔＢｔ㊃Δｕ（ｔ｜ｔ）＋ ＋ＣｔＡＮｐ－Ｎｃ－１ｔＢｔΔｕ（ｔ＋Ｎｃ｜ｔ）（１２）未来时刻输出可以由如下矩阵形式表达：Ｙ（ｔ）＝ψｔξ（ｔ｜ｔ）＋ΘｔΔｕ（ｔ）（１３）由此，在预测时域内的状态变量和输出变量都可以通过对系统当前状态量ξ（ｔ｜ｔ）和控制时域内的控制量Δｕ（ｔ）计算得到，从而实现模型预测控制算法中的预测功能㊂在实际过程中，系统的控制增量是不知道的，需要通过对合适的优化目标求解来得到控制时域内的控制序列，文献［１６］给出的目标函数如下：Ｊ（ｋ）＝ðＮｊ＝１ｘＴ（ｋ＋ｊ｜ｋ）Ｑｘ（ｋ＋ｊ｜ｋ）＋ｕＴ（ｋ＋ｊ－１）Ｒｕ（ｋ＋ｊ－１）（１４）此形式的优化目标函数可以将其转化为带有线性或非线性的二次规划，这一典型数学优化问题来解决㊂在完成每个控制周期求解后，可以得到控制时域内的一系列控制输入增量：ΔＵ∗ｔ＝［Δｕ∗ｔ，Δｕ∗ｔ＋１， ，Δｕ∗ｔ＋Ｎｃ－１］Ｔ（１５）根据模型预测控制的基本原理，控制序列中第一个元素作为实际模型预测控制的输入增量作用于系统中：ｕ（ｔ）＝ｕ（ｔ－１）＋Δｕ∗ｔ（１６）系统执行这一控制量，并根据当前状态量预测下一周期新的控制增量序列，如此的反复循环，滚动优化，直到系统完成整个控制过程㊂３㊀控制结果分析由于ＭＰＣ控制目标是拖拉机，考虑其在低速行驶过程中轨迹跟踪控制，以式（７）运动学非线性模型为预测模型，对其线性化处理，可以得到线性时变模型（１７），Ｔ为采样时间㊂在控制过程中，根据给定时刻预测模型得到拖拉机的航向角，后轴中心位置与系统实际拖拉机状态的偏差，计算得到此时刻的模型输入，重复这一过程使拖拉机快速稳定的跟踪上目标轨迹㊂ξ（ｋ＋１）＝Ａｋξ（ｋ）＋Ｂｋｕ（ｋ）（１７）其中ξ（ｋ）＝ｘ－ｘｒｙ－ｙｒφ－φｒéëêêêêùûúúúú，Ａｋ（ｋ）＝１０－ｖｒｓｉｎ（φｒ）Ｔ０１ｖｒｃｏｓ（φｒ）Ｔ００１éëêêêêùûúúúú，Ｂｋ（ｋ）＝ｃｏｓ（φｒ）Ｔ０ｓｉｎ（φｒ）Ｔ０ｔａｎ（δｆ）Ｔ／ｌｖｒＴ／ｌｃｏｓ（δｆ）éëêêêêêùûúúúúú３．１㊀正弦曲线工况正弦曲线工况是检测车辆操纵性能的行驶工况㊂在行驶过程中车辆需要不断的输入前轮转角，以期望对给定轨迹有较好的跟踪效果㊂在不断转向过程中可能会出现车辆状态发生变化或其他情况的发生，这对控制器的控制性能具有很高的要求㊂给定拖拉机车速为１０ｍ／ｓ，仿真结果如图２㊂由仿真结果可以看出，车辆在实际行驶过程中能够很好的跟踪给定的行驶路线㊂由图２（ｃ）和图２（ｄ）可知最大行驶距离偏差为－０．０２５ｍ，最大航向角偏差为０．０１ｒａｄ，由于拖拉机给定初始状态的航向角与轨迹参考值存在初始误差，因此两个偏差都是非常小的㊂在图２（ｂ）中可以看到，开始后控制器使误差逐３第９期严国军，等：基于ＭＰＣ的无人驾驶拖拉机轨迹跟踪控制渐变小，后来趋于稳定状态，说明ＭＰＣ控制器对于双移线工况跟踪效果较好㊂３．２㊀自适应ＭＰＣ控制器对于实际应用来说，如何提高控制器的速度，满足ＭＰＣ控制器对实时性的要求至关重要㊂研究发现，对于ＭＰＣ控制器，当降低预测时域Ｎｐ时，虽然控制器对轨迹的跟踪精度有所下降（特别在曲率较大地方，跟踪精度下降更为明显）但是系统的计算速度可以得到提升［１７］㊂计算速度和控制器的控制效果是相互矛盾的，如何在提升计算速度同时得到较好的控制效果是值得研究的问题㊂为了解决这个问题，笔者设计了一种自适应ＭＰＣ控制器，预测时域Ｎｐ能够根据车辆跟踪轨迹的曲率Ｋ的变化自动调节，以达到又快又好的完成控制目标㊂预测时域Ｎｐ的大小将按照下式规律㊂Ｎｐ＝Ｒｏｕｎｄ（ａ㊃｜Ｋｘ｜＋ｂ）（１８）式中，Ｎｐ是预测时域，ａ为曲率增益系数，图２㊀正弦曲线工况仿真结果Ｆｉｇ．２㊀Ｓｉｍｕｌａｔｉｏｎｒｅｓｕｌｔｓｆｏｒｓｉｎｕｓｏｉｄａｌｄｒｉｖｉｎｇｃｏｎｄｉｔｉｏｎｓ４㊀㊀重庆交通大学学报（自然科学版）㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀第３８卷图３㊀双移线工况仿真结果Ｆｉｇ．３㊀Ｓｉｍｕｌａｔｉｏｎｒｅｓｕｌｔｓｆｏｒｄｏｕｂｌｅ⁃ｓｈｉｆｔｌｉｎｅｄｒｉｖｉｎｇｃｏｎｄｉｔｉｏｎｓ㊀㊀Ｋｘ为道路曲率，ｂ为预测时域基本值，计算中ａ取为１０００，ｂ取为１０㊂为了验证自适应ＭＰＣ控制器的实际效果，选取双移线工况进行仿真实验㊂双移线工况指的是车辆在行驶过程中遇到前方障碍物变道后再返回到原来车道的工况，在现实生活中较为常见㊂车辆在换道过程中，可能会因变化的道路条件或其他情况的发生导致轮胎力饱和引起转向不足或过度转向，这都会对给定行驶轨迹的跟踪效果造成相应影响㊂拖拉机速度设定为１０ｍ／ｓ，选取ＭＰＣ控制器和自适应ＭＰＣ控制器对跟踪效果进行对比分析，其中ＭＰＣ控制器的预测时域Ｎｐ选择为３０㊁１０，其余控制器参数保持不变㊂数值仿真结果如图３，仿真曲线图３（ａ）和图３（ｂ）可以看出三种控制器都能够保证位移和航向角跟随上参考值的变化㊂图３（ｃ）和图３（ｄ）给出了三种控制器航向角和横向距离误差，可以看出当控制时域为３０时，控制效果最好，证明了增大控制时域可以提高控制效果，但从图３（ｆ）可以看出与控制时域为１０相比，其计算耗时也相对增加㊂对于设计的自适应ＭＰＣ控制器，航向角偏差和距离偏差与控制时域为１０相比，控制效果得到了明显提升，计算时间消耗也能够有所降低㊂由仿真结果可以看出，在使用自适应ＭＰＣ对车辆进行控制时，车辆在实际行驶过程中能够很好的跟踪给定的行驶路线㊂同时由图３（ｃ）和图３（ｄ）可知，最大行驶距离偏差为－０．０３ｍ，最大航向角偏差为０．０１５ｒａｄ，两个偏差都是非常小的，计算速度也得到了提升，说明自适应ＭＰＣ控制器对于双移线工况跟踪效果较好㊂因此，自适应ＭＰＣ控制器能够提升控制系统的控制效果，同时提高控制系统的计算速度，提升控制系统的实时性㊂在硬件条件较低，又希望得到很好的控制实时性的情况下，可以采用此方法㊂４㊀结㊀论基于ＭＰＣ对无人驾驶拖拉机的轨迹跟踪进行相关研究，通过对建立的拖拉机运动学非线性模型进行线性化处理，得到所需的线性时变系统，运用线性时变模型预测控制算法对行驶轨迹进行控制㊂对双移线工况和正弦曲线工况进行仿真分析，结果表明该算法能够较好的对给定轨迹进行跟踪，具有较好的动态跟踪性能㊂为提高控制器的计算速度，笔者设计了一种自适应ＭＰＣ控制器，预测时域Ｎｐ根据车辆跟踪轨迹的曲率Ｋ的变化自动调节㊂仿真结果表明，利用自适应ＭＰＣ控制器，车辆最大行驶距离偏差为－０．０３ｍ，最大航向角偏差为０．０１５ｒａｄ，同时降低了控制器的计算时间，提升控制系统的实时性，达到较好的轨迹跟踪目的㊂参考文献（Ｒｅｆｅｒｅｎｃｅｓ）：［１］ＢＥＬＬＴ．Ａｕｔｏｍａｔｉｃｔｒａｃｔｏｒｇｕｉｄａｎｃｅｕｓｉｎｇｃａｒｒｉｅｒ⁃ｐｈａｓｅｄｉｆｆｅｒｅｎｔｉａｌＧＰＳ［Ｊ］．ＣｏｍｐｕｔｅｒｓａｎｄＥｌｅｃｔｒｏｎｉｃｓｉｎＡｇｒｉｃｕｌｔｕｒｅ，２０００，２５：５３⁃６６．［２］ＲＥＩＤＦ．Ｊ．，ＺＨＡＮＧＱ，ｅｔａｌ．Ａｇｒｉｃｕｌｔｕｒａｌａｕｔｏｍａｔｉｃｇｕｉｄａｎｃｅｒｅｓｅａｒｃｈｉｎｎｏｒｔｈａｍｅｒｉｃａ［Ｊ］．ＣｏｍｐｕｔｅｒｓａｎｄＥｌｅｃｔｒｏｎｉｃｓｉｎＡｇｒｉｃｕｌｔｕｒｅ，２０００，２５：１５５⁃１６７．［３］胡静涛，高雷，白晓平，等．农业机械自动导航技术研究进展［Ｊ］．农业工程学报，２０１５，３１（１０）：１⁃１０．ＨＵＪｉｎｇｔａｏ，ＧＡＯＬｅｉ，ＢＡＩＸｉａｏｐｉｎｇ，ｅｔａｌ．Ｒｅｖｉｅｗｏｆｒｅｓｅａｒｃｈｏｎａｕｔｏｍａｔｉｃｇｕｉｄａｎｃｅｏｆａｇｒｉｃｕｌｔｕｒａｌｖｅｈｉｃｌｅｓ［Ｊ］．ＴｒａｎｓａｃｔｉｏｎｓｏｆｔｈｅＣｈｉｎｅｓｅＳｏｃｉｅｔｙｏｆＡｇｒｉｃｕｌｔｕｒａｌＥｎｇｉｎｅｅｒｉｎｇ，２０１５，３１（１０）：１⁃１０．［４］姬长英，周俊．农业机械导航技术发展分析［Ｊ］．农业机械学报，２０１４，４５（９）：４４⁃５４．ＪＩＣｈａｎｇｙｉｎｇ，ＺＨＯＵＪｕｎ．Ｃｕｒｒｅｎｔｓｉｔｕａｔｉｏｎｏｆｎａｖｉｇａｔｉｏｎｔｅｃｈｎｏｌｏｇｉｅｓｆｏｒａｇｒｉｃｕｌｔｕｒａｌｍａｃｈｉｎｅｒｙ［Ｊ］．ＴｒａｎｓａｃｔｉｏｎｓｏｆｔｈｅＣｈｉｎｅｓｅＳｏｃｉｅｔｙｆｏｒＡｇｒｉｃｕｌｔｕｒａｌＭａｃｈｉｎｅｒｙ，２０１４，４５（９）：４４⁃５４．５第９期严国军，等：基于ＭＰＣ的无人驾驶拖拉机轨迹跟踪控制［５］周兴林，伍洋，吕文莎，等．车辆行驶跑偏量在线测量研究［Ｊ］．重庆交通大学学报（自然科学版），２０１７，３６（１２）：９７⁃１０１．ＺＨＯＵＸｉｎｇｌｉｎ，ＷＵＹａｎｇ，ＬＶＷｅｎｓｈａ，ｅｔａｌ．Ｏｎｌｉｎｅｍｅａｓｕｒｅｍｅｎｔｏｆｖｅｈｉｃｌｅｄｒｉｖｉｎｇｄｅｖｉａｔｉｏｎ［Ｊ］．ＪｏｕｒｎａｌｏｆＣｈｏｎｇｑｉｎｇＪｉａｏｔｏｎｇＵｎｉｖｅｒｓｉｔｙ（ＮａｔｕｒａｌＳｃｉｅｎｃｅ）．２０１７，３６（１２）：９７⁃１０１．［６］侯江丽．基于ＧＩＳ的拖拉机自动驾驶作业路径规划方法的研究［Ｄ］．北京：中国农业大学，２００６．ＨＯＵＪｉａｎｇｌｉ．ＲｅｓｅａｒｃｈｏｎＷｏｒｋｉｎｇＰａｔｈＰｌａｎｎｉｎｇＭｅｔｈｏｄｏｆＴｒａｃｔｏｒＡｕｔｏｎｏｍｏｕｓＤｒｉｖｉｎｇＢａｓｅｄｏｎＧＩＳ［Ｄ］．Ｂｅｉｊｉｎｇ：ＣｈｉｎａＡｇｒｉｃｕｌｔｕｒａｌＵｎｉｖｅｒｓｉｔｙ，２００６．［７］郭振东．无人驾驶汽车路径识别算法研究［Ｊ］．汽车电器，２００９（５）：１４⁃１８．ＧＵＯＺｈｅｎｄｏｎｇ．Ａｌｇｏｒｉｔｈｍｒｅｓｅａｒｃｈｏｎｐａｔｈｒｅｃｏｇｎｉｔｉｏｎｏｆｐｉｌｏｔｌｅｓｓａｕｔｏｍｏｂｉｌｅ［Ｊ］．ＡｕｔｏＥｌｅｃｔｒｉｃＰａｒｔｓ，２００９（５）：１４⁃１８．［８］韩冰，陈军．拖拉机行驶路径的多项式设计［Ｊ］．农机化研究，２００６，１０（１０）：９８⁃１００．ＨＡＮＧＢｉｎｇ，ＣＨＥＮＪｕｎ．Ａｕｔｏｎｏｍｏｕｓｔｒａｃｔｏｒｔｒａｊｅｃｔｏｒｙｄｅｓｉｇｎｕｓｉｎｇｐｏｌｙｎｏｍｉａｌｆｕｎｃｔｉｏｎ［Ｊ］．ＪｏｕｒｎａｌｏｆＡｇｒｉｃｕｌｔｕｒａｌＭｅｃｈａｎｉｚａｔｉｏｎＲｅｓｅａｒｃｈ，２００６，１０（１０）：９８⁃１００．［９］龚建伟，姜岩，徐威．无人驾驶车辆模型预测控制［Ｍ］．北京：北京理工大学出版社，２０１４．ＧＯＮＧＪｉａｎｗｅｉ，ＪＩＡＮＧＹａｎ，ＸＵＷｅｉ．ＭｏｄｅｌＰｒｅｄｉｃｔｉｖｅＣｏｎｔｒｏｌｆｏｒＳｅｌｆ⁃ｄｒｉｖｉｎｇＶｅｈｉｃｌｅｓ［Ｍ］．Ｂｅｉｊｉｎｇ：ＢｅｉｊｉｎｇＩｎｓｔｉｔｕｔｅｏｆＴｅｃｈｎｏｌｏｇｙＰｒｅｓｓ，２０１４．［１０］苏成利．非线性模型预测控制的若干问题研究［Ｄ］．杭州：浙江大学，２００６．ＳＵＣｈｅｎｇｌｉ．ＲｅｓｅａｒｃｈｏｎＳｏｍｅＰｒｏｂｌｅｍｓｏｆＮｏｎｌｉｎｅａｒＭｏｄｅｌＰｒｅｄｉ⁃ｃｔｉｖｅＣｏｎｔｒｏｌ［Ｄ］．Ｈａｎｇｚｈｏｕ：ＺｈｅｊｉａｎｇＵｎｉｖｅｒｓｉｔｙ，２００６．［１１］徐健，汪慢，乔磊．欠驱动无人水下航行器三维轨迹跟踪的反步控制［Ｊ］．控制理论与应用，２０１４，３１（１１）：１５８９⁃１５９０．ＸＵＪｉａｎ，ＷＡＮＧＭａｎ，ＱＩＡＯＬｅｉ．Ｂａｃｋｓｔｅｐｐｉｎｇ⁃ｂａｓｅｄｃｏｎｔｒｏｌｌｅｒｆｏｒｔｈｒｅｅ⁃ｄｉｍｅｎｓｉｏｎａｌｔｒａｊｅｃｔｏｒｙｔｒａｃｋｉｎｇｏｆｕｎｄｅｒａｃｔｕａｔｅｄｕｎｍａｎｎｅｄｕｎｄｅｒｗａｔｅｒｖｅｈｉｃｌｅｓ［Ｊ］．ＣｏｎｔｒｏｌＴｈｅｏｒｙ＆Ａｐｐｌｉｃａｔｉｏｎｓ，２０１４，３１（１１）：１５８９⁃１５９０．［１２］刘一扬，刘明明．基于改进遗传算法的机器人运动轨迹跟踪控制［Ｊ］．机械传动，２０１６，４０（３）：３９⁃４１．ＬＩＵＹｉｙａｎｇ，ＬＩＵＭｉｎｇｍｉｎｇ．Ｔｒａｊｅｃｔｏｒｙｔｒａｃｋｉｎｇｃｏｎｔｒｏｌｏｆｒｏｂｏｔｂａｓｅｄｏｎｉｍｐｒｏｖｅｄｇｅｎｅｔｉｃａｌｇｏｒｉｔｈｍ［Ｊ］．ＪｏｕｒｎａｌｏｆＭｅｃｈａｎｉｃａｌＴｒａｎｓｍｉｓｓｉｏｎ，２０１６，４０（３）：３９⁃４１．［１３］郭烈，黄晓慧，葛平淑，等．基于反演法的智能车辆弯路换道轨迹跟踪控制［Ｊ］．吉林大学学报（工学版），２０１３，４３（２）：３２３⁃３２８．ＧＵＯＬｉｅ，ＨＵＡＮＧＸｉａｏｈｕｉ，ＧＥＰｉｎｇｓｈｕ，ｅｔａｌ．Ｌａｎｅｃｈａｎｇｉｎｇｔｒａｊｅｃｔｏｒｙｔｒａｃｋｉｎｇｃｏｎｔｒｏｌｆｏｒｉｎｔｅｌｌｉｇｅｎｔｖｅｈｉｃｌｅｏｎｃｕｒｖｅｄｒｏａｄｂａｓｅｄｏｎｂａｃｋｓｔｅｐｐｉｎｇ［Ｊ］．ＪｏｕｒｎａｌｏｆＪｉｌｉｎＵｎｉｖｅｒｓｉｔｙ（ＥｎｇｉｎｅｅｒｉｎｇａｎｄＴｅｃｈｎｏｌｏｇｙＥｄｉｔｉｏｎ），２０１３，４３（２）：３２３⁃３２８．［１４］柯文德，彭志平，蔡则苏，等．仿人机器人相似性运动轨迹跟踪控制研究［Ｊ］．自动化学报，２０１４，４０（１１）：２４０４⁃２４１３．ＫＥＷｅｎｄｅ，ＰＥＮＧＺｈｉｐｉｎｇ，ＣＡＩＺｅｓｕ，ｅｔａｌ．Ｓｔｕｄｙｏｆｔｒａｊｅｃｔｏｒｙｔｒａｃｋｉｎｇｃｏｎｔｒｏｌｆｏｒｈｕｍａｎｏｉｄｒｏｂｏｔｂａｓｅｄｏｎｓｉｍｉｌａｒｉｔｙｌｏｃｏｍｏｔｉｏｎ［Ｊ］．ＡｃｔａＡｕｔｏｍａｔｉｃａＳｉｎｉｃａ，２０１４，４０（１１）：２４０４⁃２４１３．［１５］游峰，王荣本，张荣辉，等．智能车辆换道与超车轨迹跟踪控制［Ｊ］．农业机械学报，２００８，３９（６）：４２⁃４５．ＹＯＵＦｅｎｇ，ＷＡＮＧＲｏｎｇｂｅｎ，ＺＨＡＮＧＲｏｎｇｈｕｉ，ｅｔａｌ．Ｌａｎｅｃｈａｎｇｉｎｇａｎｄｏｖｅｒｔａｋｉｎｇｃｏｎｔｒｏｌｍｅｔｈｏｄｆｏｒｉｎｔｅｌｌｉｇｅｎｔｖｅｈｉｃｌｅｂａｓｅｄｏｎｂａｃｋｓｔｅｐｐｉｎｇａｌｇｏｒｉｔｈｍ［Ｊ］．ＴｒａｎｓａｃｔｉｏｎｓｏｆＴｈｅＣｈｉｎｅｓｅＳｏｃｉｅｔｙｆｏｒＡｇｒｉｃｕｌｔｕｒａｌＭａｃｈｉｎｅｒｙ，２００８，３９（６）：４２⁃４５．［１６］ＫＵＨＮＥＦ，ＬＡＧＥＳＷＦ，ｅｔａｌ．Ｍｏｄｅｌｐｒｅｄｉｃｔｉｖｅｃｏｎｔｒｏｌｏｆａｍｏｂｉｌｅｒｏｂｏｔｕｓｉｎｇｌｉｎｅａｒｉｚａｔｉｏｎ［Ｊ］．ＰｒｏｄｅｅｄｉｎｇｓｏｆＭｅｃｈａｔｒｏｎｉｃｓａｎｄＲｏｂｏｔｏｔｉｃｓ，２００４（４）：５２５⁃５３０．［１７］曹哲．变曲率弯道四轮独立驱动电动汽车动力学稳定性控制及其悬架设计［Ｄ］．南京：东南大学，２０１７．ＣＡＯＺｈｅ．ＤｙｎａｍｉｃＳｔａｂｉｌｉｔｙＣｏｎｔｒｏｌａｎｄＳｕｓｐｅｎｓｉｏｎＤｅｓｉｇｎｏｆＦｏｕｒ⁃ｗｈｅｅｌＩｎｄｅｐｅｎｄｅｎｔＤｒｉｖｉｎｇＥｌｅｃｔｒｉｃＶｅｈｉｃｌｅｗｉｔｈＶａｒｉａｂｌｅＣｕｒｖａｔｕｒｅＣｏｒｎｅｒ［Ｄ］．Ｎａｎｊｉｎｇ：ＳｏｕｔｈｅａｓｔＵｎｉｖｅｒｓｉｔｙ，２０１７．（责任编辑：黄杨程）６㊀㊀重庆交通大学学报（自然科学版）㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀第３８卷。
车辆系统动力学
车辆系统动力学概述车辆系统动力学是研究车辆运动和控制的重要分支，主要关注车辆在不同条件下的运动特性和动力学行为。
它涉及到车辆控制、悬挂系统、轮胎力学、车辆稳定性等多个方面的知识，并在实际应用中对车辆的设计、开发和安全性能有着重要作用。
车辆运动模型在车辆系统动力学中，常用的车辆运动模型有点模型、刚体模型和多体模型。
点模型点模型是简化的车辆运动模型，将车辆简化为质点，只考虑车辆的整体运动特性，忽略车辆的细节结构和内部力学行为。
虽然点模型失去了对车辆细节的描述，但其简单性使得其在一些特定的场景中得到广泛应用，如路径规划、运动控制等。
刚体模型刚体模型是将车辆看作一个刚性物体，不考虑车辆内部部件的变形和变动。
其关注车辆整体的旋转和平移运动状态，通过刚体模型可以研究车辆的稳定性、操控性和安全性能，对车辆动力学的分析具有重要意义。
多体模型多体模型是将车辆分解为多个连接的刚体，考虑车辆内部各个部件之间的相互作用和相互影响。
多体模型可以更准确地描述车辆的运动特性，并考虑轮胎和地面之间的接触力、悬挂系统的影响等因素，对于研究车辆的运动控制和动力学行为更具有实用性。
轮胎力学轮胎是车辆系统动力学中一个重要的组成部分，其力学特性对车辆的运动和稳定性有着直接影响。
轮胎在车辆运动过程中扮演着传递动力、提供支撑力和提供制动力的重要角色。
轮胎的力学特性主要包括纵向力学、横向力学和侧向力学。
纵向力学纵向力学研究轮胎在车辆加速和制动过程中的力学行为。
在车辆加速时，轮胎需要传递动力到地面，提供足够的附着力，以确保车辆的稳定性。
在制动过程中，轮胎需要提供足够的制动力，使得车辆能够迅速停下来。
了解轮胎的纵向力学特性对于车辆的动力学行为分析和控制具有重要意义。
横向力学横向力学研究轮胎在车辆转向过程中的力学行为。
在车辆转向时，轮胎需要提供足够的侧向力，以保持车辆的稳定性。
横向力学的研究对于车辆的操控性能分析和提升具有重要意义。
侧向力学侧向力学研究轮胎在侧向偏移和滑移过程中的力学行为。
基于稳态转向特性的智能车辆换道轨迹规划
曲率进行限制，以防止车辆在换道过程中出现侧滑现象，分析了交通车对换道安全性的影响，利用多项式函数进行换道轨
迹 规 划 ，以 车 辆 侧 向 加 速 度 和 换 道 时 间 为 换 道 优 化 函 数 的 优 化 变 量 ，建 立 了 基 于 稳 态 转 向 特 性 和 换 道 安 全 距 离 的 换 道 模
和空间内的行驶轨迹[3]。而换道是车辆最基本的驾驶行 为，智能车辆换道轨迹规划的研究对提高公路交通安全 性、提高交通效率具有重要意义。
目前，国内外学者从不同角度对智能车辆的轨迹规 划问题展开了研究。陈成等人提出一种基于四阶贝塞 尔曲线的轨迹规划方法，并通过参数优化规划出曲率变 化最小的轨迹曲线，但对交通车的考虑较少，实际应用 较为困难[4]。杨志刚等人提出了等速偏移轨迹函数和正
汽车技术 · Automobile Technology
基于稳态转向特性的智能车辆换道轨迹规划*
张新锋 1,2 李传友 1,2 夏八科 1,2
（1.长安大学，汽车运输安全保障技术交通行业重点实验室，西安 710064；2.长安大学，汽车学院，西安 710064）
【摘要】为提高智能车辆在高速公路上的换道安全性，分析了车辆在高速状态下的转向特性并对换道轨迹曲线的最大
Lane Changing Trajectory Planning for Intelligent Vehicle Based
2024车辆工程毕业设计选题
选题：智能车辆路径规划与控制系统的设计与实现毕业设计概述：本毕业设计旨在通过对2024年车辆工程专业的深入学习和实践，设计并实现一个智能车辆路径规划与控制系统。
该系统将运用先进的路径规划算法，结合车辆动力学模型，实现对车辆的自主导航和控制。
设计任务与目标：1. 设计并实现一种基于机器学习的路径规划算法，能够根据环境信息自动规划出最优行驶路径。
2. 建立车辆动力学模型，通过控制算法实现对车辆的自主导航和控制。
3. 实现智能车辆与外部环境的交互，包括障碍物识别、交通信号识别等。
4. 完成系统的软硬件设计，包括硬件选型、电路设计、软件编程等。
5. 测试与优化系统性能，确保系统的稳定性和可靠性。
关键技术点：1. 路径规划算法：采用基于机器学习的A*算法，通过学习历史行驶数据，实现对未知环境的自适应规划。
2. 车辆动力学模型：建立包含速度、加速度、转向角等变量的动力学模型，用于控制车辆的行驶。
3. 传感器融合技术：利用雷达、激光雷达（LiDAR）等传感器，实现障碍物识别和环境感知。
4. 通信技术：实现智能车辆与外部系统的通信，包括GPS、蓝牙等。
设计过程：1. 确定设计方案，进行系统架构设计。
2. 搜集相关文献和资料，为算法设计和硬件选型提供参考。
3. 完成路径规划算法和车辆动力学模型的编程实现。
4. 搭建实验平台，进行系统测试和优化。
5. 完成智能车辆与外部环境的交互设计和实现。
6. 进行系统集成和测试，确保各部分功能的正常运作。
预期成果：本设计预期实现一个智能车辆路径规划与控制系统，能够根据环境信息自主规划最优行驶路径，实现对车辆的自主导航和控制。
该系统将具有以下成果：1. 实现智能车辆的自主导航和控制，提高行驶安全性和效率。
2. 提高交通拥堵情况下的通行能力，缓解交通压力。
3. 为无人驾驶技术的发展提供实践经验和理论依据。
4. 为智能交通系统的发展提供技术支持和参考案例。
总结：本毕业设计旨在通过对智能车辆路径规划与控制系统的设计与实现，深化对车辆工程专业的理解和应用。
基于MATLAB的无碳小车轨迹优化
将a、b的参数值以及式（5）代入式（4），可得转向架与车身的夹角
由于前轮与车身方向的夹角与转向架与车身的夹角互余，则可得前轮与车身方向的夹角
考虑到前轮轮轴随时间变化间歇摆动，故将θ写成关于时间的分段函数
式中：ψ=b0+0.8πrcos（0.8πt）；k∈N。
[8]李杰,谢良喜,马昭,等.无碳小车轨迹模拟及转向机构的优化[J].机械工程师,2015(7):36-38.
[9]同济大学.高等数学[M].北京:北京高等教育出版社,2006.
[10]方兴.智能车动力学模型参数辨识方法研究[D].上海:上海交通大学,2009.
[11]曹斌,张海波,朱华炳.基于槽轮机构的8字轨迹无碳小车设计[J].合肥工业大学学报(自然科学版),2014(6):661-665.
5结 论
1）设计了一种轨迹近似于“8”字型的无碳小车，详细介绍了其内部结构与工作原理，并利用解析法建立了小车转向机构以及运行轨迹的数学模型。
2）根据建立的小车轨迹模型，利用MATLAB对小车运行轨迹进行仿真，得到一个运行周期内的小车参数最优值。为了减小小车累积误差，在单周期最优值基础上进行多周期仿真，分析仿真结果，得到小车轨迹最小误差时的小车最优参数值r=0.005 35 m，b=0.013 45 m。
[16]赵华成,刘武,潘聪华,等.重力势能驱动的自行避障小车设计与制作[J].浙江水利水电学院学报,2016,28(6):73-76.（责任编辑 马忠臣）
根据式（6），利用MATLAB绘制出如图4所示的前轮摆角变化曲线。
图4 小车前轮摆角随时间变化关系
由图4可知，小车前轮每个周期内包括2次换向，2次间歇停止摆动，符合实际情况，验证了所建立方程正确。由图4易知，前轮偏向于车身一侧时，角度值为正，偏向于车身另一侧时角度值则为负。
基于车速依赖静态输出反馈的自主汽车路径跟踪控制
基于非奇异终端滑模和主动抗干扰控制的鲁棒 ＡＧＶ 路径跟随控制策
略，将复杂路径跟随问题简化为简单的偏航角跟踪问题；文献［１０］ 则
提出了一种将自适应与滑模控制相结合的新型方法，用于 ＡＧＶ 的自
动转向控制．
收稿日期 ２０２０⁃１０⁃２３
资助项目 国家自然科学基金（６２０７３０８３）；广东
省自然科学基金（ ２０１９Ｂ１５１５０２０２６）；广东省特
支计划（２０１８Ｂ０３３０３１２００６）
作者简介
姜正伟，男，硕士生，主要研究方向为自主
汽车．ｊｉａｎｇｌｕｃｋ０９＠ ｆｏｘｍａｉｌ．ｃｏｍ
李攀硕（ 通信作者） ，女，博士，教授，主要
研究方向为时变系统、切换系统、网络化控制
遗传算法来优化 ＰＩＤ 控制器中的参数，避免了控制器参数转向的繁
琐和费时问题．自适应控制与滑模控制也被应用于路径跟踪控制中：
文献［７］ 提出了一种基于无模型自适应控制的无人驾驶汽车横向控
制方案，将汽车路径跟踪控制问题转化成预瞄偏差角跟踪问题；文献
［８］ 提出了一种基于李雅普诺夫函数（ Ｌｙａｐｕｎｏｖ） 的自适应 ＲＢＦ 神经
ＤＯＩ：１０．１３８７８ ／ ｊ．ｃｎｋｉ．ｊｎｕｉｓｔ．２０２１．０１．００６
姜正伟１ 李鹏旭２ 张斌１ 李攀硕１
基于车速依赖静态输出反馈的自主汽车路径跟踪控制
摘要
本文设计了一种新的基于静态输出
反馈的增益调度控制器，可使自主汽车
在车速时变且状态不全可测的情况下，
完成路 径 跟 踪 并 保 证 车 身 的 横 向 稳 定
控制器，并给出其中参数求取方法，所提
方法在实际应用中简单易行；最后在两
基于动力学系统的状态估计算法
基于动力学系统的状态估计算法赵天骐;江晓东;李鹏;白浩;于力【摘要】状态估计的收敛性是电网在线实时监测和控制的关键问题,常用的高斯-牛顿最小二乘算法在系统出现严重的拓扑错误以及存在不可观状态变量时难以收敛.针对这一问题,本文提出基于动力学系统的状态估计算法,通过构造商梯度动力系统,使其退化的稳定平衡流形与状态估计的最小二乘解对应,然后追踪该动力学系统的轨迹从而得到原状态估计问题的解.本文从非线性动力学系统理论出发,证明了该商梯度动力学系统是渐近稳定的,从而保证了算法的收敛性.最后用IEEE 14节点和IEEE 118节点算例对算法进行测试,验证了该算法的有效性.【期刊名称】《电力系统及其自动化学报》【年(卷),期】2018(030)008【总页数】6页(P81-86)【关键词】状态估计;动力学系统;加权最小二乘;不可观测性【作者】赵天骐;江晓东;李鹏;白浩;于力【作者单位】天津大学电气自动化与信息工程学院,天津 300072;天津大学电气自动化与信息工程学院,天津 300072;南方电网科学研究院有限责任公司,广州510080;南方电网科学研究院有限责任公司,广州 510080;南方电网科学研究院有限责任公司,广州 510080【正文语种】中文【中图分类】TM711电力系统状态估计是能量管理系统EMS（ener⁃gy management system）的主要功能之一，在监测和控制电力系统的可靠运行方面发挥着重要作用。
状态估计器通过电压、电流、线路功率、注入功率等测量来估计整个系统的状态，即每个母线的电压幅值和相角。
这些测量由数据采集与监视控制系统的远动终端提供。
状态估计结果为其他EMS功能，如安全分析、最优潮流、电压稳定性分析等提供基础。
因此状态估计的收敛性是电网在线实时监测和控制的关键。
基于高斯-牛顿迭代法的加权最小二乘WLS（weighted least squares）算法是最常用的状态估计算法。
基于动态系统稳定估计器的机器人变刚度轨迹规划
基于动态系统稳定估计器的机器人变刚度轨迹规划
谢啸;张涵;汤自林;高霄;肖晓晖
【期刊名称】《中南大学学报:自然科学版》
【年(卷),期】2022(53)4
【摘要】针对现有基于动态系统稳定估计器(SEDS)的机械臂轨迹规划中无法兼顾运动精度和能量消耗的问题,提出变刚度轨迹规划的方法。
首先,采用SEDS对示教轨迹进行拟合,得到从空间任一起点到终点的收敛轨迹。
然后,基于人体上肢刚度模型,通过实验得到肌电信号与上肢末端刚度的映射关系,并使用高斯混合模型GMM 和高斯混合回归GMR学习示教的刚度。
最后,结合学习到的轨迹和刚度进行阻抗控制,然后进行抗干扰和变刚度实验。
研究结果表明:与定刚度轨迹规划方法相比,本文所提方法位置误差减小了78.1%,能耗降低16.1%。
机械臂能在到达目标点的位置精度与能量消耗之间取得较好的平衡,且当其受到外界干扰后,会根据控制器发出的期望位置调整自身运动,最终仍能收敛到目标点,具有较强的抗干扰能力。
【总页数】9页(P1250-1258)
【作者】谢啸;张涵;汤自林;高霄;肖晓晖
【作者单位】武汉大学动力与机械学院
【正文语种】中文
【中图分类】TP24
【相关文献】
1.基于变刚度纤维曲线铺放的机器人铺放路径规划及运动仿真
2.基于质心稳定的四足机器人轨迹规划与仿真
3.基于谐波轨迹和中枢模式发生器的工业机器人在线轨迹规划
4.基于Simulink/SimMechanics的四足机器人足端轨迹规划及动态仿真分析
5.煤矸石分拣机器人动态目标稳定抓取轨迹规划
因版权原因，仅展示原文概要，查看原文内容请购买。
基于伺服运动系统的三步非线性控制方法
基于伺服运动系统的三步非线性控制方法
高兴泉;孙浩;杨昊
【期刊名称】《科学技术创新》
【年(卷),期】2024()6
【摘要】为了提高伺服运动系统的瞬态性能,加快系统的响应速度,获得更优的轨迹跟踪效果,本文提出了伺服运动系统三步非线性控制方法。
首先假定伺服运动系统达到稳定状态,求得类稳态控制律;其次考虑参考目标的动态变化,求出前馈控制律;接着利用参考目标与实际输出之间的差值设计误差反馈控制律,最后通过仿真验证了所提方法的有效性。
【总页数】4页(P75-78)
【作者】高兴泉;孙浩;杨昊
【作者单位】吉林工业职业技术学院信息工程学院;吉林化工学院信息与控制工程学院
【正文语种】中文
【中图分类】TP273
【相关文献】
1.一种基于积分反推原理的非线性伺服控制方法
2.基于Backstepping方法的齿隙非线性伺服系统神经网络控制
3.一种基于交流伺服系统的非线性控制方法
4.一种基于积分反推原理的非线性伺服控制方法
5.含齿隙非线性的双电机驱动伺服系统控制研究--基于反演积分自适应方法
因版权原因，仅展示原文概要，查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
{
[
]}
（ 10 ） θ t = θ0 ± （ 11 ）
该解析表达式表达的是汽车在给定速度下， 对应于不同的转角输入其运动学的响应 ， 可以较 为准确地反映车辆的运动轨迹， 而且数值计算效 率高、 实时性好。 2． 2． 2 模型参数识别 k2 ， 稳态动力学模型存在参数 k1 、 在实车以及 k2 不仅仅是前轮、 k1 、 后轮的 主流动力学模型中， 侧偏刚度， 通常无法直接给出， 需要经过参数识别 得出。 本文利用 Carsim 稳态转向实验数据， 通过
Illustration of traffic vehicle trajectory prediction
第6 期
等： 基于车辆稳态动力学特性的汽车动态轨迹规划 孙浩，
· 173·
获得。 首先， 通过“采样 ”将不同时刻交通车的位 置投影到道路网格中。 则未来任意时刻交通车在 该坐标系下的坐标均可以由式 （ 4 ） 确定。 式 （ 4） 得出该交通车在未来任意时刻所占据的空间 位置。
· 172·
国防科技大学学报
第 35 卷
1
整体方案描述
2
2． 1
车辆动态轨迹规划
交通车轨迹预估以及搜索空间建立
设 本文介绍的轨迹规划方法采用“模块化 ” 计思想， 根据功能进行模块划分和设计， 如图 1 所 。“汽车行驶环境模块 ” 示 包含道路信息， 如车道 ； “交通车辆模块 ” 宽度、 车道数目、 路面附着系统 ； “轨迹规划模块 ” 预估交通车状态 在每次规划周 期开始时获得当前时刻下的主车以及相关交通信 ； “轨迹跟随控制模块 ” 息并进行轨迹规划 接受规 划轨迹并产生方向盘转角、 油门开度、 制动踏板角 ； “车辆动力学模块 ” 度等控制信号 接受到控制信 号后产生相应的响应， 即实际轨迹； 主车状态在规 划周期开始时实时更新。
态轨迹规划算法。该算法在交通车轨迹预估基础上建立搜索空间， 利用车辆稳态动力学模型作为轨迹发生 器， 在搜索空间中对轨迹发生器产生的轨迹进行评价， 根据驾驶意图和优化条件选择最优轨迹 。采用基于最 优加速度预瞄理论的轨迹跟踪算法， 建立了七自由度车辆动力学模型， 并在 Simulink 环境下搭建仿真平台， 进 行超车仿真实验。实验结果表明该算法可行 、 有效。 关键词： 驾驶辅助系统； 动态轨迹规划； 车辆动力学； 轨迹决策； 轨迹跟踪 中图分类号： U461． 99 文献标志码： A 文章编号： 1001 － 2486 （ 2013 ） 06 － 0171 － 06
0 r
（ 2）
虽然通过适当传感可以获取交通车当前时刻 u（ t） ） 也 且状态方程 f（ x（ t） ， 的初始状态值 x（ 0 ） ， 可通过经验获得， 但状态方程的输入 u（ t） ∈ U（ U 所以未来的行驶轨 为外界输入集合 ） 无法确定， 迹并不确定， 因此估算交通车的行驶轨迹只有概 率和统计上的意义。 然而在实际情况下， 大多数车 在大多数时候遵循基本的交通行驶模式 ， 因此本 文中合理地假定交通车保持当前状态 （ 速度和方 向） 不变， 并在此前提下对其未来轨迹进行估算 ， 如式（ 3 ） 。 很显然轨迹估算的周期越短， 该假设也
基于此假设进行交通车轨迹预估， 如图 3 所 示， 以主车规划时刻质心为坐标原点， 主车行驶方 向为 x 轴的笛卡尔坐标系下， 进行交通车轨迹预 估。 交通车的轨迹估算基于简单的物体运动模型
图2 Fig． 2
轨迹规划模块 Fig． 3
图3
交通车轨迹预估示意图
Trajectory planning block
（ 4） Y t = Y0 ± u
同理， 可以将所有感兴趣交通车未来任意时 刻的位置投影到该坐标系下， 如图 4 ， 所有预估轨 “时间”与 “空间 ”信息的主 迹共同组成同时包含 车轨迹规划搜索空间。 通过这样的方式， 在一个规 划周期内， 将动态环境的时间变量转化为静态环 境的空间变量。
L（ 1 + Ku ） uδ 1 － sin t uδ L（ 1 + Ku2 ） uδ t L（ 1 + Ku2 ）
ห้องสมุดไป่ตู้
收稿日期： 2013 － 04 － 02 基金项目： 国家自然基金资助项目（ 51175215 ） Email： sunhao0913@ gmail． com； 作者简介： 孙浩（ 1988 —） ， 男， 山东聊城人， 博士研究生， Email： suminzhang@ 163． com 张素民（ 通信作者） ， 男， 讲师， 博士，
图4 Fig． 4
安全轨迹示意图
最小二乘辨识方法获得。 k2 ） = v err （ k1 ， k2 ） = ω err （ k1 ， k1 ， k2 ） δ， ∑ （ f（ u， k1 ， k2 ） δ， ∑ （ g（ u， － f carsim ）
2
Illustration of safe trajectory
Ｒ =
u ωr
（ 8）
Y0 ， 若车辆初始位置为 X0 ， θ0 ， 那么在 t 时刻 后， 车辆的状态可以解析地表达为： X t = X0 + u L（ 1 + Ku2 ） uδ cos t uδ L（ 1 + Ku2 ）
2
{y
x ti = x t0 + v tx × t i
ti
(
)
（ 9）
= y t0 + v ty × t i
第 35 卷 第 6 期 2013 年 12 月
国 防 科 技 大 学 学 报 JOUＲNAL OF NATIONAL UNIVEＲSITY OF DEFENSE TECHNOLOGY
Vol． 35 No． 6 Dec． 2013
基于车辆稳态动力学特性的汽车动态轨迹规划 *
孙 浩， 张素民
( 吉林大学 汽车仿真与控制国家重点实验室， 吉林 长春 130022 ) 摘 要： 针对高动态环境下驾驶辅助系统（ ADAS ） 的轨迹规划问题， 提出基于车辆稳态动力学特性的动
*
2］ 文献［ 提出一种自由环境下车辆轨迹规 ， 划算法 但 没 有 讨 论 结 构 化 环 境 中 轨 迹 规 划 问 3］对非 完 整 机 器 人 轨 迹 规 划 问 题 进 题 。 文献［ 1］中 行了系统研究 ， 提出多种解决方法 。 文献［ 用多项式 表 达 汽 车 轨 迹 ， 考虑了车辆运动学和 动力学约 束 ， 但对终点状态未知的轨迹规划没 4］ 有讨论 。 文献［ 考虑车辆纵向动力学 ， 并沿指 5］对 不 同 定路径进行轨 迹 规 划 与 决 策 。 文 献［ 优化条件下的轨迹规划方法进行了总结 。 以上 研究均取 得 了 不 错 的 研 究 成 果 ， 但是较少同时 考虑汽车横向动力学以及规划过程交通车状态 的变化 。 并 且 大 多 假 定 终 点 状 态 已 知 ， 这与实 际情况不相符 。 本文在已有研究基础之上， 结合实际应用， 提 出一种基于车辆稳态动力学的汽车动态轨迹规划 方法。
对汽车行驶交通环境中交通参与物位置和运 动状态的估计是进行汽车轨迹规划的前提 ， 也是 保障汽车安全行驶的关键。交通车的动力学可用 下式表达： = f（ x（ t） ， x u（ t） ） （ 1） u 为交通车的连续输入， 上式中 x 是状态变量， 所 以在 t = r 时刻下， 车辆状态为 x（ r） = x（ 0 ） + u（ τ） ） dτ ∫ f（ x（ τ） ，
图1 Fig． 1
功能流程图
就越合理。 x（ r） = x（ 0 ） + 0 ） dτ ∫ f（ x（ τ） ，
0 r
Functional flowchart
（ 3）
轨迹规划模块是本文研究内容的核心， 为了 更加逼近真实应用以及更好地进行算法调试 、 升 级， 轨 迹 规 划 也 分 成 若 干 子 系 统， 如 图 2 所 示。 “传感器” 模块感知交通车、 道路信息并将其转换 到规划时刻以主车质心为坐标原点的车体坐标系 ； “轨 迹 生 下， 并将 感 兴 趣 信 息 传 递 到 需 要 模 块 成” 模块根据主车当前状态和稳态动力学模型产 ； “驾驶意图 ” 生待决策轨迹簇 模块将驾驶员输入 “轨迹决策” ； “轨迹决策 ” 的意图传给 模块 模块根 ， 据传感信息建立搜索空间 并结合驾驶员意图从 待决策轨迹簇中决策出最优轨迹 。
若任意时刻、 任意交通车， 对于规划轨迹 L， 均有 HL （ ti ） ∩ Tj （ ti ） = O （ 5）
Dynamic trajectory planning based on vehicle steady dynamics
SUN Hao ，ZHANG Sumin
（ State Key Laboratory of Automobile Simulation and Control ，Jilin University，Changchun 130022 ， China） Abstract： A dynamic trajectory planning algorithm based on vehicle steadystate dynamics for driver assistance systems （ ADAS ） under high dynamic environment is proposed． The algorithm built a ＇search space＇on the basis of traffic vehicle trajectory prediction and used the vehicle steadystate kinetic model as a trajectory generator． Every trajectory produced by the generator was evaluated in the search space and the optimal trajectory under optimal conditions was selected． In order to realize the closedloop dynamic simulation ，the corresponded trajectory tracking algorithms and vehicle dynamics model were also proposed． A simulation platform under Simulink environment was built for simulation tests． The results show that in the intelligent overtaking test case，the proposed algorithm is able to overtake safely and to meet the needs of intelligent assistance systems． Key words： ADAS； dynamic trajectory planning； vehicle dynamics； trajectory decision making； trajectory tracking