运筹学 第二章线性规划的对偶理论(研究生)
合集下载
运筹学第二章__线性规划的对偶理论a管理精品资料

原问题 决策变量X 松弛变量XS
基变量XB 非基变量XN
对偶问题 松弛变量YS 决策变量Y
非基变量YN 基变量YB
证明: (1)由 max z CX max z CX
AX b X 0
AX X S b X 0, X S 0
得: min w Yb
min w Yb
YA C
YA Y S C
将上述结果,代入原问题的约束方程,得二
元线性方程组
2 x3 3x4 20 3x3 2 x4 20
解得 x3 x4 4
所以原问题的最优解为 X00,0,4,4T,
相应的最大值Z=28。
原问题与对偶问题解的对应关系:
第四节 影子价格 (LP模型计算结果的经济解释)
在最优条件下,原问题和对偶问题的目 标函数分别是:
对偶问题: max z=24y1+ 15y2 +30y3 - 10y4 s.t - 4y1- 3y2 + 0y3 + 2y4 ≥ 7 2y1+ y2 + 5y3 – 2y4 = 4 - 6y1+ 2y2 + 3y3 + 4y4 ≤-3 y1 ≤ 0 , y2≥0, y3无约束,y4≥0
原问题与对偶问题的一般对应关系见表2-2。
矩阵形式: 原问题
max z CX AX b X 0
对偶问题
min w Yb YA C Y 0
第二节 原问题与对偶问题的一般对应关系
例1、例2.结论:LP对偶问题的对偶问题就是原问题。
例3. 写出下列LP的对偶问题
原问题: min z=7x1+ 4x2 -3x3 s.t - 4x1+ 2 x2 - 6x3 ≤ 24 → y1 ≤0 -3x1+ x2 +2x3 ≥ 15 → y2 ≥ 0 5x2 +3x3 = 30 → y3 无约束 2x1- 2x2 +4x3 ≥ -1 → y4 ≥0 x1 ≤ 0 , x2取值无约束,x3≥0
运筹学课件第二章线性规划的对偶理论及其应用

对偶问题同时解
– 原问题为基础可行解,对偶问题为非可行解,但满足
互补松弛条件;则当对偶问题为可行解时,取得最优 解
13
2.2.5 原问题检验数与对偶问题的解
• 在主对偶定理的证明中我们有:对偶(min型)变量的最 优解等于原问题松弛变量的机会成本,或者说原问题松 弛变量检验数的绝对值
• 容易证明,对偶问题最优解的剩余变量解值等于原问题 对应变量的检验数的绝对值
1
1/2 5/2
1
1
0
1/2 3/2
0
0
0
1/2 3/2
OBJ=
39
9/2
3
6
6
0
3/2
3/2
cj - zj
1/2
0
0
0
0
3/2 -M-3/2
0
x4
4
0
0
1
1
1
1
3
5
x1
6
1
0
2
2
0
1
1
3
x2
4
0
1
1
(1)
0
1
2
OBJ=
42
5
3
7
7
0
2
1
cj - zj
0
0
1
1
0
2 -M+1
0
x4
ቤተ መጻሕፍቲ ባይዱ
8
0
1
0
0
1
0
1
5
x1
数值,
g(Y0)=Y0b= CBB1 b
而原问题最优解的目标函数值为
f(X0)=CX0= CBB1 b 故由最优解判别定理可知Y0 为对偶问题的最优解。证毕。
– 原问题为基础可行解,对偶问题为非可行解,但满足
互补松弛条件;则当对偶问题为可行解时,取得最优 解
13
2.2.5 原问题检验数与对偶问题的解
• 在主对偶定理的证明中我们有:对偶(min型)变量的最 优解等于原问题松弛变量的机会成本,或者说原问题松 弛变量检验数的绝对值
• 容易证明,对偶问题最优解的剩余变量解值等于原问题 对应变量的检验数的绝对值
1
1/2 5/2
1
1
0
1/2 3/2
0
0
0
1/2 3/2
OBJ=
39
9/2
3
6
6
0
3/2
3/2
cj - zj
1/2
0
0
0
0
3/2 -M-3/2
0
x4
4
0
0
1
1
1
1
3
5
x1
6
1
0
2
2
0
1
1
3
x2
4
0
1
1
(1)
0
1
2
OBJ=
42
5
3
7
7
0
2
1
cj - zj
0
0
1
1
0
2 -M+1
0
x4
ቤተ መጻሕፍቲ ባይዱ
8
0
1
0
0
1
0
1
5
x1
数值,
g(Y0)=Y0b= CBB1 b
而原问题最优解的目标函数值为
f(X0)=CX0= CBB1 b 故由最优解判别定理可知Y0 为对偶问题的最优解。证毕。
第二章对偶理论
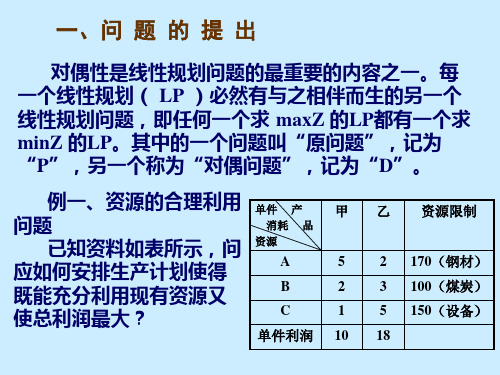
3 5
x1 , x2 , x3 0
解:首先将原式变形
max Z 2 x1 3 x2 4 x3
2 x 3 x2 5 x3 2
3 x1 x2 7 x3 3
x1 4 x2 6 x3
5
x1 , x2 , x3 0
注意:以后不强调等式右段项 b≥0,原因在对偶单
纯型表中只保证 而j 不0 保证
=(1.1),分别是
(P_)_ 和__(D)的可行解。Z=10 ,W=40,故有
C X < Y b ,弱对偶定理成立。由推论⑴可知,W 的最
小值不能小于10,Z 的最大值不能超过40。
例二、已知
p : max Z x1 2x2
D : minW 2 y1 y2
x1 x2 x3 2
2x1 x2 x3 1
n
j 1
aij
yi
cj
(对偶问题)
yi 0
目标函数 约束条件
原问题
对偶问题
max
min
≤
≥
变量数量 约束条件个数
约束条件个数 变量数量
例三、
23
x1
x2
原问题
12 y1 2
2
≤ 12
8
y2
1
2
≤
8
16 y3 4 0 ≤ 16 12 y4 0 4 ≤ 12
对偶问题 2 3
二、线性规划的对偶理论
原问题 问题无界
无可 行解
对偶问题 无可 行解
问题无界
(对)
y1 y1
y1
y2 y2 0, y2
2 1 0
无可 行解
推论⑶.在一对对偶问题(P)和(D)中,若一个可 行(如P),而另一个不可行,(如D),则该可行的 问题无界。
运筹学(第2章 线性规划的对偶理论)

min w 15 y1 24 y 2 5 y 3 6 y 2 y 3 y4 2 s.t 5 y1 2 y 2 y 3 y5 1 yi 0
分别用单纯形法求解上述2个规划问题,得到最终单纯形表如 下表:
原问 题最 优表
XB x3 x1 x2
-2 3 -3 1 5 7 1 -4 -6
2 y1 3 y2 y3 2 3 y y 4 y 3 1 2 3 5 y1 7 y2 6 y3 4 y1 , y2 , y3 0
(2) 非对称型对偶问题 若给出的线性规划不是对称形式,可以先化成对 称形式再写对偶问题。也可直接按教材表2-2中的对 应关系写出非对称形式的对偶问题。
y2
y3
1/4
1/2
-4/5
15/2 15/2
1
0 0
0
1 0
-1/4
1/2 7/2
1/4
-3/2 3/2
j
原问题与其对偶问题的变量与解的对应关系: 在单纯形表中,原问题的松弛变量对应对偶 问题的变量,对偶问题的剩余变量对应原问 题的变量。
弱对偶性;强对偶性;
最优性; 无界性; 互补松弛性
性质1 对称性定理:对偶问题的对偶是原问题 min W= Y b s.t. YA ≥ C Y≤0
对偶性质(Dual property)
性质4 强对偶性:若原问题及其对偶问题均具有可行解, 则两者均具有最优解,且它们最优解的目标函数值相等, 即 max z min w
故
证明:将原问题化成标准形式
m ax z c j x j
j 1 n n
yi 0 (i 1,, m)
是对偶问题的可行解, 又因
运筹学第二章线性规划的对偶理论

(5.5) (5.6)
4.3 对偶问题的基本性质
证: 设B是一可行基,于是A=(B,N)
max z=CBXB+ CNXN BXB+BXN +Xξ=b X,XB,Xξ ≥0
其中Yξ=(Yξ1, Yξ2)
min ω =Yb YB-Yξ1=CB YN-Yξ2=CN Y, Yξ1 Yξ2 ≥0
(5.5) (5.6)
x1﹐x2 ≥0
关系?
对原模型设: 1 2
A= 4 0 b=(8,16,12)T C=(2,3) 04
X=(x1,x2)T Y=(y1,y2 ,y3 ) 则可得:
4.1 对偶问题的提出
min ω=8 y1+16y2 +12y3
y1+4y2
≥2
2 y1 +4y3≥3
与
y1 , y2 ,y3≥0 12
max z=2x1+3x2 x1+ 2x2 ≤8
4x1
≤16
4x2 ≤12
x1﹐x2 ≥0
有何关 系?
对愿模型设: A= 4 0 04
b=(8,16,12)T C=(2,3)
X=(x1,x2)T
Y=(y1,y2 ,y3 ) 则可得:
max z=CX AX≤b (5.1) 和
min ω =Yb YA ≥ C (5.2)
120
A=
1 -3
0 2
1 1
1 -1 1
b=(2,3,-5,1)T C=(5,4, 6)
确定约束条件
YA
C
x1 ≥0 ﹐x2≤0, x3 无约束
解:因原问题有3个变 于是 量,4个约束条件, 所以对偶问题4个 变量,3个约束条
运筹学 线性规划的对偶理论

线性规划单纯形表
初始单纯形表
cs xs b x A c
max z=cx+ 0xs s.t. Ax+xs= b x0, xs0
xs I 0
j
迭代单纯形表
x
cB xB B-1b B-1A c - cBB-1A
xs
B-1 - cBB-1
j
从数学上提出对偶问题
当线性规划问题找到最优解z*时,有:
如果极大化原始问题中一个约束是“≥”约束,则对偶问 题中相应的变量≤0
其他对偶关系
max z=cx s.t. Ax ≤ b
x ≥0
Ax ≥ b Ax = b x≤0
min w=bTy s.t. ATy ≥ CT y≥0
y≤0 y
free
ATy ≤ cT
x
free
ATy = cT
原始问题的经济解释
1、原始问题是利润最大化的生产计划问题
总利润(元) 单位产品的利润(元/件)
产品产量(件)
max z = c1 x 1 + c 2 x 2 L + c n x n s.t. a11 x 1 + a12 x 2 L + a1n x n + x n +1 + x n+2 a 21 x 1 + a 22 x 2 L + a 2 n x n
c - cBB-1A 0 - cBB-1 0 取y = (cBB-1)T 可得: ATy cT y0
cB xB B b 当xB=B-1b为原问题的最优解时, y
-1
如何选取y,使 w = bTy 最小?
min w= bTy
s.t. ATy CT y0
运筹学第2章-线性规划的对偶理论

❖ 影子价格不是市场价格,而是在现有技术和管理条件下, 新增单位资源所能够创造的价值,是特定企业的一种边 际价格;不同企业或同一企业不同时期,同种资源的影 子价格可能不同;当市场价格高于影子价格,可以卖出; 相反,则应买进,以获取更大收益
Ma例x:Z ( 2第x一1 章3例x22)
2 x1 2 x2 12
当原问题和对偶问题都取得最优解时,这 一对线性规划对应的目标函数值是相等的:
Zmax=Wmin
二、原问题和对偶问题的关系
1、对称形式的对偶关系
(1)定义:若原问题是
MaxZ c1 x1 c2 x2 cn xn
a11x1 a12 x2 a1n xn b1
s.t.a21
x1
a22
二、 手工进行灵敏度分析的基本原则 1、在最优表格的基础上进行; 2、尽量减少附加计算工作量;
5y3 3
,y
2
3
0
(用于生产第i种产 品的资源转让收益不 小于生产该种产品时 获得的利润)
对偶变量的经济意义可以解释为对工时及原材 料的单位定价 ;
若工厂自己不生产产品A、B和C,将现 有的工时及原材料转而接受外来加工时, 那么上述的价格系统能保证不亏本又最富 有竞争力(包工及原材料的总价格最低)
内,使得产品的总利润最大 。
MaxZ 2x1 3x 2
2x1 2x2 12
s.t.54xx12
16 15
x1, x 2 0
它的对偶问题就是一个价格系统,使在平衡了 劳动力和原材料的直接成本后,所确定的价格系统 最具有竞争力:
MinW 12y1 16y2 15y3
2y1 4y2
2
s.t.2y1y,1y
y1, y2, , ym 0
Ma例x:Z ( 2第x一1 章3例x22)
2 x1 2 x2 12
当原问题和对偶问题都取得最优解时,这 一对线性规划对应的目标函数值是相等的:
Zmax=Wmin
二、原问题和对偶问题的关系
1、对称形式的对偶关系
(1)定义:若原问题是
MaxZ c1 x1 c2 x2 cn xn
a11x1 a12 x2 a1n xn b1
s.t.a21
x1
a22
二、 手工进行灵敏度分析的基本原则 1、在最优表格的基础上进行; 2、尽量减少附加计算工作量;
5y3 3
,y
2
3
0
(用于生产第i种产 品的资源转让收益不 小于生产该种产品时 获得的利润)
对偶变量的经济意义可以解释为对工时及原材 料的单位定价 ;
若工厂自己不生产产品A、B和C,将现 有的工时及原材料转而接受外来加工时, 那么上述的价格系统能保证不亏本又最富 有竞争力(包工及原材料的总价格最低)
内,使得产品的总利润最大 。
MaxZ 2x1 3x 2
2x1 2x2 12
s.t.54xx12
16 15
x1, x 2 0
它的对偶问题就是一个价格系统,使在平衡了 劳动力和原材料的直接成本后,所确定的价格系统 最具有竞争力:
MinW 12y1 16y2 15y3
2y1 4y2
2
s.t.2y1y,1y
y1, y2, , ym 0
第2章 线性规划的对偶理论

≤9
y1≤0, y2≥0, y3无约束
2.1 线性规划的对偶模型 Dual model of LP
1.本节以实例引出对偶问题; 2.介绍了如何写规范与非规范问题的对偶问题;
作业:教材P61 T 1、2 下一节:对偶性质
2.2 对偶性质
Dual property
2.2 对偶性质 Dual property
时得到最优解,C CB B 1 A 是 X=(X B,X N)的检验数 CB CB B 1B 和
CN CB B1N 的合并。
令 Y CB B1 ,由 C CB B 1 A 0与 CB B 1 0 得
YA C Y 0
可见,这是Y是对偶问题的一个可行解。 思考:Y右边的部分是什么?
C X°≤Y°AX≤Y°b
这一性质说明了两个线性规划互为对偶时,求最大值的 线性规划的任意目标值都不会大于求最小值的线性规划 的任一目标值,不能理解为原问题的目标值不超过对偶 问题的目标值。
2.2 对偶性质 Dual property
由这个性质可得到下面几个结论:
(1)(LP)的任一可行解的目标值是(DP)的最优值下界; (DP)的任一可行解的 目标是(LP)的最优值的上界;
【例2.3】 写出下列线性规划的对偶问题
max Z 4x1 3x2
5x1 x2 6 7x1x135x2x2108 x1 0, x2 0
【解】这是一个规范形式的线性规划,它的对偶问题求 最小值,有三个变量且非负,有两个“ ≥”约束,即
min w 6 y1 8 y2 10 y3
5yy1172yy22
y3 3y3
4
3
yi 0,i 1,2,3
2.1 线性规划的对偶模型 Dual model of LP
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
以上两个线性规划分别称为线性规划的原问题和对偶问题。
第二节
原问题和对偶问题
一、对称对偶规划
二、非对称对偶规划
三、一般对偶规划 四、原问题和对偶问题的对应关系
一、对称的对偶规划
若两个线性规划分别是
Max z c1 x1 c2 x 2 ..... cn x n
Min w b1 y1 b2 y2 ..... bm ym
令
60 b 40 35
Y ( y1 , y2 , y3 )
x1 x max z 15 7 9 12 2 x3 x4 5 2 4 3 2 1 3 1 2 x1 0 x 0 2 x3 0 x 0 4 x1 2 60 x2 40 4 x3 5 35 x 4
y1' y1 等式约束对应自由变量 y2' y2
' " ' " 令 y1 y1 y1 , y2 y2 y2
写出它的对偶规划
' " ' " min w 10 y1 10 y1 8 y2 8 y2 ' " ' " 5 y1 5 y1 2 y2 2 y2 5 ' " ' " y1 y1 4 y2 4 y2 3 ' " ' " y1 y1 3 y2 3 y2 3 ' " ' " 8 y1 8 y1 2 y2 2 y2 4 y' , y" , y ' , y" 0 1 1 2 2
max z 15 x1 7 x2 9 x3 12 x4 5 x1 2 x2 4 x3 2 x4 60 3 x1 2 x2 x3 4 x4 40 s .t . 3 x1 x2 2 x3 5 x4 35 x , x , x , x 0 1 2 3 4
解 先将约束条件变形为“≤”形式 max z x1 x2 5 x3 7 x4
例5. 写出下面线性规划的对偶规划
max z x1 x2 5 x3 7 x4 x1 3 x2 2 x3 x4 25 2 x 7 x3 2 x4 60 1 30 s .t . 2 x1 2 x2 4 x3 5 x4 10 x1 , x2 0
A B C D 含量(单位/公斤) 原料拥有量 (单位) 60 40 35
x1
糖 蛋白质 脂肪 单价 (元/公斤) 5 3 3 15
x2
2 2 1 7
x3
4 1 2 9
x4
2 4 5 12
建立其数学模型。
解:设甲厂安排A、B、C、D的产量分别为x1、 x2、 x3、 x4 公斤,总产值为z 元。于是,例1的数学模型 为:
解:设y1,y2和y3(元/单位)分别代表乙厂收购糖、蛋 白质和脂肪的单价,乙厂收购原料付出的总费用为w元, 于是例2的数学模型为:
min w 60 y1 40 y2 35 y3 5 y1 3 y2 3 y3 15 2 y1 2 y2 y3 7 s .t . 4 y1 y2 2 y3 9 2 y 4 y 5 y 12 2 3 1 y1 , y2 , y3 0
一般对偶规划的特点
(1)原问题是“max,=,≤” 形式,对偶问题是“min, =,≥”形式 (2)原问题的每个等式约束,对应对偶问题一个自由变 量,原问题的每个不等式约束,对应对偶问题的一个非负 变量;反之亦然,即原问题中的每个非负变量对应的是对 偶问题中的一个不等式约束,而原始问题中的每个自由变 量对应对偶问题中的一个等式约束。 (3)原问题目标函数中的系数c就是对偶问题约束条件的 右端常数项,而原问题约束的右端常数项就是对偶问题目 标函数中的系数。 (4)如果用矩阵和向量形式写出问题(P)和(D)的约束, 可以看出这两个问题的约束系数矩阵互为转置。
a11 y1 a21 y2 .....am 1 ym c1 a11 x1 a12 x2 .....a1n xn b1 和 a21 x1 a22 x2 .....a2 n xn b2 a12 y1 a22 y2 .....am 2 ym c2 s .t . .................................... s .t . .................................... a x a x .....a x b a y a y .....a y c m1 1 m2 2 mn n m 2n 2 mn m n 1n 1 x j 0 j 1, 2, .....n yi 0 i 1, 2, .....m
max z CX AX b X 0
则称它们是一对对称的对偶规划。
min w Yb YA C Y 0
对称对偶规划还可以写成表格形式,称为对偶表
Max z
原问题(求极大)
c1 x1 c2 x2
a12 a22 … am2 c2
Min w
… …
… … … … …
不等式约束对应非负变量
二、非对称对偶规划
max z CX AX b X 0
min w Yb
YA C
叫做非对称的对偶规划。非对称的对偶规划可以由对 称对偶规划推出。 例4:写出下列线性规划问题的对偶规划。 max z 5 x1 3 x2 3 x3 4 x4
北京物资学院运筹学教学课件
第二章
线性规划的对偶理论
北京物资学院信息学院 2010年10月
本章主要内容
第一节、对偶问题的提出 第二节、原问题与对偶问题 第三节、对偶问题的基本性质 第四节、影子价格 第五节、对偶单纯形方法
第六节、灵敏度分析
第七节、线性规划的求解软件
第一节、对偶问题的提出
例1 甲食品厂用糖、蛋白质和脂肪三种原料生产四种复 合食品A、B、C、D,复合食品中含有各种原料的数量、 复合食品的单价、三种原料的拥有量分别如下表所示, 问甲厂如何安排生产才能使总产值达到最大?
5 x1 x2 x3 8 x4 10 2 x1 4 x2 3 x3 2 x4 8 x 0 ( j 1, 2, 3, 4) j
解:将上述线性规划化成对称对偶规划的形式
max z 5 x1 3 x2 3 x3 4 x4 5 x1 x2 x3 8 x4 10 5 x1 x2 x3 8 x4 10 s .t . 2 x1 4 x2 3 x3 2 x4 8 2 x 4 x 3 x 2 x 8 1 2 3 4 x j 0 ( j 1, 2, 3, 4)
C (15,7,9,12)
5 2 4 2 A 3 2 1 4 3 1 2 5
x1 x2 X x3 x 4
min w 60 y1 40 y2 35 y3 5 y1 3 y2 3 y3 15 2 y1 2 y2 y3 7 s .t . 4 y1 y2 2 y3 9 2 y 4 y 5 y 12 2 3 1 y1 , y2 , y3 0
cn xn
a1n a2n … amn cn
右端 项
b1 b2 … bm
对 偶 问 题 求极小
b1 b2 … bm
y1 y2
a11 a21 …
ym
am1 c1
右端项
对偶规划中的两个问题分别称为原问题和对偶问题 (互为对偶)。
一对对称形式的对偶规划之间具有下面的对应关系。 (1)若一个模型为目标求“极大”,约束为“小于等于” 的不等式,则它的对偶模型为目标求“极小”,约束是 “大于等于”的不等式。即“max,≤”和“min,≥”相对 应。 (2) 一个模型是m个约束,n个变量,则它的对偶模型为n 个约束,m个变量。从约束系数矩阵看:一个模型中为A, 则另一个模型中为AT。 (3)原问题目标函数系数是对偶问题的约束条件右端项; 原问题的约束条件右端项是对偶问题的目标函数系数。 (4)两个规划模型中的变量皆非负。
y1 min w 60 40 35 y2 y 3 5 3 3 15 y1 2 2 1 y 7 4 1 2 2 9 y3 2 4 5 12 y 0 1 y2 0 y 0 3
得 min w 10 y1 8 y2 5 y1 2 y2 5 y1 4 y2 3 s .t . y1 3 y2 3 8 y 2 y 4 2 1 y1 , y2 无符号限制
s .t .
三、一般对偶规划
max z c j x j
例1和例2的数学模型比较
max z 15 x1 7 x2 9 x3 12 x4 5 x1 2 x2 4 x3 2 x4 60 3 x1 2 x2 x3 4 x4 40 s .t . 3 x1 x2 2 x3 5 x4 35 x , x , x , x 0 1 2 3 4
例3:写出下列线性规划的对偶规划
min z 15 x1 24 x2 5 x3 s .t . 6 x2 x3 2 5 x1 2 x2 x3 1 x , x , x 0 2 3 1
