长方体与正方体易错题整理二
五下数学 长方体与正方体易错题训练 50题 带答案

长方体与正方体易错题训练50题1、一个正方体每个面的面积都是9平方厘米,这个正方体的棱长总和是(36)厘米。
2、一个长方体的长是5厘米,宽是3厘米,高是4厘米,它的表面积是(94 )平方厘米。
3、一个长方体不同方向三个面的面积分别是6平方厘米,12平方厘米,18平方厘米,则这个长方体的表面积是(72)平方厘米。
4、一个正方体的棱长是2厘米,把它的棱长扩大到原来的3倍,现在这个正方体的表面积是(216 )平方厘米。
5、正方体的棱长扩大到原来的3倍,表面积会扩大到原来的(9)倍。
6、把2个棱长3厘米的正方体拼成一个长方体,表面积比原来两个正方体减少( 18 )平方厘米,这个长方体的体积是( 54 )立方厘米。
7、把一根长80厘米,宽5厘米,高3厘米的长方体木料锯成长都是40厘米的两段,表面积比原来增加了(30)平方厘米。
8、一个长方体棱长之和是84厘米,长是8厘米,宽是7厘米,高是(6厘米),体积是(336 立方厘米)。
9、在括号里填上适当的数:4.3立方米=(4300)立方分米11.8立方分米=(11800)立方厘米3540立方厘米=(3.54 )立方分米6立方米40立方分米=(6.04)立方米5.5平方米=(5500)平方分米5立方分米180立方厘米=(5.18 )立方分米6.08升=(6)升(80)毫升2.4立方米=(2)立方米(400 )立方分米10、一个长方体的,长、宽、高都扩大到原来的2倍,它的表面积扩大到原来的(4)倍,它的体积扩大到原来的(8 )倍。
11、一个长8分米,宽0.7米,高5分米的长方体盒子,最多能够装下(24)个棱长为2分米的正方体木块。
12、一个长20厘米,宽20厘米,高15厘米的长方体纸盒内,最多能够放(700)个棱长为2厘米的正方体木块。
13、把3个棱长是4厘米的正方体木块粘合成一个长方体,这个长方体的体积是(192 )立方厘米,表面积比原来的3个小正方体表面积的和减少(64)平方厘米.14、将一个长为8分米宽为6分米,高为5分米的长方体木块切割成棱长为2分米的小正方体,一共可以割成(24 )块,把这些小正方体排成一行,一共长( 4.8 )米。
六上数学长方体和正方体表面积易错题
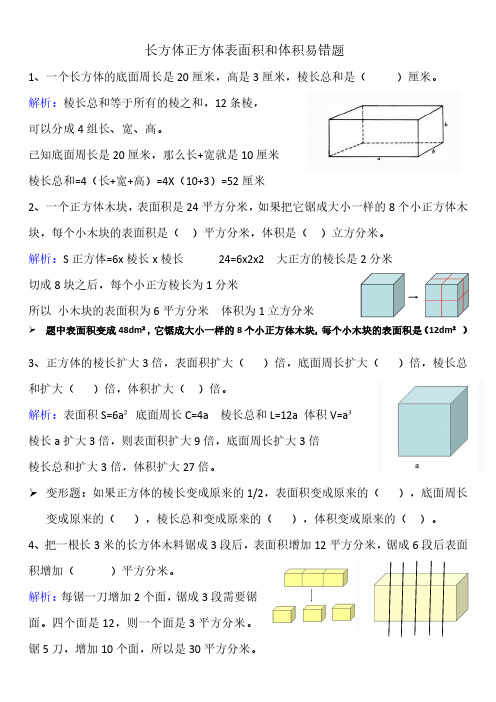
长方体正方体表面积和体积易错题1、一个长方体的底面周长是20厘米,高是3厘米,棱长总和是()厘米。
解析:棱长总和等于所有的棱之和,12条棱,可以分成4组长、宽、高。
已知底面周长是20厘米,那么长+宽就是10厘米棱长总和=4(长+宽+高)=4X(10+3)=52厘米2、一个正方体木块,表面积是24平方分米,如果把它锯成大小一样的8个小正方体木块,每个小木块的表面积是()平方分米,体积是()立方分米。
解析:S正方体=6x棱长x棱长24=6x2x2大正方的棱长是2分米切成8块之后,每个小正方棱长为1分米所以小木块的表面积为6平方分米体积为1立方分米题中表面积变成48dm²,它锯成大小一样的8个小正方体木块,每个小木块的表面积是(12dm²)3、正方体的棱长扩大3倍,表面积扩大()倍,底面周长扩大()倍,棱长总和扩大()倍,体积扩大()倍。
解析:表面积S=6a²底面周长C=4a棱长总和L=12a体积V=a³棱长a扩大3倍,则表面积扩大9倍,底面周长扩大3倍棱长总和扩大3倍,体积扩大27倍。
变形题:如果正方体的棱长变成原来的1/2,表面积变成原来的(),底面周长变成原来的(),棱长总和变成原来的(),体积变成原来的()。
4、把一根长3米的长方体木料锯成3段后,表面积增加12平方分米,锯成6段后表面积增加()平方分米。
解析:每锯一刀增加2个面,锯成3段需要锯2刀,增加了4个面。
四个面是12,则一个面是3平方分米。
要锯成6段,需要锯5刀,增加10个面,所以是30平方分米。
5、一个长方体,如果高增加2厘米就变成了一个正方体,这时表面积增加了56平方厘米,原来长方体的表面积是()平方厘米。
解析:要求原来长方体的表面积需要求出长宽高。
根据题意长方体的高增加2cm就变成了一个正方体,可以得出原来长方体的长和宽相等,且比高大2cm。
由题意高增加2cm,表面积增加56cm²。
人教版五年级数学下册长方体和正方体重点易错题解析40例

人教版五年级数学下册长方体和正方体重点易错题解析(精选40例)【1】长方体的位置任意改变,体积不变。
(√)易错题解析:一个物体不论横着放、竖着放或还其他位置摆放,物体所占空间大小不变,即物体的体积和位置无关。
【2】有6个面,12条棱、8个顶点的物体就是长方体。
(×)错题解析:一个物体是长方体,必须中间的四条棱要垂直于上下底面,而有6个面,12条棱、8个顶点的物体有可能是6个面的斜棱柱,中间的四条棱与底面不垂直。
【3】长方体的三条棱分别叫做长方体的长、宽、高。
(×)错因解析:长方体相交于一个顶点处的三条棱分别叫做长方体的长、宽、高,而长方体中任意的三条棱有可能为三条相等的长(或宽,或高),也有可能有两条相等的长(或宽,或高)。
订正:长方体相交于一个顶点处的三条棱分别叫做长方体的长、宽、高。
【4】长方体的棱可以分成4组,每组3条棱,分别是长、宽、高。
(×)错因解析:长方体有12条棱,除相对的两个面都为正方形外,其中4条长,4条宽,4条高长度分别相等,因此长方体的棱可以分成3组,每组3条棱长度相等。
订正:长方体的棱可以分成3组,每组4条棱,分别是4条长、4条宽、4条高。
【5】在长方体中,只有相对的棱长度相等。
(×)错题解析:长方体中,长和宽、宽和高、长和高并不相对,但是当长方体相对两个面完全相同,如上、下面完全相同,此时长、宽、高三个数值中,有两个数值可能相等。
订正:在长方体中,不是相对的棱长度可能相等。
【6】一个长方体,不可能有8条棱的长度都相等。
(×)错题解析:在长方体中,周围的四个面是完全相同的长方形,此时如另一组相对的面是两个完全相同的正方形,此时这两个正方形的8条边长长度相等。
订正:一个长方体,可能有8条棱的长度都相等。
【7】长方体中最多有4个面完全相同。
(√)易错题解析:长方体相对的面如果是正方形,此时周围的四个面是形状和大小完全相同的长方形,如某些牙膏盒,某些装日光灯的包装盒,都是这样的长方体。
苏教版六年级长方体与正方体易错题2

苏教版六年级长方体与正方体易错题2
长方体与正方体易错题2(必须画图)
1、一个长方体正好可以切成完全相同的3个小正方体,3个小正方体的棱长总和比长方体的
棱长总和增加了120厘米。
原来长方体的棱长总和是多少厘米?
2、一根长方体钢材,长6分米,宽和高都是2分米,从一端锯下一个尽可能大的正方体
原来长方体的表面积减少了多少平方分米?
3、把一根长1分米的长方体钢条,沿着横截面锯下长0.3分米的一段后,表面积增加了24平方厘米。
原来长方体钢条的体积是多少立方分米?
4、一个长方体容器,长32厘米,宽20厘米,高12厘米,里面的水深9厘米。
如果把这个容器盖紧竖起来,右面着地,那么此时容器中的水深多少厘米?
5、一个长方体,如果高减少2厘米,长、宽不变;或长减少4厘米,宽、高不变;或宽减少3厘米,长、高不变,体积都是减少60立方厘米,原来长方体的表面积是多少平方厘米?
6、把一根棱长4分米的正方体钢材,锻造成宽2分米、高2.5分米的长方体钢材。
锻造后钢材长多少米?
7、用一张长40厘米、宽20厘米的长方形铁皮做一个深5厘米的无盖的长方体容器(焊
处和铁皮厚度不计)。
容积最大是多少立方厘米?
8、一个棱长10厘米的正方体木块,在它的前、后两面的正中心挖去一个相通的长方体
洞口是边长2厘米的正方形。
剩下部分的体积是多少立方厘米?
9、一个长方体长12厘米,宽8厘米,高3厘米,把它切成棱长是2厘米的小正方体,一共可以切多少个?
10、做1节长5米、横截面是边长4厘米的长方体水管,至少需要多少平方米的材料?。
长方体正方体易错题整理

长方体正方体易错题整理一、概念类1. 判断:长方体的6个面一定都是长方形。
(×)题目解析:长方体有6个面,通常情况下六个面都是长方形,但特殊的长方体有两个相对的面是正方形,其余四个面是长方形。
例如底面是正方形的长方体盒子,它的上底面和下底面是正方形,四个侧面是长方形。
2. 正方体是特殊的长方体。
(√)题目解析:正方体具备长方体的所有特征,它的六个面都是正方形,是长、宽、高都相等的长方体,所以正方体是特殊的长方体。
二、表面积计算类1. 一个无盖的长方体玻璃鱼缸,长5分米,宽4分米,高3分米,制作这个鱼缸至少需要多少平方分米的玻璃?错误答案:(5×4 + 5×3+4×3)×2=94(平方分米)正确答案:5×4+(5×3 + 4×3)×2 = 74(平方分米)题目解析:因为鱼缸无盖,所以只需要求5个面的面积之和。
错误答案是按照有盖的长方体表面积公式计算的,正确的做法是用底面面积(长×宽)加上四周四个面的面积(前后两个面:长×高×2,左右两个面:宽×高×2)。
2. 一个正方体的棱长总和是72分米,求它的表面积。
错误做法:先求棱长:72÷12 = 6(分米),然后计算表面积:6×6×6 = 216(平方分米),但是有些同学可能会忘记先求棱长,直接用72×72之类的错误计算。
题目解析:正方体有12条棱且都相等,棱长总和是72分米,所以棱长为72÷12 = 6分米。
正方体表面积 = 棱长×棱长×6,所以表面积是6×6×6 = 216平方分米。
三、体积计算类1. 一个长方体的长、宽、高分别扩大到原来的2倍,它的体积扩大到原来的多少倍?错误答案:2倍正确答案:8倍题目解析:设原长方体的长、宽、高分别为a、b、c,则原体积为V_1 = abc。
长方体和正方体易错题

长方体和正方体易错题1.长方体的前面的长是长方体的长度,宽是长方体的宽度,右面的长是长方体的高度,宽是长方体的宽度,上面的长是长方体的长度,宽是长方体的高度。
2.特殊的长方体有2个面是正方形和4个面是长方形。
表面积是2(长×宽+长×高+宽×高)。
3.长方体的长是水平面上的长边,宽是短边,高是垂直于水平面的边。
长方体的表面积可以先算2(长×宽+长×高+宽×高),再算6×长×宽,也可以先算2(长×宽+长×高+宽×高+长×宽),再减去4×长×宽。
正方体的表面积是6×边长的平方。
长方体的体积是长×宽×高,正方体的体积是边长的立方。
也可以写成统一公式V= lwh。
5.设长方体的高为h,则2(lw+lh+wh)=2×92,即XXX又l=10,w=8,代入得h=9.底面积是lw=80.6.表面积扩大9倍,体积扩大27倍。
长方体相对的两个正方形是底面和顶面,其它4个是侧面。
7.通风管是3个面,无盖的鱼缸是5个面,四周贴商标纸是5个面,教室四周和顶部粉刷是5个面,游泳池抹水泥是4个面,火柴内盒是2个面,火柴外盒是3个面,抽屉是6个面,邮箱是5个面。
书套和相册套是4个面。
8.设正方体的底面边长为a,则a+2a=30,解得a=10.底面积是10×10=100平方厘米,表面积是6×10×10=600平方厘米。
9.通风管的横截面积是4×4=16平方分米,长度为1米,所需铁皮面积为16×100=1600平方厘米。
10.正方体的边长为96÷4=24厘米,表面积为6×24×24=3456平方厘米。
无盖的正方体盒子的侧面积为4×24×h,底面积为24×24,总面积为4×24×h+24×24.由题意可得4×24×h+24×24=3456,解得h=12.所需硬纸面积为4×24×12+2×24×24=1728平方厘米。
长方体与正方体表面积易错点

长方体与正方体表面积易错点易错点1——概念不清,单位换算错误易错题(1)一个正方体的棱长总和是24厘米,它的表面积是()平方厘米;体积是()立方厘米。
【错误分析:第一种错误是把正方体的12条棱记成8条,;第二种错误是把表面积和体积混淆了。
】解答:24 8易错题(2)一个通风管长为5米,横截面是边长为100分米的正方形。
求做10根这样的通风管需要多少平方米的铁皮?错误答案:(5×100+100×100+5×100)×2=(500+10000+500)×2=22000(平方米)错误分析:没有统一单位,同时题目是要求10根通风管面积。
所以在做题时,首先观察单位不同,要注意统一单位。
看题目求的总量是几根的。
正确答案:100分米=10米(10×10+5×10+5×10)×2=200×2=400(平方米)400×10=4000(平方米)易错点2——没有根据实际情况来分析和解决,如计算无盖立方体的表面积时,要去掉没有的那个面。
易错题(1)一个鱼缸长为6cm,宽为4cm,高为2cm。
求鱼缸表面积。
错误答案:(6×4+4×2+6×2)×2=(24+8+12)×2=88(平方厘米)错误分析:鱼缸只有五个面,不能直接用表面积公式计算。
所以在计算鱼缸的表面积时只要算左右、前后以及下面这五个面的面积总和。
正确答案:(4×2+6×2)×2+6×4=(8+12)×2+24=64(平方厘米)易错点3——棱长、面积、体积的变化★说明:不管是长方体还是正方体的面积、体积变化都根据计算公式和积的变化规律进行判断。
棱长扩大n倍,棱长之和扩大n倍,表面积扩大n²倍,体积扩大n³倍。
易错题(1)长方体的长、宽、高同时都缩小3倍,它的表面积缩小()倍.A.3 B.9 C.6 D.27【根据长方体的表面积公式:s=(ab+ah+bh)×2,再根据因数与积的变化规律,积扩大或缩小的倍数等于因数扩大或缩小倍数的乘积】解答:B易错题(2)正方体的棱长扩大为原来的3倍,它的棱长之和、表面积和体积分别怎么变化?【①棱长之和的变化:根据正方体的棱长之和公式C=12a,可以判断一个因数12不变,另一个因数a扩大到原来的3倍,那么棱长之和也扩大为原来的3倍。
五年级长方体与正方体经典易错例题

五年级长方体与正方体经典易错例题一、填空题。
1. 一个正方体的棱长总和是72分米,它的表面积是()平方分米,体积是()立方分米。
- 解析:正方体有12条棱且每条棱长度相等,已知棱长总和是72分米,那么每条棱的长度为72÷12 = 6分米。
正方体的表面积公式为6a^2(a为棱长),所以表面积为6×6^2=6×36 = 216平方分米;体积公式为a^3,体积为6^3=216立方分米。
2. 一个长方体的长是8厘米,宽是6厘米,高是5厘米,它的棱长总和是()厘米。
- 解析:长方体的棱长总和=(长 + 宽+高)×4,所以(8 + 6+5)×4=(14 + 5)×4 = 19×4=76厘米。
3. 一个长方体的长、宽、高分别扩大到原来的3倍,它的表面积扩大到原来的()倍,体积扩大到原来的()倍。
- 解析:设原长方体的长、宽、高分别为a、b、c,则原表面积S_1 = 2(ab+bc + ac),原体积V_1=abc。
长、宽、高扩大后的长、宽、高分别为3a、3b、3c,新表面积S_2=2(3a×3b + 3b×3c+3a×3c)=2×9(ab + bc+ac)=9×2(ab + bc + ac)=9S_1,所以表面积扩大到原来的9倍;新体积V_2 = 3a×3b×3c=27abc = 27V_1,所以体积扩大到原来的27倍。
4. 一个正方体的棱长是5厘米,把它切成两个完全一样的长方体,这两个长方体的表面积之和比原来正方体的表面积增加了()平方厘米。
- 解析:把正方体切成两个完全一样的长方体,增加的表面积是正方体两个面的面积。
正方体一个面的面积为5×5 = 25平方厘米,增加了25×2=50平方厘米。
二、判断题。
5. 长方体的6个面一定都是长方形。
()- 解析:错误。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
长方体与正方体易错题整理二
班级: 姓名: 成绩:
一、综合基础题(按要求完成)
1、一个底面是边长为4分米的正方形、高为5分米的长方体水箱,里面装满水,把它倒入棱长6分米的正方体水箱,水面距箱口多少分米?
2、一块石板,长1.5米,宽0.3米,厚0.2米,如果每立方分米石料重2.7千克,这块石板重多少千克?
3、一种油桶,地面是边长为2分米的正方形,高36厘米,把这样的一桶油注入容积是720毫升的瓶子里,可以装多少瓶?
4、把下面的长方体木料切割成最大的正方体。
最多能切成多少个这样的正方体?切成的每个正方体的体积是多少立方厘米?
5、下面的物体是由一个正方体与一个长方体组合而成的。
求这个物体的表面积与体积。
6、长方体的长是12厘米,高是8厘米,阴影部分两个面的面积和是180平方厘米。
这个长方体的体积是多少立方厘米?
7、一个长方体长5分米,宽2分米,高3分米。
如果要使这个长方体的表面积增加20平方分米,宽和高不变,长要增加多少分米?(要求:先画示意图,再算一算。
)
8、张老师将一个长方体平均分成了两部分,下图是其中的一部分,请你计算出这个立体图形的体积。
(单位:厘米)
9、如图是一个长方体的空心管,掏空部分的长方体的长为12厘米,宽为7厘米。
求这根空心管的体积是多少立方厘米?
10、一个长方体纸箱的底面与侧面展开都是一个正方形,已知底面周长是20分米,它的体积是多少立方分米?
11、有一个空的长方体容器A和一个盛有水的长方体容器B,水深24厘米。
将容器B中的水倒一部分到容器A中,使两个容器中水的高度相等,这时水深是多少厘米?(要求:用方程解)
二、要求:先画图,再计算
1、有一块长30厘米、宽20厘米的长方形硬纸板,在四个角分别剪去面积相等的正方形后,正好折成一个深5
2、有一张长24厘米、宽18
方形做纸盒,这个纸盒的容积是多少立方厘米?
3、一个底面是正方形的长方体铁箱,如果把它的侧面展开,正好得到一个边长为12分米的正方形,求铁箱的容积。
1、在一个长25cm,宽20cm的长方体玻璃缸中,有一块棱长10cm的正方体铁块,这时水深15cm,把这块铁块从玻璃缸中取出,玻璃缸的水深多少厘米?
2、在一个长20分米,宽15分米的水箱中,有10分米深的水,如果在水中沉入一个棱长是30cm的正方体铁块,那么现在水箱中的水深多少分米?
3、一个石块放入一个长和宽都是25cm,水深9cm的长方体玻璃缸中,结果水面上升到12cm(水没有溢出),这个石块的体积是多少?
1、一个正方体的高增加2厘米,得到的新长方体的表面积比原正方体表面积增加了56平方厘米,求正方体的体积。
2、一块长方体木块,沿着高锯掉2厘米后,成为一个正方体,表面积减少40
平方厘米,求原来长方体木块的体积。
3、一根木料,沿着横截面的方向截成4段,表面积比原来增加了18平方分米,求原来这段木料的体积是多少平方米?
6米
三、体积与表面积的变化。
1、下面图中每个正方体的棱长都是a厘米,下面各图的表面积分别是多少?
()()()n个
()
2、下面每个小正方体体积是1立方厘米,拼成下面形状,表面积和体积分别是多少?
分别至少再加几个小正方体,就能拼成一个大正方体?
()()()()。
