材料力学第27讲 Chapter3-2第三章 能量法(卡氏定理)
合集下载
材料力学能量法第3节 卡式定理
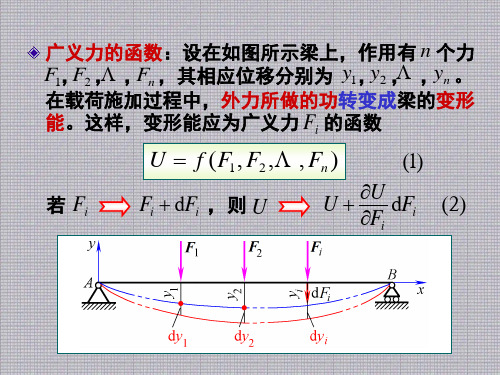
q 2 M ( x) (l x) M e 2
M 1 M e
(2)计算 B 截面转角 B
M q 2 1 M ( x) (l x) M e M e 2 M ( x) M ( x) Bq M e dx EI M e 1 l q 2 [ ( l x ) M ] ( 1 ) d x e EI 0 2 3 l ql 顺时针转向 Me EI 6 ql 3 顺时针转向 B 令 Me 0 6 EI
2
1 dFi dyi U dFi yi 2
(3)
比较(2)(3)式
1 dFi dyi U dFi yi (3) 2 U ( F1 , F2 , Fn ) yi i 1,2,3,... Fi
U U dFi Fi
(Hale Waihona Puke 2)梁的变形能对某一载荷 Fi 的偏导数,等于 在该载荷处沿载荷方向的位移,这就是卡氏定理, 也称卡氏第二定理。由意大利工程师 A 卡斯蒂利亚 诺(1847-1884)于1873年提出的。卡氏定理对其他 线弹性结构也是适用的。
广义力的函数:设在如图所示梁上,作用有 n 个力 y2 , , yn 。 F1, F2 , , Fn ,其相应位移分别为 y1, 在载荷施加过程中,外力所做的功转变成梁的变形 能。这样,变形能应为广义力 Fi 的函数
U f ( F1, F2 ,, Fn )
若 Fi
(1) ( 2)
Fi dFi , 则 U
U U dFi Fi
卡式定理的推导 —— 改变加力的次序 (1)先施加 dFi :在施加 dFi 时,其作用点沿 dFi 方向的 1 dF dy 位移为 dyi ,梁的变形能为 i i;
材料力学第三章 能量法

三、卡氏第二定理(线弹性体)
Di
Vc Fi
在线弹性范围内
余能定理 Vc V
Di
V Fi
卡氏第二定理: 线弹性杆件或杆系的应变能对于 作用在该杆件或杆系上的某一荷 载的变化率,就等于与该荷载相 应的位移。
卡氏第二定理适用于一切受力状态下的线弹性体。
卡氏第二定理公式D及i 含义VF:i
若结构的应变能 V 表示为F1、F2 …Fi …的函数,则应变 能对任一载荷Fi的偏导数等于Fi作用点沿Fi方向位移。
C
与需求位移相应的虚设外力
F。求偏导后令其为零。
(2)列弯矩方程
M
x
F 2
ql 2
x
qx 2 2
0
x
l 2
M
x
F 2
ql 2
x
qx 2 2
0
x
l 2
(3)求梁的应变能
M 2 l/2
x
1
V 2 0
dx
2EI
EI
l/2
0
F 2
ql 2
x
qx 2 2
2 dx
1 EI 1 EI
V W
一、杆件基本变形的应变能
(一)轴向拉伸(压缩)
1、杆的应变能
轴力沿轴线不变的情况:
dW Fd(Dl) W Dl1 Fd(Dl) 0
线弹性范围内 W 1 FDl
1
2
V
F
W
FN
2
F Dl Dl
FNl EA
应变能
V
FN2l 2EA
F
l
Dl
F
Dl d (Dl)
Dl1
Dl
(一)轴向拉伸(压缩)
材料力学-能量法

U
l
N 2( x)dx 2EA
l
M
2 n
(
x
)dx
2GI P
l
M 2( x)dx 2EI
(9-8)
注意:叠加法不能用于计算外力功和变形能。
例1 试分别计算图示各梁的变形能 例1图
解:求各梁的变形能 a b
c
Ua
0l
M 2( x)dx 2EI
0l
(
Px)2 2EI
dx
P 2l3 6EI
Ub
0l
M 2( x)dx 2EI
W 1 P
2
(9-2)
式中: P —— 广义力(力、力偶)
——广义位移(线位移、角位移)
广义力与广义位移相对应。如广义力是力,相应的广义
位移就是线位移(沿力方向的线位移);如广义力是力偶, 相应的广义位移就是角位移(在力偶作用处的角位移)。
(二)变形能和比能
1. 轴向拉伸与压缩时的变形能
a. 轴力为常量: ( N P,l Nl )
材料力学
能量法
一、外力功与变形能
本章考虑杆件在线弹性范围内的能量法计算问题。
能量法——利用功和能的概念来解决变形体的位移、变 形和内力等计算的方法。
在线弹性范围内,外力功 W 全部转变为变形能 U,不 考虑能量的损耗。因此有
W=U
(一)外力功
1. 常力作功(P 为恒力)
W P
(9-1)
2. 变力作功(P 从0逐渐增加到最终值)
EA
U W 1 Pl N 2l
2
2EA
(9-3)
u
U V
N2 2EA2
2
2E
1
2
u 为比能,即单位体积的变形能。
卡氏定理材料力学

2Ma 3EI
(
)
DF FD
CD段:
M (x)
Mx , 2a
M (x) F
x,
MC
CB段: M (x) M ,
M (x) 2a x, a F
2a
C
M
AB段: M (x) 0,
M (x) x, F
a
B
A FAx
(4)带入卡氏定理求解。
Dx
l
M (x) M (x) d x EI F
FAy
2a
MC, 在D截面虚设一水平力F 。 MC
DF
C
(2)取刚架为研究对象, a
受力图如图所示。
M
FD
FAx F
B
a
A FAx
FAy
FD
F
1 2a
(M
MC)
FAy
(3)分段列出弯矩方程及偏导方程。
2a
CD段:
MC
M
( x1 )
[F
1 2a
(M
MC
)]x1
Cx aM 2
x
1
DF FD
M (x1) F
新位移 i 上也做功,系统的总的应变能为
V
Fi
i
1 2
Fi
i
(2)
由(1)=(2),并忽略二阶小量,得
V Fi
i
V Fi
i
若将结构的应变能表示为载荷F1,F2, ,Fn 的 函数,则应变能对任一载荷Fi的偏导数,等于Fi作用
点沿Fi作用方向的位移 i ,称为卡氏第二定理。
说明 (1)卡氏定理只适用线弹性结构。
i
V Fi
FN (x) FN (x) d x L EA Fi
材料力学能量法

按二种方式加载
(2)先作用 i,再作用 1,P2,…,Pi,…,则 先作用dP 再作用P 先作用 , ,
(3)由于 1=U2,略去二阶微量,则有 由于U 略去二阶微量, 由于 2.用卡氏定理计算基本变形 用卡氏定理计算基本变形 (1)拉压变形 拉压变形
为分段常量时: 当N(x)为分段常量时: 为分段常量时
广义力及单位广义力共同作用下,结构的变形能: 广义力及单位广义力共同作用下,结构的变形能: (1)先作用单位力 0(=1),再作用 1,P2,…,Pi,…,结构变形能为: 先作用单位力P 先作用单位力 ,再作用P , ,结构变形能为:
?U+U0
P1
P2 f
Pn
△1
△2
△n
P1
P2
δ
1
Pn
△1
f
△2 △n
U1= P1δ11/2 + ( P2δ22/2 + P1δ12 )
U1= P1δ11/2 + ( P2δ22/2 + P1δ12 )
作用方式2: 再作用P 作用方式 :先作用 P2,再作用 1: 再作用
U2= P2δ22/2
两种作用方式结果相同: 两种作用方式结果相同: 功的互等定理: 功的互等定理:
1.证明 证明 设线弹性结构在约束情况下,无刚体位移,外力为 广义), 设线弹性结构在约束情况下,无刚体位移,外力为P1,P2,…,Pi,…(广义 , , 广义 相应在力方向的位移为d 相应在力方向的位移为 1,d2,…,di…。则变形能是广义力的函数: , 。则变形能是广义力的函数:
变形能的微分是: 变形能的微分是: (1)同时作用 1,P2,…,Pi+dPi,…,则 同时作用P 同时作用 , ,
材料力学中的能量法

记为 M,F 。 S ,F N ,T
(3)单位力所做的外力虚功为 We =1·
杆件的内力虚功为
* * * * W ( M d F d F d d T d) j i S N l 0
单位力法的虚位移原理表达式为
* * * * (10-16) 1 Δ ( M d F d F d d T d) j S N l 0
解:如图11-4b所示,在点 C及点D应加一对大小相等, 方向相反,且均垂直于杆CD的力。 根据功的互等定理: F B F F l F 0 .0 8 k N B C D lC D
§10-4、10-5 虚位移原理及单位力法
. 虚位移原理 (1)刚体 虚位移 —— 满足约束条件的假想的任意微小位移。 虚位移原理 ——作用于刚体上的力对于任何虚位移所作的 总功等于零(平衡的必要和充分条件)。
由于以上分析中没有涉及材料的物理性质, (11-15)式适用于弹性体和非弹性体问题。式中Fi为广义力,M ,
Δi FS , FN , T是由荷载产生的内力,
d , dd ,
* *
* d j 为广义虚位移,d* ,
为微段的变形虚位移。
Ⅱ. 单位力法(单位载荷法)
(1) 因为由荷载引起的位移,满足约束条件和变形连续条
(c)
(d) 将(a),(d)式代入(11-14)式 ,得梁的虚位移原理表达式为
* * F Δ ( M d F d ) 0 i i S l n 0
即
i 1
* * F Δ ( M d F d ) i i S l i 1 0
n
外力虚功=内力在微段变形虚位移上的虚功(或虚应变能)
2 2 lM M ( x ) ( x ) 1 2 U d x d x (3) l 0 2 EI EI 2 2 l 2
材料力学第26讲 Chapter3-1第三章 能量法(应变能 余能)

利用功和能的概念求解可变形固体的位移、变形及内力等 的方法,统称为能量方法。
能量方法是用有限元法解固体力学问题的重要基础。
4
能量方法用途很广:
不仅适用于线弹性问题; 也可用于非线性弹性问题; 曲杆问题;
5
本章要介绍的几种能量方法:
应变能原理-卡氏第一定理 余能原理-卡氏第二定理 虚位移原理及单位力法
6
§3–2 应变能 余能
应变能的计算:
I. 应变能
外力缓慢做功W ,无损失地转化为应变能 (不
转化成动能、热能) ,贮存于弹性体内部。
V W
7
一、 线弹性问题
1. 轴向拉压杆件应变能的计算
W 1 Fl
2
l Fl
W F 2l 2EA
F
EA
W=V 功能原理
V
EAl2
2l
F 2l V 2 EA
5P1P2l3 48EI
23
进一步分析
21
P1
P2
12
l
l
2
2
21P16(E 2l)Il2(3l2l)458P1E l3I
l
l
2
2
12P26(E 2l)Il2(3l2l)4 58 P2 E lI3
P112 P221 ====== 功的互等定理 ======
第一组力在第二组力作用所产生位移上做的功 等于第二组力在第一组力作用所产生位移上做的功。
17
4.3 弯曲杆件应变能的计算
V
V vdV
V
1 2
dV
V
1 2E
2dV
l
A21E(M Izy)2dAdl l
A21E(M Iz )2y2dAdl
d l dx M 2 l 2EIz
能量方法是用有限元法解固体力学问题的重要基础。
4
能量方法用途很广:
不仅适用于线弹性问题; 也可用于非线性弹性问题; 曲杆问题;
5
本章要介绍的几种能量方法:
应变能原理-卡氏第一定理 余能原理-卡氏第二定理 虚位移原理及单位力法
6
§3–2 应变能 余能
应变能的计算:
I. 应变能
外力缓慢做功W ,无损失地转化为应变能 (不
转化成动能、热能) ,贮存于弹性体内部。
V W
7
一、 线弹性问题
1. 轴向拉压杆件应变能的计算
W 1 Fl
2
l Fl
W F 2l 2EA
F
EA
W=V 功能原理
V
EAl2
2l
F 2l V 2 EA
5P1P2l3 48EI
23
进一步分析
21
P1
P2
12
l
l
2
2
21P16(E 2l)Il2(3l2l)458P1E l3I
l
l
2
2
12P26(E 2l)Il2(3l2l)4 58 P2 E lI3
P112 P221 ====== 功的互等定理 ======
第一组力在第二组力作用所产生位移上做的功 等于第二组力在第一组力作用所产生位移上做的功。
17
4.3 弯曲杆件应变能的计算
V
V vdV
V
1 2
dV
V
1 2E
2dV
l
A21E(M Izy)2dAdl l
A21E(M Iz )2y2dAdl
d l dx M 2 l 2EIz
材料力学(II)第三章 PPT课件
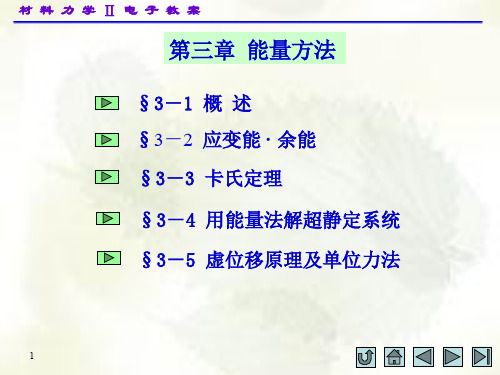
T 2l 2GIp
GIp 2l
2
5
材料力学Ⅱ电子教案
(c) 弯曲
第三章 能量方法
纯弯曲
Vε
W
1 2
M e
M e2l 2EI
M 2l 2EI
横力弯曲
Vε
l M 2 (x) d x 0 2EI
6
材料力学Ⅱ电子教案
第三章 能量方法
可以把应变能统一写成
Vε
W
1 2
FΔ
式中,F 为广义力,可以代表一个力,一个力偶,一对力或一
§3-2 应变能 ·余能
Ⅰ 应变能 (1)线弹性体
1. 基本变形形式【材料力学(Ⅰ)】 利用应变能 Vε 在数值上等于外力功W,可得
(a) 轴向拉(压)杆
4
Vε
W
1 2
FDl
FN2l 2EA
EA 2l
Dl 2
材料力学Ⅱ电子教案
第三章 能量方法
(b) 扭转
Vε
W
1 2
M
e
M e2l 2GIp
由结点A的平衡方程,得
F
FN 2sin
(3)
由于 为小角度,
所以 sin tan D
(4)
lLeabharlann 19材料力学Ⅱ电子教案
将(4)式代入(3)式,得
FN
Fl 2Δ
将(5)式代入(2)式,得
或写成
3
Δ
F
l
EA
F ( Δ)3 EA l
F 和D的关系如图b所示。
20
第三章 能量方法
2EA
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
V(s)
ds M2(s) 2EI
曲线坐标形式
3 PR3
2 EI
V(
)
Rd M2() 2EI
极坐标形式
34
解:(2)求水平位移
M
施加一水平力F
A
M () P ( R R c o s) F R s in
R
BF
Bx
V F
F 0
0
M()
EI
M() F
Rd
F 0
P
E 1 I
[ P R (1 c o s)]R s inR d
l FNl EA
E 2 lA 1 A x2 E 2 lA 2 A ysin 4 5 0 A xc o s4 5 02
12
V E 2 lA 1 A x2 E 2 lA 2 A ys in 4 5 0 A xc o s4 5 02
1 EA,l
450
A
由卡氏第一定理得
V 0; (Ax )
因为只有第i个载荷相应的位移有一微小增量di,其余载荷相 应的位移保持不变,则外力功的变化可写作:
dWFi di
7
功能原理
dV V(1 , i2 n)di
dWFi di
Fi
V(1,2 i
n)
卡氏第一定理
弹性杆件的应变能对于杆件上某一位移的变化率,等于该
位移相应的荷载。
卡氏定理适用于一切受力状态下的弹性杆件。 卡氏定理对非线性弹性杆件也适用。
x
M
2 AB
(
y)dy
l
M
2 BC
( y)dy
0 2EI
x 2EI
(x y)
0
f ( x) V
xMAB(y)MAB(y)dy l MBC(y)MBC(y)dy
F F 0 0 EI
F
x EI
F
36
M A B (y ) P ( L y ) F ( x y )
M A B ( x ) (x y)
V P (Ay )
2
EA
P
E l1 A A x E l2 A A ys in 4 5 0 A xc o s 4 5 0( c o s 4 5 0 ) 0 E l2 A A ysin4 5 0 A xco s4 5 0(sin4 5 0)P l2 2l1 2l
13
E l1 A A x E l2 A A ys in 4 5 0 A xc o s 4 5 0( c o s 4 5 0 ) 0
dx dx dx 2a ( Fx)2 0 2 EI
a (F 2a)2 0 2 EI
2a ( Fx)2 0 2 EI
28
V
d x dx d x a ( F x ) 2
0 2EI
a (Fa )2 0 2 EI
a (Fx)2 0 2EI
dx dx dx 2a ( Fx)2 0 2 EI
l [(FxM)]2 dx
0 2EI
0 2EI
接下来先完成求导工作, 不要去做积分!
V
l (FxM)1dx
下面先完成M=0的代入,
M M 0 0 EI
M 0 进而完成积分!
l F x d x
0 EI
F l2 2EI
22
若假想在自由端作用一力矩M的方 向与前面相反,结果将有何变化?
先求导
代入F=0
(与前同)
26
例5 求图示结构AB间的相对位移(各杆的弯曲刚度为EI)。
aF B
2a
A
a
F
F
aF B
2a
A
a
F
F
V ?
AB
V F
27
aF B
1A
a2
F
F
3
2a
4
5
6
F
V
d x dx d x a ( F x ) 2
0 2EI
a (Fa )2 0 2 EI
a (Fx)2 0 2EI
转角。(梁的弯曲刚度为EI,长为l)。
解(1): 求挠度
F
l
V
l M 2(x) dx
l (Fx)2 dx
F 2l3
0 2EI
0 2EI
6EI
x
O
wc
V F
F l3
3EI
21
F
解(2): 求转角 V
l
M
M
假想在自由端作用一力矩M
x
O
V M M 0
V
lM
2 (x)dx
F
f ( x ) xMAB(y)MAB(y)dy
0 EI
F
F 0
x
E 1 I
[ P (L y)] [ (xy)]d y
0
E P I
x[y2(Lx)yLx]dy
0
P EI
x3
3
(Lx)x2
2
Lx2
Px2 6EI
(3L
x)
37
作业 P94:3-7(b); 3-8(a,b) (第二册) P95: 3-9(a)
下次课讲用能量法解超静定系统
38
R
A
B
P
33
解: (1)求竖直位移
M
曲杆的内力: FN , Fs , M
FN()Pcos
A
R
F
s
FN B
Fs()Psin
P
M () P (R R c o s)By
V P
0
M()
EI
M() P
Rd
直杆:
V
dx M2(x) 2EI
E 1 I
P [R (1cos
)]2R d
0
() 曲杆:
dWc i dFi
17
dVcVc(F1 ,F Fi2 Fn)dFi
dWc i dFi
弹i性杆V 件c的(F余1,F F 能i2对于Fn杆)件上某一载余荷能的定变化理率,等于该荷
载相应的位移。
余能定理适用于一切受力状态下的弹性杆件。
余能定理对非线性弹性杆件也适用。
18
i
Vc(F1,F2 Fi
Fn)
a (F 2a)2 0 2 EI
2a ( Fx)2 0 2 EI
AB
V F
a
0
Fx EI
xdx
a
0
Fa EI
adx
a
0
Fx EI
xdx
2a
0
Fx EI
xdx
a 0
F 2a EI
2adx
2a
0
Fx EI
xdx
AB
F EI
(
a3 3
a3
) a
3
8a3
4 a 3
8a3
33
3
11Fa3 EI
E l2 A A ysin4 5 0 A xco s4 5 0(sin4 5 0)P Ay (2 21)Ax
l11Ax21l2 AyAx 0
Ax212 AyAx 0
1
l2
Ay Ax
2P EA
Ay
Ax
2
2Pl EA
l2 2l1 2l
Ax
Pl EA
,
Ay (2
21) Pl EA
与解法一结果相同
材料力学 II
(2)
Energy Method—Part 2
第廿七讲
1
内容
1. 应变能和余能的计算 2. 卡氏定理 3. 用能量法解超静定系统 4. 虚位移原理及单位力法
2
线弹性问题应变能的普遍表达式
V LF 2 N E 2(A x)dxLT 2 G 2(Ix P )dxLM 22 E (Ix)dx
Ay 2l2Ax 2l2 l1
Ay
2
21Pl EA
()
11
解(2): 用卡氏第一定理
关键: V V(Ax,Ay)
1
Ax
450
2
l2
l1 Ay
变形协调关系
Ax l1; A ysin4 5 0 A xco s4 5 0 l2
450
V
FN21l1 FN22l2 2EA 2EA
E2lA1 l12 E2lA2 l22
29
例6 求铰B两侧截面的相对转角(各杆的弯曲刚度为EI)。
q MM
E I ,l
B
E I ,l
解:在铰B处施加一对力矩MB,则
B
V M
M 0
30
qM
q MM
xO
A EI,l
B A EI,l
B
E I ,l
C
Ml
xO
M AB (x)
M l
x
M
1 2
qx
2
V
l
M
2 AB
( x )dx
l
M
2 BC
fid i
i 1
可见,最终梁内的应变能应是关于i (i=1,2…n)的函数,即
V V (1 , 2 n)
第i个载荷的f-变化曲线
fi Fi
O
i
i
6
F1 F2 Fi
Fn
1 2 i di n
若与第i个载荷相应的位移有一微小增量di,则梁内应变能的
变化dV应写作: dV V(1 , i2 n)di
14
II. 卡氏第二定理
F1 F2 Fi
Fn
1 2 i
n
图示梁(材料为线性,也可为非线性)
作用n个集中载荷Fi (i=1,2…n),相应位移为i (i=1,2…n),
15
F1 F2 Fi
Fn
