材料力学:第12章:能量法
合集下载
材料力学能量法第3节 卡式定理
q 2 M ( x) (l x) M e 2
M 1 M e
(2)计算 B 截面转角 B
M q 2 1 M ( x) (l x) M e M e 2 M ( x) M ( x) Bq M e dx EI M e 1 l q 2 [ ( l x ) M ] ( 1 ) d x e EI 0 2 3 l ql 顺时针转向 Me EI 6 ql 3 顺时针转向 B 令 Me 0 6 EI
2
1 dFi dyi U dFi yi 2
(3)
比较(2)(3)式
1 dFi dyi U dFi yi (3) 2 U ( F1 , F2 , Fn ) yi i 1,2,3,... Fi
U U dFi Fi
(Hale Waihona Puke 2)梁的变形能对某一载荷 Fi 的偏导数,等于 在该载荷处沿载荷方向的位移,这就是卡氏定理, 也称卡氏第二定理。由意大利工程师 A 卡斯蒂利亚 诺(1847-1884)于1873年提出的。卡氏定理对其他 线弹性结构也是适用的。
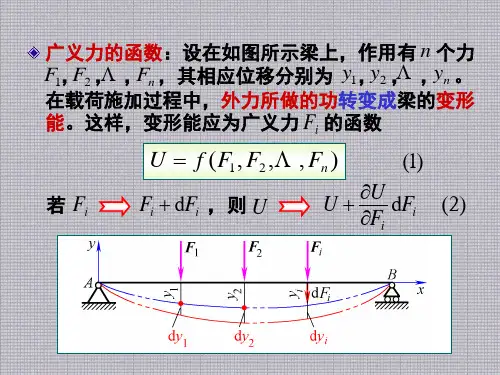
广义力的函数:设在如图所示梁上,作用有 n 个力 y2 , , yn 。 F1, F2 , , Fn ,其相应位移分别为 y1, 在载荷施加过程中,外力所做的功转变成梁的变形 能。这样,变形能应为广义力 Fi 的函数
U f ( F1, F2 ,, Fn )
若 Fi
(1) ( 2)
Fi dFi , 则 U
U U dFi Fi
卡式定理的推导 —— 改变加力的次序 (1)先施加 dFi :在施加 dFi 时,其作用点沿 dFi 方向的 1 dF dy 位移为 dyi ,梁的变形能为 i i;
材料力学能量法

限制条件:不适 用于求解动力学 问题如振动、冲 击等
适用范围:适用 于求解线性问题 如弹性、塑性等
限制条件:不适 用于求解非线性 问题如塑性、蠕 变等
材料力学能量法的发展趋势和未来 展望
材料力学能量法的发展趋势
计算方法:发展高效、准确 的数值计算方法
应用领域:拓展应用领域如 航空航天、生物医学等
柱的压缩问题
问题描述:柱在轴向 压力作用下的压缩问 题
应用实例:桥梁、建 筑等结构中的柱在受 压时的变形和破坏
能量法分析:利用能 量法分析柱的受压变 形和破坏过程
结论:能量法在柱的 压缩问题中的应用可 以有效地预测柱的变 形和破坏情况为工程 设计提供依据。
弹性体的振动问题
添加 标题
弹性体振动问题的背景:在工程中弹性体的振动问题非常常见如桥梁、建筑物、机械设备等。
定义和原理
材料力学能量法: 一种研究材料力学 问题的方法通过分 析能量变化来求解 问题。
基本概念:能量、 应力、应变、位移 等。
原理:根据能量守 恒定律材料的变形 和破坏过程中能量 会发生变化通过分 析这些变化可以求 解问题。
应用:广泛应用于 结构分析、优化设 计等领域。
能量法的应用范围
结构力学:分析结构受力、变形和稳定性 材料力学:分析材料应力、应变和断裂 流体力学:分析流体流动、压力和速度 热力学:分析热传导、对流和辐射 电磁学:分析电磁场、电磁波和电磁感应 声学:分析声波传播、反射和吸收
能量法的基本假设
材料是连续、均匀、各向同性的
材料是线弹性的应力与应变成正 比
添加标题
添加标题
材料是弹性的满足胡克定律
添加标题
添加标题
材料是各向同性的应力与应变的 关系与方向无关
用能量法研究夹芯梁的弯曲挠度计算

2
z
∫
h
2
z
zbdz +
zbdz +
ME t
D
∫
h
2
h
+t
2
( M + dM) E t
D
∫
h
2
Et Ec
zbdz
h
+t
2
(6)
12G c D
QE t
- z ö÷ +
ç
τc =
( ht + t 2 )
2D è 4
ø 2D
Δ=
(7)
2 夹芯梁弯曲挠度
由文献[12ꎬ13] 可知梁截面弯矩、剪力导致的
2
Q 1 ∂Q 1
C ∂P
M 2 ∂M 2
D ∂P
dx
dx +
(18)
P ( l - a ) 2 ( l + 2a ) P ( l - a )
=
+
48D
4C
3 算例分析
(1) 试验 1
文献[14] 采用三点弯曲试验研究了1.81
1.87
3.21
1.89
4.58
300
19.76
入式(10) 中可得:
M 2 E t z 2 M 2 E c z 2 Q 2 E 2t
+
+
u=
2D
2D
8G t D 2
2
2
éê æ h + ö - 2 ùú +
ç
÷
t
z
êë è 2
úû
ø
Q 2 E 2c æ h 2 2 ö2 Q 2 E 2t
-z ÷ +
ç
( ht + t 2 ) 2 +
8G c D 2 è 4
3
ø 8 û 12
z
∫
h
2
z
zbdz +
zbdz +
ME t
D
∫
h
2
h
+t
2
( M + dM) E t
D
∫
h
2
Et Ec
zbdz
h
+t
2
(6)
12G c D
QE t
- z ö÷ +
ç
τc =
( ht + t 2 )
2D è 4
ø 2D
Δ=
(7)
2 夹芯梁弯曲挠度
由文献[12ꎬ13] 可知梁截面弯矩、剪力导致的
2
Q 1 ∂Q 1
C ∂P
M 2 ∂M 2
D ∂P
dx
dx +
(18)
P ( l - a ) 2 ( l + 2a ) P ( l - a )
=
+
48D
4C
3 算例分析
(1) 试验 1
文献[14] 采用三点弯曲试验研究了1.81
1.87
3.21
1.89
4.58
300
19.76
入式(10) 中可得:
M 2 E t z 2 M 2 E c z 2 Q 2 E 2t
+
+
u=
2D
2D
8G t D 2
2
2
éê æ h + ö - 2 ùú +
ç
÷
t
z
êë è 2
úû
ø
Q 2 E 2c æ h 2 2 ö2 Q 2 E 2t
-z ÷ +
ç
( ht + t 2 ) 2 +
8G c D 2 è 4
3
ø 8 û 12
材料力学 能量法

3
13 Pa 12 EI
3
M
能量法
例:图示梁,抗弯刚度为EI,承受均布载荷q及
集中力X作用。用图乘法求: (1)集中力作用端挠度为零时的X值; (2)集中力作用端转角为零时的X值。
能量法
解:(1)
ql / 8
2
1 wC EI
Xal 2a Xa 2 2a ql 3 a 2 3 2 3 12 2
l P 2 得:P wC1 m 2E I 2 ml 由此得: C wC1 8E I
2
能量法
例:长为 l 、直径为 d 的圆杆受一对横向压力 P 作用,
求此杆长度的伸长量。已知E和m。
能量法
解:由位移互等定理知,①杆的伸长量等于 ②杆直径的减小量
l
①
d
②
e d e d
4 P P d d E AE
能量法
例:已知简支梁在均布载荷 q 作用下,梁的中点挠
度
5ql w 384E I
4
。求梁在中点集中力P作用下(见
图),梁的挠曲线与梁变形前的轴线所围成的面积A。
A
能量法
A
5ql q A P 384E I
能量法
4
可用于线弹性材料,也可用于非线弹性材料。
能量法
§12-7 单位载荷法 莫尔积分
P1
P2
C
用虚功原理可以导出计算结构一点位移的单位载荷法
能量法
P1
P2
C
Fs ( x)
C
M ( x)
1 M ( x)d
M ( x) d dx EI
P0 1 Fs ( x)
材料力学13能量法

1 1 V F2 22 F111 F2 21 2 2
功的互等定理:
F1 12 F2 21
即:F1 力在由F2力引起的位移上所作的功,等于F2 力在由F1力引起的位移上所作的功。
若F1 = F2 ,则得
位移互等定理:
12 21
即: F2引起的F1 作用点沿 F1方向的位移,等于同 样大小的力F1 引起的F2作用点沿 F2方向的位移。
( F1 F2 ) L F1 L F2 L F1F2 L V 2 EA 2 EA 2 EA EA
2
2
2
L
2) F1 单独作用下:
F1 F2
F1 L V 1 2 EA
3)F2 单独作用下:
F22 L V 2 2 EA
2
L F1 F2
L
V1 V 2 V
证毕。
b Px1 l ( 0 ≤x1 ≤ a) a CB段: M(x2 ) = RB x2 = Px2 l ( 0 ≤x2≤ b) 2
AC段:M(x1 ) = RA x1 =
13-3 应变能的普遍表达式
基础知识
广义
线弹性结构上受一个外力作用,任一点的位移与该力成正比。
线弹性结构上任意一点的广义位移与各广义力成线性 齐次关系。 比例加载时,线弹性结构上任一外力作用点沿外力方 向的位移与该点的广义力成正比。
P12 l1 P1作功为 V 3 2 EA
(5)应变能是可逆的。(跳板跳水)
总功仍为上述表达式。
直接利用功能原理求位移的实例
利用能量法求解时,所列 例 求简支梁外力P作用点C的挠度。 弯矩方程应便于求解。
解:
A x1 RA l a
P
功的互等定理:
F1 12 F2 21
即:F1 力在由F2力引起的位移上所作的功,等于F2 力在由F1力引起的位移上所作的功。
若F1 = F2 ,则得
位移互等定理:
12 21
即: F2引起的F1 作用点沿 F1方向的位移,等于同 样大小的力F1 引起的F2作用点沿 F2方向的位移。
( F1 F2 ) L F1 L F2 L F1F2 L V 2 EA 2 EA 2 EA EA
2
2
2
L
2) F1 单独作用下:
F1 F2
F1 L V 1 2 EA
3)F2 单独作用下:
F22 L V 2 2 EA
2
L F1 F2
L
V1 V 2 V
证毕。
b Px1 l ( 0 ≤x1 ≤ a) a CB段: M(x2 ) = RB x2 = Px2 l ( 0 ≤x2≤ b) 2
AC段:M(x1 ) = RA x1 =
13-3 应变能的普遍表达式
基础知识
广义
线弹性结构上受一个外力作用,任一点的位移与该力成正比。
线弹性结构上任意一点的广义位移与各广义力成线性 齐次关系。 比例加载时,线弹性结构上任一外力作用点沿外力方 向的位移与该点的广义力成正比。
P12 l1 P1作功为 V 3 2 EA
(5)应变能是可逆的。(跳板跳水)
总功仍为上述表达式。
直接利用功能原理求位移的实例
利用能量法求解时,所列 例 求简支梁外力P作用点C的挠度。 弯矩方程应便于求解。
解:
A x1 RA l a
P
材料力学第2版 课后习题答案 第12章 变形能法
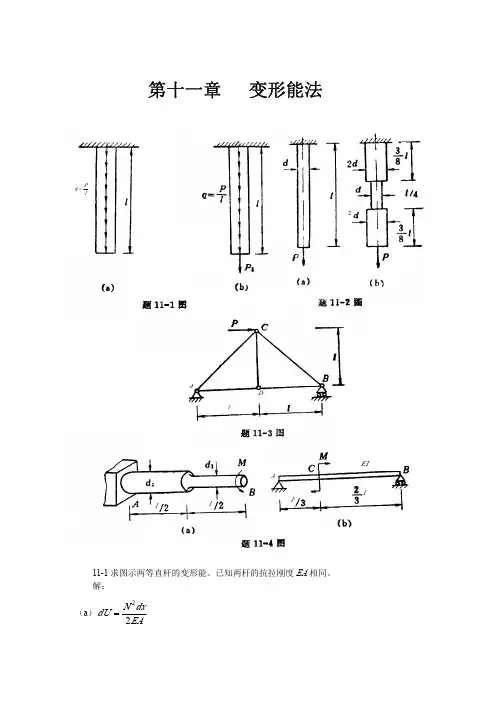
3 d1 ; 2
(b) 梁的抗弯刚度EI,略去剪切变形的影响。 解: (a) M n1 = m
M n2 = m U2 = J P2 =
9.6m 2 l Gπd14
U1 = J P1 =
m 2l 4GJ P1 π 4 d1 32
m 2l 4GJ P2 π 4 5.06π 4 d2 = d1 32 32
故
U a 16 = Ub 7
11-3 图示桁架各杆材料相同,截面面积相等,试求在 P 力作用下,桁架的变形能。 解:
支反力
R Ax = P R Ay = R B =
各杆的轴力和变形能如表所示 杆号 1 内力 Ni 杆长 各杆的变形能 Ui
P 2
2P 2
2l
2 P 2 l (4 EA)
2
− 2P 2
求 θA
M 0 ( x1 ) = −1 M 0 ( x 2 ) = −1
θA =
1 EJ
⎡ ⎛L ⎤ 1 ⎞ − P⎜ + x2 ⎟(− 1)⎥ dx 2 ∫0 (− Px1 )(− 1)dx1 + 2EJ ∫0 2 ⎢ ⎠ ⎣ ⎝2 ⎦
2
L
L
1 L2 1 = ⋅P⋅ + EJ 8 2 EJ =
求 δB
0
2l
l l l
2 P 2 l (4 EA)
0
3 4 5ຫໍສະໝຸດ P 2 P 2P 2 l (8EA) P 2l (8 EA)
故珩架的变形能为
5
U = ∑ Ui =
i =1
2 2 + 1 P 2l P 2l = 0.957 4 EA EA
11-4 试计算图示各杆的变形能。 (a) 轴材料的剪切弹性模量为G, d 2 =
材料力学II能量法的应用补充
压杆的临界载荷——极值点失稳问题
压杆的临界载荷——极值点失稳问题
曲线OA部分为稳定平衡,极值点以后部 分为不稳定平衡。A点为临界状态。
对于受轴向压力P作用的扁锥,力P与轴 向位移间的关系如图b所示。不仅存在相 对极大值A点,还存在相对极小值B点。 这类无分支点的稳定问题也称为跳跃 (snap)问题。
能量法的应用
能量法研究梁的横向剪切效应 能量法研究杆件的冲击应力 能量法研究压杆的临界载荷 能量法研究梁柱纵横弯曲变形与应力计
算等问题 此外,另一重要应用为求解静不定问题。
梁的横向剪切效应
梁的横向剪切效应
梁的横向剪切效应
梁的横向剪切效应
梁的横向剪切效应
梁的横向剪切效应
将(a)式代入到公式(5)可得临界载荷为
Fcr
EIw''2 dx
l
w'2 dx
l
l
EI(
a
l2
2
sin
x
l
)2
dx
( a cos x )2 dx
2EI l2
ll
l
所得解答与精确解相同。之所以如此,是因为 假设的挠曲线方程就是真实的挠曲线方程。
例 2 如图所示细长 压杆,一端固定、另 一端自由,承受集度 为q的轴向均布载荷 作用。试用能量法确 定载荷q的临界值qcr。
平衡;
若ΔΠ<0,原始状态ΔΠ=max,属于不稳
定平衡;
若ΔΠ=0,势能不变,属于随遇平衡。
平衡相关物理概念从数学观点看可以归 结为寻求势能函数的极小值和极大值的 微分或变分问题。
压杆的临界载荷
两类失稳形式: 弹性体的平衡问题,其稳定性取决于结
专题能量法求位移lecture
计算转角的莫尔定理
P1 P2 P3
C
x
c
l
原受力结构
EIz
1c
L
M
0
x
M
x
dx
EI Z
1C
x
l 克隆结构
EIz
莫尔定理—又称单位力法 适用范围—线性弹性结构
例:如图所示:简支梁AB,跨长为L,抗弯刚度为 EI Z
。梁上受均布载荷作用,载荷集度为q,试求出梁跨中点C的
挠度 f c 及端面B的转角 B
L
U
N 2x dx
0 2EA
dx
N(x) dx qdx
N ( x)
二.扭转变形能的计算:
1.M n 常量
U
W
M
2 n
L
2GI P
2.M n M n x
U M n2 xdx
L 2GI P
三.弯曲变形能的计算:
1. M z 常量 U M z2l 2EIZ
2. M z M z x
U M 2 xdx L 2EIZ
1 2
Fa 1 EA
2
2 F 2
EA
2a
(
2
2)
Fa 3 2 EA 2
例3 用卡氏第二定理求B点的挠度。EI为常数。
F
F
解:
A
C l x2
l x1 B (1)弯矩方程及导数
M1(x1) Fx1
M 2 (x2 ) F (l x2 ) Fx2
M1 F
x1
M 2 F
l
x2
(2)卡氏第二定理求挠度
(4)求解多余未知力: 将力-位移间物理关系,代入变形协 调条件,得补充方程。由补充方程解出多余未知力。
材料力学第12章 能量法
范围内工作时,其轴线弯曲成为一段圆弧,如图12.5(a)所示。两端横截
面有相对转动,其夹角为θ ,由第7章求弯曲变形的方法可以求出
图12.5 与前面的情况相似,在线弹性范围内,当弯曲外力偶矩由零逐渐增加到M0时
,梁两端截面相对于转动产生的夹角也从零逐渐增加到θ ,M0与θ 的关系也
是斜直线,如图12.5(b)所示,所以杆件纯弯曲变形时的应变能为
dW在图12.2(a)中以阴影面积来表示。拉力从零增加到FP的整个加载过程
中所做的总功则为这种单元面积的总和,也就是说是△OAB的面积,即
可以将以上的分析推广到其他受力情况,因而静载荷下外力功的计算式可以
写为 式中的 F是广义力,它可以是集中力或集中力偶;Δ 是与广义力F相对应的
位移,称为广义位移,它可以是线位移或角位移。式(12.2)表明,当外力
在工程实际中,最常遇到的是横力弯曲的梁。这时梁横截面上同时有剪力和
弯矩,所以梁的应变能应包括两部分:弯矩产生的应变能和剪力产生的应变 能。在细长梁的情况下,剪切应变能与弯曲应变能相比,一般很小,可以不
计,常只计算弯曲应变能。另外,此时弯矩通常均随着截面位置的不同而变
化,类似于式(12.5)与式(12.9),梁的弯曲应变能为
表面上的剪力与相应的位移方向垂直,没有做功。因此,单元体各表面上的 剪切力在单元体变形过程中所做的功为
故单元体内积蓄的应变能为
则单元体内积蓄的应变比能为
下
这表明,vε 等于γ 直线
的面积。由剪切胡克定律=Gγ ,比能又可以写成下列形式
(3)扭转 如图12.4(a)所示的受扭圆轴,若扭转力偶矩由零开始缓慢增加到最终值T
,积蓄在弹性体内的应变能Vε 及能量耗损Δ E在数值上应等于载荷所做的功 ,既 如果在加载过程中动能和其他形式的能量耗损不计,应有
材料力学能量法
wA
F
A
B
x
l
②列弯矩方程 M =-Fx ( 0 ≤ x < l ) ③求外力功W 和应变能Ve
1 W FwA 2
1 F 2l 3 FwA 2 6 EI
2 l ( Fx ) dx M 2 dx F 2l 3 Ve 0 2 EI 0 2 EI 6 EI l
Fl 3 wA 3EI
l
由功能原理有
由平衡方程和对称条件有 F1 F2 ,Dl1 Dl2
2 F1 cos + F3 F
1 1 F Dl3 ( F1Dl1 + F2 Dl2 + F3Dl3 ) 2 2
(1) Dl3
(2) (3)
F
Dl1
(2)、(3)代入(1)得 Dl3 cos Dl1
变形几何方程
即 D1= d11F1+d12F2+ … +d1iFi + … +d1nFn …… Di= di1F1+di2F2+ … +diiFi + … +dinFn …… 其中dij 是与载荷无关的常数。 注意:各载荷和位移都是指最终值,所以是常数。
材料力学 中南大学土木建筑学院
16
设各外载荷有一增量,于是位移亦有一增量。载荷 在位移增量上所作的元功为:
( )
仅仅只能求力作用点与力相对应的位移, 其它位移的求解有待进一步研究功能原理。
材料力学 中南大学土木建筑学院
10
图示对称结构,各杆抗拉刚度EA均相等。 ①由平衡方程,通过功能原理导出变形几 何方程;②由平衡方程结合功能原理求出 各杆内力。
解:A点的位移等于③杆的变形Dl3。
B
F
A
B
x
l
②列弯矩方程 M =-Fx ( 0 ≤ x < l ) ③求外力功W 和应变能Ve
1 W FwA 2
1 F 2l 3 FwA 2 6 EI
2 l ( Fx ) dx M 2 dx F 2l 3 Ve 0 2 EI 0 2 EI 6 EI l
Fl 3 wA 3EI
l
由功能原理有
由平衡方程和对称条件有 F1 F2 ,Dl1 Dl2
2 F1 cos + F3 F
1 1 F Dl3 ( F1Dl1 + F2 Dl2 + F3Dl3 ) 2 2
(1) Dl3
(2) (3)
F
Dl1
(2)、(3)代入(1)得 Dl3 cos Dl1
变形几何方程
即 D1= d11F1+d12F2+ … +d1iFi + … +d1nFn …… Di= di1F1+di2F2+ … +diiFi + … +dinFn …… 其中dij 是与载荷无关的常数。 注意:各载荷和位移都是指最终值,所以是常数。
材料力学 中南大学土木建筑学院
16
设各外载荷有一增量,于是位移亦有一增量。载荷 在位移增量上所作的元功为:
( )
仅仅只能求力作用点与力相对应的位移, 其它位移的求解有待进一步研究功能原理。
材料力学 中南大学土木建筑学院
10
图示对称结构,各杆抗拉刚度EA均相等。 ①由平衡方程,通过功能原理导出变形几 何方程;②由平衡方程结合功能原理求出 各杆内力。
解:A点的位移等于③杆的变形Dl3。
B
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解: M ( ) PR (1 cos ) M ( ) R (1 cos )
0
AB 2
0
3 PR 3 EI
ቤተ መጻሕፍቲ ባይዱ
2 2 M ( ) M ( ) PR (1 cos ) R d 2 R d EI EI 0 0
d
例:半圆形小曲率曲杆的A端固定,在自 由端作用扭转力偶矩m,曲杆横截面为圆形,
的集中力P垂直于轴线所在的平面。试求A点的
垂直位移。已知GIp、EI为常量。
解:T ( ) PR(1 cos ) , M ( ) PR sin T 2 ( ) M 2 ( ) U Rd Rd 2G I p 2E I l l
3 P R P R 4G I p 4E I 1 W P AV 2
M ( x) M ( x) dx EI
0
l
M ( x ) Px ,
M ( x ) 1
B
l
M ( x) M ( x) dx EI
0
0
l
2 Px Pl dx EI 2 EI
例:计算图(a)所示开口圆环在 P力作用
下切口的张开量 Δ AB 。EI=常数。
2
2
2 2 2 P 2b 2 a 3 P2a 2 b3 P a b 2 2 6 EI l 2 EI l 3 2 EI l 3
1 W P vC 2
由U W,得: Pa 2 b 2 vC 3EI l
例:试求图示四分之一圆曲杆的变形能,
并利用功能原理求B截面的垂直位移。已知EI
2
U
l
l
1 W P vB 2
Pl 由 U W,得 v B 3EI
3
例:试求图示梁的变形能,并利用功能原 理求C截面的挠度。
解:
U
l
Pb Pa x1 x2 2 a b M ( x) l l dx dx1 dx 2 2E I 2E I 2E I 0 0
注意:上式中应看成广义位移,把单位力看成与广 义位移对应的广义力
P
例:试用莫尔定
A
l
x
B
理计算图(a)所示
悬臂梁自由端B
的挠度和转角。
A
1
B
x
1
A B
x
解: (1) 在B截面作用一单位力 , 如图 (b) 所示 M ( x ) Px ,
0
M ( x) x
0
3 Px 2 vB dx Pl EI l 3EI 0 (2) 在B截面作用一单位力偶 , 如图 (c) 所示
W1 U 1
[( M ( x ) M 0 ( x )]2 U 0 U 1 dx 2E I l
l
M ( x) M 0 ( x) M 2 ( x) [ M 0 ( x )]2 dx dx dx 2E I 2E I EI l l
M M x )MMx) ( x ) ( ( x) ( 1 E I dx dx EI l
0 l
0
l
M ( x) M ( x) 莫尔定理 dx EI (莫尔积分)
M ( x) M 0 ( x) dx EI
0
对于组合变形: l
l
N ( x) N 0 ( x) T ( x) T 0 ( x) M ( x) M 0 ( x) dx dx dx EA GI p EI l l
为常量。
解: M ( ) PR sin
U
l
M 2 ( ) Rd 2E I
( PR sin ) P R 2 E I Rd 8 EI 0
2 2
2
3
1 W P BV 2
由U W,得:
BV
PR
4 EI
3
R
例:轴线为半圆形的平面曲杆,作用于A端
2 3 2 3
由U W,得:
AV 3 PR PR 2GI p 2 EI
3 3
R
§12-3 单位载荷法
P1
P2
C
P1
P2
C
M ( x)
U
l
M ( x) dx 2E I
2
P0 1
C
M ( x)
0
[ M ( x )] U0 dx 2E I l
0
2
P1 P2
P0
第十二章
能量法 述
§12-1 概
在弹性范围内,弹性体在外力作用下发
生变形而在体内积蓄的能量,称为弹性变形能,
简称变形能。
物体在外力作用下发生变形,物体的变
形能在数值上等于外力在加载过程中在相应位
移上所做的功,即
U=W
§12-2 杆件变形能计算
一、轴向拉伸和压缩
1 Pl 1 U W P l 2 P EA 2
三、弯曲
2 2 1 ml m l M l 纯弯曲: W 1 m m U 2 EI 2E I 2E I 2
横力弯曲:U
M ( x) 2 E I ( x ) dx l
2
四、组合变形 截面上存在几种内力,各个内力及相应的 各个位移相互独立,力独立作用原理成立,各 个内力只对其相应的位移做功。
N ( x) T ( x) M ( x) U dx dx dx l 2 E A( x ) l 2G I p ( x ) l 2 E I ( x)
2
2
2
例:试求图示悬臂梁的变形能,并利用功 能原理求自由端B的挠度。
解:
M ( x) P x
2 3 ( Px ) 2 M ( x) P l dx dx 2E I 2E I 6 EI 0
P l N l 2 EA 2 EA
N ( x) U dx 2 EA( x ) l
2
P
2
2
P
l
l
二、扭转
m
m
2
2
ml 1 1 m l T l U W m m 2 G I p 2G I p 2G I p 2 2 T ( x) U dx 2G I p ( x ) l
C
M ( x) M 0 ( x)
[( M ( x ) M 0 ( x )]2 U1 dx 2E I l
P0 作功:
共做功 P1 、P2 作功: U W1 U 0 U 1 1 P0 在上又作功: P0 1 P1 P2
U0
C
