Eviews数据统计与分析教程12章 面板数据(Panel Data)模型
计量经济面板数据模型及EVIEWs软件的实现

面板数据模型的分析及Eviews实现一、面板数据和模型概述在经济学研究和实际应用中,我们经常需要同时分析和比较横截面观察值和时间序列观察值结合起来的数据,即:数据集中的变量同时含有横截面和时间序列的信息。
这种数据被称为面板数据(panel data),它与我们以前分析过的纯粹的横截面数据和时间序列数据有着不同的特点。
简单地讲,面板数据因同时含有时间序列数据和截面数据,所以其统计质既带有时间序列的性质,又包含一定的横截面特点。
因而,以往采用的计量模型和估计方法就需要有所调整。
例1 表1中展示的数据就是一个面板数据的例子。
其他类似的例子还有:历次人口普查中有关不同年龄段的受教育状况;同行业不同公司在不同时间节点上的产值等。
这里,不同的年龄段和公司代表不同的截面,而不同时间节点数据反映了数据的时间序列性。
研究和分析面板数据的模型被称为面板数据模型(panel data model)。
它的变量取值都带有时间序列和横截面的两重性。
一般的线性模型只单独处理横截面数据或时间序列数据,而不能同时分析和对比它们。
面板数据模型,相对于一般的线性回归模型,其长处在于它既考虑到了横截面数据存在的共性,又能分析模型中横截面因素的个体特殊效应。
当然,我们也可以将横截面数据简单地堆积起来用回归模型来处理,但这样做就丧失了分析个体特殊效应的机会。
二、一般面板数据模型介绍 符号介绍:ity ——因变量在横截面i 和时间t 上的数值;j it x ——第j 个解释变量在横截面i 和时间t 上的数值;假设:有K 个解释变量,即K j ,,2,1 =;有N 个横截面,即N i ,,2,1 =; 时间指标T t ,,2,1 =。
记第i 个横截面的数据为⎪⎪⎪⎪⎪⎭⎫⎝⎛=iT i i i y y y y21; ⎪⎪⎪⎪⎪⎭⎫⎝⎛=K iT iT iT Ki i i K i i i i x x x x x x x x x X 212221212111;⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=iT i i i μμμμ 21 其中对应的i μ是横截面i 和时间t 时随机误差项。
面板数据模型 计量经济学 EVIEWS建模课件

⑶当使用一个Pool序列名时,EViews认为将 准备使用Pool序列中的所有序列。EViews会自动 循环查找所有截面识别名称,并用识别名称来替 代“?”。然后会按指令使用这些替代后的名称 了。Pool序列必须通过Pool对象来定义,因为如 果没有截面识别名称,占位符“?”就没有意义。
使用基本名和截面识别名称组合命名。截面 识别名称可以放在序列名中的任意位置,只要保 持一致即可。例如:GDP_JPN,GDP_USA,GDP_UK等; 其中“GDP”作为序列的基本名。
⑴通过View/Cross-Section Identifiers或选 择工具条的Define按钮,可以显示Pool中的截面成 员识别名称,并可以对其进行编辑。
⑵通过sheet按钮定义一组序列名, 序列名是 由基本名和所有截面识别名构成的。在Pool中的关 键是序列命名: 各序列名的命名规则可以使用基 本名和“?”占位符构成,其中“?”代表截面识 别名。如序列名为GDPJPN,GDPUSA,GDPUK,相应 的Pool序列命名时就要输入GDP?。如果序列名为 JPNGDP,USAGDP,UKGDP,则为 ?GDP。
⑴通过确定工作文件样本来指定堆积数据表中 要包含哪些时间序列观测值。
⑵打开Pool,选择View/Spreadsheet(stacked data),EViews会要求输入序列名列表,可以输入 普 通 序 列 名 或 Pool 序 列 名 。 如 果 是 已 有 序 列 , EViews 会 显 示 序 列 数 据 ; 如 果 这 个 序 列 不 存 在 , EViews会使用已说明的Pool序列的截面成员识别名 称建立新序列或序列组。
⒉ 堆积数据 选择View/Spreadsheet(stacked data), EViews会要求输入序列名列表。
Eviews统计第十二章

Eviews 统计分析 从入门到精通 三、混合横截面模型
如果我们认为一个面板数据在时间和截面个体之间均无显著性 差异,那么就可以直接把面板数据混合在一起用普通最小二乘 法(OLS)估计参数,这样的模型就是混合横截面模型,如公 式12-5所示。
yit i xit vit
i 1 k
(2)在Test type下拉列 表框中选择Summary选 项,Test for unit root in 选择组中选择level单选按 钮,Include in test eqution选项组中选择 Individual intercept,其 他选项选择默认设置。
i 1 k
12 2
其中,i = 1, 2, …, N表示个体成员,t = 1, 2, …, T代表时间跨度。
Eviews 统计分析 从入门到精通
模型中不随时间变化的非观测效应与误差项相关。均值截距项在不 同的截面成员时间是相同的,代表截面个体成员截距项,表示个体成员 的截距对整体截距的偏离。 对于固定效应模型,通常的处理方法是准差分处理后使用OLS估计 方法或使用最小二乘虚拟变量法(LSDV)进行估计;如果其误差项不 满足满足相互独立和同方差假定,则需要使用GLS进行估计。
Eviews 统计分析 从入门到精通
案例12.2
Eviews 统计分析 从入门到精通
设置要点 (1)在Depandent Variable输入框 中输入待模型的被解释变量 (2)在 Regressors and AR terms 选项组下的Cross-section specifics输入框中输入解释变量 名称。 (3)选择估计形式。
ˆ ˆ ) 1 ( ˆ ˆ )12 4 W ( w GLS w GLS
eviews面板数据模型详解
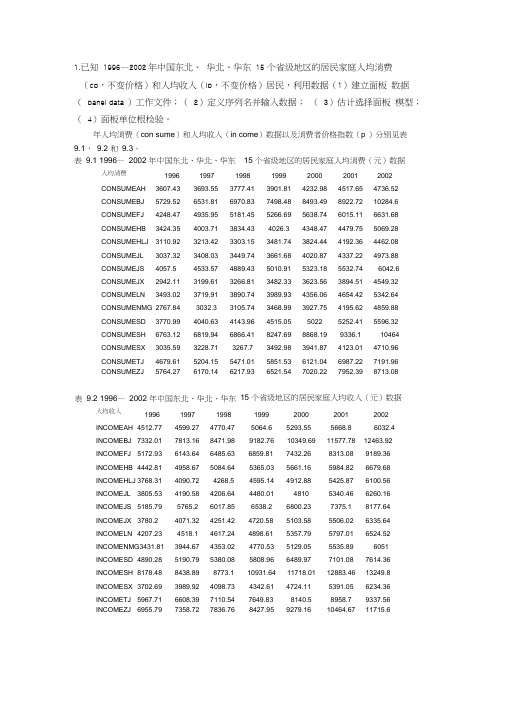
1.已知 1996—2002年中国东北、 华北、华东 15 个省级地区的居民家庭人均消费(cp ,不变价格)和人均收入(ip ,不变价格)居民,利用数据(1)建立面板 数据( panel data )工作文件;( 2)定义序列名并输入数据; ( 3)估计选择面板 模型;( 4)面板单位根检验。
年人均消费(con sume )和人均收入(in come )数据以及消费者价格指数(p )分别见表 9.1, 9.2 和 9.3。
表 9.1 1996— 2002 年中国东北、华北、华东 15 个省级地区的居民家庭人均消费(元)数据人均消费1996 1997 1998 1999 2000 2001 2002 CONSUMEAH 3607.43 3693.55 3777.41 3901.81 4232.98 4517.65 4736.52 CONSUMEBJ 5729.52 6531.81 6970.83 7498.48 8493.49 8922.72 10284.6 CONSUMEFJ 4248.47 4935.95 5181.45 5266.69 5638.74 6015.11 6631.68 CONSUMEHB3424.354003.71 3834.43 4026.3 4348.47 4479.75 5069.28 CONSUMEHLJ 3110.92 3213.42 3303.15 3481.74 3824.44 4192.36 4462.08 CONSUMEJL 3037.32 3408.03 3449.74 3661.68 4020.87 4337.22 4973.88 CONSUMEJS 4057.5 4533.57 4889.43 5010.91 5323.18 5532.74 6042.6 CONSUMEJX 2942.11 3199.61 3266.81 3482.33 3623.56 3894.51 4549.32 CONSUMELN3493.023719.91 3890.74 3989.93 4356.06 4654.42 5342.64 CONSUMENMG 2767.84 3032.3 3105.74 3468.99 3927.75 4195.62 4859.88 CONSUMESD 3770.99 4040.63 4143.96 4515.05 5022 5252.41 5596.32 CONSUMESH 6763.12 6819.94 6866.41 8247.69 8868.19 9336.1 10464 CONSUMESX 3035.59 3228.71 3267.7 3492.98 3941.87 4123.01 4710.96 CONSUMETJ 4679.61 5204.15 5471.01 5851.53 6121.04 6987.22 7191.96 CONSUMEZJ5764.276170.146217.936521.547020.227952.398713.08人均收入1996 1997 1998 1999 2000 2001 2002 INCOMEAH 4512.77 4599.27 4770.47 5064.6 5293.55 5668.86032.4INCOMEBJ 7332.01 7813.16 8471.98 9182.76 10349.69 11577.78 12463.92 INCOMEFJ 5172.93 6143.64 6485.63 6859.81 7432.26 8313.08 9189.36 INCOMEHB 4442.81 4958.67 5084.64 5365.03 5661.16 5984.82 6679.68 INCOMEHLJ 3768.31 4090.72 4268.5 4595.14 4912.88 5425.87 6100.56 INCOMEJL 3805.53 4190.58 4206.64 4480.01 4810 5340.46 6260.16 INCOMEJS 5185.79 5765.2 6017.85 6538.2 6800.23 7375.1 8177.64 INCOMEJX 3780.2 4071.32 4251.42 4720.58 5103.58 5506.02 6335.64 INCOMELN 4207.23 4518.1 4617.24 4898.61 5357.79 5797.01 6524.52 INCOMENMG3431.81 3944.67 4353.02 4770.53 5129.05 5535.89 6051 INCOMESD 4890.28 5190.79 5380.08 5808.96 6489.97 7101.08 7614.36 INCOMESH 8178.48 8438.89 8773.1 10931.64 11718.01 12883.46 13249.8 INCOMESX 3702.69 3989.92 4098.73 4342.61 4724.11 5391.05 6234.36 INCOMETJ 5967.71 6608.39 7110.54 7649.83 8140.5 8958.7 9337.56 INCOMEZJ 6955.797358.727836.768427.959279.1610464.6711715.615 个省级地区的居民家庭人均收入(元)数据表 9.2 1996— 2002 年中国东北、华北、华东< >\ Uinni«d X NewPage -/ 程如下:表9.3 1996 — 2002年中国东北、华北、华东物价指数1996 1997 1998 1999 2000 2001 2002 PAH 109.9 101.3 100 97.8 100.7 100.5 99 PBJ 111.6 105.3 102.4 100.6 103.5 103.1 98.2 PFJ 105.9 101.7 99.7 99.1 102.1 98.7 99.5 PHB 107.1 103.598.4 98.1 99.7 100.5 99 PHLJ 107.1 104.4 100.4 96.8 98.3 100.8 99.3 PJL 107.2 103.7 99.2 98 98.6 101.3 99.5 PJS 109.3 101.7 99.4 98.7 100.1 100.8 99.2 PJX 108.4 102 101 98.6 100.3 99.5 100.1 PLN 107.9 103.1 99.3 98.6 99.9 100 98.9PNMG 107.6 104.5 99.3 99.8 101.3 100.6100.2PSD 109.6 102.8 99.4 99.3 100.2 101.8 99.3 PSH 109.2 102.8 100 101.5 102.5 100 100.5 PSX 107.9 103.1 98.6 99.6 103.9 99.8 98.4 PTJ109 103.1 99.5 98.9 99.6 101.2 99.6 PZJ107.9102.899.798.810199.899.1(1)建立面板数据工作文件首先建立工作文件Tetcli from DB .Update sslectei from DB... Stor* selected to DB... Copy.s^lectedL . selectelFrijit Selected15个省级地区的消费者物价指数Ssntple: E c 回 r@sidGenerate Series. BDisplay Filter *New Obj set...建立面板数据库在窗口中输入15个不同省级地区的标识AH BJ FJHB HLJJL JS JX LNNMG SD SH sx TJ ZJI(2)定义序列名并输入数据产生3*15个尚未输入数据的变量名。
EVIEWS面板数据分析操作教程及实例解析

模型选择对分析结果影响
模型适用性
根据研究目的和数据特征选择合 适的面板数据模型,如固定效应 模型、随机效应模型等。
模型假设
确保所选模型满足基本假设,如 线性关系、误差项独立同分布等 ,否则可能导致结果不准确。
模型比较与选择
通过比较不同模型的拟合优度、 参数显著性等指标,选择最优模 型进行分析。
操作规范性与结果可靠性保障措施
操作步骤规范
结果验证与解读
对分析结果进行验证,确保结果的合理性和准确性 ;同时,正确解读分析结果,避免误导读者。
严格按照EVIEWS软件的操作步骤进行分析 ,避免操作失误或遗漏关键步骤。
数据分析报告
编写详细的数据分析报告,包括数据来源、 处理方法、模型选择、分析结果及解读等, 以便读者全面了解分析过程。
方和来估计模型参数。
广义最小二乘法(GLS)
02
当存在异方差性或自相关性时,采用广义最小二乘法进行参数
估计,以提高估计效率。
最大似然法(ML)
03
适用于随机效应模型等复杂面板数据模型,通过最大化似然函
数来估计模型参数。
模型诊断与检验
残差分析
检查残差是否满足独立同分布等假设条件, 以评估模型的拟合效果。
07 EVIEWS面板数 据分析操作注意 事项
数据质量对分析结果影响
数据来源
确保数据来自可靠、权威的来源,避免使用不准确或存在偏见的数 据。
数据完整性
检查数据是否存在缺失值、异常值或重复值,这些问题可能导致分 析结果失真。
数据处理
对数据进行适当的预处理,如清洗、转换和标准化,以提高数据质量 和一致性。
增强了解决实际问题的能力
通过实例解析和操作演示,学员们学会了如何运用所学知识解决实际问题,提高了分析 问题和解决问题的能力。
Eviews面板数据模型估计

4361.555
3890.580 4077.961 5317.862 3612.722 4360.420 3877.345 5011.976 8651.893 3793.908 6145.622
4457.463
4159.087 4281.560 5488.829 3914.080 4654.420 4170.596 5159.538 9336.100 4131.273 6904.368
4571.439 6624.316 4787.606 4968.164 4780.090
4997.843
4878.296 6793.437 5088.315 5363.153 5063.228
5382.808
5271.925 7316.567 5533.688 5797.010 5502.873
6143.565
建立好Pool对象以后,选择View/Spreadsheet (stacked data),EViews会要求输入序列名列表。
大多数情况下,不同截面成员的数据从上到下依次堆积,每一 列代表一个变量,每一列内数据都是按年排列的。如果数据按年排 列,要确保各年内截面成员的排列顺序要一致。
生成新的序列
• 打开原始pool数据,点击工具栏中的poolgenr键,在 弹出的对话框中输入要生成的公式,如: cp?=consume?/p?,ip?=income?/p?
4.如何估计Pool方程
单击Pool工具栏的Estimate选项打开如下对话框:
(1)因变量 在因变量对话框中输入Pool变量或Pool变量表达式。 (2)估计方法 Fixed and Random下: Cross-secti(个体效应)有三个选项,分别表示无、固定和随机个 体效应。 Period(时点效应)有三个选项,分别表示无、有固定和有随机时 点效应。 Weights有五个选项,分别表示无加权、个体的GLS法、个体SUR法、 时点GLS法和时点SUR法。 (3)估计设置 Method有两个选项:LS和TSLS Sample为样本区间。
Panel data简介

Panel data 简介及其在eviews 中的应用武汉大学经济学系数量经济学教研室《实践教改项目组》编制面板数据(panel data )回归模型与规则的时间序列或截面数据回归模型的区别在于其变量有两个下标,它同时使用截面数据和时间序列数据。
一、panel data 的优点面板数据相对于时间序列数据或截面数据的优点:1.能提供给研究者大量的数据点,这样可以增加自由度并减少解释变量间的共线性,从而改进计量经济估计的有效性。
为了估计模型参数,样本点越多越好。
样本点越多,估计的结果有效性越好,当样本点足够多时,估计结果可以视为具有一致性; 2. 面板数据模型可以从多层面分析经济问题。
3. 与时间序列数据或截面数据相比,面板数据能够更好的进行识别并控制和检验更复杂的行为模型。
二、模型的基本结构和分类面板数据回归模型的主要结构如下:T t N i u a X y it it it ,,2,1,,,2,1,/==++=β (1)其中,i 表示截面维度,可以表示家庭,个人,公司,国家等等;t 表示时间序列维度,是面板数据所研究的时间区间;it X 为解释变量,β为1⨯K 维向量,K 为解释变量的个数,β是斜率,a 是截距。
模型的矩阵形式为:11221111111121111111221111111111⨯⨯⨯⨯⨯⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛''''''+⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛NT NT N T T k NT NT N T T NT NT NT N T T u u u u u u X X X X X X y y y y y y βα 其中()k t t itX X X ,11,1,''=' 众所周知,随机误差项it u 包含了模型解释变量所不能解释的所有其它因素,并且it u 满足一些经典假设,这些假设是我们估计模型参数的基础。
eviews面板数据模型分析——面板数据模型与应用

2.2 固定效应模型(fixed effects model) 。
解释设定个体固定效应模型的原因。假定有面板数据模型 yit = 0 + 1 xit +2 zi +it, i = 1, 2, …, N; t = 1, 2, …, T 其中0 为常数, 不随时间、 截面变化;每个个体回归函数的斜率1 相同; zi 表示随个体变化,但不随时间变化的难以观测的变量。上述模型可以 被解释为含有 N 个截距,即每个个体都对应一个不同截距的模型。令 i = 0 +2 zi,于是变为 yit = i + 1 xit +it, i = 1, 2, …, N; t = 1, 2, …, T 以家庭消费性支出与可支配收入关系为例, 省家庭平均人口数就是这样 的一个变量,即对于短期面板,这是一个基本不随时间变化的量,但是 对于不同的省份,这个变量的值是不同的。 因为 zi 是不随时间变化的量, 所以当对个体固定效应模型中的变量进行 差分时,可以剔除那些随个体变化,但不随时间变化的 zi 的影响。
yit = i + Xit ' +it, i = 1, 2, …, N; t = 1, 2, …, T
其中i是随机变量,表示对于i个个体有i个不同的截距项,且其变化与Xit 有关系;Xit为k 1阶回归变量列向量(包括k个回归量),为k 1阶回归 系数列向量,对于不同个体回归系数相同,yit为被回归变量(标量),it 为误差项(标量),则称此模型为个体固定效应模型。
2.2 固定效应模型(fixed effects model) 。
个体固定效应模型的强假定条件是, E(iti, Xit) = 0, i = 1, 2, …, N
i 作为随机变量描述不同个体建立的模型间的差异。 因为i 是不可观测
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
EViews统计分析基础教程
二、Pool对象的基本操作
1.Pool对象的建立
在创建Pool对象前应首先建立一个能进行面板数据分析的工 作 文 件 。 首 先 打 开 EViews 软 件 , 在 主 菜 单 栏 中 选 择 “ File”|“New”|“Workfile…” 选 项 , 在 弹 出 的 对 话 框 “Workfile structure type”的下拉菜单中选择“Balanced Panel” (平衡面板)选项。在右侧的“Frequency”中选择数据频率, 在“Start”和“End”中输入起至日期,在“Number of cross” 中输入截面数据成员的个数。在“Names”中为该工作文件 命名,再单击“OK”按钮即可生成一个给定频率的平衡面板 工作文件。
EViews统计分析基础教程
二、Pool对象的基本操作
1.Pool对象的建立
在将标识名称输入完毕后,可直接关闭该Pool对话框。系统 会自动保存在Pool对象中输入的信息。需说明的是,Pool对 象本身不包含任何时间序列和数据,它只是对数据结构的一 个基本描述。因此,当删除所建立的Pool对象时,并不同时 删除它所使用的序列对象。
EViews统计分析基础教程
第12章 面板数据(Panel Data)模型
重点内容:
• Pool对象的建立
• Pool对象数据分析
• Pool对象模型估计
EViews统计分析基础教程
一、Panel Data模型原理
面板数据模型的基本形式是 y it = it + xit it + µ it 其中, i t是模型的常数项; i t是k×1维参数向量,k是模 型中解释变量的个数; xit是外生变量向量;µ t是均值为0且 i 同方差的随机误差项,并且不同样本下的随机误差项是相互 独立的;T是每个截面样本下的时期总数,N是截面样本总 数。
EViews统计分析基础教程
二、Pool对象的基本操作
2.Pool对象数据的输入
在实际应用中,通常将三维数据转化为二维数据。首先向读 者介绍一下堆积数据和非堆积数据两种数据结构形式,然后 分别介绍每一种数据结构的导入方法。 (1)堆积数据 Pool数据的堆积形式为将一个变量的所有数据放在一起,并 与其他变量的数据分开。数据堆积的方式有两种,一种是按 截面成员堆积,一种是按日期堆积。按截面成员堆积的数据 是将不同截面成员的数据从上至下排列,每一列代表一个变 量。
EViews统计分析基础教程
二、Pool对象的基本操作
2.Pool对象数据的输入
(2)非堆积数据 在非堆积数据中,给定的截面数据和变量是放在一起的,但 同其他的截面成员和变量的数据是分开的。每一个截面成员 的观测值被放在一纵列中,每一列是截面成员不同时期的样 本观测值。 非堆积数据形式的导入方法与第三章所介绍的数据导入方法 相同。
EViews统计分析基础教程源自二、Pool对象的基本操作
1.Pool对象的建立
在建立好的工作文件中创建Pool对象。选择工作文件工具栏 中的“Object”|“New Object”选项,在打开的对话框中选择 “Pool”选项,将弹出图12-1所示的Pool对象窗口。单击该窗 口工具栏中的“Name”功能键可为该Pool对象命名。系统默 认的名称为“pool01”“pool02”等。
EViews统计分析基础教程
二、Pool对象的基本操作
2.Pool对象数据的输入
对于堆积形式的数据可以采用手动方式输入,也可以采用 Pool对象中的数据导入方式输入。但要注意的是,数据必须 是平衡的,如果采用导入方式,则源文件中截面成员的排列 顺序与Pool对象中的截面成员标识名称的顺序要保持一致。 对于截面成员堆积数据,每个截面成员的样本期应该是一致 的;对于时期堆积数据,每个时期必须包含相同数目的截面 成员,并且排列顺差应该是一致的。当观测值为空值(NA) 时,应用“–”代替,以保证数据总体结构平衡。
EViews统计分析基础教程
三、Pool对象模型估计
在“Dependent variable”(因变量)中输入Pool变量或者Pool 变量的表达式; 在“Estimation method”中设定估计形式; 在“Cross-section”(截面成员)和“Period”(时期)的下拉 菜单中可对影响方式进行设定; 在“Regressors and AR() terms”中输入解释变量; “Method”提供了两种估计方法,一种是最小二乘估计法 ( LS ) , 一 种 是 两 阶 段 最 小 二 乘 估 计 法 ( TSLS ) 。 “Sample”为样本期的设定,系统默认下为截面成员的最大 样本值。其右侧有个复选框“Balance Sample”,可在各截面 成员间进行数据排除。
EViews统计分析基础教程
二、Pool对象的基本操作
1.Pool对象的建立
在Pool对象的编辑窗口中输入截面成员的标识名称,例如做 中国省际面板数据分析时,选取中部五省份为截面成员,即 湖南、湖北、河南、江西和安徽,分布用字母HN,HB,HE, JX,AH表示。这些截面成员各名称之间可用空格隔开,也 可以通过回车键进行换行,即每一个名称占一行。需注意的 是,截面成员的标识名称的设定需简单,便于操作。通常可 以在截面成员标识名称前加下划线“_”。如下图所示。
EViews统计分析基础教程
二、Pool对象的基本操作
3.Pool对象数据的分析
打开Pool对象窗口,选择工具栏中的 “View”|“Descriptive Statistics…”选项,得到下图所示的对话框。
EViews统计分析基础教程
二、Pool对象的基本操作
3.Pool对象数据的分析
在编辑栏中输入要计算描述统计量的序列名称,可以是普 通序列,也可以是Pool序列; 在“Sample”中选定样本类型; 在“Data organization”中指定计算方法。
EViews统计分析基础教程
二、Pool对象的基本操作
2.Pool对象数据的输入
(1)堆积数据 在含有Pool对象的工作文件中,打开Pool对象,单击其工具 栏中的“View”|“Spreadsheet(stacked data)…”选项,在弹 出的对话框中输入序列名称 。如果是已经存在的序列, EViews会显示出序列中的数据;如果是不存在的序列, EViews会根据Pool对象的截面成员标识名称建立新的序列对 象。在该对话框中输入完序列名称后单击“OK”按钮,即可 得 到 图 12-3 所 示 的堆积形式 的 数据表 。 点击工 具 栏中的 “Edit+/-”键可对数据进行编辑,用户可用手动方式逐个进 行输入,也可以通过“复制粘帖”方式输入。
一、Panel Data模型原理
分类: 通常情况下,可将面板数据模型分为三类: 变截距模型:当模型中系数向量 i t相同即均为,而截距 项 i t是不同时,则应建立变截距模型; 变系数模型:当模型中系数向量 i t和截距项 i t均发生变 化时,则应建立变系数模型; 截距和系数均不变的模型:当模型中系数向量 i t和截距项 i t均相同时,即同为 和,则应建立截距和系数均不变的 模型。
EViews统计分析基础教程
二、Pool对象的基本操作
2.Pool对象数据的输入
(1)堆积数据 如果用户采用导入方式输入数据,可在Pool对象窗口工具栏 中选择“Proc”|“Import Pool data(ASCII,XLS,WK?)…”选 项,然后在弹出的窗口中选择源文件的路径和名称后会得到 下图所示的导入数据的对话框。
EViews统计分析基础教程
二、Pool对象的基本操作
2.Pool对象数据的输入
(1)堆积数据 在“Series order”中指定数据的排列方式,“In Columns”为 纵向排列,“In Rows”为横向排列。在“Group observations” 中指定数据堆积形式,“By Cross-section”为按截面成员堆 积,“By Date”为按时期堆积。在“Upper-left data cell”的编 辑 栏 中 指 定 EXCEL 工 作 表 中 数 据 的 起 始 单 元 格 。 在 “Ordinary and Pool”的编辑栏中输入序列名称,例如,I? M?。如果输入的系列名是Pool序列名,EViews软件会用截 面成员的标识名称创建序列或命名序列;如果是普通序列名, 则会创建单个序列。其他各项内容的设定与第三章介绍的数 据导入相同。设定好各项内容后单击“OK”按钮就完成了数 据的读入。
EViews统计分析基础教程
本章小结:
• 了解面板数据模型的基本原理 • 掌握Pool对象的建立方法 • 掌握Pool对象的数据输入方法
EViews统计分析基础教程
三、Pool对象模型估计
通过Pool对象可以对固定影响、随机影响变截距模型和固定 影响变系数模型进行估计。常用的方法有最小二乘估计法、 加权最小二乘法等。
EViews统计分析基础教程
三、Pool对象模型估计
在EViews操作中,单击Pool对象工具栏中的“Estimate”或者 选择“Proc”|“Estimate”选项,将弹出下图所示的对话框。
EViews统计分析基础教程
一、Panel Data模型原理
当参数值不随截面数据成员的不同而改变时,可将面板数据 模型写为如下形式
yi = i + xi i + µ i
yi和xi向量中的每一分量代表第i个截面样本下的数据序列, 常数项i 和参数i不受不同截面样本数据的影响。
EViews统计分析基础教程
