传热学-第二章(二)
合集下载
传热学第二章 第二节 导热微分方程式
∂t ∂z
)
+
qv
第二节 导热微分方程式
若物性参数 λ、c 和 ρ 均为常数：
∂t ∂τ
=
a(
∂2t ∂x2
+ ∂2t ∂y2
+
∂2t ∂z2
)
+
qv ; ρc
or
∂t = a∇2t + qv
∂τ
ρc
a = λ — 热扩散率（导温系数） [m2 s] ρc （Thermal diffusivity）
dxdydz ⋅ dτ
[J]
第二节 导热微分方程式
[导入与导出净热量]:
[1] = [dQ x − dQ x+ dx ] + [dQ y − dQ y + dy ] + [dQ z − dQ z + dz ]
[1] = − ( ∂ q x + ∂ q y + ∂ q z ) d x d y d z d τ
qw
=
−
λ
(
∂t ∂n
)n
−
(
∂t ∂n
)
n
=
qw λ
第二类边界条件相当于已知任何时刻物体边界面 法向的温度梯度值
稳态导热： qw = const (恒热流边界条件）
非稳态导热： q w = f (τ )
第二节 导热微分方程式 特例：绝热边界面： 绝热边界条件
qw
=
−λ
⎛ ⎜⎝
∂t ∂n
⎞ ⎟⎠w
=
对特定的导热过程：需要得到满足该过程的补充 说明条件的唯一解
单值性条件：确定唯一解的附加补充说明条件
完整数学描述：导热微分方程 + 单值性条件 单值性条件包括四项：几何、物理、时间、边界
传热学 第2章 稳态导热
t t t t c Φ x x y y z z
3、常物性且稳态:
2t 2t 2t Φ a 2 2 2 0 x y z c
如果边界面上的热流密度保持为常数，则 q | w 常数 当边界上的热流密度为零时，称为绝热边界条件
t t qw 0 0 n w n w
18
（3）第三类边界条件 给出了物体在边界上与和它直接接触的流体之 间的换热状况。 根据能量守恒，有：
返回
2.1.1 各类物体的导热机理
气体：气体分子不规则热运动时相互碰撞的结果，高温的气体分子运 动的动能更大 固体：自由电子和晶格振动 对于导电固体，自由电子的运动在导热中起着重要的作用，电的良导 体也是热的良导体 对于非导电固体，导热是通过晶格结构的振动，即原子、分子在其平 衡位置附近的振动来实现的
返回
2.2.2 定解条件
导热微分方程式是能量守恒定律在导热过程中的应用，是一切导热 过程的共性，是通用表达式。 完整数学描述：导热微分方程 + 定解条件 定解条件包括初始条件和边界条件两大类，稳态问题无初始条件 初始条件：初始时刻的状态表示为： =0，t =f (x,y,z)
边界条件： 给出了物体在边界上与外界环境之间在换热上的联系或相互作用
2、推导基本方法：傅里叶定律 + 能量守恒定律 在导热体中取一微元体
进入微元体的总能量+微元体内热源产生的能量-离开微元体的总能量= 微元体内储存能的增加
11
Ein Eg Eout Es
d 时间段内：
Ein Φx Φy Φz d Eiout Φxdx Φy dy Φz dz d
传热学第2章
根据第一类边界条件时的结果:
dt tw1 tw2 1
（此时壁温tw1和tw2为未知）
dr
ln r1 r
r2
与以上两个边界条件共三式变形后
相加,可消去tw1和tw2，得：
单层圆筒壁的单位管长热流量：
ql
tf1 tf2 1 1 ln r2 1
tf1 tf 2
1 1 ln d 2 1
h1 2r1 2 r1 h2 2r2 h1d1 2 d1 h2d 2
x h2 t x t f 2
根据第一类边界条件时的结果: （此时壁温tw1和tw2为未知）
q dt tw1 tw2 dx
与以上两个边界条件共三式变形后 相加,可消去tw1和tw2，得：
单层平壁的热流密度：
q
tf1 tf2
1 1
k tf1 tf2
h1 h2
多层平壁的热流密度：
接触热阻的定义：
Rc
tc
接触热阻的影响因素： 粗糙度
挤压压力 硬度匹配情形 空隙中介质的性质
减小接触热阻的措施： 表面尽量平整 增加挤压压力
两表面一软一硬 涂导热姆
第七节 二维稳态导热
应用领域：房间墙角，地下埋管，矩形保温层，短肋片
二维稳态导热微分方程：
2t x2
2t y 2
0
解析法
二维稳态导热问题的研究手段：
几种导热过程的形状因子
第二章重点：
1.各种稳态导热问题的数学模型 和求解方法
2.临界热绝缘直径问题
3.肋片性能分析
请同学们思考一个问题:
肋高越大，肋的散热面积越大，因而采用 增加肋高的方法可以增加肋的散热量。这 种方法在实际换热器设计中是否可行？若 可行，是否会有某些局限性？
《传热学》课后习题答案-第二章
第二章 思考题 1 试写出导热傅里叶定律的一般形式，并说明其中各个符号的意义。
t q＝－gradt n x ，其中： gradt 为空间某点的温 答：傅立叶定律的一般形式为： 度梯度； n 是通过该点的等温线上的法向单位矢量，指向温度升高的方向； q 为该处的热流
密度矢量。 2 已知导热物体中某点在 x,y,z 三个方向上的热流密度分别为 热密度矢量？
W /( m 2 .K ) 。同时，有一股辐射能透过薄膜投射到薄膜与基板的结合面上，如附图所示。 t 60 基板的另一面维持在温度 t1 30 ℃。生成工艺要求薄膜与基板结合面的温度 0 ℃，试
确定辐射热流密度 q 应为多大？薄膜的导热系数
f 0.02W /( m.K )
, 基板的导热系数
2-3 有一厚为 20mm 的平板墙，导热系数为 1.3 W /( m.K ) 。为使每平方米墙的热损失不超过 1500W,在外表面上覆盖了一层导热系数为 0.12 W /( m.K ) 的保温材料。已知复合壁两侧的温 度分别为 750℃及 55℃，试确定此时保温层的厚度。 解：依据题意，有
q
1 2 1 2
q1
解：
Q Aq 41.95W q2 5200 44.62 q 116 . 53 1 所以
1 2 3 1 2 3 ＝116.53W/ m 2
t1 t 2
q2
t1 t 2
1 1
5200w / m
2-10 某些寒冷地区采用三层玻璃的窗户，如附图所示。已知玻璃厚δg=3 ㎜，空气夹层宽δ 。玻璃面向室内的表面温度 ti=15℃，面向室外 air=6 ㎜，玻璃的导热系数λg=0.8W/（m·K） 的表面温度 to=-10℃，试计算通过三层玻璃窗导热的热流密度。 解： 2-11 提高燃气进口温度是提高航空发动机效率的有效方法。 为了是发动机的叶片能承受更高 的温度而不至于损坏， 叶片均用耐高温的合金制成， 同时还提出了在叶片与高温燃气接触的 表面上涂以陶瓷材料薄层的方法， 如附图所示， 叶片内部通道则由从压气机来的空气予以冷 却。陶瓷层的导热系数为 1.3W/（m·K） ，耐高温合金能承受的最高温度为 1250K，其导热 系数为 25W/(m·K)。在耐高温合金与陶瓷层之间有一薄层粘结材料，其造成的接触热阻为 10-4 ㎡· K/W。 如果燃气的平均温度为 1700K， 与陶瓷层的表面传热系数为 1000W/(㎡· K)， 冷却空气的平均温度为 400K，与内壁间的表面传热系数为 500W/(㎡·K)，试分析此时耐高 温合金是否可以安全地工作？ 解： 2-12 在某一产品的制造过程中，厚为 1.0mm 的基板上紧贴了一层透明的薄膜，其厚度为 0.2mm。薄膜表面上有一股冷却气流流过，其温度为 20℃，对流换热表面传热系数为 40
t q＝－gradt n x ，其中： gradt 为空间某点的温 答：傅立叶定律的一般形式为： 度梯度； n 是通过该点的等温线上的法向单位矢量，指向温度升高的方向； q 为该处的热流
密度矢量。 2 已知导热物体中某点在 x,y,z 三个方向上的热流密度分别为 热密度矢量？
W /( m 2 .K ) 。同时，有一股辐射能透过薄膜投射到薄膜与基板的结合面上，如附图所示。 t 60 基板的另一面维持在温度 t1 30 ℃。生成工艺要求薄膜与基板结合面的温度 0 ℃，试
确定辐射热流密度 q 应为多大？薄膜的导热系数
f 0.02W /( m.K )
, 基板的导热系数
2-3 有一厚为 20mm 的平板墙，导热系数为 1.3 W /( m.K ) 。为使每平方米墙的热损失不超过 1500W,在外表面上覆盖了一层导热系数为 0.12 W /( m.K ) 的保温材料。已知复合壁两侧的温 度分别为 750℃及 55℃，试确定此时保温层的厚度。 解：依据题意，有
q
1 2 1 2
q1
解：
Q Aq 41.95W q2 5200 44.62 q 116 . 53 1 所以
1 2 3 1 2 3 ＝116.53W/ m 2
t1 t 2
q2
t1 t 2
1 1
5200w / m
2-10 某些寒冷地区采用三层玻璃的窗户，如附图所示。已知玻璃厚δg=3 ㎜，空气夹层宽δ 。玻璃面向室内的表面温度 ti=15℃，面向室外 air=6 ㎜，玻璃的导热系数λg=0.8W/（m·K） 的表面温度 to=-10℃，试计算通过三层玻璃窗导热的热流密度。 解： 2-11 提高燃气进口温度是提高航空发动机效率的有效方法。 为了是发动机的叶片能承受更高 的温度而不至于损坏， 叶片均用耐高温的合金制成， 同时还提出了在叶片与高温燃气接触的 表面上涂以陶瓷材料薄层的方法， 如附图所示， 叶片内部通道则由从压气机来的空气予以冷 却。陶瓷层的导热系数为 1.3W/（m·K） ，耐高温合金能承受的最高温度为 1250K，其导热 系数为 25W/(m·K)。在耐高温合金与陶瓷层之间有一薄层粘结材料，其造成的接触热阻为 10-4 ㎡· K/W。 如果燃气的平均温度为 1700K， 与陶瓷层的表面传热系数为 1000W/(㎡· K)， 冷却空气的平均温度为 400K，与内壁间的表面传热系数为 500W/(㎡·K)，试分析此时耐高 温合金是否可以安全地工作？ 解： 2-12 在某一产品的制造过程中，厚为 1.0mm 的基板上紧贴了一层透明的薄膜，其厚度为 0.2mm。薄膜表面上有一股冷却气流流过，其温度为 20℃，对流换热表面传热系数为 40
传热学第2章2
Department of Power Engineering, North China Electric Power University (Beijing 102206) 杨立军 知识产权与使用权归华北电力大学能源与动力工程学院所有
NCEPU
矩形、 矩形 、 三角形直肋及矩形环肋的肋片效率见书中 41、42页图 页图2 14、 15。 第41、42页图2－14、2－15。
Φs
Department of Power Engineering, North China Electric Power University (Beijing 102206) 杨立军 知识产权与使用权归华北电力大学能源与动力工程学院所有
NCEPU
代入导热微分方程式， 代入导热微分方程式，得
d 2t hP − ( t − t∞ ) = 0 2 dx λ Ac
sinh ( mH ) = Aλ mθ 0 cosh ( mH ) x =0
NCEPU
肋片效率定义： 肋片效率定义： 肋片的实际散热量 Φ 与假设整个肋 片都具有肋基温度时的理想散热量Φ0之比
2. 肋片效率
式中t 式中tm、θm分别为肋面的平均温度和平均过余温度， t0、 分别为肋面的平均温度和平均过余温度， θ0分别为肋基温度与肋基过余温度。 分别为肋基温度与肋基过余温度。 小于1 由于θm< θ0 ，所以肋片效率ηf 小于1。 因为假设肋表面各处h都相等， 因为假设肋表面各处 h都相等 ， 所以等截面直肋的 平均过余温度可按下式计算： 平均过余温度可按下式计算： L L cosh m ( H − x ) 1 1 dx = θ 0 tanh ( mH ) θ m = ∫ θ dx = ∫ θ 0 H 0 cosh ( mH ) mH H 0 tanh ( mH ) 可见，肋片效率是mH的函数 的函数。 可见，肋片效率是mH的函数。 ηf = mH NCEPU
NCEPU
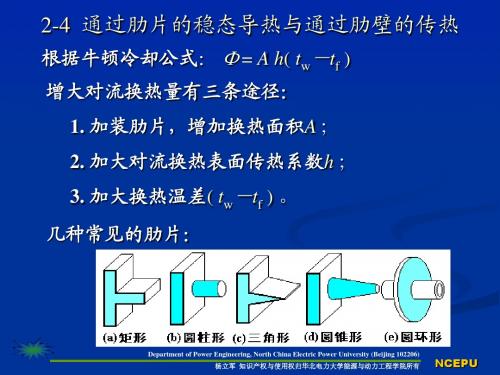
矩形、 矩形 、 三角形直肋及矩形环肋的肋片效率见书中 41、42页图 页图2 14、 15。 第41、42页图2－14、2－15。
Φs
Department of Power Engineering, North China Electric Power University (Beijing 102206) 杨立军 知识产权与使用权归华北电力大学能源与动力工程学院所有
NCEPU
代入导热微分方程式， 代入导热微分方程式，得
d 2t hP − ( t − t∞ ) = 0 2 dx λ Ac
sinh ( mH ) = Aλ mθ 0 cosh ( mH ) x =0
NCEPU
肋片效率定义： 肋片效率定义： 肋片的实际散热量 Φ 与假设整个肋 片都具有肋基温度时的理想散热量Φ0之比
2. 肋片效率
式中t 式中tm、θm分别为肋面的平均温度和平均过余温度， t0、 分别为肋面的平均温度和平均过余温度， θ0分别为肋基温度与肋基过余温度。 分别为肋基温度与肋基过余温度。 小于1 由于θm< θ0 ，所以肋片效率ηf 小于1。 因为假设肋表面各处h都相等， 因为假设肋表面各处 h都相等 ， 所以等截面直肋的 平均过余温度可按下式计算： 平均过余温度可按下式计算： L L cosh m ( H − x ) 1 1 dx = θ 0 tanh ( mH ) θ m = ∫ θ dx = ∫ θ 0 H 0 cosh ( mH ) mH H 0 tanh ( mH ) 可见，肋片效率是mH的函数 的函数。 可见，肋片效率是mH的函数。 ηf = mH NCEPU
《传热学讲义—第二章》
第二章稳态导热本章重点：具备利用导热微分方程式建立不同边界条件下稳态导热问题的数学模型的能力第一节 通过平壁的导热1-1第一类边界条件研究的问题：（D 几何条件：设有一单层平■壁，厚度为a,其宽度、高度远大丁其厚度（宽度、高度 是厚度的10倍以上）。
这时可认为沿高度与宽度两个方向的温度变化率很小，温度只沿厚度 方向发生变化。
（届一维导热问题）（2） 物理条件：无内热源，材料的导热系数入为常数。
（3） 边界条件：假设平壁两侧表面分别保持均匀稳定的温度t wi 和t w2 , t wi t w2。
（为第一类边界条件，同时说明过程是稳态的）求：平■壁的温度分布及通过平■壁的热流密度值。
方法1导热微分方程：采用直角坐标系，这是一个常物性、无内热源、一维稳态导热 问题（温度只在x 方向变化）。
导热微分方程式为： 史 0 （2-1） dx 2边界条件为：t x0 t w 1 , t x t w 2（2-2）对式（2-1）连续积分两次，得其通解：t c 1x c 2t w 2 t w 1这里C 1、C 2为常数，由边界条件确定，解得：C1C 2 t w 1最后得单层平壁内的温度分布为：t t w 1 %」曳x由丁 a 、t w 1、t w 2均为定值。
所以温度分布成线性关系，即温度分布曲线的斜率是常数（温度梯度），虫―宜const（2-6）dx0—1I~Dfl ——单屋平惬(2-3)(2-4)(2-5)热流密度为：q 史—(t W l t w2) W /m2(2-7)dx若表面积为A,在此条件下，通过平壁的导热热流量则为：qA A— t W考虑导热系数随温度变化的情况:通过平壁的导热热流密度为:dt dtq 0(1 bt) —dx dx竺一1 ]bt t 0 1 2 b t W1 t W21式中，0 1 2bt W1 t W21 22 m则q —(t W1 t W2)从上式可以看出，如果以平壁的平均温度t m虹上来计算导热系数，则平壁的热流密2度仍可用导热系数为常数时的热流密度计算式:(2-8)对丁导热系数随温度线形变化，即0(1 bt),此时导热微分方程为: d dt °0 dx dx解这个方程，最后得:t2bt2bt 2 Wi W2t W2)t W1(t W it、W 一t W2说明：壁内温度不再是直线规律, 而是按曲线变化。
传热学课件第二章导热基础理论
也称导温系数,
单位为m2/s。
其大小反映物体被瞬态加热或冷却时温度变化的快慢。
导热微分方程式的简化
(1) 物体无内热源：V = 0 t a2t
(2) 稳态导热： t 0 a2t V 0 c
(3)稳态导热、无内热源：
2t 2t 2t 2t = 0，即 x2 y2 z2 0
（4）热流密度
q d
dA
nt dA
热流密度的大小和方向可 以用热流密度矢量q 表示
q
d
q d n
dA
热流密度矢量的方向指向温度降低的方向。
在直角坐标系中，热流密度矢量可表示为
q qxi qy j qzk
qx、qy、qz分别表示q在三个坐标方向的分量的大小。
2. 2 导热的基本定律—傅里叶定律
第二章 导热基础理论
例内重基 题容点本 赏精难要 析粹点求
基本要求
1． 理解温度场、等温面（线）、温度梯 度、热流密度等概念。
2． 掌握傅立叶定律及其应用。 3. 掌握热导率和热扩散率的定义、意
义、影响因素和确定方法。 4． 能写出典型简单几何形状物体导热问
题的数学描述表达式。
重点与难点
重点： 1. 傅里叶定律与热导率。 2. 导热微分方程及单值性条件。 难点： 1. 傅里叶定律的矢量表达式。 2. 导热微分方程及单值性条件。
标量形式的付里叶定律表达式为
q t
n
对于各向同性材料, 各方向上的导热系数相等,
q qxi qy j qzk
gradt t i t j t k x y z
q
t x
传热学第二章--稳态导热精选全文
t
无内热源，λ为常数，并已知平 t1
壁的壁厚为，两个表面温度分别 维持均匀而恒定的温度t1和t2
t2
c t ( t ) Φ x x
d 2t dx2
0
o
x 0,
x ,
t t
t1 t2
x
直接积分，得：
dt dx
c1
t c1x c2
2024/11/6
35
带入边界条件：
c1
t2
t1
c t
1 r2
r 2
r
t r
1
r 2 sin
sin
t
r2
1
sin 2
t
Φ
2024/11/6
26
6 定解条件 导热微分方程式的理论基础：傅里叶定律+能 量守恒。 它描写物体的温度随时间和空间变化的关系； 没有涉及具体、特定的导热过程。通用表达式。
完整数学描述：导热微分方程 + 单值性条件
4
2 等温面与等温线
①定义
等温面：温度场中同一瞬间同温度各点连成的 面。 等温线：在二维情况下等温面为一等温曲线。
t+Δt t
t-Δt
2024/11/6
5
②特点
t+Δt t
t-Δt
a) 温度不同的等温面或等温线彼此不能相交
b)在连续的温度场中，等温面或等温线不会中
止，它们或者是物体中完全封闭的曲面（曲
它反映了物质微观粒子传递热量的特性。
不同物质的导热性能不同：
固体 液体 气体
金属 非金属
金属 12~418 W (m C) 非金属 0.025 ~ 3W/(mC)
合金 纯金属
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
tw1 tw2 1 ln(r2 r1) r 2
若 tw1 tw2 :
d 2t 0 dr2
向上凹
若 tw1 tw2 :
d 2t dr 2
0
向上凸
下面来看一下圆筒壁内部的热流密度和热流分布情况
t
tw1
(tw1
ln( r tw2 ) ln( r2
r1 ) r1 )
dt tw1 tw2 1 dr ln(r2 r1) r
2.3.2 通过圆筒壁的导热
1 单层圆筒壁
圆柱坐标系：
c t
1 r
(r t ) r r
1 r2
(
t ) z
(
t ) Φ z
假设单管长度为l，圆筒壁的外半 径小于长度的1/10。
一维、稳态、无内热源、常物性：
d (r dt ) 0
(a)
dr dr
第一类边界条件：
r r
r1时 r2时
• 假设各层之间接触良好，可以近似地认 为接合面上各处的温度相等
t2
t3 t4
❖ 边界条件： x 0
n
x i i1
t t1 t tn1
❖ 热阻：
r1
1 1
, , rn
n n
t1
t2
t3
t4
三层平壁的稳态导热
由热阻分析法：
q
t1 tn1
n
ri
i 1
t1 tn1
n i i1 i
问：现在已经知道了q，如何计算其中第 i 层的右侧壁温？
第一层：q
1 1
(t1
t2
)
t2
t1
q
1 1
第二层：q
2 2
(t2
t3
)
t3
t2
q
2 2
第
i
层：q
i i
(ti
ti11)
ti1
ti
q
i i
多层、第三类边条
q
1 h1
tf1 tf2
n
i1
i i
1 h2
tf1 h1
t2
t3
h2
tf2
单位：
W m2
传热系数？
？
？
tf1
t1
t2
t3
t2
tf2
三层平壁的稳态导热
t1 t2
o
线性分布
t
t2
t1
x
t1
dt
t2
t1
dx
带入Fourier 定律
q
t2
t1
t
t
(A)
r
R A
热阻分析法适用于一维、稳态、无内热源的情况
2 多层平壁的导热
• 多层平壁：由几层不同材料组成
t1
• 例：房屋的墙壁 — 白灰内层、水泥 沙浆层、红砖（青砖）主体层等组成
Φ tw1 tw(n1)
n
i1
1
2i
L
ln
ri1 ri
ql
tw1 tw(n1)
n
i1
1
2i
ln
ri1 ri
W W m
通过单位长度圆筒壁的热流量
单层圆筒壁，第三类边界条件，稳态导热
ql r1 2r1h1 (t f 1 tw1 ) ql
tw1 tw2 1 ln r2
2 r1
h1
ql r 2 2r2h2 (tw2 t f 2 )
h2
ql
1
tf1 tf 2 1 ln r2
1
h1 2r1 2 r1 h2 2r2
tf1 tf 2 Rl
W m
通过单位长度圆筒壁传热过程的 热阻 [mK/W]
多层圆筒壁传热
ql
1
tf1 tf2
n
1
ln di1
1
h1d1 i1 2i di h2dn1
2.3.3 通过球壳的导热
类似地，可通过球壳的导热推导出2-33，2-34，2-35式
Φ A dt
dx
当＝(t), A=A(x)时，
Φ (t) A(x) dt
dx
分离变量后积分，并注意到热流量Φ与x 无关(稳态)，得
x2 x1
dx A( x)
tt1Φ2 (t)d(tt()ttA22(x)ttdd11x)t
t2
t1
(t
)
t2 t1
(t2Biblioteka t1 )t2t1
(t )dt
t2 t1
q dt tw1 tw2
dr r ln(r2 r1)
W m2
虽然是稳态导热，但 热流密度 q 与半径 r
成反比！
Φ
2
rlq
tw1 ln( r2
tw2 r1 )
tw1 tw2 R
2 l
W
长度为 l 的圆筒 壁的导热热阻
4 n层圆筒壁 •由 不 同 材 料 构 成 的 多 层 圆 筒 壁 ， 其 导热热流量可按总温差和总热阻计算
Φ
tf1 tf2
1
1
W
h1A A h2 A
为了增加传热量，可以采取哪些措施?
（1）增加温差（tf1 - tf2），但受工艺条件限制 （2）减小热阻：
a) 金属壁一般很薄( 很小)、热导率很大，故导热热阻一般可忽略
§2-3 典型一维稳态导热问题的分析解
本节将针对一维、稳态、常物性、无内热源情况，考察平 板和圆柱内的导热。 直角坐标系： c t ( t ) ( t ) ( t ) Φ
x x y y z z
2.3.1 通过平壁的导热
1 单层平壁的导热
a 几何条件：一维大平壁厚度；
b 物理条件：、c、 已知；无内热源
t tw1 t tw2
对上述方程(a)积分两次:
第一次积分
第二次积分
r
dt dr
c1
t c1 ln r c2
tw1 c1 ln r1 c2 ; tw2 c1 ln r2 c2
应用边界条件 获得两个系数
c1
tw2 tw1 ln( r2 r1)
;
c2
tw1
(tw2
tw1)
ln r1 ln( r2 r1)
t
tw1
tw2 ln( r2
tw1 r1 )
ln(
r
r1 )
将积分常数带入通解
显然，温度呈对数曲线分布
圆筒壁内温度分布：
t
tw1
(tw1
tw2
)
ln( r ln( r2
r1 ) r1 )
•圆筒壁内温度分布曲线的形状？
dt tw1 tw2 1; dr ln(r2 r1) r
d 2t dr 2
2.3.4 带第二类、第三类边界条件的导热实例
2.3.5 变截面或变导热系数的一维问题
求解导热问题主要有两种途径：
(1) 求解导热微分方程，获得温度场；根据Fourier定律计 算热流量;
(2) 对于稳态、无内热源、第一类边界条件下的一维导热
问题，可以不通过温度场而直接应用Fourier定律获得 热流量。此时， 一维Fourier定律：
(t1 t2 )
x2 x1
dx A( x)
当 随温度呈线性分布时，即 ＝ 0＋at，则
0
a t1
t2 2
实际上，不论 如何变化，只要能计算出平均导热系
数，就可以利用前面讲过的所有定导热系数公式，只
是需要将换成平均导热系数。
§2-4 通过肋片的导热
第三类边界条件下通过平壁的一维稳态导热：
c 时间条件： 稳态导热 : t 0
d 边界条件：第一类
o x
根据上面的条件可得：
控制
方程
c t ( t ) Φ x x
d2t dx2
0
边界
条件
第一类边条：
x 0,
x ,
t t
tw1 tw2
t
x
直接积分，得：
dt dx
c1
t c1x c2
带入边界条件：
c1
t2
t1
c2 t1