中文版传热学-第二章
合集下载
中文版传热学-第二章
19
In-Class Problems
在任意直角坐标系下，对于以下两种关于第三类边界条件的表 达形式，你认为哪个对？简述理由。
t x
tw
h(t f t w )
w
tf
t x h(t w t f )
w
2019/1/14
20
Quick Review：
1 重要概念：温度场、温度梯度、导热系数及其性质、 导温系数（热扩散率）定义及性质；
体的导热
2-4 通过肋片的导热
2-5 具有内热源的导热及多维导热
2019/1/14 22
§2-3 通过平壁，圆筒壁，球壳和其它变截面物体的导热
本节将针对一维、稳态、常物性、无内热源情况，考察平板和 圆柱内的导热。 直角坐标系：
c
t t t t ( ) ( ) ( ) Φ x x y y z z
2 导热微分方程式的理论基础及推导过程
3 导热微分方程式的一般形式、组成、及在推导给定条 件下的具体形式；
4 灵活运用导热微分方程，如温度的空间分布通过导热 方程与时间分布建立联系等 5 定解条件？边界条件？三类边界条件的数学表达式？
2019/1/14 21
第二章 导热基本定律及稳态导热
2-1 导热基本定律 2-2 导热微分方程式及定解条件 2-3 通过平壁、圆筒壁、球壳和其它变截面物
Φxdx
dy
Φ y dy Φ y
Φ z dz
t ( )dxdydz y y
y o x
t Φz ( )dxdydz z z
Φy
dx
Eout
2019/1/14
t t t Ein ( ) ( ) ( ) dxdydz x x y y z z
传热学(第二章)
(2-32)
热阻
R=
1 1 1 ( 4πλ r r2 1
(2-33)
由球坐标系一般形式的导热微分方程
1 T 1 T 1 T T (λr2 + 2 2 (λ ) + 2 (λ sin θ ) + Φ = ρcp r2 r r) r sin θ r sin θ θ θ τ
2 1
λ1
第二章
导热基本定律及稳态导热
2-3 通过平壁,圆筒壁,球壳和其他变截面物体的导热 通过平壁,圆筒壁,
1 T 1 T T T (λr + 2 (λ ) + (λ ) + Φ = ρcp τ r r r) r z z d dt 简化变为 dr (r dr ) = 0 (2-25)
⒉ 通过圆筒壁的导热 由导热微分方程式(2—12)
⒉ 通过圆筒壁的导热 根据热阻的定义,通过整个圆筒壁的导热热阻为 (2-29) 29) 与分析多层平壁—样,运用串联热阻叠加的原则,可得通过图2-9所示的多层圆筒壁的 导热热流量 2πl(t1 t4 ) Φ= (2-30) ln( d2 / d1) / λ1 + ln( d3 / d2 ) / λ2 + ln( d4 / d3) / λ3 ⒊ 通过球壳的导热 导热系数为常数,无内热源的空心球壁.内,外半径为r1,r2,其内外表面均匀 恒定温度为t1,t2,球壁内的温度仅沿半径变化,等温面是同心球面. 由傅立叶定律得: dt 各同心球面上的热流率q不相等,而热流量Φ相等. Φ = 4πr2λ dr dr Φ 2 = 4πλdt r
的热传导微分方程:
T(r,τ ) τ ρc 当 λ = const 时, 2T(r,τ ) + Φ = p T(r,τ ) λ λ τ [λT(r,τ )] + g(r,τ ) = ρcp
《传热学》第二章 稳态导热
断面周长： 断面面积：
进行负内热源处理后等截面直肋导热微分方程组如下：
（假定肋端绝热）
定义： 令：
—— 过余温度
使导热微分方程齐次化：
并解出其通解为：
代入边界条件求出c1和c2，并代入通解，得出特解：
等截面直肋的温度分布：
肋端过余温度：
肋片散热量：
当考虑肋端散热时，计算肋片散热量时可采用假想肋高
n层圆筒壁的单位管长热流量：
二、第三类边界条件
常物性时导热微分方程组如下：
根据第一类边界条件时的结果: （此时壁温tw1和tw2为未知） 与以上两个边界条件共三式变形后 相加,可消去tw1和tw2，得：
单层圆筒壁的单位管长热流量：
三、临界热绝缘直径
有绝缘层时的管道总热阻：
当dx增大时： 增 大 减 小
代入肋片效率定义，得到：
肋片效率计算式：
m和l对肋片效率的影响分析：
a. m一定时，l越大，Φ越大，但ηf越低
采用长肋可以提高散热量，但却使肋片散热有效性降低
b. l一定时，m越大，ηf越低
可采用变截面肋片设法降低m
根据肋片效率计算散热量的方法（查线图法）：
矩形及三角形直肋的肋片效率
环肋的肋片效率
h较小时
应用实例：细管，电线 电线的绝缘层外直径小于临界热绝缘直径时， 可起到散热作用
第四节 具有内热源的平壁导热
应用领域：混凝土墙壁凝固
研究对象：厚度为2δ的墙壁，内热源强度为qv， 两边为第三类边界，中间为绝热边界， 取墙壁的一半为研究对象建立导热微分方程 常物性时导热微分方程组如下：
积分两次，得：
《传热学》
第二章 稳态导热
导热微分方程：
稳态时满足：
《传热学》第二章热传导
第二章热传导一、名词解释1．温度场：某一瞬间物体内各点温度分布的总称。
一般来说，它是空间坐标和时间坐标的函数。
2．等温面(线)：由物体内温度相同的点所连成的面（或线）。
3．温度梯度：在等温面法线方向上最大温度变化率。
4．热导率：物性参数，热流密度矢量与温度降度的比值，数值上等于1 K／m的温度梯度作用下产生的热流密度。
热导率是材料固有的热物理性质，表示物质导热能力的大小。
5．导温系数：材料传播温度变化能力大小的指标。
6．稳态导热：物体中各点温度不随时间而改变的导热过程。
7．非稳态导热：物体中各点温度随时间而改变的导热过程。
8．傅里叶定律：在各向同性均质的导热物体中，通过某导热面积的热流密度正比于该导热面法向温度变化率。
9．保温(隔热)材料：λ≤0.12 W/(m·K)(平均温度不高于350℃时)的材料。
10．肋效率：肋片实际散热量与肋片最大可能散热量之比。
11．接触热阻：材料表面由于存在一定的粗糙度使相接触的表面之间存在间隙，给导热过程带来额外热阻。
12．定解条件(单值性条件)：使微分方程获得适合某一特定问题解的附加条件，包括初始条件和边界条件。
二、填空题1．导热基本定律是_____定律，可表述为。
（傅立叶，）2．非稳态导热时，物体内的_____场和热流量随_____而变化。
（温度，时间）3．导温系数的表达式为_____，单位是_____，其物理意义为_____。
（a=λ/cρ,m2/s,材料传播温度变化能力的指标）4．肋效率的定义为_______。
（肋片实际散热量与肋片最大可能散热量之比。
）5．按照导热机理，水的气、液、固三种状态中_______态下的导热系数最小。
（气）6．一般，材料的导热系数与_____和_____有关。
（种类，温度）7．保温材料是指_____的材料.（λ≤0.12 W/(m·K)(平均温度不高于350℃时)）8．已知材料的导热系数与温度的关系为λ＝λ0(1+bt)，当材料两侧壁温分别为t1、t2时，其平均导热系数可取下的导热系数。
传热学 第2章 稳态导热
t t t t c Φ x x y y z z
3、常物性且稳态:
2t 2t 2t Φ a 2 2 2 0 x y z c
如果边界面上的热流密度保持为常数，则 q | w 常数 当边界上的热流密度为零时，称为绝热边界条件
t t qw 0 0 n w n w
18
（3）第三类边界条件 给出了物体在边界上与和它直接接触的流体之 间的换热状况。 根据能量守恒，有：
返回
2.1.1 各类物体的导热机理
气体：气体分子不规则热运动时相互碰撞的结果，高温的气体分子运 动的动能更大 固体：自由电子和晶格振动 对于导电固体，自由电子的运动在导热中起着重要的作用，电的良导 体也是热的良导体 对于非导电固体，导热是通过晶格结构的振动，即原子、分子在其平 衡位置附近的振动来实现的
返回
2.2.2 定解条件
导热微分方程式是能量守恒定律在导热过程中的应用，是一切导热 过程的共性，是通用表达式。 完整数学描述：导热微分方程 + 定解条件 定解条件包括初始条件和边界条件两大类，稳态问题无初始条件 初始条件：初始时刻的状态表示为： =0，t =f (x,y,z)
边界条件： 给出了物体在边界上与外界环境之间在换热上的联系或相互作用
2、推导基本方法：傅里叶定律 + 能量守恒定律 在导热体中取一微元体
进入微元体的总能量+微元体内热源产生的能量-离开微元体的总能量= 微元体内储存能的增加
11
Ein Eg Eout Es
d 时间段内：
Ein Φx Φy Φz d Eiout Φxdx Φy dy Φz dz d
传热学-第二章
金属 非金属; 固相 液相 气相
不同物质热导率的差异：构造差别、导热机理不同
1、气体的热导率
气体 0.006~0.6W (m C)
0 C : 空气 0.0244W (m C) ; 20 C : 空气 0.026W (m C)
气体的导热：由于分子的热运动和相互碰撞时发生的能量传递
dt dx
表示t只与x有关，是一维导热；
t x
表示t只与x有关，是一维导热，且在Δ x内dt/dx保持不变。
§2-2 导热微分方程式（Heat Diffusion Equation） 傅里叶定律： q -grad t [ W m2 ]
确定热流密度的大小，应知道物体内的温度场: t f ( x, y, z, ) 确定导热体内的温度分布是导热理论的首要任务 一、导热微分方程式 理论基础：傅里叶定律 + 热力学第一定律 假设：(1) 所研究的物体是各向同性的连续介质 (2) 热导率、比热容和密度均为已知 (3) 物体内具有内热源；强度 qv [W/m3]; 内热源均匀分布；qv 表示单位体积的导热 体在单位时间内放出的热量
T
大多数建筑材料和绝热材料具有多孔或纤维结构 多孔材料的热导率与密度和湿度有关
、湿度
保温材料：国家标准规定，温度低于350度时热导率小于 0.12W/(mK) 的材料（绝热材料）
t dt t 问题： 、 、 有何区别？ x dx x
t 表示t除与x有关还与其他因素有关，如y、z、时间等； x
t t t q x ; q y ; q z x y z
注：傅里叶定律只适用于各向同性材料 各向同性材料：热导率在各个方向是相同的
有些天然和人造材料，如：石英、木材、叠层塑料板、叠层 金属板，其导热系数随方向而变化 —— 各向异性材料
传热学第二章--稳态导热精选全文
t
无内热源，λ为常数，并已知平 t1
壁的壁厚为，两个表面温度分别 维持均匀而恒定的温度t1和t2
t2
c t ( t ) Φ x x
d 2t dx2
0
o
x 0,
x ,
t t
t1 t2
x
直接积分，得：
dt dx
c1
t c1x c2
2024/11/6
35
带入边界条件：
c1
t2
t1
c t
1 r2
r 2
r
t r
1
r 2 sin
sin
t
r2
1
sin 2
t
Φ
2024/11/6
26
6 定解条件 导热微分方程式的理论基础：傅里叶定律+能 量守恒。 它描写物体的温度随时间和空间变化的关系； 没有涉及具体、特定的导热过程。通用表达式。
完整数学描述：导热微分方程 + 单值性条件
4
2 等温面与等温线
①定义
等温面：温度场中同一瞬间同温度各点连成的 面。 等温线：在二维情况下等温面为一等温曲线。
t+Δt t
t-Δt
2024/11/6
5
②特点
t+Δt t
t-Δt
a) 温度不同的等温面或等温线彼此不能相交
b)在连续的温度场中，等温面或等温线不会中
止，它们或者是物体中完全封闭的曲面（曲
它反映了物质微观粒子传递热量的特性。
不同物质的导热性能不同：
固体 液体 气体
金属 非金属
金属 12~418 W (m C) 非金属 0.025 ~ 3W/(mC)
合金 纯金属
传热学第2章稳态热传导
（2）该平壁热力学能的变化速率；
λсρ
（3）x=0m和x=0.5m两处温度 随时间的变化速率。
t w1 t=450-320x-160x2
ΦV
t w2
0 δ 0.5 x
2.3 典型一维稳态导热问题的分析解
2.3.1 通过平壁的导热
h (8 ~ 10)
1. 第一类边界条件下单层平壁的导热
假设；大平壁λ= 常数，表面积A，厚度δ，
无内热源，平壁两侧维持均匀恒定
温度 tw1, tw2，且tw1> tw2。
t
A
λ
确定（1）平壁内的温度分布；
tw1
（2）通过此平壁的热流密度。
tw2 ф
0 x dx δ x
导热数学描述（导热微分方程+边界条件）
d 2t dx2
0
B.C x 0 t tw1
t
A
λ
tw1
x t tw2
tw2
求解微分方程，得通解：
dx
t
A
λ
tw1
tw2 ф
0 x dx δ x
大小和方向
结论
t
tw1
tw1
tw2
x
q tw1 tw2
✓ 当λ= 常数时，平壁内温度分布呈线性分布，
且与λ无关。
t
✓ 通过平壁内任何一个等温面的
A tw1
λ
热流密度均相等，与坐标x无关。
✓ 导热热阻（Conductive resistance）
1. 定义：温度场描述了各个时刻物体内所有各点 的温度分布。
t f ( x, y, z, )
2. 分类：
按温度场是否随时间变化
• 稳态温度场： t 0
传热学-第二章k5
对于矩形截面的直肋片： 对于矩形截面的直肋片：
b >> δ故而P = 2(b + δ ) ≈ 2b
δ 0 Qx
b
Qc
Qx+dx dx H
x
A
c
= δb
mH =
2h
λδ
⋅H
对于圆形截面的直肋片（针形肋片） 对于圆形截面的直肋片（针形肋片）:
hP mH = ⋅H λ Ac
P = πd Ac = πd 2 4
二、肋片效率与肋片的工程计算
肋片效率： 1. 肋片效率：从散热的角度评价加装肋片后换热 效果（Fin efficiency） 效果（
th ( mH ) hP Φ = λ Acθ 0 mth ( mH ) = θ 0 th ( mH )= hPθ 0 H mH m
hPθ 0 H 表示整个肋片均处于肋基温度时传递的热 流量，也就是肋片传导热阻为零时向环境散失的 流量， 热流量。 热流量。
总换热面积： 总换热面积：
A0 = Ar + Af
Ar Af
t0
tf ， h
换热量： Φ 0 = Ar h ( t0 − t f ) + Af η f h ( t0 − t f ) 换热量：
= h ( t0 − t f
)( A + A η )
r f f
Ar + η f Af = A0 h ( t0 − t f ) A0 Ar + η f Af η0 = 其中： 其中： Ar + Af
接触热阻是普遍存在的， 接触热阻是普遍存在的，而目前对其研究又不充 分，往往采用一些实际测定的经验数据。 往往采用一些实际测定的经验数据。 通常， 通常，对于导热系数较小的多层壁导热问题接触热阻 多不予考虑； 多不予考虑；但是对于金属材料之间的接触热阻就是 不容忽视的问题。 不容忽视的问题。 影响接触热阻的因素: 影响接触热阻的因素:
《传热学》第2章-稳态导热
第一类边界条件： x 0 , t t w1 积分得:
控制方程
边界条件
x , t tw 2
t
dt 1 2 0 ( 1 bt ) c1 0 ( t bt ) c1 x c2 tw1 dx 2
代入边界条件，得:
1 1 2 2 ( t bt ) c 0 c , ( t bt 1 2 0 w2 w 2 ) c1 c 2 0 w1 2 w1 2 1 2 c ( t bt 2 0 w1 w1 ) 2 t w1 t w 2 1 c [ 1 b( t w1 t w 2 )] 0 1 2
tw 2 tw3
2
tw3 tw4
3
tw1 tw4 tw1 tw4 3 相加可得： q R ,1 R ,2 R ,3 R ,i
i 1
例2-1：有一锅炉炉墙，三层，内层为230mm的耐火 砖层，中间为50mm厚的保温层，外层为240mm的 红砖层，导热系数分别为1.10 W/(m.K) ，0.072 W/(m.K) ，0.58W/(m.K)，已知炉墙内外表面温度 为500℃与50℃，求炉墙的导热热流密度和红砖墙的 最高温度。
第二章 稳态导热
Steady-State Conduction —— One Dimension
主要内容
掌握稳态导热。
§2-1 §2-2 §2-3 §2-4 §2-5 §2-6
通过平壁的导热 通过复合平壁的导热 通过圆筒壁的导热 具有内热源的平壁导热 通过肋片的导热 通过接触面的导热
对各层直接应用单层大平壁的热量计算式 tw1 tw 2 tw1 tw 2 第一层平壁 : q1 , 变换 : q1 R ,1 t w1 t w 2 1 R ,1
控制方程
边界条件
x , t tw 2
t
dt 1 2 0 ( 1 bt ) c1 0 ( t bt ) c1 x c2 tw1 dx 2
代入边界条件，得:
1 1 2 2 ( t bt ) c 0 c , ( t bt 1 2 0 w2 w 2 ) c1 c 2 0 w1 2 w1 2 1 2 c ( t bt 2 0 w1 w1 ) 2 t w1 t w 2 1 c [ 1 b( t w1 t w 2 )] 0 1 2
tw 2 tw3
2
tw3 tw4
3
tw1 tw4 tw1 tw4 3 相加可得： q R ,1 R ,2 R ,3 R ,i
i 1
例2-1：有一锅炉炉墙，三层，内层为230mm的耐火 砖层，中间为50mm厚的保温层，外层为240mm的 红砖层，导热系数分别为1.10 W/(m.K) ，0.072 W/(m.K) ，0.58W/(m.K)，已知炉墙内外表面温度 为500℃与50℃，求炉墙的导热热流密度和红砖墙的 最高温度。
第二章 稳态导热
Steady-State Conduction —— One Dimension
主要内容
掌握稳态导热。
§2-1 §2-2 §2-3 §2-4 §2-5 §2-6
通过平壁的导热 通过复合平壁的导热 通过圆筒壁的导热 具有内热源的平壁导热 通过肋片的导热 通过接触面的导热
对各层直接应用单层大平壁的热量计算式 tw1 tw 2 tw1 tw 2 第一层平壁 : q1 , 变换 : q1 R ,1 t w1 t w 2 1 R ,1
传热学 第二章 对流换热
δtt
tw
第一节 对流换热分析及牛顿冷却定律 一、边界层概念
在层流边界层中， 在层流边界层中，热量的传递只能依靠流体层与层间的 导热作用，此时对流换热较弱。在紊流边界层中， 导热作用，此时对流换热较弱。在紊流边界层中，层流底 层的热量传递方式仍是导热， 层的热量传递方式仍是导热，但在层流底层以外存在着对 因而对流换热较强。 流，因而对流换热较强。所以对流换热实际上是包括流体 层流的导热和层流以外的对流共同作用的综合传热过程。 层流的导热和层流以外的对流共同作用的综合传热过程。 若同一流体在相同的温度下流过同一壁面时， 若同一流体在相同的温度下流过同一壁面时，则层流底层 越薄，对流换热越强烈。 越薄，对流换热越强烈。
第一节 对流换热分析及牛顿冷却定律 一、边界层概念
（一）速度边界层 当粘性流体流过固体壁面时， 当粘性流体流过固体壁面时，若用仪器测出沿壁面法线方 方向不同点的速度u，将得到如图所示的速度分布图。 向Y方向不同点的速度 ，将得到如图所示的速度分布图。 方向不同点的速度 它表明从y=0处u=0开始，速度u随着 方向离壁面的距离 它表明从 处 开始，速度 随着y方向离壁面的距离 开始 随着 的增加而迅速增大，经过厚度为δ的薄层 的薄层， 接近达到主流 的增加而迅速增大，经过厚度为 的薄层，u接近达到主流 速度u ，这个y= 的薄层即为速度边界层 的薄层即为速度边界层， 为边界层厚 速度 ∞，这个 δ的薄层即为速度边界层， δ为边界层厚 度。边界层厚度理论上应等于由壁面到流体达到主流速度 点之间的距离，但这个点的位置难于准确确定， 点之间的距离，但这个点的位置难于准确确定，故通常把 u/ u∞=0.99处离壁面的垂直距离定义为边界层厚度。实验 处离壁面的垂直距离定义为边界层厚度。 处离壁面的垂直距离定义为边界层厚度 表明δ与壁面尺寸 相比是一个极小的量。 与壁面尺寸L相比是一个极小的量 表明 与壁面尺寸 相比是一个极小的量。
工程热力学与传热学(中文) 第2章 热力学第一定律
H = f (T , v ) ∆ H 1− 2 =
∫
2
1
dH = H 2 − H 1
∫ dH
=0
什么条件下，热力学能和焓值可以同时为零”？ 什么条件下，热力学能和焓值可以同时为零”
2-4-4 开口系统稳定流动能量方程式
（The first law applied to open system - steady flow） ）
dm 2
2. 表示
入口处： δ W f 1 = p1 A1dx1 = p1dV1 = p1v1dm1 入口处： 出口处： 出口处： δ W f 2 = p 2 A2 dx 2 = p 2 dV 2 = p 2 v 2 dm 2 单位质量工质： 单位质量工质： w f 1 =
δW f 1
dm1
= p1v1
例 题
2. 一活塞汽缸中的气体经历了两个过程，从状态 到状态 ， 一活塞汽缸中的气体经历了两个过程，从状态1 到状态2， 气体吸热500kJ，活塞对外做功 到状态3 气体吸热 ，活塞对外做功800kJ。从状态 到状态 。从状态2到状态 是一个定压的压缩过程，压力为400kPa，气体向外散热 是一个定压的压缩过程，压力为 ， 450kJ。并且已知 1=2000kJ，U3=3500kJ。 。并且已知U ， 。 试计算2-3过程中气体体积的变化 过程中气体体积的变化。 试计算 过程中气体体积的变化。
Q
W
a: 一部分用于增加工质的热力学能。 一部分用于增加工质的热力学能。 b: 另一部分以作功的方式传递到外界。 另一部分以作功的方式传递到外界。
∆u
（2）对于1kg工质 ：q = w + ∆ u ） （3）适用条件：a: 可逆过程，不可逆过程。 ）适用条件： 可逆过程，不可逆过程。
∫
2
1
dH = H 2 − H 1
∫ dH
=0
什么条件下，热力学能和焓值可以同时为零”？ 什么条件下，热力学能和焓值可以同时为零”
2-4-4 开口系统稳定流动能量方程式
（The first law applied to open system - steady flow） ）
dm 2
2. 表示
入口处： δ W f 1 = p1 A1dx1 = p1dV1 = p1v1dm1 入口处： 出口处： 出口处： δ W f 2 = p 2 A2 dx 2 = p 2 dV 2 = p 2 v 2 dm 2 单位质量工质： 单位质量工质： w f 1 =
δW f 1
dm1
= p1v1
例 题
2. 一活塞汽缸中的气体经历了两个过程，从状态 到状态 ， 一活塞汽缸中的气体经历了两个过程，从状态1 到状态2， 气体吸热500kJ，活塞对外做功 到状态3 气体吸热 ，活塞对外做功800kJ。从状态 到状态 。从状态2到状态 是一个定压的压缩过程，压力为400kPa，气体向外散热 是一个定压的压缩过程，压力为 ， 450kJ。并且已知 1=2000kJ，U3=3500kJ。 。并且已知U ， 。 试计算2-3过程中气体体积的变化 过程中气体体积的变化。 试计算 过程中气体体积的变化。
Q
W
a: 一部分用于增加工质的热力学能。 一部分用于增加工质的热力学能。 b: 另一部分以作功的方式传递到外界。 另一部分以作功的方式传递到外界。
∆u
（2）对于1kg工质 ：q = w + ∆ u ） （3）适用条件：a: 可逆过程，不可逆过程。 ）适用条件： 可逆过程，不可逆过程。
传热学-第2章
第二章 稳态热传导 12
在导热体中取一微元体 热力学第一定律：
Q U W
W 0, Q U
d 时间内微元体中： [导入与导出净热量]+ [内热源发热量] = [热力学能的增加]
1、导入与导出微元体的净热量 d 时间内、沿 x 轴方向、经 x 表面导入的热量：
dQx qx dydz d
t t1
n i
x
i 1
t tn1
t1 t2 t3 t4
热阻：
r1
1 , , rn n 1 n
第二章 稳态热传导
三层平壁的稳态导热
30
q
t1 t n 1
由热阻分析法：
ri
i 1
n
t1 t n 1
i i 1 i
n
问：现在已经知道了q，如何计算其中第 i 层的右侧壁温？
第一章复习
(1) 导热
傅里叶定律：
(2) 对流换热 牛顿冷却公式： (3) 热辐射
斯忒藩－玻耳兹曼定律 ：
dt Φ A dx
Aht
A T 4
(4) 传热过程
(t f 1 t f 2 ) (t f 1 t f 2 ) Φ 1 1 Rh1 R Rh 2 Ah1 A Ah2
多层、第三类边条
tf1
q
tf1 tf 2 1 n i 1 h1 i 1 i h2
h1 t2 t3
h2 tf2
W 单位： 2 m
传热系数？ tf1
？
t1 t2 t3 t2
？ tf2
32
三层平壁的稳态导热
第二章 稳态热传导
一台锅炉的炉墙由三层材料叠合而成.最里面的是耐火黏土砖,厚 115MM;中间是B级硅藻土砖,厚125MM;最外层为石棉板,厚 70MM.已知炉墙内外表面温度分别为485℃ 和60 ℃ , 试求每平方 米炉墙的热损失及耐火黏土砖和硅藻土砖分界面上的温度。 解：各层的导热系数可根据估计的平均温度从手册中查出。第一 次估计的平均温度不一定正确，待算得分界面温度时，如发现不 对，可重新假定每层的平均温度。经几次试算，逐步逼近，可得 合理的数值。这里列出的是几次试算后的结果： W 3 0.116 /(m K ) W 1 1.12W /(m K ) 2 0.116 /(m K )
在导热体中取一微元体 热力学第一定律：
Q U W
W 0, Q U
d 时间内微元体中： [导入与导出净热量]+ [内热源发热量] = [热力学能的增加]
1、导入与导出微元体的净热量 d 时间内、沿 x 轴方向、经 x 表面导入的热量：
dQx qx dydz d
t t1
n i
x
i 1
t tn1
t1 t2 t3 t4
热阻：
r1
1 , , rn n 1 n
第二章 稳态热传导
三层平壁的稳态导热
30
q
t1 t n 1
由热阻分析法：
ri
i 1
n
t1 t n 1
i i 1 i
n
问：现在已经知道了q，如何计算其中第 i 层的右侧壁温？
第一章复习
(1) 导热
傅里叶定律：
(2) 对流换热 牛顿冷却公式： (3) 热辐射
斯忒藩－玻耳兹曼定律 ：
dt Φ A dx
Aht
A T 4
(4) 传热过程
(t f 1 t f 2 ) (t f 1 t f 2 ) Φ 1 1 Rh1 R Rh 2 Ah1 A Ah2
多层、第三类边条
tf1
q
tf1 tf 2 1 n i 1 h1 i 1 i h2
h1 t2 t3
h2 tf2
W 单位： 2 m
传热系数？ tf1
？
t1 t2 t3 t2
？ tf2
32
三层平壁的稳态导热
第二章 稳态热传导
一台锅炉的炉墙由三层材料叠合而成.最里面的是耐火黏土砖,厚 115MM;中间是B级硅藻土砖,厚125MM;最外层为石棉板,厚 70MM.已知炉墙内外表面温度分别为485℃ 和60 ℃ , 试求每平方 米炉墙的热损失及耐火黏土砖和硅藻土砖分界面上的温度。 解：各层的导热系数可根据估计的平均温度从手册中查出。第一 次估计的平均温度不一定正确，待算得分界面温度时，如发现不 对，可重新假定每层的平均温度。经几次试算，逐步逼近，可得 合理的数值。这里列出的是几次试算后的结果： W 3 0.116 /(m K ) W 1 1.12W /(m K ) 2 0.116 /(m K )
传热学讲义—第二章
第二章 稳态导热本章重点：具备利用导热微分方程式建立不同边界条件下稳态导热问题的数学模型的能力第一节 通过平壁的导热1-1 第一类边界条件 研究的问题：（1）几何条件：设有一单层平壁，厚度为δ，其宽度、高度远大于其厚度（宽度、高度是厚度的10倍以上）。
这时可认为沿高度与宽度两个方向的温度变化率很小，温度只沿厚度方向发生变化。
（属一维导热问题）（2）物理条件：无内热源，材料的导热系数λ为常数。
（3） 边界条件：假设平壁两侧表面分别保持均匀稳定的温度1w t 和2w t ，21w w t t >。
（为第一类边界条件，同时说明过程是稳态的）求：平壁的温度分布及通过平壁的热流密度值。
方法1 导热微分方程：采用直角坐标系，这是一个常物性、无内热源、一维稳态导热问题（温度只在 x 方向变化）。
导热微分方程式为：022=dxtd （2-1）边界条件为：10w x t t == ， 2w x t t ==δ （2-2）对式（2-1）连续积分两次，得其通解： 21c x c t += （2-3）这里1c 、2c 为常数，由边界条件确定 ，解得：⎪⎩⎪⎨⎧=-=11221ww w t c t t c δ （2-4）最后得单层平壁内的温度分布为： x t t t t w w w δ211--= （2-5）由于δ 、1w t 、2w t 均为定值。
所以温度分布成线性关系，即温度分布曲线的斜率是常数（温度梯度），const t t dx dt w w =-=δ12 （2-6）热流密度为：)(21w w t t dx dt q -=-=δλλ2/m W （2-7） 若表面积为 A, 在此条件下 , 通过平壁的导热热流量则为 :t A qA ∆==Φδλ W （2-8）考虑导热系数随温度变化的情况：对于导热系数随温度线形变化，即)1(0bt +=λλ，此时导热微分方程为：0=⎪⎭⎫⎝⎛dx dt dx d λ 解这个方程，最后得：⎥⎦⎤⎢⎣⎡++-+⎪⎭⎫ ⎝⎛+=+)(211212121121122w w w w w w t t b x t t bt t bt t δ 或 x tt t t b b t b t w w w w w δ12211)(21122-⎥⎦⎤⎢⎣⎡+++⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+说明：壁内温度不再是直线规律，而是按曲线变化。
传热学第2章 稳态传热
ch2 稳态导热 18
A1 A2 A3 RλA1 RλA2
B C D RλB RλC
E1 E2
E3
RλE1 RλE2
当复合平壁的各材料 BCD的导热系数相差较 大时，二维导热问题， 计算方法:采用热阻图 计算后，乘上修正系数， 表2-1。
RλA3
RλD
RλE3
t R
2014-6-1
d dt (r )0 dr dr
(a)
r r1时 t t w1 第一类边界条件： r r2时 t t w2
2014-6-1 ch2 稳态导热 20
第一次积分 对上述方程 (a)积分两次 : 第二次积分
应用边界条件
dt r c1 dr
t c1 ln r c2
t w1 c1 ln r1 c2 ; t w2 c1 ln r2 c2
边界 条件
x
11
改写（1）（2）（3），得：
tw1 tw 2 dt q c1 dx
(1)
q x 0 q x
dt - dx dt =- dx
h1 (t f 1 tw1 )
x 0
(2) (3)
h2 (tw 2 t f 2 )
x
W W
m
通过单位长度圆筒壁的热流量
各层圆筒壁之间的温度 twi 与多层平壁 的计算方法类似。
2014-6-1 ch2 稳态导热 24
3.3 第三类边界条件单层圆筒壁的稳态导热
t w1 t w 2 ql r2 1 ln 2 r1
h1 h2
通过单位长度 圆筒壁传热过 程的热阻 [mK/W]
dt c1 t c1 x c2 dx
A1 A2 A3 RλA1 RλA2
B C D RλB RλC
E1 E2
E3
RλE1 RλE2
当复合平壁的各材料 BCD的导热系数相差较 大时，二维导热问题， 计算方法:采用热阻图 计算后，乘上修正系数， 表2-1。
RλA3
RλD
RλE3
t R
2014-6-1
d dt (r )0 dr dr
(a)
r r1时 t t w1 第一类边界条件： r r2时 t t w2
2014-6-1 ch2 稳态导热 20
第一次积分 对上述方程 (a)积分两次 : 第二次积分
应用边界条件
dt r c1 dr
t c1 ln r c2
t w1 c1 ln r1 c2 ; t w2 c1 ln r2 c2
边界 条件
x
11
改写（1）（2）（3），得：
tw1 tw 2 dt q c1 dx
(1)
q x 0 q x
dt - dx dt =- dx
h1 (t f 1 tw1 )
x 0
(2) (3)
h2 (tw 2 t f 2 )
x
W W
m
通过单位长度圆筒壁的热流量
各层圆筒壁之间的温度 twi 与多层平壁 的计算方法类似。
2014-6-1 ch2 稳态导热 24
3.3 第三类边界条件单层圆筒壁的稳态导热
t w1 t w 2 ql r2 1 ln 2 r1
h1 h2
通过单位长度 圆筒壁传热过 程的热阻 [mK/W]
dt c1 t c1 x c2 dx
传热学-第二章导热基本定律及稳态传热
1、导入微元体的净热量
d 时间X方向流入与流出微元体的热流量
dQx
- dQxdx
- qx x
dxdydz d
( t ) dxdydz d
x x
d 时间Y方向流入与流出微元体的热流量
dQy
- dQydy
- q y y
dy dxdz d
y
( t ) dxdydz d
y
2.4 导热微分方程及定解条件
影响热导率的因素：物质的种类、材料成分、温度、压力及 密度等。
2.3 导热系数
2.3.1 气体导热系数
气体导热——由于分子的无规则热运动以及分子间 的相互碰撞
1 3
vlcv
v 3RT M
V 气体分子运动的均方根 m/s L 气体分子两次碰撞之间的平均自由程 m
Cv气体的定容比热 J/kg·℃
2.3 导热系数
2.4 导热微分方程及定解条件
建立数学模型的目的：
求解温度场 t f x, y, z,
步骤： 1）根据物体的形状选择坐标系, 选取物体中的 微元体作为研究对象； 2）根据能量守恒, 建立微元体的热平衡方程式； 3）根据傅里叶定律及已知条件, 对热平衡方程式 进行归纳、整理，最后得出导热微分方程式。
通过某一微元面积dA的热流：
dA q
d
q dA
t
n
dA
t
dydz
t
dxdz
t
பைடு நூலகம்
dxdy
n
x
y
z
2.2导热的基本定律
例：判断各边界面的热流方向
2.3 导热系数
由傅里叶定律可得，导热系数数学定义的具体形式为：
q t n
d 时间X方向流入与流出微元体的热流量
dQx
- dQxdx
- qx x
dxdydz d
( t ) dxdydz d
x x
d 时间Y方向流入与流出微元体的热流量
dQy
- dQydy
- q y y
dy dxdz d
y
( t ) dxdydz d
y
2.4 导热微分方程及定解条件
影响热导率的因素：物质的种类、材料成分、温度、压力及 密度等。
2.3 导热系数
2.3.1 气体导热系数
气体导热——由于分子的无规则热运动以及分子间 的相互碰撞
1 3
vlcv
v 3RT M
V 气体分子运动的均方根 m/s L 气体分子两次碰撞之间的平均自由程 m
Cv气体的定容比热 J/kg·℃
2.3 导热系数
2.4 导热微分方程及定解条件
建立数学模型的目的：
求解温度场 t f x, y, z,
步骤： 1）根据物体的形状选择坐标系, 选取物体中的 微元体作为研究对象； 2）根据能量守恒, 建立微元体的热平衡方程式； 3）根据傅里叶定律及已知条件, 对热平衡方程式 进行归纳、整理，最后得出导热微分方程式。
通过某一微元面积dA的热流：
dA q
d
q dA
t
n
dA
t
dydz
t
dxdz
t
பைடு நூலகம்
dxdy
n
x
y
z
2.2导热的基本定律
例：判断各边界面的热流方向
2.3 导热系数
由傅里叶定律可得，导热系数数学定义的具体形式为：
q t n
最新-传热学第二章 稳态导热-PPT文档资料
2019/4/19 8
4 付里叶定律(Fourier’s Law) 第一章中给出了稳态条件下的付里叶定律，这 里可推广为更一般情况。 n dt dn t q grad t n t1 t t+dt x 热流密度在x, y, z 方向 的投影的大小分别为：
0
t2
δ
x
t t t q ;q ;q x y z x y z
第二章 稳态导热
§2-1 基本概念 §2-2 一维稳态导热
2019/4/19
1
分析传热问题基本上是遵循经典力学的研究 方法，即针对物理现象建立物理模型，而后 从基本定律导出其数学描述(常以微分方程的 形式表达，故称数学模型)，接下来考虑求解 的理论分析方法。 导热问题是传热学中最易于采用此方法处理 的传热方式。
2019/4/19 7
系统中某一点所在的等温面与相邻等温面 之间的温差与其法线间的距离之比的极限 为该点的温度梯度，记为gradt。
t t t t t gradt Lim n i j k n 0 n n x y z
注：温度梯度是向量；正向朝着温度增加 的方向
2019/4/19 16
假设：(1) 所研究物体是各向同性的连续介质； (2) 热导率、比热容和密度均为已知 (3) 物体内具有内热源；强度 [W/m3]; 表示单位体积的导热体在单位时间内放出 的热量
z
dz+dz dy
dx
导入微元体的总热流量 +内热源的生成热 =导出微元体的总热流量 +内能的增量
2019/4/19
dy+dy dz
dx+dx
x
17
4 付里叶定律(Fourier’s Law) 第一章中给出了稳态条件下的付里叶定律，这 里可推广为更一般情况。 n dt dn t q grad t n t1 t t+dt x 热流密度在x, y, z 方向 的投影的大小分别为：
0
t2
δ
x
t t t q ;q ;q x y z x y z
第二章 稳态导热
§2-1 基本概念 §2-2 一维稳态导热
2019/4/19
1
分析传热问题基本上是遵循经典力学的研究 方法，即针对物理现象建立物理模型，而后 从基本定律导出其数学描述(常以微分方程的 形式表达，故称数学模型)，接下来考虑求解 的理论分析方法。 导热问题是传热学中最易于采用此方法处理 的传热方式。
2019/4/19 7
系统中某一点所在的等温面与相邻等温面 之间的温差与其法线间的距离之比的极限 为该点的温度梯度，记为gradt。
t t t t t gradt Lim n i j k n 0 n n x y z
注：温度梯度是向量；正向朝着温度增加 的方向
2019/4/19 16
假设：(1) 所研究物体是各向同性的连续介质； (2) 热导率、比热容和密度均为已知 (3) 物体内具有内热源；强度 [W/m3]; 表示单位体积的导热体在单位时间内放出 的热量
z
dz+dz dy
dx
导入微元体的总热流量 +内热源的生成热 =导出微元体的总热流量 +内能的增量
2019/4/19
dy+dy dz
dx+dx
x
17
《传热学》第二章课件_chapter2
2、导热系数的相对大小和典型数据
金属 非金属; 固相 液相 气相
在常温（20℃）条件下
纯铜： 399 W (m K)
碳钢： 36.7 W/ (m K)
水： 0.599 W (m K)
空气： 0.0259 W (m K)
传热学 Heat Transfer
传热学 Heat Transfer
沿x 轴方向导入与导出微元体净热量
Φx Φx dx
同理可得：
t dxdydz x x
t dxdydz y y
沿 y 轴方向导入与导出微元体净热量
Φy Φy dy
0
δ
x
传热学 Heat Transfer
3. 一块厚度为 的平板，平板内有均匀的内热源， ，平板一侧绝热，平板另一侧与温 热源强度为 度为tf 的流体对流换热，且表面传热系数为h。
传热学 Heat Transfer
4. 已知一单层圆筒壁的内、外半径分别为 r1、r2，
导热系数为常量，无内热源，内、外壁面维持均
匀恒定的温度tw1，tw2 。
3.对各向异性材料必须做一定的修改；
4.当导热发生的过程时间极短或空间尺度极小时，
傅里叶定律不在适合。
传热学 Heat Transfer
2-2 导热问题的数学描写
作用：导热微分方程式及定解条件是对导热体的 数学描述，是理论求解导热体温度分布的基础。
t f ( x, y, z, )
理论：导热微分方程式建立的基础是： 热力学第一定律+傅里叶定律 方法：对导热体内任意的一个微小单元进行分析， 依据能量守恒关系，建立该处温度与其它变量之间 的关系式。
最新传热学第二章 稳态热传导PPT课件
实用计算中，大多数材料的导热 系数都可以用线性近似关系，即 λ= λ0（a+bt），式中，t为温度， a,b为常量， λ0是直线段的延长线 在纵坐标轴上的截距。
3 、保温材料（隔热、绝热材料）
把导热系数小的材料称保温材料。我国规
t 定： ≤ 350 ℃ 时， ≤ 0.12w/mk 保温材
料导热系数界定值的大小反映了一个国家保 温材料的生产及节能的水平。 越小，生产及 节能的水平越高。
传热学第二章 稳态热传导
1.重点内容：
① 傅立叶定律及其应用； ② 导热系数及其影响因素； ③ 导热问题的数学模型。
2.掌握内容：一维稳态导热问题的分析解法 3.了解内容：多维导热问题
导热特点
1)物体之间不发生宏观相对位移。
2)依靠微观粒子（分子、原子、电子等）的无规 则热运动。
3)是物质的固有本质。
微元体的导热热平衡分析
① 通过 x=x 、 y=y 、 z=z ，三个微元表面而导 入微元体的热流量：фx 、фy 、фz 的计算。 根 据傅立叶定律得
x
t x
dydz
y
t y
dxdz
(a) 通过 x=x+dx 、 y=y+dy 、 z=z+dz 三个微元 表面而导出微元体的热流量ф x+dx 、ф y+dy 、ф z+dz 的计算。根据傅立叶定律得：
物体的温度场通常用等温面或等温线表示。
等温线图的物理意义： 若每条等温线间的温度间隔相等时，等
温线的疏密可反映出不同区域导热热流 密度的大小。
三 、导热基本定律
1 、导热基本定律（傅立叶定律） 1 ）定义：在导热现象中，单位时间内通过给 定截面所传递的热量，正比例于垂直于该截 面方向上的温度变化率，而热量传递的方 向与温度升高的方向相反，即 ~ t
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
纯 3 铜 W 9 ( C m 8 ; 大 ) 2 .7 理 W ( C m 石 )
0 C :冰 2 .2W 2 ( m C ; 水 ) 0 .5W 5(1 m C)
蒸汽 0.01W 83 (m C)
2020/7/15
5
A 气体的导热系数 气 体 0.0 ~00W .6 6 (m K)
§2-2 导热微分方程式及定解条件（续）
b 导出微元体的总热流量Eout
采用Taylor级数展开，并忽略高阶项，则有
Φxdx Φx Φ xx dxΦx x(xtdydz)dx
Φx x(xt)dxdydz
Φx
dy
Φ ydy
Φ ydyΦ y y( y t)ddxydz
y
Φ zdzΦ z z( z t)ddx ydz
2-1 导热基本定律
2-2 导热微分方程式及定解条件
2-3 通过平壁、圆筒壁、球壳和其它变截面物 体的导热
2-4 通过肋片的导热
2-5 具有内热源的导热及多维导热
2020/7/15
9
§2-2 导热微分方程式及定解条件
1 导热微分方程式的推导 为什么需要导热微分方程？ 理论基础：Fourier 定律 + 能量守恒定律 导热微分方程式
2020/7/15友情提示：非直角坐标系下的导热微分方程式自己看 15
c t x( x t) y( y t) z( z t) Φ
非稳态项
扩散项
源项
？ 是不是有了导热微分方程式，就可以获得温度分布呢
答案是否定的！
定解条件(单值性条件)
导热微分方程 + 定解条件 + 求解方法 = 确定的温度场
o
Φy
x dx
2020/7/15E ou E tin x( x t) y( y t) z( z t) dd y x d z
Φxdx
13
§2-2 导热微分方程式及定解条件（续）
c 内热源的生成热 QgΦ dVΦ dxdydz
d 热力学能的增量 Qst Φctdxdydz ？
定解条件包括四项：几何、物理、时间、边界 下面详细介绍边界条件！
2020/7/15
16
§2-2 导热微分方程式及定解条件（续）
边界条件：规定了物体与外部环境之间的换热条件，包括以下三类：
特点：(a) 气体的导热系数基本不随压力的改变而变化 (b) 随温度的升高而增大 (c) 随分子质量减小而增大
B 液体的导热系数 液 体 0.~ 007.W 7(m C)
特点：(a) 随压力的升高而增大 p
(b) 随温度的升高而减小 T
2020/7/15
6
C 固体的导热系数
金属 1~ 241W 8(m C)
图2-1 温度场的图示
3
2 导热基本定律——Fourier Law
对于一维情况， A dt
dx
对于三维直角坐标系情况，有
qx
t x
qy
t y
qz
t z
gratdtti t jtk x y z
q x ti y tj z tk t n tn
2020/7/15
图2-2 温度梯度
通用形式的
Fourier Law
下面我们来考察一个矩形微元六面体，如下图所示。
x
x+dx
zy
dx
x
2020/7/15
10
假设：(1) 所研究的物体是各向同性的连续介质
(2) 导热系数、比热容和密度均为已知
(3) 物体内具有内热源；强度 Φ [W/m3]; 内热源均匀
分布；
2020/7/15
11
§2-2 导热微分方程式及定解条件（续）
非金 0 属 .02~5 3W(m C)
特点：纯金属：
T
合金和非金属：T
金属的导热系数与温度的依变关系参见图2-7
保温材料：国家标准规定，温度低于350度时导热系数 小于 0.12W/(mK) 的材料（绝热材料）
2020/7/15
7
图2-7 导热系数对温度的依变关系
2020/7/15
8
第二章 导热基本定律及稳态导热
第二章 导热基本定律及稳态导热
2-1 导热基本定律
2-2 导热微分方程式及定解条件
2-3 通过平壁、圆筒壁、球壳和其它变截面物 体的导热
2-4 通过肋片的导热
2-5 具有内热源的导热及多维导热
2020/7/15
1
§2-1 导热基本定律
1 几个基本概念: 温度场、等温面、等温线、温度梯度、热流密度矢量
根据能量守恒定律有：
导入微元体的总热流量in + 微元体内热源的生成热 g =
导出微元体的总热流量 out + 微元体热力学能的增量 st
Φ ydy
a 导入微元体的总热流量Ein
Φx
dy/15
Φy
dx
Φxdx
Φ
x
t x
dydz
Φ
y
t y
dxdz
Φ
z
t z
dxdy
in Φ x Φ y Φ z x td y d z y td x d z z td x d 1y 2
把Qin、Qout、Qg、Qst 带入前面的能量守恒方程
Q inQgQ outQst
得： c t x( x t) y( y t) z( z t) Φ
这就是三维、非稳态、变物性、有内热源的导热微分方 程的一般形式。
2020/7/15
14
§2-2 导热微分方程式及定解条件（续）
2 几种特殊情况
(1) 若物性参数 、c 和 均为常数：
t a ( x 2 2 t y 2 2 t z 2 2 t) Φ c; or t a 2 t Φ c
a —热扩散率（导温系 [m数 2 s]） c
(2) 无内热源、常物性： t a2t
物理
意义
(3) 稳态、常物性： 2t 0
？
(4) 稳态、常物性、无内热源：2t 0
4
§2-1 导热基本定律（续）
3 导热系数(热导率) q
- grad t
(1)物理意义：热导率的数值就是物体中单位温度梯度、单位时
间、通过单位面积的导热量 W(m C。) 热导率的数值表征物质
导热能力大小，由实验测定。
(2) 影响因素：物质的种类、材料成分、温度、湿度、压力、密度等
金属 非;金固 属相 液相 气相
(1) 温度场： tf(x,y,z,)
三维非稳态温度场： tf(x,y,z,)
三维稳态温度场： tf(x,y,z)
二维稳态温度场： tf(x,y)
一维稳态温度场： t f (x)
2020/7/15
2
§2-1 导热基本定律（续）
(2) 等温线 (3) 等温面 (4) 等温面和等温线的特点
2020/7/15
0 C :冰 2 .2W 2 ( m C ; 水 ) 0 .5W 5(1 m C)
蒸汽 0.01W 83 (m C)
2020/7/15
5
A 气体的导热系数 气 体 0.0 ~00W .6 6 (m K)
§2-2 导热微分方程式及定解条件（续）
b 导出微元体的总热流量Eout
采用Taylor级数展开，并忽略高阶项，则有
Φxdx Φx Φ xx dxΦx x(xtdydz)dx
Φx x(xt)dxdydz
Φx
dy
Φ ydy
Φ ydyΦ y y( y t)ddxydz
y
Φ zdzΦ z z( z t)ddx ydz
2-1 导热基本定律
2-2 导热微分方程式及定解条件
2-3 通过平壁、圆筒壁、球壳和其它变截面物 体的导热
2-4 通过肋片的导热
2-5 具有内热源的导热及多维导热
2020/7/15
9
§2-2 导热微分方程式及定解条件
1 导热微分方程式的推导 为什么需要导热微分方程？ 理论基础：Fourier 定律 + 能量守恒定律 导热微分方程式
2020/7/15友情提示：非直角坐标系下的导热微分方程式自己看 15
c t x( x t) y( y t) z( z t) Φ
非稳态项
扩散项
源项
？ 是不是有了导热微分方程式，就可以获得温度分布呢
答案是否定的！
定解条件(单值性条件)
导热微分方程 + 定解条件 + 求解方法 = 确定的温度场
o
Φy
x dx
2020/7/15E ou E tin x( x t) y( y t) z( z t) dd y x d z
Φxdx
13
§2-2 导热微分方程式及定解条件（续）
c 内热源的生成热 QgΦ dVΦ dxdydz
d 热力学能的增量 Qst Φctdxdydz ？
定解条件包括四项：几何、物理、时间、边界 下面详细介绍边界条件！
2020/7/15
16
§2-2 导热微分方程式及定解条件（续）
边界条件：规定了物体与外部环境之间的换热条件，包括以下三类：
特点：(a) 气体的导热系数基本不随压力的改变而变化 (b) 随温度的升高而增大 (c) 随分子质量减小而增大
B 液体的导热系数 液 体 0.~ 007.W 7(m C)
特点：(a) 随压力的升高而增大 p
(b) 随温度的升高而减小 T
2020/7/15
6
C 固体的导热系数
金属 1~ 241W 8(m C)
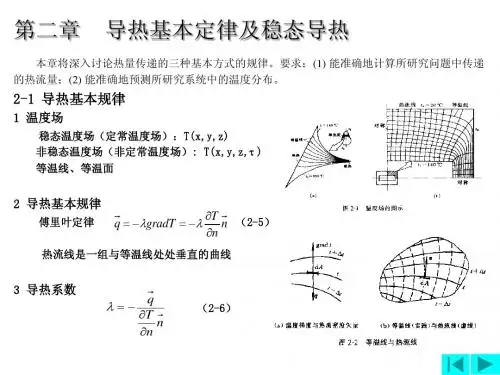
图2-1 温度场的图示
3
2 导热基本定律——Fourier Law
对于一维情况， A dt
dx
对于三维直角坐标系情况，有
qx
t x
qy
t y
qz
t z
gratdtti t jtk x y z
q x ti y tj z tk t n tn
2020/7/15
图2-2 温度梯度
通用形式的
Fourier Law
下面我们来考察一个矩形微元六面体，如下图所示。
x
x+dx
zy
dx
x
2020/7/15
10
假设：(1) 所研究的物体是各向同性的连续介质
(2) 导热系数、比热容和密度均为已知
(3) 物体内具有内热源；强度 Φ [W/m3]; 内热源均匀
分布；
2020/7/15
11
§2-2 导热微分方程式及定解条件（续）
非金 0 属 .02~5 3W(m C)
特点：纯金属：
T
合金和非金属：T
金属的导热系数与温度的依变关系参见图2-7
保温材料：国家标准规定，温度低于350度时导热系数 小于 0.12W/(mK) 的材料（绝热材料）
2020/7/15
7
图2-7 导热系数对温度的依变关系
2020/7/15
8
第二章 导热基本定律及稳态导热
第二章 导热基本定律及稳态导热
2-1 导热基本定律
2-2 导热微分方程式及定解条件
2-3 通过平壁、圆筒壁、球壳和其它变截面物 体的导热
2-4 通过肋片的导热
2-5 具有内热源的导热及多维导热
2020/7/15
1
§2-1 导热基本定律
1 几个基本概念: 温度场、等温面、等温线、温度梯度、热流密度矢量
根据能量守恒定律有：
导入微元体的总热流量in + 微元体内热源的生成热 g =
导出微元体的总热流量 out + 微元体热力学能的增量 st
Φ ydy
a 导入微元体的总热流量Ein
Φx
dy/15
Φy
dx
Φxdx
Φ
x
t x
dydz
Φ
y
t y
dxdz
Φ
z
t z
dxdy
in Φ x Φ y Φ z x td y d z y td x d z z td x d 1y 2
把Qin、Qout、Qg、Qst 带入前面的能量守恒方程
Q inQgQ outQst
得： c t x( x t) y( y t) z( z t) Φ
这就是三维、非稳态、变物性、有内热源的导热微分方 程的一般形式。
2020/7/15
14
§2-2 导热微分方程式及定解条件（续）
2 几种特殊情况
(1) 若物性参数 、c 和 均为常数：
t a ( x 2 2 t y 2 2 t z 2 2 t) Φ c; or t a 2 t Φ c
a —热扩散率（导温系 [m数 2 s]） c
(2) 无内热源、常物性： t a2t
物理
意义
(3) 稳态、常物性： 2t 0
？
(4) 稳态、常物性、无内热源：2t 0
4
§2-1 导热基本定律（续）
3 导热系数(热导率) q
- grad t
(1)物理意义：热导率的数值就是物体中单位温度梯度、单位时
间、通过单位面积的导热量 W(m C。) 热导率的数值表征物质
导热能力大小，由实验测定。
(2) 影响因素：物质的种类、材料成分、温度、湿度、压力、密度等
金属 非;金固 属相 液相 气相
(1) 温度场： tf(x,y,z,)
三维非稳态温度场： tf(x,y,z,)
三维稳态温度场： tf(x,y,z)
二维稳态温度场： tf(x,y)
一维稳态温度场： t f (x)
2020/7/15
2
§2-1 导热基本定律（续）
(2) 等温线 (3) 等温面 (4) 等温面和等温线的特点
2020/7/15