曲柄连杆机构运动及动力特性分析
（7）
用近似式计算活塞速度，在 α =0°、90°、
以式
dβ dt
=
λ × cosα cos β
× dα dt
代入，得
j = rω2[cos(α + β ) + λ cos2 α ]
cos β
cos3 β
（11）
这是活塞加速度的准确表达式。
将式（7）对时间求导，则可得活塞加速度的
近似表达式
j = rω2 (cosα + cos 2α )
连杆比 λ 是一个重要的结构设计参数。采用较大 中心的圆周速度 rω ，随连杆比 λ 的增大， ve 略有
的 λ (即较短连杆)，可使发动机高度减小，重量减轻， 增大。
但同时也使活塞的加速度和连杆的摆角加大，相应的
活塞的平均速度
往复运动质量的惯性力和活塞的测推力加大。与得失 相比，对汽车发动机来说，更重要的是发动机的高度 和重量上的得益。所以设计时总要选用短连杆。即使
g
0
体的绝对压强； Ah 为活塞的投影面积。
pg
>
p 0
时，Pg
是正值，其作用方向是活塞的下
行方向，负值 P 的作用方向相反。 g
1.3.2 曲柄连杆机构所受的外力
对一个单缸机的曲柄连杆机构来说，如果忽略
各运动副的摩擦阻力和阻力矩不计，忽略构件重力
不记，则它所受的外力就只有：
（1）作用于活塞的气体作用力
记活塞加速度出现极值时的曲轴转角为 α je ，则 按式（12）应有
dj dα
α je
=
sin α je (1+ 4λ cosα je )
=
0
（13）
·12·
设计与研究
机械 2006 年第1 期 总第33 卷
由此式解得 α je
=
0°、180°、
arc cos(−
1 )
4λ
，
而对应的加速度极值为：
l
杆大小头孔中心的距离，α 是曲轴转角， β 是连杆 转角。
因
cos β = (1− λ 2 sin2 α )1/2 = 1− λ 2 sin2 α − λ 4 sin4 α − .......
2
8
（2）
———————————————
收稿日期：2005－10－10 作者简介：李斌（1963－），男，汉族，四川南充人，在读博士，副教授，主要从事机电一体化技术，机械动力学及仿真方面的研究工作。
dt
dt cos β
dt
cos2 β dt
将式 dβ = λ × cosα × dα ，dα = ω 代入式（5），
dt
cos β dt dt
则有
v = rω sin(α + β ) cos β
（6）
此式是活塞速度的准确表达式。
将活塞位移的近似式（4）对时间求导，可得活
塞速度的近似式
v = rω(sinα + λ sin 2α ) 2
对于较大的连杆来说，式（3）中含 λ 的三次以上个高
Cm
=
2S (60 n)
=
Sn 30
=
2 π
rω
=
0.6366rω
（10）
式中： S 为活塞行程， n 为曲轴每分钟转角数，
次项的数值也很小，可略去不计，即得活塞位移近似 式为
ω
=
πn 30
。
x = r[(1− cosα ) + λ (1− cos 2α )] 4
（12）
用近似式计算活塞加速度，在 α = 0°和 180°
是没误差，在 α = 90°和 270°时误差最大。当
180°、270°时没有误差,在其他曲拐转角时有误 差。但即使对 λ = 0.32 的机构，最大误差也不大于 0.0057 rω ，相对误差小于 0.83％。对于 λ < 0.32 的 机构误差更小。
当α
=
0
90
,
0
270
时，
β max
=
±λ (1 +
1 λ2 ) 6
β& = λω cosα cos β
近似公式 最大值
β& = λω cosα (1 + 1 λ2 sin 2 α ) 2
当 α = 00 ,1800 时， β&max = ±λω
精确公式
β&& = −λ(1 − λ2 )ω 2 sinα cos3 β
·10·
设计与研究
机械 2006 年第1 期 总第33 卷
曲柄连杆机构运动及动力特性分析
李斌，杨春雷，刘勇
（西南石油大学 机电工程条件下作变速运动，因此它在工作中的受力极其复杂。本文针对柴油机曲柄连杆机构进
行了运动和动力特性分析，得出了机构中主要零件的运动规律和所承受的力及力矩。从而为设计曲柄连杆机构和减小发
P g
；
（2）作用于曲轴动力输出端的旋转阻力矩 M；
（3）机体对活塞的支承力 N；
（4）机体对曲轴的支承力。
其中 N 可认为垂直于气缸的中心线并通过活塞
销中心；机体对曲轴前、后两个主轴颈的支承力的
合力则方向不明，但可以用以沿曲柄方向得力 K 和
一垂直于曲柄方向的力 T 来表示。见图 2。
上止点 N
x
按近似式画出活塞的速度随曲轴转角的变化的 曲线。当活塞由上止点向下止点运动时，其速度为 正，反之为负。0°～90°和 270°～360°之间，
λ = 0.32 时，近似式算出的 j 和 j 比准确值小
90
270
0.0178 rω2 ，相对误差约为 5.3％。对于 λ < 0.32 时
的机构，计算误差更小。
je α=00 = rω 2 (1 + λ)
j e
α =1800
= −rω2 (1− λ)
1 2 ω λ λ j = −r (8 + ) e α=arccos(−1/ 4λ )
因
cosα
< 1 ，故第三个加速度值只在 λ
>
1 4
时
才出现。
1.2 连杆的运动分析
连杆的运动是随活塞平移和绕活塞销摆动两种 运动的复合。连杆随活塞平移的速度和加速度就是 活塞的速度和加速度。连杆绕活塞销摆动的角位移 β ，从连杆与气缸中心线重合时算起。在 α = 0°～ 180°范围内 β 为正值，α = 180°～360°范围内 β 为负值。
1 运动及动力特性分析
1.1 活塞的运动分析
正置曲柄连杆机构见图 1，其曲轴回转中心线和 活塞销中心线均与气缸中心弦线相交。这是车用往 复式内燃机常用的一种曲柄连杆机构，活塞的位移
x 由其上止点开始计量。
x = r[(1− cosα ) + 1 (1− cos β )] λ
（1）
式中：λ 是连杆比（ λ = r ）， r 是曲柄半径， l 是连
机械 2006 年第1 期 总第33 卷
设计与研究
·11·
把式（2）代入式（1），并利用三角函数的倍角
活塞速度个出现一个极值 v 。 e
公式予以化简，最后可得
记活塞速度达到极值时曲轴转角为 α ，则有 ve
x = r(a + a cosα + a cos 2α
0
1
2
+a 4
cos
4α
+
a 6
cos
通过对活塞的计算和活塞和连杆之间的运动关 系分析，可得连杆的角位移、角速度和角加速如表 1 所示。
角位 移β
角速 度 β&
角加 速度
β&&
表 1 连杆运动规律
精确公式
计算公式 β = arcsin(λ sin α )
近似公式 最大值 精确公式
β = λ sin α (1 + 1 λ 2 sin 2 α ) 6
LI Bin，YANG Chun-lei，LIU Yong
(College of Mechanical Engineering, South-West Petroleum University，Chengdu 610500，China) Abstract：The crank-connecting rod mechanism makes variable movement under the high-pressure and in high temperature, so it is complicated that the crank-connecting rod mechanism has received force at work. Thought the analysis of the characteristics of movement and force, the article which establishes the foundation for the design of crank-connecting rod and reducing the vibration of engine obtains the characteristics of movement and force of the major part in the mechanism. Key words：crank-connecting rod mechanism；movement analysis；dynamic characteristic
解出未知力 K′ 、 N′ 、 T ′ 、 M ′ ，可以先利用力的
分解与平移定理将此力系中的 Pg 、 Pj 二力予以转
化。如图 2， Pg 和 Pj 合在一起可以用一个沿连杆中 心线作用的力 S（简称连杆力）和一个垂直于气缸
曲柄连杆机构的运动与受力分析讲解学习
定义“曲拐当量质量”为：
则： Prqmqdr2
mqdmqx2mqbrb
如果曲拐的某一曲柄臂上设有平衡重，其质量为 m p ，而其质心
距曲轴轴线的距离为 p ，则平衡重的旋转惯性力为：
Prpmpp2r2mprp
定义“平衡重当量质量”为：
mpd
mp
p
r
（1-32）
则： Prpmpdr2 （1-33）
（2）活塞速度：在0 ºCA~90 ºCA之间和 270 ºCA~360 ºCA之间，活塞速度各出现 一个正极值和负极值。 （3）活塞加速度：在上止点前后活塞加 速度是正值，方向是活塞下行的方向，往 复惯性力朝上；在下止点前后活塞加速度 是负值，方向是活塞上行的方向，往复惯 性力朝下。根据极值方法求解，可得：
1.2.2.2 单个曲拐的旋转惯性力
曲轴上曲柄不平衡部 分的质量分为两部分：
（1）曲柄销部分：
图1-10 单曲拐的旋转惯性力
Prxmqxr2 （1-28）
（r为曲柄半径）
（2）曲柄臂部分： Prbmqbb2 （1-29）
（ b 为曲柄臂质心至曲轴轴线的垂直距离）
整个曲拐的旋转惯性力就是：
P rq P rx 2 P rb r2 m q x2 m qbrb
由式（1-3）知：
arc s i（n1-12）
极值： e arcsin角速度： l Nhomakorabead
dt
cos cos
cos 1 2 sin 2
1 （1-13）
2
角速度极值：le
角加速度：l d d l t c s i o n d d s tc o c s s2 o i n s d d t
1.2.2.3 连杆的惯性力
第一章_曲柄连杆机构的运动与受力分析
此惯性力作用于活塞销上，并通过活塞销作用于连杆，进而 传递到曲轴、机体mhx j （1-26）
此惯性力作用于连杆小头上，并通过连杆作用于曲轴，再传 到机体。 在进行曲柄连杆机构总体受力分析时（对机体、被曲轴驱动 的轴系…），考虑整个活塞组件的往复惯性力：
1.2.1 气体作用力 作用于活塞顶上的气体作用力： Pg ( pg p0 ) Fh （式中，Fh是活塞投影面积）
pg p0 时， Pg 是正值，其作用方向是活塞下行方向。 2 以 F cm 与 为单位，则： p0 以bar为单位， h 若 pg
当
Pg 10 pg p0 Fh
dv d sin d cos d j r cos sin 2 dt dt cos dt cos dt
将式（1-6）代入上式，得：
2 cos cos 2 j r 2 cos cos
e arcsin
d cos 角速度： l dt cos cos 1 （1-13） 2 2 2 1 sin
角速度极值： le
d dt
sin d sin d l l cos 角加速度： cos 2 dt cos dt
dx d 1 d v r sin sin dt dt dt d cos d 将式（1-3）对时间求导，得： （1-6） dt cos dt d 代入上式，且记曲轴角速度：
活塞速度： 可得： v r
（1-10）（精确式）
将式（1-8）对时间求导，得：
j r 2 cos cos2
第九章-曲柄连杆机构动力学分析
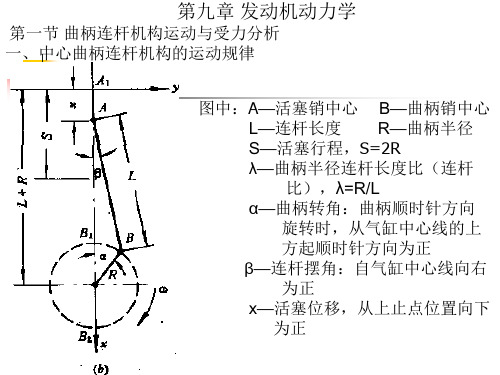
Pj m j a m j R 2 cos m j R 2 cos2 PjI PjII
（2）、旋转惯性力Fr=mrRω2 2、沿气缸中心线的总作用力F 总作用力F是缸内气体作用力Fg与往复惯性力的代数和 F=Fg+Fj 气体作用力 D 2 Fg p g - p? g 4
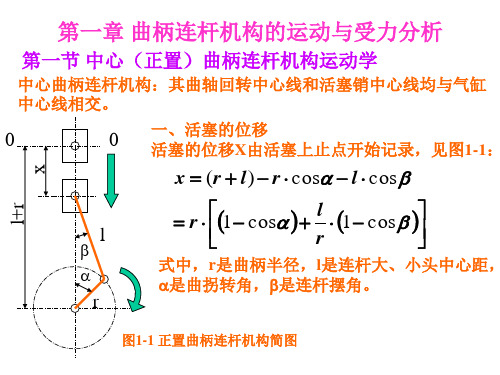
1、活塞位移x：
x ( L R) ( L cos R cos )
2 2
R(1 cos ) L(1 1 sin )
（精确式）
R x R(1 cos ) (1 cos 2 ) x I x II （近似式） 4
近似式与精确式相比误差很小，如当λ =1/3.5时，曲柄转角为 90度时误差为最大，在0.003R左右，此精度在工程上已足够。
பைடு நூலகம்
（精确式）
1 2 L sin 1 1 3 cos2 （近似式） 2
2
在α =90º 或270º 时达到极值：
Le
2 (1 2 )1 / 2
（精确式）
1 （近似式） 2 摆动角速度和角加速度精确式中分母均近似等于 1 ，因此两者均 随α 近似按简谐规律变化。
L L 1 m j m p m 1 m p m l L 作旋转运动的不平衡质量mr，包括曲柄换算质量mk和连杆换算
L1 mr mk m 2 mk1 2mk 2 mL R L
到大头中心的质量m2，集中作用于曲柄销中心，即
三、曲柄连杆机构作用力和力矩 1、惯性力 、 （1）旋转惯性力 （1）、 往复惯性力
2、活塞速度：
sin( ) v R cos
发动机曲柄连杆机构运动及动力特性分析与仿真
第 一种情 况 ： 当
时，活 塞加速 度在 曲
４
轴转 动 一 圈的范 围 内有两 个 极值 ： 在 ， ０ 处 ， ＝ 。 即上 止 点处 ， 塞加速 度 极大 值为 ： 活
作 者简 介 ：李鹏 （９ ６ ）男 ，在 读硕 士 ，主要 研 究方 向 为内燃 机动 态 设计 。 １８ －
（ ５ ）
结 合（） 分析 ：速度 １对 曲轴 转角 作一 次 ４式 ，
Ｖａ≈＋ ｃ ／＋ ２，其所在位置 （ 表 示 ， ｘ Ｒｏ １ ２ ｘ ｖ） ｍ
图 １ 曲柄 连 杆 机 构 简 图
、 ．
ｘ ＝ ａ ｃｃｏｓ— ｒ
／＋—２ — ８ —１ １ ２
—
发 动机 曲柄连 杆 机 构 由活塞 组 、连 杆 组和 曲 轴 组三 大 部分 组成 。 １ 图 是正 置式 曲柄 连杆 机构 运
机 电技术
２１ 年 ６ ０１ 月
ａ ＝Ｒ ｏ（＋２ ｃ １ ）
Байду номын сангаас
（） ６
，
一
（ ） ＋
（） ８
在 ，＝１０ 处 ，即下 止 点处 ，活塞 加速度 极 小值 ８。
１ 连杆 运 动学分 析 ． ２
为：ａ， Ｒ ｏ （一 ＝一 ｃ １ ）
１
（） ７
＝ ・ Ｄ （） ９
速度 近似 式代 入 ，可 得 曲柄连 杆机 构 的往 复惯 性
力为：
＝ ｍ， ｃ （ Ｓ￣ ｃｓ ａ － Ｒ ｏ Ｃ Ｏ＋２ ｏ ２ ） Ｏ
一
４
结合 （） 分析 ：活 塞加 速度 极值 的大 小及 位 ５式 置有 两 种情 况 ：
１
动和动力分析简图，其 中活塞组和连杆小端沿气 缸 中心 线 做往 复 直线 运 动 ， 曲轴组 和连 杆 大端 作 回转运 动 。运 动 过程 中 ，各 部 件 的速度 和 加速 度
柴油机的曲柄连杆机构运动及动力特性分析解读
曲柄连杆机构运动及动力特性分析学生姓名：学号：专业：院（系）：完成时间：摘要本文针对柴油机曲柄连杆机构运动和动力特性分析，运用自己在理论力学、高等数学、线性代数、工程力学等科目的知识，深入的分析了曲柄连杆机构在运动过程中的运动规律，并且用代数的方法精确地了得出了机构在运动过程中机构中主要零件的运动规律和所承爱的力及力矩变化关系式，并且以EA1113柴油机为例，进行了精确的计算。
从而为设计曲柄连杆机构和减小发动机震动提供了理论支持。
关键词：曲柄连杆机构；运动分析；力学分析特性目录第1章柴油机介绍.......................... .. (4)1.1柴油机概述 (4)1.2柴油机系统的机构及工作原理 (4)第2章柴油机的运动和力析 (5)2.1曲柄连杆机构的类型 (5)2.2曲柄连杆机构运动分析 (6)2.2.1活塞位移 (7)2.2.2活塞的速度 (8)2.2.3活塞的加速度 (9)2.3曲柄连杆机构中的作用力 (9)2.3.1气缸内工作物质的作用力 (9)2.3.2机构的惯性力 (11)2.4本章小结 (17)第3章国内外柴油机的发展现状 (17)前言人们想起柴油车，总会想起浓烟滚滚、噪音大等等问题，其实随着2003年第三代电控高压共轨喷射系统的发展，噪音问题和柴油机震动问题都有了改善，新一代的柴油发动机在保障噪音低和震动小的前提下，还拥有经济性好，动力大等优点。
这吸引了国际上有关大公司对柴油发动机的热情，也大大促进了柴油车在国外的销售，如今欧洲柴油车已经抢夺了汽油车的半壁江山，而部分车型，比如路虎在欧洲90％都是柴油版本。
柴油车的优点如此突出，然而振动问题和噪声问题却日益突出，致使其零部件磨损加重、噪声升高、寿命降低、工作条件恶化。
柴油机的曲轴是整个发动机中最重要的零件之一。
它的受损及破坏可能引起柴油机其它零件的损坏，特别是随着发动机的强化与技术发展，使曲轴的工作条件愈发苛刻。
曲柄连杆机构概述
曲柄连杆机构受力分析
3．离心力——是指曲柄、连杆轴颈、连杆大头等围绕曲轴轴线做圆周运 动产生的离心惯性力，简称离心力，用FC表示。
离心力在垂直方向上的分力Fcy，与惯性力Fj的 方向总是一致的，因而加剧了发动机的上、下振动 。
而水平方向的分力Fcx则使发动机产生水平方向 的振动。
此外，离心力使连杆大头的轴承和轴颈受到又 一附加载荷，增加了它们的变形和磨损。
曲柄连杆机构受力分析
曲柄连杆机构受力分析
曲柄连杆机构在工作时做变速运动，受力情况相当复杂，气体压力、往复 惯性力、旋转运动的离心力、相对运动件接触表面的摩擦力等都作用在曲柄连 杆机构上。
（1）气体压力
（2）往复惯性力
（3）旋转运动的离心力
（4）相对接处表—在发动机工作循环的每个行程中，气
曲柄连杆机构受力分析
4．摩擦力——任何一对互相压紧并做 相对运动的零件表面之间都存在摩擦力。 在曲柄连杆机构中，活塞、活塞环与气缸 壁之间，以及曲轴、连杆轴承与轴颈之间 都存在摩擦力，摩擦力是造成零件配合表 面磨损的根源。
感谢您的观看
曲柄连杆机构的组成
曲柄连杆机构的作用 曲柄连杆机构的组成 曲柄连杆机构的工作条件
曲柄连杆机构的作用
将燃烧的油气混合气作用在活塞顶上的压力转变为曲轴旋转运动 而对外输出动力。
曲柄连杆机构的组成
机体组
活塞连杆组
曲轴飞轮组
曲柄连杆机构的工作条件
曲柄连杆机构是在高温、高压、高速和化学腐蚀的环境中工作的。 高温：最高可达 2500K以上 ； 高压：最高可达 5MPa—10MPa； 高速：最高可达 3000 r/min—6000 r/min； 化学腐蚀：可燃混合气和燃烧废气直接接触机件；
曲柄连杆机构运动及动力特性分析
λ = 0.32 时，近似式算出的 j90 和 j270 比准确值小
0.0178 rω 2 ，相对误差约为 5.3％。对于 λ < 0.32 时 的机构，计算误差更小。 则 记活塞加速度出现极值时的曲轴转角为 α je ， 按式（12）应有
dj α je = sin α je (1 + 4λ cos α je ) = 0 dα
& = λω cos α (1 + λ2 sin 2 α ) β
& 当 α = 0 ,180 时， β max = ± λω
&& = −λ (1 − λ2 )ω 2 β sin α cos 3 β
0 0
1 2
根据达伦伯原理，上述各力应与曲柄连杆机构 的质量惯性力 Pj 和旋转惯性力 Pr 构成平衡力系，既 然 Pg 、 Pj 、 Pr 、N 在同一气缸中心平面，故 K 和 T 也处于同一平面上。为了便于从这些力的平衡关系 解出未知力 K ′ 、 N ′ 、 T ′ 、 M ′ ，可以先利用力的 分解与平移定理将此力系中的 Pg 、 Pj 二力予以转 化。如图 2， Pg 和 Pj 合在一起可以用一个沿连杆中 心线作用的力 S（简称连杆力）和一个垂直于气缸 中心线的侧推力 N 来代替。其中
上止点 N s=2r x
1 因 cos α < 1 ，故第三个加速度值只在 λ > 4 时 才出现。
1.2 连杆的运动分析 连杆的运动是随活塞平移和绕活塞销摆动两种 运动的复合。连杆随活塞平移的速度和加速度就是 活塞的速度和加速度。连杆绕活塞销摆动的角位移 β ，从连杆与气缸中心线重合时算起。在 α = 0°～
1 3 a0 = 1 + λ + λ 3 + LL 4 64 a1 = −1
第三章曲柄机构受力分析
第三章曲柄机构受力分析3.1曲柄连杆机构运动学曲柄连杆机构的任务是将活塞的往复运动转化为曲柄的旋转运动，在往复活塞式汽车发动机中基本上采用两种曲柄连杆机构；中心曲柄连杆机构；偏心曲柄连杆机构。
（l）、中心曲柄连杆机构：其气缸轴线通过曲轴轴线。
这种机构的运动特性完确定，其中r为曲柄半径，L为连杆长度（连杆大小头孔中心间距全由连杆比λ=rι离）（2）、偏心曲柄连杆机构：其气缸轴线偏离曲柄轴线。
这种机构的特性参数除连杆比λ，还有偏心率ξ=℮，其中ℯ为气缸轴线相对曲轴轴γ线的偏移量。
下面讨论应用最广泛的中心曲柄连杆结构的运动学。
3.1.1中心曲柄连杆机构运动学中心曲柄连杆机构在汽车发动机中应用最广泛。
机构简图如图3一1所示。
它在运动时，活塞A作往复直线运动，曲柄OB作旋转运动，连杆AB作平面复合运动。
研究曲柄连杆机构图运动学的重点是研究活塞的运动规律，因为曲柄的运动状态比较简单，连杆的运动虽然较复杂，但可把它看成一部分随活塞A运动，另一部分随连杆轴径B运动，其运动所引起的其他后果对我们所研究的问题影响较小。
图3一2中，O点表示曲轴中心，A点表示活塞销中心位置、也就是活塞的位置，OB表示曲柄半径:，AB表示连杆长度l。
曲柄转角α是从气缸轴线顺着曲柄转动方向度量。
当α二0º时，对应的Aˊ和Βˊ表示活塞和连杆轴径在上止点位置；当α﹦180º时，对应的Aˊ和Βˊ表示活塞和连杆轴径在下止点位置。
β为连杆轴线偏离气缸轴线的角度，称为连杆摆动角，逆时针为正、顺时针为负。
下面分别研究曲柄、活塞和连杆的运动规律：1、曲柄运动通常近似地认为汽车发动机中曲柄是作匀谏转动，其转角α=360π60t=6nt度。
式中t表示时间，n表示汽车发动机转速（转/分）。
角速度ω=dαdt =πn30弧度/秒≈常数。
因为认为曲柄是作匀速转动，所以ω一个参数确定了曲轴的运动状态。
2、活塞位移从图3一2可知，活塞位移：Χ=ΑΑ=ΑΟ−ΑΟ=ΑΟ−ΑC−CO=r+L−r cosα−L cosβ=r1+1λ−cosα+1λcosβ由上式知，位移x与r有关，不同型号的汽车发动机r是不一样的，为了便于比较分析不同大小汽车发动机活塞位移变化规律，常引用无量纲位移（又称位移系数）χ=χr，即用χ与r的相对值表示变化规律。
曲柄连杆机构动力学分析与计算
第一章绪论1.1内燃机概述汽车自19世纪诞生至今，已经有100多年的历史了。
汽车工业从无到有，以惊人的速度在发展着，汽车工业给人类的近代文明带来翻天覆地的变化，在人类的文明进程中写下了宏伟的篇章。
汽车工业是衡量一个国家是否强大的重要标准之一，而内燃机在汽车工业中始终占据核心的地位。
内燃机是将燃料中的化学能转变为机械能的一种机器。
由于内燃机的热效率高（是当今热效率最高的热力发动机）、功率范围广、适应性好、结构简单、移动方便、比质量（单位输出功率质量）轻、可以满足不同要求等特点，已经广泛的应用于工程机械、农业机械、交通运输（陆地、内河、海上和航空）和国防建设事业当中。
因此，内燃机工业的发展对整个国民经济和国防建设都有着十分重要的作用。
1.1.1世界内燃机简史内燃机的出现和发明可以追溯到1860年，来诺伊尔（J.J.E.Lenoir1822~1900年）首先发明了一种叫做大气压力式的内燃机，这种内燃机的大致工作过程是：空气和煤气在活塞的上半个行程被吸入气缸内，然后混合气体被火花点燃；后半个行程是膨胀行程，燃烧的煤气推动着活塞下行，然后膨胀做功；活塞上行时开始排气。
这种内燃机和现代主流的四冲程内燃机相比，在燃烧前没有压缩行程，但基本思想已经有了雏形。
这种内燃机的热效率低于5%，最大功率只有4.5KW，1860~1865年间，共生产了约5000台。
1867年奥拓（Nicolaus A.Otto，1832~1891年）和浪琴（Eugen Langen，1833~1895年）发明了一种更为成功的大气压力式内燃机。
这种内燃机是利用燃烧所产生的缸内压力，随着缸内压力的升高，在膨胀行程时加速一个自由活塞和齿条机构，他们的动量将使得缸内产生真空，然后大气压力推动活塞内行。
齿条则通过滚轮离合器和输出轴相啮合，然后输出功率。
这种发动机的热效率可以达到11%，共生产了近5000台。
由于煤气机必须使用气体燃料，而当时的气体燃料的来源非常困难，这从某种意义上讲就阻碍了煤气机的进一步发展。
汽车发动机曲柄连杆机构动力学分析
汽车发动机曲柄连杆机构动力学分析摘要：本文对汽车发动机的曲柄连杆机构的动力学特性进行分析，创建D6114B发动机的仿真动力学模型，利用ANSYS有限元分析软件软件得出发动机曲柄连杆机构的曲轴模态数据，分别对活塞、曲轴、连杆的受力进行分析，研究进油口、润滑油槽位置布置，为发动机机械构造设计提供参考。
关键字：发动机；曲柄连杆机构；动力学曲柄连杆机构的动力学特性对于汽车发动机的可靠性、振动效果、噪声等有很大关联，利用机械系统动力学有限元分析平台（ANSYS）创建D6114B发动机的仿真动力学模型，分析发动机曲柄连杆机构的曲轴、连杆的模态数据，对准确的掌握D6114B发动机曲柄连杆机构的零部件动力学特性具有一定的参考价值。
1. 汽车发动机曲柄连杆机构动力学模型汽车发动机曲柄连杆机构是由缸体、曲轴、连杆、飞轮活塞，构成。
上柴D6114B发动机的曲柄连杆机构的动力学模型结构如图1所示图1上柴D6114B发动机的曲柄连杆机构的动力学模型结构图缸体与曲轴连接铰链中有一条为转动铰链，其余为圆柱铰链，飞轮与曲轴固定，连接杆与曲轴之间的连接采用转动铰链，其大头一端连接曲轴，小头一端连接活塞，活塞与缸体之间采用圆柱铰链连接。
利用以上模型的各个部件的几何位置参数和质量参数建立CAD数据模型，传入给机械系统动力学有限元分析平台（ANSYS）进行分析和计算，活塞1-8作用在各缸体气压力学特性输入ANSYS如图1所示：图1 发动机各缸气体压力特性得出发动机曲柄连杆机构的曲轴模态数据结果如表1所示模态阶数 1 2 3 4 5 6 7 8 9 10频率124.8 149.9 335.4 372.1 398.0 490.7 599.2 632.1841.1 947.2模态阶数11 12 13 14 15 16 17 18 19 20频率1015.3 1264.3 1340.6 1369.2 1413.9 1465 1664 17451862.5 2394.92. 曲柄连杆机构动力学分析当对活塞逐级施加压力0-12/104pa，对应曲轴转速2200r/min，活塞运动其对气缸的侧推力在-7804~6960N之间周期性变化，侧推力对汽缸壁的磨损影响很大。