电子电路基础第四章习题参考答案
《数字电子技术基础》第四章习题答案
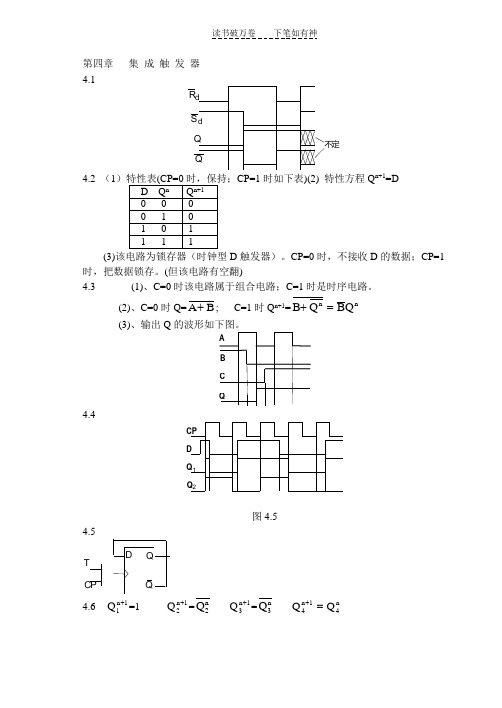
第四章 集 成 触 发 器 4.1R d S d Q Q不定4.2 (1CP=1时如下表)(2) 特性方程Q n+1=D(3)该电路为锁存器(时钟型D 触发器)。
CP=0时,不接收D 的数据;CP=1时,把数据锁存。
(但该电路有空翻)4.3 (1)、C=0时该电路属于组合电路;C=1时是时序电路。
(2)、C=0时Q=A B +; C=1时Q n+1=B Q BQ nn+= (3)、输出Q 的波形如下图。
A B C Q4.4CP D Q 1Q 2图4.54.5 DQ QCPT4.6 Q 1n 1+=1 Q 2n 1+=Q 2n Q n 13+=Q n 3 Q Q 4n 14n+=Q1CP Q2Q3Q44.7 1、CP 作用下的输出Q 1 Q 2和Z 的波形如下图; 2、Z 对CP 三分频。
DQ QCPQ1DQ QQ2ZRd CP Q1Q2Z14.8由Q D J Q KQ J Q KQ n 1n n n n +==+=⋅得D 触发器转换为J-K 触发器的逻辑图如下面的左图;而将J-K 触发器转换为D 触发器的逻辑图如下面的右图CPD Q QJKQ QDQ QJ KCP4.9CP B CA4.10CP X Q1Q2Z4.11 1、555定时器构成多谐振荡器 2、u c, u o 1, u o 2的波形u c u o 1u o 2t t t 1.67V3.33V3、u o 1的频率f 1=1074501316..H z ⨯⨯≈ u o 2的频率f 2=158H z4、如果在555定时器的第5脚接入4V 的电压源,则u o 1的频率变为1113001071501232....H z ⨯⨯+⨯⨯≈4.12 图(a)是由555定时器构成的单稳态触发电路。
1、工作原理(略);2、暂稳态维持时间t w =1.1RC=10ms(C 改为1μF);3、u c 和u o 的波形如下图:u ou ct t tu i (ms)(ms)(ms)5 10 25 30 45 503.33V4、若u i 的低电平维持时间为15m s ,要求暂稳态维持时间t w 不变,可加入微分电路4.13由555定时器构成的施密特触发器如图(a)所示 1、电路的电压传输特性曲线如左下图; 2、u o 的波形如右下图;3、为使电路能识别出u i 中的第二个尖峰,应降低555定时器5脚的电压至3V 左右。
电路基础 第四章习题解答

图4‐4(a)
图4‐4(b)
4-5 解:画出三个电源独立作用时各自的电路图,如图(a)、(b)、(c)所示 图(a)中,根据分流定律
I ' 12 6 4A 6 12
图(b)中,根据欧姆定律
I ' '
36 2 A 12 6
图(c)中,根据欧姆定律
根据叠加原理
6 I 1 I 6 12 3 I I ' I ' ' I ' ' ' I ' ' '
(2 2) i1 2isc 8i1 6 2i1 (2 4) isc (2 8)i1 0
解得
i sc
6 1 .5 A 4
故一端口电路的等效电阻
uoc 6 Req 4 isc 3 2
2 u oc 2 . 25 W 4 R eq
得到戴维宁等效电路图(c)所示。由最大功率传输定理得 RL Req 4 时获得最 大功率
Pmax
图(a)
图(b)
图(c)
把15V电压源电路,应用外加电源法求等效电阻 Req ,可得
6 12 u u u 4 8 6//12 6 12 8 4 3 u - 4u2 u u 3 2 u2 0 i 4 6//12 4 4 u2
说明该电路的等效电阻
Req
故等效电路为一电流为7.5A的理想电流源,即该电路只有诺顿等效电路,如图(b1)所 示,而不存在戴维宁等效电路模型。
代入得
1 I 4 2 I I 3A 3
(a)
(b)
(c)
4-7 解:根据叠加定理,设响应
电路与电子技术基础第四章习题答案
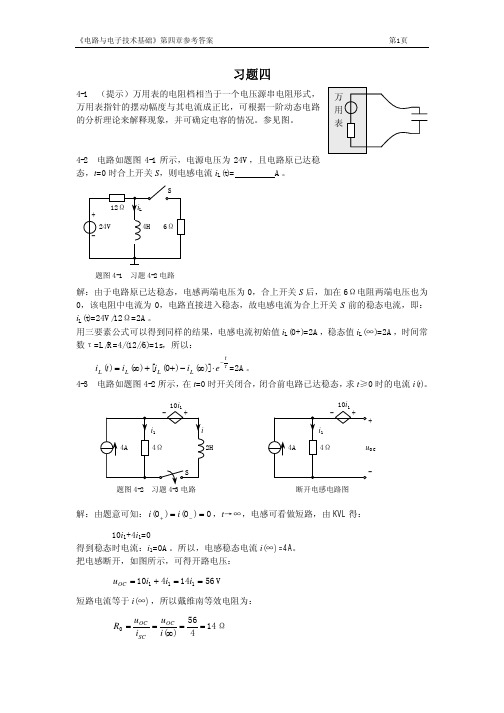
解:本题是求零输入响应,即在开关处于 a 时,主要是电感储能,当开关投向 b 后, 讨论由电感的储能所引起的响应。所以对图(a)t≥0 时的电路可列出 di L L + Ri L = 0 t≥0 dt 及 iL(0)=i(t)=10(mA) 其解为: i L (t ) = 10e
而
t≥0
i R (t ) = −i L (t ) = −10e −10 t (mA)
7
t≥0
其波形图见图(b)、图(c)所示。 4-5 电路如题图 4-4 所示,开关接在 a 端为时已久,在 t=0 时开关投向 b 端,求 3Ω电 1Ω a b 阻中的电流。 i (t ) 解:因为 u c (0) = 3 × 2 = 6(V ) (注意:当稳态以后电容为开路,所以流过 1 3A Ω和电容串联支路的电流为零, 因此电容两端的电 压就是并联支路 2Ω支路两端的电压) 当开关投向 b 时电流的初始值为
S 12Ω + 24V iL 4H 6Ω
题图 4-1
习题 4-2 电路
解:由于电路原已达稳态,电感两端电压为 0,合上开关 S 后,加在 6Ω电阻两端电压也为 0,该电阻中电流为 0,电路直接进入稳态,故电感电流为合上开关 S 前的稳态电流,即: iL(t)=24V/12Ω=2A。 用三要素公式可以得到同样的结果,电感电流初始值 iL(0+)=2A,稳态值 iL(∞)=2A,时间常 数τ=L/R=4/(12//6)=1s,所以:
当 t=0 时,开关打开,由于电感电流、电容电压均不跃变,有: i L (0 + ) = i L (0 − ) = 0.03( A) 1k u c (0 + ) = u c (0 − ) = 120(V ) 当 t≥0 时,根据基尔霍夫定律有
数字电子技术基础教材第四章答案

习题44-1 分析图P4-1所示得各组合电路,写出输出函数表达式,列出真值表,说明电路得逻辑功能。
解:图(a):;;真值表如下表所示:其功能为一位比较器。
A>B时,;A=B时,;A<B时,图(b):真值表如下表所示:功能:一位半加器,为本位与,为进位。
图(c):真值表如下表所示:功能:一位全加器,为本位与,为本位向高位得进位。
图(d):;;功能:为一位比较器,A<B时,=1;A=B时,=1;A>B时,=14-2 分析图P4-2所示得组合电路,写出输出函数表达式,列出真值表,指出该电路完成得逻辑功能。
解:该电路得输出逻辑函数表达式为:因此该电路就是一个四选一数据选择器,其真值表如下表所示:,当M=1时,完成4为二进制码至格雷码得转换;当M=0时,完成4为格雷码至二进制得转换。
试分别写出,,,得逻辑函数得表达式,并列出真值表,说明该电路得工作原理。
解:该电路得输入为,输出为。
真值表如下:由此可得:完成二进制至格雷码得转换。
完成格雷码至二进制得转换。
4-4 图P4-4就是一个多功能逻辑运算电路,图中,,,为控制输入端。
试列表说明电路在,,,得各种取值组合下F与A,B得逻辑关系。
解:,功能如下表所示,两个变量有四个最小项,最多可构造种不同得组合,因此该电路就是一个能产生十六种函数得多功能逻辑运算器电路。
4-5 已知某组合电路得输出波形如图P4-5所示,试用最少得或非门实现之。
解:电路图如下:4-6 用逻辑门设计一个受光,声与触摸控制得电灯开关逻辑电路,分别用A,B,C表示光,声与触摸信号,用F表示电灯。
灯亮得条件就是:无论有无光,声信号,只要有人触摸开关,灯就亮;当无人触摸开关时,只有当无关,有声音时灯才亮。
试列出真值表,写出输出函数表达式,并画出最简逻辑电路图。
解:根据题意,列出真值表如下:由真值表可以作出卡诺图,如下图:C AB 00 10 11 100 1由卡诺图得到它得逻辑表达式为: 由此得到逻辑电路为:4-7 用逻辑门设计一个多输出逻辑电路,输入为8421BCD 码,输出为3个检测信号。
电子电路第四章习题及参考答案

习题四4-1 电路如题图4-1所示,i (t )=10mA 、R =10k Ω、L =1mH 。
开关接在a 端为时已久,在t =0时开关由a 端投向b 端,求t ≥0时,u (t )、i R (t )和i L (t ),并绘出波形图。
解:本题是求零输入响应,即在开关处于a 时,主要是电感储能,当开关投向b 后,讨论由电感的储能所引起的响应。
所以对图(a)t ≥0时的电路可列出00≥=+t Ri dtdiL L L及 i L (0)=i (t )=10(mA ) 其解为:0)(1010)(710≥==--t mA e et i t tL τS R L 73310101010--=⨯==τ 则 0)(10010101010))(0()1)(0()(77101033≥-=⨯⨯⨯-=-=-==-----t V e e e LR Li e Li dt di L t u t ttL t L L L τττ 而 0)(10)()(710≥-=-=-t mA e t i t i t L R其波形图见图(b)、图(c)所示。
4-2 电路如题图4-2所示,开关接在a 端为时已久,在t =0时开关投向b 端,求3Ω电阻中的电流。
解:因为 )(623)0(V u c =⨯= (注意:当稳态以后电容为开路,所以流过1Ω和电容串联支路的电流为零,因此电容两端的电压就是并联支路2Ω支路两端的电压)当开关投向b 时电流的初始值为)(236)0()0(A R u i c ===S RC i 3130)(=⨯===∞τ,故根据三要素法得: 0)(2)(31≥=-t A e t i t4-3 电路如题图4-3所示,开关在t <0时一直打开,在t =0时突然闭合。
求u (t )的零输入响应和零状态响应。
解:因为u (t )=u c (t ),所以求出u c (t )即可。
方法一:直接用三要素法:(注意,开关闭合以后,时间常数由两个电阻并联后,再与电容构成RC 电路)L (t ) i (t L(a)10(b) (c) 题图4-1 习题4-1电路及波形图(t )题图4-2 习题4-2电路S C R 23)1//2(0=⨯==τ)(32)2//1(1)()(221)0(V u V u c c =⨯=∞=⨯= 所以)1(322)322(32))()0(()()(5.05.05.0≥-+=-+=∞-+∞=----t ee e eu u u t u tt t tc c c c 零状态响应零输入响应τ方法二:分别求出零输入响应和零状态响应(可以直接解微分方程,也可以直接利用结论)零输入响应:02)(215.05.00'≥=⨯==---t e V e eU u tt tc τ零状态响应:0))(1(32)1(11212)1(5.05.0"≥-=-⨯+⨯=-=---t V e e eRI u t t ts cτ4-4 电路如题图4-4所示,已知 ⎩⎨⎧≥<=010)(t t t u s 且u c (0)=5V 。
电子电路基础习题册参考答案-第四章

第四章集成运算放大器的应用§4-1 集成运放的主要参数和工作点1、理想集成运放的开环差模电压放大倍数为Aud=∞,共模抑制比为K CMR= ∞,开环差模输入电阻为ri= ∞,差模输出电阻为r0=0 ,频带宽度为Fbw=∞。
2、集成运放根据用途不同,可分为通用型、高输入阻抗型、高精度型和低功耗型等。
3、集成运放的应用主要分为线性区和非线性区在分析电路工作原理时,都可以当作理想运放对待。
4、集成运放在线性应用时工作在负反馈状态,这时输出电压与差模输入电压满足关系;在非线性应用时工作在开环或正反馈状态,这时输出电压只有两种情况;+U0m 或-U0m 。
5、理想集成运放工作在线性区的两个特点:(1)up=uN ,净输入电压为零这一特性成为虚短,(2)ip=iN,净输入电流为零这一特性称为虚断。
6、在图4-1-1理想运放中,设Ui=25v,R=1.5KΩ,U0=-0.67V,则流过二极管的电流为10 mA ,二极管正向压降为0.67 v。
7、在图4-1-2所示电路中,集成运放是理想的,稳压管的稳压值为7.5V,Rf=2R1则U0=-15 V。
二、判断题1、反相输入比例运算放大器是电压串联负反馈。
(×)2、同相输入比例运算放大器是电压并联正反馈。
(×)3、同相输入比例运算放大器的闭环电压放大倍数一定大于或等于1。
(√)4、电压比较器“虚断”的概念不再成立,“虚短”的概念依然成立。
(√)5、理想集成运放线性应用时,其输入端存在着“虚断”和“虚短”的特点。
(√)6、反相输入比例运算器中,当Rf=R1,它就成了跟随器。
(×)7、同相输入比例运算器中,当Rf=∞,R1=0,它就成了跟随器。
(×)三、选择题1、反比例运算电路的反馈类型是(B )。
A.电压串联负反馈B.电压并联负反馈C.电流串联负反馈2、通向比例运算电路的反馈类型是(A )。
A.电压串联负反馈B.电压并联负反馈C.电压串联正反馈3、在图4-1-3所示电路中,设集成运放是理想的,则电路存在如下关系(B )。
数字电子技术基础(第四版)课后习题答案-第四章
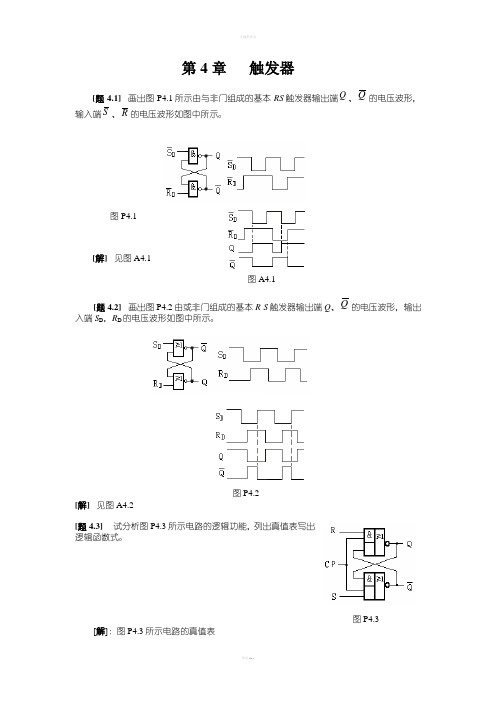
第4章触发器[题4.1]画出图P4.1所示由与非门组成的基本RS触发器输出端Q、Q的电压波形,输入端S、R的电压波形如图中所示。
图P4.1[解]见图A4.1图A4.1[题4.2]画出图P4.2由或非门组成的基本R-S触发器输出端Q、Q的电压波形,输出入端S D,R D的电压波形如图中所示。
图P4.2[解]见图A4.2[题4.3]试分析图P4.3所示电路的逻辑功能,列出真值表写出逻辑函数式。
图P4.3 [解]:图P4.3所示电路的真值表S R Q n Q n+1 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 0 1 0 0 1 1 0 1 1 1 1 0 0* 1 110*由真值表得逻辑函数式 01=+=+SR Q R S Q nn[题4.4] 图P4.4所示为一个防抖动输出的开关电路。
当拨动开关S 时,由于开关触点接触瞬间发生振颤,D S 和D R 的电压波形如图中所示,试画出Q 、Q 端对应的电压波形。
图P4.4[解] 见图A4.4图A4.4[题4.5] 在图P4.5电路中,若CP 、S 、R 的电压波形如图中所示,试画出Q 和Q 端与之对应的电压波形。
假定触发器的初始状态为Q =0。
图P4.5[解]见图A4.5图A4.5[题4.6]若将同步RS触发器的Q与R、Q与S相连如图P4.6所示,试画出在CP信号作用下Q和Q端的电压波形。
己知CP信号的宽度tw= 4 t Pd 。
t Pd为门电路的平均传输延迟时间,假定t Pd≈t PHL≈t PLH,设触发器的初始状态为Q=0。
图P4.6图A4.6[解]见图A4.6[题4.7]若主从结构RS触发器各输入端的电压波形如图P4.7中所给出,试画Q、Q端对应的电压波形。
设触发器的初始状态为Q=0。
图P4.7[解] 见图A4.7图A4.7R各输入端的电压波形如图P4.8所示,[题4.8]若主从结构RS触发器的CP、S、R、D1S。
试画出Q、Q端对应的电压波形。
电路分析基础第四版课后习题第四章第五章第六章答案
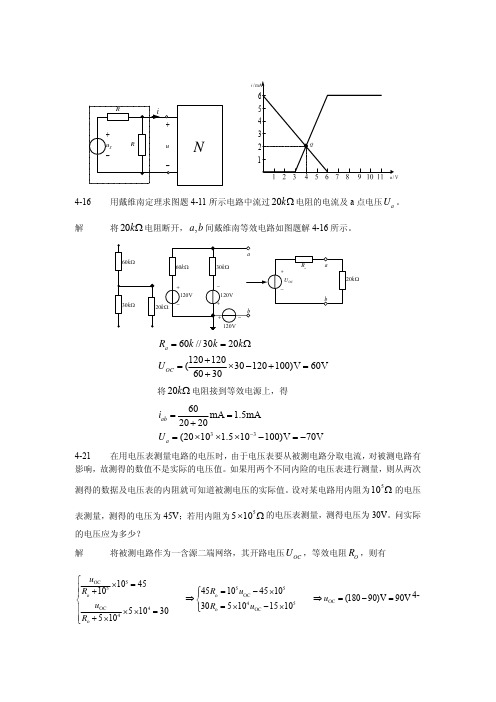
/i4-16 用戴维南定理求图题4-11所示电路中流过20k Ω电阻的电流及a 点电压。
a U 解将电阻断开,间戴维南等效电路如图题解4-16所示。
20k Ω,a bk Ω60//3020120120(30120100)V 60V6030a OCR k k k U ==Ω+=×−+=+ 将电阻接到等效电源上,得20k Ω3360mA 1.5mA2020(2010 1.510100)V 70V ab a i U −==+=×××−=− 4-21 在用电压表测量电路的电压时,由于电压表要从被测电路分取电流,对被测电路有影响,故测得的数值不是实际的电压值。
如果用两个不同内险的电压表进行测量,则从两次测得的数据及电压表的内阻就可知道被测电压的实际值。
设对某电路用内阻为的电压表测量,测得的电压为45V ;若用内阻为510Ω5510×Ω的电压表测量,测得电压为30V 。
问实际的电压应为多少? 解将被测电路作为一含源二端网络,其开路电压,等效电阻OC U O R ,则有5OC 555o o OC OC 454OCo OC 4o 10451045104510(18090)V 90V 30510151051030510u R R u u u R u R ⎧×=⎪⎧+=−×⎪⎪⇒⇒=⎨⎨=×−×⎪⎪⎩××=⎪+×⎩−=4-28 求图题4-20所示电路的诺顿等效电路。
已知:12315,5,10,R R R =Ω=Ω=Ω。
10V,1A S S u i ==解对图题4-20所示电路,画出求短路电流和等效内阻的电路,如下图所示SC i对左图,因ab 间短路,故0,0i i α==,10A 0.5A 155SC i ==+ 对右图,由外加电源法,106ab R α=Ω− 4-30 电路如图题4-22所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章习题
4.1一电容0.5 F C =,其电流电压为关联参考方向,如其端电压()
41 V t u e -=-,0t ≥,求0t ≥时的电流i ,粗略画出其电压与电流的波形,电容的最大储能是多少?
4.2一电容0.5 F C =,其电流电压为关联参考方向,如其端电压4cos 2 V u t =,t -∞<<+∞,
求其电流i ,粗略画出其电压与电流的波形,电容的最大储能是多少?
4.3一电容0.2 F C =,其电流如4.3图所示,若已知在0t =时,电容电压()00u =,求其端电压,并画波形。
题 4.3 图
4.4一电感 H L 2.0=,其电流电压为关联参考方向。
如通过它的电流A e i t )1(52--=,
0≥t ,求0≥t 时的端电压,并粗略画出其波形,电感的最大储能是多少?
4.5 一电感 H L
5.0=,其电流电压为关联参考方向。
如通过它的电流tA i 5sin 2=, t -∞<<+∞,求端电压 u ,并粗略画出其波形。
4.6一电感H L 4=,其端电压的波形如题3-6所示,已知 0)0(=i ,求其电流,并画出其波形。
题 4.6 图
4.7 题图4.7所示电路中已知100S U V =、1000R =Ω、1C F μ=,开关K 合上以前电容来充
过电.0t =时,K 合上,计算0t +
=时,i ,di
dt ,及22d i dt。
题图4.7
(参考答案)
252()()11
()(0)1
(0)100/1(0)(0)10/C C du t di t i t dt R dt RC di i A s dt RC d i di A s dt RC dt
++++
=-=-=-=-=-=
4.8 给定电路如题图4.8所示,100S U V =,10R =Ω,1L H =,0t =时合上,计算0t +=时
di
dt 及22d i dt
的值。
题图4.8
(参考答案)
1
(0)(0)100/L di u A s dt L ++== 22211(0)(0)(0)1000/L du d i di R A s dt L dt L dt +++⎡⎤==-=-⎢⎥⎣⎦
4.9 题图4.9所示电路中,已知100S U V =,110R =Ω,220R =Ω,320R =Ω,K 闭合前电路处于稳态,0t =时K 闭合,试求1(0)i +及2(0)i +。
题图4.9
(参考答案)
1110(0)(0)3
i i A +-==
23(0)5(0)3S C U u i A R ++
-==
4.10 在题图4.10所示电路中,参数为1232R R R ===Ω。
1m g s =,1L H =,2C F =,直
流电源5E V =,电容上无初始电荷。
当0t =时,K 闭合。
求(0)i +、(0)di
dt
+。
题图4.10
(参考答案)
(0)
(0)1/L u i A s L
+'=
=
4.11在题图4.11所示电路中,12126,1,2,1,(0)1,(0)2s I A L H L H R i A i A --====Ω==,问K 闭合后2(0)i +和2()i ∞各的多少?
题图4.11
(参考答案)
22(0)(0)2i i A +-==
2()3i A ∞=
4.12 电容40C F μ=,经过一电阻放电,放电过程结束时电阻消耗的能量为5J ,若在放电开始后3
5.5610s -⨯时,电容放出的能量它开始时储存能量的一半,试问放电前电容的端电压是多少?所接电阻之值是多少? (参考答案)
()RC t
c e t u -=500
Ω=07.401R
4.13 题图4.13电路中,10,200,(0)2,45)C S R C F u V u t V μ-=Ω==-,求开关K 合上后()i t 和()C u t 。
题图4.13
(参考答案)
500500() 3.167 1.197sin(31477.13)()0.3170.075sin(31412.87)
t C t
u t e t i t e
t --∴=+-=-++。
