拉普拉斯变换表
拉普拉斯变换及其逆变换表

拉普拉斯变换及其反变换表1.表A-1 拉氏变换的基本性质2.表A-2 常用函数的拉氏变换和z变换表3. 用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开,然后逐项查表进行反变换。
设)(s F 是s 的有理真分式11n 1n n n 011m 1m m m a s a s a s a b s b s b s b )s (A )s (B )s (F ++++++++==----ΛΛ (m n >)式中系数n 1n 10a ,a ,...,a ,a -,m1m 10b ,b ,b ,b -Λ都是实常数;n m ,是正整数。
按代数定理可将)(s F 展开为部分分式。
分以下两种情况讨论。
① 0)(=s A 无重根这时,F(s)可展开为n 个简单的部分分式之和的形式。
∑=-=-++-++-+-=n 1i iin n i i 2211s s c s s c s s c s s c s s c )s (F ΛΛ 式中,Sn 2S 1S ,,,Λ是特征方程A(s)=0的根。
i c 为待定常数,称为F(s)在i s 处的留数,可按下式计算:或式中,)(s A '为)(s A 对s 的一阶导数。
根据拉氏变换的性质,从式(F-1)可求得原函数② 0)(=s A 有重根设0)(=s A 有r 重根1s ,F(s)可写为 =nni i 1r 1r 111r 11r r 1r s s c s s c s s c )s s (c )s s (c )s s (c -++-++-+-++-+-++--ΛΛΛ 式中,1s 为F(s)的r 重根,1+r s ,…, n s 为F(s)的n-r 个单根;其中,1+r c ,…, n c 仍按式(F-2)或(F-3)计算,r c ,1-r c ,…, 1c 则按下式计算: 原函数)(t f 为ts n 1r i i t s 122r 1r 1r r 1e c e c t c t )!2r (c t )!1r (c ∑+=---+⎥⎦⎤⎢⎣⎡+++-+-=Λ (F-6)。
Laplace变换表

J 0 at
sn
1 s
74③
1 s2 a2
75
③
I 0 at
1 s2 a2
76
J 0 2 at
1 a e s s
1
77
ebt I 0 at
s b
2
a2
78
tJ o at
tI 0 at
J 0 a t t 2b
1
sin 2 at
e
a s
53
t
sh 2 at
e
a s
54 55
1 bt e eat t 2 sh at t 2 (1 cos at ) t 2 1 ch at t
sa s b sa a ln 2 Arth sa s
56
ln
s2 a2 s2
57
s2 a2 ln s2
2
a2
2
13
2i s 2 a 2s a
2
m 1
2 m 1
s ia
m 1
s ia
m 1
m 1
2 m 1
14
s ia
m 1
s ia
m 1
15
ebt sin at
25
26
1 s s a2
2 2
27
1 s s a2
3 2
28
1 s s a2
3 2
29
1 sin at at cos at 2a 3 1 sin at at cos at 2a 1 1 1 cos at 3 t sin at 4 a 2a
(完整版)拉普拉斯变换表

拉普拉斯变换及反变换1. 表 A-1 拉氏变换的基本性质1齐次性线性定理叠加性2微分定一般形式理L[af ( t)] aF (s)L[ f1 (t ) f 2 ( t )] F1 ( s) F2 ( s) L[ df (t ) ] sF (s) f (0)dtL[d 2 f (t) 2f()dt 2 ] s F (s) sf (0) 0n nd f (t ) n n k ( k 1 )L dt n s F (s) k 1 s f (0) f ( k 1) (t ) d k 1 f (t )dt k 1初始条件为 0 时一般形式3积分定理初始条件为 0 时4延迟定理(或称 t 域平移定理)5衰减定理(或称 s 域平移定理)6终值定理7初值定理8卷积定理L[d n f (t) ndt n ] s F (s)L[ f (t)dt]F (s) [ f (t)dt] t 0s sL[ f (t)(dt)2 ] F (s)[ f (t )dt]t 0[ f (t)( dt) 2 ] t 0s2 ss2共 n个n共 n个nF (s) 1 nL[ f (t )(dt) ] 1 [ f (t)( dt) ] t 0nk 1 sn ks共 n个F (s)L[ f (t )( dt) n ]s nL[ f (t T )] e Ts F ( s)L[ f ( t)e at ] F (s a)lim f (t ) lim sF (s)t s0lim f (t ) lim sF ( s)t 0 st 1 ( ) 2 ( ) ] [ t 1 ( ) 2 ( ) ] 1() 2()[ f d L f f t dL f t t F s F s0 012.表 A-2 常用函数的拉氏变换和z 变换表拉氏变换E(s)111 e Ts1s12s13s1s n 11s a1( s a) 2as( s a)b a( s a)(s b)s2 2ss2 2( s a) 2 2s a( s a)2 21s (1 / T ) ln a 时间函数 e(t)δ(t)T (t )(t nT )n01(t )tt 22ntn!e atte at1 e ate at e btsin tcos te at sin te at cos ta t / T23.用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开,然后逐项查表进行反变换。
拉普拉斯变换表word版本

拉普拉斯变换表附录A 拉普拉斯变换及反变换收集于网络,如有侵权请联系管理员删除收集于网络,如有侵权请联系管理员删除收集于网络,如有侵权请联系管理员删除3. 用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开,然后逐项查表进行反变换。
设)(s F 是s 的有理真分式1110111)()()(a s a s a s a b s b s b s b s A s B s F n n n n m m m m ++++++++==----ΛΛ (m n >) 式中系数n n a a a a ,,...,,110-,m m b b b b ,,,110-Λ都是实常数;n m ,是正整数。
按代数定理可将)(s F 展开为部分分式。
分以下两种情况讨论。
① 0)(=s A 无重根 这时,F(s)可展开为n 个简单的部分分式之和的形式。
∑=-=-++-++-+-=ni ii n n i i s s c s s c s s c s s c s s c s F 12211)(ΛΛ (F-1) 式中,n s s s ,,,21Λ是特征方程A(s)=0的根。
i c 为待定常数,称为F(s)在i s 处的留数,可按下式计算:)()(lim s F s s c is s i i-=→ (F-2) 或is s i s As B c ='=)()( (F-3)式中,)(s A'为)(s A 对s 的一阶导数。
根据拉氏变换的性质,从式(F-1)可求得原函数[]⎥⎦⎤⎢⎣⎡-==∑=--n i i i s s c L s F L t f 111)()(=t s n i i ie c -=∑1 (F-4) ② 0)(=s A 有重根 设0)(=s A 有r 重根1s ,F(s)可写为())()()()(11nr rs s s s s s s B s F ---=+Λ =nn i i r r r r r r s s c s s c s s c s s c s s c s s c -++-++-+-++-+-++--ΛΛΛ11111111)()()(收集于网络,如有侵权请联系管理员删除式中,1s 为F(s)的r 重根,1+r s ,…, n s 为F(s)的n-r 个单根;其中,1+r c ,…, n c 仍按式(F-2)或(F-3)计算,r c ,1-r c ,…, 1c 则按下式计算:)()(lim 11s F s s c rs s r -=→ )]()([lim 111s F s s dsd c rs s r -=→- M)()(lim !11)()(1s F s s dsd j c rj j s s j r -=→- (F-5) M)()(lim )!1(11)1()1(11s F s s dsd r c rr r s s --=--→ 原函数)(t f 为[])()(1s F L t f -= ⎥⎦⎤⎢⎣⎡-++-++-+-++-+-=++---n n i i r r r r r r s s c s s c s s c s s c s s c s s c L ΛΛΛ111111111)()()( t s nr ii t s r r r r ie c e c t c t r c t r c ∑+=---+⎥⎦⎤⎢⎣⎡+++-+-=1122111)!2()!1(Λ (F-6)。
拉普拉斯变换表-互联网类

拉普拉斯变换表-互联网类关键信息项:1、拉普拉斯变换的定义和基本原理2、常见函数的拉普拉斯变换公式3、拉普拉斯变换的性质4、逆拉普拉斯变换的方法5、拉普拉斯变换在互联网领域中的应用场景6、协议的生效日期和有效期限7、协议的更新和修订机制11 拉普拉斯变换的定义和基本原理拉普拉斯变换是一种数学变换,用于将时域函数转换为复频域函数。
其定义为对于函数 f(t),其拉普拉斯变换 F(s) 定义为:\F(s) =\int_0^\infty f(t) e^{st} dt\其中,s =σ +jω 是复变量,σ 为实部,ω 为虚部。
111 拉普拉斯变换的目的在于将微分方程转化为代数方程,从而简化系统的分析和设计。
12 常见函数的拉普拉斯变换公式以下是一些常见函数的拉普拉斯变换:单位阶跃函数 u(t) 的拉普拉斯变换为 1/s。
指数函数 e^at 的拉普拉斯变换为 1/(s a)。
正弦函数sin(ωt) 的拉普拉斯变换为ω/(s^2 +ω^2)。
余弦函数cos(ωt) 的拉普拉斯变换为 s/(s^2 +ω^2)。
121 更多复杂函数的拉普拉斯变换可以通过基本函数的组合和性质推导得出。
13 拉普拉斯变换的性质包括线性性质、微分性质、积分性质、位移性质、卷积性质等。
131 线性性质:若 Lf1(t) = F1(s),Lf2(t) = F2(s),则对于任意常数a,b,有 Laf1(t) + bf2(t) = aF1(s) + bF2(s)。
132 微分性质:若 Lf(t) = F(s),则 Lf'(t) = sF(s) f(0)。
133 积分性质:若 Lf(t) = F(s),且 f(t) 在 t = 0 处连续,则L∫f(t)dt = F(s)/s + f^(-1)(0)/s。
134 位移性质:若 Lf(t) = F(s),则 Le^at f(t) = F(s a)。
135 卷积性质:若 Lf1(t) = F1(s),Lf2(t) = F2(s),则 Lf1(t) f2(t) =F1(s)F2(s)。
(完整版)拉普拉斯变换及其逆变换表
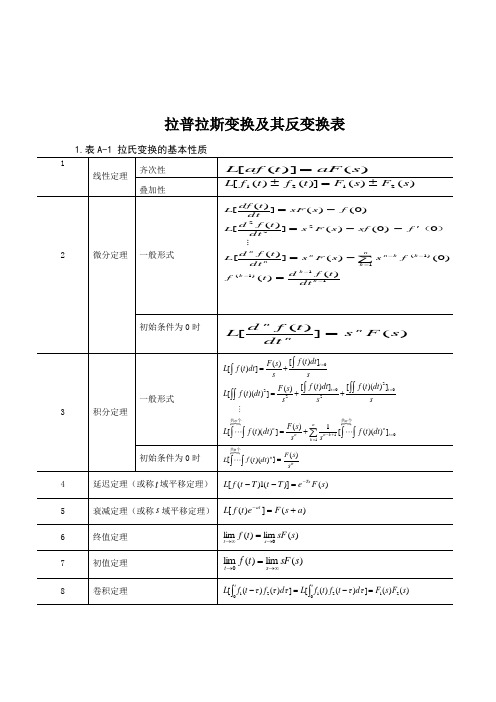
拉普拉斯变换及其反变换表3. 用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开,然后逐项查表进行反变换。
设)(s F 是s 的有理真分式11n 1n nn11m 1m mmas a s a s a b s b s b s b )s (A )s (B )s (F ++++++++==---- (m n >)式中系数n1n 1a ,a ,...,a ,a-,m1m 1b ,b ,b ,b - 都是实常数;n m ,是正整数。
按代数定理可将)(s F 展开为部分分式。
分以下两种情况讨论。
① 0)(=s A 无重根这时,F(s)可展开为n 个简单的部分分式之和的形式。
∑=-=-++-++-+-=n1i iinnii2211ss cs s c s s c s s c s s c )s (F 式中,Sn 2S 1S ,,, 是特征方程A(s)=0的根。
i c 为待定常数,称为F(s)在i s 处的留数,可按下式计算: )s (F )s s (lim c is s i-=→或is s i)s (A )s (B c='=式中,)(s A '为)(s A 对s 的一阶导数。
根据拉氏变换的性质,从式(F-1)可求得原函数[]t s n 1i i n 1i i i 11i e c s s cL )s (F L )t (f -==--∑∑=⎥⎦⎤⎢⎣⎡-==② 0)(=s A 有重根设0)(=s A 有r 重根1s ,F(s)可写为())s s ()s s ()s s ()s (B s F n1r r 1---=+=nnii1r 1r 111r 11r r 1rss cs s c s s c )s s (c )s s (c )s s (c -++-++-+-++-+-++-- 式中,1s 为F(s)的r 重根,1+r s ,…, n s 为F(s)的n-r 个单根;其中,1+r c ,…, n c 仍按式(F-2)或(F-3)计算,r c ,1-r c ,…, 1c 则按下式计算:)s (F )s s (lim c r1s s r-=→)]s (F )s s ([dsdlim c -=)s (F )s s (dsd lim !j 1c -=)s (F )s s (dsdlim )!1r (1c --=原函数)(t f 为 [])()(1s F L t f -=⎥⎦⎤⎢⎣⎡-++-++-+-++-+-=s s cs s c s s c )s s (c )s s (c )s s (c L e c e c t c t )!2r (c t )!1r (c ∑+⎥⎦⎤⎢⎣⎡+++-+-= (F-6)。
拉普拉斯变换及Z变换表

式中, s1 为 F(s)的 r 重根, sr 1 ,…, s n 为 F(s)的 n-r 个单根; 其中, c r 1 ,…, cn 仍按式(F-2)或(F-3)计算, cr , cr 1 ,…, c1 则按下式计算:
c r lim ( s s1 ) r F ( s )
s s1
c r 1 lim
z 2 ze aT cos T z 2 ze aT cos T e 2 aT
2
sa (s a) 2 2
1 s (1 / T ) ln a
z za
3. 用查表法进行拉氏反变换 用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开,然后逐项查表进行 反变换。设 F ( s ) 是 s 的有理真分式
1 s2
1 s3
t
t2 2
Tz ( z 1) 2
T 2 z ( z 1) 2( z 1)3
lim (1) n n z ( ) n a 0 n! a z e aT
z z e aT
1 s n 1
1 sa
tn n!
e at te
at
1 (s a) 2
a s(s a) ba ( s a )( s b)
F (s)
B ( s ) bm s m bm 1 s m 1 b1 s b0 A( s ) a n s n a n 1 s n 1 中系数 a 0 , a1 ,..., a n 1 , a n , b0 , b1 , bm 1 , bm 都是实常数; m , n 是正整数。按代数定理可 将 F ( s ) 展开为部分分式。分以下两种情况讨论。 ①
表a2常用函数的拉氏变换和z变换表拉氏变换es时间函数et42112用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开然后逐项查表进行反变换
拉普拉斯变换表

拉普拉斯变换的基本性质
由于拉普拉斯变换是傅里叶变换在复频域(即s域)中的推广,因而也具有与傅里叶变换的性质相应的一些性质。
这些性质揭示了信号的时域特性与复频域特性之间的关系,利用这些性质可使求取拉普拉斯正、反变换来得简便。
关于拉普拉斯变换的基本性质在表5-1中列出。
对于这些性质,由于读者在工程数学课中已学习过了,所以不再进行证明,读者可复习有关的工程数学书籍。
表5-1 拉普拉斯变换的基本性质
利用式(5-5)和拉普拉斯变换的性质,可以求出和导出一些常用时间常数的拉
普拉斯变换式,如表5-2中所列。
利用此表可以方便地查出待求的像函数
或原函数
表5-2 拉普拉斯变换表
()()t U t f ()s F ()t f。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
419
附录A 拉普拉斯变换及反变换
1.表A-1 拉氏变换的基本性质 1
线性定理
齐次性 [()]()L af t aF s =
叠加性
1212[()()]()()L f t f t F s F s ±=±
2
微分定理
一般形式
=
-=][ '- -=-=----=-∑1
1
)1()
1(1
22
2)
()()
0()()(0)0()(])([)0()(])
([
k k k k n
k k n n n
n dt t f d t f f s s F s dt t f d L f sf s F s dt t f d L f s sF dt t df L )( 初始条件为0时
)(])([s F s dt
t f d L n n
n =
3
积分定理
一般形式
∑⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰==+-===+=+
+=+=
n
k t n n k n n n
n t t t dt t f s s s F dt t f L s
dt t f s dt t f s s F dt t f L s
dt t f s s F dt t f L 10
102
2022
]))(([1)(])()([]))(([])([)(]))(([])([)(])([个
共个
共
初始条件为0时
n n n s
s F dt t f L )
(]))(([=⎰⎰个
共
4 延迟定理(或称t 域平移定理) )()](1)([s F e T t T t f L Ts -=--
5 衰减定理(或称s 域平移定理) )(])([a s F e t f L at +=-
6 终值定理 )(lim )(lim 0
s sF t f s t →∞
→=
7 初值定理
)(lim )(lim 0
s sF t f s t ∞
→→=
420
8 卷积定理
1212120
[()()][()()]()()t t
L f t f d L f t f t d F s F s τττττ-=-=⎰⎰
2.表A-2 常用函数的拉氏变换和z 变换表 序
号 拉氏变换E(s)
时间函数e(t) Z 变换E(z)
1 1
δ(t)
1 2 Ts
e --11
∑∞
=-=0
)()(n T nT t t δδ
1
-z z 3 s
1 )(1t
1
-z z 4 21s
t
2
)1(-z Tz
5 3
1s 2
2t
3
2
)1(2)1(-+z z z T
6 11+n s
!n t n
)(!)1(lim 0aT n n n a e
z z a n -→-∂∂- 7 a
s +1 at e -
aT
e z z
-- 8 2
)(1a s +
at
te
- 2
)(aT aT e z Tze ---
9 )
(a s s a
+ at
e
--1
)
)(1()1(aT aT e z z z e ----- 10 )
)((b s a s a
b ++-
bt at e e ---
bT
aT e z z
e z z ----- 11 2
2ωω
+s t ωsin
2
sin 2cos 1
z T
z z T ωω-+ 12 2
2ω+s s t ωcos
1
cos 2)cos (2
+--T z z T z z ωω 13 2
2
)(ω
ω
++a s t e at ωsin - aT
aT aT e T ze z T
ze 22cos 2sin ---+-ωω 14
2
2)(ω+++a s a s
t e
at
ωcos -
aT
aT aT e T ze z T ze z 222cos 2cos ---+--ωω
421
15
a
T s ln )/1(1- T t a /
a
z z - 3. 用查表法进行拉氏反变换
用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开,然后逐项查表进行反变换。
设)(s F 是s 的有理真分式
11
10
111)()()(a s a s a s a b s b s b s b s A s B s F n n n n m m m m ++++++++==---- (m n >) 式中系数n n a a a a ,,...,,110-,m m b b b b ,,,110- 都是实常数;n m ,是正整数。
按代数定理可将
)(s F 展开为部分分式。
分以下两种情况讨论。
① 0)
(=s A 无重根
这时,F(s)可展开为n 个简单的部分分式之和的形式。
∑=-=-++-++-+-=n
i i
i
n n i i s s c s s c s s c s s c s s c s F 122
11)( (F-1)
式中,n s s s ,,,21 是特征方程A(s)=0的根。
i c 为待定常数,称为F(s)在i s 处的留数,可按下式计算: )()(lim s F s s c i s s i i
-=→ (F-2)
或
i
s
s i s A s B c ='=
)()
( (F-3)
式中,
)(s A '为)(s A 对s 的一阶导数。
根据拉氏变换的性质,从式(F-1)可求得原函数
[]⎥⎦⎤⎢⎣⎡-==∑=--n i i i s s c L s F L t f 11
1
)()(=t
s n i i i
e c -=∑1
(F-4)
② 0)
(=s A 有重根
设0)
(=s A 有r 重根1s ,F(s)可写为
())
()()()
(11n r r
s s s s s s s B s F ---=
+
422
=
n
n i i r r r r r r s s c s s c s s c s s c s s c s s c -+
+-++-+-++-+-++-- 11
111111)()()(
式中,1s 为F(s)的r 重根,1+r s ,…, n s 为F(s)的n-r 个单根;
其中,1+r c ,…, n c 仍按式(F-2)或(F-3)计算,r c ,1-r c ,…, 1c 则按下式计算:
)()(lim 11
s F s s c r s s r -=→
)]()([lim
111
s F s s ds
d
c r s s r -=→-
)()(lim !11)()
(1s F s s ds
d j c r j j s s j
r -=→- (F-5)
)()(lim )!1(11)1()
1(11s F s s ds
d r c r r r s s --=--→
原函数)(t f 为
[])()(1s F L t f -=
⎥⎦⎤⎢⎣⎡-++-++-+-++-+-=++---n n i i r r r r r r s s c s s c s s c s s c s s c s s c L 11
111
1111)()()
( t s n
r i i t s r r r r i
e c e c t c t r c t r c ∑+=---+⎥⎦
⎤⎢⎣⎡+++-+-=112211
1
)!2()!1( (F-6)。
