四年级学而思_1--12讲
小学数学奥数辅导讲座(四年级)

- 1 -小学四年级奥数辅导讲座第1讲速算与巧算(一)第2讲速算与巧算(二)第3讲高斯求和第4讲 4,8,9整除的数的特征第5讲弃九法第6讲数的整除性(二)第7讲找规律(一)第8讲找规律(二)第9讲数字谜(一)第10讲数字谜(二)第11讲归一问题与归总问题第12讲年龄问题第13讲鸡兔同笼问题与假设法第14讲盈亏问题与比较法(一)第15讲盈亏问题与比较法(二)第16讲数阵图(一)第17讲数阵图(二)第18讲数阵图(三)第19将乘法原理第20讲加法原理(一)第21讲加法原理(二)第22讲还原问题(一)第23讲还原问题(二)第24讲页码问题第25讲智取火柴第26讲逻辑问题(一)第27讲逻辑问题(二)第28讲最不利原则第29讲抽屉原理(一)第30讲抽屉原理(二)第1讲速算与巧算(一)计算是数学的基础,小学生要学好数学,必须具有过硬的计算本领。
准确、快速的计算能力既是一种技巧,也是一种思维训练,既能提高计算效率、节省计算时间,更可以锻炼记忆力,提高分析、判断能力,促进思维和智力的发展。
我们在三年级已经讲过一些四则运算的速算与巧算的方法,本讲和下一讲主要介绍加法的基准数法和乘法的补同与同补速算法。
例1 四年级一班第一小组有10名同学,某次数学测验的成绩(分数)如下:86,78,77,83,91,74,92,69,84,75。
求这10名同学的总分。
分析与解:通常的做法是将这10个数直接相加,但这些数杂乱无章,直接相加既繁且易错。
观察这些数不难发现,这些数虽然大小不等,但相差不大。
我们可以选择一个适当的数作“基准”,比如以“80”作基准,这10个数与80的差如下:6,-2,-3,3,11,-6,12,-11,4,-5,其中“-”号表示这个数比80小。
于是得到总和=80×10+(6-2-3+3+11-=800+9=809。
实际计算时只需口算,将这些数与80的差逐一累加。
为了清楚起见,将这一过程表示如下:通过口算,得到差数累加为9,再加上80×10,就可口算出结果为809。
打印学而思小学奥数36个精彩讲座总汇全-90页文档资料

第1讲计算综合(一)繁分数的运算,涉及分数与小数的定义新运算问题,综合性较强的计算问题.1.繁分数的运算必须注意多级分数的处理,如下所示:甚至可以简单地说:“先算短分数线的,后算长分数线的”.找到最长的分数线,将其上视为分子,其下视为分母.2.一般情况下进行分数的乘、除运算使用真分数或假分数,而不使用带分数.所以需将带分数化为假分数.3.某些时候将分数线视为除号,可使繁分数的运算更加直观.4.对于定义新运算,我们只需按题中的定义进行运算即可.5.本讲要求大家对分数运算有很好的掌握,可参阅《思维导引详解》五年级[第1讲循环小数与分数].1.计算:71147 182621358 1333416⨯+⨯-÷【分析与解】原式=712372317 461224 1488128 131233+⨯=⨯=-2.计算:【分析与解】注意,作为被除数的这个繁分数的分子、分母均含有5199.于是,我们想到改变运算顺序,如果分子与分母在5199后的两个数字的运算结果一致,那么作为被除数的这个繁分数的值为1;如果不一致,也不会增加我们的计算量.所以我们决定改变作为被除数的繁分数的运算顺序.而作为除数的繁分数,我们注意两个加数的分母相似,于是统一通分为1995×0.5.具体过程如下:原式=5919(3 5.22)19930.41.6 910() 52719950.51995 19(6 5.22)950+-⨯÷+⨯-+3.计算:1111111987 -+-【分析与解】原式=11198711986-+=198613973-=198739734.计算:已知=181111+12+1x+4=,则x等于多少?【分析与解】方法一:1118x 68114x 112x 7111+11148x 62+214x 1x+4+====+++++++交叉相乘有88x+66=96x+56,x=1.25. 方法二:有11131118821x 4+==+++,所以18222133x 4+==++;所以13x 42+=,那么x =1.25. 5.求944,43,443,...,44...43个这10个数的和.【分析与解】方法一:方法二:先计算这10个数的个位数字和为39+4=31⨯;再计算这10个数的十位数字和为4×9=36,加上个位的进位的3,为36339+=; 再计算这10个数的百位数字和为4×8=32,加上十位的进位的3,为32335+=; 再计算这10个数的千位数字和为4×7=28,加上百位的进位的3,为28331+=; 再计算这10个数的万位数字和为4×6=24,加上千位的进位的3,为24327+=; 再计算这10个数的十万位数字和为4×5=20,加上万位的进位的2,为20222+=; 再计算这10个数的百万位数字和为4×4=16,加上十万位的进位的2,为16218+=; 再计算这10个数的千万位数字和为4×3=12,加上百万位的进位的1,为12113+=; 再计算这10个数的亿位数字和为4×2=8,加上千万位的进位的1,为819+=;最后计算这10个数的十亿位数字和为4×1=4,加上亿位上没有进位,即为4.所以,这10个数的和为4938271591.6.如图1-1,每一线段的端点上两数之和算作线段的长度,那么图中6条线段的长度之和是多少? 【分析与解】 因为每个端点均有三条线段通过,所以这6条线段的长度之和为:7.我们规定,符号“○”表示选择两数中较大数的运算,例如:3.5○2.9=2.9○3.5=3.5.符号“△”表示选择两数中较小数的运算,例如:3.5△2.9=2.9△3.5=2.9.请计算:23155(0.625)(0.4)333841235(0.3)( 2.25)3104⨯+ 【分析与解】原式8.规定(3)=2×3×4,(4)=3×4×5,(5)=4×5×6,(10)=9×10×11,….如果111(16)(17)(17)-=⨯,那么方框内应填的数是多少?【分析与解】111(17)()1(16)(17)(17)(16)=-÷=-=161718111516175⨯⨯-=⨯⨯.9.从和式11111124681012+++++中必须去掉哪两个分数,才能使得余下的分数之和等于1?【分析与解】因为1116124+=,所以12,14,16,112的和为l,因此应去掉18与110.10.如图1-2排列在一个圆圈上10个数按顺时针次序可以组成许多个整数部分是一位的循环小数,例如1.892915929.那么在所有这种数中。
学而思2011年暑假新四年级超常123班难题汇总
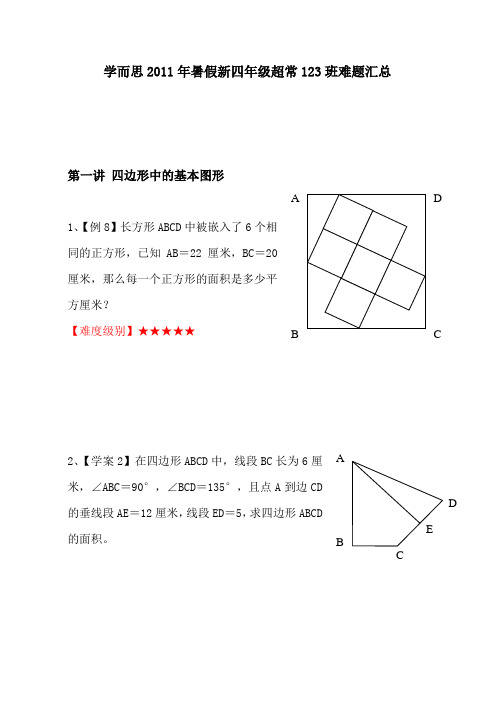
学而思2011年暑假新四年级超常123班难题汇总第一讲四边形中的基本图形1、【例8】长方形ABCD中被嵌入了6个相同的正方形,已知AB=22厘米,BC=20厘米,那么每一个正方形的面积是多少平方厘米?【难度级别】★★★★★2、【学案2】在四边形ABCD中,线段BC长为6厘米,∠ABC=90°,∠BCD=135°,且点A到边CD 的垂线段AE=12厘米,线段ED=5,求四边形ABCD 的面积。
D C3、【学案3】等腰梯形ABCD 中,交于O 点的两条对角线互相垂直,三角形ECB 是直角三角形,OC 比AO长20厘米。
已知三角形ADE 的面积是250平方厘米,则梯形ABCD 的面积是多少平方厘米?4、【学案4】一块边长为180厘米的正方形铁片,四角各被截去一个边长为40厘米的小正方形铁片,现在要从剩下的铁片中剪出一块完整的正方形铁片来,剪出的正方形面积最大为多少平方厘米?5、【作业5】请仅用刻度尺画一个面积是5平方厘米的正方形,保留必要的作图痕迹。
O B C D EA第二讲乘法原理6、【例7】1到1999的自然数中,有多少个与5678相加时,至少发生一次进位?7、【例8】有______个四位数满足下列条件:它的各位数字都是奇数,它的各位数字互不相同,它的每个数字都能整除它本身。
8、【学案1】计算机上编程序打印出前10000个正整数:1,2,3,……,10000时,不幸打印机有毛病,每次打印数字3时,它都打印出x,问其中被错误打印的共有多少个数?9、【学案4】有9张同样大小的圆形纸片,其中标有数码“1”的有1张,标有数码“2”的有2张,标有数码“3”的有3张,标有数码“4”的有3张,把这9张圆形纸片如图所示放置在一起,但标有相同数码的纸片不许挨在一起。
(1)如果M处放标有数码“3”的纸片,一共有多少种不同的放置方法?(2)如果M处放标有数码“2”的纸片,一共有多少种不同的放置方法?10、【越玩越聪明】在例6的后面。
学而思-五年制10级思维训练体系(7级上)四年级解题能力超常班-第1讲教程文件

学而思-五年制10级思维训练体系(7级上)四年级解题能力超常班-第1讲简单的抽屉原理1.理解抽屉原理的基本含义。
2.能运用抽屉原理对一些简单问题进行说明。
3.能使用最不利原则进行分析。
知识要点最不利原则所谓“最不利原则”是指完成某一项工作先从最不利的情况下考虑,然后研究任意情况下可能的结果。
由此得到充分可靠的结论。
抽屉原理如果把n+1个苹果任意放入n个抽屉,那么必定有一个抽屉里至少有两个苹果。
抽屉原理1:如果把多于n件物品任意放到n个抽屉中,那么必有1个抽屉至少有2件物品。
抽屉原理2:如果把多于m×n件物品任意放到n个抽屉中,那么必有1个抽屉至少有m +1件物品。
例1围棋盒中装有黑子和白子各180粒,一次最少取出多少粒才能保证至少有20粒棋子颜色相同?(2007年第五届“走进美妙的数学花园”中国青少年数学论坛趣味数学解题能力展示大赛四年级初赛第12题)袋中有外形完全一样的红、黄、蓝三种颜色的小球各15个,每个小朋友只能从中摸出2个小球。
至少有_____个小朋友摸球,才能保证一定有两个人模的球的颜色一样。
口袋里有蓝色球6个,红色球2个,黄色球19个,至少要取多少个小球才能保证至少有5个小球同色?体育用品的仓库里有许多足球、排球和篮球,有66个同学来仓库拿球,要求每个人至少拿一个,最多拿两个球,问至少有多少名同学所拿的球的种类是完全一样的?一个布袋里有大小相同颜色不同的一些木球,其中红色的有10个,黄色的有8个,蓝色的有3个,绿色的有1个。
请问:⑴一次至少要取出多少个球,才能保证取出的球至少有三种颜色?⑵一次至少要取出多少个球,才能保证其中必有红球和黄球?例6用红、蓝两种颜色将一个2×5方格图中的小方格随意涂色(见下图),每个小方格涂一种颜色。
是否存在两列,它们的小方格中涂的颜色完全相同?测试题1.要想保证至少有5个人的属相相同,但不能保证有6个人的属相相同,那么总人数应该在什么范围内?2.今有乒乓球盒22个,每个盒子内最多可放六个球,试说明这些盒子中,至少有四个盒子里所放球数相同。
学而思讲义四年级第一讲(整数与数列)

2
四年级秋季班(七级下) 1.1
2010 年四年级秋季班 第一讲 整数与数列 程雪
第 n 项=首项+公差×(n-1)
2、项数公式:什么时候用?——知道首项、末项及公差,求项数
项数=(末项-首项)÷公差+1
3、求和公式(高斯公式) :什么时候用?——任何一个等差数列求和
和=(首项+末项)×项数÷2
辅助记忆:装皮鞋 4、中项公式:什么时候用?——对于容易找到中项的等差数列求和
和=中项×项数
注意:高斯公式与中项公式的联系 高斯公式:和=(首项+末项)×项数÷2 =(首项+末项)÷2 ×项数
中项(也即平均数)
二、常用公式 2 1、从 1 开始连续奇数求和=项数 2 即:1 + 3 + 5 + 7 + … +(2n-1)= n 图示: 1 3 5 7 9
2、金字塔数列=中项 2 即:1 + 2 + 3 + … +(n-1)+ n +(n-1)+ … + 3 + 2 + 1 = n 图示:
三、平方差公式:a - b =(a+b)×(a-b) ……两数平方差=两数和×两数差 几何证明:
2Hale Waihona Puke 2b a 2 2 a - b 表示的是图中大正方形减去黑色小正方形后的空白部分的面积,沿虚线将空白部分减 成两部分再拼接起来,即为一个长方形的面积。该长方形长为 a+b,宽为 a-b,面积为(a+b) ×(a-b) ,得证。 特例: 两数相差为 1,其平方差就是两数和 2 2 37 -36 =(37+36)×(37-36)=37+36 四、平方差公式拓展: (逆向思维)既然平方差=和×差,那么两个数相乘能否转化为平方差的形式呢? 1、若两数的奇偶性相同,则这两数的乘积可化为平方差的形式。 如:41×39 41=a+b,39=a-b ,利用和差公式即可算出 a=40,b=1(a 即是 41 与 39 的平均数) 2 2 所以 41×39=(40+1)×(40-1)=40 -1 2、进而,若两数相差不大,且两数和为整十整百时,乘积改写为平方差可简化计算 2 2 如:68×72=(70-2)×(70+2)=70 -2 =4900-4=4896 五、自然数列的平方和公式 2 2 2 2 1 +2 +3 +…+n =n(n+1) (2n+1)÷6 图示证明: 1 2 3 … n n 3 2 3 … … n
四年级数学第12讲课后习题

第12讲差倍问题
1.大胖吃的包子的数量比小胖的倍还多个,已知大胖比小胖多吃了个,那么小胖吃了
________个。
A. 10
B. 45
C. 6
2.学而思网校竞赛班比启航班多名学员,而且竞赛班的人数是启航班人数的倍,那么启航班有________名学员。
A. 300
B. 100
C. 50
3.小鹿为找工作准备了中、英文两份简历。
中文简历的字数比英文简历单词数的倍多个,而且中文简历字数比英文简历单词数多。
那么,中文简历的字数是________个。
A. 100
B. 320
C. 200
4.一个车间男工人比女工人多人,其中男工人数是女工人数的倍,男工人有________人,女工人有________人。
A. 120 20
B. 20 120
5.李爷爷家养的鸭比鹅多只,鸭的只数是鹅的倍,李爷爷家养的鸭有________只,鹅有
________只。
A. 24 8
B. 12 36
C. 36 12
【答案】1. A 2. B 3. B 4. A 5. C
第 1 页,共 1 页。
完整小学新编学而思合集完整版

完整小学新编学而思合集HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】完整小学学而思合集高清无密(2013-06-02 01:18:14)转载▼分类:小学标签:教育二年级奥数和阅读写作:【2801】2011一升二年级数学竞赛班-8讲【3211】2011秋季二年级数学竞赛班-12讲【4716】2012春季二年级数学竞赛班-14讲【3746】2012寒假二年级数学竞赛班-8讲【2802】2011暑期二升三数学竞赛班-12讲【6031】糖果星球探秘:二升三年级“畅享语文”成长计划暑期班12讲【3747】精灵旅行团:2012年寒假二年级说话写话训练营10讲6531:小柿子星球探秘:二年级“畅享语文”成长计划秋季班(6级)共11讲三年级奥数和阅读写作:【3212】2011秋季三年级奥数竞赛班-16讲【3779】2012寒假三年级奥数竞赛班-10讲【4860】2012春季三年级奥数竞赛班-16讲【4861】2012春季三年级奥数零基础班-10讲【6039】三升四奥数暑期班14讲4863人教春季三年级数学同步8讲6055人教版三年级上册数学满分班16讲7429北师版三年级下册数学满分班(教材精讲+奥数知识拓展)14讲4209+2012年寒假五年制小学三年级数学超常班12讲【6032】杮子星球探秘,三升四年级畅想语文成长计划暑期班12讲【3230】精灵旅行团:2011秋季三年级阅读写作训练营12讲【3783】精灵旅行团:2012寒假三年级阅读写作训练营8讲【4865】精灵旅行团:2012春季三年级阅读写作训练营12讲四年级奥数及阅读写作:【2799】2011暑期三升四数学强化班共14讲[6040]2012四升五年级奥数暑期班18讲【3297】2011秋季四年级上册人教数学课内同步班8讲【4772】人教四年级下册数学同步8讲【3208】2011秋季四年级数学强化班,18讲【3947】2012寒假奥数强化班10讲【6057】人教版四年级上册数学满分班14讲【4770/4771】2011春季四年级数学竞赛班18讲7088第13届中环杯四年级初赛冲刺VIP班12讲3948+2012寒假四年级奥数竞赛班10讲1891:四年级奥数必考知识点系统复习全能班(上)9讲6063北师版四年级上册数学满分班(教材精讲+奥数知识拓展)17讲7431北师版四年级下册数学满分班(教材精讲+奥数知识拓展)18讲【6033】6033乐学星球探秘:四升五年级畅想语文成长计划暑期班11讲【3231】精灵旅行团:2011秋季四年级阅读写作训练营12讲【3945】精灵旅行团:2012寒假四年级阅读写作训练营10讲【4775】精灵旅行团:2012春季四年级阅读写作训练营10讲五年级奥数及阅读写作:【3209】2011秋季五年级数学强化班共20讲,【4817】2011原春季五年级奥数强化班20讲【3768】2011原寒假五年级奥数强化班共16讲【2921】2011原暑假五年级奥数强化班共18讲2925崔兆玉2011五年级奥数年卡74讲7421人教五年级下册数学满分班15讲[6059]人教版五年级上册数学满分班16讲3299+2011秋季五年级数学课内同步班(人教版)8讲4820+2012春季五年级数学课内同步班(人教版)8讲3769+2012寒假五年级数学零基础班14讲6071苏教版五年级上册数学满分班14讲(教材精讲+奥数知识拓展)7427苏教版五年级下册数学满分班(教材精讲+奥数知识拓展)14讲6065北师版五年级上册数学满分班14讲7433北师版五年级下册数学满分班13讲【6102】小升初总复习:2012五升六年级语文暑期班12讲【3232】精灵旅行团:2011秋季五年级阅读写作训练营10讲【3773】精灵旅行团:2012寒假五年级阅读写作训练营10讲【4822】精灵旅行团:2012春季五年级阅读写作训练营10讲【3058】小学语文知识大全—小学阅读技巧魔法班-4讲【2666】小学语文必学写作技巧之非常作文训练营-10讲3618小学语文知识大全——小学语文基础知识精讲(上)9讲3721:小学语文知识大全——小学语文基础知识精讲(下)8讲2515:春季五年级语文阅读课外拓展班6讲2516:春季小学语文总复习小升初冲刺班8讲3809:五年制小学五年级语文阅读写作综合提高共10讲六年级奥数及阅读写作:【2819】2011年暑期五升六数学课内预习班人教8讲上册【4851】2012春季六年级数学课内同步班人教12讲【6463】人教版六年级上册数学满分班(教材精讲)14讲【6464】人教版六年级上册数学满分班(教材精讲)18讲4【6535】2012六年级培优数学秋季班(竞赛班)22讲2974:六升初一有理数四则运算必备3讲2975-六升初一不等式(组)解法攻略3讲2976-六升初一几何证明与推理初步3讲2977-六升初一二元一次方程组全透析3讲7556北师版六年级下册数学满分班(教材精讲+奥数知识拓展)17讲4547+12华杯赛初赛六年级VIP全能班8讲8375+2013高年级华杯复赛考前冲刺班(五、六年级)10讲【3065】小学语文经典课程:精讲心理描写2讲【3371】小学语文经典课程:文章立意有深度-1讲【3372】小学语文经典课程:分析文段作用,领会句子含义1讲【3409】小学语文经典课程:叙事文阅读2讲【3629】小学语文经典课程:运用对比手法塑造人物形象1讲3057:小学语文知识大全—古诗文奥秘赏析-1讲4992:小学语文知识大全—8课时突破小学记叙文阅读考点5453:小学语文知识大全—8课时文言文轻松入门7194:小学语文知识大全—小学分类作文全攻略--9讲3059:小学语文知识大全—小学写作技巧宝典班--5讲6727:柿子星球探秘:四年级“畅享语文”成长计划秋季班12课时(14级)7、5717庄海燕考试速记系列:如何快速记忆小学语文知识4讲2、7336百变精灵阅读满分班(记叙文+说明文+文言文)共20讲六年级及小升初:【2912】2011年六-小升初年级奥数年卡{竞赛班}2806+3295+3921+4847.共70讲【2914】(3296+4857+3925+2808)2011六年级六年级语文年卡(竞赛班)-42讲[7563]小升初总复习:2013六年级语文下半学年卡24讲[2917-75] (2851+3229+3927+4853) 2011六年级小升初英语年卡6520+1+英语“坑爹”题目大汇总——小升初190多讲六年级奥数七大专题3340:组合专题3393:几何专题3656/2966:数论专题4136:行程专题八、玩转小学英语语法共30课时:【3532】六大时态6讲【3679】五大句型5讲【3822】词法大全12讲【3695】被动语态2讲【4456】三大从句5讲九、亲子英语口语【5450】和孩子一起学口语(亲子英语课程)共20讲【3914】学而思乐学口语一级7讲【3748】学而思乐学口语二级8讲【3784】学而思乐学口语三级8讲【3937】学而思乐学口语四级9讲【3772】学而思乐学口语五级10讲【3926】学而思乐学口语六级10讲[6572 ](1-10)乐学英语预备级:2012秋季听说6747 (1-17)乐学英语五级:2012秋季听说读[6746] (1-15)乐学英语四级:2012秋季听说读写6745 (1-15)乐学英语三级2012秋季听说读写训练营(三、四年级)6538 (1-15)乐学英语二级:2012秋季听说读写训练6573 (1-15)乐学英语一级:2012秋季听说读4523剑桥少儿英语预备级(上)1-7讲5325剑桥少儿英语预备级(上)8-15讲7027剑桥少儿英语预备级(下)1-8讲7082剑桥少儿英语预备级(下)9-15讲十、3225/4998:自然拼音一级二级三级和10次国际音标和自然拼音全掌握十、剑桥少儿英语一40讲、二级40讲、三级40讲新概念第一册整套编号:5501+5692+4282+3228共58讲【2183】新概念一册同步强化班 15课时【2523】新概念英语一册同步强化15讲新概念第二册整套:80讲新概念英语二册L1-L80 2185+2524+2814新概念第三册:40讲十二、单词记忆:【7044】过目不忘背单词--小学核心词汇1000词上-11讲【7103】过目不忘背单词-小学核心词汇1000词(中)11讲十二、英语阅读写作核心词:5442/3099编号共10课时一年级奥数全部国学经典各40课时6078共欠11-40讲千字文:5909欠18-40讲弟子规:6222孟子40讲:6221欠21-40讲论语:6220欠12-40讲三字经:5172--小魔方大智慧:世界冠军教你玩转异形魔方4682--小魔方大智慧:世界冠军教你玩转魔方(三阶魔方还原基础必备)5532 小魔方大智慧:世界冠军庄海燕教你玩....5171--世界记忆锦标赛经典项目:超速记忆扑克牌5714---庄海燕考试速记系列:如何快速记忆英语单词5718_庄海燕考试速记系列:如何快速记忆初....。
学而思(四年级)目30讲全

合用标准准数,各数与基准数的差的和叫做累学而思(四年级)若是你需要更多的各种奥数计差。
由例 1 获取:教材,课程同步教材,同步总和数 =基准数×加数的个数+累计第 1 讲速算与巧算(一)练习题,培优练习题,期中差,第 2 讲速算与巧算(二)期末单元试卷,平均数 =基准数 +累计差÷加数的个第 3讲高斯求和各种致富管理文学作品书籍数。
第4讲4, 8, 9 整除的数的特点维修书籍大人物传记在使用基准数法时,应采用与各第 5讲弃九法都是电子档。
能够联系我数的差较小的数作为基准数,这样才第 6 讲数的整除性(二)468453607简单计算累计差。
同时考虑到基准数第 7 讲找规律(一)微信电话与加数个数的乘法能够方便地计算出第 8 讲找规律(二)来,所以基准数应尽量采用整十、整第 9 讲数字谜(一)百的数。
第 10 讲数字谜(二)例 2 某农场有 10 块麦田,每块的产量第 11 讲归一问题与归总问题以下(单位:千克):第 12 讲年龄问题462,480,443,420,473,429 ,第 13 讲鸡兔同笼问题与假设法例 1 四年级一班第一小组有10名同468, 439,475 , 461。
求平均每块麦第 14 讲盈亏问题与比较法(一)学,某次数学测试的成绩(分数)如田的产量。
第 15 讲盈亏问题与比较法(二)下:解:选基准数为 450,则第 16 讲数阵图(一)86, 78, 77, 83, 91, 74, 92,累计差 =12+ 30-7- 30+23- 21第 17 讲数阵图(二)69,84,75。
+18-11+25+11第 18 讲数阵图(三)求这 10 名同学的总分。
=50,第 19 将乘法原理解析与解:平常的做法是将这10 个数平均每块产量 =450 + 50÷ 10 =第 20 讲加法原理(一)直接相加,但这些数纷乱无章,直接455(千克)。
第 21 讲加法原理(二)相加既繁且易错。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四年级第一讲:乘法原理基础班1、有五顶不同的帽子,两件不同的上衣,三条不同的裤子。
从中取出一顶帽子、一件上衣、一条裤子配成一套装束。
问:有多少种不同的装束?2、四角号码字典,用4个数码表示一个汉字。
小王自编一个"密码本",用3个数码(可取重复数字)表示一个汉字,例如,用"011"代表汉字"车"。
问:小王的"密码本"上最多能表示多少个不同的汉字?3、"IMO"是国际数学奥林匹克的缩写,把这3个字母写成三种不同颜色。
现在有五种不同颜色的笔,按上述要求能写出多少种不同颜色搭配的"IMO"?4、在右图的方格纸中放两枚棋子,要求两枚棋子不在同一行也不在同一列。
问:共有多少种不同的放法?5、要从四年级六个班中评选出学习和体育先进集体各一个(不能同时评一个班),共有多少种不同的评选结果?6、甲组有6人,乙组有8人,丙组有9人。
从三个组中各选一人参加会议,共有多少种不同选法?7、如下图,在三条平行线上分别有一个点,四个点,三个点(且不在同一条直线上的三个点不共线).在每条直线上各取一个点,可以画出一个三角形.问:一共可以画出多少个这样的三角形?8、在自然数中,用两位数做被减数,用一位数做减数.共可以组成多少个不同的减法算式?9、一个篮球队,五名队员A、B、C、D、E,由于某种原因,C不能做中锋,而其余四人可以分配到五个位置的任何一个上.问:共有多少种不同的站位方法?10、由数字1、2、3、4、5、6、7、8可组成多少个①三位数?②三位偶数?③没有重复数字的三位偶数?④百位为8的没有重复数字的三位数?⑤百位为8的没有重复数字的三位偶数?11、某市的电话号码是六位数的,首位不能是0,其余各位数上可以是0~9中的任何一个,并且不同位上的数字可以重复.那么,这个城市最多可容纳多少部电话机?解答1.30种。
2.1000个。
3.60种。
4.400种。
提示:第一枚棋子有25种放法,去掉这枚棋子所在的行和列,还有16个空格,所以第二枚棋子有16种放法。
5.30种。
6.432种。
7.1×4×3=12(个).8.90×9=810(个).9.4×4×3×2×1=96(种).10.①8×8×8=512(个);②4×8×8=256(个);③4×7×6=168(个);④1×7×6=42(个);⑤1×3×6=18(个).11.9×10×10×10×10×10=900000(部).提高班1.用四种颜色给右图的五块区域染色,要求每块区域染一种颜色,相邻的区域染不同的颜色。
问:共有多少种不同的染色方法?2.由数字1、2、3、4、5、6、7、8可组成多少个①三位数?②三位偶数?③没有重复数字的三位偶数?④百位为8的没有重复数字的三位数?⑤百位为8的没有重复数字的三位偶数?答案1. 48种。
2.①8×8×8=512(个);②4×8×8=256(个);③4×7×6=168(个);④1×7×6=42(个);⑤1×3×6=18(个).第二讲:加法原理基础班1.南京去上海可以乘火车、乘飞机、乘汽车和乘轮船。
如果每天有20班火车、6班飞机、8班汽车和4班轮船,那么共有多少种不同的走法?2.光明小学四、五、六年级共订300份报纸,每个年级至少订99份报纸。
问:共有多少种不同的订法?3.将10颗相同的珠子分成三份,共有多少种不同的分法?4.在所有的两位数中,两位数码之和是偶数的共有多少个?5.用1,2,3这三种数码组成四位数,在可能组成的四位数中,至少有连续两位是2的有多少个?6.下图中每个小方格的边长都是1。
有一只小虫从O点出发,沿图中格线爬行,如果它爬行的总长度是3,那么它最终停在直线AB上的不同爬行路线有多少条?7.如下图,从甲地到乙地有三条路,从乙地到丙地有三条路,从甲地到丁地有两条路,从丁地到丙地有四条路,问:从甲地到丙地共有多少种走法?8.书架上有6本不同的画报和7本不同的书,从中最多拿两本(不能不拿),有多少种不同的拿法?9.如下图中,沿线段从点A走最短的路线到B,各有多少种走法?10.在1~1000的自然数中,一共有多少个数字0?11.在1~500的自然数中,不含数字0和1的数有多少个?12.十把钥匙开十把锁,但不知道哪把钥匙开哪把锁,问:最多试开多少次,就能把锁和钥匙配起来?答案1.38种。
2.10种。
提示:没有年级订99份时,只有三个年级各订100份一种订法;只有一个年级订99份时,另外两个年级分别订100份和101份,有6种订法;有两个年级订99份时,另外一个年级订102份,有3种订法。
3.8种。
4.45个。
提示:两个数码都是奇数的有5×5(个),两个数码都是偶数的有4×5(个)。
5.21个。
提示:与例5类似,连续四位都是2的只有1种,恰有连续三位是2的有4种,恰有连续两位是2的有16种。
6.10条。
提示:第一步向下有5条,第一步向上有1条,第一步向左或向右各有2条。
7.3×3+2×4=17(种).8.6+7+15+21+6×7=91(种).提示:拿两本的情况分为2本画报或2本书或一本画报一本书.9.(1)6;(2)10;(3)20;(4)35.10.9+180+3=192(个).11.8+8×8+3×8×8=264(个).12.9+8+7+6+5+4+3+2+1=45(次).我们通常解题,总是要先列出算式,然后求解。
可是对有些题目来说,这样做不仅麻烦,而且有时根本就列不出算式。
这一讲我们介绍利用加法原理在“图上作业”的解题方法。
提高班1. 用五种颜色给右图的五个区域染色,每个区域染一种颜色,相邻的区域染不同的颜色。
问:共有多少种不同的染色方法?11.小明要登15级台阶,每步登1级或2级台阶,共有多少种不同登法?12.小明要登20级台阶,每步登2级或3级台阶,共有多少种不同登法?13.有一堆火柴共10根,每次取走1~3根,把这堆火柴全部取完有多少种不同取法,答案1. 420种。
解:如上图所示,按A,B,C,D,E顺序染色。
若B,D颜色相同,则有5×4×3×1×3=180(种);若B,D颜色不同,则有5×4×3×2×2=240(种)。
共有不同的染色方法180+240=420(种)。
2. 987种。
3. 114种。
4. 274种。
提示:取走1根有1种方法,取走2根有2种方法,取走3根有4种方法。
将1,2,4作为数列的前三项,从第4项起每项都是它前三项的和,得到1,2,4,7,13,24,44,81,149,274。
第10项274就是取走10根火柴的方法数。
第三讲:排列基础班1.计算2.某铁路线共有14个车站,这条铁路线共需要多少种不同的车票.3.有红、黄、蓝三种信号旗,把任意两面上、下挂在旗杆上都可以表示一种信号,问共可以组成多少种不同的信号?4.班集体中选出了5名班委,他们要分别担任班长,学习委员、生活委员、宣传委员和体育委员.问:有多少种不同的分工方式?5.由数字1、2、3、4、5、6可以组成多少没有重复数字的①三位数?②个位是5的三位数?③百位是1的五位数?④六位数?解答1.(1)30;(2)2002;(3)156;(4)1.第四讲:组合基础班1.计算:①C315;②C19982000;③C34×C28;④P28-C68.2.从分别写有1、2、3、4、5、6、7、8的八张卡片中任取两张作成一道两个一位数的加法题.问:①有多少种不同的和?②有多少个不同的加法算式?3.某班毕业生中有10名同学相见了,他们互相都握了一次手,问这次聚会大家一共握了多少次手?4.在圆周上有12个点.①过每两个点可以画一条直线,一共可以画出多少条直线?②过每三个点可以画一个三角形,一共可以画出多少个三角形?5.如图,图上一共有六个点,且六个点中任意三个点不共线,问:①从这六个点中任意选两点可以连成一条线段,这些点一共可以连成多少条线段?②从这六个点中任意选两点可以作一条射线,这些点一共可以作成多少条射线?(射线是一端固定,经另一点可以无限延长的.)6.下图中共有4×4=16个小方格,要把A,B,C,D四个不同的棋子放在方格里,每行和每列只能出现一个棋子,共有多少种放法?解答1.①455;②1999000;③112;④28.2.①C28=28;②P28=56.3.C28=45.4.①C212=66;②C312=220.5.①C26=15;②P26=30.6.16×9×4×1=576(种)或4!×4!=576(种)提高班1. 5件不同的商品陈列在橱窗内,排成一排。
(1)如果某件商品不放在中间,有几种不同排法?(2)如果某件商品不能放在两端,有几种不同排法?2.有四封不同的信,随意投入三个信筒里,有多少种不同投法?解答1.(1)5×4×3×2×1-4×3×2×1=96;(2)3×4×3×2×1=72。
2. 34=81(种)第五讲:排列、组合基础班1.有6名同学参加象棋决赛,得冠军和亚军的名单有几种可能的情况?2.一个口袋装有6个小球,另一个口袋装有5个小球,所有小球的颜色都不相同。
(1)从两个口袋中任取一个小球,有多少种不同的取法?(2)从两个口袋中各取一个小球,有多少种不同的取法?3.某市电话号码是五位数,每一数位上的数码可以是0,l,2,…8,9中的任意一个(数字可以重复出现,如00000也算一个电话号码)那么这个城市最多有多少个电话号码?4.在“希望杯”足球赛中,共有27支小足球队参赛。
(l)如果这27个队进行单循环赛(两队间只比赛一次,称作一场),需要比赛多少场?(2)如果这27个队进行淘汰赛,最后决出冠军,共需比赛多少场?5.如上图,从A地到B地有两条路;从B地到D地有两条路;从A地到C地只有一条路;从C地到D地有3条路。
那么从A地到D地有多少种不同走法?6.5件不同的商品陈列在橱窗内,排成一排。
(1)如果某件商品不放在中间,有几种不同排法?(2)如果某件商品不能放在两端,有几种不同排法?7.有四封不同的信,随意投入三个信筒里,有多少种不同投法?8.下图中共有4×4=16个小方格,要把A,B,C,D四个不同的棋子放在方格里,每行和每列只能出现一个棋子,共有多少种放法?9.由数字0、1、2、3、4可以组成多少个①三位数?②没有重复数字的三位数?③没有重复数字的三位偶数?④小于1000的自然数?答案1.由乘法原理,有6×5种不同情况。
