学而思四年级超常班试题+答案
2020年超常思维数学4年级初赛试题+答案
2020年超常(数学)思维与创新能力测评(四年级初赛)姓名：考试时间：60分钟满分：100分考试说明(1)本试卷包括25道不定项选择题(可能有几个选项正确),每小题4分。
(2)每道题的分值按正确选项的个数平均分配，但是如有错选，则该题不得分。
1.将一个已知面积、形状、大小的图形分成两部分，即其两部分拼起来就是原来的图形.请由左侧的图形找出被分解后的两个图形，即五个选项中的其中两个.()....2.计算1+3+5+7+…+2019+2021=().A.10112 B.10002 C.9992 D.9982 E.以上都不正确3.有七个图形，中间五个是选项，左侧的图形经过中间的图形切割后，成为右侧的分离图形，请将中间这个切割线找出来.().....4.甲、乙、丙三个小朋友共有贺年卡90张，如果甲给乙3张后，乙又送给丙5张，那么三人的贺年卡张数刚好相同，则乙原来有贺年卡()张.A.28 B.29 C.30 D.31 E.32E D C B A D C B A5.左侧图形为问题图形，右侧图形为答案图形，请你根据左侧问题图形的排列关系，或变化关系找出接下来的一个图形.()2566.1÷(2÷4)÷(4÷8)÷(8÷16)÷(16÷32)=()A.8 B.4 C.64 D.32 E.167.要使前后两个图形内所填数字的运算规律一致，则问号处应填入的数字是(A.96).B.86C.116D.106E.以上都不正确8.房间里有四个人，他们的年龄之和是89岁，其中最小的是10岁，他与最大者的年龄之和比另外两人的年龄之和大9岁.他们中任何一人的年龄都不可能是().A.31 B.33 C.35 D.37 E.399.在下图中间圆圈内填一个数后，计算每条线段两端的两数之差(大减小),再把这三个差相加，则其和的最小值是().43A.41B.32C.13D.18E.2810.2021年1月1日是星期五，10年后，即2031年1月1日是().A.星期三B.星期四C.星期五D.星期六E.星期日11.一台计算机被编程用于搜索计数用的数所含的数字个数.例如，当它搜索了123456789101112后，那它已搜索到了15个数字.当计算机开始这一任务并搜索到前1788个数字，那么它搜索的最后一个计数用的数是().A.533 B.632 C.645 D.1599 E.168912.在三个相互接触的球(图A)上可以放上一个球(图B).在图C,D,E 和F 的每一种情况可以放上()个球.A B E C D FA.C—3,D—6,E—7,F—10B.C—4,D—7,E—8,F—11C.C—2,D—7,E—8,F—10D.C—3,D—6,E—7,F—8E.C—3,D—6,E—7,F—913.摩托车骑手甲和自行车骑手乙同时由A地去B地.走过全程的时，乙停下来休息，当他休息完准备继续出发时，发现甲距B地还有全程的甲到达B地后一刻也不停留，马上向A地返回.究竟是甲先到达A地，还是乙先到达B 地，以下正确的说法是().A.谁先到取决于两人的速度B.谁先到取决于A,B之间的距离C.两人同时到达D.甲先到A地E.乙先到B地14.图中的大长方形由面积分别为12cm²,24cm²,36cm²,48cm²的四个小长方形组成，则阴影部分的面积为()cm².A.4B.5C.6D.8E.1015.左侧图形为问题图形，右侧图形为答案图形，请你根据左侧问题图形的排列关系，或变化关系找出接下来的两个图形.()A. B. C. D. E.16.图中格子点的位置的间距为1cm,则该封闭图形的面积是()cm².A.50B.50.5C.51D.51.5E.5217.13.5吨货物分装在一批箱子里，箱子本身的质量极轻(可忽略),每个箱子所装货物都不超过350kg.则最少可以用()辆载重为1.5吨的卡车一次性运走这批货物.A.9B.10C.11D.12E.2018.如图，相互补充能成为正方形的图形对为().235681112的臣A.1—2,3—4,5—6,7—8,9—10,11—12B.1—3,2—4,5—7,6—8,9—11,10—12C.1—8,2—6,3—11,4—7,5—9,10—12D.1—9,2—7,3—11,4—10,5—8,6—12E.1—9,2—6,3—11,4—7,5—12,8—1019.如图，今有9块3种颜色的小方块：3块红色(R),3块白色(W),3块蓝色(B).把它们摆入一个3×3的大方格中去，使每一行和每一列都有3种不同颜色的小方块，如果用转动大方格而改变小方格位置的摆法不算，有()种摆法.A.12B.9C.6D.3E.以上都不对20.左侧有一大方块，内有九个小方格，左上角的画面为初始画面，有问号的小方格为欲知画面的方格.初始画面必须向右或向下做连续翻转，且每隔一线翻转一次，直到求出在问号位置的画面为止.在右边五个答案中，有一个画面即为在问号位置的画面，请你将这个画面找出，然后选出正确的答案.().....21.小明做普通的乘法，用字母E 代表偶数数字，用字母0代表奇数数字，乘式是OE E ×E EE O EE +E O E0E E 则得到的4位数数字之和为().A.22 B.23 C.24 D.36 E.2522.圆上有6个点，两两连成一条线段，我们称之为“弦”.这些弦在圆内可能有()个交点.A.12 B.13 C.14 D.15 E.1623.0是AB 的中点，青蛙从A 跳到B,称之为关于中心0作了一次“对称跳”,记为T(O).对任意给定的△ABC,一只青蛙从Po开始，T(A)至P ₁,然后T(B)至P2,再T(C)至P₃;继续T(A)至P₄,T(B)至Ps,再T(C)至P₆,…,以下正确的是().ED C B AA.青蛙将越跳越远.B.青蛙将最终跳入三角形内.C.P6与Po重合，即六次跳动回到原处.D.Pi₂与P₀重合，即十二次跳动回到原处.E.是否跳回原地，与在三角形内还是三角形外无关.24.如图，9个点P,Q,R,S,..,W,X等距离位于一个圆周上，那么顶点属于集合{P,Q,R,S,…,W,X},圆心落在其内部的不同三角形的个数是()个.A.14B.21C.30D.42E.4825.对一个非零自然数做如下操作：如果是偶数则除以2;如果是奇数则加1.如此进行直到为1,操作停止.经过9次操作变为1的数有()个.A.13B.21C.34D.65E.以上都不正确2020年超常(数学)思维与创新能力测评(四年级初赛答案)姓名：考试时间：60分钟满分：100分考试说明(1)本试卷包括25道不定项选择题(可能有几个选项正确),每小题4分。
2017年4月第十一届北京学而思杯四年级数学试卷解析
34
【考点】计数，有序枚举 【难度】☆☆☆ 【答案】6 【分析】1,2,9 这三个数字的位置是确定的，如下图：
12 34
9
将 5,6,7,8 这四个数字填入剩下的四个方格内，经有序枚举可得如下 6 种情况：
127 348 569
1 26 3 48 5 79
126 3 47 5 89
125 3 46 7 89
1 25 3 47 6 89
5
1 25 3 48 6 79
四、 填空题Ⅳ（共 4 道小题，每题 8 分，共 32 分） 13. 如果一个数的各位数字从左到右构成等差数列，我们就称这个数为“等差数”，例如：135、8642 均
是“等差数”，153 就不是“等差数”，那么一共有________个三位“等差数”． 【考点】计数，有序枚举 【难度】☆☆☆☆ 【答案】45 【分析】当这个三位数中有数字 0 时：“等差数”有 210,420,630,840，共 4 个；
16. 请在下图的每个方格中填入 1~6 中的一个数字，使得每行、每列和每个粗线宫内数字都不重复．且 每个箭头上从线尾到箭头的尖，数字依次变大．那么，五位数 ABCDE ________．
3
【考点】组合，数独 【难度】☆☆☆☆ 【答案】63451 【分析】
3
A BCDE
3 156 2 4 4 62 135 253461 146 253 5 21346 634512
14. 一个三位数，若在前面添上数字 4，则组成的四位数是 8 的倍数；若在前面添上数字 5，则组成的
四位数是 9 的倍数；若在前面添上数字 6，则组成的四位数是 11 的倍数．那么这个三位数是________．
【考点】数论，整除特征
【难度】这个三位数为
2021 年超常思维竞赛 数学 四年级含答案
2021年超常思维竞赛数学四年级考试时间：100分钟满分150分1. 如图所示，请从下面左侧两组图形的相对排列关系，找出下面右侧两组图形应有的相对排列关系，那么正确的选项为（）.2. 数数看：下图有（）个三角形.A.15B.16C.17D.18E.193. 根据下图所示的规律，推知M=（）.A.1547B.1692C.1977D.2020E.20214. 如图所示，在下面五个图形中与其他四个图形不同的是（）.5. 数学家诺伯特·维纳是控制论的创始人，在他获得哈佛大学博士学位的授予仪式上，有人好奇地询问他的年龄，因为他看上去还像一个小孩，他的回答很有趣，他说：“我的年龄的立方是一个四位数，年龄的四次方是一个六位数，这两个数刚好把0～9这10个数字全部用上了，不重复也不遗漏.”则诺伯特·维纳当年（）岁.A.10B.12C.14D.16E.186. 下列图形中与其他三个图形不一样的是( ). A.（1） B.（2） C.（3） D.（4） E.都一样7. “1后面有100个零”这个数是10100. 1940年，爱德华·卡斯纳和詹姆士·纽曼把10100这个大数叫作“古戈”(googol)，古戈在实际生活中是个非常大的数，可是在数学研究中古戈又显得太小了. 为了能表示更大的数，数学家又规定了“古戈布来克斯”(googolplex)，一个古戈布来克斯等于1010100或写成10googol，它有一万亿亿亿亿亿亿亿亿亿亿亿亿个零.已知：102=10×10=100.(102)3=102×102×102=102+2+2=106=1000000.1023=102×2×2=108=100000000.那么100 (00)⏟2000个0等于（）个古戈的乘积.A.12B.14C.16D.18E.208. 如图所示，正方形的边长依次是2，4，6，8，10，阴影部分的面积是（）.A.10B.20C.30D.40E.509. 如图所示，是一个未完成的大正方体，则还缺少（）个小正方体才能完成.A.14B.15C.16D.17E.1910. 画线联结下图中相邻的圆圈，最终使所有圆圈通过联结线可连在一起；联结线可以沿着圆圈的8个方向联结，但不能相互交叉(图1)；每个圆圈内的数表示与它联结的圆圈数量(如图2中数字7，表示分别联结了7个圆圈). 图3中所有和圆圈5联结的圆圈中数字之和是（）.A.11B.13C.15D.17E.1911. 下列这些图形的表示方法是一个正方形的每边都接着一个三角形，第一组有8个小圆点，第二组有21个小圆点，第三组有40个小圆点，则推出第四组有（）个小圆点.A.60B.61C.63D.65E.6712. 如图所示，由8个正六边形以及它们顶点间的连线组成一只蝴蝶，那么该图形中共有（）个平行四边形.A.9B.10C.11D.12E.以上都不是13. 如图所示，相同的汉字代表相同的数字，不同的汉字代表不同的数字，那么“启智杯”，代表的三位数最大是（）.+ 启智智启杯杯奖奖杯杯A.920B.820C.720D.620E.520 14. 如图所示，一群学生参观了某博物馆. 他们从大门P入馆，从大门Q离馆. 在参观中，他们除了一道门没有经过外，馆内其他每道门都经过一次并且仅为一次. 他们没有经过的门是（）.A.RB.SC.TD.UE.V15. 小明模仿诸葛亮草船借箭，自己玩了一个草船借箭的数学游戏，他知道曹军总共有3880支箭. 曹军向小明的草船一支一支射箭，射了一段时间，小明下令士兵撤退，曹军立即停止射箭. 此时小明算了一下，自己借到箭的数量和曹军剩余箭的数量的乘积是射箭过程中最大的数(即使曹军再向草船射箭也不能超过这个数)，那么关于小明一共借了多少支箭，以下答案不正确的有（）.(假设射箭过程中箭全部射在草船上.)A.1840B.1885C.1990D.2000E.202116. 方格中的图形符号“◇”“○”“▽”“☆”代表填入方格中的数，相同的符号表示相同的数.如图所示，若第一列、第三列、第二行、第四行的四个数的和分别为36，50，41，37，则第三行的四个数的和为（）.A.11B.22C.33D.44E.5517. 一个图形序列从左到右按照下图所示规律排列，那么第102个图形是 A，B，C，D，E中的（）.A. B. C. D. E.不确定18. 如图所示，已知△ABC的面积是12cm2，以正六边形的边长为正方形的边长，向外作了6个正方形，最后以正方形的边长为等边三角形的边长，作了6个小等边三角形，这6个小三角形的面积之和是（）cm2.A.10B.12C.14D.20E.2419. 如图所示，有A，B，C，D，E五个区域，另有五种不同的颜色，规定相邻的两个区域不能染上相同的颜色，则一共有（）种不同的染色方法.A.100B.120C.420D.500E.202120. 一个2021位整数的第一位数字是4，已知这个数中任意相邻的两个数字按顺序组成的两位数都可以被19或23整除，这个数的个位数字可能是( ).A.3B.5C.6D.7E.821. 从1970年起，我开始收集日历且以后每年都这样做，直到以后每一年至少可用一本已经收集到的日历来代用时，我将停止收集. 则必须收集日历的最后年份是（）年.A.1978B.1980C.1988D.1996E.202122. 如图所示，小张驾车从T出发，经过A，B，C，D，E各一次后，最后回到T，不允许走重复路线. 图中道路旁边的数值表示汽车经过这段公路所用的小时数. 小张完成计划的行程至少要用（）h.A.29B.30C.31D.32E.以上都不是23. 将一些正方形用如图一样的方式填满一个矩形盒子，则我们称这些正方形可以被组装成一个“锯齿状矩形”. 下图为一个6×4的锯齿状矩形，它是由39个大小相同的正方形所构成的，则一个9×7的锯齿状矩形内有（）个这样大小相同的小正方形.A.91B.101C.111D.121E.以上都不是24. 由若干个单位立方体组成一个较大的立方体，然后把这个大立方体的某些面涂上油漆. 油漆干后，把大立方体拆成单位立方体，发现有45个单位立方体的任何一面都没有油漆. 那么大立方体有（）面被涂过油漆.A.4B.5C.6D.7E.以上都不是25. 在下图的每个空格内填入1~5中的一个数字，使得每行、每列所填的5个数字互不相同，虚线框内提示数表示框内两位数对个位进行四舍五入后的结果(如12四舍五入后为10，35四舍五入后为40). 那么第5列从上到下的5个数字组成的五位数是（）.A.24315B.23415C.21345D.23145E.以上都不对26. 某数学竞赛结束后，主办方给第一、二、三名颁发奖金，这些奖金按3∶2的比例分成两部分，较多的那一份作为第一名的奖金；较少的那一份又再按3∶2的比例分成两部分，分别作为第二名及第三名的奖金. 已知第三名的奖金比第一名的奖金少2200元，则第二名的奖金是（）元.A.800B.1000C.1100D.1200E.以上都不对27. AC Milan(意大利)，Barcelona(西班牙)，Chelsea(英格兰)，Dortmund(德国)四支欧洲职业足球队进行单循环比赛，即每两队都要进行一场比赛，其中胜方积3分，负方积0分，平后则双方各积1分，结果如下：如果AC Milan对Barcelona的比赛结果是1∶0，那么AC Milan获胜，请由上面表格中的资料判断出AC Milan对 Dortmund的比赛结果是（）(按队伍先后顺序写)A.0:3B.0:2C.1:1D.1:3E.以上都不对28. 已知1+2+3+45+6+78+9=144，若只允许将1，2，3，4，5，6，7，8，9中某些数字依序合并为一个数且添上加法符号，那么，还有（）种其他不同的方法可以将它们组成和为144的等式.A.1B.2C.3D.4E.以上都不对29. 题图数字谜中，不同字母表示不同数字，A，B，C，D，E所代表的数字依次成等差数列. M所代表的数字旋转180°是W所代表的数字，W所代表的数字旋转180°是M所代表的数字，那么该乘法竖式的积是（）.A.12915B.19215C.20115D.20215E.以上都不对30. 在左下表中，在有公共边的两格内的数同时加上1或同时减去1叫作一次操作，经过有限次操作后由左下表变为右下表，那么右下表中A处的数是（）.A.2B.5C.2020D.2022E.以上都不对2021 2021年超常思维竞赛数学四年级答案考试时间：100分钟满分150分。
2011学而思四年级超长班试题2
第五讲简单的统计20、【例8不超过最低额度a立方米时，只付基本费3元和每户每月额定c保险费；如果每月用气量超过最低额度a立方米时，超过部分应按b元/立方米的标准付费，并知道保险费c不超过5元。
试根据以上提供的资料确定a，b，c的值。
第六讲定义新运算21、【学案4】小明来到红毛族探险，看到下面几个红毛族的算式：8×8＝8，9×9×9＝5，9×3＝3，（93＋8）×7＝837。
老师告诉他，红毛族算术中所用的符号“＋、－、×、÷、（）、＝”与我们算术中的意义相同，进位也是十进制，只是每个数字虽然与我们写法相同，但代表的数却不同。
请你按红毛族的算术规则，完成算式：89×57＝______。
22、【例7】定义a*b为a与b之间（包括a、b）所有与a奇偶性相同的自然数的平均数，例如：7*14=(7+9+11+13)÷4=10，18*10=(18+16+14+12+10)÷5=14。
在算式口*(19*99)=80的方格中填入恰当的自然数后可使等式成立，那么所填的数是多少？23、【例8】如有a#b新运算，a#b表示a、b中较大的数除以较小数后的余数。
例如：2#7=1，8#3=2，9#16=7，21#2=1。
如21#(21#x)=5，则x可以是______(x 小于50)。
第七讲游戏与策略本讲是博弈论的入门，例如：①大自然是平衡的，保护平衡就可以胜利，破坏平衡就会失败；②寻找制胜点；③当无法找到胜利的方法时保证自己不输也是对策，保证了自己不输，最终的结果就是对方输；④增强自己或者削弱对手是两种很有意思的对策，有时增强自己可以获胜，但有时增强自己却无法获胜必须削弱对手24、【作业1】甲乙二人轮流报数，报出的数只能是1～７的自然数。
同时把所报数一一累加起来，谁先使这个累加和达到80，谁就获胜。
问怎样才能确保获胜？25、【学案3】15个小球围成一圈，甲、乙两人轮流从中取一个或者相邻的两个，如果两球中间有一个空位置，则不难将这两个球同时拿走，谁取走最后一个球谁就获胜，甲先拿，谁将获胜？26、【作业6】100个“+”号排成一排，甲乙轮流将“+”号改成“-”号，每次只能改一个或相邻的两个，谁将最后一个“+”改成“-”，谁获胜，获胜的策略是什么？27、【作业5】在一个6×5的棋盘上，甲乙二人轮流往棋盘的方格内放棋子。
学而思2011年暑假新四年级超常123班难题汇总
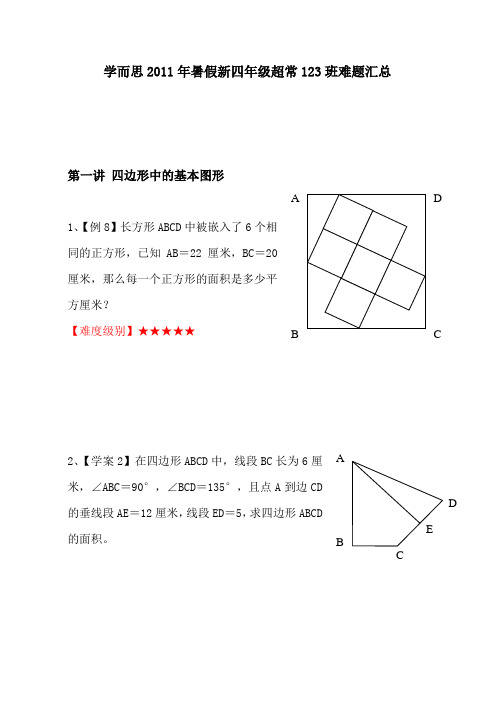
学而思2011年暑假新四年级超常123班难题汇总第一讲四边形中的基本图形1、【例8】长方形ABCD中被嵌入了6个相同的正方形，已知AB＝22厘米，BC＝20厘米，那么每一个正方形的面积是多少平方厘米？【难度级别】★★★★★2、【学案2】在四边形ABCD中，线段BC长为6厘米，∠ABC＝90°，∠BCD＝135°，且点A到边CD 的垂线段AE＝12厘米，线段ED＝5，求四边形ABCD 的面积。
D C3、【学案3】等腰梯形ABCD 中，交于O 点的两条对角线互相垂直，三角形ECB 是直角三角形，OC 比AO长20厘米。
已知三角形ADE 的面积是250平方厘米，则梯形ABCD 的面积是多少平方厘米？4、【学案4】一块边长为180厘米的正方形铁片，四角各被截去一个边长为40厘米的小正方形铁片，现在要从剩下的铁片中剪出一块完整的正方形铁片来，剪出的正方形面积最大为多少平方厘米？5、【作业5】请仅用刻度尺画一个面积是5平方厘米的正方形，保留必要的作图痕迹。
O B C D EA第二讲乘法原理6、【例7】1到1999的自然数中，有多少个与5678相加时，至少发生一次进位？7、【例8】有______个四位数满足下列条件：它的各位数字都是奇数，它的各位数字互不相同，它的每个数字都能整除它本身。
8、【学案1】计算机上编程序打印出前10000个正整数：1,2,3,……,10000时，不幸打印机有毛病，每次打印数字3时，它都打印出x，问其中被错误打印的共有多少个数？9、【学案4】有9张同样大小的圆形纸片，其中标有数码“1”的有1张，标有数码“2”的有2张，标有数码“3”的有3张，标有数码“4”的有3张，把这9张圆形纸片如图所示放置在一起，但标有相同数码的纸片不许挨在一起。
(1)如果M处放标有数码“3”的纸片，一共有多少种不同的放置方法？(2)如果M处放标有数码“2”的纸片，一共有多少种不同的放置方法？10、【越玩越聪明】在例6的后面。
2022年超常思维数学4年级试题+答案
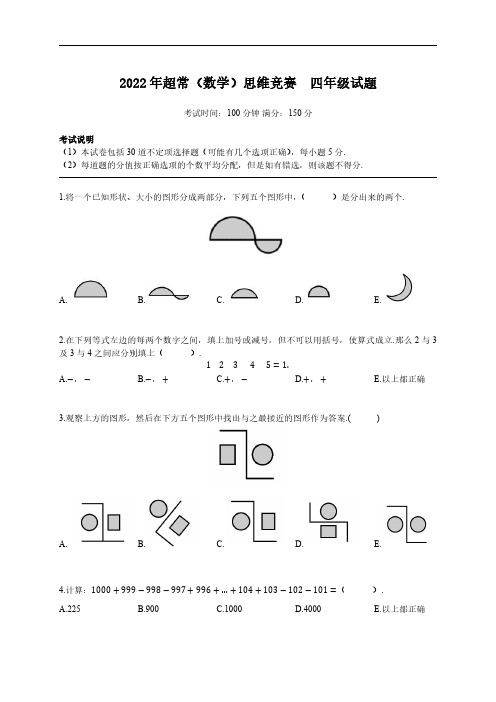
2022年超常（数学）思维竞赛四年级试题考试时间：100分钟满分：150分考试说明（1）本试卷包括30道不定项选择题（可能有几个选项正确），每小题5分.（2）每道题的分值按正确选项的个数平均分配，但是如有错选，则该题不得分.1.将一个已知形状、大小的图形分成两部分，下列五个图形中，（）是分出来的两个.A. B. C. D. E.2.在下列等式左边的每两个数字之间，填上加号或减号，但不可以用括号，使算式成立.那么2与3及3与4之间应分别填上（）.12345=1.A.−，−B.−，+C.+，−D.+，+E.以上都正确3.观察上方的图形，然后在下方五个图形中找出与之最接近的图形作为答案.()A. B. C. D. E.4.计算：1000+999−998−997+996+…+104+103−102−101=（）.A.225B.900C.1000D.4000E.以上都正确5.如图，在标准的8×8的棋盘(带有黑白相间的正方形格子)上，有204个正方形(64个1×1的正方形，49个2×2的正方形，等等).那么，有（）个这样的正方形，其中每个正方形的面积黑白各占一半.A.120B.83C.84D.102E.以上都不对6.爱迪生家的大门非常重，一位朋友对这位发明家埋怨道：“你有没有办法让这门开关起来不费劲？”爱迪生笑着回答：“我家的大门设计得非常合理.那个门与一个打水的装置连接，来访问我的人每推一次门都可以往水槽里加20升水.”后来，爱迪生想，如果每次推门能往水槽里加水25升，那么比原来少推12次门，水槽就可装满了.那么，爱迪生家的水槽能装（）升水.A.1000B.1100C.1200D.1300E.以上都不对7.下列五个选项中含有甲部分的特点而不含有乙部分的特点的是（）.A. B. C. D. E.8.在一个密封的瓶中，放进一个细菌，1分钟后瓶中就充满了细菌.已知每个细菌每秒钟分裂一次，一个变成两个.如果开始放进两个细菌，（）秒后瓶中充满细菌.A.30B.45C.58D.59E.以上都不对9.如图，在一片树叶上放一张透明的方格纸，方格纸上的小正方形边长为1cm.这片树叶的面积最接近于（）cm2.A.6B.9C.18D.20E.2710.找规律：问号处应该填（）.A.3B.4C.9D.7E.811.在保龄球游戏的最近一局中小鹏得198分，从而把若干局的平均分由177分提高到178分.为了把他的平均分提高到179分，下一局他必须得（）分.A.179B.180C.199D.200E.以上都不对12.小超晨跑，在他前面有5人，回头一看，发现后面也有5人，那么跑道上共有（）人.A.5B.6C.10D.11E.以上都不对13.把图(a)所示的9块正方形拼字板不留缝隙地拼到图(b)所示的3×3的方格内，其中阴影部分可以组成一个汉字，这个字是（）.A.深B.港C.数D.理E.中14.把1~7这七个数分别填入下图所示的“○”内，使每条线段上三个数的和都等于14，则中间“○”应填（）.A.7B.6C.5D.4E.以上都不对15.如图所示的物体由相邻面粘在一起的7个木制立方体组成，各立方体的每边长皆为1cm.该物体总的表面积等于（）cm2.A.30B.26C.31D.36E.以上都不对16.设为正整数，形如2−1的质数称为梅森数，例如：25−1=31是梅森数.曾经有一段时期已知世界上最大的梅森数是274207281−1，那么它的个位数是（）.A.1B.3C.5D.7E.917.两人划了10次拳，男士出了3次石头、6次剪子、1次布，女士出了2次石头、4次剪子、4次布.没有平局，但是忘记了出拳次序.则下列说法正确的是().A.男士以3胜7负失败B.男士以7胜3负胜利C.女士以4胜6负失败D.女士以6胜4负胜利E.无法判断18.如图，给定一个棱长为6m的实心立方体，从每个面的中部到对面的中部开设一个正方形孔，三个孔在立方体的中间相交，这样产生的正方形窗口的边长为2m，这个新立方体的总表面积是（）m2.A.72B.144C.288D.320E.以上都不对19.如果一个三位数的本身增加3，那么它的各位数字之和就减少到原来的13，则这样的三位数有（）个.A.1B.3C.10D.20E.以上都不对20.一家四口，父亲、母亲、儿子和女儿，他们的年龄和是71岁.已知父亲比母亲大3岁，女儿比儿子大2岁.4年前，全家的年龄之和为56岁.那么，下列（）是该家庭成员的年龄.A.33B.30C.6D.4E.以上都不对21.下列的除法算式中，相同的汉字表示相同的数字，不同的汉字表示不同的数字，那么两位数勤思=().A.32B.42C.52D.62E.以上都不对22.用数字1，2，3，4，5，6，7，8，9构造9个九位数(不一定互不相同)，在每个数中每个数字都刚好使用一次.则这9个九位数的和的末尾最多能有（）个0.A.1B.2C.4D.9E.以上都不对23.从所给的五个选项中，选择最合适的一个填入问号处，使之呈现一定的规律性.()A. B. C. D. E.24.对某自然数：①能被3整除的话，就将其变为用3除后所得的数.②不能被3整除的话，将其变为此数加1后所得的数.如此反复变换，直到最后为1.例如，自然数7，按照7→8→9→3→1如此变换4次就为1了.那么，1~99中，通过变换5次首次变为1的数有()个(不到5次变换即为1的除外）.A.1B.3C.10D.19E.以上都不对25.小明有一块4×4的方格板如图所示.他希望在板上放尽可能多的棋子，规则是每个小方格中至多放1颗棋子，而且在每行、每列和对角线上至多放3颗棋子，这样最多可在方格板上放置（）颗棋子.A.9B.10C.11D.14E.以上都不对26.河的左岸有4艘船，横渡到对岸的时间分别为：A需要2min，B需要4min，C需要8min，D 需要16min.目前只有一名船夫，一条船的后面只能再拴一条船，而且此时渡河所费时间为拴在一起的两条船中最慢那条船所用的时间.现在每次用一条船牵一条船渡河，然后再开一条船回到左岸.如此反复，直到把所有的船都开到右岸，请问最少需要()min.当然，换船和拴船的时间忽略不计.A.6B.12C.24D.30E.6027.如图所示，图中正八边形有()个.A.1B.3C.5D.8E.928.李明、韩梅梅、张晓丽三名同学一起吃草莓，数量分别是：1枚、2枚、3枚（顺序非对应).李明：“韩梅梅和我吃了相同数量的草莓.”韩梅梅：“张晓丽和我吃了相同数量的草莓.”张晓丽：“我比李明只多吃了1枚.”已知，至少吃了3枚草莓的人说的是真话.那么，().A.李明1枚，韩梅梅2枚，张晓丽3枚B.李明1枚，韩梅梅3枚，张晓丽2枚C.李明2枚，韩梅梅1枚，张晓丽3枚D.李明2枚，韩梅梅3枚，张晓丽1枚E.李明3枚，韩梅梅1枚，张晓丽2枚29.小明每天定时到达车站，随即乘坐与此同时到达的家里来接的车回家.有一天，小明稍微早一些到了车站，于是就开始步行向家走，在途中的A点与来接的车错过了.如果这个时间司机发现了小明，那么他会比平时早30min到家，不巧司机没有发现小明，还像平时一样向车站开去了.当小明从A地点开始又走了35min的时候，被到车站后马上返回的车追上了，从这开始小明乘车，结果，还是在平时的时间点回到了家.则小明的步行速度与车的速度之比是().这里假定车的速度以及小明的步行速度都是常数，并且，上车所花的时间忽略不计.A.1:3B.1:4C.1:5D.1:6E.1:730.在《最强大脑》第二季中，有一个超高难度的挑战项目，那就是蜂巢迷宫.如图所示是一个简易的蜂巢迷宫，一共有14间房间，每相邻两间房间之间都有一个通道.挑战者要从最左边的房间出发，最终到达最右边的房间.如果挑战者只能向右走(包括右上、右下)，那么挑战者从起点到终点一共有()种不同的走法.A.11B.21C.31D.51E.612022年超常（数学）思维竞赛四年级答案。
学而思小学四年级数学入学测试(难题)超常班选拔考试)
学校________________ 班级________________ 姓名_________________ 联系电话__________________密 封 线 内 不 要 答 题2016年学而思数学超常班选拔考试 四年级一、 填空题（每题6分，共96分，将答案填在下面的空格处）1. 计算：666666666666666+-⨯÷=__________．2. 规定图形表示运算a b c +-，图形表示运算y w x z +--，则计算＋＝__________．3. 珂珂老师带着20名学生围成一圈做游戏：从某一个同学开始顺时针从1开始依次连续报数，报含有数字7的数（如7，17，71等）或7的倍数的同学击1次掌．如此进行下去，当报到100时，所有同学共击掌__________次．4.四个非零自然数的和为38，四个自然数的乘积的最小值是__________，最大值是_________．5. 如图，大平行四边形ABCD 的面积是48平方厘米，小平行四边形CEFG 的面积是6平方厘米，则阴影三角形BDF 的面积是__________平方厘米．6. 家具厂生产一批桌椅，原计划每天生产30套，12天完成．实际只用原来时间的一半就完成了任务，那么实际每天比原计划多生产__________套．7. 如图所示，一个小正方形和6个一样的小长方形组成一个大正方形，已知小长方形的长比宽长2厘米，则大正方形的面积是__________平方厘米．8. 在一条笔直的公路上，可可和凡凡从相距100米的地方同时出发，相向跑步，以后方向都不变，可可每秒跑6米，凡凡每秒跑4米．出发__________秒时，他们相距200米.9. 将48本书分给两组小朋友，已知第二组比第一组多5人．如果把书全部分给第一组，那么每人4本，有剩余；每人5本，书不够．如果把书全分给第二组，那么每人3本，有剩余；每人4本，书不够．问第二组有__________人．10. 若干名棋手进行单循环赛，即任两名棋手间都要赛一场．胜利者得2分，平局各得1分，负者得0分．比赛完成后，前4名依次得8、7、5、4分，则一共有__________名棋手．11. 如图，含有字母A 或者字母B 的平行四边形有__________个．BA12. 如图，在三角形ABC 中，已知3BC DC =，并且三角形ABC 的面积是24平方厘米，则三角形ADB 的面积是__________平方厘米．13. 箱子里红、白两种玻璃球，红球数是白球数的3倍多2个，每次从箱子里取出7个白球、15个红球．取若干次以后，箱子里剩下3个白球、53个红球．那么箱子里原有红球__________个．14. 已知五位数2016□能被9整除，则“□”中填上合适的数字是__________．15. 有A 、B 、C 三个人，每人戴一顶帽子，帽子上写有一个不为0的数，已知其中有1个数为其它2个数之和，每个人都可以看见其他人帽子上的数但看不到自己帽子上的数．他们都很聪明不会有失误的推理，他们所说的话均为真话，并且会将当时已经确知的事全部说出来． A 说：“我不知道我帽子上的数．”B 说：“我帽子上的数是10．”C 帽子上的数是__________．DCBA16. 套娃是俄罗斯的一种民间工艺品．大套娃里面有小套娃，小套娃里面有更小的套娃．现在有一个特产商店里出售这种六重套娃，一整套套娃的价格是8700元，当然也可以单卖，而且相邻大、小套娃的差价是300元．请问：在这种六重套娃之中，最小的套娃要卖__________元钱．二、 解答题（17、18题每题12分，19、20题每题15分，共54分，写出必要步骤，否则不得分）17. 在长方形ABCD 中，E 是AB 的中点，F 是ED 的中点．已知AB 等于6厘米，AD 等于4厘米．求：（1） 长方形ABCD 的面积? （2） 梯形ADCE 的面积?（3） 阴影部分三角形AEF 的面积?D18. 四位数的数字顺序重新排列后，可以得到一些新的四位数．现有一个四位数码互不相同，且没有0的四位数M ，它比重排的新数中最大的小3834，比新数中最小的大4338．求这个四位数．19. 如图，线段AB 和CD 垂直且相等，点E 、F 、G 是线段AB 的四等分点，点E 、H 是线段CD的三等分点，从A 、B 、C 、D 、E 、F 、G 、H 这8 个点中任选3个作为顶点构成三角形．（1）已知CFE △面积为2，则三角形CDB △的面积是多少． （2）面积是CFE △面积2倍的三角形有多少个．（3）面积与CFE △面积相等的三角形（不包括CFE △）有多少个．20. 三个环行跑道如图排列，每个环行跑道周长为210厘米；甲、乙两只爬虫分别从A 、B 两地按箭头所示方向出发，甲爬虫绕1、2号环行跑道作“8”字形循环运动，乙爬虫绕3、2号环行跑道作“8”字形循环运动，已知甲、乙两只爬虫的速度分别为每分钟20厘米和每分钟15厘米.则：甲、乙两爬虫第二次相遇时，甲爬虫爬了多少厘米?学校________________ 班级________________ 姓名_________________ 联系电话__________________密 封 线 内 不 要 答 题321BA（1） 经过多长时间，甲、乙两爬虫第一次相遇?（2） 甲、乙两爬虫第二次相遇时，甲爬虫爬了多少厘米?学校________________ 班级________________ 姓名_________________ 联系电话__________________密 封 线 内 不 要 答 题2016年学而思数学超常班选拔考试 四年级一、 填空题（每题6分，共96分，将答案填在下面的空格处）1.计算：666666666666666+-⨯÷=__________．【答案】6662. 规定图形表示运算a b c +-，图形表示运算y w x z +--，则计算＋＝__________．【答案】23. 珂珂老师带着20名学生围成一圈做游戏：从某一个同学开始顺时针从1开始依次连续报数，报含有数字7的数（如7，17，71等）或7的倍数的同学击1次掌．如此进行下去，当报到100时，所有同学共击掌__________次． 【答案】304. 四个非零自然数的和为38，四个自然数的乘积的最小值是__________，最大值是_________．【答案】35；81005. 如图，大平行四边形ABCD 的面积是48平方厘米，小平行四边形CEFG 的面积是6平方厘米，则阴影三角形BDF 的面积是__________平方厘米．【答案】246. 家具厂生产一批桌椅，原计划每天生产30套，12天完成．实际只用原来时间的一半就完成了任务，那么实际每天比原计划多生产__________套． 【答案】30套7. 如图所示，一个小正方形和6个一样的小长方形组成一个大正方形，已知小长方形的长比宽长2厘米，则大正方形的面积是__________平方厘米．【答案】648. 在一条笔直的公路上，可可和凡凡从相距100米的地方同时出发，相向跑步，以后方向都不变，可可每秒跑6米，凡凡每秒跑4米．出发__________秒时，他们相距200米. 【答案】309. 将48本书分给两组小朋友，已知第二组比第一组多5人．如果把书全部分给第一组，那么每人4本，有剩余；每人5本，书不够．如果把书全分给第二组，那么每人3本，有剩余；每人4本，书不够．问第二组有__________人．【答案】15人10. 若干名棋手进行单循环赛，即任两名棋手间都要赛一场．胜利者得2分，平局各得1分，负者得0分．比赛完成后，前4名依次得8、7、5、4分，则一共有__________名棋手． 【答案】611. 如图，含有字母A 或者字母B 的平行四边形有__________个．BA【答案】4812. 如图，在三角形ABC 中，已知3BC DC =，并且三角形ABC 的面积是24平方厘米，则三角形ADB 的面积是__________平方厘米． 【答案】16DCBA13. 箱子里红、白两种玻璃球，红球数是白球数的3倍多2个，每次从箱子里取出7个白球、15个红球．取若干次以后，箱子里剩下3个白球、53个红球．那么箱子里原有红球__________个．【答案】158只14. 已知五位数2016□能被9整除，则“□”中填上合适的数字是__________．【答案】915. 有A 、B 、C 三个人，每人戴一顶帽子，帽子上写有一个不为0的数，已知其中有1个数为其它2个数之和，每个人都可以看见其他人帽子上的数但看不到自己帽子上的数．他们都很聪明不会有失误的推理，他们所说的话均为真话，并且会将当时已经确知的事全部说出来．A 说：“我不知道我帽子上的数．”B 说：“我帽子上的数是10．”C 帽子上的数是__________． 【答案】516. 套娃是俄罗斯的一种民间工艺品．大套娃里面有小套娃，小套娃里面有更小的套娃．现在有一个特产商店里出售这种六重套娃，一整套套娃的价格是8700元，当然也可以单卖，而且相邻大、小套娃的差价是300元．请问：在这种六重套娃之中，最小的套娃要卖__________元钱． 【答案】700二、 解答题（17、18题每题12分，19、20题每题15分，共54分，写出必要步骤，否则不得分）17. 在长方形ABCD 中，E 是AB 的中点，F 是ED 的中点．已知AB 等于6厘米，AD 等于4厘米．求：（1） 长方形ABCD 的面积? （2） 梯形ADCE 的面积?（3） 阴影部分三角形AEF 的面积?D【答案】24平方厘米 ；（4分）18平方厘米；（4分）（3）连接AC ，11348S AEF S ABC S ABCD D D ===正（平方厘米）．（4分） 18. 四位数的数字顺序重新排列后，可以得到一些新的四位数．现有一个四位数码互不相同，且没有0的四位数M ，它比重排的新数中最大的小3834，比新数中最小的大4338．求这个四位数． 【答案】设组成这个四位数的四个数码为a ，b ，c ，d (91a b c d ≥>>>≥)，则有383443388172abcd dcba -=+=，（4分） 可得999()90()81727992180a dbc -+⨯-==+，（4分） 则8ad -=，2b c -=，9a =，1d =，194338M cb =+，且M 的四位数字分别为1、c 、b 、9，由于8917+=的个位数字为7，所以b ，c 中有一个为7，但2b c -=，所以c 不能为7，故7b =，5c =，157943385917M =+=．（4分）19. 如图，线段AB 和CD 垂直且相等，点E 、F 、G 是线段AB 的四等分点，点E 、H 是线段CD的三等分点，从A 、B 、C 、D 、E 、F 、G 、H 这8 个点中任选3个作为顶点构成三角形．（1）已知CFE △面积为2，则三角形CDB △的面积是多少． （2）面积是CFE △面积2倍的三角形有多少个．（3）面积与CFE △面积相等的三角形（不包括CFE △）有多少个．【答案】（1）9（4分）（2）三角形三个顶点不能共线，所以不能三个点都在AB 上，一定有一个或两个点在CD 上．只含C 点：CFB △、CFA △、CEG △ 3个 只含H 点：HAB △1个只含D 点：DAB △ 1个含C 、H 点：0个 含H 、D 点：HDG △1个学校________________ 班级________________ 姓名_________________ 联系电话__________________密 封 线 内 不 要 答 题共有31116+++=个．（5分）（3）只含C 点：CAE △、CFG △、CGB △ 3个 只含H 点：1HAF △、HEG △、HFB △ 3个 只含D 点：DAF △、DEG △、DFB △ 3个 含C 、H 点：CHG △1个 含H 、D 点：AHD △、FHD △2个共有3331212++++=个．（6分）20. 三个环行跑道如图排列，每个环行跑道周长为210厘米；甲、乙两只爬虫分别从A 、B 两地按箭头所示方向出发，甲爬虫绕1、2号环行跑道作“8”字形循环运动，乙爬虫绕3、2号环行跑道作“8”字形循环运动，已知甲、乙两只爬虫的速度分别为每分钟20厘米和每分钟15厘米.则：甲、乙两爬虫第二次相遇时，甲爬虫爬了多少厘米?321BA（1） 经过多长时间，甲、乙两爬虫第一次相遇?（2） 甲、乙两爬虫第二次相遇时，甲爬虫爬了多少厘米?【答案】（1）根据题意，甲爬虫爬完半圈需要210220 5.25÷÷=分钟，乙爬虫爬完半圈需要2102157÷÷=分钟．由于甲第一次爬到1、2之间要5.25分钟，第一次爬到2、3之间要10.5分钟，乙第一次爬到2、3之间要7分钟，所以第一次相遇的地点在2号环形跑道的上半圈处．(210105)(2015)9+?=（分钟）（6分）（2）由于甲第一次爬到2、3之间要10.5分钟，第二次爬到1、2之间要15.75分钟，乙第一次爬到1、2之间要14分钟，所以第二次相遇的地点在2号环形跑道的下半圈处． 第二次相遇时，两只爬虫爬了(2102105)(2015)15⨯+÷+=分钟．所以甲、乙两爬虫第二次相遇时，甲爬虫爬了2015300⨯=厘米．（8分）。
2013年四年级秋创新班选拔答案
2013年学而思四年级秋季超常班选拔考试参考答案一、填空题1、10047407400740007++++=个________． 【答案】原式114941104040040004000711444077444517=+++++⨯=+=个个个2、甲、乙两人同时从A 、B 两地出发，相向而行．出发3分钟后，两人相距300米；出发7分钟后，两人也相距300米．那么A 、B 两地相距________米．【答案】750米3、甲、乙两人在笔直的公路上练习跑步，若甲让乙先跑20米，则甲跑5秒可追上乙；若让乙先跑2秒，则甲跑4秒可追上乙．甲的速度是________米/秒．【答案】124、如图，大正方形的每条边长都被截成6厘米和8厘米两部分，如图连接后内部构成一个小正方形．那么三角形②的面积比三角形①大________平方厘米． （提示：在一个直角三角形中，两条直角边的长度分别为a 和b ，斜边的长度为c ，那么它们一定满足：222a b c +=．这就是著名的勾股定理）【答案】1平方厘米5、一天，小慧和刘老师一起谈心，小慧问：“老师，您今年有多少岁啊？”刘老师 回答说：“你猜猜，当我像你这么大时，你才1岁；当你到我这么大时，我就34 岁了．”那么刘老师今年的年龄是________岁．【答案】小慧和刘老师的年龄差是一定的，设为1倍量，那么两人的年龄差是：(341)311-÷=（岁），所以，刘老师今年的年龄是：111223+⨯=（岁）．6、下图中共有________个正方形．【答案】16941(41)240+++++⨯=（个）7、黑板上写着200以内的所有偶数．擦去其中一个后，余下的所有偶数之和为9998．那么擦去的数字是________．【答案】1028、定义两种新运算[]a 和{}a ，[]a 表示求a 的整数部分；{}a 表示求a 的小数部分．如[7.23]7=，{7.23}0.23=．若[]{}8.24 4.28x x +=+，那么x =________．【答案】12.52二、简答题1、200个苹果分给一些小朋友，要求：（1）每个小朋友都分到了苹果，且个数都为偶数个；（2）小朋友分得的苹果个数各不相同．按照上述条件，这些苹果最多可以分给多少个小朋友？【答案】最小的13个偶数之和24626182++++= ；最小的14个偶数之和24628210++++= ．因此最多可以分给13个小朋友．2、有四张数字卡片0、1、2、3，利用它们可以组合出一些一位或多位数，如2，32，102，3012等．那么共可组合出多少个小于2000的数？【答案】将组合的数按位数分类：一位数4个；两位数339⨯=个；三位数33218⨯⨯=（个）；四位数13216⨯⨯⨯=（个）共4918637+++=（个）．3、请在内填上合适的数，使除法算式成立．【答案】97080120809÷=4、16支队伍参加羽毛球比赛．比赛分为小组赛和淘汰赛，赛程如下：（1）每4支队伍分为一个小组，共4小组．小组赛采取单循环赛制（任意两队赛且只赛一次），按积分决出小组第一、二名的队伍，获得出线权；（2）8支获得出线权的队伍通过淘汰赛决出冠、亚、季军．按这样的赛制，一共需要进行了多少场比赛？【答案】小组赛共进行了6424⨯=（场），淘汰赛共进行了8场，共32场．注意：决出季军还需再进行一场比赛．08三、解答题1、小琦和大琦在400米的环形跑道上跑步锻炼．小琦在前，大琦在后，相距100米．哨声一向，两人同时、同向开始跑步．已知小琦的速度是4米/秒，大琦的速度是6米/秒．那么大琦第10次追上小琦时，他离自己的出发点多远？【答案】第一次追上需要100(64)50÷-=（秒）；之后每次追上需要400(64)200÷-=（秒）． 第10次追上，用时5092001850+⨯=（秒），大琦共跑了1850611100⨯=（米）． 1110040027300÷= ，即大琦回到出发点后又多跑了300米．考虑到环形跑道，离出发点的距离为400300100-=（米）．2、有六张完全相同的直角三角形卡片，将每个三角形的一个锐角拼在一起，可以拼出240︒．有多少种形状的直角三角形卡片满足条件？（两个三角形的三个内角对应相等，那么它们是同一种形状的三角形）【答案】设两个角度分别为x 、y ，那么90x y +=︒．拼成240︒有四种情况：6x ；5x y +，42x y +，33x y +．（1）6240x =︒，解得40x =︒，50y =︒，符合条件．（2）5240x y +=︒，解得37.5x =︒，62.5y =︒，符合条件．（3）42240x y +=︒，解得30x =︒，60y =︒，符合条件．（4）33240x y +=︒，但由90x y +=︒知，33270x y +=︒，无解．因此共有三种形状的直角三角形满足条件．。
2016年四年级超常班选拔
学
校
姓
名
电
话
班
次
5. 马丁和海绵宝宝分别从甲、乙两地同时出发，相向而行。出发 6 小时后，两人在距离甲乙两地中点 15 千 米的丙地相遇；两人相遇后继续前进，4 小时后马丁到达乙地，而海绵宝宝到达了丁地，那么：
密 封 线 内 不 要 答 题 ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※
。
密 封 线 内 不 要 答 题 ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※
【解析】 x 7 x x 1 + x 2 ++ x 6 =7x 21 63 ，解得：x=12。 7. 下图中，“超常班选拔”这几个汉字表示 0~9 中的数字。不同的汉字表示不同的数字，相同的汉字表示相同 的数字，那么“超常班选拔”= 。
※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※
2011学而思三升四超常班选拔答案
考试总分120分，填空题10题，每题5分1 计算：(12342010201120104321)2011++++++++++++÷=解答：2011.2 学校排练节目，如果每行排8人，则有一行少2人，如果每行排9人，则有一行少7人，一共有 人。
（两次排队行数一样）【分析】 两种分配方案只所以相差725-=人，是因为两种分配方案每行相差981-=人，对应的求出一共排了515÷=行，一共有58238⨯-=人。
3停车场停了三轮车和小轿车共20辆，车轮总共72个，那么三轮车有 辆【分析】三轮车有8辆4甲、乙、丙三人今年的年龄分别为12、15、34岁，那么 年后甲的年龄等于乙与丙的年龄之差。
【分析】7年 5观察下面排列的规律，第9行各个数之和与第10行各个数之和相差... (6)12345512341234321【分析】 答案：126 长方形的长是50厘米，截去一个最大的正方形后，余下一个长方形，这个长方形的周长是 厘米。
【分析】 截去的最大的正方形边长等于长方形的宽，余下的长方形的周长502100⨯=（厘米） 712011之间同时被3、5、7除都余2的数有 个。
【分析】 [3,5,7]105=，所以这些数为2、107、212⋅⋅⋅⋅⋅⋅，20111051916÷=⋅⋅⋅⋅⋅⋅，所以总共有19120+=2011学而思 乐加乐 超常班选拔考试（三升四）（个）.8某书的页码是连续的自然数1，2，3，4，…9，10…当将这些页码相加时，某人把其中一个页码错加了两次，结果和为2011，则这书共有______页。
【分析】如果这本书的页数超过62页，那么页码之和超过12362632016+++⋅⋅⋅++=。
所以页数不大于+++⋅⋅⋅+=，无论将62页，又因为如果这本书的页数不到62页，那么页码之和小于123611891哪个页码重复加两遍，都不会使页码和达到2011，所以这本书有62页。
因为-=。
四年级2019超常班选拔数学试题
学校班级姓名联系电话密 封 线 内 不 要 答 题考生须知1．本试卷共4页，20题2．本试卷满分150分，考试时间90分钟3．在试卷密封线内填写学校、班级、姓名、联系电话一、 填空题（每题6分，共96分，将答案填在下面的空格处）1. 2006＋200.6＋20.06＋2.006＋994＋99.4＋9.94＋0.994＝__________．2. 定义x ☆37y x y =+．（1☆1）+（2☆2）+（3☆3）+…+（10☆10）=__________．3.M 是两位数，如果11M A B ÷= ，当A B +的和最大时，M =__________．4. 五位打工者一天的辛苦劳动后共获得330元工资，由于工种不同，获得最高工资者比其他四位分别多得12、14、21和28元，获得最低工资者的工资是__________元．5. 一次足球赛比赛中，所有参赛队的每两个队比赛一场，共比赛了15场，那么有__________个队参赛．6. 春节前夕，一个富翁向一些乞丐施舍一笔钱．一开始他准备给每人100元，结果剩下350元，他决定每人多给20元．这时从其他地方闻讯赶来了5个乞丐，如果他们每个人拿到的钱和其他乞丐一样多，富翁还需要再增加550元．原有__________名乞丐．7. A 、B 两地相距90千米，甲骑自行车每小时行15千米，乙开汽车，每行1千米比甲少用3分钟，甲、乙两人同时从A 出发去B 地，乙到B 地后立即返回，当乙遇到甲时，他们距离B 地__________千米．8. 如图，用8个相同的小长方形拼成一个大长方形，求阴影部分的面积是__________平方厘米．9. 如图，三角形ABC 面积为90平方厘米，BD =2DC ，AE :EC =2:3，求阴影部分三角形CDE 的面积__________平方厘米．ABCDE10. 如图，请在右图每个方框中填入一个不是8的数字，使乘法竖式成立．则乘积的结果为__________．11. 有若干根长度相等的火柴棒，把这些火柴棒摆成如图的图形．照这样摆下去，到第10行为止一共用了__________根火柴棒．12. 一天，红太狼和灰太狼同时从“野猪林”出发，到“天堂镇”．红太狼一半路程溜达，一半路程奔跑．灰太狼一半时间溜达，一半时间奔跑．如果它们溜达的速度相同，奔跑的速度也相同，则先到“天堂镇”是__________．13. 将一个能被5整除的三位数的首、末数字交换后，还是三位数，它的5倍也是三位数，它的后两住数字的和是60的约数，求满足条件的最大的三位数是__________．14. 下面的算式是按规律排列的：11+、23+、35+、47+、19+、211+、313+、415+、117+、219+、321+、423+、125+⋯⋯那么，第__________个算式的两数之和是2008．15. 在一张四边形的纸上共有10个点，如果把四边形的顶点算在一起，则一共有14个点．已知这些点中的任意三个点都不在同一直线上．按下面规定把这张纸剪成一些三角形：⑴ 每个三角形的顶点都是这14个点中的3个；⑵ 每个三角形内，都不再有这些点． 那么，这张四边形的纸最多可以剪出__________个三角形．16. 老罗在退休时共有264万元的积蓄，他将这些钱分为4份，除了三个儿子各给一份外，另有一份自己留做养老金．若他把这份养老金给大儿子，则大儿子所得的钱等于二儿子及三儿子所得的钱之总和；若他把这份养老金给二儿子，则二儿子所得的钱等于大儿子及三儿子所得的钱之总和的两倍；若他把这份养老金给三儿子，则三儿子所得的钱等于大儿子及二儿子所得钱之总和的三倍．请问老罗准备拿来当养老金的部分为__________万元．2019年学而思数学超常班选拔考试四年级二、 解答题（17、18题每题12分，19、20题每题15分，共54分，写出必要步骤，否则不得分）17.妈妈带儿子小虎到超市买了两件商品，小虎把一件商品标价中个位上的零忽略了，他付给收银员162元，但是收银员说应当付270元．求这两种商品的单价差是多少元？18.将1分、2分、5分和1角的硬币投入19个盒子中，使每个盒子里都有硬币，且任何两个盒子里的硬币的钱数都不相同．问：（1）至少需要投入多少硬币？（2）这时，所有的盒子里的硬币的总钱数至少是多少？19.6条谜语让50人猜，每条谜语每人猜一次，共猜对了178次，已知每人至少猜对了2条，只猜对2条的有16人，只猜对4条的有9人，只猜对3条和只猜对5条的人数一样多．那么6条谜语全猜对的有多少人？20.8点10分，有甲、乙两人以相同的速度分别从相距60米的A，B两地顺时针方向沿着长方形ABCD（见图）的边走向D点，甲8点20分到D后，丙、丁两人立即以相同的速度从D点出发，丙由D逆时针向A走去，8点24分与乙在E点相遇，丁由D顺时针向C走去，8点30分在F点被乙追上，则连接三角形BEF的面积为多少平方米．AB CD。
学而思杯四年级试卷详解
2017第十一届学而思杯四年级试题详解一、填空题Ⅰ（每题8分，共80分） 1. 计算（1）16 1.740.3+++=． （2）65 1.735 1.7⨯+⨯=．【答案】（1）22；（2）170 【考点】小数巧算 【解析】（1）加减法凑整（2）提取公因数2. 如下图，每个小正方形的面积为1，则图中“2017”的面积是 ．【答案】34.5【考点】格点多边形【解析】面积为1的小正方形有30个，面积为0.5的小三角形有9个．3. 甲乙丙丁四人排成一行拍照，有 种不同的排法． 【答案】24【考点】加乘原理【解析】乘法原理即可快速解决：432124⨯⨯⨯=（种）．4. 已知五位数403□□是99的倍数，请问这个五位数是 ．【答案】40392 【考点】整除特征【解析】方法一：99的整除特征，从右往左两位一段求和，和为4+3+□□，是99的倍数，可以推出=994392=□□－－．方法二：试除法，40399994087÷=，40399740392-=．5. 学而思在淘宝上买书架，高书架100元一个，矮书架80元一个，最后花了960元买了10个书架，其中高书架有 个．【答案】8【考点】鸡兔同笼【解析】假设法解决：假设全是矮书架，那10个矮书架共需8010800⨯=（元），比960元少了960800160=－（元），每把一个矮书架换成高书架，多花1008020=－（元），所以高书架有160208÷=（个）．6. 艾迪、薇儿和大宽一共买了960元的零食，已知艾迪支付了总费用的一半，薇儿比大宽多支付了100元，那么大宽付了 元． 【答案】190【考点】和差倍问题【解析】艾迪支付了9602480÷=（元），所以薇儿和大宽共支付了剩下480元，其中薇儿多支付100元，所以用和差问题，推出大宽付了4801002190÷=（－）（元）．7. 甲乙两人从相距1000米的A 、B 两地同时出发，相向而行，甲每秒能走3米，乙每秒能走2米， 秒后两人将相遇． 【答案】200【考点】相遇问题【解析】路程和÷速度和=相遇时间．8. 只能被1和它本身整除的自然数叫做质数，例如：2、3、5、7、11、13；那么90到100之间有 个质数． 【答案】1【考点】因倍质合 【解析】质数为97．9. 如图所示，圆圈中分别填入1到5这5个数，每个三角形顶点上的三个数之和都是10，那么中间圆圈A 上填的数是 ．【答案】5【考点】数阵图【解析】两个三角形顶点上所有数之和为10×2=20，比1234515++++=多了5，而圆圈A正好被算了两次，所以圆圈A 上填的是5．10. 下图中，每个小正方形的面积为1，请问图中面积为4的长方形（包括正方形）共有个．A【答案】12【考点】图形计数【解析】面积为4的长方形分为2×2的正方形和1×4的长方形，前者有8个，后者有4个．二、填空题Ⅱ（每题9分，共36分）11. 下图是一个乘法竖式，最后的乘积结果为 ．0×4719□□□□□□□□□□□□□□□【答案】94799 【考点】数字谜【解析】个位分析法推出第一个乘数个位为7，进而推出第一个乘数十位为1，此时第一个乘数乘7为五位数，乘4为四位数，这样的乘数只可能是2017，20174794799⨯=．12. 甲乙丙三个小朋友参加学而思杯考试，满分200分，最后三个人得分各不相同，三个人总分正好能被20和17整除，请问分数最高的甲至少得 分． 【答案】115【考点】最值问题【解析】三人总分最高为2003=600⨯（分），而这个总分正好被20和17整除，所以总分为2017340⨯=（分），此时要求所有人得分各不相同，并且分数最高的人得分尽量低，此时应尽量平分，34031131÷=，再稍作调整，得到三人分数分别为112，113，115．13. 某印刷厂接到订单要印刷一批书，如果每天印刷30本，则会比规定时间晚4天完成任务；为了如期完成任务，印刷厂决定每天多印刷5本，这样刚好能在规定时间完成印刷，那么印刷厂总共要印刷 本书． 【答案】840【考点】盈亏问题【解析】经典盈亏变形题目，把天数变得一样多即可，这儿我们把时间都统一为规定时间，将第一次多的4天给去掉，这样第一次就会比订单要求少印430120⨯=（本），再用总差÷每份差=份数，得出天数为120÷5=24（天），再用30244840⨯+=（）（本）或30524840+⨯=（）（本），即可算出答案．14. 如图所示，D 是AB 的中点，E 为BC 边靠近B 点的三等分点，已知三角形ADF 的面积为3，三角形CEF 的面积为8，那么三角形ABC 的面积为 ．【答案】30【考点】等积变形 【解析】三角形DBF 和三角形ADF 等高，面积相等，都为3；三角形BEF 和三角形CEF 等高，前者为后者的一半，即824÷=，此时得出大三角形CDB 面积为84315++=，大三角形ACD 与三角形CDB 等高，面积相等，都为15，所以三角形ABC 面积为30．三、填空题Ⅲ（每题10分，共40分）15. 如下图所示，在三角形中内接一个正方形和一个三角形，得到一个新的图形，我们称之为一次操作，下图为两次操作之后的结果，那么5次操作后，得到的图形里，共能找到 个三角形．【答案】31【考点】归纳与递推 【解析】原来有1个，每次操作后，三角形增加6个，所以5次操作后变为16531+⨯=（个）16. 好未来小学展开了一项名叫“我最喜欢的学科”的调查，问卷上只有数学和英语两个选项，学生们可以给自己喜欢的学科打勾（可以不选）；最后发现，有1000人参与了这次调查，共有1300个勾，其中只喜欢数学的有100人，喜欢英语的学生中有一半同样喜欢数学，那么只喜欢一门学科的有 人． 【答案】500【考点】容斥原理/鸡兔同笼【解析】根据容斥原理知道，所有学生分为4类：只喜欢数学，只喜欢英语，两门都喜欢，CBADEF83两门都不喜欢；其中把只喜欢数学的100人去掉，还剩900人，勾还剩130********-=（个）；设两门都喜欢的有x 人，那么只喜欢英语的也有x 人，两门都不喜欢的有9002x （－）人， 两门都喜欢的最后打了2x 个勾，只喜欢英语的打了x 个勾，两门都不喜欢的最后没有打勾；所以列出方程21200x x +=，算出400x =，所以只喜欢数学的100人，只喜欢英语的400人，只喜欢一门的为100400500+=（人）．17. 将从1如果一直写下去，肯定会在某行出现连续的两个数字“0”，我们把这样连续两个“0”叫做“双黄蛋”，那么第三个“双黄蛋”出现在第 行． 【答案】156【考点】页码问题/周期问题【解析】数表规律为：从1开始连续自然数，每个数字占一格，写7个数字就换行；第一个“双黄蛋”出现在写100的时候，第二个“双黄蛋”出现在写200的时候； 第三个“双黄蛋”应该出现在写300的时候，不过以防万一，我们算下100、200和300，他们的“0”是否在同一行里，此处我们算下300后一个“0”在哪个位置： 1~9：9个数字；10~99，180个数字；100~300，2013603⨯=（个）数字，所以后一个“0”是第918060379++=（个）数字，算下这个数字的位置，79271131÷=，发现写300时，后一个“0”在第一列，前一个“0”在上一行最后一列，两个“0”不在同一行，所以不符合“双黄蛋”的要求． 同样方法，可以推出100和200都是符合要求的； 所以第三个“双黄蛋”只能出现在写400的时候，这时会再多写100个三位数，即多写300个数字，所以写400时，后一个“0”是第7923001092+=（个）数字，用周期问题算出位置：10927156÷=，所以第三个“双黄蛋”出现在第156行．18. 右图中，三角形ABC 是一个直角三角形，角ABC 是90度，AB =6，BC =8，AD =13，BC和AD 平行，BD 和CE 平行，BF 和DE 平行，那么阴影部分面积为 ．13FEDCB A86【答案】24【考点】等积变形【解析】如下图进行三次等积变形，三角形DEF 面积等于三角形BDE 的面积，三角形BDE 的面积等于三角形BCD 的面积，三角形BCD 的面积等于三角形ABC 的面积，三角形ABC 面积为68224⨯÷=，因此三角形DEF 面积为24．四、填空题Ⅳ（每题11分，共44分）19. 已知三位数abc ̅̅̅̅̅，交换数字顺序后得到另外两个三位数bca ̅̅̅̅̅和cab̅̅̅̅̅，这三个三位数恰好组成一个等差数列，并且a =1，b ＜c ，求bc ̅̅̅= ． 【答案】48【考点】位值原理【解析】方法一：枚举法尝试，从b =1开始尝试；方法二：位值原理解决2×bca ̅̅̅̅̅=abc ̅̅̅̅̅+cab̅̅̅̅̅，位值原理得210010)(10010)(10010)b c a a b c c a b ⨯++=+++++（，整理得20020211011101b c a a b c ++=++；继续整理得：18910881b a c =+，743b a c =+，将a =1代入得743b c =+，最后尝试得b =4，c =8，bc ̅̅̅=48．20. 甲乙两人分别从A 、B 两地同时出发，相向而行，甲的速度是乙的2倍，两人相遇后继续前行，各自到达B 、A 两地后立即返回，甲到达B 地后速度减半，乙到达A 地后速度翻倍，最后在C 点相遇，已知A 、B 两地相距300米，请问A 、C 两地相距 米． 【答案】100【考点】相遇问题【解析】我们一段一段的分析路程，即可解决这个问题：刚开始甲的速度是乙的2倍，所以第一次相遇时，路程也应该是2倍的关系，甲走了200米，乙走了100米；甲再往前走100米即可到达B 点，此时乙走的路程为甲的一半，即50米；当甲到达B 点后，速度减半，此时甲乙速度相等，乙再走150米到A 地，此时甲也走了150米；最后乙速度翻倍，变为甲的2倍，所以最后150米的距离，甲走了50米，乙走了甲的2倍100米，最后如图所示，AC 距离100米．68ABCDEF1313FEDCB A8613FEDCB86A21. 有6个数字2、3、4、5、6、7，从中选择4个互不相同的数字，组成一个四位数abcd̅̅̅̅̅̅̅，关于这个四位数，艾迪、薇儿、博士和大宽有以下的对话： 艾迪：“这个四位数是63的倍数．” 薇儿：“前两位ab ̅̅̅是一个质数．”博士：“两位数bd̅̅̅̅是一个质数．” 大宽：“后两位cd̅̅̅是一个平方数．” 已知他们之中只有3人的对话是正确的，所以abcd̅̅̅̅̅̅̅是 ． 【答案】4725【考点】因倍质合/整除特征【解析】对于这类问题，我们着重于去找出矛盾，此处看博士和大宽的对话，根据博士的话，bd ̅̅̅̅是一个质数，d 只能是3、7；而根据大宽的对话，cd̅̅̅是一个平方数，d 只 能是4、5和6，此时两人之间必有一人说错，所以艾迪和薇儿说的都是对的； 根据艾迪的话，此数是63的倍数，即同时被7和9整除；根据被9整除，这个四 位数数字和为9的倍数，而我们发现任选四个数字，和最小为234514+++=， 最大为456722+++=，所以这四个数字之和只能为18．下面我们讨论下博士和大宽到低谁对谁错；如果博士对，那么ab ̅̅̅和bd̅̅̅̅都是质数， b 和d 一个选3，另一个选7，此时根据数字和为18，可以轻易推出a 和c 一个选2，另一个选6；此时试验下来，abcd̅̅̅̅̅̅̅可能为2367、6723，两个都不是7的倍 数，排除这种可能，所以博士的对话是错的，大宽的对话才是对的，cd̅̅̅是一个平 方数．观察后两位cd̅̅̅是一个平方数，只可能是25、36、64； 如果cd ̅̅̅是25，根据9的整除特征，得出前两个数字分别为4和7，此时ab ̅̅̅只能是 47，四位数4725是7的倍数，符合条件；如果cd̅̅̅是36，根据9的整除特征，得出前两个数字分别为4和5，或者2和7， 然而4和5或者2和7都无法组出质数，不符合条件，排除；如果cd ̅̅̅是64，根据9的整除特征，得出前两个数字分别为3和5，此时ab ̅̅̅是个质 数，只能是53，四位数5364不是7的倍数，不符合条件，排除；所以答案是 4725．22. 黑板上从1开始写了很多平方数：1、4、9、16……我们把相邻两个平方数相减，求出来的差写在两个数之间，例如：1和4相减，求出来3，将3写在1和4之间，变成1、3、4……再把4和9相减，求出来5，将5写在4和9之间，变成1、3、4、5、9……这样操作完之后，整个数列变成了1、3、4、5、9、7、16． 然后我们把数列里所有的数连在一起，组成一个很长的数：13459716……我们把这个数叫做“学而思数”．2001001005015015010050ABC（1）这个数从左往右第10个数字是．（2）黑板上第一次出现“484”时，这个8是从左往右第个数字．（3）从左往右第600个数字是．【答案】（1）2；（2）91；（3）0．【考点】杂题【解析】（1）写出前10个数字：1345971692，第10个数字为2；（2）我们知道相邻两个平方数的差为奇数，而484三个数字都是偶数，所以写出484有以下三种可能：=⨯，当写到22的平方时出现；①4842222②484前面48是某个平方数的后半部分，但平方数个位不可能是8，排除；③484前面4是某个平方数的后半部分，简单尝试后，结果比22的平方大很多；数字，平方数之差到22222143-=，43是第21个平方差，前面所有平方差共有：+=（）（个）数字，所以写完22的平方484后，共写了543892 41214238⨯+-⨯=（个）数字，所以8是从左往右第91个数字．（3）从上表，我们写到31的平方数后，粗略估计，离600个数字还差的比较远，所以我们试下写完所有四位平方数，也就是写到99的平方数：⨯=（个）数字；一位平方数221~3：313二位平方数224~9：93212（）（个）数字；-⨯=三位平方数2210~31：319366（）（个）数字；-⨯=四位平方数2232~99：9931)4272（（个）数字；-⨯=平方差写到了22-=，是第98个平方差：9998197一位平方差：4个数字；二位平方差：494290（）（个）数字；-⨯=三位平方差：98493147-⨯=（）（个）数字；++++++=（个）数字；算出写完99的平方后，共写了31266272490147594-=（个）数字，再往后写6个数字，99的平方后面应该是还差600594622-=，再往后是100的平方，即10000，所以第600个数字是0．10099199。
2022年超常思维百科4年级试题+答案
2022年第三届超常(百科)思维与创新能力测评四年级试题考试时间：80分钟满分：80分考试说明：不定项选择题（本试卷共40题，每题2分，每题给出的四个选项中，至少有一个正确答案，多选、错选、不选均不得分。
少选且正确的，分值按正确选项的个数平均分配。
）1.北京时间2022年4月16日上午，（）航天员翟志刚、王亚平、叶光富顺利结束“太空出差”，回到阔别半年之久的地球，圆满完成飞行任务。
A.神舟五号B.神舟六号C.神舟十号D.神舟十三号2.中国首位进行出舱活动的女航天员是（），她迈出了中国女性舱外太空行走第一步。
A.王亚平B.刘洋C.杨利伟D.李亚平3.2021年12月9日，“天宫课堂”第一课正式开讲。
在课堂上，我们看到泡腾片扔进水中的产生的气泡不再上浮，而是相互挤压，水球也被气泡撑得更大。
这一现象与太空的（）有关。
A.真空环境B.缺氧环境C.低压环境D.微重力环境4.（）体现了社会主义核心价值观在价值导向上的定位，是立足社会层面提要求。
A.富强、民主、文明、和谐B.自由、平等、公正、法治C.爱国、敬业、诚信、友善D.富强、和谐、自由、敬业5.2022年8月30日，中共中央政治局向党的十九届七中全会建议，中国共产党第二十次全国代表大会于（）在北京召开。
A.2022年9月16日B.2022年9月26日C.2022年10月1日D.2022年10月16日6.我国实行九年义务制教育，《中华人民共和国义务教育法》规定的“义务性”包括（）。
A.让适龄儿童、少年接受义务教育是学校、家长和社会的义务。
B.家长不送学生上学，家长要承担责任；C.学校不接受适龄儿童、少年上学，学校要承担责任；D.学校不提供相应的教育条件，情节严重的对直接责任人依法给予行政处分。
7.我国《道路交通安全法》规定，不满（）的儿童不准在道路上骑自行车。
A.8周岁B.10周岁C.12周岁D.14周岁8.我们体内所有的细胞都需要空气中的（）来维持生命，它可以帮助我们正常地生活和工作。
深圳小学四年级学而思奥数超常班而选拔考试卷答案
学校________________ 班级________________ 姓名_________________ 联系电话__________________密 封 线 内 不 要 答 题2017年学而思数学超常班选拔考试 四年级一、 填空题（每题6分，共96分，将答案填在下面的空格处）1. 2006＋200.6＋20.06＋2.006＋994＋99.4＋9.94＋0.994＝__________．【答案】原式=（2006+994）+（200.6+99.4）+（20.06+9.94）+（2.006+0.994）=3000+300+30+3 =3333．2. 定义x ☆37y x y ．（1☆1）+（2☆2）+（3☆3）+…+（10☆10）=__________． 【答案】（1☆1）+（2☆2）+（3☆3）+…+（10☆10）31713272337331071010(12310) 5503.M 是两位数，如果11M A B ，当A B 的和最大时，M __________．【答案】984. 五位打工者一天的辛苦劳动后共获得330元工资，由于工种不同，获得最高工资者比其他四位分别多得12、14、21和28元，获得最低工资者的工资是__________元． 【答案】获得最高工资者的工资是 33012142128581 元，所以获得最低工资者的工资是812853 元．5. 一次足球赛比赛中，所有参赛队的每两个队比赛一场，共比赛了15场，那么有__________个队参赛． 【答案】66. 春节前夕，一个富翁向一些乞丐施舍一笔钱．一开始他准备给每人100元，结果剩下350元，他决定每人多给20元．这时从其他地方闻讯赶来了5个乞丐，如果他们每个人拿到的钱和其他乞丐一样多，富翁还需要再增加550元．原有__________名乞丐．【答案】题目可以转化为：每个乞丐（一开始的个数）给100元，多350元，每个乞丐（一开始的个数）给120元，多12×50-550=50元.根据盈亏问题一开始乞丐个数（350-50）÷（120-100）=15（个）．7. A 、B 两地相距90千米，甲骑自行车每小时行15千米，乙开汽车，每行1千米比甲少用3分钟，甲、乙两人同时从A 出发去B 地，乙到B 地后立即返回，当乙遇到甲时，他们距离B 地__________千米．【答案】因为甲骑自行车每小时行15千米， 所以甲骑车行1千米需要4分钟．因为乙每行1千米比甲少用3分钟，’所以乙每分钟行1千米，即每小时行60千米． 因为A 、B 两地相距90千米，所以从甲、乙同时从A 出发，到乙从B 地返回遇到甲， 两人共行了90×2 =180（千米），所花的时间是180÷(15 +60)=2.4(小时)．所以当乙遇到甲时，他们距离B 的距离是90-15×2.4=54(千米)．8. 如图，用8个相同的小长方形拼成一个大长方形，求阴影部分的面积是__________平方厘米． 【答案】阴影部分面积是900平方厘米．9. 如图，三角形ABC 面积为90平方厘米，BD =2DC ，AE :EC =2:3，求阴影部分三角形CDE 的面积__________平方厘米．BC【答案】18平方厘米.10. 如图，请在右图每个方框中填入一个不是8的数字，使乘法竖式成立．则乘积的结果为__________．888×【答案】11. 有若干根长度相等的火柴棒，把这些火柴棒摆成如图的图形．照这样摆下去，到第10行为止一共用了__________根火柴棒．【答案】1行：4根；2行：10根：3行：18根规律为：4、10、18 相邻两个数之间的差构成等差数列6、8、10所以10行的图形用了 4681022130 根火柴棒．12. 一天，红太狼和灰太狼同时从“野猪林”出发，到“天堂镇”．红太狼一半路程溜达，一半路程奔跑．灰太狼一半时间溜达，一半时间奔跑．如果它们溜达的速度相同，奔跑的速度也相同，则先到“天堂镇”是__________． 【答案】由最简单的平均速度公式可以知道灰太狼的平均速度要高于红太狼的平均速度，那么先到“天堂镇”的应该是灰太狼．13. 将一个能被5整除的三位数的首、末数字交换后，还是三位数，它的5倍也是三位数，它的后两住数字的和是60的约数，求满足条件的最大的三位数是__________． 【答案】由三位数能被5整除，可知这个三位数的末位数字是0或5．由这个三位数的首、末数字交换后还是三位数，可知这三位数的末位数字5． 由三位数的5倍也是三位数，可知这三位数的首位数字是1．故设该三位数是15xx 可能是1，2，3，…，8，9．因为x +5是60的约数，且z 要尽可能大，所以x =7． 故所求的三位数是175．14. 下面的算式是按规律排列的：11 、23 、35 、47 、19 、211 、313 、415 、117 、219 、321 、423 、125 ⋯⋯那么，第__________个算式的两数之和是2008． 【答案】1003这个和的前项是一个周期数列1，2，3，4循环，后项是一个奇数数列．和为2008，那么后项要在2004～2007之间，只能是2005和2007．分别看一下他们前面的数是不是所需要的数即可．2005是第1003项，前面是3，2005+3=2008满足题意． 2007是第1004项，前面是4，和不满足．所以只能是第1003．15. 在一张四边形的纸上共有10个点，如果把四边形的顶点算在一起，则一共有14个点．已知这些点中的任意三个点都不在同一直线上．按下面规定把这张纸剪成一些三角形： ⑴ 每个三角形的顶点都是这14个点中的3个； ⑵ 每个三角形内，都不再有这些点． 那么，这张四边形的纸最多可以剪出__________个三角形．【答案】当四边形内只有1个点时，则可剪出4个三角形；当四边形内只有2个点时，则可以剪出6个三角形；当四边形内只有3个点时，则最多可以剪出8个三角形；由此可见，四边形内每增加1个点，就可以多剪出2个三角形．因此，四边形内有10个点时，最多可剪出三角形42922 （个）．16. 老罗在退休时共有264万元的积蓄，他将这些钱分为4份，除了三个儿子各给一份外，另有一份自己留做养老金．若他把这份养老金给大儿子，则大儿子所得的钱等于二儿子及三儿子所得的钱之总和；若他把这份养老金给二儿子，则二儿子所得的钱等于大儿子及三儿子所得的钱之总和的两倍；若他把这份养老金给三儿子，则三儿子所得的钱等于大儿子及二儿子所得钱之总和的三倍．请问老罗准备拿来当养老金的部分为__________万元． 【答案】121万元二、 解答题（17、18题每题12分，19、20题每题15分，共54分，写出必要步骤，否则不得分）1. 妈妈带儿子小虎到超市买了两件商品，小虎把一件商品标价中个位上的零忽略了，他付给收银员162元，但是收银员说应当付270元．求这两种商品的单价差是多少元？ 【答案】收银员要收的钱与小虎算出的价格相差270-162=108(元)．因为小虎将一件商品标价中个位上的零忽略了， 所以这件商品被他错看成了 108÷（10-1）=12（元）， 于是这件商品的真实价格应是 12×10=120(元)．所以另外一件商品的价格是 270 -120 =150（元）． 于是两件商品的单价分别是120元和150元．1501203088888×学校________________ 班级________________ 姓名_________________ 联系电话__________________密 封 线 内 不 要 答 题2. 将1分、2分、5分和1角的硬币投入19个盒子中，使每个盒子里都有硬币，且任何两个盒子里的硬币的钱数都不相同．问： （1）至少需要投入多少硬币？（2）这时，所有的盒子里的硬币的总钱数至少是多少？ 【答案】只取一枚有1分、2分、5分、10分（1角）4种；取二枚有1＋1＝2（分），2＋2＝4（分），5＋5＝10（分），10＋10＝20（分）（2角）， 1＋2＝3（分），1＋5＝6（分），1＋10＝11（分）（1角1分），2＋5＝7（分），2＋10＝12（分）（1角2分），5＋10＝15（分）（1角5分）， 共10种，其中重复2种（2分、10分），加上只取一枚的共12种不同币值；取三枚时，可将以上取两枚的10种情况，分别加1分、2分、5分、10分，共有40种情况．从小到大取出7种不重复的币值为：8分、9分、13分、14分、16分、17分、21分，加上上述12种共19种．公用硬币的枚数为：1×4＋2×8＋3×7＝41（枚）． 总钱数为：1＋2＋3＋…＋17＋20＋21＝194（分）．3. 6条谜语让50人猜，每条谜语每人猜一次，共猜对了178次，已知每人至少猜对了2条，只猜对2条的有16人，只猜对4条的有9人，只猜对3条和只猜对5条的人数一样多．那么6条谜语全猜对的有多少人？【答案】因为50个人猜6条谜语，每条谜语每人猜一次，所以共有506300 （条）因为共猜对了178次，所以共猜错了300178122 （次）．因为只猜对2条的有16人，所以这16人共猜错了16(62)64 （次），因为猜对4条的有9人，所以这9人猜错了9(64)18（次），于是还剩122641840 （次）被猜错．而猜对6条的人猜错0条，所以这40条是被猜对3条的人或猜对5条的人猜错的．因为猜对3条和猜对5条的人数一样，所以猜对3条和猜对5条的都各有40[(63)(65)]10 (人) ．于是6条谜语全猜对的人数是5016910105 （人）．4. 8点10分，有甲、乙两人以相同的速度分别从相距60米的A ，B 两地顺时针方向沿着长方形ABCD （见图）的边走向D 点，甲8点20分到D 后，丙、丁两人立即以相同的速度从D 点出发，丙由D 逆时针向A 走去，8点24分与乙在E 点相遇，丁由D 顺时针向C 走去，8点30分在F 点被乙追上，则连接三角形BEF 的面积为多少平方米．A BCD【答案】2497.5平方米【分析】如下图所示，假设8点20分时，乙走到了M 点，由于甲、乙两人速度相同，因此有AB AM AD ，也即60MD AB 米，此时丙、丁从D 点出发．单独看乙和丙，两人做了一个相遇运动，相遇的时间是4分钟，相遇路程是60米，因此两人的速度和为15米/分．单独看乙和丁，两人做了一个追及运动，追及的时间是10分钟，追及路程也是60米，因此两人的速度差为6米/分．又因为丙和丁的速度相同，因此有乙的速度为 156210.5 米/分．乙花了14分钟走到E 点，走了10.514147 米，AE 长度为1476087 米．同理乙花了20分钟走到F 点，走了10.520210 米，DF 长度为2106010545 米．因此有：63002610405787.52497.5BEF ABCD ABE BCF DEF S S S S S △△△平方米。
学而思小学四年级数学超常班选拔考试(难题)
第1页 共4页 第2页 共4页2015—2016年深圳学而思 超常班选拔考试四年级 数学考 生 须 知1．本试卷共4页，20道题，满分150分，考试时间90分钟． 2．在试卷上认真填写学校名称、班级和姓名．3．答案填写在答题卡上，写在试卷上无效，请用黑色字迹签字笔作答．16题，每题6分，共96分，将答案填在下面的空格处） ．计算：27 3.6 6.427=⨯+⨯____________． ．小乐四次测试的成绩分别为98分，95分，90分和93分，这四次测试的平均分是__________分． ．4名工人3小时一共做了60个零件，按照这样的速度，12名工人8小时能做__________个零件． ．数一数，下图中共有__________个三角形．．如图，边长为10厘米的正方形ABCD 里有一个三角形BEF ，AE =4厘米，FC =6厘米，三角形BEF 的面积是_________平方厘米．．一个长方形的长和宽都是整数厘米，周长是30厘米，这个长方形的面积最大是__________平方厘米． ．如图，点D 是BC 边上的中点，AE 的长度是EC 长度的3倍，如果三角形ABC 的面积是48平方厘米，那么三角形EDC 的面积是__________平方厘米．8．下图中包含☆的长方形有__________个.9．小超家和小越家相距2880米，小超每分钟走48米，小越每分钟走32米，两人同时出发相向而行，经过__________分钟两人相遇．10．用数字1、4、5、8、0能组成__________个没有重复数字的三位偶数．11．在一个宽为1米的长方形花坛周围铺上边长为1米的正方形石板路，如下图，如果花坛长2米，则会用到10块石板，如果花坛长度是3米，则会用到12块石板，如果花坛长度为a 米（a 为整数），则会用到__________块石板．（用含有a 的式子表示）12．四位数462a 既是3的倍数，又是8的倍数，a =_________．13．1~100中，所有4的倍数的和是_________．14．一个数的所有数字和是23，每个数位上的数字各不相同，且不为0，这个数最大是__________．15．四年级2班布置联欢会的现场，每位男生吹12个气球，每位女生吹8个，全班45个人一共吹了460个气球，这个班有_________名女生．16．甲、乙两人现在的年龄和是63岁，当甲年龄等于乙现在年龄一半时，乙当时的年龄等于甲现在的岁数，那么甲现在__________岁．FED CBAEDCBA☆第3页 共4页 第4页 共4页二、解答题（17题12分，18题12分，19题15分，20题15分，共54分，写出必要步骤，否则不得分） 17．如图，长方形ABCD 的长9cm AB =，12cm CF =，阴影部分ACE ∆的面积是218cm ．（1）三角形ACF 的面积是多少平方厘米？（4分） （2）CE 的长度是多少厘米？（5分）（3）长方形ABCD 的面积是多少平方厘米？（6分）18．数列：21，34，67，210，313，616，219……按照一定的规律排列． （1）这个数列的第20个是什么？（4分）（2）数列中157□的分子是几？（5分）（3）数列中第几个数的分子和分母之和是418？（6分）19．如图，宁宁、涛涛和浩浩三人合坐一辆出租车从学校回家．他们约定：共同乘坐的部分所产生的费用由乘坐者平均分摊；单独乘坐部分所产生的费用由乘坐者单独承担．（如：一段路程有3人乘坐，一共花费12元，则每人分担4元；一段路程只有1人乘坐，花费5元，则这5元由这1人承担．）此出租车没有起步价，且每公里的价格一样．结果三人承担的费用分别是6元、15元、21元．宁宁家离学校12公里． （1）这次坐车的一共花了多少元？（4分）（2）图中三段路程，每段路程的费用分别是多少元？（6分） （3）浩浩家离学校有多少公里？（5分）20．甲、乙、丙三人沿湖边练习跑步，三人同时从湖边的某一点出发，乙、丙两人顺时针跑，甲逆时针跑，在甲与乙第一次相遇后5分钟第一次遇到丙，再过15分钟第二次遇到乙．已知甲的速度是乙的1.5倍，湖的周长为8000米．（1）甲、乙两人经过几分钟第一次相遇？（3分） （2）甲、丙两人经过几分钟第一次相遇？（3分） （3）甲、乙、丙三人的速度分别是多少？（6分） （4）丙沿湖边跑一圈需要多长时间？（3分）912FED CBA学校 班级 姓名 考号 指导老师密 封 线 内 禁 止 答 题2015年深圳学而思秋季超常班选拔考试四年级考 生 须 知1. 本试卷共4页，20题2. 本试卷满分150分，考试时间90分钟3. 在试卷密封线内填上填写学校、班级、姓名、联系电话一、填空题（共16题，每题6分，共96分，将答案填在下面的空格处）1. 计算：27 3.6 6.427=⨯+⨯____________．【解析】270．2. 小乐四次测试的成绩分别为98分，95分，90分和93分，这四次测试的平均分是__________分． 【解析】()98+95+90+934=94÷分．3. 4名工人3小时一共做了60个零件，按照这样的速度，12名工人8小时能做__________个零件．【解析】1名工人1小时做6043=5÷÷个，12名工人8小时能做5128=480⨯⨯个．4. 数一数，下图中共有__________个三角形．【解析】13个．5. 如图，边长为10厘米的正方形ABCD 里有一个三角形BEF ，AE =4厘米，FC =6厘米，三角形BEF的面积是_________平方厘米．【解析】38．6. 一个长方形的长和宽都是整数厘米，周长是30厘米，这个长方形的面积最大是__________平方厘米． 【解析】78=56⨯平方厘米．7. 如图，点D 是BC 边上的中点，AE 的长度是EC 长度的3倍，如果三角形ABC 的面积是48平方厘米，那么三角形EDC 的面积是__________平方厘米．【解析】488=6÷平方厘米．8. 下图中包含☆的长方形有__________个.【解析】412=48⨯个．9. 小超家和小越家相距2880米，小超每分钟走48米，小越每分钟走32米，两人同时出发相向而行，经过__________分钟两人相遇．【解析】()288048+32=36÷分钟．10. 用数字1、4、5、8、0能组成__________个没有重复数字的三位偶数． 【解析】431+332=30⨯⨯⨯⨯．11. 在一个宽为1米的长方形花坛周围铺上边长为1米的正方形石板路，如下图，如果花坛长2米，则会用到10块石板，如果花坛长度是3米，则会用到12块石板，如果花坛长度为a 米（a 为整数），则会用到__________块石板．（用含有a 的式子表示）【解析】26a +．12. 四位数462a 既是3的倍数，又是8的倍数，a =_________． 【解析】3a =．13. 1~100中，所有4的倍数的和是_________． 【解析】()4+100252=1300⨯÷．14. 一个数的所有数字和是23，每个数位上的数字各不相同，且不为0，这个数最大是__________． 【解析】1+2+3+4+5+6=21，最大的数为854321．15. 四年级2班布置联欢会的现场，每位男生吹12个气球，每位女生吹8个，全班45个人一共吹了460个气球，这个班有_________名女生．【解析】20名．FEDCBAECBA☆学理科到学而思16. 甲、乙两人现在的年龄和是63岁，当甲年龄等于乙现在年龄一半时，乙当时的年龄等于甲现在的岁数，那么甲现在__________岁．【解析】27岁．二、解答题（17题12分，18题12分，19题15分，20题15分，共54分，写出必要步骤，否则不得分）17. 如图，长方形ABCD 的长9AB cm =，12CF cm =，阴影部分ACE ∆的面积是218cm ．（1） 三角形ACF 的面积是多少平方厘米？（4分） （2） CE 的长度是多少厘米？（5分）（3） 长方形ABCD 的面积是多少平方厘米？（6分）【解析】（1）29122=54cm ⨯÷．（2）()54182126CE cm =-⨯÷=．（3）1826=6AD cm =⨯÷，长方形的面积是96=54⨯平方厘米．18. 数列：21，34，67，210，313，616，219……按照一定的规律排列．（1） 这个数列的第20个是什么？（4分）（2） 数列中157□的分子是几？（5分）（3） 数列中第几个数的分子和分母之和是418．（6分）【解析】此数列的分子是一个周期数列，分母是一个等差数列．（1）分子：203=62÷ ，分子为3；分母：1+193=58⨯，第20个是358．（2）157是这个数列的第()15713+1=53-÷个，分子是533=172÷ ，分子为3．（3）418=2+416=3+415=6+412，其中416不在分母是数列中，415是第139个，412是第138个；对于分子来说，第139个分子是2，第138个分子是6，所以6412满足要求，是第138个．19. 如图，宁宁、涛涛和浩浩三人合坐一辆出租车从学校回家．他们约定：共同乘坐的部分所产生的费用由乘坐者平均分摊；单独乘坐部分所产生的费用由乘坐者单独承担．（如：一段路程有3人乘坐，一共花费12元，则每人分担4元；一段路程只有1人乘坐，花费5元，则这5元由这1人承担．）此出租车没有起步价，且每公里的价格一样．结果三人承担的费用分别是6元、15元、21元．宁宁家离学校12公里．（1） 这次坐车的一共花了多少元？（4分）（2） 图中三段路程，每段路程的费用分别是多少元？（5分） （3） 浩浩家离学校有多少公里？（6分）【解析】（1）6+15+21=42元．（2）第①段：63=18⨯元，第②段：()15-62=18⨯元，第③段：21156-=元．（3）前两段花的钱一样，说明前两段都是12公里，第③段花了6元，所以为123=4÷公里，浩浩家离学校有12+12+4=28公里．20. 甲、乙、丙三人沿湖边练习跑步，三人同时从湖边的某一点出发，乙、丙两人顺时针跑，甲逆时针跑，在甲与乙第一次相遇后5分钟第一次遇到丙，再过15分钟第二次遇到乙．已知甲的速度是乙的1.5倍，湖的周长为8000米．（1） 甲、乙两人经过几分钟第一次相遇？（3分） （2） 甲、丙两人经过几分钟第一次相遇？（3分） （3） 甲、乙、丙三人的速度分别是多少？（6分） （4） 丙沿湖边跑一圈需要多长时间？（3分）【解析】（1）5+15=20分．（2）20+5=25分．（3）甲、乙两人的速度和为800020=400÷米/分，甲的速度是乙的1.5倍，乙的速度为()4001+1.5=160÷米/分，甲的速度是160 1.5=240⨯米/分，甲、丙的速度和是800025=320÷米/分，丙的速度是32024080-=米/分．（4）800080=100÷分．912FED CBA。
四年级超常班详解
联系电话：62164116/ 82618899
【答案】：15 【解析】：取一等奖中最后 4 名同学的平均分作为基准数．根据题目中的条件一有前六人 平均分 前十人平均分 2 ． 这说明在计算前十人的平均分时， 前六人共多出 6 2 12 (分)， 用来弥补后四人的分数．因而四人的平均分比前十名的平均分少 12 4 3 (分)．根据题目 中的条件二，当一等奖的后四人调整为二等奖后，二等奖者平均每人提高 2 分，这四人提 供 2 （20 4）=48 分，分给二等奖的 24 人，平均每人供给 48 4 12 (分)．综上可知，原来一 等奖的平均分比二等奖的平均分多 3 12 15 (分)． 五、 填空题（每题 12 分，共 24 分）
45 11 34 .
12. 任何大于 1 的自然数 n 阶乘表示方法为： n ! n (n 1) (n 2) 1 , 0! 1 ．现已知：
a ! b ! c ! 127 , 那么, 三位数 abc 有
【答案】：10 【解析】： 5! 120 ，
10. 一个三位数， 如果它的每一位数字都不小于另一个三位数对应数位上的数字， 就称它“吃 掉”另一个三位数， 例如： 532 吃掉 311， 123 吃掉 123， 但 726 与 267 相互都不被吃掉． 那 么，能吃掉 678 的三位数共有 【答案】：24 【解析】：即求百位数不小于 6，十位数不小于 7，个位不小于 8 的自然数．百位数不小于 6， 有 4 种；十位数不小于 7，有 3 种；个位不小于 8，有 2 种．由乘法原理，能吃掉 678 的三位数 共有 4 3 2 24 种． 11. 下图中不同的汉字表示不同的数字，相同的汉字表示相同的数字，那么，“四+年+级+学 +而+思+超+常”= . 个．
2021第4届学而思杯四年级(Word解析)
2021第4届学而思杯四年级（Word解析）2021年第四届全国学而思综合能力测评小学四年级（2021年4月7日）一、填空题（每题5分，共20分）1．定义：一天的“幸福指数”是12M?M2，其中M代表今天是星期几．例如，今天是4月7日星期一，那么今天的幸福指数就是12?1?12=11．那么，2021年劳动节（5月1日，星期四）的幸福指数是_________．2．在右图“学而思培优”的标志中，共有_________个四边形．3．学而思在“五一劳动节”即将发行新版积分卡．如果旧版积分卡上共出现300位老师，新版积分卡上共出现400位老师，其中有150位老师在新旧两版积分卡中都出现了，那么，在新旧两版积分卡上共出现了_________位老师．4．粗心的俊俊想要计算“1+2+3+4+5+6+7+8+9+10”的和，但他不慎把其中的一个数加了两次，结果得到了64．那么，俊俊把_________加了两次．二、填空题（每题6分，共24分）5．盛盛在玩一种“跑酷”游戏，他在跑道上奔驰，并拾起跑道上的金币．他每跑1米，会得到8分，每拾到一个金币，会得到15分．在一次游戏中，盛盛共跑了38米，得了2021分，那么，盛盛平均每米会拾到_________个金币．6．在下面的乘法竖式中，如果方框内填的数字都不是1和4，那么将竖式补充完整后，最后一行的乘积是_________．7．请你在下面的5个方框中，不重复的填入1～5这5个数字，组成一个算式（不允许添加括号）．要使得这个算式最后的计算结果是整数并且最大，这个最大的结果是_________．1 / 138．如下图，ABCD和ABEF都是长方形，如果长方形ABEF的面积是30平方厘米，那么阴影部分的面积是_________平方厘米．三、填空题（每题7分，共28分）9．甲乙丙丁4个队进行单循环赛，每两个队都要比赛一场．每场比赛胜者得3分，负者不得分，平局则双方各得1分．比赛全部结束后，发现甲队战胜了乙队，但甲队是最后一名（不与其它队并列），而乙队却是第一名（也不与其它队并列）．那么，这4个队的得分按甲乙丙丁的顺序组成的四位数是 _________．10．甲、乙、丙3人在一个周长是300米的环形跑道上同时出发，出发地和行走方向如图所示．已知，出发 15 秒后乙和丙第一次相遇，又过了10秒，甲和乙第一次相遇．那么，再经过_________秒，甲第一次追上丙．11．有些数，它们既可以表示成两个不同质数的和，也可以表示成两个不同质数的乘积，我们称这样的数是“未来数”．那么，两位数中，最大的“未来数”是_________．12．A、B、C、D、E、F六个人相约去照相（所有人都可以负责摄影），安排如图所示．他们6人的身高依次递增， A最矮，F最高．照相要求所有后排的人必须比所有前排的人高（摄影师身高不限），那么，共有________种不同的安排方式．四、填空题（每题8分，共32分）13．有一个神奇的五位数，它能同时被1、3、5、7、9、11、13、15 整除，却不能被2、4、6、8、10、12、14、16 中的任何一个数整除．那么，这个五位数是_________．2 / 1314．下图是一个正六边形，面积是360平方厘米，A、B、C、D分别是四条边的中点．那么，阴影部分的面积是_________平方厘米．15．如图，一个小正四面体印章，每面刻着1至4中的一个数字，各面数字互不相同．小明用这个小正四面体印章在右图的三角形格子内滚动，从任意一格以任意摆放方法开始，到任意一格结束，但要求每格恰好经过一次．那么，当滚动结束后，所有小三角形格中印下的数字之和共有_________种不同的取值．16．有12张卡牌，分别写着1～12，不同卡牌上的数互不相同．甲、乙、丙分别抓取其中的四张牌，进行游戏．规则如下：比赛分4轮，每轮三人各出一张牌（出过的牌不能再出），并计算三张牌的和，如果和比中间牌的3倍小，则出最小牌的人获胜，反之，则出最大牌的人获胜．如果和等于中间牌的3倍，则无人获胜．（例如：甲、乙、丙分别出的是 2、4、1，则乙获胜）．已知：① 四轮都有人获胜；② 甲四轮出牌顺序依次是 3、4、8、1，结果只有前 3 轮获胜；③ 乙第一次出了他手中四张牌中最小的牌；④ 乙、丙两人手中四张牌的和相等．那么，乙所拥有的四张牌的乘积是 _________．五、解答题（每题8分，共16分） 17．计算：（1）952?91?99 （2）4.7?8.4+9.4?19+4.7?3.618．计算：（1）12+1?2+22?2?3?32?…+92?9?10?1023 / 13（2）(202120212021?202120212021)?(20212021?20212021)六、解答题（每题15分，共30分）19．甲、乙两人平时喜欢散步．甲从A地出发，每走5分钟就要休息2分钟，需要50分钟走到B地．乙从B地出发，每走4分钟就要休息1分钟，需要74分钟走到A地．已知，A、B两地的距离是3600米．（1）如果甲不休息，走完全程需要多少分钟？（2）有一天，甲、乙分别从A、B两地同时出发，相向而行（各自按先走后休息的方法走），经过25分钟后，甲、乙还相距多少米？（3）接（2）问，甲、乙继续行走，当两人第一次相遇时，甲从出发开始总共走了多少米？20．把从1开始的自然数按照下图方式排列（下图只给出了这个数表的一部分）．如果我们认为1在第0行第0列，6在第上2行第0列，12在第0行第左2列，19在第下2行第右1列．请问：（1）在第上2行第右3列的数是多少？（2）自然数2021在第几行第几列？（要求写出方向）（3）从1开始向上数100个数（1算作第1个，向后依次是2，6，14……），那么，这100个数的和是多少？4 / 132021年第四届全国学而思综合能力测评小学四年级参考答案1 32 11 94 2 8 12 723 550 13 450454 9 14 2105 3 15 46 94658 16 3150 96 15 3644 17 18 19 （1）16（1）715 （1）36；（2）235 （2）20002 （2）500；（3）2160 7 8 10 50 20 （1）45；（2）第上5行第右28列；（3）646999 部分解析一、填空题（每题5分，共20分）1．定义：一天的“幸福指数”是12M?M2，其中M代表今天是星期几．例如，今天是4月7日星期一，那么今天的幸福指数就是12?1?12=11．那么，2021年劳动节（5月1日，星期四）的幸福指数是_________．【考点】定义新运算【难度】☆ 【答案】32【解析】12?4?42=32．2．在右图“学而思培优”的标志中，共有_________个四边形．【考点】几何计数【难度】☆ 【答案】8【解析】有5个大四边形和3个重叠的，共8个．3．学而思在“五一劳动节”即将发行新版积分卡．如果旧版积分卡上共出现300位老师，新版积分卡上共出现400位老师，其中有150位老师在新旧两版积分卡中都出现了，那么，在新旧两版积分卡上共出现了_________位老师．【考点】容斥原理【难度】☆ 【答案】550【解析】300+400?150=550．4．粗心的俊俊想要计算“1+2+3+4+5+6+7+8+9+10”的和，但他不慎把其中的一个数加了两次，结果得到了64．那么，俊俊把_________加了两次．【考点】等差数列5 / 13感谢您的阅读，祝您生活愉快。
2021年超常思维英语4年级试题+答案
2021年超常思维竞赛外语四年级考试时间：80分钟满分：100分一、词汇。
选出最佳答案。
（答案只有一个）()1.My______is my brother’s son.A.cousinB.nieceC.nephewD.grandson()2.A room used for sleeping in is the_______.A.living roomB.kitchenC.bathroomD.bedroom()3.A policeman to a policewoman as a waiter to a/an______.A.actorB.waitressC.customerD.cashier()4.The meals between7:00and9:00is breakfast,What is the meals between19:00 and21:00?A.dinnerB.breakfastC.lunchD.food()5.I’ve got_______above my eye.A.earB.eyebrowC.noseD.tongue()6.The duck quacks and the bee______.A.miaowsB.roarsC.barksD.buzzes()7.If you want to travel by plane,you need to go to the_______.A.train stationB.airportC.bus stationD.fire station ()8.A parking lot is where you can______.A.play footballB.park your carC.go shoppingD.walk your dog ()9.Which fruit doesn’t have to be peeled when we eat them?A.orangesB.applesC.bananasD.grapefruit ()10.Hopeless means having no hope,then what does homeless mean?A.have a homeB.at homeC.without a homeD.go home()11.David works in a pet clinic.He helps sick animals.What is David’s job?He’s a_____.A.vetB.farmerC.firemanD.doctor()12.Which word is not like the others?A.byB.inC.underD.go()13.The teacher writes on the_______.A.chairB.boardC.deskD.door()14.The period between classes when children do not study is called a______.A.recessB.textbookC.headteacherD.PE()ually we put books on the shelf,then where do we put bowls and plates?_______________A.On the armchair.B.In the fridge.C.In the cupboard.D.In the restroom. ()16.As write to a writer,work to a worker,teach to a teacher,cook to a______.A.cookerB.cookC.cookingD.cooked()17.As feet to shoes,hands to_______.A.socksB.fingersC.glovesD.hat()18.Red foxes_______for food under the snow.A.makeB.cookC.waveD.dig()19.Which is NOT junk food?_______.A.DumplingsB.ColaC.CrispsD.Fried chips()20.Where do you go for help when you have a fever?_______.A.Ice cream shopB.Shopping MallC.HospitalD.Pet clinic二、不定项选择。