数学建模简单13个例子共40页
数学建模简单13个例子全解

数学建模简单13个例子全解数学建模是一种将数学方法和技术应用于实际问题解决的过程。
它是数学领域的一个重要分支,具有广泛的应用和重要的研究价值。
数学建模能够帮助我们理解和解决许多复杂的现实问题,对于推动科学研究和技术开发具有重要作用。
在现代科学和工程领域,数学建模被广泛运用于各种领域,包括物理、生物、经济、环境、社会等。
通过数学建模,我们可以通过数学方法对问题进行抽象和化简,然后利用数学工具和技术进行分析和求解。
数学建模的过程通常包括问题定义、模型构建、模型分析和模型验证等步骤,其中数学模型的选择和建立是关键的一步。
数学建模的重要性在于它能够帮助我们更好地理解和解决复杂的现实问题。
通过数学建模,我们可以用精确的数学语言和方法描述问题,通过数学分析和计算实现对问题的量化和定量化,为问题的解决提供科学的依据和方法。
数学建模还能够帮助我们发现问题中的规律和关联,提供新的洞察和预测,促进科学的发展和技术的创新。
本文将介绍数学建模的概念和重要性,并给出简单13个例子的全解。
通过这些例子,我们可以更加深入地了解数学建模的基本方法和技巧,培养和提高自己的数学建模能力,为解决实际问题提供有益的借鉴和参考。
描述如何利用数学建模解决鱼群聚集问题,并阐述模型的步骤和应用在鱼群聚集模型中,我们希望通过数学建模来解释鱼群在水中聚集的现象,并找到一种合适的模型来描述鱼群的行为。
步骤:收集数据:首先,我们需要收集关于鱼群聚集的现实数据。
这些数据可以包括鱼群的数量、鱼群的密度、鱼群的移动速度等。
建立模型:基于收集到的数据,我们可以建立一个数学模型来描述鱼群的聚集行为。
常用的模型包括离散模型和连续模型。
离散模型:离散模型将鱼群视为一组个体,每个个体根据一定的规则进行移动和相互作用。
常见的离散模型包括离散元胞自动机模型和离散粒子模型等。
连续模型:连续模型将鱼群视为一个连续的流体,采用偏微分方程来描述鱼群密度的演化。
常见的连续模型包括Navier-Stokes方程和Birds模型等。
数学建模的简单实例ppt课件
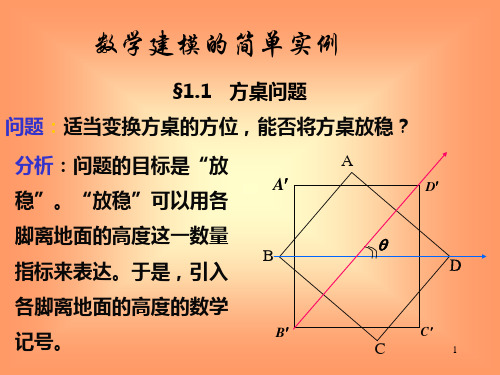
§1.1 方桌问题
问题:适当变换方桌的方位,能否将方桌放稳?
分析:问题的目标是“放
A
A
D
稳”。“放稳”可以用各
脚离地面的高度这一数量
B
指标来表达。于是,引入
各脚离地面的高度的数学
记号。
B
C
C
1
依次记 A、B、fc fD
A
D
fA( ) fB ( ) fC ( ) fD ( )
2
注意到,在任何情况下,总有三只脚能同时着地,且这三 只脚中总有两只脚处在对角位置上,于是我们记:
f ( ) fB( ) fD( ) g( ) fA( ) fC ( )
则 有 , f ( ) g( ) 0
仓库;可关闭2号或3号仓库。 公司不主张仓库的个数 超过4个。 由于向客户供货的运费和仓库改建的费用
均由公司负担, 故需建模为公司选择方案。
若有可能, 应将所建模型推广为适应于类似地更一般 情 形 下 的 方 案 选 择。
13
问题分析
公司的目标是费用尽可能小
费用是怎样构成的
工厂到仓库
运输费用
工厂到客户 问题分析
0
cij Ai到B j及Ck的单位运输费;
d jk B j到Ck的单位运输费;
e1 B1扩建的月增费; e5 B5的月增费; e2 , e3 B2 , B3变更时发生的费用;
保留B2 关闭B2
;
xij
Ai
到B
j
及C
的运
k
量;
新建B5 不建B5
;
y jk
B
j
到C
的运
数学建模简单实例

一些简单实例
% 用二分法求山崖高度 k = 0.05; g = 9.81; left = 0.0; right = 3.9; eps = 1.0; while (abs(eps) > 0.1) t2 = (left + right) / 2; t1 = 3.9 - t2; h2 = 340 * t2; h1 = g * (t1 + exp(-k * t1) / k) / k - g / k^2; eps = h1 - h2; if (eps > 0) left = t2; 运行结果为: else >> shanyagaodu1 right = t2; t2 = end 0.1871 end h= t2 63.6130 h = 340 * t2
2 2
A(0,b) 航母,速度V1
θ1 θ2
O
B(0,-b) 护卫舰,速度V2
X
令:
a2 1 2ab h 2 b, r 2 a 1 a 1
10
一些简单实例
则上式可简记成 :
x ( y - h) r y (tan 2 ) x b (护卫舰的路线方程) y (tan 1 ) x b (航母的路线方程)
n
25
an=0
一些简单实例
对第二问:假设还贷k个月后,利率发生了
变化。则第k个月后还应还给银行的总金额
为:
ak= a0(1+r)k-x[(1+r)k-1]/[(1+r)-1]
而我们可以将此总金额作为最初的贷款额,
而需还贷的时间则是n-k个月。
26
D L
间内,车辆仍将向前行驶一段距离 L。
4
一些简单实例
数学建模经典例题

A题机组组合问题当前的科学技术还不能有效地存储电力,所以电力生产和消费在任何时刻都要相等,否则就会威胁电力系统安全运行。
又由于发电机组的物理特性限制,发电机组不能够随心所欲地发出需要的电力。
为了能够实时平衡变化剧烈的电力负荷,电力部门往往需要根据预测的未来电力负荷安排发电机组起停计划,在满足电力系统安全运行条件下,追求发电成本最小。
在没有电力负荷损耗以及一个小时之内的电力负荷和发电机出力均不变的前提下,假定所有发电机组的发电成本都是由3部分组成,它们是启动成本(Startup Cost),空载成本(No load cost)和增量成本(Incremental Cost)。
需要考虑的约束有:1.负荷平衡约束:任何小时,电力负荷之和必须等于发电机发电出力之和。
2.系统备用约束:处于运行状态的发电机的最大发电能力减去其出力称为该发电机的备用容量,处于停运状态的发电机的备用容量为0。
任何小时,发电机的备用容量之和必须大于系统备用要求。
3.输电线路传输容量约束:线路传输的电能必须在它的传输容量范围内。
4.发电机组出力范围约束:处于运行状态的发电机组的发电出力必须小于其最大发电能力(Pmax, MW)。
5.机组增出力约束(Ramp Up, MW/h):发电机组在增加发电出力时,不能太快,有一个增加出力的速度上限,在一定时间内(通常是10分钟,为简单起见,本题取1个小时)不能超过额定范围。
6.机组降出力约束(Ramp Down, MW/h):与机组增出力约束类似,发电机组在减少发电出力时也有一个减少出力的速度上限。
问题1:3母线系统有一个3母线系统,其中有2台机组、1个负荷和3条输电线路,已知4个小时的负荷和系统备用要求。
请求出这4个小时的最优机组组合计划。
最终结果应该包括总成本、各小时各机组的状态、各小时各机组的发电出力和各小时各机组提供的备用。
所有数据请见下面图及表格,“3BusData”目录中还有包含了本题所有表格数据的5个xml文件。
数学建模举例
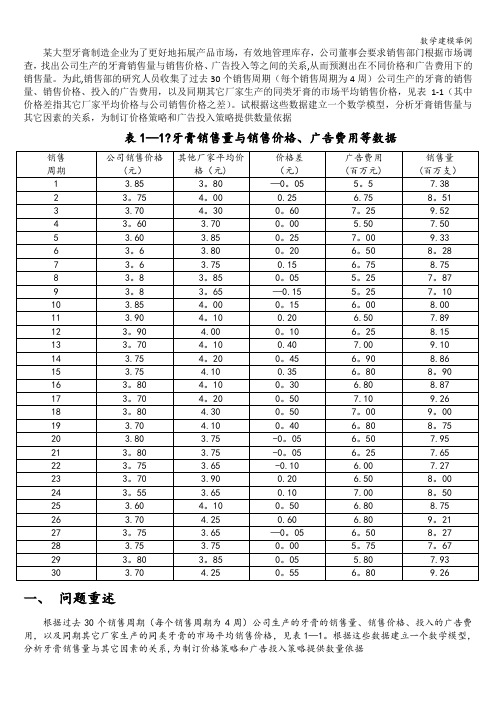
某大型牙膏制造企业为了更好地拓展产品市场,有效地管理库存,公司董事会要求销售部门根据市场调查,找出公司生产的牙膏销售量与销售价格、广告投入等之间的关系,从而预测出在不同价格和广告费用下的销售量。
为此,销售部的研究人员收集了过去30个销售周期(每个销售周期为4周)公司生产的牙膏的销售量、销售价格、投入的广告费用,以及同期其它厂家生产的同类牙膏的市场平均销售价格,见表1-1(其中价格差指其它厂家平均价格与公司销售价格之差)。
试根据这些数据建立一个数学模型,分析牙膏销售量与其它因素的关系,为制订价格策略和广告投入策略提供数量依据表1—1?牙膏销售量与销售价格、广告费用等数据一、问题重述根据过去30个销售周期(每个销售周期为4周)公司生产的牙膏的销售量、销售价格、投入的广告费用,以及同期其它厂家生产的同类牙膏的市场平均销售价格,见表1—1。
根据这些数据建立一个数学模型,分析牙膏销售量与其它因素的关系,为制订价格策略和广告投入策略提供数量依据二、 问题分析由于牙膏是生活必需品,对大多属顾客来说,在购买同类产品的牙膏是更多地会在意不同品牌之间的价格差异,而不是它们的价格本身.因此,在研究各个因素对销量的影响时,用价格差代替公司销售价格和其他厂家平均价格更为合适。
三、 模型假设1. 画出牙膏销售量与价格差,公司投入的广告费用的散点图2. 由散点图确定两个函数模型,再由这两个函数模型解出回归模型3. 对模型进行改进,添加新的条件确定更好的回归模型系数,得到新的回归模型4.对模型进一步改进,确定最终的模型四、 符号约定牙膏销售量为y,其他厂家平均价格和公司销售价格之差(价格差)为x1,公司投入的广告费用为x2,其他厂家平均价格和公司销售价格分别为x3和x4,x1=x3-x4。
基于上面的分析,我们仅利用1x 和2x 来建立y 的预测模型。
五、 模型的建立和求解1. 基本模型利用表1—1的数据用matlab 作出y 与x1的散点图(图1—1),y 与x2的散点图(图1-2) 代码如下:x1=[—0.05 0.25 0。
数学建模简单示例

否则一处的车辆将会越积越多。
例4 飞机失事时,黑匣子会自动打开,发射 出某种射线。为了搞清失事原因,人们必须 尽快找回匣子。确定黑匣子的位置,必须确 定其所在的方向和距离,试设计一些寻找黑 匣子的方法。由于要确定两个参数,至少要 用仪器检测两次,除非你事先知道黑匣子发 射射线的强度。
方法一
点光源发出的射线在各点处的照度与其到点光源的 2 的平方成反比,即
例2 某人第一天由 A地去B地,第二天由 B地沿原路返回 A 地。问:在什么条件下, 可以保证途中至少存在一地,此人在两天 中的同一时间到达该地。
分析 本题多少 有点象 数学中 解的存在 性条件 及证明,当 然 ,这里的情况要简单得多。 假如我们换一种想法,把第二天的返回改变成另一人在同 一天由B去A,问题就化为在什么条件下,两人至少在途中 相遇一次,这样结论就很容易得出了:只要任何一人的到 达时间晚于另一人的出发时间,两人必会在途中相遇。
初中数学建模的若干简要案例

初中数学建模的若干简要案例初中数学建模学习案例1 :----- 与自行车有关的问题(小组学习实践)课题:了解自行车中的数学问题,应用学过的数学知识,解决以下问题。
问题1 :用自己或同学的一辆自行车为观察对象,观察并解决下列问题:( 1 )我观察的这辆自行车是什么牌子的?( 2 )它的直径是_______cm ,轮子转动一周,在地面走过的距离是_______cm ,精确到1cm 。
( 3 )自行车中轴的大齿轮盘的齿数是_______齿,后轴的小齿轮(飞轮)的齿数是_______,中轴的大齿轮被踏动一周时,后轴的小齿轮在链条传动下,不计算惯性将转动_______周(保留2 位小数)。
问题2 :如果你有自行车,并骑车上学,你能借助于自行车,测量出从你的家到学校的路程吗?请你设计一个测量方案,并尽可能地通过实际操作测量出从你的家到学校的路程。
问题3 :如果你的(或你的朋友)自行车是可以变速的自行车(如山地车、多飞轮的自行车)、请你观察一下在这辆自行车上有几个(中轴上的)大轮盘,几个飞轮,它们都各有多少齿?记录这些数据。
如果你骑车时每一秒脚蹬一圈,请你根据上面测量的数据计算出这辆自行车运行时最大的速度和最小的速度各是每小时多少公里?:选做问题4 :你认为对问题 3 中的自行车的各个齿轮的齿数安排的合理吗?你能发现或提出什么样的问题?如果有可能请你做设计改进的话,你会做什么?求解工作的表格省略初中数学数学建模案例 2 :----- 线路设计问题(自学、探索、创新实践)课题:为所在小区设计一个最佳的邮政投递路线, 、一个合理的保安巡逻路线。
实施建议:1: 按居住地成立4-6 人的小组,对你们要研究的小区, 进行观察, 收集必要的数据和信息,( 如平面图, 楼的门洞的朝向, 道路情况, 小区的进出口位置等). 发挥各自的特长,分工合作完成测量方案的设计、实测、作图、计算、论证、比较、计算机文稿录入、结果介绍等。
简单数学建模100例完整

简单数学建模100例(可以直接使用,可编辑优秀版资料,欢迎下载)“学”以致用-----简单数学建模应用问题100例数学教学过程中学习了一个数学公式后,需要做大量的应用题,通过训练来加深理解所学公式。
但是在生活中又有多少实际问题是可以直接套用公式的呢?理想状态下的公式直接运用,在生产及生活中的实例是少之又少。
为此学生总感到学了数学没有什么实际用处,所以对学习数学少有兴趣。
数学建模的引入对培养学生利用数学方法分析、解决实际问题的能力开辟了一条有效的途径,让中职学生从中体会到数学是来源于生活并应用于生活的.数学建模是一种思维方式,它是一个动态的过程,通过此过程可以将一个实际的问题,经过模型准备、模型假设、模型构成、模型解析、模型检验与应用等五个具体步骤,转变为可以用数学方法(公式)来解决的,在理想状态下的数学问题,上述的整个流程统称为数学建模如果想解决某个实际问题(也许它和数学没有直接的关系),可以按下面流程对问题进行数学建模。
一.模型准备先了解该问题的实际背景和建模目的,尽量弄清要建模的问题属于哪一类学科的问题,可能需要用到哪些知识,然后学习或复习有关的知识,为接下来的数学建模做准备.由于人们所掌握的专业知识是有限的,而实际问题往往是多样和复杂的,模型准备对做好数学建模问题是非常重要的.二.模型假设有了模型准备的基础,要想把实际问题变为数学问题还要对其进行必要合理的简化和假设.明确了建模目的又掌握了相关资料,再去除一些次要因素.以主要矛盾为主来对该实际问题进行适当的简化并提出一些合理的假设。
模型假设不太可能一蹴而就,可以在模型的不断修改中得到逐步完善.三.模型构成在模型假设的基础上,选择适当的数学工具并根据已知的知识和搜集的信息来描述变量之间的关系或其他数学结构(如数学公式、定理、算法等).做模型构成时可以使用各种各样的数学理论和方法,但要注意的是在保证精度的条件下尽量用简单的数学方法是建模时要遵循的一个原则.四.模型解析在模型构成中建立的数学模型可以采用解方程、推理、图解、计算机模拟、定理证明等各种传统的和现代的数学方法对其进行求解,其中有些可以借助于计算机软件来做这些工作。
