4.2解一元一次方程(二)
六年级上册数学习题课件 4.2.2用移项法解一元一次方程 鲁教版

夯实基础
14.【中考·聊城】在如图所示的2016年6月份的月历表中, 任意框出表中竖列上三个相邻的数,这三个数的和不 可能是( )
A.27 B.51
C.69
D.72
夯实基础
【点拨】设框出的三个数中最上面的数为x,则中间的 数为x+7,最下面的数为x+14, 故三个数的和为x+x+7+x+14=3x+21. 当3x+21=27时,x=2;当3x+21=51时,x=10; 当3x+21=69时,x=16;当3x+21=72时,x=17,但 x=17这种情况不存在.故选D. 【答案】D
a(x+1)=12
a+x 的解,则 a 的值是 5 .
夯实基础
7.已知关于 x 的方程 3a-x=x2+3 的解为 x=2,则 式子 a2-2a+1 的值是 1 .
夯实基础
8.解方程 3x-4=3-2x 的过程的正确顺序是( C ) ①合并同类项,得 5x=7; ②移项,得 3x+2x=3+4; ③系数化为 1,得 x=75. A.①②③ B.③②① C.②①③ D.③①②
探究培优
22.【中考·安徽】《九章算术》中有一道阐述“盈不足 术”的问题,原文如下: 今有人共买物,人出八,盈三;人出七,不足四. 问人数,物价各几何? 译文为: 现有一些人共同买一个物品,每人出8元,还盈余3 元;每人出7元,则还差4元,问共有多少人?这个 物品的价格是多少?
探究培优
请解答上述问题.
夯实基础
15.解方程:x-3=-12x-4. 错解:移项,得 x-12x=-4-3.合并同类项,得12x =-7.系数化为 1,得 x=-14.
诊断:在解方程移项时,所移的项一定要变号,但 有的学生不管移的项还是没移的项一律都变号或都 不变号,这两种做法都是不正确的.
2022六年级数学上册 第四章 一元一次方程 2解一元一次方程(2)课件 鲁教版五四制

即
x-1=-2
x=-2+1 x=-1
练习
1.解下列方程: (1)2(3—x)=9; (2)−3(x +3) =24; (3)11x +1 =5(2x + 1); (4)5(x—1)=1;
x =-1.5 x =-11
x =4
x=1.2
(5)2 — (1—x)= —2;
5.某商店购进一批运动服,每件售价120元, 可获利20%,这种运动服每件的进价是多少 元?
解:设这种运动服每件的进价是X元。 根据题意,得(1+20%)X=120
120%X=120
X=100 答:这种运动服每件的进价是100元。
6.植树节某班要栽100棵树,有5名同学每人都栽了2棵, 其余的同学每人栽3棵,正好全部栽完,问这个班共有多 少名学生?
如果设一听果奶饮料x元,那么可列出方程 4(x+0.5)+x=10-3
想一想
(1)上面这个方程列的对吗?你还能列出不同的方程吗?
(2)怎样解所列的方程?
你知道一听果奶饮料多少 钱吗?解出你所列的方程。
例3 解方程:4(x+0.5)+x=7.
此方程与上课时所学方程有何差异?
方程中含 有括号
须先去括号
4.2 解一元一次方程(2)
小颖到超市准备买1听果奶饮料和4听可乐,营业员告诉她一 听可乐比一听果奶饮料多0.5元,小颖给了营业员10元钱,营 业员找回了3元,大家帮助小颖算算一听果奶饮料多少钱?
小颖到超市准备买1听果奶饮料和4听可乐,营业员告诉她一 听可乐比一听果奶饮料多0.5元,小颖给了营业员10元钱,营 业员找回了3元,大家帮助小颖算算一听果奶饮料多少钱?
合并同类项
4.2 解一元一次方程的算法

4.2 解一元一次方程的算法42 解一元一次方程的算法在数学的世界里,方程就像是一座桥梁,连接着已知和未知。
而一元一次方程,作为方程家族中的“基础成员”,其解法有着重要的地位和广泛的应用。
今天,咱们就来好好聊聊解一元一次方程的算法。
一元一次方程,形式通常是 ax + b = 0 (其中 a 和 b 是常数,且 a ≠ 0)。
解这样的方程,其实就是找出那个能让等式成立的未知数 x 的值。
先来说说最基本的思路。
我们的目标是把方程逐步变形,最终让 x 单独在等式的一边。
比如说,对于方程 3x + 5 = 14,第一步,我们要把常数项 5 移到等式右边,变成 3x = 14 5,这一步依据的是等式的基本性质:等式两边同时加上或减去同一个数,等式仍然成立。
接下来,计算 14 5 得到 3x = 9。
然后,为了让 x 单独出现,因为3 乘以 x 等于 9,所以 x 就等于 9 除以 3,即 x = 3。
这一步的依据是等式两边同时乘以或除以同一个非零数,等式仍然成立。
再举个例子,方程-2x + 7 = 1,先把 7 移到右边得到-2x = 1 7,也就是-2x =-6。
这时,两边同时除以-2,算出 x = 3。
有时候,方程可能会稍微复杂一点,比如有括号。
像 2(x 3) + 5 =11,这时候我们先运用乘法分配律把括号去掉,得到 2x 6 + 5 = 11,整理一下就是 2x 1 = 11。
然后把-1 移到右边变成 2x = 11 + 1,即2x = 12,最后得出 x = 6。
还有分母的情况,比如(x + 1) / 2 = 3。
这时候要先把分母去掉,两边同时乘以 2,得到 x + 1 = 6,接着算出 x = 5。
解一元一次方程的过程,其实就是不断运用等式的基本性质,进行变形和化简。
通过这些步骤,我们就能找到那个神秘的 x 的值。
在实际应用中,一元一次方程的解法用处可大了。
比如说,我们在计算物品的单价、行程问题中的速度、工程问题中的工作效率等等,都可能会用到一元一次方程。
解一元一次方程(第二课时 移项与合并同类项)(课件)七年级数学上册(苏教版)

探索与思考
如何求方程3x+20=4x-25的解?
3x+20 = 4x-25
3x+20-4x-20=4x-25-4x-20
3x-4x=-25-20
-x=-45
x=45
把它变成x=a(常数)的形式
等式两边都含有
x的项和不含字母的常数项。
利用等式性质1,将等式
变为x=a(常数)的形式
合并同类项
探索与思考
数学(苏科版)
七年级 上册
第四章 一元一次方程
4.2 解一元一次方程
第二课时 移项与合并同类项
课前回顾
等式的两边都加上(或减去)同一个数(或同一个式子),所得的结
果仍是等式。
如果a=b,那么a±c=a±c
等式两边都乘以同一个数,或都除以同一个不为0的数,结果仍相等。
如果a=b,那么ac = bc
如果a=b,那么
因为这批书的总数是一个定值,
表示它的两个式子应相等
(2)每人分3本,还剩余20本,则这批书共
(3x+20)
_______ 本;
(3)每人分4本,还缺25本,则这批书共 (4x-25)
______本;
3x+20=4x-25
(4)根据题意可列方程为________________________
等式左右两边都有未知数,如何求得方程的解呢?
合并同类项: 7x=24
系数化为1 :
24
x= .
7
(4) x+ =
x-3
1
2
移项:x- x=-3-2
1
2
合并同类项: x=-5
系数化为1 :x=-10.
利用移项与合并同类项移项解方程
苏科版七年级上册数学4.2《解一元一次方程》课件 (共20张PPT)

移项、合并同类项,得 5x=10
系数化为1,得 x=2
讲授新课
如何解方程 x 2 x 1 3? 0.2 0.5
解:去分母,得 5(x-2)-2(x+1)=3 去括号,得 5x-10-2x-2=3 移项、合并同类项,得 3x=15 系数化为1,得 x=5
讲授新课
解一元一次方程有哪些步骤? 一般步骤:去分母;去括号;移项;合并同类项; 未知数系数化为1.
讲授新课 例3、解方程:2x=5x-21 思考:方程2x=5x-21变形为2x-5x=-21 解:两边都减去5x,得 从形式上发生了什么变化? 2x-5x=-21 合并同类项,得 -3x=-21 两边都除以-3,得 x=7 方程中的某些项改变符号后,可以从方程的一边移到另一 边,这样的变形叫做移项 .
讲授新课
例4、解方程:x-3=4- 1 x
解:移项,得
1 x+
2 x=4+3
合并同类项,得3 2 x=7
两边都除以
3,得2
14 x=
2
3
方 乘程2 ,32 都x=能7的把两未边知都数除的以系32数或化 3
为1.
注意:(1)移项时,通常把含有未知数的项移到等号的左边,
把常数项移到等号的右边.
(2)移项要改变符号.
5x=15 系数化为1,得 x=3
(2) x 1 x 3 2
解:去分母,得 x-1=2(x+3) 去括号,得 x-1=2x+6 移项、合并同类项,得 -x=7 系数化为1,得 x=-7
移项,得 -4x=7-3-3
合并同类项,得 -4x=1
两边除以-4,得
1 x=-
4
(2)x-3 =2(x+1) 解:去括号,得 x-3=2x+2 移项,得 x-2x=2+3 合并同类项,得 -x=5 两边除以-1,得 x=-5
课时编号4.2解一元一次方程.2(去括号)
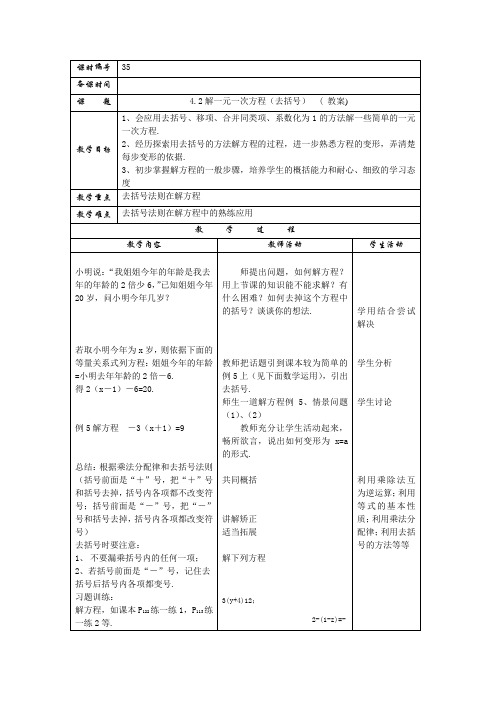
不要漏乘括号内的任何一项;
若括号前面是“-”号,记住去括号后括号内各项都变号
板书设计
情境创设
1、
2、
例1:……
……
……
例2:……
……
……
习题……
……
……
作业布置
P102
课后随笔
注意解法的灵活性,不要过分强求学生按固定格式来解,可适当引导学生找出较好的解题方法和书写过程.
共同概括
讲解矫正
适当拓展
解下列方程
3(y+4)12;2-(1-z)=-2;
2(3y-4)+7(4-y)=4y;4x-3(20-x)=6x-7(9-x);
3(2y+1)=2(1+y)+3(y+3)
学用结合尝试解决
学生分析
学生讨论
利用乘除法互为逆运算;利用等式的基本性质;利用乘法分配律;利用去括号的方法等等
教学重点
去括号法则在解方程
教学难点
去括号法则在解方程中的熟练应用
教学过程
教学内容
教师活动
学生活动
小明说:“我姐姐今年的年龄是我去年的年龄的2倍少6,”已知姐姐今年20岁,问小明今年几岁?
若取小明今年为x岁,则依据下面的等量关系式列方程:姐姐今年的年龄=小明去年年龄的2倍-6.
得2(x-1)-6=20.
3.有什么收获?
初步掌握了解方程的一般步骤,培养自己的概括能力和耐心、细致的学习态度.
师提出问题,如何解方程?用上节课的知识能不能求解?有什么困难?如何去掉这个方程中的括号?谈谈你的想法.
教师把话题引到课本较为简单的例5上(见下面数学运用),引出去括号.
练习52 4.2 解一元一次方程(2)

学校班级姓名考号________________考试时间 ______________装订线内不要答题 ◆◆◆◆◆◆◆◆◆◆◆◆◆装◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆订◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆线◆◆◆◆◆◆◆◆ 2014-2015学年度七年级数学练习五十二 4.2 解一元一次方程(2) 本试卷共印6个班:初一9、10、11、12、14、15, 命题人:朱学范 时间:2014-11-19 一、选择题 1、方程3x+6=2x -8移项后,正确的是( ) A .3x+2x=6-8 B .3x -2x=-8+6 C .3x -2x=-6-8 D .3x -2x=8-6 2、方程7(2x-1)-3(4x-1)=11去括号后,正确的是( ) A .14x-7-12x+1=11 B. 14x-1-12x-3=11 C. 14x-7-12x+3=11 D. 14x-1-12x+3=11 3、如果代数式75-x 与94+x 的值互为相反数,则x 的值等于( ) A.29 B.29- C.92 D. 92- 4、如果123-n ab 与1+n ab 是同类项,则n 是( ) A.2 B.1 C.1- D.0 5、已知矩形周长为20cm ,设长为x cm ,则宽为 ( ) A.x -20 B.x -10 C.x 220- D. 220x - 6.如果x=1是方程x x m 2)(312=--的解,那么关于y 的方程2)3(--y m = )52(-y m 的解是( ) A. 10- B. 0 C. 34 D. 4 二、填空题. 7.方程2x-0.3=1.2+3x 移项得 . 8.方程12-(2x -4)= -(x -7)去括号得 . 9.若︱a ﹣1︱+(b+2)2=0,则a b = . 10.若3x+2与﹣2x+1互为相反数,则x-2的值是 . 11.若2(4a ﹣2)﹣6 = 3(4a ﹣2),则代数式a 2﹣3a + 4= . 12.代数式5m +14与5(m -14)的的值互为相反数,则m 的值为__________. 13.已知关于x 的方程x ax -=+42的解是21,则________=a.14.若0)22.0(6232=++-y x ,则_________22=+y x . 15.已知4-=x 是方程a x x -=+482的解,则_______12=+a a . 三、解答题.16.解下列方程(1) 312+=-x x (2) 234-=x x(3) x x 4613+=- (4)x x 2143+=+(5)454436+=-y y (6) 12131-=+x x(7)x x x x 43987--=+- (8) x x x 59182511-+=+(9)3(2x+5)=2(4x+3)-3 (10)4y ﹣3(20﹣y)=6y ﹣7(9﹣y)(11)|4x-1|=7 (12)2|x-3|+5=1317.已知2-=x 是方程612-=--k x 的解,求k 的值.18.已知:m my m y -=+21 (1)当4=m 时,求y 的值; (2)当4=y 时,求m 的值19.已知单项式5322b am +-与n m b a 253-的和是单项式,求2005)(n m +的值.20.观察方程32[23(x -4)-6]=2x+1的特点,你有好的解法吗?写出你的解法.21. a 为什么整数时,方程x ax =-4的解为整数?22.已知a 是整数,且a 比0大,比10小.请你设法找出a 的一些数值,使关于x 的方程1―21ax=―5的解是偶数,看看你能找出几个.22.2a —3x=12是关于x 的方程.在解这个方程时,粗心的小虎误将-3x 看做3x ,得方程的解为x=3.请你帮助小虎求出原方程的解.。
2024年秋新苏科版七年级上册数学教学课件 4.2 一元一次方程及其解法

解含有分母的一元一次方程时,方程各项都乘所有分母的最小公倍数,从而约去分母,这个过程叫作去分母. 不要漏乘没有分母的项.
B
变形名称
依据
具体做法
注意事项
去分母
等式的基本性质2.
依据
等式的基本性质1.
目的
把含有未知数的项移到方程的一边,把常数项移到另一边.
移项与加法交换律的区别移项是把某些项从等式的一边移到另一边,移动的项要变号;而加法交换律中加数交换位置只是改变排列的顺序,不改变符号.
一元一次方程:等号两边都是整式,且只含有一个未知数,未知数的次数都是1的方程,叫作一元一次方程. 一元一次方程包含三个要素:一是只含有一个未知数;二是等号两边都是整式;三是未知数的次数都是1.三者缺一不可.
②③
解析:
示例
解一元一次方程
_
概念
方程中的某些项改变符号后,可以从方程的一边移到另一边,这样的变形叫作移项.
第4章 一元一次方程
4.2 一元一次方程及其解法
七上数学 SK
1.理解一元一次方程的概念,能判断一个方程是不是一元一次方程,发展抽象能力.2.能根据等式的基本性质解一元一次方程,掌握解一元一次方程的方法.3.了解解一元一次方程的一般步骤,能熟练地解数字系数的一元一次方程.4.能根据一元一次方程的特点,灵活选择合适的步骤解一元一次方程,提高运算能力.
方程两边同时乘各分母的最小公倍数.
(1)不要漏乘不含分母的项;(2)当分子是多项式时,去分母后应将分子作为一个整体加上括号.
变形名称
依据
具体做法
注意事项
去括号
乘法分配律、去括号法则.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.2解一元一次方程(二)
(30分钟50分)
一、选择题(每小题4分,共12分)
1. 解方程-2(x-5)+3(x-1)=0 时,去括号正确的是()
(A) -2x-10+3x-3=0
(B) -2x+10+3x-1=0
(C) -2x+10+3x-3=0
(D) -2x+5+3x-3=0
1
2. 解方程4(y -1 )-y =2(y +3)的步骤如下:
解:①去括号,得4y-4-y=2y+1
②移项,得4y+y-2y=1+4
③合并同类项,得3y=5
④系数化为1,得得.
3
经检验y=5不是方程的解,则上述解题过程中是从第几步出错的() 3
(A) ①(B) ②(C) ③(D) ④
3. 方程2-“一4=:」-7去分母得()
3 6
(A) 2-2(2x-4)=-(x-7)
(B) 12-2(2x-4)=-x-7
(C) 12-2(2x-4)=-(x-7)
(D) 12-(2x-4)=-(x-7)
二、填空题(每小题4分,共12分)
4. 解方程:4(2x+3)=8(x-1)-5(x-2) 的解是____________ .
1 1
5. 当x= ________ 时,代数式—(x +1与-(x +2 )的差是1.
2 3
6. 若代数式y-5+5"2—上)的值是2,则y= .
4 6 4
三、解答题(共26分)
7. (8分)当x取什么值时,代数式X—8与代数式1 -^x的值相等.
3 2 6
第-1 - 页
8. (8分)已知关于x 的方程x • m = mX —m .
2 6 ⑴ 当m 为何值时,方程的解为x=4;
⑵当m=4时,求方程的解.
【拓展延伸】
9. (10 分)若 abc=1,解方程 2ax 2bx 2cx
=1.
ab+a + 1 bc+b+1 ca+c+1 答案解析
1.【解析】选C.将方程去括号,得 -2x+10+3x-3=0,故选 C.
2. 【解析】选B.第②步应为4y-y-2y=1+4而不是4y+y-2y=1+4.
3. 【解析】选C.方程两边同时乘以6得:
得:12-2(2x-4)=-(x-7).
4. 【解析】去括号,得8x+12=8x-8-5x+10,
移项,合并同类项,得5x=-10, 系数化1,得x=-2.
答案:x=-2
亠 1 1
由题意得 一(x +1 )-一(x +2 ) = 1,解得 x=7.
2 3
答案:7
由题意得,y+5汉(2-丫)= 2,解得y=2. 4 6 4
答案:2
去括号,得 2x-16=3-8+x.
移项,得 2x-x=3-8+16.
合并同类项,得x=11.
所以,当x=11时,代数式-―8
与代数式 3 【归纳整合】解方程中常见的错误有四种:
(1)去分母时不含分母的项忘记乘以最小公倍数;
(2)去分母时,分子是多项式,忘记加括号;
第-2 - 页
(3) 移项不变号;
7.【解析】 去分母,得 由题意得:X —8 3 2(x-8)=3-(8-x).
1 _8-x
2 6
5.【解析】
6.【解析】
1 8 —x 一- --- 的值相等.
2 6
(4)不验算或检验.
4 4m _
8. 【解析】⑴ 将x=4代入方程中有
2 6 去分母得12+6m=4m-m,
移项,合并同类项得-3m=12,解得m=-4. ⑵当m=4时,方程为x . 4 = 4x二4,
2 6
去分母得3x+24=4x-4,
移项,合并同类项得x=28.
9. 【解析】因为abc=1,所以原方程可变形为:化简整理为:
2(b+1]x 亠2cx [ 2(b+1)x 亠2cx =〔,
bc b 1 ca c 1 ' bc b abc ca c 1 ' 化简整理为:
2x b abc bc 1
1,2x=1,x bca bc b 2
1
所以x = * 1 2是原方程的解.
2。
