高三数学填空题专练(17)新人教版
2020届高三数学精准培优专练17:椭圆(一)

1.若椭圆x 216+y 2b 2=1过点(-2,3),则其焦距为( )A .2 5B .2 3C .4 5D .4 32.已知椭圆x 2a 2+y 2b 2=1(a>b>0)的焦点分别为F 1,F 2,b =4,离心率为35.过F 1的直线交椭圆于A ,B 两点,则△ABF 2的周长为( )A .10B .12C .16D .203.已知椭圆的中心在坐标原点,焦点在x 轴上,且长轴长为12,离心率为13,则该椭圆方程为( )A.x 2144+y 2128=1B.x 236+y 220=1C.x 232+y 236=1D.x 236+y 232=1 4.若椭圆x 29+y 24+k=1的离心率为45,则k 的值为( )A .-21B .21C .-1925或21 D.1925或215.若椭圆x 2+my 2=1的焦点在y 轴上,且长轴长是短轴长的两倍.则m 的值为( )A.14B.12 C .2 D .46.如图,已知椭圆C :x 2a 2+y 2b 2=1(a>b>0),其中左焦点为F(-25,0),P 为C 上一点,满足|OP|=|OF|,且|PF|=4,则椭圆C 的方程为( )A.x 225+y 25=1B.x 236+y 216=1C.x 236+y 210=1D.x 245+y 225=1 7.若焦点在x 轴上的椭圆x 22+y 2m =1的离心率为12,则m 等于( )A. 3B.32C.83D.238.已知椭圆x 2a 2+y 2b 2=1(a>b>0)的左、右焦点分别为F 1,F 2,过F 2的直线与椭圆交于A ,B 两点,若△F 1AB 是以A 为直角顶点的等腰直角三角形,则椭圆的离心率为( )A.22 B .2-3 C.5-2 D.6- 39.设斜率为22的直线l 与椭圆x 2a 2+y 2b 2=1(a>b>0)交于不同的两点,且这两个交点在x 轴上的射影恰好是椭圆的两个焦点,则该椭圆的离心率为( )A.33B.12C.22D.1310.已知椭圆C :x 2a 2+y 2b 2=1(a>b>0)的离心率为32,四个顶点构成的四边形的面积为4,过原点的直线l(斜率不为零)与椭圆C 交于A ,B 两点,F 1,F 2分别为椭圆的左、右焦点,则四边形AF 1BF 2的周长为( )A .4B .4 3C .8D .8 311.已知直线l :y =kx 与椭圆C :x 2a 2+y 2b 2=1(a>b>0)交于A ,B 两点,其中右焦点F 的坐标为(c ,0) ,且AF 与BF 垂直,则椭圆C 的离心率的取值范围为( ) A .[22,1) B .(0,22] C .(22,1) D .(0,22)12.在平面直角坐标系xOy 中,椭圆C 的中心为原点,焦点F 1,F 2在x 轴上,离心率为22.过F 1的直线l 交C 于A ,B 两点,且△ABF 2的周长为16,那么C 的方程为________. 13.若椭圆的方程为x 210-a +y 2a -2=1,且此椭圆的焦距为4,则实数a =________.14.若椭圆C :x 2a 2+y 2b 2=1(a>b>0)的左、右焦点与短轴的两个顶点组成一个面积为1的正方形,则椭圆C 的内接正方形的面积为________.15.已知F 1、F 2为椭圆x 2a 2+y 2b 2=1(a>b>0)的左、右焦点,M 为椭圆上一点,MF 1垂直于x 轴,且∠F 1MF 2=60°,则椭圆的离心率为________.16. 一个底面半径为2的圆柱被与底面所成角是60°的平面所截,截面是一个椭圆,则该椭圆的焦距等于________.17.已知F 1,F 2分别是椭圆C :x 2a 2+y 2b 2=1(a>b>0)的左、右焦点,若椭圆C 上存在点P ,使得线段PF 1的中垂线恰好经过焦点F 2,则椭圆C 的离心率的取值范围是________. 18.如右图,已知椭圆x 2a 2+y 2b 2=1(a>b>0),F 1,F 2分别为椭圆的左、右焦点,A 为椭圆的上顶点,直线AF 2交椭圆于另一点B.(1)若∠F 1AB =90°,求椭圆的离心率;(2)若椭圆的焦距为2,且AF 2→=2F 2B →,求椭圆的方程.19.设F 1,F 2分别是椭圆C :x 2a 2+y 2b 2=1(a>b>0)的左、右焦点,M 是C 上一点且MF 2与x 轴垂直,直线MF 1与C 的另一个交点为N.(1)若直线MN 的斜率为34,求C 的离心率;(2)若直线MN 在y 轴上的截距为2,且|MN|=5|F 1N|,求a ,b.1.若椭圆x 216+y 2b 2=1过点(-2,3),则其焦距为( )A .2 5B .2 3C .4 5D .4 3答案 D 解∵椭圆过(-2,3),则有416+3b 2=1,b 2=4,c 2=16-4=12,c =23,2c =432.已知椭圆x 2a 2+y 2b 2=1(a>b>0)的焦点分别为F 1,F 2,b =4,离心率为35.过F 1的直线交椭圆于A ,B 两点,则△ABF 2的周长为( )A .10B .12C .16D .20答案 D 解析 如图,由椭圆的定义知△ABF 2的周长为4a ,又e =c a =35,即c =35a ,∴a 2-c 2=1625a 2=b 2=16.∴a =5,△ABF 2的周长为20. 3.已知椭圆的中心在坐标原点,焦点在x 轴上,且长轴长为12,离心率为13,则该椭圆方程为( )A.x 2144+y 2128=1B.x 236+y 220=1C.x 232+y 236=1D.x 236+y 232=1 答案 D 解析 ∵2a =12,c a =13,∴a =6,c =2,b 2=32.∴椭圆的方程为x 236+y 232=1. 4.若椭圆x 29+y 24+k=1的离心率为45,则k 的值为( )A .-21B .21C .-1925或21 D.1925或21答案 C 解析 若a 2=9,b 2=4+k ,则c =5-k.由c a =45,即5-k 3=45,得k =-1925; 若a 2=4+k ,b 2=9,则c =k -5.由c a =45,即k -54+k =45,解得k =21.5.若椭圆x 2+my 2=1的焦点在y 轴上,且长轴长是短轴长的两倍.则m 的值为( )A.14B.12C .2D .4答案 A 将原方程变形为x 2+y 21m=1.由题意知a 2=1m ,b 2=1,∴a =1m ,b =1.∴1m =2,∴m =14. 6.如图,已知椭圆C :x 2a 2+y 2b 2=1(a>b>0),其中左焦点为F(-25,0),P 为C 上一点,满足|OP|=|OF|,且|PF|=4,则椭圆C 的方程为( )A.x 225+y 25=1B.x 236+y 216=1C.x 236+y 210=1D.x 245+y 225=1 答案 B 解析 设椭圆的焦距为2c ,右焦点为F 1,连接PF 1,如图所示. 由F(-25,0),得c =2 5.由|OP|=|OF|=|OF 1|,知PF 1⊥PF.在Rt △PFF 1中,由勾股定理,得|PF 1|=|F 1F|2-|PF|2=(45)2-42=8.由椭圆定义,得|PF 1|+|PF|=2a =4+8=12,从而a =6,得a 2=36,于是b 2=a 2-c 2=36-(25)2=16,所以椭圆C 的方程为x 236+y 216=1.7.若焦点在x 轴上的椭圆x 22+y 2m =1的离心率为12,则m 等于( )A. 3B.32C.83D.23答案 B 解析 ∵a 2=2,b 2=m ,∴c 2=2-m.∵e 2=c 2a 2=2-m 2=14.∴m =32.8.已知椭圆x 2a 2+y 2b 2=1(a>b>0)的左、右焦点分别为F 1,F 2,过F 2的直线与椭圆交于A ,B 两点,若△F 1AB 是以A 为直角顶点的等腰直角三角形,则椭圆的离心率为( )A.22 B .2-3 C.5-2 D.6- 3答案 D 设|F 1F 2|=2c ,|AF 1|=m ,若△ABF 1是以A 为直角顶点的等腰直角三角形,则|AB|=|AF 1|=m ,|BF 1|=2m.由椭圆的定义可得△ABF 1的周长为4a ,即有4a =2m +2m ,即m =(4-22)a ,则|AF 2|=2a -m =(22-2)a ,在Rt △AF 1F 2中,|F 1F 2|2=|AF 1|2+|AF 2|2,即4c 2=4(2-2)2a 2+4(2-1)2a 2,即有c 2=(9-62)a 2,即c =(6-3)a ,即e =ca =6-39.设斜率为22的直线l 与椭圆x 2a 2+y 2b 2=1(a>b>0)交于不同的两点,且这两个交点在x 轴上的射影恰好是椭圆的两个焦点,则该椭圆的离心率为( )A.33B.12C.22D.13答案 C 解析 由题意知,直线l 与椭圆x 2a 2+y 2b 2=1(a>b>0)两个交点的横坐标是-c ,c ,所以两个交点分别为(-c ,-22c),(c ,22c),代入椭圆得c 2a 2+c 22b 2=1,两边同乘2a 2b 2,则c 2(2b 2+a 2)=2a 2b 2.因为b 2=a 2-c 2,所以c 2(3a 2-2c 2)=2a 4-2a 2c 2,所以c 2a 2=2或12.又因为0<e<1,所以e =c a =22,故应选C.10.已知椭圆C :x 2a 2+y 2b 2=1(a>b>0)的离心率为32,四个顶点构成的四边形的面积为4,过原点的直线l(斜率不为零)与椭圆C 交于A ,B 两点,F 1,F 2分别为椭圆的左、右焦点,则四边形AF 1BF 2的周长为( )A .4B .4 3C .8D .8 3答案 C 解析 由⎩⎪⎨⎪⎧c a =32,2ab =4,c 2=a 2-b 2,解得⎩⎨⎧a =2,b =1.周长为4a =8.11.已知直线l :y =kx 与椭圆C :x 2a 2+y 2b 2=1(a>b>0)交于A ,B 两点,其中右焦点F 的坐标为(c ,0) ,且AF 与BF 垂直,则椭圆C 的离心率的取值范围为( ) A .[22,1) B .(0,22] C .(22,1) D .(0,22)答案 C 解析 由AF 与BF 垂直,运用直角三角形斜边的中线即为斜边的一半,可得|OA|=|OF|=c ,由|OA|>b ,即c>b ,可得c 2>b 2=a 2-c 2,即c 2>12a 2,可得22<e<1.故选C.12.在平面直角坐标系xOy 中,椭圆C 的中心为原点,焦点F 1,F 2在x 轴上,离心率为22.过F 1的直线l 交C 于A ,B 两点,且△ABF 2的周长为16,那么C 的方程为________. 解析 根据椭圆焦点在x 轴上,可设椭圆方程为x 2a 2+y 2b 2=1(a>b>0).∵e =22,∴c a =22.根据△ABF 2的周长为16得4a =16,因此a =4,b =22,所以椭圆方程为x 216+y 28=1.13.若椭圆的方程为x 210-a +y 2a -2=1,且此椭圆的焦距为4,则实数a =________.答案 4或8解析 ①当焦点在x 轴上时,10-a -(a -2)=22,解得a =4.②当焦点在y 轴上时,a -2-(10-a)=22,解得a =8.14.若椭圆C :x 2a 2+y 2b 2=1(a>b>0)的左、右焦点与短轴的两个顶点组成一个面积为1的正方形,则椭圆C 的内接正方形的面积为________.答案 43解析 由已知得,a =1,b =c =22,所以椭圆C 的方程为x 2+y 212=1,设A(x 0,y 0)是椭圆C 的内接正方形位于第一象限内的顶点,则x 0=y 0,所以1=x 02+2y 02=3x 02,解得x 02=13,所以椭圆C 的内接正方形的面积S =(2x 0)2=4x 02=43.15.已知F 1、F 2为椭圆x 2a 2+y 2b 2=1(a>b>0)的左、右焦点,M 为椭圆上一点,MF 1垂直于x 轴,且∠F 1MF 2=60°,则椭圆的离心率为________.答案 33 解析 方法一:∵|F 1F 2|=2c ,MF 1⊥x 轴,∴|MF 1|=233c ,|MF 2|=433 c. ∴2a =|MF 1|+|MF 2|=23c.∴e =2c 2a =33.方法二:由F 1(-c ,0),将x =-c 代入x 2a 2+y 2b 2=1,得y =b 2a ,∵|F 1F 2||MF 1|=3,∴2cb 2a = 3.∵b 2=a 2-c 2,∴2ac a 2-c 2=3,即2e 1-e2= 3.解得e =-3(舍),e =33.16. 一个底面半径为2的圆柱被与底面所成角是60°的平面所截,截面是一个椭圆,则该椭圆的焦距等于________. 答案 43解析 ∵底面半径为2的圆柱被与底面成60°的平面所截,其截面是一个椭圆,∴这个椭圆的短半轴长为2,长半轴长为2cos60°=4.∵a 2=b 2+c 2,∴c =42-22=23,∴椭圆的焦距为4 3.17.已知F 1,F 2分别是椭圆C :x 2a 2+y 2b 2=1(a>b>0)的左、右焦点,若椭圆C 上存在点P ,使得线段PF 1的中垂线恰好经过焦点F 2,则椭圆C 的离心率的取值范围是________.答案 [13,1)解析 设P(x ,y),则|PF 2|=a -ex ,若椭圆C 上存在点P ,使得线段PF 1的中垂线恰好经过焦点F 2,则|PF 2|=|F 1F 2|,∴a -ex =2c ,∴x =a -2c e =a (a -2c )c .∵-a ≤x ≤a ,∴a (a -2c )c ≤a ,∴c a ≥13,∴13≤e<1.故椭圆C 的离心率的取值范围是[13,1).18.如右图,已知椭圆x 2a 2+y 2b 2=1(a>b>0),F 1,F 2分别为椭圆的左、右焦点,A 为椭圆的上顶点,直线AF 2交椭圆于另一点B. (1)若∠F 1AB =90°,求椭圆的离心率;(2)若椭圆的焦距为2,且AF 2→=2F 2B →,求椭圆的方程. 答案 (1)22 (2)x 23+y 22=1解析 (1)若∠F 1AB =90°,则△AOF 2为等腰直角三角形.所以有|OA|=|OF 2|,即b =c. 所以a =2c ,e =c a =22.(2)由题知A(0,b),F 2(1,0),设B(x ,y),由AF 2→=2F 2B →,解得x =32,y =-b 2.代入x 2a 2+y 2b 2=1,得94a 2+b 24b 2=1. 即94a 2+14=1,解得a 2=3.所以椭圆方程为x 23+y 22=1.19.设F 1,F 2分别是椭圆C :x 2a 2+y 2b 2=1(a>b>0)的左、右焦点,M 是C 上一点且MF 2与x 轴垂直,直线MF 1与C 的另一个交点为N.2020届高三数学精准培优专练十七:椭圆(一)2019届高三数学精准培优专练十七:椭圆(一) (1)若直线MN 的斜率为34,求C 的离心率;(2)若直线MN 在y 轴上的截距为2,且|MN|=5|F 1N|,求a ,b.答案 (1)12 (2)a =7,b =27解析 (1)根据c =a 2-b 2及题设知M ⎝⎛⎭⎫c ,b 2a ,b 2a 2c =34,2b 2=3ac. 将b 2=a 2-c 2代入2b 2=3ac ,解得c a =12,c a =-2(舍去).故C 的离心率为12.(2)由题意,原点O 为F 1F 2的中点,MF 2∥y 轴,所以直线MF 1与y 轴的交点D(0,2)是线段MF 1的中点.故b 2a =4,即b 2=4a.① 由|MN|=5|F 1N|,得|DF 1|=2|F 1N|.设N(x 1,y 1),由题意知y 1<0,则⎩⎨⎧2(-c -x 1)=c ,-2y 1=2,即⎩⎪⎨⎪⎧x 1=-32c ,y 1=-1.代入C 的方程,得9c 24a 2+1b 2=1.② 将①及c =a 2-b 2代入②得9(a 2-4a )4a 2+14a =1. 解得a =7,b 2=4a =28.故a =7,b =27.。
【题型专项特训】三年级数学上册第三单元测量专项训练——填空题(人教版,含答案)

三年级数学上册第三单元测量专项训练——填空题一、填空题1.下面的回形针我估计长约(________)厘米,实际量得(________)厘米(________)毫米。
2.填上合适的单位名称。
小红身高120(______)小朋友每天大约要睡9(______)小东体重35(______) 1米-2分米=(______)分米3.分米可以用字母(________)表示,毫米可以用字母(________)表示。
4.100秒=(______)分(______)秒 70毫米=(______)厘米4米=(______)分米=(______)厘米 5分=(______)秒6吨+35千克=(______)千克 2千克=(______)克5.量出下面线段的长度。
长(__________)毫米6.纸条长(________)厘米(________)毫米。
7.在括号里填上“>”“<”或“=”。
5米(______)600厘米 300米(______)300分米8分米(______)200厘米 4分米(______)40厘米1900毫米(______)2分米 64毫米(______)6厘米5毫米30毫米(______)2厘米 32毫米(______)9厘米2毫米8.认一认,写出下面铅笔的长度。
铅笔长(______)厘米(______)毫米9.量一量。
10.下图中回形针的长度是(________)厘米(________)毫米。
11.填上合适的时间、质量或长度单位。
脉搏跳10次大约用了8(________);一名三年级学生的体重是35(________);一个回形针的长度是28(________)。
12.我们每人身上都有“身体尺”,例如:拃(如图),请你测量一下自己的一拃大约(__________)厘米,用手量一量,估一估这份试卷的宽大约(__________)厘米。
13.填上适合的单位名称。
小亮过马路等红绿灯用了40(________);教室的高度大约是3(________);高铁的速度大约是每小时行驶200(________);一本数学书大约重300(________)。
2021高三数学(理)一轮复习专练4函数及其表示含解析

2021高三数学(理)人教版一轮复习专练4函数及其表示含解析专练4函数及其表示命题范围:函数的概念及其表示、映射、函数的对应法则、函数的定义域、值域.[基础强化]一、选择题1.已知集合A到集合B的映射f:(x,y)→(x+2y,2x-y),在映射f下对应集合B中元素(3,1)的A中元素为()A.(1,3) B.(1,1)C.(3,1)D.(5,5)2.下列各组函数中,表示同一函数的是()A.f(x)=|x|,g(x)=错误!B.f(x)=错误!,g(x)=(错误!)2C.f(x)=x2-1x-1,g(x)=x+1D.f(x)=x+1·错误!,g(x)=错误!3.已知函数f(错误!+1)=x+1,则函数f(x)的解析式为()A.f(x)=x2B.f(x)=x2+1(x≥1)C.f(x)=x2-2x+2(x≥1)D.f(x)=x2-2x(x≥1)4.函数y=错误!的定义域为()A.(-∞,1]B.[-1,1]C.[1,2)∪(2,+∞)D。
错误!∪错误!5.若函数y=f(x)的定义域为[1,2 019],则函数g(x)=错误!的定义域为()A.[0,2 018]B.[0,1)∪(1,2 018]C.(1,2 018] D.[-1,1)∪(1,2 018]6.[2020·葫芦岛一中测试]已知f(x)是一次函数,且f[f(x)]=x+2,则函数f(x)=()A.x+1 B.2x-1C.-x+1 D.x+1或-x-17.[2020·邢台一中测试]如图所表示的函数解析式为()A.y=错误!|x-1|,0≤x≤2B.y=错误!-错误!|x-1|,0≤x≤2C.y=32-|x-1|,0≤x≤2D.y=1-|x-1|,0≤x≤28.已知函数f(x)=错误!若f(a)+f(1)=0,则实数a的值等于()A.-4 B.-1C.1 D.49.已知函数f(x)=-x2+4x,x∈[m,5]的值域是[-5,4],则实数m的取值范围是()A.(-∞,-1) B.(-1,2]C.[-1,2]D.[2,5]二、填空题10.函数f(x)=错误!的定义域为________.11.[2020·广东珠海测试]已知函数f(x)=错误!且f(a)=-3,则f(6-a)=________。
题型突破三年级上册数学第三单元题型专项训练-填空题人教版(含答案)

第三单元测量填空题专项训练解题策略数学填空题,绝大多数是计算型(尤其是推理计算型)和概念(性质)判断型的试题,应答时必须按规则进行切实的计算或者合乎逻辑的推演和判断。
求解填空题的基本策略是要在“准”、“巧”、“快”上下功夫。
常用的方法有直接法、特殊化法、数行结合法、等价转化法等。
一、直接法。
这是解填空题的基本方法,它是直接从题设条件出发、利用定义、定理、性质、公式等知识,通过变形、推理、运算等过程,直接得到结果。
【例1】(2021·广东南沙区)填上适合的单位名称。
小亮过马路等红绿灯用了40();教室的高度大约是3();高铁的速度大约是每小时行驶200();一本数学书大约重300()。
分析:根据生活实际、对时间单位、面积单位和数据大小的认识,可知计量小亮过马路等红绿灯用的时间用“秒”作单位;计量教室的高度用“米”作单位;高铁的速度大约是每小时行驶200千米;一本数学书大约重300克。
据此解题即可。
小亮过马路等红绿灯用了40秒;教室的高度大约是3米;高铁的速度大约是每小时行驶200千米;一本数学书大约重300克。
故答案为:秒米千米克【例2】(2021·广东天河区·三年级期末)7000米=()千米;9厘米=()毫米。
分析:(1)低级单位米化高级单位千米,除以进率1000。
(2)高级单位厘米化低级单位毫米,乘进率10。
7000÷1000=7;9×10=907000米=7千米;9厘米=90毫米。
故答案为:7 90二、计算法。
有些填空题实质是容易算错的计算题,这时可以把它当作一般的计算题,直接算出结果,但是要细心,适当结合运算律使运算更简单。
【例1】(2021·全国三年级单元测试)一支铅笔长2分米,另一支铅笔长15厘米,这两支铅笔一共有()厘米。
分析:分米和厘米之间的进率是10,据此将2分米换算成厘米。
再将两支铅笔的长度相加求和。
2分米=20厘米20厘米+15厘米=35厘米则这两支铅笔一共有35厘米。
高三数学考前基础知识专练:三角函数的图像与性质

高三数学基础知识专练三角函数的图像与性质一、填空题(本大题共14小题,每小题5分,共70分,将答案填在答题卡上) 1、已知角α的终边上一点),3(m P -,且m 42sin =α,则m 的值为 . 2、将函数)32sin(π+=x y 的图像上的所有点向右平移个单位6π,再将图像上所有点的横坐标变为原来的21倍(纵坐标不变),则所得的图像的函数解析式为 . 3、函数216sin lg x x y -+=的定义域为 . 4、函数)32sin(32π+=x y 的周期、振幅依次是 . 5、函数)42sin(log 21π+=x y 的单调减区间为 .6、若函数)2||,0)(sin()(πϕωϕω<>+=x x f的部分图像如图所示,则=+ϕω . 7、已知22πθπ<<-,且a =+θθcos sin ,其中)1,0(∈a ,则关于θtan 的值,在以下四个答案中,可能正确的是 (请填写正确答案的题号). (1)-3;(2)3或31;(3)31-;(4)-3或31-. 8、函数)10(sin 2)(<<=ωωx x f 在区间]3,0[π上最大值为2,则=ω .9、方程x x 41sin =π的解的个数是 . 10、已知)2cos()(),2sin()(ππ-=+=x x g x x f ,则下列命题中正确的序号是 .(1)函数)()(x g x f y +=的最小正周期为π2;(2)函数)()(x g x f y =是偶函数;(3)将函数)(x f y =的图像向左2π平移个单位可以得到函数)(x g 的图像; (4)将函数)(x f y =的图像向右平移2π个单位可以得到函数)(x g 的图像.11、设函数)52sin(2)(ππ+=x x f ,对任意R x ∈,都有)()()(21x f x f x f ≤≤成立,则||21x x -的最小值为 .12、函数],0[|,cos ||sin |π∈+=x x x y 的值域是 .13、半径为1的圆的圆心位于坐标原点,点P 从点)0,1(A 出发,以逆时针方向等速沿单位xy32π32π3π-32πO1圆的圆周旋转,已知P 在1秒内旋转的角度)0(πθθ<<,经过2秒到达第三象限,经过14秒又回到出发点A ,则角=θ . 14、关于函数))(32sin(4)(R x x x f ∈+=π,有下列命题:(1)由0)()(21==x f x f ,可得21x x -必是π的整数倍; (2))(x f y =的表达式可以改写为)62cos(4π-=x y ;(3))(x f y =的图像关于点)0,6(π-对称;(4))(x f y =的图像关于直线6π-=x 对称. 其中正确命题的序号是 (将你认为正确的命题的序号都填上).二、解答题:15、设()f x a b =⋅ .其中向量(2sin ,2cos 1),a x x ωω=+(2cos ,2cos 1)b x x ωω=- (Ⅰ) 当1,(0,)2x πω=∈时,求函数()f x 的值域;(Ⅱ)当ώ=-1时,求函数()f x 的单调递减区间.16、已知函数2πππ()12sin 2sin cos 888f x x x x ⎛⎫⎛⎫⎛⎫=-++++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.求: (I )函数()f x 的最小正周期; (II )函数()f x 的单调增区间.参考答案1、5±或02、x 4sin3、),0(],4[ππ --4、32,4π 5、Z k k k ∈+-],8,8(ππππ6、621π+ 7、(3) 8、439、710、(1)(4) 11、2 12、[1,2] 13、74π或75π14、(2)(3)15、解:f (x )a b ==22sin cos 2cos 1sin 2cos 2x x x x x ωωωωω+-=+ =2sin(2)4x πω+(Ⅰ)当ω=1时,()2sin(2)4f x x π=+∵(0,)2x π∈,∴52444x πππ<+<, 2sin(2)124x π-<+≤, ∴1()2f x -<≤, 函数()f x 的值域是(1,2]-.(Ⅱ)当ω=-1时,()2sin(2)4f x x π=-+=2sin(2)4x π--, 求函数()f x 的单调递减区间即求函数y=2sin(2)4x π-的递增区间令222,242k x k k Z πππππ-≤-≤+∈ ,解得388k x k ππππ-≤≤+∴当ω=-1时,函数()f x 的单调递减区间是[388k k ππππ-+,],k Z ∈.16、解:ππ()cos(2)sin(2)44f x x x =+++πππ2sin(2)2sin(2)2cos 2442x x x =++=+=. (I )函数()f x 的最小正周期是2ππ2T ==;(II )当2ππ22πk x k -≤≤,即πππ2k x k -≤≤(k ∈Z )时,()2cos 2f x x =是增函数,故函数()f x 的单调递增区间是π[ππ]2k k -,(k ∈Z ).。
届高三数学填空题专练
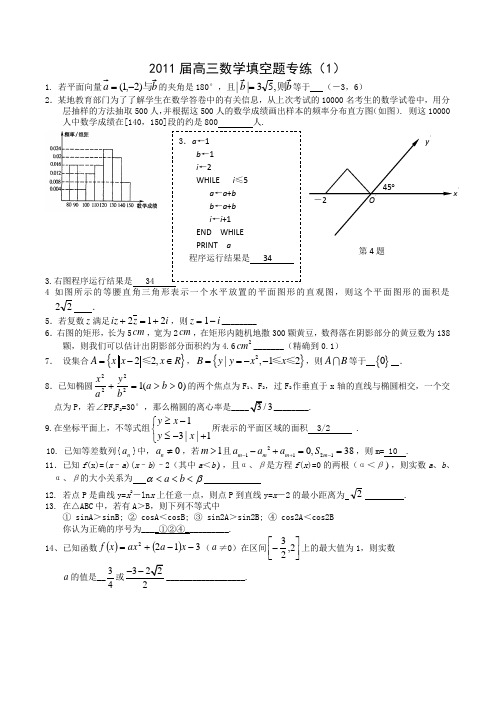
1. 若平面向量b a 与)2,1(-=的夹角是180°,且b b 则,53||=等于 (-3,6)2.某地教育部门为了了解学生在数学答卷中的有关信息,从上次考试的10000名考生的数学试卷中,用分层抽样的方法抽取500人,并根据这500人的数学成绩画出样本的频率分布直方图(如图). 则这10000人中数学成绩在[140,150]段的约是800 人.3.右图程序运行结果是 344如图所示的等腰直角三角形表示一个水平放置的平面图形的直观图,则这个平面图形的面积是22 .5.若复数z 满足i z iz 212+=+,则=z i -1________6.右图的矩形,长为5cm ,宽为2cm ,在矩形内随机地撒300颗黄豆,数得落在阴影部分的黄豆数为138颗,则我们可以估计出阴影部分面积约为4.62cm _______(精确到0.1) 7. 设集合{}22,A x x x R =-∈≤,{}2|,12B y y x x ==--≤≤,则AB 等于 {}0 .8.已知椭圆)0(12222>>=+b a by a x 的两个焦点为F 1、F 2,过F 2作垂直于x 轴的直线与椭圆相交,一个交点为P ,若∠PF 1F 2=30°,那么椭圆的离心率是____3/3________.9.在坐标平面上,不等式组⎩⎨⎧+-≤-≥1||31x y x y 所表示的平面区域的面积 3/2 .10. 已知等差数列{n a }中,0n a ≠,若1m >且211210,38m m m m a a a S -+--+==,则m= 10 .11.已知f (x)=(x –a )(x –b )–2(其中a <b ),且α、β是方程f (x )=0的两根(α<β),则实数a 、b 、α、β的大小关系为 βα<<<b a12. 若点P 是曲线y=x 2-ln x 上任意一点,则点P 到直线y=x -2的最小距离为 2 . 13. 在△ABC 中,若有A >B ,则下列不等式中① sinA >sinB; ② cosA <cosB; ③ sin2A >sin2B; ④ cos2A <cos2B 你认为正确的序号为____①②④__________.14、已知函数()()3122--+=x a ax x f (a ≠0)在区间⎥⎦⎤⎢⎣⎡-2,23上的最大值为1,则实数 a 的值是__34或322--__________________.3.a ←1 b ←1 i ←2WHILE i ≤5a ←a +b b ←a +b i ←i +1END WHILE PRINT a 程序运行结果是 34 ′ y ′O ′ -2 45︒ 第4题1.已知a b ∈R ,,且i 3,i 2++b a (i 是虚数单位)是一个实系数一元二次方程的两个根,那么+a b = -1 .2.设命题p: 134≤-x ,命题q:,0)1()12(2≤+++-a a x a x 若p ⌝是q ⌝的必要不充分条件,则实数a 的取值范围是_____________⎥⎦⎤⎢⎣⎡21,03.不等式823≤++k y x 表示的平面区域包含(0, 0)及(1, 1)两点, 则k 的取值范围是_____[-8,3] ___________ _4.集合A={x| x 2+x-6=0}, B={x| ax+1=0}, 若B ⊆A ,则a=__ 31210或或-________ 5.过点)3,2(--,且与x 轴、y 轴的截距相等的直线方程是 02y -3x 05==++或y x6.双曲线C 与椭圆2214924x y +=的焦点相同,离心率互为倒数,则双曲线C 的渐近线的方程是_____x y 562±=_____ 7.已知12cos 1cos sin =-⋅ααα,32)(tg -=-βα,则)2(tg αβ-等于_81_________8.一个几何的三视图如图所示:其中,主视图中△ABC 的边长是2的正三角形,俯视图为正六边形,那么该几何体几的体积为 32.9. 设12,F F 为椭圆143+=左、右焦点,过椭圆中心任作一条直线与椭圆交于,P Q 两点,当四边形12PF QF 面积最大时,12PF PF ⋅的值等于 2 .10.定义在R 上的函数()x f 满足()023=+⎪⎭⎫ ⎝⎛+x f x f 且函数⎪⎭⎫ ⎝⎛-=43x f y 为奇函数,给出下列命题 ①函数()x f 的最小正周期是23②函数()x f 的图象关于点)0,43(-对称③函数()x f 的图象关于y 轴对称其中真命题的是____②__③___(把你认为正确的填上)11.设函数f (x )=x 3-22x -2x +5.若对任意x ∈[-1,2],都有f (x )>m ,则实数m 的取值范围是m ∈(-∞,27)________.12.函数f (x )定义域为R ,x 、y ∈R 时恒有f (xy )=f (x )+f (y ),若f (27+)+f (27-)=2,则f (1261()1261-++f )= -4 13.设两个向量1e 、2e 满足|1e |=2,|2e |=1,1e 与2e 的夹角为600,若向量2172e e +=λ与向量21e e λ+=的夹角为锐角,则实数λ的取值范围是_____________),214()214,21()7,(+∞---∞ 14若函数())4(log -+=xax x f a (a >0且a ≠1)的值域为R ,则实数a 的取值范围是04a <≤或1a ≠________________.2011届高三数学填空题专练(3)1. O 为平面上定点,A , B , C 是平面上不共线的三点,若(OB OC -)·(OB OC +2OA -)=0, 则∆ABC 的形状是 .2. 在平行四边形ABCD 中,点,,A B C 对应的复数分别是4i,34i,35i ++-,则点D 对应的复数是 .3. 在所有的两位数中,任取一个数,则这个数能被2或3整除的概率为 .4. L , M, N 分别为正方体1111ABCD A B C D -的棱111,,A B AD CC 的中点,则平面LMN 与平面1AB C 的位置关系是 (填“平行”,“相交但不垂直”或“垂直”之一).5. 在等差数列{}n a 中,11101,aa <-若它的前n 项和n S 有最大值,则使n S 取得最小正数的n = .6. 四面体A -BCD 中,AC =BD , BC =AD AB =CD =4,则四面体A -BCD 外接球的面积为 .7. 已知p :“3201x x -≥-”和q :“22530x x -+>”,则p ⌝是q 的 条件.8. 如图给出的是计算1111246100++++的值的一个程序框图,其中判断框内应填入的条件是 .9. 若向量a =)(,2x x ,b =)(3,2x -,且a ,b 的夹角为钝角, 则x 的取值范围是 .10. 甲. 乙两人约定在6时到7时之间在某处会面,并约定先到者等候另一人15分钟,过时即可离去,则两人会面的概率是.11. 某地区有1500染给另外2个用户,若不清除病毒,则在第22小时内该地区感染此病毒的用户数为 (237242 1.5102<⨯<).12. 一个正三棱柱的三视图如图所示,则这个几何体的表面积是 .13. 如图,开始时桶A 中有a 升水,t 分钟后剩余的水量符合指数衰减函数1e nt y a -=⋅ (其中e, n 为常数),此时桶B 中的水量就是2e nt y a a -=-⋅,假设过5分钟后桶A 和桶B 中的水量相等,则再过.. 分钟,桶A 中只有水8a升. 14. 已知函数y =f (x )是定义在R 上的奇函数,且对于任意x ∈R ,都有(3)()f x f x +=-,若f (1)=1,tan 2α=, 则(2005sin cos )f αα的值为 .参考答案1. 等腰三角形2. 48i -3. 234. 平行5. 196. 25π7. 必要不充分8. 100i ≤.9. )(1,3-∞-()()14,0,33-+∞ 10. 71611. 2321-12. 2483+ 13. 10 14. -12011届高三数学填空题专练(4)1.设全集为R ,11A xx ⎧⎫=<⎨⎬⎩⎭,则C R A=__________________; 2.已知向量)1,(m =,若2||=,则m =______________; 3.抛物线)0(42<=a ax y 的焦点坐标是_____________;4.ABC ∆的内角A 、B 、C 的对边也为a 、b 、c ,若a 、b 、c 成等比数列,且c =2a ,则_________cos =B5.已知等差数列{}n a 中,664=+a a ,其前5项和S 5=10,则其公差d =_________6.已知2()(1)xf x f x ⎧=⎨-⎩ (4)(4)x x <≥ 则____________)5(=f7.如果实数+∈R b a ,,且b a >,那么ab b ,和)(21b a +由大到小的顺序是____________ 8.以双曲线191622=-x y 的焦点为顶点,顶点为焦点的椭圆方程是______________ 9.已知)sin ,2(cos αα=a ,)1sin 2,1(-=αb ,且),2(ππα∈,若52=⋅b a ,则tan()4πα+=__________________10.设直线12=+my x 的倾斜角为α,若),2[)32,(+∞--∞∈ m ,则角α的取值范围是__________________11.已知数列{}n a 满足a 1=2,nn n a a a -+=+111(+∈N n ), 则___________20074321=⋅⋅⋅⋅⋅⋅a a a a a12.已知数列ABC ∆的两顶点A 、C 是椭圆192522=+y x 的二个焦点,顶点B 在椭圆上,则________________sin sin sin =+CA B13.定义两种运算:22b a b a -=⊕,2)(b a b a -=⊗则2)2(2)(-⊗⊕=x xx f 是_______________函数,(填奇、偶、非奇非偶,既奇又偶四个中的一个)14.给定下列结论:①已知命题p :R x ∈∃,1tan =x ;命题q :01,2>+-∈∀x x R x ,则命题“p ∧q ”是假命题; ②已知直线l 1:013=-+y ax ,l 2:x - b y + 1= 0,则21l l ⊥的充要条件是3-=ba; ③若21)sin(=+βα,31)sin(=-βα,则βαtan 5tan =; ④圆012422=+-++y x y x ,与直线x y 21=相交,所得的弦长为2;⑤定义在R 上的函数)()1(x f x f -=+,则)(x f 是周期函数;其中正确命题的序号为________________(把你认为正确的命题序号都填上)参考答案1. [0,1]2. 3±3. (a ,0)4.43 5. 216. 87.b ab b a ,),(21+8.125922=+y x 9. 7110.),43[)6,0(πππ11. 3 12.54 13. 奇 14 ③⑤2011届高三数学填空题专练(5)1.已知函数2(3)log f x =,则(5)f 的值是2.已知()312f x ax a =+-在[1,1]-上存在零点0x (01x ≠±),则a 的取值范围是 3.0tan 20cos10tan 20240cos -= 4.复数121iz i+=-的虚部为 5.直线2(1)(3)750m x m y m ++-+-=与直线(3)250m x y -+-=垂直的充要条件是 6.圆224460x y x y +-++=截直线x-y-5=0所得弦长等于7.已知椭圆221259x y +=与双曲线22197x y -=在第一象限内的交点为P ,则点P 到椭圆右焦点的距离等于___ ___8.设m 、n 是不同的直线,α、β、γ是不同的平面,有以下四个命题:(1)//////αββγαγ⎫⇒⎬⎭(2)//m m αββα⊥⎫⇒⊥⎬⎭(3)//m m ααββ⊥⎫⇒⊥⎬⎭(4)////m n m n αα⎫⇒⎬⊂⎭,其中,假命题有 __(把你认为正确的命题序号都填上).9.一个正三棱柱的侧面展开图是一个边长为6cm 的正方形,则此三棱柱的体积为 cm 3.10.若判断框内填入10≤k ,则下面的程序框图输出的结果为__ ____11.数列{}n a 为等比数列,n S 为其前n 项和.已知11a =,第10题图3q =,364k S =,则k a = .12.某商场有四类食品,其中粮食类、植物油类、动物性食品类及果蔬类分别有40种、10种、30种、20种,现从中抽取一个容量为20的样本进行食品安全检测。
第7章 扇形统计图 题型专练(填空题)-2024-2025学年数学人教版六年级上册(含答案解析)

2024-2025学年上学期六年级数学第7章扇形统计图题型专练-填空题1.下面的统计图记录了小青家三月份部分费用的支出情况,支出水电等费用500元,伙食费占总费用的35%,支出伙食费( )元。
2.六(1)班共有50人进行了一次单元测试,全班没有人不及格,情况如下图所示。
其中20%表示( )。
3.某校60名同学共植树180棵。
5个班完成总任务的百分比如图所示。
C组种植了54棵,C组完成总任务的( )%;D组种植了( )棵。
4.下图是一所学校六年级学生的一次晨练情况调查统计图。
从图中信息可以看出,跑步人数是跳绳人数的( ),跳绳人数是跑步人数的( )倍。
5.枫枫家一个月的各种开支统计如图,已知在服装上的花费为2700元,则枫枫家每月还房贷元。
6.某校为了了解本校学生参加课外体育锻炼的情况,随机调查了本校300名学生,并做成了扇形统计图(如图)。
本次调查中“从不参加”课外体育锻炼的学生有( )人,“经常参加”所对应的圆心角的度数是( )度。
7.2022年,第24届冬季奥运会在北京成功举办,下图是我国奥运健儿在此届奥运会上获得奖牌的分布情况。
(1)我国获得的铜牌数量占总奖牌数的( )。
(2)此届奥运会我国获得9块金牌,那么我国一共获得( )块奖牌。
8.如图是红旗小学参加全市“古诗词大赛”的获奖情况统计图。
(1)获得( )等奖的人数最多。
(2)获得优秀奖的人数占获奖总人数的( )%。
(3)根据统计,红旗小学获得优秀奖的有2人,照这样计算,红旗小学获奖的一共( )人,获得一等奖的有( )人。
(4)获得二等奖的人数比获得三等奖的人数少( )%。
9.如图是对“某校六年级300名学生喜欢的球类运动”调查后作出的统计图,观察统计图,回答问题。
(1)( )球类运动最受欢迎,有( )人。
(2)喜欢篮球运动的有( )人,足球运动的有( )人。
(3)排球运动的学生比喜欢足球运动的学生少( )%。
10.下图是一种奶粉的成分含量统计图,看图回答问题。
数列的通项与求 和

当 d ( , 0 ) ( 0, ) 时, a30 7.5, .
2 1 3 10 d , 2 4
数学备课大师 目录式免费主题备课平台
数学备课大师 目录式免费主题备课平台
高三数学基础知识专练
一.填空题(共大题共 14 小题,每小题 5 分,共 70 分)
1
数列的通项与求和
a , n为偶数 1、设数列{an}的首项 a1 a 1 , 且 ,则 a4= 2 n a n 1 4 1 a , n为奇数 n 4
2
2
(d 0) ,
a 30
(3)所给数列可推广为无穷数列 a n ,其中 a1 , a 2 , , a10 是首项为 1,公差为 1 的等差 数列,当 n 1 时,数列 a10n , a10n1 , , a10 ( n1) 是公差为 d n 的等差数列. 研究的问题可以是:试写出 a10 ( n1) 关于 d 的关系式,并求 a10 ( n1) 的取值范围.
k=_____. 二.解答题 15. 设数列 {an} 的前 n 项和为 Sn, 且方程 x2-anx-an=0 有一根为 Sn-1, n=1, 2, 3, …. [来 源:学§科§网] (Ⅰ)求 a1,a2; (Ⅱ) {an}的通项公式.
16. 已 知 数 列 a1 , a 2 , , a30 , 其 中 a1 , a 2 , , a10 是 首 项 为 1 , 公 差 为 1 的 等 差 数 列 ;
9、 a n 3 3 ( ) 10、11 11、
4 3
n 1
n 2 3n 2 2
12、
n2 n 2 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011届高三数学填空题专练(17)
1.已知|)7||3lg(|,++-<∈x x a R x 恒成立,则a 的取值范围是 . 2.已知x 、y x 0 1 3 4 y
2.2 4.3 4.8 6.7
从散点图分析,y 与x ˆ= . 3.设)(x f y =是一次函数,,1)0(=f 且)13(),4(),1(f f f 成等比数列,则++)4()2(f f …=+)2(n f .
4. 已知一物体在两力1(lg2,lg2)F =、)2lg ,5(lg 2=F 的作用下,发生位移
(2lg 5,1)S =,则所做的功是__ ___.
5. 已知两点),4,0()0,3(B A 、动点),(y x P 在线段AB 上运动,则xy 的最大值为 .
6. 设c b a 、、分别是ABC ∆中C B A ∠∠∠、、所对边的边长,则直线0sin =++c ay x A )(与
0sin )(sin =+-C y B bx 的位置关系是 .
7. 若圆01222=++-+y ax y x 和圆12
2=+y x 关于直线1-=x y 对称,过点),(a a C - 的圆P 与y 轴相切,则圆心P 的轨迹方程是 . 8. 如图(下面)已知点F 1、F 2分别是椭圆22
221x y a b
+=的左、
右焦点,过F 1且垂直于x 轴的直线与椭圆交于A 、B 两点,若
△ABF 2为正三角形,则该椭圆的离心率e 是 .
9. 若),(11y x P 是直线0),(:=y x f l 上的一点,
),(22y x Q 是直线l 外一点,则方程
),(),(),(2211y x f y x f y x f +=表示的直线与直线l 的位置关系是 .
10. 已知圆,42
2
=+y x 过A (4,0)作圆的割线ABC ,则弦BC 中点的轨迹方程为 .
11. 设向量(1,)a x =,(,1)b x =,,a b 夹角的余弦值为()f x ,则()f x 的单调增区间是 .
12. 如图所示,在宽2公里的河两岸有A 、B 两个城市,它们的直线距离为10公里,A 城到河岸的垂直距离|AA 1|=5公里,B 城到河岸的垂直距离|BB 1|=1公里,现在选址建桥(河两岸近似看作两条平行直线,且桥垂直河岸),使得从A 到B 的路程最短,则最短路程为 公里.
13.已知,m R ∈若22250{(,)|30
}{(,)|25},0x y x y x x y x y mx y -+≥⎧⎪
-≥⊆+≤⎨⎪+≥⎩
实数m 的取值范围为 .
14. 已知n a n =,把数列{}n a 的各项排列成如下的三角形状: 1a
2a 3a 4a 5a 6a 7a 8a 9a
……………………………………
记(,)A m n 表示第m 行的第n 个数,则(10,12)A =___________
参考答案
x
F 1 F 2
B
A
1、1<a ,
2、2.6 ,
3、 )32(+n n ,
4、2,
5、49
144,6、重合,7、0122
=+--y x y , 8、
3
3
,9、过点Q 且与l 平行,10、4)2(22=+-y x ,11、[1,1]-,12、262+, 13、4[0,]3,14、93。
