数列找规律万能公式word精品
找规律万能公式

找规律万能公式
第一个是等差数列,差为4,所以f(n)=5+4(n-1)=4n+1。
第二个也是等差数列,差为-5,所以f(n)=2-5(n-1)=7-5n。
万能公式不大可能,最简单办法是在坐标系里画出相应点,然后看点
的大致分布,然后选择相应函数,最后根据数值求出具体函数;比如这两
个题目,点分布基本为直线,对应的函数就是一次函数,也就是等比数列,可以按y=ax+b进行求解。
找规律填空的意义
实际上在于加强对于一般性的数列规律的熟悉,虽然它有很多解,但
主要是培养你寻找数列一般规律和猜测数列通项的能力(即运用不完全归
纳法的能力)。
以便于在碰到一些不好通过一般方法求通项的数列时,能够通过前几
项快速准确地猜测到这个数列的通项公式,然后再用数学归纳法或反证法
或其它方法加以证明,绕过正面的大山,快速地得到其通项公式。
所以找
规律填空还是有助于我们增强解一些有难度又有特点的数列的。
万能找规律方法
在此我就不多说了,因为列出的就是10元1次方程组,直接告诉大家结果:
a=-1/576
b=11/128
c=-611/336
d=1375/64
e=-149087/960
f=1133
g=90563/128
h=-580513/288
i=109725/32
2.得出通式的x的最高次项为10-1=9
3.列出通式:
f(x)=a x^9+b x^8+c x^7+d x^6+e x^5+ f x^4+g x^3+h x^2+Ix+j
4.列出要求的方程
在此我就简单的表示,用f(x)表示对应的函数
f(1)=1,f(2)=3,f(3)=5,f(4)=7,f(5)=9,f(6)=2,f(7)=4,f(8)=6,f(9)=8,f(10)=10
j=-872819/280
f(x)=
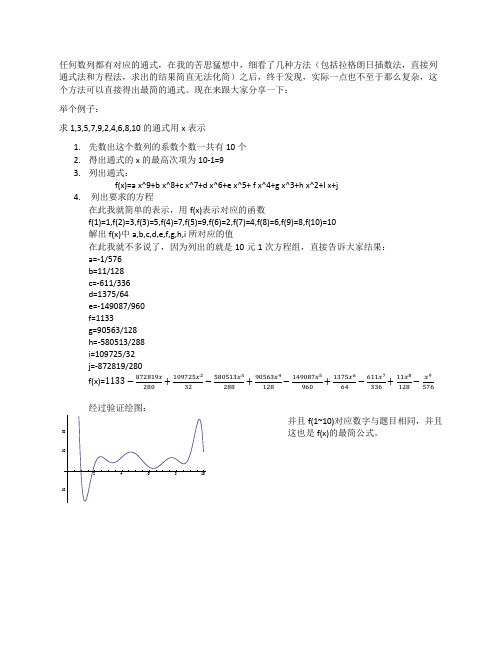
经过验证绘图:
并且 f(1~10)对应数字与题目相同,并且这也是f(x)的最简公式。
任何数列都有对应的通式,在我的苦思猛想中,细看了几种方法(包括拉格朗日插数法,直接列通式法和方程法,求出的结果简直无法化简)之后,终于发现,实际一点也不至于那么复杂,这个方法可以直接得出最简的通式。现在来跟大家分享一下:
举个例子:
求1,3,5,7,9,2,4,6,8,10的通式用x表示
1.先数
数列找规律万能公式

数列找规律公式数列找规律用拉格朗日插值。
拉格朗日“提出”了这种方法,所谓的插值,就是“插”“值”,就是指找出一个通过给出离散数据点的函数。
即,数列中给出数据可以表示为在坐标系上的点,x坐标就是第几项,y坐标就是该项的值。
比如说,“1 ,3,7,8,0,5,9,2,4,6”这个数列可以表示为:在Mathematica中用几行简单的代码即可做到:接下来,我们找出这些点都在哪一个函数上面,接着下来把下一项的项数带进去,就得到了下一项的值——这实际上就是通项公式!事不宜迟,马上来试一试!首先,我们先来看看拉格朗日插值公式是怎么样的:好吧,我知道小学生又看不懂了。
那下面我们先试一一个简单的数列:1、8、27…那下一个是什么呢?首先,这表示存在一个函数。
当自变量分别为1、2、3时函数值为1、8、27。
于是我们可以设一个函数:接下来就是关键的一步了!小学生可以不懂这是怎么回事。
但有什么问题?考试会用就行了(如果你不介意再解释一下一些其他的问题...比如未知数、自变量和分数的运算)。
容易看到,整个式子是三项的和,每一个点都有一项。
对于每一个单独的点来说,分子是这一点的函数值乘上x与其他点的自变量的差。
而分母就是该店的自变量和其他点的自变量的差的积。
于是,一个通项公式就出来了。
是于是我们迫不及待地把x=4带进去,得到58.至此,大功告成。
等等,什么答案写着是64?别管了,肯定是盗版书印错答案了。
有什么可能拉格朗日大牛会错呢?什么,我们的规律不对?正确的是y=x^3?好的,让我看看。
嗯…难道是拉格朗日错了?但是前面我们的估算也是没问题的啊。
再仔细看一下坑爹的高数课本,才发现原来是我们一直搞错了。
如果我们给的是n个点,那么拉格朗日给出的函数将会是(n-1)次的。
这不坑爹吗…用公式之前还得想清楚这个函数是几次的,而且如果是更高次数的还没办法加上点去求(更别说斐波那契数列这样的用递归定义的数列了)。
这就意味着,就算是1、2、3、4、5、6…这样的数列,拉格朗日插值法在耗尽你大量的考试时间去求出通项公式以后,还会给出一个超级坑爹的答案!那么这个方法还有什么用!别急,前面的计算都是为后面做铺垫的。
(完整word版)初中数学找规律常见公式

一、基本方法——看增幅(一)如增幅相等(此实为等差数列):对每个数和它的前一个数进行比较,如增幅相等,则第n个数可以表示为:a+(n-1)b,其中a为数列的第一位数,b为增幅,(n-1)b为第一位数到第n位的总增幅.然后再简化代数式a+(n-1)b.例:4、10、16、22、28……,求第n位数.分析:第二位数起,每位数都比前一位数增加6,增幅相都是6,所以,第n位数是:4+(n-1)×6=6n-2 (二)如增幅不相等,但是,增幅以同等幅度增加(即增幅的增幅相等,也即增幅为等差数列).如增幅分别为3、5、7、9,说明增幅以同等幅度增加.此种数列第n位的数也有一种通用求法.基本思路是:1、求出数列的第n-1位到第n位的增幅;2、求出第1位到第第n位的总增幅;3、数列的第1位数加上总增幅即是第n位数.举例说明:2、5、10、17……,求第n位数.分析:数列的增幅分别为:3、5、7,增幅以同等幅度增加.那么,数列的第n-1位到第n位的增幅是:3+2×(n-2)=2n-1,总增幅为:[3+(2n-1)]×(n-1)÷2=(n+1)×(n-1)=n2-1所以,第n位数是:2+n2-1=n2+1此解法虽然较烦,但是此类题的通用解法,当然此题也可用其它技巧,或用分析观察凑的方法求出,方法就简单的多了.(三)增幅不相等,但是,增幅同比增加,即增幅为等比数列,如:2、3、5、9,17增幅为1、2、4、8.(三)增幅不相等,且增幅也不以同等幅度增加(即增幅的增幅也不相等).此类题大概没有通用解法,只用分析观察的方法,但是,此类题包括第二类的题,如用分析观察法,也有一些技巧.二、基本技巧(一)标出序列号:找规律的题目,通常按照一定的顺序给出一系列量,要求我们根据这些已知的量找出一般规律.找出的规律,通常包序列号.所以,把变量和序列号放在一起加以比较,就比较容易发现其中的奥秘.例如,观察下列各式数:0,3,8,15,24,…….试按此规律写出的第100个数是.解答这一题,可以先找一般规律,然后使用这个规律,计算出第100个数.我们把有关的量放在一起加以比较:给出的数:0,3,8,15,24,…….序列号:1,2,3,4,5,…….容易发现,已知数的每一项,都等于它的序列号的平方减1.因此,第n项是n2-1,第100项是1002-1.(二)公因式法:每位数分成最小公因式相乘,然后再找规律,看是不是与n2、n3,或2n、3n,或2n、3n有关.例如:1,9,25,49,(),(),的第n为(2n-1)2(三)看例题:A:2、9、28、65.增幅是7、19、37.,增幅的增幅是12、18答案与3有关且.即:n3+1B:2、4、8、16.增幅是2、4、8...答案与2的乘方有关即:2n(四)有的可对每位数同时减去第一位数,成为第二位开始的新数列,然后用(一)、(二)、(三)技巧找出每位数与位置的关系.再在找出的规律上加上第一位数,恢复到原来.例:2、5、10、17、26……,同时减去2后得到新数列:0、3、8、15、24……,序列号:1、2、3、4、5分析观察可得,新数列的第n项为:n2-1,所以题中数列的第n项为:(n2-1)+2=n2+1(五)有的可对每位数同时加上,或乘以,或除以第一位数,成为新数列,然后,在再找出规律,并恢复到原来.例:4,16,36,64,?,144,196,…?(第一百个数)同除以4后可得新数列:1、4、9、16…,很显然是位置数的平方.(六)同技巧(四)、(五)一样,有的可对每位数同加、或减、或乘、或除同一数(一般为1、2、3).当然,同时加、或减的可能性大一些,同时乘、或除的不太常见.(七)观察一下,能否把一个数列的奇数位置与偶数位置分开成为两个数列,再分别找规律.三、基本步骤1、先看增幅是否相等,如相等,用基本方法(一)解题.2、如不相等,综合运用技巧(一)、(二)、(三)找规律3、如不行,就运用技巧(四)、(五)、(六),变换成新数列,然后运用技巧(一)、(二)、(三)找出新数列的规律4、最后,如增幅以同等幅度增加,则用用基本方法(二)解题四、练习题例1:一道初中数学找规律题0,3,8,15,24,······2,5,10,17,26,·····0,6,16,30,48······(1)第一组有什么规律?(2)第二、三组分别跟第一组有什么关系?(3)取每组的第7个数,求这三个数的和?2、观察下面两行数2,4,8,16,32,64,...(1)5,7,11,19,35,67...(2)根据你发现的规律,取每行第十个数,求得他们的和.(要求写出最后的计算结果和详细解题过程.)3、白黑白黑黑白黑黑黑白黑黑黑黑白黑黑黑黑黑排列的珠子,前2002个中有几个是黑的?4、3^2-1^2=8×15^2-3^2=8×27^2-5^2=8×3……用含有N的代数式表示规律写出两个连续技术的平方差为888的等式五、对于数表1、先看行的规律,然后,以列为单位用数列找规律方法找规律2、看看有没有一个数是上面两数或下面两数的和或差。
常见数列公式范文

常见数列公式范文1.等差数列公式:一个等差数列中的每个数字与其前一个数字的差值都相等。
表达式为an = a1 + (n - 1)d,其中an表示数列中的第n个数字,a1表示数列中的第一个数字,d表示公差。
2.等比数列公式:一个等比数列中的每个数字与其前一个数字的比值都相等。
表达式为an = a1 * r^(n - 1),其中an表示数列中的第n个数字,a1表示数列中的第一个数字,r表示公比。
3. 斐波那契数列公式:斐波那契数列的前两个数字为1,从第三项开始,每一项都是前两项的和。
表达式为fn = fn-1 + fn-2,其中fn表示数列中的第n个数字,fn-1表示数列中的第n-1个数字,fn-2表示数列中的第n-2个数字。
4. 调和数列公式:调和数列是指数列的倒数。
表达式为an = 1/n,其中an表示数列中的第n个数字。
5. 平方数列公式:平方数列是指数列的平方。
表达式为an = n^2,其中an表示数列中的第n个数字。
6. 立方数列公式:立方数列是指数列的立方。
表达式为an = n^3,其中an表示数列中的第n个数字。
7. 阶乘数列公式:阶乘数列是指n的阶乘。
表达式为an = n!,其中an表示数列中的第n个数字。
8. 三角数列公式:三角数列是指等差数列的前n项和。
表达式为an = n * (n + 1) / 2,其中an表示数列中的第n个数字。
9.素数数列公式:素数数列是只包含素数的数列。
素数是只能被1和自身整除的正整数。
10. 自然数数列公式:自然数数列是指从1开始的连续的正整数序列。
表达式为an = n,其中an表示数列中的第n个数字。
11. 平行四边形数列公式:平行四边形数列是指一个与等差数列和等差数列之和成等差关系的数列。
表达式为an = n^2 + an-1,其中an表示数列中的第n个数字,an-1表示数列中的第n-1个数字。
12.算术-几何数列公式:算术-几何数列是指一个等差数列和等比数列的乘积数列。
(完整word版)高中数学_数列求和及数列通项公式的基本方法和技巧

数列求和的基本方法和技巧关键词:数列求和 通项分式法错位相减法反序相加法分组法分组法合并法数列是高中代数的重要内容,又是学习高等数学的基础•在高考和各种数学竞赛中都占有重要的地位数列求和是数列的重要内容之一,除了等差数列和等比数列有求和公式外,大部分数列的求和都需要一定 的技巧•下面,就几个历届高考数学来谈谈数列求和的基本方法和技巧、利用常用求和公式求和利用下列常用求和公式求和是数列求和的最基本最重要的方法 1、等差数列求和公式: S nn(a1 an)na !n(n 1)d2 2[例]求和 1 + X 2 + X 4+ X 6+…x 2n+4(x 工 0)解: ••• X M0•••该数列是首项为1,公比为X 2的等比数列而且有n+3项 当x 2= 1即X =±1时和为n+3评注:(1)利用等比数列求和公式•当公比是用字母表示时,应对其是否为 1进行讨论,如本 题若为“等比”的形式而并未指明其为等比数列,还应对 X 是否为0进行讨论.(2)要弄清数列共有多少项,末项不一定是第n 项.2n 1对应高考考题:设数列 1,( 1+2 ),•••,( 1+2+2 2 ), ..... 的前顶和为 S n,则S n的值。
2、等比数列求和公式:S nn^ 印(1 q n )1 q3、S nnkk 1 1n(n 1) 25、S nnk3k 11 2[才(n 1)]22a 1 a n q 1 q(q 1)n214、S nk—n(n 1)(2 n 1)k 16当黑忖1即篡詳主1对?和為自然数方幕和公式:(q 1)二、错位相减法求和错位相减法求和在高考中占有相当重要的位置,近几年来的高考题其中的数列方面都出了这方面的内容。
需要我们的学生认真掌握好这种方法。
这种方法是在推导等比数列的前n项和公式时所用的方法,这种方法主要用于求数列{a n • b n}的前n项和,其中{ a n }、{ b n }分别是等差数列和等比数列•求和时一般在已知和式的两边都乘以组成这个数列的等比数列的公比q ;然后再将得到的新和式和原和式相减,转化为同倍数的等比数列求和,这种方法就是错位相减法[例]求和:S n 1 3x 5x2 7x3(2n 1)x n 1(X 1)解:由题可知,{(2n 1)x n1}的通项是等差数列{2n —1}的通项与等比数列{x n1}的通项之积设xS n 1x 3x2 5x3 7x4(2n 1)x n.................... ②(设制错位)①一②得(1 x)S n 1 2x 2x22x32x42x n1(2n1)x n(错位相减)再利用等比数列的求和公式得:(1 x)Snn 11 x1 2x - (2n 1)x n1 xS (2n S n1)xn 11 ;2n 1)x n (1 x)2(1 x)注意、1要考虑当公比x为值1时为特殊情况2错位相减时要注意末项此类题的特点是所求数列是由一个等差数列与一个等比数列对应项相乘。
数列万能公式
数列万能公式
数列万能公式是一种用来计算等差数列求和的公式,它也可以用来计算等比数列求和。
这个公式最早是由法国数学家波尔基(Blaise Pascal)在17th世纪发明的,并得到了英国数学家斯特鲁姆(Strum)的补充和发展。
数列万能公式是一种用来计算数列求和的公式,可以用来计算等差数列、等比数列或者任意序列的求和问题。
数列万能公式的正确形式是:若n为正整数,a1为等差数列的首项,d为公差,an为等差数列的末项,则该等差数列的前n项和S(n)可以用如下公式表示:
S(n) = n/2 * (a1 + an)
以上是数列万能公式的正确形式,它可以用来计算等差数列求和。
而等比数列的前n项和T(n)也有相应的计算公式,即T(n) = a1 * (1 - q^n) / (1 - q)
其中,q为等比数列的公比,a1为等比数列的首项。
数列万能公式可用来计算任意序列的求和问题,例如:
若a1,a2,…,an为任意序列,则该序列的前n项和
S(n)可以用如下公式表示:
S(n) = a1 + a2 + … + an
数列万能公式的最大优点是,它可以根据数列的不同性质,使用不同的公式来计算求和问题。
它可以帮助人们快速准确地计算出数列求和。
此外,这个公式对理解抽象概念也有很大的帮助,例如,可以利用它来计算组合数量和极限等概念。
它可以说是数学的抽象概念的实用工具。
总之,数列万能公式是一种用来计算数列求和的公式,它可以用来计算等差数列、等比数列或者任意序列的求和问题,不但可以帮助人们计算出数列求和,而且还能帮助人们理解抽象概念。
数学找规律公式大全
数学找规律公式大全一、数字规律。
1. 等差数列。
- 定义:如果一个数列从第二项起,每一项与它的前一项的差等于同一个常数,这个数列就叫做等差数列。
- 通项公式:a_n=a_1+(n - 1)d,其中a_n表示第n项的数值,a_1是首项(数列的第一项),n是项数,d是公差(相邻两项的差值)。
- 例如:数列1,3,5,7,·s,a_1=1,d = 2,那么第n项a_n=1+(n - 1)×2=2n - 1。
2. 等比数列。
- 定义:如果一个数列从第二项起,每一项与它的前一项的比值等于同一个常数,这个数列就叫做等比数列。
- 通项公式:a_n=a_1q^n - 1,其中a_n表示第n项的数值,a_1是首项,n是项数,q是公比(相邻两项的比值)。
- 例如:数列2,4,8,16,·s,a_1=2,q = 2,则第n项a_n=2×2^n - 1=2^n。
3. 数字规律中的其他常见类型。
- 平方数数列:1,4,9,16,·s,通项公式为a_n=n^2。
- 立方数数列:1,8,27,64,·s,通项公式为a_n=n^3。
- 斐波那契数列:1,1,2,3,5,8,·s,从第三项起,每一项都等于前两项之和,即a_n=a_n - 1+a_n - 2(n≥slant3)。
二、图形规律。
1. 点的规律。
- 在平面直角坐标系中,如果点的坐标呈现一定规律。
例如,点(1,1),(2,4),(3,9),(4,16)·s,横坐标为n,纵坐标为n^2。
2. 多边形边数与内角和的规律。
- 多边形内角和公式:(n - 2)×180^∘,其中n为多边形的边数。
例如三角形(n = 3)内角和为(3 - 2)×180^∘=180^∘;四边形(n = 4)内角和为(4 -2)×180^∘=360^∘。
3. 图形数量规律。
- 例如,用小棒摆三角形,摆1个三角形需要3根小棒,摆2个三角形需要5根小棒(共用一条边),摆3个三角形需要7根小棒。
数列找规律万能公式
数列找规律公式数列找规律用拉格朗日插值.拉格朗日“提出”了这种方法,所谓得插值,就就是“插”“值",就就是指找出一个通过给出离散数据点得函数。
即,数列中给出数据可以表示为在坐标系上得点,x坐标就就是第几项,y坐标就就是该项得值。
比如说,“1 ,3, 7,8, 0,5,9,2,4,6”这个数列可以表示为:在Mathematica中用几行简单得代码即可做到:接下来,我们找出这些点都在哪一个函数上面,接着下来把下一项得项数带进去,就得到了下一项得值-—这实际上就就是通项公式!事不宜迟,马上来试一试!首先,我们先来瞧瞧拉格朗日插值公式就是怎么样得:好吧,我知道小学生又瞧不懂了。
那下面我们先试一一个简单得数列:1、8、27…那下一个就是什么呢?首先,这表示存在一个函数。
当自变量分别为1、2、3时函数值为1、8、27。
于就是我们可以设一个函数:接下来就就是关键得一步了!小学生可以不懂这就是怎么回事。
但有什么问题?考试会用就行了(如果您不介意再解释一下一些其她得问题、、、比如未知数、自变量与分数得运算).容易瞧到,整个式子就是三项得与,每一个点都有一项.对于每一个单独得点来说,分子就是这一点得函数值乘上x与其她点得自变量得差.而分母就就是该店得自变量与其她点得自变量得差得积。
于就是,一个通项公式就出来了.就是于就是我们迫不及待地把x=4带进去,得到58、至此,大功告成。
等等,什么答案写着就是64?别管了,肯定就是盗版书印错答案了。
有什么可能拉格朗日大牛会错呢?什么,我们得规律不对?正确得就是y=x^3?好得,让我瞧瞧。
嗯…难道就是拉格朗日错了?但就是前面我们得估算也就是没问题得啊.再仔细瞧一下坑爹得高数课本,才发现原来就是我们一直搞错了。
如果我们给得就是n个点,那么拉格朗日给出得函数将会就是(n-1)次得。
这不坑爹吗…用公式之前还得想清楚这个函数就是几次得,而且如果就是更高次数得还没办法加上点去求(更别说斐波那契数列这样得用递归定义得数列了).这就意味着,就算就是1、2、3、4、5、6…这样得数列,拉格朗日插值法在耗尽您大量得考试时间去求出通项公式以后,还会给出一个超级坑爹得答案!那么这个方法还有什么用!别急,前面得计算都就是为后面做铺垫得。
(完整word版)求数列的通项公式方法总结,推荐文档
题型四:求数列的通项公式一.公式法:当题中已知数列是等差数列或等比数列,在求其通项公式时我们就可以直接利用等差或等比数列的公式来求通项,只需求得首项及公差公比。
二.当题中告诉了数列任何前一项和后一项的递推关系即:n a 和a n-1的关系时我们可以根据具体情况采用下列方法1、叠加法:一般地,对于型如)(1n f a a n n +=+类的通项公式,且)()2()1(n f f f +++Λ的和比较好求,我们可以采用此方法来求n a 。
即:11221()()()n n n n n a a a a a a a ---=-+-++-L 1a +(2)n ≥;【例1】已知数列{}n a 满足11211,2n n a a a n n+==++,求数列{}n a 的通项公式。
解:(1)由题知:121111(1)1n n a a n n n n n n +-===-+++ 112211()())n n n n n a a a a a +(a -a a ---∴=-+-++……1111111()()()121122n n n n =-+-++-+---…… 312n=- 2、叠乘法:一般地对于形如“已知a 1,且n1n a a +=f (n )(f (n )为可求积的数列)”的形式可通过叠乘法求数列的通项公式。
即:121121n n n n n a a a a a a a a ---=⋅⋅⋅⋅L (2)n ≥; 【例2】在数列{n a }中,1a =1, (n+1)·1+n a =n ·n a ,求n a 的表达式。
解:由(n+1)·1+n a =n ·n a 得11+=+n n a a n n , 1a a n =12a a ·23a a ·34a a …1-n n a a =n n n 11433221=-⋅⋅Λ 所以n a n 1= 3、构造法:当数列前一项和后一项即n a 和a n-1的递推关系较为复杂时,我们往往对原数列的递推关系进行变形,重新构造数列,使其变为我们学过的熟悉的数列(等比数列或等差数列)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数列找规律公式
数列找规律用拉格朗日插值。
拉格朗日提出”了这种方法,所谓的插值,就是插”值”,就
是指找出一个通过给出离散数据点的函数。
即,数列中给出数据可以表示为在坐标系上的点,
x坐标就是第几项,y坐标就是该项的值。
比如说,“ 1,3,7,8,0,5,9,2,4,6”这个数列可以表示为:
在Mathematica中用几行简单的代码即可做到:
1艸』-± data = (11 3r 7, 6 r 0T5 r 3, 2^4 f 6}
{!■# 31了F S r口*5 / 9 r 2 f 41£ _■
■■[二=ListPlot [data]
T omleneri 巢売
网^uokLcofir
-i -
接下来,我们找出这些点都在哪一个函数上面,
接着下来把下一项的项数带进去, 就得到了
-2 -
("叼-1) 9一叼+1) T 仗IT 働)
(叼 ~ 丁j-〔)(与一叼熬売网 gtSjrfcoFft )
好吧,我知道小学生又看不懂了。
那下面我们先试一一个简单的数列: 1、8 27…那下一个是什么呢?
首先,这表示存在一个函数。
当自变量分别为 1、2、3时函数值为1、8、27。
于是我们可
以设一个函数:
珈=1 f 仏)=1 叼=2 畑)=8
T&rnLsnafi
衍=3
親澎曲r25In
接下来就是关键的一步了! 小学生可以不懂这是怎么回事。
但有什么问题?考试会用就行了
(如果你不介意再解释一下一些其他的问题
…比如未知数、自变量和分数的运算)。
下一项的值一一这实际上就是通项公式!
事不宜迟,马上来试一试!
首先,我们先来看看拉格朗日插值公式是怎么样的:
-3 -
f — 1 x — 2 3- 1 3-2
TornLenerj
眾亮冈;juokr.corri
容易看到,整个式子是三项的和,每一个点都有一项。
对于每一个单独的点来说, 分子是这
一点的函数值乘上 x 与其他点的自变量的差。
而分母就是该店的自变量和其他点的自变量的
差的积。
于是我们迫不及待地把 x=4带进去,得到58.
至此,大功告成。
等等,什么答案写着是 64?别管了,肯定是盗版书印错答案了。
有什么可能拉格朗日大牛 会错呢?
什么,我们的规律不对?正确的是
y=x A 3?好的,让我看看。
嗯 …难道是拉格朗日错了?但
是前面我们的估算也是没问题的啊。
再仔细看一下坑爹的高数课本, 才发现原来是我们一直搞错了。
如果我们给的是n 个点,那
么拉格朗日给出的函数将会是 (n-1)次的。
这不坑爹吗…用公式之前还得想清楚这个函数是几次的, 而且如果是更高次数的还没办法加 上点去
求(更别说斐波那契数列这样的用递归定义的数列了)。
rr 一 2 工一3
3+27'
=6T 2 — 11T + 6.
于是,一个通项公式就出来了。
是 6x 2 — 11T + 6.
这就意味着,就算是1、2、3、4、5、6…这样的数列,拉格朗日插值法在耗尽你大量的考试时间去求出通项公式以后,还会给出一个超级坑爹的答案!
那么这个方法还有什么用!
别急,前面的计算都是为后面做铺垫的。
现在才是主要内容。
无论是分布得多么奇怪的点,拉格朗日插值法总能给出一条经过这些点的函数图象。
也就是说,就算是1、2、3、4、5、6、(1568)这样明显不靠谱的答案也是“有规律的”。
因为你总可以设一个六次多项式,找出这个数列的通项公式。
所以说:
1 、3 、5、7、9、(1598),是对的
3、1 、
4、1 、
5、9、2、(999),是对的
1,1,2,3,5,7,(8989),是对的
2,4,6,8,(5),是对的
如果老师斗胆把你的答案批错的话,你大可以把这篇文章打印出来,然后跟老师说:“这个空填任何数都是可以的,因为你总可以设一个n次多项式,然后……”
- 4 -。
