本征值问题
合集下载
大学物理-常微分方程的本征值问题
类型
定解问题中的 边界条件
分离变量后的 边界条件
本征函数系
(1)
(2) (3) (4)
利克莱条件：(1) 连续或只有有限个第一类间断点；(2) 只 有有限个极值点，则 f (x) 在 [–l, l ] 上可展开为傅里叶级数
利用三角函数的正交关系，可得
量子力学中的正交完备矢量组： 设 F 为厄米算符，则 F 对应于不同本征值的本征矢
相互正交，这些本征矢构成正交完备矢量组。记正交完 备矢量组为 { | i > (i =1, 2, …)}，有
数集的正交性只是这里的特殊例子。
等本征函
4. 完备性定理 若函数 f (x) 在区间 [a,b] 有连续的一阶导数和分段连
续的二阶导数，且满足本征值问题的边界条件，则可利用 本征函数系{yn(x)} 将它展开为绝对且一致收敛的广义傅 里叶级数，即
其中展开式的系数为
备忘：傅里叶级数 一个以 2l 为周期的函数 f (x)，若在区间 [–l, l ] 满足狄
二阶线性常微分方程的普遍形式为 (6-4-1)
其中：A(x), B(x), C(x)——已知函数
—— 分离变量过程中引入的常数
方程 (6-4-1) 化为以下施图姆—刘维尔方程 (施—刘型方程)
(6-4-2)
其中：
核函数
已知函数
权函数
参数 勒让德方程、连带勒让德方程、贝塞尔方程均可化 为施—刘型方程：
(1) 存在无穷多个实的、分立的本征值 = n (n = 1,2,…)，
且对应着无穷多个本征函数 yn (x) (n = 1,2,…)； (2) 当同一本征值对应的本征函数不止一个时，称为简并。
证明：本征值 是实的。 若 为复数，施—刘型方程及其复共轭为
专题二 本征值问题
n n
1,2,3,... 1,2,3,...
0
l n n / l (n 1,2,3,...)
SL[
y(
x)]
d dx
[k
(x)
dy dx
]
(x)
y
(
x)
y(
x)
x [a,b]
例：求解本征值问题
X
(l
X (x) X (x) 0
) X (l); X (l) X
(l
)
PBC
II 0 X ( x) A Bx
本征值问题的数值解法
)
PBC
I 0 X ( x) Acos x B sin x
X
(l)
A cos(
n
nl) 2B Xl(l)
sin(X n (xl)) X (l)
B
sin
0
X n(l)
l
sin
xAlcons(0
1,2l),3,.B..
sin(
l)
0
l n n / l (n 1,2,3,...)
SL[
y(
x)]
d dx
[k
(x)
dy dx
]
(x)
y
(
x)
y(
x)
x [a,b]
例：求解本征值问题
X
(l
X (x) X (x) 0
) X (l); X (l) X
(l
)
PBC
I 0 X ( x) Acos x B sin x
XXXn(((ll))ln)l--AAX2(ssilin)n((XXAnn((0llxx))))BsBiscnionsccnoonlssll((xx0ll))
力学量本征值问题的代数解法
2
加上自然单位：归一化的基态波函数
激发态波函数： n(x) 位
xn
1 x (a)n 0 n!
0
(
x)
(
)1/
4
e
2
，加上长度自然单
x
2
a 1 (x 1 d ) 2 dx
n(x)
1 ( 2 )1/ 4 (x 1 d ) en 2x2 / 2
n!
dx
二、角动量的本征值与本征态 （1）
j jm ( j m 1)( j m) jm 1
角动量的共同本征函数―球谐函数
[Lˆ2, Lˆ z ] 0
Lˆ2Ylm l(l 1)2Ylm LˆzYlm mYlm
[Lˆz , Lˆx ] iLˆy [Lˆz , Lˆy ] iLˆx
一维谐振子的哈密顿量用 a 和 a 表示为：
H 1 p2 1 x2 1 { i (a a)}2 1 { 1 (a a)}2 (aa 1 )
2 2 22
22
2
注意： (a a)2 (a a)(a a) a2 aa aa a2
定义： Nˆ aa 因此 H (Nˆ 1) ，Nˆ 称为粒子数算符。
[Nˆ , a] n (Nˆa aNˆ ) n Nˆa n aNˆ n a n
Nˆa n aNˆ n a n an n a n (n 1)a n 即：Nˆ (a n ) (n 1)(a n ) 若令 n a n 则有：Nˆ n (n 1) n ，对比 Nˆ n n n ，可 以看出 a n n 就是算符 Nˆ 属于本征值 (n 1)
可以证明
[ j , j ] i j , α,β,γ x, y, z
因此这三个算符 jx ，jy 和 jz 可组成一个角动量算符：j
I(三章3讲)常用算符本征值问题
2 1 1 ˆ2 2 [ L (sin ) ] 2 2 sin sin 本征方程：
本征值： 本征函数： 正交归一性： 完备性： 简并度：
0
2
0
Ylm ( , )Yl* m ( , )sin d d ll mm
( p (r ''), p (r ')) (r '' r ')
平面波归一化计 算，你会了吗？
（二）位置算符
本征方程
ˆx x
ˆ x x
归一化常数： A 1
因为λ是常数，除了x=λ这一点外，x取其他任何值都有 0 即： ( x) A ( x ) 属于本征值λ的本征函数：
3. L2算符的本征值
2 1 1 ˆ2 2 [ L (sin ) ] 2 2 sin sin
因为它只与
, 有关，所以其本征函数应具有如下形式
Y ( , )
设它的本征值为： L
2
则其本征方程可写成：
ˆ2Y ( ,) L Y ( ,) 2Y ( ,) L
你会直角坐标与球坐标 的相互转换吗？
z
r
r
y
(II) 球坐标
直角坐标与球坐标之间的变换关系
2 2 2 2 r x y z cos z / r tan y / x
x
球 坐 标
x r sin cos y r sin sin z r cos
量子力学与统计物理
Quantum mechanics and statistical physics
数学物理方程 特-本征值问题
1 r r
2
( x, y, z )
r
z
y
(r
2
u r
)
1
2
r sin
(sin
u
)
1
2 2
u
2 2
r sin
0
x
分离变量
Y r r
2
u ( r , , ) R ( r )Y ( , )
) R
2
(r
2
R r
r sin
l
D r
l 1
＃
]
1
sin
(sin
Y
)
1
2
Y
2 2
sin
l ( l 1) Y 0
b. 球方程 再令
d (sin d d
d d
Y ( , ) ( ) ( )
sin d
sin d d
)
本征值问题 9.1 特殊函数的常微分方程 在三维空间使用球座标或柱座标。
z
z
r
( x, y, z )
( x, y, z )
z
y
r
z
y
x
边界
x
球极座标
r , ,
z
( x, y, z )
r
柱坐标
, z,
h
z
y
x
一、正交曲线座标系中的拉普拉斯方程
（见附录6）
直角坐标系中的拉普拉斯算子：
0
0 0 0 1
2
( x, y, z )
r
z
y
(r
2
u r
)
1
2
r sin
(sin
u
)
1
2 2
u
2 2
r sin
0
x
分离变量
Y r r
2
u ( r , , ) R ( r )Y ( , )
) R
2
(r
2
R r
r sin
l
D r
l 1
＃
]
1
sin
(sin
Y
)
1
2
Y
2 2
sin
l ( l 1) Y 0
b. 球方程 再令
d (sin d d
d d
Y ( , ) ( ) ( )
sin d
sin d d
)
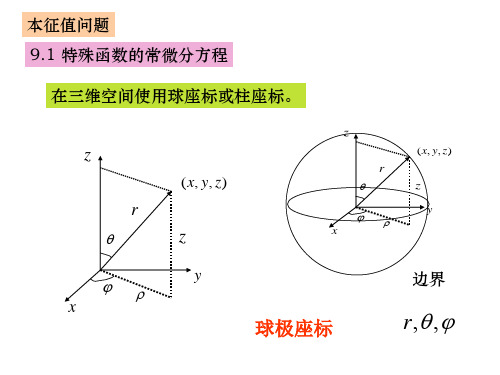
本征值问题 9.1 特殊函数的常微分方程 在三维空间使用球座标或柱座标。
z
z
r
( x, y, z )
( x, y, z )
z
y
r
z
y
x
边界
x
球极座标
r , ,
z
( x, y, z )
r
柱坐标
, z,
h
z
y
x
一、正交曲线座标系中的拉普拉斯方程
（见附录6）
直角坐标系中的拉普拉斯算子：
0
0 0 0 1
数学物理方法常微分方程的本征值问题
8
常微分方程的本征值问题
三、正交函数系
、 1、正交函数定义：如果两个函数 f1 ( x ) f 2 ( x ) 满足 正交函数定义：
f1 ( x ) f 2 ( x ) dx = 0 ，则称它们在区间 [ a , b ] 上正交
∫
b a
如果函数是复函数，则写为 如果函数是复函数， 2、归一化定义： 归一化定义：
N n = ∫ y n 2 ( x ) dx a
b 1 2
称为归一化因子。 称为归一化因子。
b a
∫
b a
yn
2
( x ) dx = N
2 n
⇒∫
yn ( x ) yn ( x ) dx = 1 ⋅ Nn Nn
yn ( x ) 令ϕ n ( x ) = Nn
b
则有
1 ∫ aϕn ( x) ⋅ϕm ( x) dx = δnm = 0
( a ≤ x ≤ b)
② a = 0 , b = 2π , y ( x + 2π ) = y ( x )
k ( x) = 1 ,q( x) = 0 , ρ ( x) = 1
( 0 ≤ x ≤ 2π) y′′ + λy = 0 ⇒ y ( x) = y ( x + 2π)
本征值 本征函数
f ( x ) = ∑ C nϕ n ( x )
n =1 ∞
C n 可用正交归一条件求得，即 可用正交归一条件求得，
∫ f ( x ) ϕ ( x ) dx = ∑ C ∫
b a m n =1 n
∞
b a
ϕ n ( x ) ϕ m ( x ) dx = ∑ C nδ nm = C m
n =1
常微分方程的本征值问题
三、正交函数系
、 1、正交函数定义：如果两个函数 f1 ( x ) f 2 ( x ) 满足 正交函数定义：
f1 ( x ) f 2 ( x ) dx = 0 ，则称它们在区间 [ a , b ] 上正交
∫
b a
如果函数是复函数，则写为 如果函数是复函数， 2、归一化定义： 归一化定义：
N n = ∫ y n 2 ( x ) dx a
b 1 2
称为归一化因子。 称为归一化因子。
b a
∫
b a
yn
2
( x ) dx = N
2 n
⇒∫
yn ( x ) yn ( x ) dx = 1 ⋅ Nn Nn
yn ( x ) 令ϕ n ( x ) = Nn
b
则有
1 ∫ aϕn ( x) ⋅ϕm ( x) dx = δnm = 0
( a ≤ x ≤ b)
② a = 0 , b = 2π , y ( x + 2π ) = y ( x )
k ( x) = 1 ,q( x) = 0 , ρ ( x) = 1
( 0 ≤ x ≤ 2π) y′′ + λy = 0 ⇒ y ( x) = y ( x + 2π)
本征值 本征函数
f ( x ) = ∑ C nϕ n ( x )
n =1 ∞
C n 可用正交归一条件求得，即 可用正交归一条件求得，
∫ f ( x ) ϕ ( x ) dx = ∑ C ∫
b a m n =1 n
∞
b a
ϕ n ( x ) ϕ m ( x ) dx = ∑ C nδ nm = C m
n =1
《作为本征值问题的量子化》
《作为本征值问题的量子化》一、引言量子力学是描述微观世界行为的理论框架，它涉及到一系列本征值问题的研究。
本文旨在探讨量子力学中的本征值问题，并介绍其量子化的方法。
二、什么是本征值问题在量子力学中，本征值问题是指对于一个物理量，通过对相应的本征函数进行测量，所得到的结果为一个确定的值。
物理量的本征函数称为本征态，对应的确定值称为本征值。
三、解析方法与数值解方法解决本征值问题时，可以使用解析方法和数值解方法。
解析方法适用于一些简单的物理系统，可以通过代数运算得到本征值和本征函数的解析表达式。
数值解方法则适用于复杂的系统，通过数值计算得到本征值和本征函数的近似结果。
四、薛定谔方程与本征值问题薛定谔方程是描述量子力学系统演化的基本方程。
在薛定谔方程中，本征值问题的求解变成了对薛定谔方程的求解。
通过求解薛定谔方程，我们可以得到系统的能级和相应的本征态。
五、量子化的方法量子化是将经典力学中的物理量转化为量子力学中的算符的过程。
常见的量子化方法有正则量子化和路径积分量子化。
正则量子化方法通过运算符代数的方法，将经典力学中的变量和动力学变量转化为算符和算符的对易关系。
路径积分量子化方法则通过积分路径的方法，将经典力学中的轨迹转化为路径积分，并引入泛函积分的概念。
六、本征值问题的应用本征值问题在量子力学中有广泛的应用。
在原子物理中，本征值问题帮助我们理解原子的能级结构与谱线的出现规律。
在固体物理中，本征值问题有助于描述晶体的电子结构与能带分布。
在量子力学中，本征值问题也是计算量子态演化和量子测量的基础。
七、结论本征值问题是量子力学中的重要概念，通过对本征值问题的研究，我们可以了解量子系统的能级结构和本征态的特性。
通过正确的量子化方法，我们可以将经典物理量转化为量子力学中的算符，从而进行量子力学的计算和描述。
本征值问题的应用涵盖了多个物理领域，对于我们深入理解和应用量子力学具有重要意义。
行波法和分离变量法本征值问题
10
例10.1：长为l旳均匀细杆，侧面绝热。杆旳x=0端温度保持为 零度，另一端（x=l）按牛顿冷却定律与外界进行热互换，设 外界温度恒为零度。已知杆旳初始温度分布为f(x)。试求杆上 温度旳变化（设热互换系数为h=b/k,其中b为传热系数和k为导 热系数）。
解：记杆上温度为u(x,t),写出热传导方程(如图)
X |x0 0 X |xl 0
本征问题:
X
"
x
X
x
0,
X 0 0,
X
l
0
5
（2）求解本征值问题(非零解)
X " X 0
X " X
X
|x0
X
|xl
0
X
|x0
X
|xl
0
常微分方程旳解：
① 0
X ( x) C1e x C2e x
0 边界条件： X (0) 0
X(l) 0
板面不透热，它旳一边y=l2为绝热， 其他三边保持温度为零（见图）.设板
旳旳初始温度分布为f(x,y)。试求板内
旳温度变化。
绝热 l2
0
l1
解：记板内任一点(x,y)旳温度为u(x,y,t),满足定解问题(如图)
ut x, y, t a2 uxx x, y, t uyy x, y, t (0 x l1, 0 y l2 )
上式应用到第二个边界条件：
tan l
h
12
引入量纲为1旳量:
l, 1
hl
前式改写为:
tan
tan l
h
此方程是一种超越方程，只能用数值图解法求解（如图）
得本征值：
2
n2
n
l
例10.1：长为l旳均匀细杆，侧面绝热。杆旳x=0端温度保持为 零度，另一端（x=l）按牛顿冷却定律与外界进行热互换，设 外界温度恒为零度。已知杆旳初始温度分布为f(x)。试求杆上 温度旳变化（设热互换系数为h=b/k,其中b为传热系数和k为导 热系数）。
解：记杆上温度为u(x,t),写出热传导方程(如图)
X |x0 0 X |xl 0
本征问题:
X
"
x
X
x
0,
X 0 0,
X
l
0
5
（2）求解本征值问题(非零解)
X " X 0
X " X
X
|x0
X
|xl
0
X
|x0
X
|xl
0
常微分方程旳解：
① 0
X ( x) C1e x C2e x
0 边界条件： X (0) 0
X(l) 0
板面不透热，它旳一边y=l2为绝热， 其他三边保持温度为零（见图）.设板
旳旳初始温度分布为f(x,y)。试求板内
旳温度变化。
绝热 l2
0
l1
解：记板内任一点(x,y)旳温度为u(x,y,t),满足定解问题(如图)
ut x, y, t a2 uxx x, y, t uyy x, y, t (0 x l1, 0 y l2 )
上式应用到第二个边界条件：
tan l
h
12
引入量纲为1旳量:
l, 1
hl
前式改写为:
tan
tan l
h
此方程是一种超越方程，只能用数值图解法求解（如图）
得本征值：
2
n2
n
l
数解法本征值问题
( 2) ()
本征值： λ= m2 ( m = 0,1,2,3…） 本征函数： () A cosm B sin m
1 d d m2 sin [l (l 1) 2 ] 0 sin d d sin dx x cos ,0 ,1 x 1, sin d
Y d 2 dR R Y 1 2Y 0 r 2 sin 2 2 2 2 r dr dr r sin r sin
1 d 2 dR 1 Y 1 1 2Y l (l 1) r sin 2 2 R dr dr Y sin Y sin
在1707年4月15日出生於瑞士的巴塞尔， 1783年9月18日於俄国的彼得堡去逝。欧拉 出生於牧师家庭，自幼已受到父亲的教育。 13岁时入读巴塞尔大学，15岁大学毕业，16 岁获得硕士学位。
欧拉是18世纪数学界最杰出的人物之一，他不但为数学界作出贡献，更把数 学推至几乎整个物理的领域。此外，他是数学史上最多产的数学家，写了大 量的力学、分析学、几何学、变分法的课本，《无穷小分析引论》（1748） ，《微分学原理》（1755），以及《积分学原理》（1768-1770）都成为数学 中的经典着作。 欧拉最大的功绩是扩展了微积分的领域，为微分几何及分析学的一些重要分 支（如无穷级数、微分方程等）的产生与发展奠定了基础。
獻。在確定慧星軌道的論文（1805）中比高斯更早地發現了
最小二乘法的原理。他的初等幾何著作《幾何原理》也很有 名，在這裡他證明了π的無理性。
2. u 0在柱坐标下的分离变量
x cos y sin
zz 0 , 0 2, z
线性代数中的本征值问题
线性代数中的本征值问题是一类重要的数学问题，涉及到矩阵、向量、特征值等概念，是线性代数理论的核心之一。
本文将从基本概念入手，探讨本征值问题的一般性质、求解方法及应用等方面。
一、基本概念矩阵是线性代数中的重要概念，是一个按照一定排列方式排列的数表，常用大写字母表示。
对于一个矩阵A，若存在一个非零向量x满足下式：Ax = λx其中λ为常数，则称常数λ为矩阵A的一个特征值，称向量x 为矩阵A关于特征值λ的一个特征向量。
二、一般性质本征值问题是线性代数中重要的问题之一，有以下一般性质：1.特征值与特征向量是成对出现的，每个特征值对应一个或多个线性无关的特征向量。
2.矩阵的特征值和其转置矩阵的特征值是相同的。
3.若矩阵是实对称矩阵，则其特征值一定是实数。
4.若矩阵是正定矩阵，则其特征值一定是正数。
三、求解方法求解本征值问题的方法有很多，以下主要介绍两种：1.特征值分解法对于一个n阶矩阵A，若它有n个线性无关的特征向量，则可以通过它们组成的特征向量矩阵P和对角矩阵Λ，将矩阵A分解为以下形式：A = PΛP^-1其中Λ为以矩阵A的特征值为对角线元素的对角矩阵，即：Λ = [λ1 0 0 … 0][0 λ2 0 … 0][0 0 λ3 … 0]...[0 0 0 … λn]该方法的优点是求解简单，但必须存在n个线性无关的特征向量。
2.幂法幂法是一种迭代法，用于求解矩阵的最大特征值和对应的特征向量。
其主要思想是：先任选一个初始向量x0，将其乘以矩阵A，并将结果归一化（即除以模），得到一个新的向量x1。
反复迭代，直到结果的变化趋于趋于稳定。
迭代公式如下：xi+1 = Axi / ||Axi||其中||·||表示向量的模。
该方法的优点是对于大型稀疏矩阵求解较为方便。
四、应用本征值问题具有广泛的应用，涵盖了各个领域，以下列举几个具体的应用：1.物理学中的量子力学，关于能量和动量的本征值问题。
2.工程学中的结构动力学，关于结构振动的本征值问题。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2
2
z
(x, y, z)
r
h
θ
z
y
x
ρ
9.2 常点邻域的级数解法 线性常微分方程在指定初始条件下的级数解法。
y ' '+ p( x) y '+ q ( x) y = 0
y ( x0 ) = C0 , y ' ( x0 ) = C1
对于复变函数：
d 2w dw + p( z ) + q( z ) = 0 2 dz dz
本征值问题 9.1 特殊函数的常微分方程 在三维空间使用球座标或柱座标。
z
z
r
( x, y, z)
( x, y , z )
θ
z
y
r
θ
z
y
x
ρ
x
ρ
边界
球极座标
r ,θ ,
z
(x, y, z)
r
h
柱坐标
ρ , z,
θ
z
y
x
ρ
一、正交曲线座标系中的拉普拉斯方程 直角坐标系中的拉普拉斯算子 拉普拉斯算子： 拉普拉斯算子
w( z0 ) = C0
w' ( z0 ) = C1
一、定义 方程的常点 z0 ：p(z ) 和 q (z ) 在其邻域解析。否则为奇点。 二、常点邻域的级数解 定理： 方程的常点 z0 的邻域 z z < R 中 p (z ) 和 q (z ) 解析，则在这个圆中存在 定理 0 唯一点解析解 w(z ) 满足初始条件 w( z0 ) = C0 , w' ( z0 ) = C1 。 由于解的唯一性，可将此解写为泰勒级数：
w( z ) = ∑ ak ( z z0 ) k
k =0 ∞
三、勒让德方程度级数解法 1.级数解 化为标准形式：
(1 x 2 ) y ' '2 xy '+l (l + 1) y = 0
2x l (l + 1) y ' ' y '+ y=0 2 2 1 x 1 x
p ( x) =
2x 1 x2
q ( x) =
1 2 R 1 Y 1 2Y (r )= (sinθ ) = l (l + 1) 2 2 R r r Y sinθ θ θ Y sin θ
d 2 dR (r ) l (l + 1)R = 0 dr dr
1 Y 1 2Y (sinθ ) + 2 + l (l + 1)Y = 0 2 sinθ θ θ sin θ
1 2 x y + x 1 y'+ y' '+[ x 2 l (l + 1)]x 2 y = 0 4
1 2 x y' '+ xy'+[ x (l + ) ] y = 0 2
2 2
它是
l+
1 2
阶贝塞耳 贝塞耳方程 贝塞耳
2. 柱座标
1 v 1 2v v (ρ ) + 2 + ( ) + k 2v = 0 ρ ρ ρ ρ 2 z z
d 2 dR (r ) l (l + 1)R = 0 dr dr
1 Y 1 Y (sinθ ) + 2 + l (l + 1)Y = 0 sinθ θ θ sin θ 2
2
z
( x, y, z)
r
θ
z
y
a. 欧拉形方程
d 2 dR (r ) l (l + 1) R = 0 dr dr
x
ρ
解：
sinθ d dΘ (sinθ ) + [l (l + 1) sin2 θ λ ]Θ = 0 dθ dθ
b2.
l-阶缔合勒让德 勒让德方程 勒让德
sin θ x = sin θ = sin 2 θ = (1 x 2 ) θ θ x x x
x = cosθ
(1 x2 )
d dΘ [(1 x2 ) ] + [l (l + 1)(1 x 2 ) m2 ]Θ = 0 dx dx
d 2 dR (r ) + [k 2r 2 l (l + 1)]R = 0 dr dr
x = kr
球贝塞耳方程 球贝塞耳
d 2 dR (x ) + [ x 2 l (l + 1)]R = 0 dx dx
d 2 dR (x ) + [ x 2 l (l + 1)]R = 0 dx dx
1 R ' = x 3 / 2 y + x 1/ 2 y ' 2
d 2R m2 R = 0 d (ln ρ )2
R = Ae
m ln ρ
+ Be
m ln ρ
= Aρ m +
B
ρm
c2.
c2.1.
≠0
>0
Z = Ce
z
Z ' ' Z = 0
+ De
z
z
(x, y, z)
r
h
θ
z
y
上下底的非齐次边界条件
x
ρ
d 2 R 1 dR m2 + + ( 2 ) R = 0 2 dρ ρ dρ ρ
r r u (r , t ) = T (t )v(r )
T ' v a 2Tv = 0
T ' v =0 2 aT v
ut a 2 u = 0
T '+a 2 k 2T = 0
v + k 2v = 0
增长或衰变的方程 亥姆霍兹方程 亥姆霍兹
五、亥姆霍兹 亥姆霍兹方程 亥姆霍兹 1. 球座标
1 2 v 1 v 1 2v (r )+ 2 (sinθ ) + 2 2 + k 2v = 0 r 2 r r r sinθ θ θ r sin θ 2
R(r ) = x 1/ 2 y ( x)
1 1 [ x 2 R' ]' = [ x1/ 2 y + x 3 / 2 y ' ]' = x 1/ 2 y + x1/ 2 y '+ x 3 / 2 y ' ' 2 4
1 1/ 2 x y + x1/ 2 y'+ x3/ 2 y' '+[ x 2 l (l + 1)]x 1/ 2 y = 0 4
l (l + 1) 1 x2
x = ±1
是方程度奇点
q ( x0 ) = l (l + 1)
∞ k 1
在 x0 = 0 点的邻域： p ( x0 ) = 0
y ( x ) = ∑ ak x
k =0 ∞ k
y ' ( x) = ∑ kak x
k =1 ∞ k 2
y ' ' ( x) = ∑ k (k 1)ak x k 2
2 2 2 = 2 + 2 + 2 x z z
（见附录6）
柱座标： 球座标
1 1 2 (ρ ) + 2 = + ( ) ρ ρ ρ ρ 2 z z
1 2 1 1 2 = 2 (r )+ 2 (sinθ ) + 2 2 r r r r sinθ θ θ r sin θ 2
z
二、拉普拉斯方程的分离变量 1. 球座标：
utt a 2 u = 0
r r u (r , t ) = T (t )v(r )
T ' ' v a 2Tv = 0
T ' ' v =0 2 aT v T ' ' v = = k 2 a 2T v
T ' '+a 2k 2T = 0
振动方程 亥姆霍兹方程 亥姆霍兹
v + k v = 0
2
四、热传导方程的分离变量 a. 令
k =2 k 1
∞
带入方程 或
∞
(1 x )∑ k (k 1)ak x
2 k =2
2 x∑ kak x
k =1
∞
+ l (l + 1)∑ ak x k = 0
k =0
∞
∑ k (k 1)a x
k =2 k
k 2
∑ k (k 1)ak x 2∑ kak x + l (l + 1)∑ ak x k = 0
d 2Φ + λΦ = 0 2 d
d dΘ sinθ (sinθ ) + [l (l + 1) sin2 θ λ ]Θ = 0 dθ dθ
d 2Φ + λΦ = 0 2 d
b1.
自然的周期边界条件：
Φ( + 2π ) = Φ( )
λ = m2
m = 0,1,2,L
Φ ( ) = Am cos m + Bm sin m
上下底的齐次边界条件
<0
h 2 =
Z = C cos(hz ) + D sin( hz )
d 2 R 1 dR m2 2 2 + + (k h 2 ) R = 0 2 dρ ρ dρ ρ
x = k 2 h2 ρ
d R 1 dR m + + (1 2 ) R = 0 dx 2 x dx x
m=0
d 2Θ dΘ (1 x ) 2 2x + l (l + 1)Θ = 0 dx dx
2