四川公务员笔试行测资料分析公式大全
公务员考试行测资料分析公式汇总推荐文档

同比增长率本期数 ::A 上年同期数:B冋比增长率:m% 已知: 本期数 A 和上年同期数B 求:冋比增长率 m%公式: m% A BA B 100%B已知: 本期数 A 和冋比增长率m%求:上年同期数B公式: B -A1 m%已知:上年同期数 B 和同比增长率 m% 求:本期数 A公式:A B (1m%)环比增长率本期数:A上期数:C 环比增长率:n%已知: 本期数 A 和上期数C 求:环比增长率n%公式: n% A C 100%C已知: 本期数 A 和环比增长率 求:上期数C公式:C - A1 n%已知:环比增长率 n%和上期数 C 求:本期数A公式:A C (1 n%)本期数:A 上年同期数: 已知 公式 已知 公式:已知 公式已知 公式已知 公式:B本期数A 和上年同期数 X AB 本期数 A 和同比增长率A X m%1 m%上年同期数 B 和同比增长量 A B X 本期数 A 和同比增长量B A X 本期数 同比增长量 同比增长率:m% 求:同比增长量同比增长量 Xm% 求:同比增长量 X 求:本期数求:上年同期数 m%A 和同比增长量 X100%A X求:同比增长率m% 本期数:A 上期数:C 环比增长率:n% 环比增长量已知:本期数 A 和上期数C 求:环比增长量Y公式: Y A D已知: 本期数 A 和环比增长率 求:环比增长量Y公式:Y — —n%1 n%已知:上期数 C 和环比增长量 Y 求:本期数A环比增长量Y第n年相比于第n-2年的增速(1 m%)(1 m%- n%)-1B,这n年的年均增长率为1、已知第m年的数据指标为A,年均增长率为,求第n年的数据指标B,根据上式展开2、已知第m年的数据指标为A,第n年为B,年均增长率。
第n年相对于第m年的增长B B— B—率为,且一1,即1 —。
根据上式可知,(1 )n-m -,则有(1 )n-m1,A A A(n-m)且大于(n-m),在选项差距较大时,一般使用公式(n-m),即n m比重公式: A C Y已知: 本期数A和环比增长量Y求:上期数C公式: C A Y已知: 本期数A和环比增长量Y求:环比增长率n%公式: n%Y100%A Y跨年份增长假设第n年某指标为A,同比增长m%,增速同比增长n个百分点,则第n-2年该指标A (1 m%)1 ( m n%)年均增长量一段时间内某一数据指标平均每年增长的数量。
公务员行测数学常用公式汇总大全

公务员考试行测数学常用公式汇总大全1、等差数列(1)s n =2)(1n a a n +⨯=na 1+21n(n-1)d ;(2)项数n =da a n 1-+1; (3)若m+n=k+i ,则:a m +a n =a k +a i ;(4)前n 个奇数:1,3,5,7,9,…(2n —1)之和为n 2(其中:n 为项数,a 1为首项,a n 为末项,d 为公差,s n 为等差数列前n 项的和) (5)a n =a 1+(n -1)d ;(6)若a,A,b 成等差数列,则:2A =a+b ;2、基础代数公式1. 完全立方公式:(a±b)3=(a±b )(a 2μab+b 2)2. 立方和差公式:a 3+b 3=(a ±b)(a 2+μab+b 2)3. a m ·a n =a m +n a m ÷a n =a m -n (a m )n =a mn (ab)n =a n ·b n 4. 平方差公式:(a +b )·(a -b )=a 2-b 2 5. 完全平方公式:(a±b)2=a 2±2ab +b 23、不等式1.abc c b a 3222≥++ abc c b a 33≥++推广:n n n x x x n x x x x ......21321≥++++2.一阶导为零法:连续可导函数,在其内部取得最大值或最小值时,其导数为零。
3.两项分母列项公式:)(a m m b +=(m 1—a m +1)×ab4.三项分母裂项公式:)2)((a m a m m b ++=[)(1a m m +—)2)((1a m a m ++]×ab 25.一元二次方程求根公式:ax 2+bx+c=a(x-x 1)(x-x 2)其中:x 1=a ac b b 242-+-;x 2=aacb b 242---(b 2-4ac ≥0)根与系数的关系:x 1+x 2=-a b ,x 1·x 2=ac6.ab b a 2≥+ ab b a ≥+2)2( ab b a 222≥+ abc c b a ≥++3)3(4、工程问题工作量=工作效率×工作时间; 工作效率=工作量÷工作时间; 工作时间=工作量÷工作效率; 总工作量=各分工作量之和; 注:在解决实际问题时,常设总工作量为1或最小公倍数5、几何边端问题(1)方阵问题:1.空心方阵:方阵总人数=(最外层每边人数)2-(最外层每边人数-2×层数)2 =(最外层每边人数-层数)×层数×4=中空方阵的人数。
公务员考试资料分析公式大全

公务员考试资料分析公式大全2.百分点表示相对指标的变化幅度,可直接相加减。
例如,从10%增长到20%,增长了10个百分点,而不是10%。
基期、现期、增长量、增长率基期量是对比参照时期的具体数值,现期量是相对于基期量的数值,增长量是现期量相对于基期量的变化量。
平均增长量是一段时间内平均每期的变化量,而增长率是现期量相对于基期量的变化指标。
年均增长率和间隔增长率年均增长率是基期量经过n个周期变为末期量B的情况下,计算出的平均增长率。
但当|x|>10%时,利用公式计算存在一定误差。
间隔增长率是已知第二期和第三期的增长率,求第三期相对于第一期的增长率。
混合增长率混合增长率是已知部分的增长率,求整体的增长率。
例如,A的增长率是a,B的增长率是b,而“A+B”的增长率是r,其中r介于a、b之间,且偏向于基数较大一方的增长率。
同比增长和环比增长同比增长是与历史同期相比的增长情况,而环比增长是与相邻上一个统计周期相比的增长情况。
平均数、比重、倍数、翻番和指数平均数包括现期平均数和基期平均数,其中A为现期总量,a为对应增长率,B为现期份数,b为对应增长率。
比重指部分在整体中所占的百分比,用个百分数或者“几成”表示。
倍数是A是B的多少倍,A÷B;而翻番是翻几番变为原来数值的倍。
指数是描述某种事物相对变化的指标值,假设基数为100,其他值与基期相比得到的数值。
删除有问题的段落。
1.修改每段话:算法可以帮助我们计算各种数值的变化。
例如,如果现在比过去增长了20%,那么我们可以用算法100×(1+20%)=120来计算。
同样地,如果现在比过去降低了20%,那么我们可以用算法100×(1-20%)=80来计算。
如果我们想知道某个数是原来的多少倍,我们可以用倍数进行计算。
例如,某城市2000年的人均住房使用面积达到14.8平方米,比1978年的3.8平方米高出3.9倍。
另外,我们也可以用翻番来计算数量加倍的情况。
公务员考试——行测常用公式汇总

公务员考试——行测常用数学公式汇总一、基础代数公式1.平方差公式:( a+b)3( a-b)= a2- b22.完全平方公式:( a±b)2=a2±2ab+ b2完全立方公式:( a±b)3=a3±3a2b+3ab2±b33.同底数幂相乘 : a m3a n=a m+n(m、n 为正整数, a≠0)同底数幂相除:m n m-na ÷a=a(m、n为正整数,a≠0)a a-p 0=1(a≠0)=(a≠0, p 为正整数)4.等差数列:(1)前 n 项和公式:Sn==na1+1n(n-1)d;2na n1n 为奇数2(2)中项求和:Sn nn 为奇数a n a n1222(3)通项公式:a n=a1+(n-1)d;(5)等差中项:若a,A,b 成等差数列,则:2A=a+b;(6)对称公式:若m+n=k+i,则: a m+a n=a k+a i;通项公式推论: a m-a n=(m-n)d(其中: n 为项数, a1 为首项, an 为末项, d 为公差, sn 为等差数列前 n 项的和)5.等比数列:(1)通项公式:a n=a12q n-1;a 1q n a n qa11q 1(2)前n项和公式:Sn1q1qna1q12(3)等比中项:若a,G,b 成等比数列,则: G=ab;(4)对称公式:若m+n=i+j ,则:a m a n a i a j;(其中: n 为项数, a1为首项, a n为末项, q 为公比, Sn 为等比数列前 n 项的和)二、基础几何公式1.三角形:不在同一直线上的三点可以构成一个三角形;三角形内角和等于180°;三角形中任两边之和大于第三边、任两边之差小于第三边;(1)角平分线:三角形一个的角的平分线和这个角的对边相交,这个角的顶点和交点之间的线段 , 叫做三角形的角的平分线。
(2)三角形的中线:连结三角形一个顶点和它对边中点的线段叫做三角形的中线。
公务员考试行测常见基础公式汇总

公务员考试行测常见基础公式汇总公务员考试中,行政职业能力测验(简称行测)是重要的组成部分。
其中涉及到众多的知识点和公式,掌握这些基础公式对于提高解题效率和准确性至关重要。
下面为大家汇总了一些行测常见的基础公式。
一、数量关系1、等差数列通项公式:$a_n = a_1 +(n 1)d$,其中$a_n$表示第$n$项的值,$a_1$表示首项,$d$表示公差。
例如,已知一个等差数列的首项为 3,公差为 2,求第 10 项的值。
则$a_{10} = 3 +(10 1)×2 = 21$等差数列求和公式:$S_n =\frac{n(a_1 + a_n)}{2}$,其中$S_n$表示前$n$项的和。
例如,求上述等差数列前 10 项的和,$a_{10} = 21$,则$S_{10}=\frac{10×(3 + 21)}{2} = 120$2、等比数列通项公式:$a_n = a_1×q^{n 1}$,其中$q$为公比。
例如,一个等比数列的首项为 2,公比为 3,求第 5 项的值。
则$a_{5} = 2×3^{5 1} = 162$等比数列求和公式:$S_n =\frac{a_1(1 q^n)}{1 q}$($q ≠1$)3、行程问题相遇问题:$S =(v_1 + v_2)×t$,其中$S$表示路程,$v_1$、$v_2$表示两个物体的速度,$t$表示相遇时间。
例如,甲、乙两人分别以 5 米/秒和 3 米/秒的速度相向而行,经过10 秒相遇,求他们最初的距离。
则$S =(5 + 3)×10 = 80$米追及问题:$S =(v_1 v_2)×t$例如,甲以 8 米/秒的速度追赶以 5 米/秒速度前行的乙,经过 10 秒追上,求他们最初的距离差。
则$S =(8 5)×10 = 30$米4、工程问题工作总量=工作效率×工作时间例如,一项工程,甲单独完成需要 10 天,乙单独完成需要 15 天,两人合作需要的时间为:$1÷(\frac{1}{10} +\frac{1}{15})=6$天5、利润问题利润=售价成本利润率=利润÷成本×100%例如,一件商品成本为 80 元,售价为 100 元,则利润为$100 80 =20$元,利润率为$20÷80×100\%= 25\%$二、资料分析1、增长率增长率=(现期量基期量)÷基期量×100%例如,某地区去年的 GDP 为 100 亿元,今年为 120 亿元,则增长率为$(120 100)÷100×100\%= 20\%$2、平均数平均数=总数÷个数例如,某班级 5 名学生的成绩分别为 80、90、85、95、70 分,平均成绩为$(80 + 90 + 85 + 95 + 70)÷5 = 84$分3、比重比重=部分÷整体×100%例如,某公司总人数为 500 人,其中男性 250 人,则男性所占比重为$250÷500×100\%= 50\%$三、判断推理1、集合推理“所有的 S 都是P”可以推出“有的 S 是P”“某个 S 是P”可以推出“有的 S 是P”2、翻译推理“如果……那么……”:前推后“只有……才……”:后推前3、逻辑论证加强论证:增加论据、建立联系、补充前提削弱论证:削弱论据、切断联系、否定前提四、言语理解与表达虽然言语理解与表达部分没有像数量关系和资料分析那样有明确的公式,但一些解题技巧和规律还是需要掌握的。
2024国考行测资料公式汇总

2024国考行测资料公式汇总一、概述随着国家发展和改革的不断推进,国家公务员考试作为选拔和录用优秀人才的重要途径,备受关注和热议。
而国家公务员考试中的行政职业能力测验(简称行测),作为其中的一项重要考试科目,涵盖了诸多知识点和应试技巧。
其中,数学实在是行测中的一大难点,而其中的公式更是让考生头疼的部分。
我们特整理了以下2024国考行测资料公式,以便考生备考时能够更好地复习和掌握相关知识点。
二、数量关系题目公式1. 平均值计算公式平均值 = 总值 / 个数2. 比例计算公式两者之比 = 较多者 / 较少者3. 反比例计算公式两者之比 = 较少者 / 较多者4. 增减百分比计算公式百分比增加 = (增加值 / 原值) * 100百分比减少 = (减少值 / 原值) * 1005. 资料图计算公式根据柱状图、折线图或饼状图进行计算6. 存在关系计算公式混合物的平均浓度 = (已知浓度1 * 体积1 + 已知浓度2 * 体积2) / (体积1 + 体积2)三、判断推理题目公式1. 判断题公式真命题的否定为假命题假命题的否定为真命题2. 排序题公式正序排列:A<B<C逆序排列:A>B>C3. 相同字母代表相同物品四、言语理解与表达题目公式1. 近义词、反义词近义词:意思相近的词反义词:意思相反的词2. 词类变化名词→形容词→动词→副词→数词→代词→连词→介词→感叹词3. 词语搭配正词相反:冷热、高低动名结合:吃饭、送信五、综合分析题目公式1. 逻辑判断公式A→B 非B→非AA→B 非A→非B2. 选择判断公式对A的肯定是否定了B的否定3. 数字推理公式数字之和、差、乘积、商之间的规律4. 资料分析公式根据给出的数据进行图表和数据的计算和分析六、总结以上整理的2024国考行测资料公式只是行测知识点的冰山一角,但通过对这些公式的学习和掌握,能让考生更快地应对行测考试中的数量关系、判断推理、言语理解与表达、综合分析等题目类型。
公务员行测资料分析公式大全
先计算 ,然后根据a和b的大小来判断大小
21.某部分现期量为A,增长率为a%,整体现期量为B,增长率为b%
基期比重= ×
先计算 ,然后根据a和b的大小来判断大小
比重比较
22.某部分现期量为A,整体现期量为B
现期比重=
分数打下比较
23.基期比重与现期比重比较:某部分现期量为A,增长率为a%,整体现期量为B,增长率为b%
=
直除法
增长量比较
12.已知现期量与增长率x%
增长量= ×x%
特殊分数法,当 %可以被视为 时,公式可以化简为
增长率计算
13.已知基期量与增长量
增长量=
截位直除法、插值法
14.已知现期量与基期量
增长率=
截位直除法
15.如果基期量为A,经N期变为B,平均增长率为x%
= -1
代入法
增长率比较
16.已知现期量与增长量
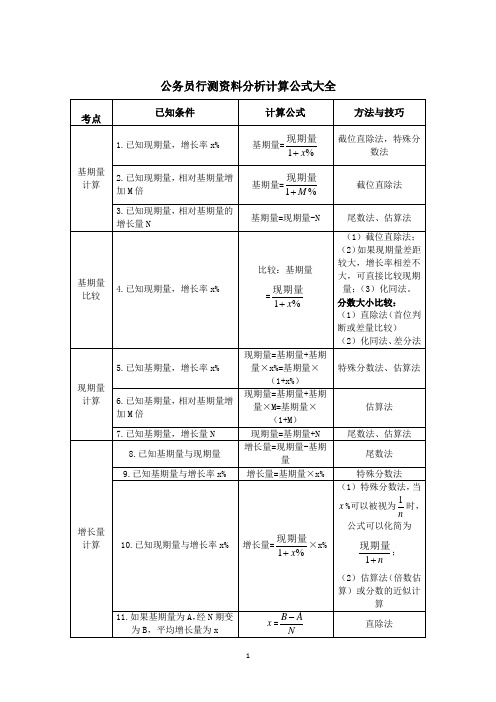
公务员行测资料分析计算公式大全
考点
已知条件
计算公式
方法与技巧
基期量计算
1.已知现期量,增长率x%
基期量=
截位直除法,特殊分数法
2.已知现期量,相对基期量增加M倍
基期量=
截位直除法
3.已知现期量,相对基期量的增长量N
基期量=现期量-N
尾数法、估算法
基期量比较
4.已知现期量,增长率x%
比较:基期量=
(1)截位直除法;(2)如果现期量差距较大,增长率相差不大,可直接比较现期量;(3)化同法。
尾数法、估算法
增长量计算
8.已知基期量与现期量
增长量=现期量-基期量
尾数法
9.已知基期量与增长率x%
增长量=基期量×x%
公务员考试行测资料分析公式汇总

同比增长率本期数:A 上年同期数:B 同比增长率:m%已知:本期数A 和上年同期数B 求:同比增长率m% 公式:%100m%⨯-=BB A 已知:本期数A 和同比增长率m% 求:上年同期数B 公式:%1m A B += 已知:上年同期数B 和同比增长率m% 求:本期数A公式:)m%1(+⨯=B A同比增长量本期数:A 上年同期数:B 同比增长率:m% 同比增长量:X已知:本期数A 和上年同期数B 求:同比增长量X公式:B A X -=已知:本期数A 和同比增长率m% 求:同比增长量X 公式:%m m%1⨯+=A X 已知:上年同期数B 和同比增长量X 求:本期数A公式:X B A +=已知:本期数A 和同比增长量X 求:上年同期数B公式:X A B -=已知:本期数A 和同比增长量X 求:同比增长率m% 公式:%100m%⨯-=XA X 环比增长率本期数:A 上期数:C 环比增长率:n%已知:本期数A 和上期数C 求:环比增长率n%公式:%100n%⨯-=CC A 已知:本期数A 和环比增长率 求:上期数C 公式:n%1+=A C 已知:环比增长率n%和上期数C 求:本期数A公式:)n%1(+⨯=C A环比增长量本期数:A 上期数:C 环比增长率:n% 环比增长量:Y已知:本期数A 和上期数C 求:环比增长量Y公式:D A -=Y已知:本期数A 和环比增长率 求:环比增长量Y 公式:n%n%1⨯+=A Y 已知:上期数C 和环比增长量Y 求:本期数A公式:Y C A +=已知:本期数A 和环比增长量Y 求:上期数C公式:Y A C -=已知:本期数A 和环比增长量Y 求:环比增长率n% 公式:%100n%⨯-=YA Y 跨年份增长假设第n 年某指标为A ,同比增长m%,增速同比增长n 个百分点,则)()(年该指标第n%m 1m%12-n -++÷=A 1-n%-m%1m%12-n n )()(年的增速年相比于第第+⨯+=年均增长量一段时间内某一数据指标平均每年增长的数量。
