齿根应力与齿根的计算方法进展与比较研究

合集下载

齿根应力与轮齿弹性变形的计算方法进展与比较研究_周长江

1926 年 , Timoshenko[ 22] 提供了第一份关于轮齿应力光弹测量的结果。1940 年 , Dolan[ 23] 根据光弹试验结果提出了与受力点位置和齿根圆角大小相关的应力集中系数。Heywood[ 24] 、Kelly[ 25] 根据光弹研究结果给出了各自的齿根应力计算的经验公式。 1955 年 , Jacobson[ 26] 根据众多的光弹研究成果提出了修正的疲劳极限公式。1967 年 , Baxter[ 27] 用三维光弹技术来确定双曲线锥齿轮三维模型中的应力分布 , 这一研究奠定了三维齿形表面应力研究的基础。近些年 , 我国的薛春玉[ 28] 、许洪斌[ 29] 等应用冻结切片三维光弹技术 , 分别对弧齿锥齿轮和分阶式双渐开线齿轮进行了试验分析。
解析法
各向同性楔模型
弹性力学法 :保角映射法
应力变形
光测力学法
实验法
计算方法
电测力学法
有限差分法
数值法边界元法
有限元法 :挠曲/ 接触分析
图 1 各类计算方法一览
1 解析法
1 .1 材料力学法这种方法使用最早。 1893 年 , Lewis[ 1] 基于材料力
学的抛物线梁理论 , 把轮齿视为等强度悬臂梁 ;首次提
出了“齿形系数”的概念 , 并推导出著名的 Lewis 公式 , 从而奠定了轮齿弯曲强度计算的理论基础。 Rand[ 2] 利
用等截面悬臂梁模型计算出轮齿的弹性变形。Walker[ 3] 在研究齿廓修形时 , 结合实验与理论分析得出了轮齿的变形。Weber[ 4] 在 Walker 研究的基础上 , 首次
光弹性法在齿轮应力和变形的研究进程中曾经起到过重要的作用 , 如 ①解析解的验证 ;②经验公式的回归拟合 ;③复杂应力场与位移场的探索性研究等。但也存在一些缺点 , 如 ①不能完全模拟材料特性和边界条件 , 存在“过度变形” ;②存在与实验原理、光路仪器、图像采集和处理相关的试验误差。因此 , 光弹法大多用于定性验证和探索性研究 , 在精细分析中作用有时受到限制。

汽车变速器齿轮的强度分析【毕业作品】

汽车变速器齿轮的强度分析摘要：随着汽车技术的不断提高，对变速器结构强度的要求越来越高，作为变速器关键部件的齿轮，工作环境恶劣，易损坏。

齿轮的质量关系着变速器能否平稳高效运转。

齿轮强度分析，是齿轮承载能力、振动、噪声、齿形优化等研究的基础。

变速器齿轮常见损坏形式有接触疲劳引起的齿面点蚀和弯曲疲劳引起的轮齿折断。

为判断是否发生损坏，需进行齿轮接触强度和弯曲强度分析。

运用经典方法分析齿轮强度，需要计算的系数很多，计算过程繁琐。

因此，有必要对其分析过程进行规范化总结归纳，并开发出带有专业特点的齿轮强度分析模块，使用户只需输入一些参数，按照一定的流程操作，即可完成齿轮强度分析。

变速器齿轮接触和弯曲问题的有限元分析，是齿轮结构设计与优化的有效手段。

建立有效的有限元分析模型，准确求解齿轮的应力与变形有重要意义。

运用有限元法进行齿轮接触和弯曲问题仿真，在接触刚度、网格划分方法、网格疏密控制、载荷作用位置等方面还存在一些问题，有必要对其进行深入研究。

目前，有限元软件中尚没有专门的齿轮应力建模与仿真模块，实现齿轮应力有限元分析模块的二次开发，可以提高工作效率，缩短设计周期。

关键词：变速器齿轮，接触强度，弯曲强度Auto ransmission gear strength analysisAbstract：With the continuous improvement of automotive technology,the demand of the transmission structural strength has become more and more increasingly.As a key component of the transmission,the working conditions of gears are poor and the gears are easy to damage.The quality of gears decides whether the transmission can operate smoothly and efficiently or not.The analysis of gear strength is the basis for the research of the gears carrying capacity,vibration,noise,profile optimization.The common forms of damage are tooth surface pitting caused by contact and tooth broken caused by bending fatigue.As to determine whether the damage occurred,the gear contact and bending strength need to ing classical method to calculate gear strength, many factors need to calculate,the process is very trouble.It is necessary to normalize and summarize the analysis process,and to develop the gear strength analysis professional module.The complete gear strength can be finished the certain input parameters are only provided.The finite element analysis of transmission gear contact and bending is an effective means of gear structural design and optimization.To establish the efficient and precise analysis of the gear contact and bending stress,there are some problems in the contact rigidity,mesh method,mesh density control,load lines.It is necessary to conduct in-depth study.There are so many gear pairs in transmission that it is difficult to analyze and calculate.At present, there is no application software having special module for gear stress simulation analysis.To develop professional modules of parametric modeling and simulation for gear stress analysis can greatly improve efficiency and shorten the design cycle.目录1绪论------------------------------------------------------------------ 1 1.1变速器齿轮强度分析的研究背景---------------------------------------- 1 1.1.1变速器齿轮失效形式------------------------------------------------ 1 1.1.2变速器齿轮强度分析方法-------------------------------------------- 1 1.2变速器齿轮强度分析与评价的研究现状---------------------------------- 2 1.2.1变速器齿轮强度分析的经典方法-------------------------------------- 2 1.2.2变速器齿轮强度分析的有限元法-------------------------------------- 3 1.2.3变速器齿轮强度评价方法-------------------------------------------- 4 1.3有限元软件ANSYS概述------------------------------------------------ 5 1.3.1 ANSYS简介-------------------------------------------------------- 5 1.3.2 ANSYS内部语言简介------------------------------------------------ 5 1.3.3 ANSYS二次开发功能------------------------------------------------ 5 1.4本文主要研究工作---------------------------------------------------- 6 2齿轮强度经典分析方法-------------------------------------------------- 7 2.1齿轮接触应力和齿根应力分析的经典方法-------------------------------- 7 2.1.1齿轮接触应力分析经典方法------------------------------------------ 7 2.1.2齿根应力分析经典方法---------------------------------------------- 7 2.2齿轮许用接触应力分析经典方法---------------------------------------- 8 2.2.1齿轮许用接触应力-------------------------------------------------- 8 2. 2. 2接触寿命系数---------------------------------------------------- 9 2.2.3润滑剂系数------------------------------------------------------- 10 2.2.4速度系数--------------------------------------------------------- 10 2.2.5粗糙度系数------------------------------------------------------- 11 2.2.6工作硬化系数----------------------------------------------------- 11 2.2.7接触尺寸系数----------------------------------------------------- 12 2.3齿轮许用齿根应力分析经典方法--------------------------------------- 12 2.3.1齿轮许用齿根应力------------------------------------------------- 122.3.2弯曲寿命系数----------------------------------------------------- 12 2.3.3相对齿根圆角敏感系数--------------------------------------------- 14 2.3.4相对齿根表面状况系数--------------------------------------------- 15 2.3.5弯曲尺寸系数----------------------------------------------------- 16 2.4本章小结----------------------------------------------------------- 16 3齿轮应力分析有限元法------------------------------------------------- 16 3.1面-面接触有限元分析关键问题---------------------------------------- 17 3.1.1接触面和目标面确定----------------------------------------------- 17 3.1.2单元类型选择----------------------------------------------------- 17 3.1.3接触协调条件----------------------------------------------------- 19 3.2斜齿轮接触应力分析有限元法----------------------------------------- 20 3.2.1单元属性定义----------------------------------------------------- 20 3.2.2网格划分方法研究与应用------------------------------------------- 21 3.2.3接触单元和目标单元生成------------------------------------------- 25 3.2.4接触应力求解与结果分析------------------------------------------- 26 3.2.5接触应力仿真影响因素分析----------------------------------------- 27 3.3斜齿轮弯曲应力分析有限元法----------------------------------------- 30 3.3.2整体单元尺寸对仿真影响分析--------------------------------------- 32 3.3.3线网格细化对仿真影响分析----------------------------------------- 34 3.3.4面网格细化对仿真影响分析----------------------------------------- 37 3.3.5网格划分控制确定------------------------------------------------- 42 3.3.6不同载荷作用位置对仿真影响分析----------------------------------- 43 3.4本章小结-------------------------------------------- 错误!未定义书签。

齿轮传动的强度设计计算

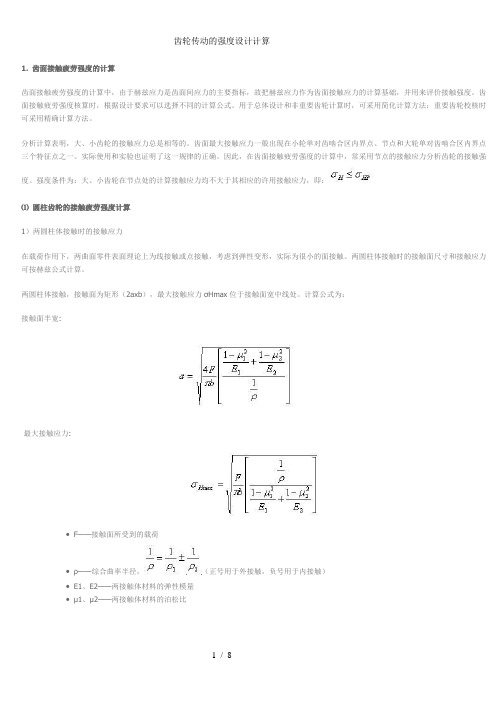
1. 齿面接触疲劳强度的计算齿面接触疲劳强度的计算中，由于赫兹应力是齿面间应力的主要指标，故把赫兹应力作为齿面接触应力的计算基础，并用来评价接触强度。

齿面接触疲劳强度核算时，根据设计要求可以选择不同的计算公式。

用于总体设计和非重要齿轮计算时，可采用简化计算方法；重要齿轮校核时可采用精确计算方法。

分析计算表明，大、小齿轮的接触应力总是相等的。

齿面最大接触应力一般出现在小轮单对齿啮合区内界点、节点和大轮单对齿啮合区内界点三个特征点之一。

实际使用和实验也证明了这一规律的正确。

因此，在齿面接触疲劳强度的计算中，常采用节点的接触应力分析齿轮的接触强度。

强度条件为：大、小齿轮在节点处的计算接触应力均不大于其相应的许用接触应力，即：⑴圆柱齿轮的接触疲劳强度计算1）两圆柱体接触时的接触应力在载荷作用下，两曲面零件表面理论上为线接触或点接触，考虑到弹性变形，实际为很小的面接触。

两圆柱体接触时的接触面尺寸和接触应力可按赫兹公式计算。

两圆柱体接触，接触面为矩形（2axb），最大接触应力σHmax位于接触面宽中线处。

计算公式为：接触面半宽:最大接触应力:•F——接触面所受到的载荷•ρ——综合曲率半径，（正号用于外接触，负号用于内接触）•E1、E2——两接触体材料的弹性模量•μ1、μ2——两接触体材料的泊松比2）齿轮啮合时的接触应力两渐开线圆柱齿轮在任意一处啮合点时接触应力状况，都可以转化为以啮合点处的曲率半径ρ1、ρ2为半径的两圆柱体的接触应力。

在整个啮合过程中的最大接触应力即为各啮合点接触应力的最大值。

节点附近处的ρ虽然不是最小值，但节点处一般只有一对轮齿啮合，点蚀也往往先在节点附近的齿根表面出现，因此，接触疲劳强度计算通常以节点为最大接触应力计算点。

参数直齿圆柱齿轮斜齿圆柱齿轮节点处的载荷为综合曲率半径为接触线的长度为，3）圆柱齿轮的接触疲劳强度将节点处的上述参数带入两圆柱体接触应力公式，并考虑各载荷系数的影响，得到：接触疲劳强度的校核公式为：接触疲劳强度的设计公式为：•KA——使用系数•KV——动载荷系数•KHβ——接触强度计算的齿向载荷分布系数•KHα——接触强度计算的齿间载荷分配系数•Ft——端面内分度圆上的名义切向力，N；•T1——端面内分度圆上的名义转矩，N.mm；•d1——小齿轮分度圆直径，mm；•b ——工作齿宽，mm，指一对齿轮中的较小齿宽；•u ——齿数比；•ψd——齿宽系数，指齿宽b和小齿轮分度圆直径的比值（ψd=b/d1）。

齿轮传动的载荷和应力

1. 齿轮传动的载荷计算(1) 直齿圆柱齿轮传动的受力分析圆周力：径向力：法向力：o d1——小齿轮的分度圆直径mmoα——分度圆压力角o T1——小齿轮传递的名义转矩(N.m)o P1为小齿轮所传递的功率（KW）o n1为小齿轮转速（rpm）作用在主动轮和从动轮上的力大小相等，方向相反。

主动轮上的圆周力是阻力，其方向与它的回转方向相反；从动轮上的圆周力是驱动力，其方向与它的回转方向相同；两轮所受的径向力分别指向各自的轮心。

齿面上的总法向力方向则为啮合点的法向方向，对于渐开线齿廓即为通过啮合点与基圆相切的啮合线方向。

(2) 斜齿圆柱齿轮传动的受力分析圆周力：径向力：轴向力：法向力：∙αt——端面分度圆压力角；∙αn——法向分度圆压力角；∙β——分度圆螺旋角；∙βt——基圆螺旋角。

(3) 直齿锥齿轮传动的受力分析法向力Fn集中作用在齿宽节线中点处，则Fn可分解为互相垂直的三个分力。

圆周力：径向力：轴向力：dm1——小齿轮齿宽中点分度圆直径mm；δ1——小锥齿轮分度圆锥角圆周力和径向力的方向判别与直齿圆柱齿轮判别方法相同，轴向力方向分别指向各自的大端。

由于锥齿轮传动两轴的空间交角为90°，因此存在以下关系：；。

负号表示方向相反。

(4) 齿轮传动的计算载荷齿轮承受载荷常表现为其传递的力矩或圆周力。

由上述力的分析计算所得出的圆周力为齿轮传动的名义圆周力。

实际工作中，由于各种因素的影响，齿轮实际承受的圆周力要大于名义圆周力。

考虑各种因素的影响，实际圆周力Ftc为：Ftc也称为计算载荷。

1）KA——使用系数。

2）KV——动载系数。

3) KHα和KFα——齿间载荷分配系数。

4) KHβ和KFβ——齿向载荷分布系数。

2. 齿轮传动应力分析齿轮传动工作过程中，相啮合的轮齿受到法向力Fn的作用，主要产生两种应力：齿面接触应力和齿根弯曲应力。

(1) 齿面接触应力σH齿轮传动工作中，渐开线齿面理论上为线接触，考虑齿轮的弹性变形，实际上为很小的面接触。

考虑齿间摩擦力的齿根弯曲应力计算

０ｒ，（，＇＝Ｍ（，＇／（１）
齿在啮合面上受沿啮合线方向的法向载荷及沿齿
面接触点切线方向的切向载荷以齿间摩擦力）的作
其中，为齿根危险截面的抗弯截面模量；
∽＝Ｆ＝ｑ）ｃｏｓａＦｘｚ ± ｓｉｎｏｔＦｘ（ｚ＋△ ２）轮强度计算方法全面
地分析了齿间摩擦力对增速传动和减速传动中大、小齿轮齿根弯曲应力的影响，并对影响程度进行了
定量计算。
（ａ）主动轮（ｂ）从动轮
１力学模型的建立
图１考虑摩擦力的轮齿力学模型
现行的齿根弯曲强度计算中只考虑了法向啮合力与该剖面上弯曲应力相比甚小，可忽略不计嘲。因力，而忽略了齿间摩擦力［１－２］。李秀莲、徐辅仁等人对此，本文主要考虑ＦｎＣＯＳＣ￣ＦＦ／ｓｉｎｏｔ，联合作用下的齿根弯曲应力。齿间摩擦力对齿根弯曲应力的影响做了研究，认为在齿间摩擦系数大的情况下可使齿根弯曲应力增加
＝
＝
＝ × ｐ ∽＝ × ｐ ∽
！竺竺ｆ：２（小齿轮的）
１＋ｆｔａｎａａｌ、 ‘ 。
图２小齿轮主动时齿】页啮合受力示意图
ｐ（＝
— —
当小齿轮为主动轮时，由图２所示关系可得：
用。为便于研究，将法向载荷沿啮合线移动到主动
轮轮齿中线的点，将切向载荷沿齿顶Ｒ点的渐开线切线也移动到轮齿中线的Ｅ点，令齿间摩擦力Ｆ，

18CrNiMo7-6和20CrMnTi材料齿根弯曲疲劳寿命对比

18CrNiMo7-6和20CrMnTi材料齿根弯曲疲劳寿命对比李道军1卢青波2刘德平3（1郑州职业技术学院电气电子工程系，河南郑州450121）（2郑州职业技术学院机械工程系，河南郑州450121）（3郑州大学机械与动力工程学院，河南郑州450001）摘要对比了齿轮钢材料18CrNiMo7-6与20CrMnTi的齿根弯曲疲劳寿命。

基于这两种材料的疲劳特性，采用SolidWorks中的GearTrax插件建立齿轮模型，并通过Workbench对齿轮的轮齿进行静力学分析；将静力学分析结果导入疲劳分析软件FE-SAFE中，结合载荷谱信息对两种材料齿轮进行疲劳寿命计算，得到齿轮的寿命云图并进行了仿真分析比较；通过试验验证了该仿真方法的可行性。

结果表明，在相同的载荷条件下，18CrNiMo7-6齿轮的疲劳寿命大于20CrMnTi齿轮的疲劳寿命，与试验结果较为接近。

该分析结果对工程实践具有一定的指导作用。

关键词疲劳寿命齿轮静力学仿真分析Comparison of Tooth Root Bending Fatigue Life Between18CrNiMo7-6and20CrMnTi MaterialsLi Daojun1Lu Qingbo2Liu Deping3（1Department of Electrical and Electronic Engineering，Zhengzhou Technical College，Zhengzhou450121，China）（2Department of Mechanical Engineering，Zhengzhou Technical College，Zhengzhou450121，China）（3School of Mechanical and Power Engineering，Zhengzhou University，Zhengzhou450001，China）Abstract In order to compare the tooth root bending fatigue life of18CrNiMo7-6and20CrMnTi gears，based on the fatigue characteristics of these two materials，the gear model is built by using the GearTrax plug-in in the3D modeling software SolidWorks.Through the finite element analysis software Workbench，the statics analysis of the single tooth of the gear is performed，and then the static analysis result is introduced into the fa⁃tigue analysis software FE-SAFE，in combination with the load spectrum information，the fatigue life of the two gears are calculated，and the obtaining life cloud maps are analyzed and compared.The feasibility of the simula⁃tion method is verified by experiments.The results show that，under the same load conditions，the fatigue life of gears with18CrNiMo7-6is slightly greater than that with20CrMnTi，it is close to the experimental results.The analysis results have a certain guiding role for engineering practice.Key words Fatigue life Gear Statics Simulation analysis0引言齿轮在机械传动领域有着举足轻重的地位，在各种机械装备中主要承担传动任务。

齿轮的许用应力

和稳定性。
齿轮材料选择与制造工艺
材料选择
常用材料包括钢、铸铁、有色金属等，应根据工作条件、承载能力和经济性等因素进行选择。
制造工艺
包括锻造、铸造、切削加工、热处理等工序，应保证齿轮的精度和表面质量，提高传动效率和承载能力。
02 许用应力概念及计算方法
许用应力定义与意义
许用应力定义
许用应力是指在工作条件下，材料或构件所能安全承受的最大应力值。
作用
广泛应用于各种机械传动系统中，如汽车、机床、钟表等，实现减速、增速、换向和分配动力等功能。
齿轮主要类型及特点
01
02
03
圆柱齿轮
包括直齿、斜齿和人字齿等，具有传动平稳、承载能力强、制造精度高等特点。
圆锥齿轮
分为直齿锥齿轮和螺旋锥齿轮，用于实现相交轴之间的传动，具有结构紧凑、传动比大等优点。
05 提高齿轮许用应力措施研究
优化设计方案以降低载荷波动
通过优化齿轮几何参数，如模数、齿数、齿宽等，降低齿轮啮合时的载荷波动。
采用变位齿轮设计，改善齿轮传动的平稳性，降低动载荷系数。
对齿轮进行修形处理，减小齿轮啮合时的冲击和振动，提高齿轮传动的平稳性。
选用高性能材料和先进制造工艺
选用高强度、高韧性的齿轮材料，如合金钢、高强度铸铁等，提高齿轮的承载能力。
确定计算载荷
同样根据齿轮受力情况，确定计算载荷的大小和方向。
计算齿面接触应力
利用赫兹公式或经验公式计算齿面接触应力。
校核齿面接触强度
将计算得到的齿面接触应力与许用接触应力进行比较，判断齿轮的接触强度是否满足要求。
国内外相关标准介绍及对比
国际标准
01
如ISO 6336等，提供了齿轮强度计算的基本方法和

齿根应力分析中加载方法的研究

２齿轮的失效形式
一
线成３￣０的直线在齿根圆角过渡处切点的面作为危险截面，载荷作
般情况下，齿轮传动的失效形式主要表现为轮齿的失效：用线与齿形中心线的交点到危险截面的距离作视为梁的高度。
★来稿日期：０１０ — ０ ★基金项目：２１－６２车辆零部件数字化设计公共平台建设（桂科能０１６０）８２０２
Ｔ＝．５× １６＝ｔ９５０Ｐ９
．
但通常情况下，这种加载方式下的齿根弯曲应力是按式（）３
计算的结果乘以重合度系数换算而得，加载示意图，图３如
’
５ ×１ × ５０
ｌＵＵＵ
：２１０ｍ１４５Ｎ‘ ｍ
（）５
ｎ
２Ｔ
（）ａ所示。
Ｋｅｏｄ：ａ；ｉｉｅｎｓｎｌｓ（Ｅ；ｏｔｏｔＳｒｓ；ｓｓｏｋｅｃｙｗｒｓＧｅｒＦｎｔｅｍｅｔａａｙｉＦＡ）Ｔｏｈｒｏ；ｔｅｓＡｎｙｒｂｎｈｅｌｓＷ
中图分类号：Ｈ１，Ｈ１２４文献标识码：Ｔ６Ｔ３．１Ａ
ｔｅｒｔｃｏｈｏｅｉａｃｍｐｕａｉｎｗｉｈｏｉｇａｘｅｎｌｏｔｃｉｔｅｗｅｎｓｎｌｏｔｎｓｉｇｅａｌｔｏｔｔｅｌａｎｅｔｒａｎａｔｔｈｄｔｃｐｏｎｔｅｉｇｅｔｏｈａｄｔｍｅｈｎａｃｂｈｅｒ
ｇａａｅｎｈｅｒｔａｆｒｌｃｌｉｎｗｉｔｎｉｏｐｔｔｎｉｌｇｎｅｃｎ；ｔｅｒｓｓｄｏｅｔｏｅｉｏｍｕａａｕｔ，ｈｃｉｅｓｙｎｃｍｕａｉｅａｄｎｆｉｔＡｉｂｔｈｃｌｃｌａｏｈｎｔｉｏｓａｒｉｆｅｉｐｅｅｔｈｃｎｑｅｉｅｓｄｉｂｅｎｃｍｕｅｓｎｆｉｌｍｎａａｓｏｗｅｔｓｌｅｒｓｎ，ｅｔｈｉｕｄｌｕｅｙｍａｓｏｐｔｒａｄｎｔｅｅｅｔｎｙｉｓａｉａｔｅｗｙｓｆｏｉｅｌｓｆｒｏｍｕｔｉｔｅｔｓｏｏｈｒｏｉｐａｔａｗｒｉａ，ｈｃｒｖｄｓｒｅｅｃｒｈｒｄｃｄｖｌｍｎ，ｎｈｒｓｆｏｔｔｎｒｃｉｌｏｋｎｌｄｗｉｐｏｉｅｅｒｎｅｏｅｏｕｔｅｅｐｅｔａｄｓｅｔｏｃｇｏｈｆｆｔｐｏｒｄｃｒｄｃｄｖｌｍｅｔｙｌｉｎｃｔ．ａｚｎｅｓｅｓｏｅｇａｏｂｏｐｔ，ｒｅｅｕｅｏｕｔｅｅｐｎｃｅｓｉａｌＩａｌｉｔｔｓｆｔｒｒｔｙｃｍｕｒｔｅｐｏｃｓｇｆｎｙｎｎｙｇｈｒｈｅｉｏｅｈｍｅｈｄｒａａｌｂｅｏａｉｇｏｅｌａｒｅｏｅｅｔｒａｓｎｌｃｎａｔｏｎｂｔｅｎｓｎｌｔｔｔｏｓｅｖｉｌｆｒｏｎｆｒ：ｄｆｃｎｔｘｅｎｌｉｅｏｔｉｔｅｗｅｉｇｏｈａａｌｄｃｏｏｈｇｃｐｅｏｎｈｎｅ，ｒｅｔｔｐｏｅｔｒｅｈｎｆｉｌｅｔｌｉｒｓｏｔｒｏａｄｍｓｉｒａｏｎｈｏｈｔ，ｒｎｈｉｈｉｌＴｅｎｔｅｍｎａｓｆｒｔｓｏｔｏｈｏｔｅｇａｏｔｏｏｏｔｐｃｃｃ．ｉｅｅｎａｙｓｓｅｏｆ

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

而由大量试验得知 ,齿根弯曲疲劳裂纹发生在局部应力最大的地方 ,且裂纹是沿着过渡曲线的法线方向 ,因此 ,着重研究折截面 ADB (图 3) 上的应力变化规律更合适 ,即“折截面法”。折截面法的特点是
图 2 平截面法
Байду номын сангаас
图 3 折截面法
① 危险截面的位置按照齿根弯曲疲劳裂纹的方向确定 ,比较接近实际情况 ;
光弹性法在齿轮应力和变形的研究进程中曾经起到过重要的作用 ,如 ①解析解的验证 ; ②经验公式的回归拟合 ; ③复杂应力场与位移场的探索性研究等。但也存在一些缺点 ,如 ①不能完全模拟材料特性和边界条件 ,存在“过度变形”; ②存在与实验原理、光路仪器、图像采集和处理相关的试验误差。因此 ,光弹法大多用于定性验证和探索性研究 ,在精细分析中作用有时受到限制。
1926 年 ,Timoshenko[22] 提供了第一份关于轮齿应力光弹测量的结果。1940 年 ,Dolan[23] 根据光弹试验结果提出了与受力点位置和齿根圆角大小相关的应力集中系数。Heywood[24 ] 、Kelly[25 ] 根据光弹研究结果给出了各自的齿根应力计算的经验公式。1955 年 ,Ja2 cobson [ 26 ]根据众多的光弹研究成果提出了修正的疲劳极限公式。1967 年 ,Baxter[27] 用三维光弹技术来确定双曲线锥齿轮三维模型中的应力分布 ,这一研究奠定了三维齿形表面应力研究的基础。近些年 ,我国的薛春玉[28 ] 、许洪斌[29 ]等应用冻结切片三维光弹技术 ,分别对弧齿锥齿轮和分阶式双渐开线齿轮进行了试验分析。
3 数值计算方法
随着计算技术和计算机的迅速发展及广泛应用 , 以有限元法为代表的数值计算方法使齿轮应力和变形分析变得方便、可靠、准确。目前齿轮工程中实用的数
© 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved.
把轮齿变形分解为弯曲变形、剪切变形和压缩变形。 Merritt[5]在 Lewis 公式中增加了考虑载荷径向分量的项。梅尔根据凯克的光弹实验结果 ,建议用“30°切线法”确定 α= 20°时渐开线齿廓的最弱截面。Niemann[6] 提出了考虑弯曲、抗压及剪切应力在内的名义应力。 Wellauer[7]引入齿宽方向分布载荷对齿根应力的影响。 Cornell[8]和 Tavakoli[9] 提出了轮齿弹性变形的数值积分法 ,综合考虑了弯曲、剪切、赫兹接触、齿根圆角半径以及轮体弹性等引起的变形。1982 年 ,AGMA 在 Lewis 公式的基础上 ,经过不断的修正 ,提出了考虑弯曲和压缩效应的弯曲强度设计公式。至此 ,齿根应力计算中的“平截面法”(图 2) 为 ISO 及绝大多数国家所采用。
图 5 单齿模型
元单齿模型 ,按集中力、分布力和模拟接触的三种情况 ,考虑模数、接触率、齿根圆角半径、压力角及齿数对轮齿应力的影响 ,提出了新的齿根应力计算公式。王玉新[36]建立了三个轮齿的二维和三维有限元模型 ,分析了直齿轮齿根应力 ,并开始注意到齿宽与平面弹性问题类型存在一定的关系。
第 28 卷第 5 期齿根应力与轮齿弹性变形的计算方法进展与比较研究 1 文章编号 :1004 - 2539 (2004) 05 - 0001 - 06
齿根应力与轮齿弹性变形的计算方法进展与比较研究
周长江1 ,2 唐进元1 ,2 吴运新1 ,2
第 28 卷第 5 期齿根应力与轮齿弹性变形的计算方法进展与比较研究 3
值解法主要有 3 种 , 有限差分法 ( FDM) 、边界元法 (BEM) 和有限元法 ( FEM) 。
有限差分法的特点是直接求解基本方程和相应定解条件的近似值 ,但它用于几何形状复杂的问题时 ,精度将降低 ,甚至收敛困难 ,因此在复杂齿轮系统强度分析方面应用不多。边界元法则是先将求解域内的控制方程用数学方法转化为求解域边界上的边界积分方程 ,再用数值解法求出边界结点上待求量的近似解 ,然后根据边界结点量计算得到区域内任意点的待求量。这种方法输入数据少 ,直接性较好 ,适合于大应力梯度的边界问题 ;但由于所用的矩阵通常为稠密阵 ,求解效率较低 ,求解规模也受到限制。
①轮齿应力分析是齿轮承载能力计算的基础 ;
②轮齿变形分析则是齿轮传动动态性能与齿廓
修形研究的依据。
在轮齿应力与变形研究方面 ,国内外的学者采用
不同的分析方法已经获得了许多有益的成果。下文就
直齿圆柱齿轮 ,简要评述了典型的静态/ 准静态计算方
法的进展 ,并进行了比较研究。
悬臂梁模型
材料力学法悬臂板模型
有限元法是一种通用的工程数值分析方法 ,应用最为广泛。同传统的计算方法相比 ,有限元法能处理复杂的载荷工况和边界条件 ,较全面地反映齿轮体的应力场、位移场、齿根应力集中与轮齿变形等。就齿根应力和轮齿变形有限元分析 ,下文从弯曲和接触两个方面进行叙述。 3. 1 齿轮弯曲强度有限元分析
传动系统变形以及齿轮制造、装配误差与磨损的影响。后来出现了改进的“悬臂板”模型和各向同性楔模
型[11] ,它们在圆弧齿的应力分析中起到了一定的作用 ,但计算精度和应用范围非常有限。 1. 2 弹性力学法
材料力学法由于模型与实际齿形相差较大 ,因而较难准确地反映复杂齿形、过渡曲线以及传动系统对轮齿应力和变形的影响。于是 ,以保角映射法为代表的平面弹性力学法应运而生。保角映射法的实质是将轮齿曲线边界映射为直线边界 ,由作用在半平面上集中力复变函数求解出半平面的位移场 ,从而得到轮齿受载点的应力和变形。其计算的精确性 ,关键在于适当地选取映射函数及其项系数。
轮齿接触问题是一种高度的非线性行为 ,涉及复杂的动力学、表面技术、材料科学等方面的工程背景。 1881 年 ,Hertz[38]提出两个弹性圆柱体接触面上的载荷分布公式 , 奠定了齿面接触强度计算的理论基础。 1908 年 ,Videky[39]把赫兹接触应力理论首先应用于计算轮齿齿面应力 ,并绘出了沿啮合线最大接触应力变化图。Jandasek , Timoshenko , Ways , Niemann ,Beeching , Nicholls , Henrio , K ser 等对点蚀的成因 ,形成初始裂纹的位置 ,点蚀的深度等进行了研究。但到目前为止 ,点蚀研究仍不够成熟。Winter[40] 指出 Hertz 接触模型的粗略性 ,即 Hertz 公式适用于弹性范围内只承受法向压力的均质各向同性体 ,而准确的接触强度评估应该考虑轮齿滑动、表面状况、边缘层杂质以及弹性流体动力学等因素 ,并根据圆盘滚动 - 滑动接触试验结果强调摩擦对接触强度具有很强烈的影响。
(1. 中南大学 , 湖南长沙 410075) (2. 重庆大学机械传动国家重点实验室 , 重庆 400044)
摘要在齿根应力与轮齿弹性变形方面 ,较为详细地评述了直齿轮的静态/ 准静态计算方法 (解析法、试验法、数值法) 的进展、特点及应用。对典型的分析方法进行了比较研究 ,并提出了作为 CAE 的核心 ,有限元法在现代齿轮传动系统设计中具有良好的应用前景。
解析法
各向同性楔模型
弹性力学法 :保角映射法
应力变形
光测力学法
实验法
计算方法
电测力学法
有限差分法
数值法边界元法
有限元法 :挠曲/ 接触分析
图 1 各类计算方法一览
1 解析法
1. 1 材料力学法这种方法使用最早。1893 年 ,Lewis[1]基于材料力
学的抛物线梁理论 ,把轮齿视为等强度悬臂梁 ;首次提出了“齿形系数”的概念 ,并推导出著名的 Lewis 公式 , 从而奠定了轮齿弯曲强度计算的理论基础。Rand[2]利用等截面悬臂梁模型计算出轮齿的弹性变形。Walk2 er[3]在研究齿廓修形时 ,结合实验与理论分析得出了轮齿的变形。Weber[4] 在 Walker 研究的基础上 ,首次
关键词齿根应力轮齿变形计算方法比较研究
引言
随着齿轮传动向重载、高速、低噪声、高可靠性的
方向发展 ,现代齿轮传动设计对系统的静/ 动态特性提
出了更高的要求。齿轮设计的主要内容在强度设计 ,
其核心是轮齿。从而 ,建立精确的计算模型 ,准确求解
受载轮齿的应力与变形意义显著。其意义是
在上述研究进程中 ,映射函数的形式和取项得到了不断的改善 ,但系数均是通过“试算法”得到 ,与理论齿形的吻合程度较差 ,计算精度不够理想。
1982 年 ,Cardou[18]开始使用“直接搜索法”电算程序 , 优化映射函数系数 , 改善了求解精度。程乃士[19～20]通过编程优化映射函数的系数 ,比较精确地求出了轮齿受载后的挠度。
④很难嵌入加工误差、装配偏差及磨损等 ;
2 实验分析方法
严格说来 ,轮齿应力与变形分析属于几何形状复杂、载荷工况多变的力学范畴 ,具有非线性、粘弹性和动态等特性。为了精确地获取轮齿的相关力学量 ,国内外学者提出了各种力学模型和理论分析方法 ,并获得了许多重要结论。而在建立这些模型和理论时 ,都曾作过一些假设和简化。因此 ,在将这些理论所得出的结果应用于实际生产之前 ,最好经由试验的检验。实验分析方法主要分为光测法和电测法 ,本文只对光测法[21]的光弹性力学法作简要的介绍。光弹性法的实质是利用光弹性材料在载荷作用下产生的瞬态双折射效应和光波干涉的结果 ,通过光弹性仪测定光程差的大小 ,应力光图随着模型形状、加载方式、边界条件等因素的变化而改变。