角的概念的推广·典型例题分析
角的概念的推广

(3)旋转量:
当旋转超过一周时,旋转量即超过360º , 角度的绝对值可大于360º .于是就会出现 720º - 540º , 等角度.
3、“象限角” 为了研究方便,我们往往在平面直角坐标系内 来讨论角: 使角的顶点与坐标原点重合,角的始边与x轴 的非负半轴重合,角的终边在第几象限,我们 就说这个角是第几象限的角。
2.角的概念的推广
⑴“旋转”形成角 一条射线由原来的位置OA, 绕着它的端点O按逆时针方向 旋转到另一位置OB,就形成角B α. 旋转开始时的射线OA叫做 角α的始边,旋转终止的射线 OB叫做角α的终边,射线的端 点O叫做角α的顶点.
O
A
B
终边 O 顶点
始边
A
⑵.“正角”与“负角”、“0º 角” 我们把按逆时针方向旋转所形成的角叫做 正角,把按顺时针方向旋转所形成的角叫做 负角,如图,以OA为始边的角α=210°,β= -150°,γ=660°,
C x轴的非正半轴上
D y轴的非正半轴上
4、终边与坐标轴重合的角的集合是( C ) A {β|β=k· 360º (k∈Z) } B {β|β=k· 180º (k∈Z) } C {β|β=k· (k∈Z) } 90º D {β|β=k· +90º 180º (k∈Z) }
5 、已知角2α的终边在x轴的上方,那么α是( ) C A 第一象限角 C 第一、三象限角 B 第一、二象限角 D 第一、四象限角
生活中很多实例会不在该范围。 体操运动员转体720º ,跳水运动员向内、 向外转体1080º ; 经过1小时,时针、分针、秒针各转了多 少度? 这些例子不仅不在范围[0º 360º ,而且 , ) 方向不同,有必要将角的概念推广到任意角, 想想用什么办法才能推广到任意角? 关键是用运动的观点来看待角的变化。
角的概念的推广

1200
O
终始边 A
AOB=1200 BOA=-1200
射线OA绕端点O旋转900到射线OB,接 着再旋转-300到OC求角AOC.
B
C
-300 900
600
O
A
AOC = AOB + BOC = 900 + (-300) = 600
各角和的旋转量等于各角旋转量的和.
例 题 1:
射线OA绕端点O顺时针旋转800到OB位 置,接着逆时针旋转2500到OC位置,然后再顺 时针旋转2700到OD位置,求 AOD的大小.
练习1:
(1).把 14850化成k 3600 00 3600, k Z
的形式是
A. 43600 450 B. 43600 3150
C. 103600 3150 D. 53600 3150
(2).在直角坐标系中,判断下列各语句的真,假.
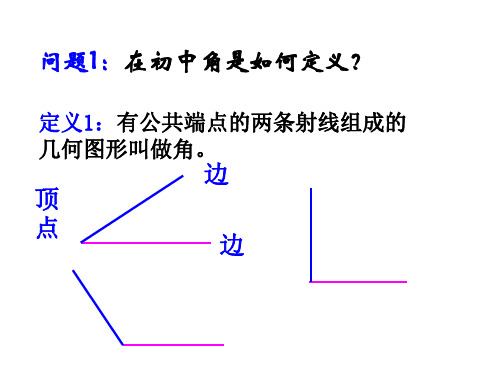
初中角的概念:
顶点
O
B
角的边
A
把公共端点的两条射线组成的图形叫做角.
角还可以看成平面内一条射线
绕着端点从一个位置旋转到另一个 位置所成的图形.
一.正角、负角、零角:
正角:一条射线绕着它的端点按逆时 针方向旋转形成的角;
负角:按顺时针方向旋转形成的角。
零角:射线没有作任何旋转。
B
终始边
-1200
1200
【例2】
在 00~3600 间,找出与下列各角终边相同的 角,并判定它们是第几象限角.
(1)150 ;(2) 650 ;(3) 950 15' .
【例3】写出与下列各角终边相同的角的集合S ,
并把 S 中适合不等式 360 720 的元素
3.1角的概念的推广与任意角的三角函数

∴cos6-sin6>1,∴lg(cos6-sin6)>0. sincosθ sincosθ ∴ <0.∴ 的符号是负号. cossin2θ cossin2θ ∴lg(cos6-sin6)的符号为正号.
题型3.三角函数的定义 例5(1)已知角 的终边上一点 P (
且 sin 2 4 y , 求 cos
1 a
sin( cos )
cos sin 2 ) (
的符
(3)已知点P(sinα-cosα,tanα)在第一象限, 则在[0,2π)内α的取值范围。
cos (4)已知 sin , ,若θ为第二象 1 a 1 a 限角,求实数a的取值范围。 3a 1
5、如果α是第三象限,那么-α, α/2,2 α的终边落在何 处?(用图表示)
练习: 已知α是第二象限的角 • (1)指出 所在的象限,并用图形表示其 变化范围. • (2)若α同时满足条件|α+2|≤4,求α的取 值区间.
题型2.三角函数符号的判断
例4 sincosθ (1)若 θ 是第二象限角,判断 的符号; cossin2θ
(2)确定 lg(cos6-sin6)的符号.
3.1 角的概念的推广与 任意角的三角函数
一、知识点 1.角的概念的推广 (1)角的分类:正角(逆转) 负角(顺转) 零角(不转) (2)终边相同角的表示: k 360 0 (k Z ) (3)直角坐标系中的象限角与坐标轴上的角. 如:终边在x轴上的角 k ( k Z ) (4)有关对称角的关系 X 轴, y轴 ,原点 如:关于y 轴对称的角 2k ( k Z ) 2.角的度量 (1)角度制与弧度制的概念 180 180 ( 弧度 ) 1弧度 ( ) 57 1 8 (2)换算关系: (3)弧长公式:l r
角的概念和推广示例解析试题

卜人入州八九几市潮王学校角的概念和推广例如解析一.本周教学内容角的概念和推广二.重点、难点本节重点是终边一样的角的概念、象限角的概念【典型例题】[例1]︒-<<︒-630990α,且α与︒120角的终边一样,求α?解:由角α与︒120角终边一样,那么︒+︒⋅=120360K α,Z K ∈令︒-<︒+︒⋅<︒-630120360990K 12121213-<<-K 又由Z K ∈,故3-=K 那么︒-=︒+︒⨯-=9601203603α即所求角α为︒-960[例2]角α是第三象限角,求2α是第几象限角? 解:由α是第三象限角,那么︒+︒⋅<<︒+︒⋅270360180360K K α,Z K ∈ 当n K2=,Z n ∈时︒+︒⋅<<︒+︒⋅135360290360n n α 当12+=n K ,Z n ∈时︒+︒⋅+<<︒+︒⋅+135180)12(290180)12(n n α︒+︒⋅<<︒+︒⋅3153602270360n n α故2α为第二象限角或者第四象限角 [例3]角α的终边与120°的终边一样,求在︒-360到︒180范围内与3α角终边一样的角的集合。
解:由角α的终边与120°终边一样,那么α︒+︒⋅=120360K ,Z K ∈︒+︒⋅=401203K α令︒<︒+︒⋅≤︒-180********K又由Z K ∈,那么1,0,1,2,3---=K 代入︒+︒⋅=401203K α 得︒︒︒-︒-︒-=160,40,80,200,320α[例4]时针指到3点后,当分针在1小时内走55分钟时,时针到分针的夹角是多少度?解:时针每走1分钟相当于转过︒-=︒-660360的角,故分针一共走过的角度为 时针每走1小时相当于转过︒-=︒-3012360的角,故时针一共走过 因此时针到分针的夹角为︒-=︒--︒-5.212)5.117(330 [例5]在一般的时钟上,自零时刻到分针与时针第一次重合,分针所转过角是多少度?解:自零时到分针与时针第一次重合,设时针转过︒x ,那么分针转过︒+)360(x ,由时针转过1°相当于经过30136012=小时,故时针转过1°相当于经过2分钟,又分针转过 1°相当于经过61分,故61)360(2⋅+=⋅x x 36011=x 11360=x 因此,当分针与时针第一次重合时,分针转过的角为[例6]{}锐角=A ,{}的角到︒︒=900B ,{}第一象限的角=C ,{}的角小于︒=90D ,求B A ,C A ,D C ,D C解:依题意,有{}︒<<︒=900ααA ,{}︒<≤︒=900ααB由︒≤︒+︒⋅9090360K 得0≤K故{}Z K K K K D C ∈≤︒+︒⋅<<︒⋅=且0,90360360αα [例7]集合{}Z K K K A ∈︒+︒⋅<<︒+︒⋅=,12036030360αα,{}Z K K K B ∈︒+︒⋅<<︒+︒⋅=,135********αα,求集合B A 解:{}Z K K K B ∈︒+︒⋅<<︒+︒⋅=,135********αα利用图象,B A 即图中阴影局部的交 故{}Z K K K B A ∈︒+︒⋅<<︒+︒⋅=,12036060360αα [例8]{}Z K K A ∈︒±︒⋅==,30120αα,{}Z K K B ∈︒+︒⋅==,9060ββ,那么集合A 和B 有何关系?解:设A ∈θ,那么︒+︒⋅=30120K θ或者︒-︒⋅=30120K θ,Z K ∈ 即︒+︒⋅-=9060)12(K θ或者︒+︒⋅-=9060)22(K θ,故B ∈θ,因此B A ⊆设B ∈θ那么Z K K ∈︒+︒⋅=,9060θ当Z n n K ∈=,2时,︒+︒⋅=90120n θ即θ)1(+=n ︒-︒⋅30120那么A ∈θ;当12-=n K ,Z n ∈时, 即︒+︒⋅=30120n θ,那么A ∈θ因此,A ∈θ,A B ⊆综上,B A =一.选择题1.〕 ①第一象限角是锐角②第二象限角比第一象限角大③三角形的内角是第一或者第二象限角④{}{}的正角小于锐角︒=90 A.0个B.1个C.2个D.3个2.以下表示中不正确的选项是〔〕A.终边在坐标轴上的角的集合是{}Z K K ∈︒⋅=,90ααB.与︒-50的终边一样的角的集合是{}Z K K ∈︒+︒⋅=,310360ααC.终边在第二、四象限的角平分线上的角的集合是{}Z K K ∈︒-︒⋅=,45360αα D.终边在直线x y =上的角的集合是{}Z K K ∈︒+︒⋅=,45180αα 3.集合{}Z K K M∈︒⋅==,45αα,{}Z K K N ∈︒±︒⋅==,4590ββ,那么集合M 和N 的关系是〔〕A.≠⊂M N B.N M = C.≠⊃M N D.不确定 二.填空题1.假设α和β的终边满足以下位置关系时,α和β满足怎样的数量关系: 〔1〕重合时,=-βα;〔2〕关于x 轴对称时,=+βα; 〔3〕关于y 轴对称时,=+βα;〔4〕关于原点对称时,=-βα。
角概念的推广

角概念的推广一、知识点归纳1.角概念的推广:平面内一条射线绕着端点从一个位置旋转到另一个位置所的图形。
按逆时针方向旋转所形成的角叫正角,按顺时针方向旋转所形成的角叫负角,一条射线没有作任何旋转时,称它形成一个零角。
射线的起始位置称为始边,终止位置称为终边。
2.象限角的概念:在直角坐标系中,使角的顶点与原点重合,角的始边与轴的非负半轴重合,角的终边在第几象限,就说这个角是第几象限的角。
如果角的终边在坐标轴上,就认为这个角不属于任何象限,它叫轴线角。
3.终边相同的角的表示:终边与终边相同(的终边在终边所在射线上),注意:相等的角的终边一定相同,终边相同的角不一定相等。
4. 几种终边在特殊位置时对应角的集合为:角的终边所在位置 角的集合X 轴正半轴{}Z k k ∈︒⨯=,360|ααY 轴正半轴{}Z k k ∈︒+︒⨯=,90360|αα X 轴负半轴{}Z k k ∈︒+︒⨯=,180360|αα Y 轴负半轴{}Z k k ∈︒+︒⨯=,270360|ααX 轴{}Z k k ∈︒⨯=,180|ααY 轴{}Z k k ∈︒+︒⨯=,90180|αα坐标轴{}Z k k ∈︒⨯=,90|αα5、角α的顶点与原点重合,角的始边与x 轴的非负半轴重合,终边落在第几象限,则称α为第几象限角.第一象限角的集合为{}36036090,k k k αα⋅<<⋅+∈Z第二象限角的集合为{}36090360180,k k kαα⋅+<<⋅+∈Z第三象限角的集合为{}360180360270,k k k αα⋅+<<⋅+∈Z第四象限角的集合为{}360270360360,k k k αα⋅+<<⋅+∈Z二、例题解析例1、自上午8点整上学到中午11点40分放学,时钟的时针和分针各转了多少度?上午8点整和中午11点40分两针所成的最小正角各是多少度?例2、给出下列命题:①小于90的角是锐角;②第二象限的角是钝角;③相等的角必是终边相同的角;④若角α和β有相同的终边,则βα-的终边必在x 轴的正半轴上.其中正确的命题序号是______________ 例3、已知 1845-=θ,在与终边相同的角中,求满足下列条件的角:(1)最小的正角 (2)最大的负角 (3)在720~360-内的角例4、若α为第三象限角,则α-,α2的终边落在何处?练习4.1、已知α为第一象限角,求α21-180是第几象限角.例5、已知α为第三象限角,求32αα,所在的象限 例6、已知集合{}Zk k k A ∈+⋅<<+⋅=,9018030180 αα,集合{}Zk k k A ∈+⋅<<-⋅=,4536045360 αα。
角的概念的推广

小结: 1、本节课我们学习正角、负角、零角的定义,
象限角的概念以及终边相同的角的表示方法, 注意:正角、负角是用射线绕端点的旋转方向定义 的,零角是射线没有做任何旋转. 2、一个角是第几象限角,关键是看这个角的 终边落在第几象限,终边相同的角的表示有两方面 的内容: (1)、与角α 终边相同的角,这些角的集合 为S={β |β =k·360°+α ,k∈Z}; (2)、在0°到360°内找与已知角终边相同 的角α ,其方法是,用所给角除以360°,所得的 商为k,余数为α (α 必须为正数),α 即为所找的 角。
结论:
所有与角α终边相同的角,连同角α在 内,可构成一个集合:
S k 360 ,k Z ,
o
即任一与角终边相同的角,都可以表示成 角与整数个圆周的和。
[例1] 在0°到360°范围内,找出与下列各角终 边相同的角,并判定它们是第几象限角. (1)-120° (2)240° (3)-950°12′ 解: (1)-120°=-360°+240° 所以与-120°角终边相同的角是240°角,它是 第三象限角. (2)640°=360°+280° 所以与640°角终边相同的角是280°角,它是 第四象限角. (3)-950°12′=(-3)×360°+129°48′ 所以与-950°12′终边相同的角是129°48′, 它是第二象限角.
[例2] 判断下列语句是否正确。
1、射线绕端点旋转的圈数越多,角就越大。 2、如图所示的∠ABC是第一象限角。
3、终边在y轴上的角的集合(用0°到360°的
k 角表示)是 S ,k Z 2
[例3]写出与下列各角终边相同的角的集合S.并把S 中适合不等式-360°≤β ≤720°的元素β 写出来: (1)60° (2)-21° (3)363°14′
角的概念与推广
30°+K·360°,K ∈ Z
与 终边相同的角的一般形式为
+K · 360°,K ∈ Z 注:
(1)K ∈ Z
(2)是任意角
(3)K·360°与 之间是“+”号,如 K·360°-30 °,应看成K·360 °+(-30 °)
(4)终边相同的角不一定相等,但相等 的角终边一定相同,终边相同的角有无数 多个,它们相差360°的整数倍。
Ⅱ y Ⅰ
终边
x
o
始边
终边
Ⅲ
终 边
终
Ⅳ
边
象限角
置角的顶点于原点
始边重合于X轴的非负半轴
终边落在第几象限就是第几象限角
y 终边
x
o
始边
终边
坐标轴上的角
终边
置角的顶点于原点
始边重合于X轴的非负半轴
终边落在坐标轴上
例如,0°、90°、180°、270°、360°、−90°、−270°等都是界限角.
练习:
(1)请用集合表示下列各角;
①0°~90°间的角 ②第一象限角
③锐角
④小于90°角.
(2)分别写出: ①终边落在x轴负半轴上的角的集合; ②终边落在y轴上的角的集合; ③终边落在第一、三象限角平分线上的角 的集合;
④终边落在四象限角平分线上的角的集 合.
小结:
1.任意角 的概念
正角:射线按逆时针方向旋转 形成的角 负角:射线按顺时针方向旋转 形成的角 零角:射线不作旋转形成的角
练习:判定下列角是第几象限的角?
30°,120°,-60°,390°, -100°, 200°,-460°
y
-330° 390°
o
30°
x
角的概念的推广典型例题

典型例题
角的概念问题
例题1 判断下列命题是否正确? 例题1:判断下列命题是否正确? 终边与始边重合的角是零角; (1)终边与始边重合的角是零角; 终边与始边都相同的角一定相等; (2)终边与始边都相同的角一定相等; 锐角都在第一象限; (3)锐角都在第一象限; 小于90 的角都是锐角; (4)小于90。的角都是锐角; 的角的终边方向相反; (5)30。与-30。的角的终边方向相反; (6)第二象限的角为钝角
例题 已知角α 的终边相同,那么α 已知角α、β的终边相同,那么α-β的 终边在 上
终边为坐标轴的角的集合
(1)终边在x轴的非负半轴上: 终边在x轴的非负半轴上:
(2)终边在x轴的非正半轴上: 终边在x轴的非正半轴上: α | α =180 + k •360 , k ∈Z
{ | α = k •360 , k ∈Z} α
{α | α = 90 + k •180 , k ∈Z}
{α | α = k •90 , k ∈Z}
(7)终边在x轴或y轴上 终边在x轴或y
(6)终边在y轴上 终边在y
已知角α所在象限, 已知角α所在象限,求 限问题
α α所在象 2α、 、
2 3
例题:已知α 例题:已知α是第二象限 角,求
α
2
是第几象Байду номын сангаас角
与α终边相同的角问题
例题:已知α=1690。。 例题:已知α=1690 (1)把α改写成 β + k •360 k ∈Z.0 ≤ β < 360 的 形式。 形式。 的终边与α相同, (2)求θ,使θ的终边与α相同, 并判断θ 且 360 < θ < 360 ,并判断θ属于第几象限 −
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
角的概念的推广·典型例题分析
例1在-720°~720°之间,写出与60°的角终边相同的角的集合S.
解与60°终边相同的角的集合为{α|α=k·360°+60°,k∈Z}.
令-720°<k·360°+60°<720°,得k=-2,-1,0,1
相应的α为-660°,-300°,60°,420°,从而S={-660°,-300°,60°,420°}.
例2把1230°,-3290°写成k·360°+α(其中0°≤α<360°,k∈Z)的形式.
分析用所给角除以360°,将余数作α.
解∵1230÷360=3余150,
∴1230°=3×360°+150°.
∵-3290÷360=-10余310,
∴-3290°=-10×360°+310°.
注意:负角除以360°,为保证余数为正角,试商时应使得到的负角的绝对值大于已知负角的绝对值.
例3写出终边在y轴上的角的集合.
解终边在y轴的正半轴上角的集合为{α|α=k·360°+90°,k∈Z}.终边在y轴的负半轴上角的集合为{α|α=k·360°+270°,k∈Z}.故终边在y轴上角的集合为
{α|α=k·360°+90°,k∈Z}∪{α|α=k·360°+270°,k∈Z}.
={α|α=2k·180°+90°,k∈Z}∪{α|α=(2k+1)·180°+90°,k∈Z}
={α|α=n·180°+90°,n∈Z}.
同样方法可写出终边在x轴上角的集合为{x|x=n·180°+90°,k∈Z}。
