毕业设计(论文)开题报告 分支限界算法的研究与实现
算法分析与设计实验五分枝—限界算法

算法分析与设计实验五分枝—限界算法1、实现0/1背包问题的LC分枝—限界算法,要求使用大小固定的元组表示动态状态空间树,与0/1背包问题回溯算法做复杂性比较。
2、实现货郎担问题的分枝—限界算法并与货郎担问题的动态规划算法做复杂性比较比较。
3、实现带有期限的作业排序的分枝—限界算法并与带有期限的作业排序贪心算法做复杂性比较。
(任选一个完成)实验六分枝—限界算法实验目的1.掌握分枝—限界的基本思想方法;2.了解适用于用分枝—限界方法求解的问题类型,并能设计相应动态规划算法;3.掌握分枝—限界算法复杂性分析方法,分析问题复杂性。
预习与实验要求1.预习实验指导书及教材的有关内容,掌握分枝—限界的基本思想;2.严格按照实验内容进行实验,培养良好的算法设计和编程的习惯;3.认真听讲,服从安排,独立思考并完成实验。
实验设备与器材硬件:PC机软件:C++或Java等编程环境实验原理分枝—限界算法类似于回溯法,也是一种在问题的解空间树上搜索问题解的算法。
但两者求解方法有两点不同:第一,回溯法只通过约束条件剪去非可行解,而分枝—限界法不仅通过约束条件,而且通过目标函数的限界来减少无效搜索,也就是剪掉了某些不包含最优解的可行解;第二,在解空间树上,回溯法以深度优先搜索,而分枝—限界法则以广度优先或最小耗费优先的方式搜索。
分枝—限界的搜索策略是,在扩展节点处,首先生成其所有的儿子结点(分支),然后再从当前的活结点表中选择下一个扩展结点。
为了有效地选择下一扩展结点,以加速搜索进程,在每一活结点处,计算一个函数值(限界),并根据这些已计算出的函数值从当前活结点表中选择一个最有利的结点做为扩展,使搜索朝着解空间树上最优解的分支推进,以便尽快找出一个最优解。
分枝—限界法常以广度优先或以最小耗费优先的方式搜索问题的解空间树(问题的解空间树是表示问题皆空间的一颗有序树,常见的有子集树和排序树)。
在搜索问题的解空间树时,分枝—限界法的每一个活结点只有一次机会成为扩展结点。
算法设计与分析 分支限界

…
13
纲要
一、分支限界的基本思想
二、背包问题
三、P和NP
14
问题定义
0-1背包问题
给定n个物品,商品i有两个属性i 和i ,分别代表重量和价格,
背包所承受的物品重量为W
0-1背包问题的目的是要选择一个物品的子集,使其总重量≤W,而价值最大。
解空间
假设解可以有向量( , ,…, )表示, ∈{0,1}, =1表示物品i被放进
(成为死节点),把剩下来的节点加到活节点的表中,然后,从这个
表中选一个节点作为下一个扩展节点。
7
分支限界法
从活节点的表中选一个节点并扩展它。这个扩展操作持续到找到解或这
个表为空为止。
选择下一个扩展节点的方法∶
1)先进先出(FIFO)
这个方法是按节点放进表中的次序从活节点表中选择节点。这个活节点
表可被看作一个队列。使用广度优先来搜索这个棵树。
在这个节点上我们得到的下界大于或等于上界,那么就没有必要在扩
展这个节点既不需在延伸这个分支。
·对于最大化问题规则正好相反:一旦上界小于或等于先前确定的下界,
那么就剪掉这个枝。
4
分支限界法
·首先,分支限界是对最优化问题可行解进行剪枝的一个方法。
·将搜索集中在有希望得到解的分支上。也就是说,在基于上下界和可
时,活节点表可用一个最大堆来表示。下一个扩展节点为最大收益的节点。
9
解空间树
扩展节点
死节点
活节点
success
10
分支限界法
使用分支限界法至少需要注意以下几点:
1.怎么样计算上界,极大值问题;
算法论文。

沈阳理工大学算法实践与创新论文题目:分支限界法学生姓名:苑怡学号:1209010201学生姓名:张薇学号:1209010202学生姓名:蔡欣彤学号:1209010204目录一.算法的简介 (3)二.原理 (4)三.步骤 (5)四.主要代码 (6)五.应用 (9)六.优点缺点 (12)参考文献 (12)一.算法的简介一种求解离散最优化问题的计算分析方法,又称分枝定界法。
它是由R.J.达金和兰德-多伊格在20世纪60年代初提出的。
这种方法通常仅需计算和分析部分允许解,即可求得最优解。
因此在求解分派问题和整数规划问题时常用此法。
采用广度优先产生状态空间树的结点,并使用剪枝函数的方法称为分枝限界法。
所谓“分支”是采用广度优先的策略,依次生成扩展结点的所有分支(即:儿子结点)。
所谓“限界”是在结点扩展过程中,计算结点的上界(或下界),边搜索边减掉搜索树的某些分支,从而提高搜索效率。
分枝限界法 - 基本方法求解一个约束条件较多的问题A,可以暂缓考虑部分条件,变换成问题B,先求B 的最优解。
B的最优解一定比A的好(或相当)。
再将原来暂缓考虑的部分条件逐步插入问题B中,得到B的若干子问题,称为分枝。
求解这些子问题,淘汰较差的解,直到所有暂缓考虑的部分条件全部插入为止。
这时求得的最优解就是问题A的最优解。
最常见的两种方式1).队列式(FIFO)分支限界法:将活结点表组织成一个队列,并按队列的先进先出原则选取下一个结点作为当前扩展结点。
2).优先队列式分支限界法:将活结点表组织成一个优先队列,并按优先队列给结点规定的优先级选取优先级最高的下一个结点作为当前扩展结点。
队列式分支限界法的搜索解空间树的方式类似于解空间树的宽度优先搜索,不同的是队列式分支限界法不搜索以不可行结点(已经被判定不能导致可行解或不能导致最优解的结点)为根的子树。
这是因为,按照规则,这样的结点未被列入活结点表。
优先队列式分支限界法的搜索方式是根据活结点的优先级确定下一个扩展结点。
实验5分支限界(精)

《算法设计与分析》实验报告实验5 分支限界算法姓名学号班级网络131实验日期2016.11.29 实验地点学院305一、实验目的:掌握分支限界算法的设计思想与设计方法。
二、实验环境1、硬件环境CPU:2.0GHz内存:4GB硬盘:100GB2、软件环境操作系统:win7编程环境:devc++编程语言:c三、实验内容1、问题有一个背包,最大限重为C,有n个物品,重量分别为W=<w1, w2, …, wn>,价值分别为V=<v1, v2, …, vn>要求使用分支限界算法找出一个装载方案,使得放入背包物品的价值之和最大。
输出装载方案和该方案下的背包所装物品总重量及总价值。
2、数据结构(1)解的结构typedef struct treenode(2)搜索空间的结构int bbfifoknap(int w[],int v[],int n,int c,int* bestValue)3、算法伪代码PackSolu(G, n, C)输入: G[]存储物品的数据结构,n表示物品个数,C表示背包容量输出:一个用来存储各个物品装入数目的数组1. Sort(G) // 将物品从大到小排序2. v<-0; w<-0; i<-0; // v表示装入背包的总值,w表示装入背包的总重,i表示物品的索引3. while i < n do4. if 背包可装下j个第i种物品5. then v<-(v+G[i].v);w<-(w+G[i].w);solu[i] = 1;6. else solu[i] = 0;7. if v >界的值best_v then 更新最优解8. while solu[i] = 0 and i > 0 do i--; // 回溯到上一个装入的物品9. if solu[i] > 0 then solu[i] = 0;w<-(w-G[i].w);v<-(v-G[i].v);i++10. if i > 0 then goto 34、算法分析时间复杂度:O(2^n)空间复杂度:O(n)5、关键代码(含注释)#include<iostream>#include<queue>using namespace std;typedef struct treenode{int weight;int value;int level;int flag;}treenode;queue<struct treenode> que;int enQueue(int w,int v,int level,int flag,int n,int* bestvalue) {treenode node;node.weight = w;node.value = v;node.level = level;node.flag = flag;if (level == n){if (node.value > *bestvalue){*bestvalue = node.value;}return 0;}else{que.push(node);}}//w为重量数组,v为价值数组,n为物品个数,c为背包容量,bestValue为全局最大价值int bbfifoknap(int w[],int v[],int n,int c,int* bestValue){//初始化结点int i=1;treenode tag, livenode;livenode.weight = 0;livenode.value = 0;livenode.level = 1;livenode.flag = 0;//初始为0tag.weight = -1;tag.value = 0;tag.level = 0;tag.flag = 0;//初始为0que.push(tag);while (1){if (livenode.weight + w[i - 1] <= c){enQueue(livenode.weight + w[i - 1], livenode.value + v[i - 1], i, 1,n,bestValue);}enQueue(livenode.weight,livenode.value, i, 0,n,bestValue);livenode = que.front();que.pop();if (livenode.weight == -1){if (que.empty() == 1){break;}livenode = que.front();que.pop();que.push(tag);i++;}}return 0;}6、实验结果(1)输入:C=10,n=4,W=<7, 4, 3, 2>,V=<9, 5, 3, 1>输出:12(2)输入:C=10,n=5,V=<10, 32, 12, 20, 18>,W=<1, 4, 2, 4, 6>输出:64四、实验总结(心得体会、需要注意的问题等)这次学习的是分支界限算法。
分支限界法实验(单源最短路径)

算法分析与设计实验报告第七次实验姓名学号班级时间12.26上午地点工训楼309实验名称分支限界法实验(单源最短路径)实验目的1.掌握并运用分支限界法的基本思想2.运用分支限界法实现单源最短路径问题实验原理问题描述:在下图所给的有向图G中,每一边都有一个非负边权。
要求图G的从源顶点s 到目标顶点t之间的最短路径。
基本思想:下图是用优先队列式分支限界法解有向图G的单源最短路径问题产生的解空间树。
其中,每一个结点旁边的数字表示该结点所对应的当前路长。
为了加速搜索的进程,应采用有效地方式选择活结点进行扩展。
按照优先队列中规定的优先级选取优先级最高的结点成为当前扩展结点。
catch (int){break;}if(H.currentsize==0) //优先队列空{break;}}}上述有向图的结果:测试结果附录:完整代码(分支限界法)Shorest_path.cpp//单源最短路径问题分支限界法求解#include<iostream>#include<time.h>#include<iomanip>#include"MinHeap2.h"using namespace std;template<class Type>class Graph //定义图类{friend int main();public:void shortest_path(int); private:int n, //图的顶点数*prev; //前驱顶点数组Type **c, //图的邻接矩阵*dist; //最短距离数组};template<class Type>class MinHeapNode //最小堆中的元素类型为MinHeapNode{friend Graph<Type>;public:operator int() const{return length;}private:int i; //顶点编号Type length; //当前路长};//单源最短路径问题的优先队列式分支限界法template<class Type>void Graph<Type>::shortest_path(int v){MinHeap<MinHeapNode<Type>> H(1000);//定义最小堆的容量为1000//定义源为初始扩展结点MinHeapNode<Type> E;//初始化源结点E.i=v;E.length=0;dist[v]=0;while(true)//搜索问题的解空间{for(int j=1;j<=n;j++)if((c[E.i][j]!=0)&&(E.length+c[E.i][j]<dist[j])){//顶点i到顶点j可达,且满足控制约束//顶点i和j之间有边,且此路径小于原先从源点i到j的路径长度dist[j]=E.length+c[E.i][j];//更新dist数组prev[j]=E.i;//加入活结点优先队列MinHeapNode<Type> N;N.i=j;N.length=dist[j];H.Insert(N);//插入到最小堆中}try{H.DeleteMin(E); // 取下一扩展结点}catch (int){break;}if(H.currentsize==0)//优先队列空{break;}}}int main(){int n=11;int prev[12]={0,0,0,0,0,0,0,0,0,0,0,0};//初始化前驱顶点数组intdist[12]={1000,1000,1000,1000,1000,1000,1000,1000,1000,1000,1000,1000 };//初始化最短距离数组cout<<"单源图的邻接矩阵如下:"<<endl;int **c=new int*[n+1];for(int i=1;i<=n;i++) //输入图的邻接矩阵{c[i]=new int[n+1];for(int j=1;j<=n;j++){cin>>c[i][j];}}int v=1; //源结点为1Graph<int> G;G.n=n;G.c=c;G.dist=dist;G.prev=prev;clock_t start,end,over; //计算程序运行时间的算法start=clock();end=clock();over=end-start;start=clock();G.shortest_path(v);//调用图的最短路径查找算法//输出从源结点到目的结点的最短路径cout<<"从S到T的最短路长是:"<<dist[11]<<endl;for(int i=2;i<=n;i++)//输出每个结点的前驱结点{cout<<"prev("<<i<<")="<<prev[i]<<" "<<endl;}for(int i=2;i<=n;i++) //输出从源结点到其他结点的最短路径长度{cout<<"从1到"<<i<<"的最短路长是:"<<dist[i]<<endl;}for(int i=1;i<=n;i++) //删除动态分配时的内存{delete[] c[i];}delete[] c;c=0;end=clock();printf("The time is %6.3f",(double)(end-start-over)/CLK_TCK); //显示运行时间cout<<endl;system("pause");return 0;}MinHeap.h#include<iostream>template<class Type>class Graph;template<class T>class MinHeap //最小堆类{template<class Type>friend class Graph;public:MinHeap(int maxheapsize=10); //构造函数,堆的大小是10~MinHeap(){delete[] heap;} //最小堆的析构函数int Size() const{return currentsize;} //Size()返回最小堆的个数T Max(){if(currentsize) return heap[1];} //第一个元素出堆MinHeap<T>& Insert(const T& x); //最小堆的插入函数MinHeap<T>& DeleteMin(T& x); //最小堆的删除函数void Initialize(T x[],int size,int ArraySize); //堆的初始化void Deactivate();void output(T a[],int n);private:int currentsize,maxsize;T *heap;};template<class T>void MinHeap<T>::output(T a[],int n) //输出函数,输出a[]数组的元素{for(int i=1;i<=n;i++)cout<<a[i]<<" ";cout<<endl;}template<class T>MinHeap<T>::MinHeap(int maxheapsize){maxsize=maxheapsize;heap=new T[maxsize+1]; //创建堆currentsize=0;}template<class T>MinHeap<T>& MinHeap<T>::Insert(const T& x){if(currentsize==maxsize) //如果堆中的元素已经等于堆的最大大小return *this; //那么不能在加入元素进入堆中int i= ++currentsize;while(i!=1 && x<heap[i/2]){heap[i]=heap[i/2];i/=2;}heap[i]=x;return *this;}template<class T>MinHeap<T>& MinHeap<T>::DeleteMin(T& x) //删除堆顶元素{if(currentsize==0){cout<<"Empty heap!"<<endl;return *this;}x=heap[1];T y=heap[currentsize--];int i=1,ci=2;while(ci<=currentsize){if(ci<currentsize && heap[ci]>heap[ci+1])ci++;if(y<=heap[ci])break;heap[i]=heap[ci];i=ci;ci*=2;}heap[i]=y;return *this;}template<class T>void MinHeap<T>::Initialize(T x[],int size,int ArraySize) //堆的初始化{delete[] heap;heap=x;currentsize=size;maxsize=ArraySize;for(int i=currentsize/2;i>=1;i--){T y=heap[i];int c=2*i;while(c<=currentsize){if(c<currentsize && heap[c]>heap[c+1])c++;if(y<=heap[c])break;heap[c/2]=heap[c];c*=2;}heap[c/2]=y;}}template<class T>void MinHeap<T>::Deactivate(){heap=0; }。
分枝限界法_实验报告

一、课题名称用分枝限界法求解单源最短路径问题二、课题内容和要求设计要求:学习算法设计中分枝限界法的思想,设计算法解决数据结构中求解单源最短路径问题,编程实现:(1)给出指定源点的单源最短路径;(2)说明算法的时间复杂度。
三、需求分析1.实现极小堆的创建,用来存储活结点表。
2.实现循环队列的创建、初始化、入队、出队等操作。
3.实现分支限界法来实现求解单元最短路径的算法。
4.实现最短路径的正确输出。
四、概要设计建立工程MinPath.dsw,加入源文件main.cpp,头文件CirQueue.h,init.h,Minpath.h和output.h. CirQueue.h中实现极小堆的创建,循环队列的创建、初始化、入队、出队等操作,Minpath.h中实现分支限界法来实现求解单元最短路径的算法。
output.h中实现最短路径的正确输出。
如下图所示:实验用例如下,通过邻接矩阵的方式写在init.h 中:五、详细设计12581134 69 7103 43292212223733352main函数:#include<iostream.h>#include"init.h"#include"CirQueue.h"#include"MinPath.h"#include"output.h"void main(){int k;int q;cout<<"------------欢迎使用本系统---------------"<<endl;cout<<"------------请选择单元路径的起点:---------------"<<endl;cout<<"------------提示:输入"<<1<<"到"<<n-1<<"之间的整数---------------"<<endl;cin>>k;cout<<"------------请选择单元路径的终点:---------------"<<endl;cin>>q;while(k<1||k>11){cout<<"------------提示:输入"<<1<<"到"<<n-1<<"之间的数,请重新输入---------------"<<endl;cin>>k;}MinPath(k);output(k,q);}init.hconst int size = 200;const int inf = 1000; //两点距离上界置为1000const int n = 12; //图顶点个数加1int prev[n]; //图的前驱顶点int dist[] = {0,inf,inf,inf,inf,inf,inf,inf,inf,inf,inf,inf}; //最短距离数组int c[n][n] = {{0,0,0,0,0,0,0,0,0,0,0,0},{0,0,2,3,4,inf,inf,inf,inf,inf,inf,inf},{0,inf,0,3,inf,7,2,inf,inf,inf,inf,inf},{0,inf,inf,0,inf,inf,9,2,inf,inf,inf,inf},{0,inf,inf,inf,0,inf,inf,2,inf,inf,inf,inf},{0,inf,inf,inf,inf,0,inf,inf,3,3,inf,inf},{0,inf,inf,inf,inf,inf,0,1,inf,3,inf,inf},{0,inf,inf,inf,inf,inf,inf,0,inf,5,1,inf},{0,inf,inf,inf,inf,inf,inf,inf,0,inf,inf,3},{0,inf,inf,inf,inf,inf,inf,inf,inf,0,inf,2},{0,inf,inf,inf,inf,inf,inf,inf,inf,2,inf,2},{0,inf,inf,inf,inf,inf,inf,inf,inf,inf,inf,0},}; //图的邻接矩阵CirQueue.hclass MinHeapNode//创建极小堆用来存储活结点表{public :int i; //顶点编号int length; //当前路长};class CirQueue//循环队列{private:int front,rear;//头指针和尾指针MinHeapNode data[size];public:CirQueue()//初始化建空队列{front = rear = 0;}void queryIn(MinHeapNode e)//元素入队操作{if((rear +1)%size != front)//队列未满{rear = (rear+1)%size; //插入新的队尾元素data[rear] = e; //在队尾插入元素 }}void queryOut()//元素出队操作{if(rear != front){front = (front+1)%size; //删除队头元素}}MinHeapNode getQuery()//读取队头元素,但不出队 {if(rear != front){return data[(front+1)%size];}return data[1];}bool empty()//判断队列是否为空{return front == rear;}bool full()//判断队列是否为满{return (rear +1)%size == front;}};//CirQueue结束MainPath.hvoid MinPath(int v){CirQueue s;//定义源为初始扩展结点MinHeapNode e;e.i = v;e.length = 0;dist[v] = 0;s.queryIn(e); //将源节点加入队列while(true){for(int j = 1;j<n;j++){if(j>=n){break;}MinHeapNode m = s.getQuery();if((c[m.i][j]<inf)&&(m.length + c[m.i][j] < dist[j]))//顶点i到顶点j可达,且从源出发途经i到j的路径长度小于当前最优路径长度{dist[j] = m.length + c[m.i][j];prev[j] = m.i;MinHeapNode mi;//加入活结点优先队列mi.i = j;mi.length = dist[j];if(s.full()){break;}s.queryIn(mi); //元素入队}}//for循环结束if(s.empty()){break;}s.queryOut(); //当该结点的孩子结点全部入队后,删除该结点 }//while循环结束}//方法结束output.hvoid output(int k,int q){int q1=q;if(dist[q1]==1000){cout<<"------------找不到此路径---------------"<<endl;return;}cout<<"最短路径长为: "<<dist[q1]<<endl;cout<<"单源最短路径为: ";int a[12]={0};int t =q1;int s=0;for(int i=0;t!=k;i++){a[i] = prev[t];t = prev[t];s=s+1;}for(i=s-1;i>-1;i--) {cout<<a[i]<<" ";}cout<<q1;cout<<endl<<"------------欢迎使用本系统---------------"<<endl; }六、测试数据及其结果分析1.选择起点:1,终点:111到11最短路径长为8,为1->3->7->10->11所获得。
分支限界法实现实验报告

队列式分支限界法将活节点表组织成一个队列,并将队列的先进先出原则选取下一个节点为当前扩展节点。
2.优先队列式分支限界法
优先队列式分支限界法将活节点表组织成一个优先队列,并将优先队列中规定的节点优先级选取优先级最高的下一个节点成为当前扩展节点。如果选择这种选择方式,往往将数据排成最大堆或者最小堆来实现。
for (j=0;j<City_Size;j++){
temp_x[j]=Best_Cost_Path[j];
}
temp_x[pNode->x[pNode->s+1]] = Best_Cost_Path[i];
temp_x[i] = Best_Cost_Path[pNode->s+1];
Node* pNextNode = new Node;
int edge2 = City_Graph[(pNode->x)[City_Size-1]][(pNode->x)[0]];
if(edge1 >= 0 && edge2 >= 0 && (pNode->cc+edge1+edge2) < Best_Cost){
Best_Cost = pNode->cc + edge1+edge2;
二、实验过程记录:
打开MicrosoftC++2008,键入代码进行编程:
源代码为:
#include <stdio.h>
#include "stdafx.h"
#include <istream>
实验三:分支限界法
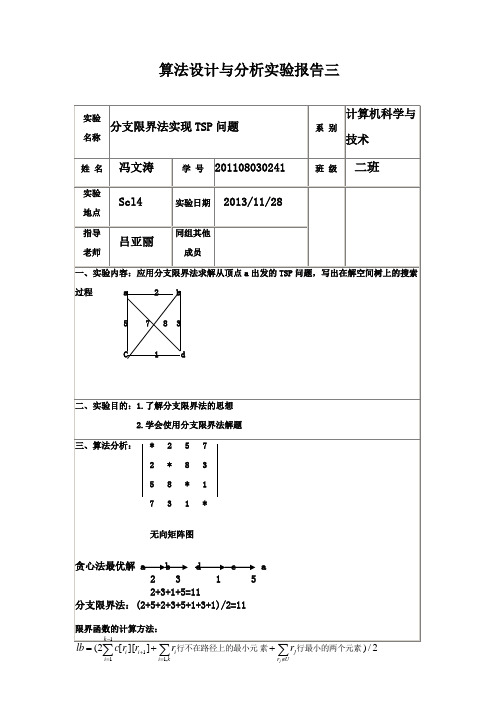
算法设计与分析实验报告三=∉=+k i U r j i i i i j ,111行最小的两个元素素行不在路径上的最小元五.实验程序:#include<iostream>#include<stack>#define N 200using namespace std;class HeapNode{public:double uprofit,profit,weight; int level,x[N];};stack<HeapNode> H;double w[N],p[N];double cw,cp,c;int n;double Bound(int i){double cleft=c-cw,b=cp;while(i<=n&&w[i]<=cleft){cleft-=w[i];b+=p[i];i++;}if(i<=n) b+=p[i]/w[i]*cleft;return b;}void AddLiveNode(double up,double cp,double cw,bool ch,int level)HeapNode nod;nod.uprofit=up;nod.profit=cp;nod.weight=cw;nod.level=level;if(level<=n) H.push(nod); }double Knap(){int i=1;cw=cp=0;double bestp=0,up=Bound(1); while(1){double wt=cw+w[i];if(wt<=c){if(cp+p[i]>bestp) bestp=cp+p[i];AddLiveNode(up,cp+p[i],cw+w[i],true,i+1); }up=Bound(i+1);if(up>=bestp)AddLiveNode(up,cp,cw,false,i+1);if(H.empty()) return bestp;HeapNode node=H.top();H.pop();cw=node.weight;cp=node.profit;up=node.uprofit;i=node.level;}}int main(){cout<<"请输入n和c:"; cin>>n>>c; cout<<"请输入w[i]"<<endl;for(int i=1;i<=n;i++) cin>>w[i];cout<<"请输入p[i]"<<endl;for(int j=1;j<=n;j++) cin>>p[j];cout<<"最优值是:"<<Knap()<<endl; return 0;}。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
毕业设计(论文)开题报告
计算机科学与信息工程学院2013 届
题目分支限界算法的研究与实现Research and application of branch threshold algorithm 课题类型应用研究课题来源老师指定
学生姓名李瑞杰学号200903010017 专业班级09届计算机科学与技术(应用)
指导教师冯慧玲职称讲师
填写日期:2013 年3 月30 日
一、本课题研究的主要内容、目的和意义
1.课题内容
以旅行售货员问题、0/1背包问题、作业分配问题、布线问题、货物装载问题为例进行算法的分析、设计、实现及模拟演示。
在分支限界法中,每一个活结点只有一次机会成为扩展结点。
活结点一旦成为扩展结点,就一次性产生其所有儿子结点。
在这些儿子结点中,导致不可行解或导致非最优解的儿子结点被舍弃,其余儿子结点被加入活结点表中。
此后,从活结点表中取下一结点成为当前扩展结点,并重复上述结点扩展过程。
这个过程一直持续到找到所需的解或活结点表为空时为止。
在现实生活中,有这样一类问题:问题有n个输入,而问题的解就由n个输入的某种排列或某个子集构成,只是这个排列或子集必须满足某些事先给定的条件。
把那些必须满足的条件称为约束条件;而把满足约定条件的排列或子集称为该问题的可行解。
满足约束条件的子集可能不止一个,也就量说可行解一般来说是不唯一的。
为了衡量可行解的优劣,事先也可能给出了一定的标准,这些标准一般以函数形式给出,这些函数称为目标函数。
那些使目标函数取极值的可行解,称为最优解。
如工作安排问题,任意顺序都是问题的可行解,人们真正需要的是最省时间的最优解。
2.研究方法
分支限界法常以广度优先或以最小耗费(最大效益)优先的方式搜索问题的解空间树。
在分支限界法中,每一个活结点只有一次机会成为扩展结点。
活结点一旦成为扩展结点,就一次性产生其所有儿子结点。
在这些儿子结点中,导致不可行解或导致非最优解的儿子结点被舍弃,其余儿子结点被加入活结点表中。
此后,从活结点表中取下一结点成为当前扩展结点,并重复上述结点扩展过程。
这个过程一直持续到找到所需的解或活结点表为空时为止。
3.课题研究的意义
用回溯算法解决问题时,是按深度优先的策略在问题的状态空间中,尝试搜索可能的路径,不便于在搜索过程中对不同的解进行比较,只能在搜索到所有解的情况下,才能通过比较确定哪个是最优解。
这类问题更适合用广度优先策略搜
索,因为在扩展结点时,可以在E-结点的各个子结点之间进行必要的比较,有选择地进行下一步扩展。
分支限界法就是一种比较好的解决最优化问题的算法。
分支限界法是由“分支”策略和“限界”策略两部分组成。
“分支”策略体现在对问题空间是按广度优先的策略进行搜索;“限界”策略是为了加速搜索速度而采用启发信息剪枝的策略。
二、文献综述(国内外相关研究现况和发展趋向)
1.常见的两种分支限界法
(1) FIFO搜索
先进先出搜索算法要依赖“队”做基本的数据结构。
一开始,根结点是唯一的活结点,根结点入队。
从活结点队中取出根结点后,作为当前扩展结点。
对当前扩展结点,先从左到右地产生它的所有儿子,用约束条件检查,把所有满足约束函数的儿子加入活结点队列中。
再从活结点表中取出队首结点为当前扩展结点,……,直到找到一个解或活结点队列为空为止。
(2) LIFO搜索
后进先出搜索算法要依赖“栈”做基本的数据结构。
一开始,根结点入栈.从栈中弹出一个结点为当前扩展结点。
对当前扩展结点,先从左到右地产生它的所有儿子,用约束条件检查,把所有满足约束函数的儿子入栈,再众栈中弹出一个结点为当前扩展结点,……,直到找到一个解或栈为空为止。
2.分支限界法与回溯法的不同
(1)求解目标:回溯法的求解目标是找出解空间树中满足约束条件的所有解,而分支限界法的求解目标则是找出满足约束条件的一个解,或是在满足约束条件的解中找出在某种意义下的最优解。
(2)搜索方式的不同:回溯法以深度优先的方式搜索解空间树,而分支限界法则以广度优先或以最小耗费优先的方式搜索解空间树。
3.解空间树的动态搜索
(1)回溯求解0/1背包问题,虽剪枝减少了搜索空间,但整个搜索按深度优先机械进行,是盲目搜索(不可预测本结点以下的结点进行的如何)。
(2)回溯求解TSP也是盲目的(虽有目标函数,也只有找到一个可行解后才
有意义)
(3)分支限界法首先确定一个合理的限界函数,并根据限界函数确定目标函数的界[down, up];然后按照广度优先策略遍历问题的解空间树,在某一分支上,依次搜索该结点的所有孩子结点,分别估算这些孩子结点的目标函数的可能取值(对最小化问题,估算结点的down,对最大化问题,估算结点的up)。
如果某孩子结点的目标函数值超出目标函数的界,则将其丢弃(从此结点生成的解不会比目前已得的更好),否则入待处理表。
三、拟采取的研究方法(方案、技术路线等)和可行性论证
1.拟采取的研究方法
分支限界有3种不同的搜索方式:FIFO、LIFO和优先队列。
以旅行售货员问题、0/1背包问题、作业分配问题、布线问题货物装载问题为例进行算法的分析、设计、实现及模拟演示。
2.系统软件及开发平台
硬件平台:
CPU:AMD X2 240 2.80GHz
内存:2.00GB
软件平台:
开发工具包:VC++6.0
服务器:运行服务器采用Windows XP
四、预期结果(或预计成果)
完成算法设计与分析中关于分支限界问题的分析,设计,实现及模拟演示。
1.以旅行售货员问题为例进行算法的分析、设计、实现及模拟演示。
2.以0/1背包问题为例进行算法的分析、设计、实现及模拟演示。
3.以作业分配问题为例进行算法的分析、设计、实现及模拟演示。
4.以布线问题为例进行算法的分析、设计、实现及模拟演示。
5.以货物装载问题为例进行算法的分析、设计、实现及模拟演示。
最后,高质量的完成论文,顺利通过毕业答辩。
五、研究进度安排
时间任务
3.04-3.11 搜集相关资料、课题调研,根据任务书初拟开发计划;
3.12-3.19 写需求规格说明书,设计每一问题的研究思路;
3.20-3.27 翻译英文文献,撰写开题报告,初步完善各种问题的解决;
3.28-
4.03 提交开题报告,并根据指导老师意见修改开题报告;
4.04-4.11 对分支限界问题进行详细设计;
4.12-4.19 完成分支限界问题的详细设计,根据导师的意见修改;
4.20-4.27 拟出解决问题的基本构架,对系统进行编码;
4.28-
5.04 对每一问题进行详细的设计;
5.05-5.12 对每一问题功能模块进行测试,在导师的指导下进行修改;
5.13-5.20 写毕业设计论文,根据指导老师的意见对其进行修改和完善;5.21-5.28 完成毕业设计论文,提交其他文档,参与毕业答辩。
六、主要参考文献
[1]Anany Levitin.算法设计与分析基础[M].潘彦,译.北京:清华大学出版社,2004:79一154
[2]严蔚敏,吴伟民.数据结构[M].北京:清华大学出版社,1997:142—147
[3]王晓东.计算机算法设计与分析(第2版)[M].北京:电子工业出版社,2005:86一113
[4]宋文,吴晟,杜亚军,算法设计与分析[M].重庆大学出版社,重庆,2008
[5]李根强,数据结构[M].中国水利水电出版社,北京,2002
[6]冯舜玺,李学武,裴伟东,算法分析导论[M].机械工业出版社,北京,2006
[7]李建学,李光元,吴春芳.数据结构课程设计案例精编[D].清华大学.2007
[8]李昌坤.JPEG2000标准算法研究及改进[D].四川大学.2005
[9]应莉 0-1背包问题及其算法计算机与现代化(2009)06-0024-03
[10]徐颖回溯法在0-1背包问题中的应用软件导刊(2008)12-0054-02
七、审核意见
指导教师对开题的意见:
指导教师签字:年月日院系审核意见:
审核人签字:年月日说明:1、该表每生一份,院系妥善存档;
2、课题来源填:“国家、部、省、市科研项目”或“企、事业单位委托”或“自拟课
题”或“其它”;课题类型填:“设计”或“论文”或“其它”。
