改进欧拉格式的matlab实现
MATLAB改进欧拉法与四阶龙格-库塔求解一阶常微分方程

姓名:樊元君学号:02 日期:一、实验目的掌握MATLAB语言、C/C++语言编写计算程序的方法、掌握改进欧拉法与四阶龙格-库塔求解一阶常微分方程的初值问题。
掌握使用MATLAB程序求解常微分方程问题的方法。
:二、实验内容1、分别写出改进欧拉法与四阶龙格-库塔求解的算法,编写程序上机调试出结果,要求所编程序适用于任何一阶常微分方程的数值解问题,即能解决这一类问题,而不是某一个问题。
实验中以下列数据验证程序的正确性。
求,步长h=。
*2、实验注意事项的精确解为,通过调整步长,观察结果的精度的变化^)三、程序流程图:●改进欧拉格式流程图:~|●四阶龙格库塔流程图:]四、源程序:●改进后欧拉格式程序源代码:function [] = GJOL(h,x0,y0,X,Y)format longh=input('h=');…x0=input('x0=');y0=input('y0=');disp('输入的范围是:');X=input('X=');Y=input('Y=');n=round((Y-X)/h);\i=1;x1=0;yp=0;yc=0;for i=1:1:nx1=x0+h;yp=y0+h*(-x0*(y0)^2);%yp=y0+h*(y0-2*x0/y0);%·yc=y0+h*(-x1*(yp)^2);%yc=y0+h*(yp-2*x1/yp);%y1=(yp+yc)/2;x0=x1;y0=y1;y=2/(1+x0^2);%y=sqrt(1+2*x0);%fprintf('结果=%.3f,%.8f,%.8f\n',x1,y1,y);:endend●四阶龙格库塔程序源代码:function [] = LGKT(h,x0,y0,X,Y)。
format longh=input('h=');x0=input('x0=');y0=input('y0=');disp('输入的范围是:');"X=input('X=');Y=input('Y=');n=round((Y-X)/h);i=1;x1=0;k1=0;k2=0;k3=0;k4=0;for i=1:1:n~x1=x0+h;k1=-x0*y0^2;%k1=y0-2*x0/y0;%k2=(-(x0+h/2)*(y0+h/2*k1)^2);%k2=(y0+h/2*k1)-2*(x0+h/2)/(y0+h/2*k1);% k3=(-(x0+h/2)*(y0+h/2*k2)^2);%k3=(y0+h/2*k2)-2*(x0+h/2)/(y0+h/2*k2);% k4=(-(x1)*(y0+h*k3)^2);%k4=(y0+h*k3)-2*(x1)/(y0+h*k3);%…y1=y0+h/6*(k1+2*k2+2*k3+k4);%y1=y0+h/6*(k1+2*k2+2*k3+k4);%x0=x1;y0=y1;y=2/(1+x0^2);%y=sqrt(1+2*x0);%fprintf('结果=%.3f,%.7f,%.7f\n',x1,y1,y);end·end*五、运行结果:改进欧拉格式结果:;}四阶龙格库塔结果:步长分别为:和时,不同结果显示验证了步长减少,对于精度的提高起到很大作用,有效数字位数明显增加。
欧拉法(euler)求解常微分方程的matlab程序及案例

欧拉法(euler)求解常微分方程的matlab程序及案例欧拉方法是最初用于求解常微分方程的数值方法之一,它是一种显式的一步法,具有易于实施的优点,特别适合初学者使用。
本文将介绍欧拉法的原理和使用MATLAB求解常微分方程的具体方法,同时给出一个简单的实例进行说明。
一、欧拉法原理考虑一个一阶常微分方程y'=f(t,y),欧拉法的基本思想是将时间步长Δt均分成n个小步长,从y(t0)开始依次计算每个时刻的值,得到一列估计值y1, y2, …, yn。
欧拉法的计算公式为:(1)y1=y(t0+Δt)=y(t0)+Δtf(t0, y0)(2)y2=y(t0+2Δt)=y(t0+Δt)+Δtf(t0+Δt, y1)(3)yn=y(t0+nΔt)=y(t0+(n-1)Δt)+Δtf(t0+(n-1)Δt, yn-1)可以看出,欧拉法的核心在于利用已知的t和y计算f(t,y),从而获得y的逼近值。
但是需要注意的是,步长Δt越小,计算所需的时间和内存就越多,而精度却并不一定提高。
因此在实际应用中需要结合具体问题选择合适的步长。
二、MATLAB求解常微分方程的具体方法(1)定义常微分方程我们以一个简单的例子开始,考虑求解y'=1-y,y(0)=0.5在[0,1]区间内的积分。
首先定义匿名函数dydt,将其传到ode45中求解:dydt=@(t,y)1-y;[t,y]=ode45(dydt,[0 1],0.5);plot(t,y,'-o')运行以上代码可以得到结果,其中plot函数用于绘制图像。
但是,由于求解过程中计算机执行到ode45函数时可能需要很长时间,因此需要更快捷的方法。
(2)利用欧拉法求解方程欧拉法求解方程首先需要定义步长Δt,这里设Δt为0.1。
定义起始值y=[0.5]、时间向量t=0:Δt:1,然后计算列向量y的估计值:t=0:0.1:1;y=zeros(size(t));y(1)=0.5;for n=1:length(t)-1y(n+1)=y(n)+0.1*(1-y(n));endplot(t,y,'-o')以上代码的执行结果与前面的ode45方法相同,但是速度更快。
四阶龙格库塔和向前欧拉方法和隐式欧拉法以及改进欧拉法教材

实验九欧拉方法信息与计算科学金融崔振威201002034031一、实验目的:1、掌握欧拉算法设计及程序实现二、实验内容:1、p364-9.2.4、p386-9.5.6三、实验要求:主程序:欧拉方法(前项):function [x,y]=DEEuler(f,a,b,y0,n);%f:一阶常微分方程的一般表达式的右端函数%a:自变量的取值下限%b:自变量的取值上限%y0:函数的初值%n:积分的步数if nargin<5,n=50;endh=(b-a)/n;x(1)=a;y(1)=y0;for i=1:nx(i+1)=x(i)+h;y(i+1)=y(i)+h*feval(f,x(i),y(i));endformat short欧拉方法(后项):function [x,y]=BAEuler(f,a,b,y0,n);%f:一阶常微分方程的一般表达式的右端函数%a:自变量的取值下限%b:自变量的取值上限%y0:函数的初值%n:积分的步数if nargin<5,n=50;endh=(b-a)/n;x(1)=a;y(1)=y0;for i=1:nx(i+1)=x(i)+h;y1=y(i)+h*feval(f,x(i),y(i));y(i+1)=y(i)+h*feval(f,x(i+1),y1);endformat short梯形算法:function [I,step,h2] = CombineTraprl(f,a,b,eps)%f 被积函数%a,b 积分上下限%eps 精度%I 积分结果%step 积分的子区间数if(nargin ==3)eps=1.0e-4;endn=1;h=(b-a)/2;I1=0;I2=(subs(sym(f),findsym(sym(f)),a)+subs(sym(f),findsym(sym(f)),b))/h;while abs(I2-I1)>epsn=n+1;h=(b-a)/n;I1=I2;I2=0;for i=0:n-1x=a+h*i;x1=x+h;I2=I2+(h/2)*(subs(sym(f),findsym(sym(f)),x)+subs(sym(f),findsym(sym(f)),x1));endendI=I2;step=n;h2=(b-a)/n;改进欧拉方法:function [x,y]=MoEuler(f,a,b,y0,n);%f:一阶常微分方程的一般表达式的右端函数%a:自变量的取值下限%b:自变量的取值上限%y0:函数的初值%n:积分的步数if nargin<5,n=50;endh=(b-a)/n;x(1)=a;y(1)=y0; for i=1:nx(i+1)=x(i)+h;y1=y(i)+h*feval(f,x(i),y(i)); y2=y(i)+h*feval(f,x(i+1),y1); y(i+1)=(y1+y2)/2; endformat short四阶龙格-库塔法:function y = DELGKT4_lungkuta(f, h,a,b,y0,varvec) %f:一阶常微分方程的一般表达式的右端函数 %h:积分步长%a :自变量的取值下限 %b:自变量的取值上限%varvec :常微分方程的变量组 format long; N = (b-a)/h;y = zeros(N+1,1); y(1) = y0; x = a:h:b;var = findsym(f); for i=2:N+1K1 = Funval(f,varvec,[x(i-1) y(i-1)]);%Funval 为程序所需要的函数 K2 = Funval(f,varvec,[x(i-1)+h/2 y(i-1)+K1*h/2]); K3 = Funval(f,varvec,[x(i-1)+h/2 y(i-1)+K2*h/2]); K4 = Funval(f,varvec,[x(i-1)+h y(i-1)+h*K3]); y(i) = y(i-1)+h*(K1+2*K2+2*K3+K4)/6; endformat short;p364-9.2.4欧拉方法(前项):1、22)(,1)0(,22'+-+-==-=-t t e t y y y t y t解:执行20步时:编写函数文件doty.m 如下: function f=doty(x,y); f=x^2-y;在Matlab 命令窗口输入:>> [x1,y1]=DEEuler('doty',0,2,1,20)可得到结果:x1 =0 0.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.70000.8000 0.9000 1.0000 1.1000 1.2000 1.3000 1.4000 1.50001.6000 1.7000 1.8000 1.90002.0000y1 =1.0000 0.9000 0.8110 0.7339 0.6695 0.6186 0.5817 0.55950.5526 0.5613 0.5862 0.6276 0.6858 0.7612 0.8541 0.96471.0932 1.2399 1.4049 1.5884 1.7906在Matlab 命令窗口输入:>> y3=-exp(-x1)+x1.^2-2*x1+2求得解析解:y3 =1.0000 0.9052 0.8213 0.7492 0.6897 0.6435 0.6112 0.59340.5907 0.6034 0.6321 0.6771 0.7388 0.8175 0.9134 1.02691.1581 1.3073 1.4747 1.6604 1.8647输入:>> plot(x1,y1,'o');hold on>> plot(x1,y3,'*');hold on可得近似值与解析解的图像比较:执行40步时:在Matlab 命令窗口输入:>> [x1,y1]=DEEuler('doty',0,2,1,40)可得到结果:x1 =0 0.0500 0.1000 0.1500 0.2000 0.2500 0.3000 0.3500 0.4000 0.4500 0.5000 0.5500 0.6000 0.6500 0.7000 0.75000.8000 0.8500 0.9000 0.9500 1.0000 1.0500 1.1000 1.15001.2000 1.2500 1.3000 1.3500 1.4000 1.4500 1.5000 1.55001.6000 1.6500 1.7000 1.7500 1.8000 1.8500 1.9000 1.95002.0000y1 =1.0000 0.9500 0.9026 0.8580 0.8162 0.7774 0.7417 0.7091 0.6798 0.6538 0.6312 0.6121 0.5967 0.5848 0.5767 0.5724 0.5719 0.5753 0.5826 0.5940 0.6094 0.6290 0.6526 0.68050.7126 0.7490 0.7897 0.8347 0.8841 0.9379 0.9961 1.05881.1260 1.1977 1.2739 1.3547 1.4401 1.5301 1.6247 1.7240 1.8279在Matlab 命令窗口输入:>> y3=-exp(-x1)+x1.^2-2*x1+2求得解析解:y3 =1.0000 0.9513 0.9052 0.8618 0.8213 0.7837 0.7492 0.7178 0.6897 0.6649 0.6435 0.6256 0.6112 0.6005 0.5934 0.5901 0.5907 0.5951 0.6034 0.6158 0.6321 0.6526 0.6771 0.70590.7388 0.7760 0.8175 0.8633 0.9134 0.9679 1.0269 1.09031.1581 1.2305 1.3073 1.3887 1.4747 1.5653 1.6604 1.7602 1.8647输入:>> plot(x1,y1,'o');hold on>> plot(x1,y3,'*');hold on可得近似值与解析解的图像比较:从上面结果可以看出,执行40步时近似解的值要接近于解析解,误差更小,结果更精确。
用MATLAB程序生动地演示欧拉公式

⽤MATLAB程序⽣动地演⽰欧拉公式下⾯的MA TLAB 程序⽣动地演⽰欧拉公式Exp(t) = cos(t) + j sin(t)% Henry-104% 本程序演⽰欧拉公式% Jan.25th,2012%h_fig1 = figure;set(h_fig1, 'unit', 'normalized', 'position', [0.1, 0.1, 0.9, 0.9]);set(h_fig1, 'defaultuicontrolunits', 'normalized');h_text1 = uicontrol(h_fig1, 'Style', 'text', 'Position', [0.71, 0.73, 0.25, 0.05],... % 创建⽂本框'String', '▲是cos 曲线的起点', 'ForegroundColor', 'r', 'FontName', '⿊体',...'FontSize', 12, 'FontWeight', 'Bold', 'BackgroundColor', [1, 1, 1]);h_text2 = uicontrol(h_fig1, 'Style', 'text', 'Position', [0.71, 0.78, 0.25, 0.05],... % 创建⽂本框'String', 'Δ是sin 和exp 曲线的起点', 'ForegroundColor', 'r', 'FontName', '⿊体',...'FontSize', 12, 'FontWeight', 'Bold', 'BackgroundColor', [1, 1, 1]);h_pushbutton1 = uicontrol(h_fig1, 'Style', 'PushButton', 'Position', [0.82, 0.12, 0.07, 0.06],...'string', '退出', 'BackgroundColor', [0.8 0.9 0.8], 'ForegroundColor', 'r', 'FontSize', 14, 'FontWeight', 'Bold',...'callback', 'delete(h_fig1),')h_axes0 = axes('Box', 'on', 'Position', [0.15, 0.18, 0.56, 0.68], 'FontSize', 8)set(gcf,'color','w');w = 0.1*pit = 0:40; % 在前进⽅向绕了2 圈%a = -ones(1,length(t));plot3(cos(w*t),t,sin(w*t),'b', 'LineWidth', 2);grid on; hold on;hc = plot3(cos(w*t),t,a,'k--'); hold on;set(hc, 'Color', 'r', 'LineWidth', 2);a=-a;hs = plot3(a,t,sin(w*t),'r-.'); hold on;set(hs, 'Color', 'k', 'LineWidth', 2);text(0.7,0.3,0.6, ' <-- CCW', 'FontSize', 14, 'FontWeight', 'Bold'); text(1,0,-1, ' ▲Cos', 'Color', 'r', 'FontSize', 14, 'FontWeight', 'Bold'); text(1,0,0, ' Δ Sin', 'FontSize', 14, 'FontWeight', 'Bold');%xlabel('x', 'FontSize', 14, 'FontWeight', 'Bold');ylabel('t', 'FontSize', 14, 'FontWeight', 'Bold');zlabel('y', 'FontSize', 14, 'FontWeight', 'Bold');title('演⽰欧拉公式y = exp(jwt) = cos(wt) + jsin(wt)', 'Color', 'b', …'FontSize', 18, 'FontWeight', 'Bold');%line([-1,-1],[39.9,39.9],[-1,1],'LineWidth',3, 'Color', 'r');line([1,1],[39.9,39.9],[-1,1],'LineWidth',3, 'Color', 'r');line([-1,-1],[0,0],[-1,1],'LineWidth',3, 'Color', 'r');line([1,1],[0,0],[-1,1],'LineWidth',3, 'Color', 'r');line([-1,-1],[0,40],[-1,-1],'LineWidth',3, 'Color', 'k');line([-1,1],[0,0],[-1,-1],'LineWidth',3, 'Color', 'b')line([-1,1],[40,40],[1,1],'LineWidth',3, 'Color', 'b')line([-1,1],[40,40],[-1,-1],'LineWidth',3, 'Color', 'b')line([-1,1],[0,0],[1,1],'LineWidth',3, 'Color', 'b')line([-1,1],[0,0],[0,0],'LineWidth',2, 'Color', 'k');line([0,0],[0,0],[-1,1],'LineWidth',2, 'Color', 'k');line([0,0],[40,40],[-1,1],'LineWidth',2, 'Color', 'k');line([0,0],[0,40],[0,0],'LineWidth',2, 'Color', 'k');line([-1,1],[40,40],[0,0],'LineWidth',2, 'Color', 'k');line([0,0],[0,40],[0,0],'LineWidth',2, 'Color', 'k');text(0,0,0.12,'O', 'FontSize', 14, 'FontWeight', 'Bold', 'Color', 'r') text(0,40,0.12,'O', 'FontSize', 14, 'FontWeight', 'Bold', 'Color', 'b')程序运⾏结果如下所⽰。
MATLAB常微分方程数值解——欧拉法、改进的欧拉法与四阶龙格库塔方法

MATLAB常微分⽅程数值解——欧拉法、改进的欧拉法与四阶龙格库塔⽅法MATLAB常微分⽅程数值解作者:凯鲁嘎吉 - 博客园1.⼀阶常微分⽅程初值问题2.欧拉法3.改进的欧拉法4.四阶龙格库塔⽅法5.例题⽤欧拉法,改进的欧拉法及4阶经典Runge-Kutta⽅法在不同步长下计算初值问题。
步长分别为0.2,0.4,1.0.matlab程序:function z=f(x,y)z=-y*(1+x*y);function R_K(h)%欧拉法y=1;fprintf('欧拉法:x=%f, y=%f\n',0,1);for i=1:1/hx=(i-1)*h;K=f(x,y);y=y+h*K;fprintf('欧拉法:x=%f, y=%f\n',x+h,y);endfprintf('\n');%改进的欧拉法y=1;fprintf('改进的欧拉法:x=%f, y=%f\n',0,1);for i=1:1/hx=(i-1)*h;K1=f(x,y);K2=f(x+h,y+h*K1);y=y+(h/2)*(K1+K2);fprintf('改进的欧拉法:x=%f, y=%f\n',x+h,y);endfprintf('\n');%龙格库塔⽅法y=1;fprintf('龙格库塔法:x=%f, y=%f\n',0,1);for i=1:1/hx=(i-1)*h;K1=f(x,y);K2=f(x+h/2,y+(h/2)*K1);K3=f(x+h/2,y+(h/2)*K2);K4=f(x+h,y+h*K3);y=y+(h/6)*(K1+2*K2+2*K3+K4);fprintf('龙格库塔法:x=%f, y=%f\n',x+h,y);end结果:>> R_K(0.2)欧拉法:x=0.000000, y=1.000000欧拉法:x=0.200000, y=0.800000欧拉法:x=0.400000, y=0.614400欧拉法:x=0.600000, y=0.461321欧拉法:x=0.800000, y=0.343519欧拉法:x=1.000000, y=0.255934改进的欧拉法:x=0.000000, y=1.000000改进的欧拉法:x=0.200000, y=0.807200改进的欧拉法:x=0.400000, y=0.636118改进的欧拉法:x=0.600000, y=0.495044改进的欧拉法:x=0.800000, y=0.383419改进的欧拉法:x=1.000000, y=0.296974龙格库塔法:x=0.000000, y=1.000000龙格库塔法:x=0.200000, y=0.804636龙格库塔法:x=0.400000, y=0.631465龙格库塔法:x=0.600000, y=0.489198龙格库塔法:x=0.800000, y=0.377225龙格库塔法:x=1.000000, y=0.291009>> R_K(0.4)欧拉法:x=0.000000, y=1.000000欧拉法:x=0.400000, y=0.600000欧拉法:x=0.800000, y=0.302400改进的欧拉法:x=0.000000, y=1.000000改进的欧拉法:x=0.400000, y=0.651200改进的欧拉法:x=0.800000, y=0.405782龙格库塔法:x=0.000000, y=1.000000龙格库塔法:x=0.400000, y=0.631625龙格库塔法:x=0.800000, y=0.377556>> R_K(1)欧拉法:x=0.000000, y=1.000000欧拉法:x=1.000000, y=0.000000改进的欧拉法:x=0.000000, y=1.000000改进的欧拉法:x=1.000000, y=0.500000龙格库塔法:x=0.000000, y=1.000000龙格库塔法:x=1.000000, y=0.303395注意:在步长h为0.4时,要将for i=1:1/h改为for i=1:0.8/h。
欧拉方法及其改进的欧拉方法的Matlab实现

11( n n y x y ++−。为了估计它,由Taylor展开得到的精确值1( n y x +是
2'
''
31( ( ( ( ( 2
n n n n h y x y x hy x y x O h +=+++ (5
2.欧拉方法、改进的欧拉方法及Matlab实现
下面主要讨论一阶常微分方程的初值问题,其一般形式为:
' 00
(,
( y f x y y x y ⎧=⎨
=⎩ (1我们知道,只要函数(, f x y适当光滑——譬如关于y满足利普希茨(Lipschitz条件
(, (, f x y f x y L y y −≤−
改进的欧拉方法是先用欧拉公式求1( n y x +的一个近似值1n y +,称为预测值,然后用梯形公式进行矫正并求得近似值1n y +。即
1111(, [(, (, ]
2n n n n n n n n n n y y f x y h h
y y f x y f x y ++++⎧=+⎪
⎨=++⎪⎩
(8 2.2.2改进的欧拉方法的误差估计
方法是一阶方法,因此它的精度不高。
2.2改进的欧拉方法
2.2.1改进的欧拉方法
用数值积分方法离散化问题(1,两端积分可得
1
1( ( (, ( (0,1, 2, n n
x n n x y x y x f x y x dx n ++−==∫
常微分方程的数值解法(欧拉法、改进欧拉法、泰勒方法和龙格库塔法)
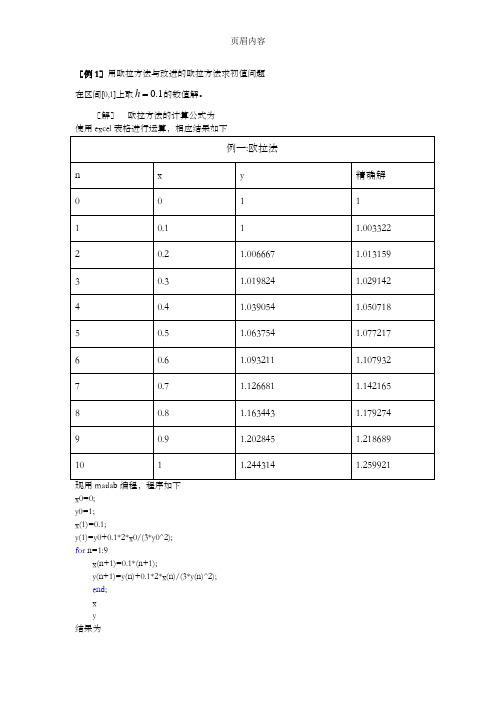
[例1]用欧拉方法与改进的欧拉方法求初值问题h 的数值解。
在区间[0,1]上取0.1[解]欧拉方法的计算公式为x0=0;y0=1;x(1)=0.1;y(1)=y0+0.1*2*x0/(3*y0^2);for n=1:9x(n+1)=0.1*(n+1);y(n+1)=y(n)+0.1*2*x(n)/(3*y(n)^2);end;xy结果为x =Columns 1 through 80.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 Columns 9 through 100.9000 1.0000y =Columns 1 through 81.0000 1.0067 1.0198 1.0391 1.0638 1.0932 1.1267 1.1634 Columns 9 through 101.2028 1.2443改进的欧拉方法其计算公式为本题的精确解为()y x=x0=0;y0=1;ya(1)=y0+0.1*2*x0/(3*y0^2);y(1)=y0+0.05*(2*x0/(3*y0^2)+2*x0/(3*ya^2));for n=1:9x(n+1)=0.1*(n+1);ya(n+1)=ya(n)+0.1*2*x(n)/(3*ya(n)^2);y(n+1)=y(n)+0.05*(2*x(n)/(3*y(n)^2)+2*x(n+1)/(3*ya(n+1)^2));end;xy结果为x =Columns 1 through 80.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 Columns 9 through 100.9000 1.0000y =Columns 1 through 81.0000 1.0099 1.0261 1.0479 1.0748 1.1059 1.1407 1.1783 Columns 9 through 101.2183 1.2600[例2]用泰勒方法解x=0.1, 0.2, …, 1.0处的数值解,并与精确解进行比较。
数值分析考试

桂林理工大学考试(考查)试卷( 学年度 第一学期)课程名称:数值分析考核专业班级:学号: 姓名: 成绩:﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍一、 简答题(4分×5=20分)1、病态线性方程组的主要判断依据有哪些?答:(1)系数矩阵的某两行(列)几乎近似相关(2)系数矩阵的行列式的值很小(3)用主元消去法解线性方程组时出现小主元(4)近似解x*已使残差向量r=b-Ax*的范数很小,但该近似解仍不符合问题要求。
2、数值计算中如何避免不稳定的算法,防止有效数字的损失?答:(1)简化计算过程,减少运算次数;(2)避免两个相近的数相减;(3)避免除数的绝对值远小于被除数的绝对值;(4)防止大数“吃掉”小数的现象;(5)使用数值稳定的算法,设法控制误差的传播。
3、解释龙格现象。
答:增加插值节点,提高插值多项式的次数,可以使插值函数在更多的点与所逼近的函数取相同的值,但会使插值函数在两端发生激烈的振荡,这就是插值计算的龙格现象。
4、阐述迭代法的基本思想。
答:就是用某种极限过程去逐步逼近线性方程组精确解得方法。
其基本思想为:先任取一组近似解初值X 0,然后按照某种迭代原则,由X 0计算新的近似解X 1,以此类推,可计算出X 2,X 3,…X K ,。
,如果{X }收敛,则取为原方程组的解。
5、叙述QR 算法的步骤。
答:对于给定的n 阶实对称矩阵A 与迭代次数M ;(1)令A 1=A ,对于k=1,2,…,M ;(2)迭代计算下一个矩阵:A k =Q k R k (对A k 作QR 分解),(3)A k =RQ(交换乘法次序),令k=k+1,A k+1=Q k T A K Q K(4)返回到2,直到k=M,输出A 的主对角元素。
二、 计算型编程题(20分×3=60分)1、 用Newton 插值拟合[0, 2*pi]上函数()sin x f x e x 。
答:function [yt,N] = NewtInterp(x,y,xt)% 已知数据点的牛顿插值% x,y:插值条件% xt:要计算的插值点,可以是多个% yt:用牛顿插值函数出xt对应的函数值数组% N: 牛顿插值多项式表达式syms t;n=length(x);ny=length(y);if n~=nyerror('插值节点x与函数值y维数不一致'); enda=zeros(1,n);N = y(1);w = 1;for k=1:n-1yy=zeros(1,n); % 记录差商for j=k+1:nyy(j) = (y(j)-y(k))/(x(j)-x(k));enda(k) = yy(k+1);w = w*(t-x(k));N = N + a(k)*w;y = yy;endyt = subs(N,'t',xt);simplify(N);N = collect(N); % 将插值多项式展开N = vpa(N, 6); % 系数转化为6位精度输入:x=[0:pi/10:2*pi];y=exp(x).*sin(x);xt=pi;[yt,N] = NewtInterp(x,y,xt)% 画图z=0:pi/20:2*pi;yz= subs(N,'t',z); %计算插值点处的函数值figure;plot(z,exp(z).*sin(z),'--r',z,yz,'-b')hold onplot(x,y,'marker','+')hold onplot(xt,yt,'marker','o')h=legend('$\exp{x}.*sin{x}$','Newton','$(x_k,y_k)$','$x=pi$');set(h,'Interpreter','latex')xlabel('x')ylabel('y')yt =7.1684e-015N =.159313e-14*t^20-.178421e-12*t^19+.578696e-11*t^18-.993977e-10*t^17+.1179 00e-8*t^16-.101872e-7*t^15+.640214e-7*t^14-.340920e-6*t^13+.131789e-5*t^12-.33 7754e-5*t^11+.19392e-4*t^10+.22800e-4*t^9+.33873e-4*t^8-.162956e-2*t^7-.110707 e-1*t^6-.333620e-1*t^5+.1611e-4*t^4+.333328*t^3+1.00000*t^2+.999992*t2、利用龙贝格算法程序计算积分x。
