北京中考数学新定义压轴题素材1
【精品中考数学】2019年北京市初三数学二模分类汇编-第15讲 新定义压轴题

【2019·房山二模】1.对于平面直角坐标系中的点P 和⊙C,给出如下定义:若⊙C 上存在点A ,使得∠APC=30°,则称P 为⊙C 的半角关联点.当⊙O 的半径为1时, (1)在点D (12,-12),E (2,0),F (0,32)中,⊙O 的半角关联点是__________; (2)直线l :32y x =--交x 轴于点M ,交y 轴于点N ,若直线l 上的点P (m ,n )是⊙O 的半角关联点,求m 的取值范围. 【答案】(1) D 、E(2) (23,0),(0,2)M N -以O 为圆心,ON 长为半径画圆,交直线MN 于点G , 可得 m ≤0设小圆⊙O 与y 轴负半轴的交点为H , 连接OG ∵ M (23,∴ OM =23,tan∠=3∴ ∠∴ △ ∴ GH ∴ 点G 3x -3-,∴ m ≥3- 3-≤第15讲 新定义压轴题⊙C ,给出如下定义:P 为图形M 上任意一点,Q 为⊙C 上任意一点,如果P ,Q 两点间的距离有最小值,那么称这个最小值为图形M 到⊙C 的“圆距离”,记作d (M -C ). (1)点C 在原点O 时,①记点A (4,3)为图形M ,则d (M -O )=______;②点B 与点A 关于x 轴对称,记线段AB 为图形M ,则d (M -O )=______;③记函数4y kx =+(0k >)的图象为图形M ,且d (M -O )1≤,直接写出k 的取值范围;(2)点C 坐标为(t ,0)时,点A ,B 与(1)中相同,记∠AOB 为图形M ,且d (M -C )=1,直接写出t 的值.【答案】解:(1)①4 ②3③k (2)10t=2t=3或 【2019·西城二模】3.对于平面内的∠MAN 及其内部的一点P ,设点P 到直线AM ,AN 的距离分别为d1,d2,称12d d 和21d d 这两个数中较大的一个为点P 关于∠MAN 的“偏率”.在平面直角坐标系xOy 中,(1)点M ,N 分别为x 轴正半轴,y 轴正半轴上的两个点.①若点P 的坐标为(1,5),则点P 关于∠MON 的“偏率”为____________;②若第一象限内点Q (a ,b )关于∠MON 的“偏率”为1,则a ,b 满足的关系为____________; (2)已知点A (4,0),B (2,,连接OB ,AB ,点C 是线段AB 上一动点(点C 不与点A ,B 重合). 若点C 关于∠AOB 的“偏率”为2,求点C 的坐标;(3)点E ,F 分别为x 轴正半轴,y 轴正半轴上的两个点,动点T 的坐标为(t ,4),⊙T 是以点T 为圆心,半径为1的圆. 若⊙T 上的所有点都在第一象限,且关于∠EOF 的“偏率”t 的取值范围. 【答案】解:(1)①5; ②a=b ;(2)∵点A (4,0),B (2,23),∴OA=4,OB=22+(23)2=4,AB=(4-2)2+(23)2=4 ∴OA=OB=AB∴△OAB 是等边三角形 ∴∠OAB=∠OBA=60°过点C 作CD ⊥OA 于点D ,CH ⊥OB 于点H ,如图, 则∠CDA=∠CHB =90° ∴△ACD∽△BCH ∴CD CH =CA CB. ∵点C 关于∠AOB 的“偏率”为2, ∴CD CH =2或CHCD =2. 当CD CH =2时,则CACB =2. ∴CA=23AB=83.∴DA=CAcos60°=43,CD=CAsin60°=433,∴OD=OA -DA=83.∴点C 的坐标为(83,433)同理可求,当CH CD =2时,点C 的坐标为(103,233)。
北师大版七年级数学上册专题2.5 新定义问题(压轴题专项讲练)(学生版)

专题2.5 新定义问题【典例1】小聪是一个聪明而又富有想象力的孩子.学习了“有理数的乘方”后,他就琢磨着使用“乘方”这一数学知识,脑洞大开地定义出“有理数的除方”概念.于是规定:若干个相同有理数(均不能为0)的除法运算叫做除方,如5÷5÷5,(﹣2)÷(﹣2)÷(﹣2)÷(﹣2)等,类比有理数的乘方.小聪把5÷5÷5记作f (3,5),(﹣2)÷(﹣2)÷(﹣2)÷(﹣2)记作f (4,﹣2).(1)直接写出计算结果,f (4,12)= ,f (5,3)= ;(2)关于“有理数的除方”下列说法正确的是 .(填序号) ①f (6,3)=f (3,6); ②f (2,a )=1(a ≠0);③对于任何正整数n ,都有f (n ,﹣1)=1; ④对于任何正整数n ,都有f (2n ,a )<0(a <0).(3)小明深入思考后发现:“除方”运算能够转化成乘方运算,且结果可以写成幂的形式,请推导出“除方”的运算公式f (n ,a )(n 为正整数,a ≠0,n ≥2),要求写出推导过程将结果写成幂的形式;(结果用含a ,n 的式子表示)(4)请利用(3)问的推导公式计算:f (5,3)×f (4,13)×f (5,﹣2)×f (6,12).【思路点拨】(1)根据题意计算即可;(2)①分别计算f (6,3)和f (3,6)的结果进行比较即可; ②根据题意计算即可判断;③分为n 为偶数和奇数两种情况分别计算即可判断; ④2n 为偶数,偶数个a 相除,结果应为正;(3)推导f (n ,a )(n 为正整数,a ≠0,n ≥2),按照题目中的做法推到即可; (4)按照上题的推导式可以将算式中的每一部分表示出来再计算. 【解题过程】解:(1)f (4,12)=12÷12÷12÷12=4,f (5,3)=3÷3÷3÷3÷3=127;故答案为:4;127.(2)①f (6,3)=3÷3÷3÷3÷3÷3=181,f (3,6)=6÷6÷6=16, ∴f (6,3)≠f (3,6),故错误;②f (2,a )=a ÷a =1(a ≠0),故正确;③对于任何正整数n ,当n 为奇数时,f (n ,﹣1)=﹣1;当n 为偶数时,f (n ,﹣1)=1.故错误;④对于任何正整数n ,2n 为偶数,所以都有f (2n ,a )>0,而不是f (2n ,a )<0(a <0),故错误; 故答案为:②.(3)公式f (n ,a )=a ÷a ÷a ÷a ÷…÷a ÷a =1÷(a n ﹣2)=(1a)n ﹣2(n 为正整数,a ≠0,n ≥2).(4)f (5,3)×f (4,13)×f (5,﹣2)×f (6,12)=127×9×(−18)×16 =−23.1.(2022•长安区模拟)用“☆”定义一种新运算:对于任何不为零的整数a 和b ,规定a ☆b =a b ﹣b 2.如(﹣1)☆2=(﹣1)2﹣22=﹣3,则(﹣2)☆(﹣1)的值为( ) A .﹣3B .1C .32D .−322.(2023秋•东港区期末)已知a 、b 皆为正有理数,定义运算符号为※:当a >b 时,a ※b =2a ;当a <b 时,a ※b =2b ﹣a ,则3※2﹣(﹣2※3)等于( ) A .﹣2B .5C .﹣6D .103.(2022•武威模拟)用“*”定义新运算,对于任意有理数a 、b ,都有a *b =b 3﹣1,则12*[3*(﹣1)]的值为( ) A .﹣1B .﹣9C .−12D .04.(2023秋•洪山区期末)定义:如果a 4=N (a >0,且a ≠1),那么x 叫做以a 为底N 的对数,记作x =log a N .例如:因为72=49,所以log 749=2;因为53=125,所以log 5125=3.则下列说法中正确的有( )个.①log 66=36;②log 381=4;③若log 4(a +14)=4,则a =50;④log 2128=log 216+log 28; A .4B .3C .2D .15.(2023秋•顺城区期末)观察下列两个等式:1−23=2×1×23−1,2−35=2×2×35−1,给出定义如下:我们称使等式a ﹣b =2ab ﹣1成立的一对有理数a ,b 为“同心有理数对”,记为(a ,b ),如:数对(1,23),(2,35)都是“同心有理数对”下列数对是“同心有理数对”的是( )A .(﹣3,47)B .(4,49)C .(﹣5,611) D .(6,713)6.(2023秋•旌阳区期末)定义一种对正整数n 的“F ”运算:①当n 为奇数时,结果为3n +5;②当n 为偶数时,结果为n 2k;(其中k 是使n2k为奇数的正整数),并且运算可以重复进行,例如,取n =26.则:若n =49,则第2021次“F ”运算的结果是( ) A .68B .78C .88D .987.(2023秋•大连月考)我们对任意四个有理数a ,b ,c ,d 定义一种新的运算:|abcd|=ad ﹣bc .则|−4−231|的值为 .8.(2023秋•郧西县月考)我们定义一种新运算,规定:图表示a ﹣b +c ,图形表示﹣x +y ﹣z ,则+的值为 .9.(2023秋•青浦区期中)若定义新的运算符号“*”为a *b =a+1b ,则(13*12)*2= . 10.(2023秋•西城区校级期中)用“△”定义新运算:对于任意有理数a 、b ,当a ≤b 时,都有a △b =a 2b ;当a >b 时,都有a △b =ab 2,那么,2△6= ;(−23)△(−3)= .11.(2023秋•绵阳期中)定义一种新的运算:x ⨂y ={x 2−2y ,x >y1,x =y−2xy ,x <y,例如2⨂1=22﹣2×1=2,2⨂3=﹣2×2×3=﹣12,1⨂1=1.计算:[(﹣3)⨂(﹣1)]+[4⨂(﹣2)]﹣(2021⨂2021)= .12.(2023•越秀区校级开学)定义两种新运算,观察下列式子:(1)x Θy =4x +y ,例如,1Θ3=4×1+3=7;3Θ(﹣1)=4×3+(﹣1)=11; (2)[x ]表示不超过x 的最大整数,例如,[2.2]=2;[﹣3.24]=﹣4; 根据以上规则,计算[1Θ(−12)]+[(−2)Θ194]= .13.(2023秋•西城区校级期中)用“☆”定义一种新运算:对于任意有理数a和b,规定a☆b= a+b+|a−b|2.(1)计算:(﹣6)☆5=.(2)从﹣9,﹣8,﹣7,﹣6,﹣5,﹣4,﹣3,﹣2,﹣1,0,1,2,3,4,5,6,7,8,9中任选两个有理数做a,b(a≠b)的值,并计算a☆b,那么所有运算结果中的最大值是.14.(2023秋•封丘县期末)对于有理数a,b,定义一种新运算“⨂”,规定a⨂b=|a+b|﹣|a ﹣b|.如3⨂5=|3+5|﹣|3﹣5|=8﹣2=6.(1)计算3⨂(﹣5)的值.(2)若(a+2)2+|b﹣1|=0,求a⨂b.15.(2023秋•茂名期中)已知a、b均为有理数,现定义一种新的运算,规定:a⨂b=a2+ab ﹣5,例如1⨂1=12+1×1﹣5.求:(1)(﹣3)⨂6的值;(2)[2⨂(−32)]﹣[(﹣5)⨂9]的值.16.(2023秋•沁阳市期中)同学们刚学完有理数相关运算后,老师又定义了一种新的“※(加乘)”运算,以下算式就是按照“※(加乘)”运算法则进行的运算:(+3)※(+4)=+7;(﹣6)※(﹣3)=+9;(+4)※(﹣3)=﹣7;(﹣1)※(+1)=﹣2;0※(+8)=+8;(﹣9)※0=+9;0※0=0.(1)综合以上情形,有如下有理数“※(加乘)”运算法则:两数进行“※(加乘)”运算,同号,异号,并把绝对值;特别地,一个数与0进行“※(加乘)”运算,都得.(2)计算:(﹣7)※(﹣4)=.(3)若(1﹣a)※(b﹣3)=0.计算:1a×b +1(a+2)×(b+2)+1(a+4)×(b+4)+1(a+6)×(b+6)+1(a+8)×(b+8)的值.17.(2023秋•晋江市期中)给出如下定义:如果两个不相等的有理数a ,b 满足等式a ﹣b =ab .那么称a ,b 是“关联有理数对”,记作(a ,b ).如:因为3−34=124−34=94,3×34=94.所以数对(3,34)是“关联有理数对”.(1)在数对①(1,12)、②(﹣1,0)、③(52,57)中,是“关联有理数对”的是 (只填序号);(2)若(m ,n )是“关联有理数对”,则(﹣m ,﹣n ) “关联有理数对”(填“是”或“不是”);(3)如果两个有理数是一对“关联有理数对”,其中一个有理数是5,求另一个有理数.18.(2022春•邗江区校级期中)阅读材料:如果10b =n ,那么b 为n 的“劳格数”,记为b =d (n ).由定义可知:10b =n 与b =d (n )表示b 、n 两个量之间的同一关系.如:102=100,则d (100)=2. 理解运用:(1)根据“劳格数”的定义,填空:d (10﹣3)= ,d (1)= ;(2)“劳格数”有如下运算性质:若m 、n 为正数,则d (mn )=d (m )+d (n ),d (mn )=d (m )﹣d (n );根据运算性质,填空:d(a 3)d(a)= ;(a 为正数)(3)若d (2)=0.3010,计算:d (4)、d (5);(4)若d (2)=2m +n ,d (4)=3m +2n +p ,d (8)=6m +2n +p ,请证明m =n =p .19.(2022春•衡阳县期末)定义:对于确定位置的三个数:a ,b ,c ,计算a ﹣b ,a−c 2,b−c 3,将这三个数的最小值称为a ,b ,c 的“分差”,例如,对于1,﹣2,3,因为1﹣(﹣2)=3,1−32=−1,−2−33=−53,所以1,﹣2,3的“分差”为−53.(1)﹣2,﹣4,1的“分差”为 ;(2)调整“﹣2,﹣4,1”这三个数的位置,得到不同的“分差”,那么这些不同“分差”中的最大值是 ;(3)调整﹣1,6,x 这三个数的位置,得到不同的“分差”,若其中的一个“分差”为2,求x 的值.20.(2022春•房山区期中)现将偶数个互不相等的有理数分成个数相同的两排,需满足第一排中的数越来越大,第二排中的数越来越小.例如,轩轩将“1,2,3,4”进行如下分组:第一列第二列第一排 1 2第二排4 3然后把每列两个数的差的绝对值进行相加,定义为该分组方式的“M值”.例如,以上分组方式的“M值”为M=|1﹣4|+|2﹣3|=4.(1)另写出“1,2,3,4”的一种分组方式,并计算相应的“M值”;(2)将4个自然数“a,6,7,8”按照题目要求分为两排,使其“M值”为6,则a的值为.(3)已知有理数c,d满足c+d=2,且c<d.将6个有理数“c,d,﹣5,﹣2,2,4”按照题目要求分为两排,使其“M值”为18,求d的值.。
中考数学压轴题之新定义经典题型

中考数学压轴题之新定义经典题型【01】.在平面直角坐标系xOy 中,C 的半径为r ,P 是与圆心C 不重合的点,点P 关于O 的反称点的定义如下:若在射线CP 上存在一点P ¢,满足2CP CP r ¢+=,则称P ¢为点P 关于C 的反称点,下图为点P 及其关于C 的反称点P ¢的示意图。
的示意图。
(1)(1)当当O 的半径为1时。
时。
①分别判断点(2,1)M ,3(,0)2N ,(1(1,,3)T 关于O 的反称点是否存在,若存在?在?求其坐标;求其坐标;②点P 在直线2y x =-+上,若点P 关于O 的反称点P ¢存在,且点P ¢不在x 轴上,求点P 的横坐标的取值范围;的横坐标的取值范围; (2)(2)当当C 的圆心在x 轴上,轴上,半径为半径为1,直线3233y x =-+与x 轴,轴,y y 轴分别交于点A ,B ,若线段AB 上存在点P ,使得点P 关于C 的反称点P ¢在C 的内部,求圆心C 的横坐标的取值范围。
的横坐标的取值范围。
yPOCx1 1【02】.在平面直角坐标系xOy 中,点P 的坐标为()11,x y ,点Q 的坐标为()22,x y ,且12x x ¹,12y y ¹,若,P Q 为某个矩形的两个顶点,为某个矩形的两个顶点,且该矩形的边均与某条坐标轴且该矩形的边均与某条坐标轴垂直,则称该矩形为点P Q ,的“相关矩形”的“相关矩形”..下图为点,P Q 的“相关矩形”的示意图意图. .(1)已知点A 的坐标为()10,,①若点B 的坐标为()31,,求点,A B 的“相关矩形”的面积;的“相关矩形”的面积;②点C 在直线3x =上,若点,A C 的“相关矩形”为正方形,求直线AC 的表达式;式;(2)O ⊙的半径为2,点M 的坐标为(),3m .若在O ⊙上存在一点N ,使得点,M N的“相关矩形”为正方形,求m 的取值范围的取值范围. .【03】对于平面直角坐标系xOy 中的点P 和⊙C ,给出如下定义:若存在过点P 的直线l 交⊙C 于异于点P 的A ,B 两点,在P ,A ,B 三点中,位于中间的点恰为以另外两点为端点的线段的中点时,则称点P 为⊙C 的相邻点,直线l 为⊙C 关于点P 的相邻线的相邻线. . (1)当⊙O 的半径为1时,时, ○1分别判断在点D (,14),E (0,-3),F (4,0)中,是⊙O 的相邻点有____________________;;○2请从○1中的答案中,任选一个相邻点,在图1中做出⊙O 关于它的一条相邻线,并说明你的作图过程相邻线,并说明你的作图过程. .○3点P 在直线3y x =-+上,若点P 为⊙O 的相邻点,求点P 横坐标的取值范围;范围;(2)⊙C 的圆心在x 轴上,半径为1,直线3233y x =-+与x 轴,y 轴分别交于点M ,N ,若线段..MN 上存在⊙C 的相邻点P ,直接写出圆心C 的横坐标的取值范围.范围.21备用图1备用图2 图1【04】定义:y 是一个关于x 的函数,若对于每个实数x ,函数y 的值为三数2+x ,12+x ,205+-x 中的最小值,则函数y 叫做这三数的最小值函数.(1)画出这个最小值函数的图象,并判断点A (1, 3)是否为这个)是否为这个最小值函数图象上的点;图象上的点;(2)设这个最小值函数图象的最高点为B ,点A (1, 3),动点M (m ,m ).①直接写出△ABM 的面积,其面积是的面积,其面积是 ; ②若以M 为圆心的圆经过B A ,两点,写出点M 的坐标;的坐标;③以②中的点M 为圆心,以2为半径作圆为半径作圆. . 在此圆上找一点P ,使22PA PB +的值最小,直接写出此最小值的值最小,直接写出此最小值. .【05】在平面直角坐标系xOy 中,对于点P 和图形W ,如果线段OP 与图形W 无公共点,则称点P 为关于图形W 的“阳光点”;如果线段OP 与图形W 有公共点,则称点P 为关于图形W 的“阴影点”. (1)如图1,已知点()13A ,,()11B ,,连接AB①在()11,4P ,()21,2P ,()32,3P ,()42,1P 这四个点中,关于线段AB 的“阳光点”是;是;②线段11A B AB P ;11A B 上的所有点都是关于线段AB 的“阴影点”,且当线段11A B 向上或向下平移时,都会有11A B 上的点成为关于线段AB 的“阳光点”.若11A B 的长为4,且点1A 在1B 的上方,则点1A 的坐标为的坐标为_________________________________________________________;; (2)如图2,已知点()13C ,,C e 与y 轴相切于点D .若E e 的半径为32,圆心E 在直线343l y x =-+:上,且E e 上的所有点都是关于C e 的“阴影点”,求圆心E 的横坐标的取值范围;的横坐标的取值范围;(3)如图3,M e 的半径是3,点M 到原点的距离为5.点N 是M e 上到原点距离最近的点,点Q 和T 是坐标平面内的两个动点,且M e 上的所有点都是关于NQT D 的“阴影点”,直接写出NQT D 的周长的最小值.的周长的最小值.图1 图2 图3yxB A OyxCOD yx11O【06】给出如下规定:在平面直角坐标系xOy 中,对于点P (x ,y ),以及两个无公共点的图形1W 和2W ,若在图形1W 和2W 上分别存在点M (1x ,1y )和N (2x ,2y ),使得P 是线段MN 的中点,则称点M 和N 被点P “关联”,并称点P 为图形1W 和2W 的一个“中位点”,此时P ,M ,N 三个点的坐标满足122x x x +=,122y yy +=.(1)已知点(0,1),(4,1),(3,1),(3,2)A B C D --,连接AB ,CD .①对于线段AB 和线段CD ,若点A 和C 被点P “关联”,则点P 的坐标为____________________;; ②线段AB 和线段CD 的一个“中位点”是1(2,)2Q -,求这两条线段上被点Q “关联”的两个点的坐标;“关联”的两个点的坐标;(2)如图1,已知点R (-(-2,02,02,0)和抛物线)和抛物线1W :22y x x =-,对于抛物线1W 上的每一个点M ,在抛物线2W 上都存在点N ,使得点N 和M 被点R “关联”,请在图1中画出符合条件的抛物线2W ;(3)正方形EFGH 的顶点分别是(4,1),(4,1),(2,1),(2,1)E F G H ------,⊙T 的圆心为(3,0)T ,半径为1.请在图2中画出由正方形EFGH 和⊙T 的所有“中位点”组成的图形(若涉及平面中某个区域时可以用阴影表示),并直接写出该图形的面积.并直接写出该图形的面积.图1 图2R【06】在平面直角坐标系中,⊙C 的半径为r ,P 是与圆心C 不重合的点,点P 关于⊙C 的限距点的定义如下:若为直线PC 与⊙C 的一个交点,满足,则称为点P 关于⊙C 的限距点,右图为点P 及其关于⊙C 的限距点的示意图.的示意图. (1)当⊙O 的半径为1时.时.①分别判断点M ,N ,T 关于⊙O 的限距点是否存在?若存在,求其坐标;在?若存在,求其坐标;②点D 的坐标为(的坐标为(2,02,02,0)),DE ,DF 分别切⊙O 于点E ,点F ,点P 在△DEF 的边上的边上..若点P 关于⊙O 的限距点存在,求点的横坐标的取值范围;取值范围;(2)保持()保持(11)中D ,E ,F 三点不变,点P 在△DEF 的边上沿E →F →D →E的方向的方向运动,⊙C 的圆心C 的坐标为(1,01,0)),半径为r .请从下面两个问题中任选一个作答一个作答. .温馨提示:答对问题1得2分,答对问题2得1分,两题均答不重复计分.问题1问题2若点P 关于⊙C 的限距点存在,且随点P 的运动所形成的路径长为,则r 的最小值为的最小值为______________________________.. 若点P 关于⊙C 的限距点不存在,则r 的取值范围为的取值范围为________. ________.xOy P ¢2r PP r ¢££P ¢P¢(3,4)5(,0)2(1,2)P ¢P ¢P ¢P ¢r p P¢【07】对于某一函数给出如下定义:若存在实数p ,当其自变量的值为p 时,其函数值等于p ,则称p 为这个函数的不变值. 在函数存在不变值时,该函数的最大不变值与最小不变值之差q 称为这个函数的不变长度.特别地,当函数只有一个不变值时,其不变长度q 为零为零..例如,下图中的函数有0,1两个不变值,其不变长度q 等于1.(1)分别判断函数1y x =-,1y x=,2y x =有没有不变值?如果有,直接写出其不变长度;其不变长度;(2)函数22y x bx =-.①若其不变长度为零,求b 的值;的值;②若13b ££,求其不变长度q 的取值范围;的取值范围;(3)记函数22()y x x x m =-³的图象为1G ,将1G 沿x=m 翻折后得到的函数图象记为2G .函数G 的图象由 1G 和2G 两部分组成,若其不变长度q 满足03q ££,则m 的取值范围为的取值范围为 . .【08】P 是⊙O 内一点,过点P 作⊙O 的任意一条弦AB ,我们把P A PB ×的值称为点P 关于⊙O 的“幂值”.(1)⊙O 的半径为5,OP = 3.①如图1,若点P 恰为弦AB 的中点,则点P 关于⊙O 的“幂值”为________________;; ②判断当弦AB 的位置改变时,点P 关于⊙O 的“幂值”是否为定值,若是定值,证明你的结论;若不是定值,求点P 关于⊙O 的“幂值”的取值范围.的取值范围.(2)若⊙O 的半径为r ,OP = d ,请参考(,请参考(11)的思路,用含r 、d 的式子表示点P 关于⊙O 的“幂值”或“幂值”的取值范围的“幂值”或“幂值”的取值范围________________________;; (3)在平面直角坐标系xOy 中,⊙O 的半径为4,若在直线33y x b =+上存在点P ,使得点P 关于⊙O 的“幂值”为1313,,请写出b 的取值范围的取值范围________________________..图1POBAO备用图备用图【09】在平面直角坐标系xOy 中,中,图形图形W 在坐标轴上的投影长度定义如下:设点),(11y x P ,),(22y x Q 是图形W 上的任意两点.若21x x -的最大值为m ,则图形W 在x 轴上的投影长度m l x =;若21y y -的最大值为n ,则图形W 在y 轴上的投影长度n l y =.如图,图形W 在x 轴上的投影长度213=-=xl ;在y 轴上的投影长度404=-=y l .(1)已知点)3,3(A ,)1,4(B .如图1所示,若图形W 为△OAB ,则=xl ,=y l .(2)已知点)0,4(C ,点D 在直线26y x =-+上,若图形W 为△OCD .当y x l l =时,求点D 的坐标.的坐标.(3)若图形W 为函数2x y =)(b x a ££的图象,其中0a b £<.当该图形.当该图形满足1£=y x l l 时,请直接写出a 的取值范围.的取值范围.x yO BA 1234123x y O 1231234图1【10】.在平面直角坐标系xOy 中,对图形W 给出如下定义:若图形W 上的所有点都在以原点为顶点的角的内部或边界上,在所有满足条件的角中,其度数的最小值称为图形的坐标角度,例如,下图中的矩形ABCD 的坐标角度是9090°.°.°.(1)已知点)3,0(-A ,)1,1(--B ,在点)0,2(C ,)0,1(-D ,)2,2(-E 中,选一点,使得以该点及点A ,B 为顶点的三角形的坐标角度为9090°,则满足条件°,则满足条件的点为的点为 ; (2)将函数2ax y =)31(££a 的图象在直线1=y 下方的部分沿直线1=y 向上翻折,求所得图形坐标角度m 的取值范围;的取值范围;(3)记某个圆的半径为r ,圆心到原点的距离为l ,且)1(3-=r l ,若该圆的,若该圆的坐标角度°££°9060m .直接写出满足条件的r 的取值范围.的取值范围. O xy D C B A –1–2–312312345。
2024年九年级中考数学压轴题-圆中的新定义问题(解析版)
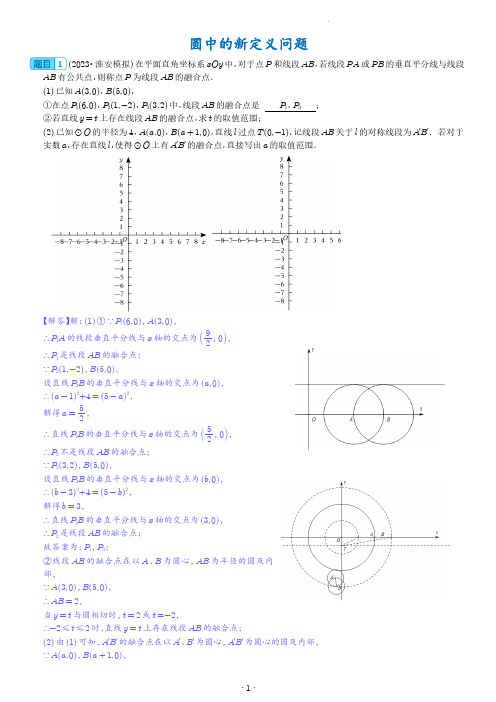
圆中的新定义问题1(2023•淮安模拟)在平面直角坐标系xOy 中,对于点P 和线段AB ,若线段PA 或PB 的垂直平分线与线段AB 有公共点,则称点P 为线段AB 的融合点.(1)已知A (3,0),B (5,0),①在点P 1(6,0),P 2(1,-2),P 3(3,2)中,线段AB 的融合点是 P 1,P 3 ;②若直线y =t 上存在线段AB 的融合点,求t 的取值范围;(2)已知⊙O 的半径为4,A (a ,0),B (a +1,0),直线l 过点T (0,-1),记线段AB 关于l 的对称线段为A B .若对于实数a ,存在直线l ,使得⊙O 上有A B 的融合点,直接写出a 的取值范围.【解答】解:(1)①∵P 1(6,0),A (3,0),∴P 1A 的线段垂直平分线与x 轴的交点为92,0,∴P 1是线段AB 的融合点;∵P 2(1,-2),B (5,0),设直线P 2B 的垂直平分线与x 轴的交点为(a ,0),∴(a -1)2+4=(5-a )2,解得a =52,∴直线P 2B 的垂直平分线与x 轴的交点为52,0,∴P 2不是线段AB 的融合点;∵P 3(3,2),B (5,0),设直线P 3B 的垂直平分线与x 轴的交点为(b ,0),∴(b -3)2+4=(5-b )2,解得b =3,∴直线P 3B 的垂直平分线与x 轴的交点为(3,0),∴P 3是线段AB 的融合点;故答案为:P 1,P 3;②线段AB 的融合点在以A 、B 为圆心,AB 为半径的圆及内部,∵A (3,0),B (5,0),∴AB =2,当y =t 与圆相切时,t =2或t =-2,∴-2≤t ≤2时,直线y =t 上存在线段AB 的融合点;(2)由(1)可知,A B 的融合点在以A 、B 为圆心,A B 为圆心的圆及内部,∵A (a ,0),B (a +1,0),∴AB =A B =1,∵⊙O 上有A B 的融合点,∴圆O 与圆A 、B 有交点,∴圆O 与圆A 、圆B 的公共区域为以O 为圆心2为半径,以O 为圆心6为半径的圆环及内部区域,当a >0时,a 的最大值为62-12=35,最小值为22-12-1=3-1,∴3-1≤a ≤35;当a <0时,a 的最大值为-22-12=-3,最小值为-62-12-1=-35-1,∴-35-1≤a ≤-3;综上所述:a 的取值范围为3-1≤a ≤35或-35-1≤a ≤-3.2(2023•西城区校级模拟)在平面内,C 为线段AB 外的一点,若以点A ,B ,C 为顶点的三角形为直角三角形,则称C 为线段AB 的直角点.特别地,当该三角形为等腰直角三角形时,称C 为线段AB 的等腰直角点.(1)如图1,在平面直角坐标系xOy 中,点M 的坐标为(-1,0),点N 的坐标为(1,0),在点P 1(2,1),P 2(-1,2),P 332,12 中,线段MN 的直角点是 P 2、P 3 ;(2)在平面直角坐标系xOy 中,点A ,B 的坐标分别为(t ,0),(0,4).①若t =4,如图2所示,若C 是线段AB 的直角点,且点C 在直线y =-x +8上,求点C 的坐标;②如图3,点D 的坐标为(m ,-2),⊙D 的半径为1,若⊙D 上存在线段AB 的等腰直角点,求出m 的取值范围.【解答】解:(1)∵P 2(-1,2),M (-1,0),∴P 2M ⊥MN ,∴P 2是线段MN 的直角点;∵M (-1,0),N (1,0),∴MN =2,∵P 332,12,∴P 3O =1,∴P 3在以O 为圆心,MN 为直径的圆上,∴∠MP 3N =90°,∴P 3是线段MN 的直角点;故答案为:P 2、P 3;(2)①∵A (4,0),B (0,4),∴OA =OB =4,∴∠OAB =∠OBA =45°.根据题意,若点C 为线段AB 的直角点,则需要分三种情况:当点B 为直角顶点,过点B 作BC 1⊥AB 于点C 1,过点C 1作C 1M ⊥y 轴于点M ,∴∠C 1BM =45°,∴C 1M =BM ,设C 1M =BM =a ,∴C 1(a ,a +4),∴-a +8=a +4,解得a =2,∴C 1(2,6);当点A 为直角顶点,过点A 作AC 2⊥AB 于点C 2,过点C 2作C 2N ⊥x 轴于点N ,∴∠C 2AN =45°,∴C 2N =AN ,设C 2N =AN =b ,∴C 2(b +4,b ),∴-(b +4)+8=b ,解得b =2,∴C 2(6,2);当点C 为直角顶点,取AB 的中点P ,则P (2,2),设C 3的横坐标为t ,则C 3(t ,-t +8),由直角三角形的性质可知,C 3P =BP =AP =22,∴(t -2)2+(-t +6)2=(22)2,解得t =4,∴C3(4,4),综上,点C的坐标为(2,6)或(6,2)或(4,4).②如图,以AB为边向下作正方形ABC1C2,连接AC1,BC2交于点C3,则C1,C2,C3是线段AB的等腰直角点.根据点A的运动可知,点C1在直线l1:x=-4上运动,C2在直线l2:y=-x-4上运动,C3在直线l3:y=-x上运动.设l2与y=-2相交于点K,l3与y=-2相交于点L,∴K(2,-2),L(2,-2).由此可得出临界情况如图:如图3(1)中,当⊙D与l1相切时,m=-5;如图3(2)中,当⊙D与l2相切时,点F为切点,连接DF,则ΔDFK为等腰直角三角形,且DF=1,∴DK=2;∴D(-2+2,-2),即m=-2+2;如图3(3)中,当⊙D与l3相切时,点G为切点,连接DG,则ΔDGL为等腰直角三角形,且DG=1,∴DL=2;∴D(2-2,-2),即m=2-2;如图3(4)中,当⊙D与l3相切时,点H为切点,连接DH,则ΔDHL为等腰直角三角形,且DH=1,∴DL=2;∴D(2+2,-2),即m=2+2;综上,符合题意的m的取值范围:-5≤m≤-2+2或2-2≤m≤2+2.3(2023•秀洲区校级二模)婆罗摩芨多是公元7世纪古印度伟大的数学家,他在三角形、四边形、零和负数的运算规则,二次方程等方面均有建树,他也研究过对角线互相垂直的圆内接四边形,我们把这类对角线互相垂直的圆内接四边形称为“婆氏四边形”;(1)若平行四边形ABCD是“婆氏四边形”,则四边形ABCD是③.(填序号)①矩形②菱形③正方形(2)如图1,RtΔABC中,∠BAC=90°,以AB为弦的⊙O交AC于D,交BC于E,连接DE、AE、BD,AB=6,sin C=35,若四边形ABED是“婆氏四边形”,求DE的长;(3)如图2,四边形ABCD为⊙O的内接四边形,连接AC,BD,OA,OB,OC,OD,已知∠BOC+∠AOD= 180°,①求证:四边形ABCD是“婆氏四边形”;②当AD+BC=4时,求⊙O半径的最小值.【解答】(1)解:∵平行四边形ABCD为⊙O的内接四边形,∴∠ABC=∠ADC,∠ABC+∠ADC=180°,∴∠ABC=∠ADC=90°,∴平行四边形ABCD是矩形,∵四边形ABCD是“婆氏四边形”,∴AC⊥BD,∴矩形ABCD是正方形,故答案为:③;(2)解:∵∠BAC=90°,AB=6,sin C=35,∴BC=10,AC=8,∴BD为直径,∴∠BED =∠DEC =90°,∵四边形ABED 是“婆氏四边形”,∴AE ⊥BD ,∴AD =DE ,AB =BE =6,设AD =DE =m ,则CD =8-m ,EC =4,在Rt ΔEDC 中,m 2+42=(8-m )2,解得m =3,∴DE =3;(3)①证明:如图2,设AC ,BD 相交于点E ,∵∠DCA =12∠AOD ,∠BDC =12∠BOC ,∠BOC +∠AOD =180°,∴∠DCA +∠BDC =12(∠AOD +∠BOC )=12×180°=90°,∴∠CED =90°,∴AC ⊥BD ,∵四边形ABCD 是⊙O 的内接四边形,∴四边形ABCD 是“婆氏四边形”;②解:过点O 作OM ⊥AD 交于M ,过O 作ON ⊥BC 交于N ,∴AM =12AD ,BN =12BC ,∠AMO =∠BNO =90°,∴∠AOM +∠OAM =90°,∵OA =BO =CO =DO ,∴∠AOM =12∠AOD ,∠BON =12∠BOC ,∵∠BOC +∠AOD =180°,∴∠AOM =∠OBN ,∴ΔOAM ≅ΔBON (AAS ),∴ON =AM =12AD ,∵AD +BC =4,设ON =AM =n ,则AD =2n ,BC =4-2n ,BN =2-n ,在Rt ΔBON 中,BO =n 2+(2-n )2=2(n -1)2+2,当n =1时,BO 有最小值2,∴⊙O 半径的最小值为2.4(2022秋•西城区期末)给定图形W 和点P ,Q ,若图形W 上存在两个不重合的点M ,N ,使得点P 关于点M 的对称点与点Q 关于点N 的对称点重合,则称点P 与点Q 关于图形W 双对合.在平面直角坐标系xOy 中,已知点A (-1,-2),B (5,-2),C (-1,4).(1)在点D (-4,0),E (2,2),F (6,0)中,与点O 关于线段AB 双对合的点是 D ,F ;(2)点K 是x 轴上一动点,⊙K 的直径为1,①若点A 与点T (0,t )关于⊙K 双对合,求t 的取值范围;②当点K 运动时,若ΔABC 上存在一点与⊙K 上任意一点关于⊙K 双对合,直接写出点K 的横坐标k 的取值范围.【解答】解:(1)当A 点是D 点的中点时,对应点为(2,-4);当B 点是D 点的中点时,对应点为(14,-4);当A 点是E 点的中点时,对应点为(-4,-6);当B 点是E 点的中点时,对应点为(8,-6);当A 点是F 点的中点时,对应点为(-8,-4);当B 点是F 点的中点时,对应点为(4,-4);当A 点是O 点的中点时,对应点为(-2,-4);当B 点是O 点的中点时,对应点为(10,-4);∴D 、F 与点O 关于线段AB 双对合,故答案为:D 、F ;(2)①设K(k,0),∵A(-1,-2),T(0,t),∴A点关于K点对称点G为(2k+1,2),T点关于K点对称点H为(2k,-t),∵点A与点T(0,t)关于⊙K双对合,∴A点关于点K的对称点在以G为圆心,∵⊙K的直径为1,∴点A关于点K的对称点在以G点为圆心,1为半径的圆上,点T关于点K的对称点在以H为圆心,1为半径的圆上,如图所示,∵点A与点T(0,t)关于⊙K双对合,∴当圆G与圆H有交点,∵GH=1+(t+2)2,∴1+(t+2)2≤2,解得-2-3≤t≤-2+3;②∵A(-1,-2),B(5,-2),C(-1,4),K(k,0),∴A点关于K点的对称点F(2k+1,2),B点关于K点的对称点E(2k-5,2),C点关于K点的对称点G(2k+1, -4),∴ΔABC上任意一点关于K点对称点在阴影区域,∵ΔABC上存在一点与⊙K上任意一点关于⊙K双对合,∴阴影区域与圆K有公共交点,∵阴影部分是由ΔEGF边上任意一点为圆心,1为半径的圆构成的区域,如图1时,k-(2k+1)=12+1,解得k=-52;如图2时,2k+1-k=12+1,解得k=12;∴-52≤k≤12时,ΔABC上存在一点与⊙K上任意一点关于⊙K双对合;过点K作KN⊥EG交于N,直线EG交x轴于点M,设直线EG的解析式为y=k x+b,∴(2k-5)k +b=2 (2k+1)k +b=-4 ,解得k =-1b=2k-3 ,∴y=-x+2k-3,∴M(2k-3,0),∵直线y=-x与y=-x+2k-3平行,∴∠KMN=45°,∴KM=2KN=322,如图3时,k-(2k-3)=322,解得k=3-322,如图4时,2k-3-k=322,解得k=3+322,∴3-322≤k≤3+322时,ΔABC上存在一点与⊙K上任意一点关于⊙K双对合;综上所述:-52≤k≤12或3-322≤k≤3+322时,ΔABC上存在一点与⊙K上任意一点关于⊙K双对合.5(2022•钟楼区模拟)概念认识:平面内,M为图形T上任意一点,N为⊙O上任意一点,将M、N两点间距离的最小值称为图形T到⊙O的“最近距离”,记作d(T-⊙O).例:如图1,在直线l上有A、C、O三点,以AC为对角线作正方形ABCD,以点O为圆心作圆,与l交于E、F两点,若将正方形ABCD记为图形T,则C、E两点间的距离称为图形T到⊙的“最近距离”.数学理解:(1)在平面内有A、B两点,以点A为圆心,5为半径作⊙A,将点B记为图形T,若d(T-⊙A)=2,则AB= 3或7.(2)如图2,在平面直角坐标系中,以O(0,0)为圆心,半径为2作圆.①将点C(4,3)记为图形T,则d(T-⊙O)=.②将一次函数y=kx+22的图记为图形T,若d(T-⊙)>0,求k的取值范围.推广运用:(3)在平面直角坐标系中,P的坐标为(t,0),⊙P的半径为2,D、E两点的坐标分别为(5,5)、(5,-5),将ΔDOE记为图形T,若d(T-⊙P)=1,则t=.【解答】解:(1)如图1中,∵d(T-⊙A)=2,∴CB=CB′=2,∵AC=5,∴AB′=5-2=3,AB=5+2=7.故答案为:3或7.(2)①如图2中,连接OC交⊙O于E.∵C(4,3),∴OC=42+32=5,∵OE=2,∴EC=3,∴d(T-⊙O)=3.故答案为:3.②如图,设直线y=kx+22与⊙O相切于E,K.连接OK,OE.∵OE⊥DE,OK⊥DK,OD=22,OE=OK=2,∴DK=OD2?OK2=(22)2-22=2,DE=OD2?OE2=(22)2-22=2,∴DE=OE=DK=OK,∴四边形DEOK是菱形,∵∠DKO=∠DEO=90°,∴四边形DEOK是正方形,∴∠ODE=∠ODK=45°,∴直线DE的解析式为y=-x+22,直线DK的解析式为y=x+22,∵d(T-⊙O)>0,∴观察图象可知满足条件的k的值为-1<k<1且k≠0.(3)如图3-1中,当点P在DE的右边时.∵D(5,5),∴∠DOP=45°,∵d(T-⊙P)=1,∴OP=5+1+2=8∴t=8.如图3-2中,当点P在∠DOE的外侧时,由题意可知OM=1,OP=1+2=3,t=-3.综上所述,满足条件的t的值为8或-3.6(2022秋•昌平区期末)已知:对于平面直角坐标系xOy中的点P和⊙O,⊙O的半径为4,交x轴于点A,B,对于点P给出如下定义:过点C的直线与⊙O交于点M,N,点P为线段MN的中点,我们把这样的点P叫做关于MN的“折弦点”.(1)若C(-2,0).①点P1(0,0),P2(-1,1),P3(2,2)中是关于MN的“折弦点”的是 P1,P2 ;②若直线y=kx+3(k≠0).上只存在一个关于MN的“折弦点”,求k的值;(2)点C在线段AB上,直线y=x+b上存在关于MN的“折弦点”,直接写出b的取值范围.【解答】解:(1)①连接OP,∵P点是弦MN的中点,∴OP⊥MN,∴∠CPO=90°,∴P点在以CO为直径的圆上,∵C(-2,0),∴P点在以(-1,0)为圆心,1为半径的圆上,∵点P1(0,0),P2(-1,1)在该圆上,∴点P1(0,0),P2(-1,1)是关于MN的“折弦点”,故答案为:P1,P2;②由①可知,P点在以(-1,0)为圆心,1为半径的圆上,设圆心D(-1,0),∵直线y=kx+3(k≠0)上只存在一个关于MN的“折弦点”,∴直线y=kx+3(k≠0)与圆D相切,过点D作DF垂直直线y=kx+3交于点F,∵直线y=kx+3与x轴交于点E-3k,0,与y轴交于点G(0,3),∴DE=-1+3k,OF=3k,OG=3,∵∠DFE=∠EOG=90°,∴ΔEGO∽ΔEFD,∴DF GO =ED EG,∴13=3k-13+3k2,解得k=3 3;(2)由(1)可知,P点在以OC为直径的圆上,∵直线y=x+b上存在关于MN的“折弦点”,∴直线y=x+b与圆D相交或相切,过D点作DF垂直直线y=x+b交于点F,∵直线y=x+b与x轴交于点(-b,0),与y轴交于点(0,b),当C点与A点重合时,b有最大值,此时D(-2,0),∴(-2+b)2=8,解得b=22+2或b=22+2(舍);当C点与B点重合时,b有最小值,此时D(2,0),∴(-b-2)2=8,解得b=22-2(舍)或b=-22-2;∴-22-2≤b≤22+2时,直线y=x+b上存在关于MN的“折弦点”.7(2022秋•东城区校级月考)如图,在平面直角坐标系xOy中,过⊙T外一点P引它的两条切线,切点分别为M,N,若60°<∠MPN<180°,则称P为⊙T的环绕点.(1)当⊙O半径为1时,①在P1(2,2),P2(2,0),P3(2,1)中,⊙O的环绕点是 P1 ;②直线y=3x+b与x轴交于点A,y轴交于点B,若线段AB上存在⊙O的环绕点,求b的取值范围;(2)⊙T的半径为2,圆心为(0,t),以-m,33m(m>0)为圆心,33m为半径的所有圆构成图形H,若在图形H上存在⊙T的环绕点,直接写出t的取值范围.【解答】解:(1)①如图,PM,PN是⊙T的两条切线,M,N为切点,连接TM,TN,当∠MPN=60°时,∵PT平分∠MPN,∴∠TPN=∠MPT=30°,∵TM⊥PM,TN⊥PN,∴∠TNP=∠PMT=90°,∴TP =2TM =2,以T 为圆心,TP 为半径作⊙T .观察图象可知:当60°<∠MPN <180°时,⊙T 的环绕点在图中的圆环内部(包括大圆上的点不包括小圆上的点),故答案为:P 1;②如图中,设小圆交y 轴的正半轴于F ,当直线y =3x +b 经过点F 时,b =1,当直线y =3x +b 与大圆相切于K (在第二象限)时,连接OK ,由题意B (0,b ),A -b 3,0,所以OB =b ,OA =b 3,AB =103b ,∵OK =2,12×AB ×OK =12×OA ×OB ,∴b =210,观察图象可知,当1<b <210时,线段AB 上存在⊙的环绕点,根据对称怀可知:当-210<b <-1时,线段AB 上存在⊙的环绕点,综上所述,满足条件的b 的值为1<b <210或-210<b <-1;(2)如图中,不妨设E -m ,33m (m >0),则点E 直线y =-33x 上,∵m >0,∴点E 在射线OE 上运动,作EM ⊥x 轴;∵E -m ,33m (m >0),∴OM =m ,EM =33m ,以E -m ,33m (m >0)为圆心,33m 为半径的⊙E 与x 轴相切,作⊙E 的切线ON ,观察图象可知:以E -m ,33m (m >0)为圆心,33m 为半径的所有圆构成图形H ,图形H 即为∠MON 的内部,包括射线OM ,ON 上,当⊙T 的圆心在y 轴的正半轴上时,假设以T 为圆心,4为半径的圆与射线ON 相切于D ,连接TD ,∵tan ∠EOM =EM OM=33,∴∠EOM =30°,∵OM ,ON 是⊙E 的切线,∴∠EON =∠EOM =30°.∴∠TOD =30°,∴OT =2DT =8,∴T (0,8),当⊙T 的圆心在y 轴的负半轴上时,且经过点O (0.0)时,T (0,-4),观察图象可知,当-4<t <8时,在图象上存在⊙T 的环绕点.8(2022秋•海淀区校级月考)对于平面直角坐标系中的线段AB 和点P (点P 不在线段AB 上),给出如下定义:当PA =PB 时,过点A (或点B )向直线PB (或PA )作垂线段,则称此垂线段为点P 关于线段AB 的“测度线段”,垂足称为点P 关于线段AB 的“测度点”.如图所示,线段AD 和BC 为点P 关于线段AB 的“测度线段”,点C 与点D为点P关于线段AB的“测度点”.(1)如图,点M(0,4)、N(2,0),①点P的坐标为(5,4),直接写出点P关于线段MN的“测度线段”的长度4;②点H为平面直角坐标系中的一点,且HM=HN,则下列四个点:Q1(0,0),Q2(3,3),Q3(1,0),Q4(0,4)中,是点H 关于线段MN的“测度点”的是;(2)直线y=-34x+6与x轴、y轴分别交于点A与点B,①点G为平面直角坐标系中一点,且GA=GB,若一次函数y=kx-14k+3上存在点G关于线段AB的“测度点”,直接写出k的取值范围为;②⊙O的半径为r,点C与点D均在⊙O上,且线段CD=65r.点K与点O位于线段CD的异侧,且KC=KD,若在线段AB上存在点K关于线段CD的“测度点”,直接写出r的取值范围为.【解答】解:(1)①∵M(0,4)、P(5,4),∴MP⎳x轴,∴点P关于线段MN的“测度线段”的长度为4,故答案为:4;②∵过点N作NF⊥MH交于F点,过点M作MG⊥NH交于点G,∵∠MFN=∠MGN=90°,∴F、G点在以MN为直径的圆上,设MN的中点为E,∵点M(0,4)、N(2,0),∴E(1,2),MN=25,∴点H关于线段MN的“测度点”在以E为圆心,5为半径的圆上,且不与M、N重合,∵Q1(0,0),Q2(3,3),Q3(1,0),Q4(0,4)中,Q1E=5,Q2E=5,Q3E=2,Q4E=5,∴Q1,Q2是点H关于线段MN的“测度点”,故答案为:Q1,Q2;(2)①当x=0时,y=6,∴B(0,6),当y=0时,x=8,∴A(8,0),∴AB的中点F(4,3),AB=10,由(1)可知,点G关于线段AB的“测度点”在以F为圆心,5为半径的圆上,且不与A、B点重合,∵一次函数y=kx-14k+3上存在点G关于线段AB的“测度点”,∴直线y=kx-14k+3与圆F相切或相交,过点F作FK垂直直线y=kx-14k+3交于点K,直线与y轴的交点为T,过点F作FL⎳KT交于交y轴于点L,过点L作SL⊥KT交于点S,∴LS =FK =5,∴LF 的直线解析式为y =kx -4k +3,∴L (0,-4k +3),T (0,-14k +3),∴TL =-10k ,∵sin ∠LTS =5-10k =11+k 2,∴k =±33,∴-33≤k ≤33时,一次函数y =kx -14k +3上存在点G 关于线段AB 的“测度点”,故答案为:-33≤k ≤33;②由(1)可知,K 点关于线段CD 的“测度点”在以CD 为直角的半圆上,且不与C 、D 重合,当CD ⎳AB ,且AB 与圆P 相切时,r 有最小值,由①可得,45=35r 6-r ,解得r =247,当CD 在AB 上时,r 有最大值,r =6,∴247≤r <6时,线段AB 上存在点K 关于线段CD 的“测度点”,故答案为:247≤r <6.9(2022•盐城一模)对于平面内的两点K 、L ,作出如下定义:若点Q 是点L 绕点K 旋转所得到的点,则称点Q 是点L 关于点K 的旋转点;若旋转角小于90°,则称点Q 是点L 关于点K 的锐角旋转点.如图1,点Q 是点L 关于点K 的锐角旋转点.(1)已知点A (4,0),在点Q 1(0,4),Q 2(2,23),Q 3(-2,23),Q 4(22,-22)中,是点A 关于点O 的锐角旋转点的是 Q 2,Q 4 .(2)已知点B (5,0),点C 在直线y =2x +b 上,若点C 是点B 关于点O 的锐角旋转点,求实数b 的取值范围.(3)点D 是x 轴上的动点,D (t ,0),E (t -3,0),点F (m ,n )是以D 为圆心,3为半径的圆上一个动点,且满足n ≥0.若直线y =2x +6上存在点F 关于点E 的锐角旋转点,请直接写出t 的取值范围.【解答】解:(1)如图,∵A (4,0),Q 1(0,4),∴OA =OQ 1=4,∠AOQ 1=90°,∴点Q 1不是点A 关于点O 的锐角旋转点;∵Q 2(2,23),作Q 2F ⊥x 轴于点F ,∴OQ 2=OF 2+Q 2F 2=22+(23)2=4=OA ,∵tan ∠Q 2OF =232=3,∴∠Q 2OF =60°,∴点Q 2是点A 关于点O 的锐角旋转点;∵Q 3(-2,23),作Q 3G ⊥x 轴于点G ,则tan ∠Q 3OG =Q 3G OG=232=3,∴∠Q3OG =60°,∴OQ 3=OG cos ∠Q 3OG =2cos60°=4=OA ,∵∠AOQ 3=180°-60°=120°,∴Q 3不是点A 关于点O 的锐角旋转点;∵Q 4(22,-22),作Q 4H ⊥x 轴于点H ,则tan ∠Q 4OH =Q 4H OH =2222=1,∴∠Q 4OH =45°,∵OQ 4=OH cos ∠Q 4OH =22cos45°=4=OA ,∴Q 4是点A 关于点O 的锐角旋转点;综上所述,在点Q 1,Q 2,Q 3,Q 4中,是点A 关于点O 的锐角旋转点的是Q 2,Q 4,故答案为:Q 2,Q 4.(2)在y 轴上取点P (0,5),当直线y =2x +b 经过点P 时,可得b =5,当直线y =2x +b 经过点B 时,则2×5+b =0,解得:b =-10,∴当-10<b <5时,OB 绕点O 逆时针旋转锐角时,点C 一定可以落在某条直线y =2x +b 上,过点O 作OG ⊥直线y =2x +b ,垂足G 在第四象限时,如图,则OT =-b ,OS =-12b ,∴ST =OS 2+OT 2=-12b 2+(-b )2=-52b ,当OG =5时,b 取得最小值,∵5×-52b =-b ×-12b ,∴b =-55,∴-55≤b <5.(3)根据题意,点F 关于点E 的锐角旋转点在半圆E 上,设点P 在半圆S 上,点Q 在半圆T 上(将半圆D 绕点E 旋转),如图3(1),半圆扫过的区域为图3(1)中阴影部分,如图3(2)中,阴影部分与直线y =2x +6相切于点G ,tan ∠EMG =2,SG =3,过点G 作GI ⊥x 轴于点I ,过点S 作SJ ⊥GI 于点J ,∴∠SGJ =∠EMG ,∴tan ∠SGJ =tan ∠EMG =2,∴GJ =355,SJ =655,∴GI =GJ +JI =3+355,∴MI =12GI =32+3510,∴OE =IE +MI -OM =352-32,即x E =t -3=352-32,解得t =352+32,如图3(3)中,阴影部分与HK 相切于点G ,tan ∠OMK =tan ∠EMH =2,EH =6,则MH =3,EM =35,∴x E =t -3=-3-35,解得t =-35,观察图象可知,-35≤t <3+352+32.10(2022秋•姜堰区期中)如图1,在平面内,过⊙T 外一点P 画它的两条切线,切点分别为M 、N ,若∠MPN ≥90°,则称点P 为⊙T 的“限角点”.(1)在平面直角坐标系xOy 中,当⊙O 半径为1时,在①P 1(1,0),②P 2-1,12,③P 3(-1,-1),④P 4(2,-1)中,⊙O 的“限角点”是②④;(填写序号)(2)如图2,⊙A 的半径为2,圆心为(0,2),直线l :y =-34x +b 交坐标轴于点B 、C ,若直线l 上有且只有一个⊙A 的“限角点”,求b 的值.(3)如图3,E (2,3)、F (1,2)、G (3,2),⊙D 的半径为2,圆心D 从原点O 出发,以2个单位/s 的速度沿直线l :y =x 向上运动,若ΔEFG 三边上存在⊙D 的“限角点”,请直接写出运动的时间t (s )的取值范围.【解答】解:(1)∵⊙O 半径为1,∴当P 为圆O 的“限角点”时,1<OP ≤2,∵OP 1=1,OP 2=52,OP 3=2,OP 4=5,∴⊙O 的“限角点”是P 2,P 3,故答案为:②③;(2)∵⊙A 的半径为2,∴当P 为圆A 的“限角点”时,2<AP ≤2,设直线l 上有且只有一个⊙O 的“限角点”P m ,-34m +b ,∴PA =2,此时AP ⊥BC ,令x =0,则y =b ,∴C (0,b ),令y =0,则x =43b ,∴B 43b ,0 ,∴tan ∠OCB =OB OC =43=AP CP ,∴CP =32,∴AC =52,∴|b -2|=52,∴b =92或b =-12;(3)∵圆心D 从原点O 出发,以2个单位/s 的速度沿直线l 移动,∴圆沿x 轴正方向移动t 个单位,沿y 轴正方向移动t 个单位,∴移动后D 点坐标为(t ,t ),设ΔEFG 边上的点P 是圆D 的“限角点”,则2<PD ≤2,在圆D 移动的过程中,当DF =2时,(t -1)2+(t -2)2=4,解得t =3-72或t =3+72,当t =3-72时,ΔEFG 边上开始出现⊙D 的“限角点”,当圆D 移动到E 点在圆上时,DE =2,(t -2)2+(t -3)2=2,解得t =5+32或t =5-32,∴3-72≤t <5-32时,ΔEFG 边上存在⊙D 的“限角点”,当圆D 再次移动到点F 在圆上时,DF =2,(t -2)2+(t -1)2=2,解得t =3+32或t 3-32,当t =3+32时,ΔEFG 三边上开始又要出现⊙D 的“限角点”;设直线EG 的解析式为y =kx +b ,直线y =x 与直线EG 的交点设为点H ,∴2k +b =33k +b=2 ,解得k =-1b =5 ,解得y =-x +5,联立方程组y =-x +5y =x,解得x =52y =52,∴H 52,52,当DH =2时,2t -52 2=4,解得t =2+52或t =-2+52,∴当t =2+52,ΔEFG 边上存在⊙D 的“限角点”,∴3+32<t ≤2+52时,ΔEFG 边上存在⊙D 的“限角点”;综上所述:3-72≤t <5-32或3+32<t ≤2+52时,ΔEFG 边上存在⊙D 的“限角点”.11(2022秋•西城区校级期中)在平面直角坐标系xOy中,已知点M(a,b),N.对于点P给出如下定义:将点P绕点M逆时针旋转90°,得到点P ,点P 关于点N的对称点为Q,称点Q为点P的“对应点”.(1)如图1,若点M在坐标原点,点N(1,1),①点P(-2,0)的“对应点”Q的坐标为 (2,0) ;②若点P的“对应点”Q的坐标为(-1,3),则点P的坐标为;(2)如图2,已知⊙O的半径为1,M是⊙O上一点,点N(0,2),若P(m,0)(m>1)为⊙O外一点,点Q为点P的“对应点”,连接PQ.①当点M(a,b)在第一象限时,求点Q的坐标(用含a,b,m的式子表示);②当点M在⊙O 上运动时,直接写出PQ长的最大值与最小值的积为.(用含m的式子表示)【解答】解:(1)①∵P(-2,0),∴P点绕点M逆时针旋转90°得到点P (0,-2),∵点P 关于点N的对称点为Q,∴Q(2,0);故答案为:(2,0);②∵Q的坐标为(-1,3),∴Q点关于N(1,1)的对称点为P (3,-1),将P 绕M点顺时针旋转90°得到点P,过P 作P F⊥x轴于点F,过点P作PE⊥x轴于点E,∵∠P OP=90°,∴∠POE+∠FOP =90°,∵∠EPO+∠EOP=90°,∴∠FOP =∠EPO,∵OP=OP ,∴ΔPOE≅△OP F(AAS),∴EO=P F=1,PE=OF=3,∴P(-1.-3),故答案为:(-1,-3);(2)①过点M作EF⊥x轴于点F,过点P 作P E⊥EF交于点E,由(1)可得ΔMPF≅△P ME(AAS),∴MF=EP ,FP=ME,∵M(a,b),P(m,0),∴EF=b+m-a,EP =b,∴P (a+b,b+m-a),∵点N(0,2),∴Q(-a-b,4-b-m+a);②P点绕O点逆时针旋转90°后得到点G,∴G(0,m),∵P (a+b,b+m-a),∴GP =2(a 2+b 2),∵M (a ,b )在圆O 上,∴a 2+b 2=1,∴GP =2,∴P 在以G 为圆心,2为半径的圆上,设G 点关于N 点的对称点为H ,则H (0,4-m ),∴QH =2(a 2+b 2)=2,∴Q 点在以H 为圆心2为半径的圆上,∴PQ 的最大值为PH +2,PQ 的最小值为PH -2,∴PQ 长的最大值与最小值的积为(PH +2)(PH -2)=2m 2-8m +14,故答案为:2m 2-8m +14.12(2022•秦淮区二模)【概念认识】与矩形一边相切(切点不是顶点)且经过矩形的两个顶点的圆叫做矩形的第Ⅰ类圆;与矩形两边相切(切点都不是顶点)且经过矩形的一个顶点的圆叫做矩形的第Ⅱ类圆.【初步理解】(1)如图①~③,四边形ABCD 是矩形,⊙O 1和⊙O 2都与边AD 相切,⊙O 2与边AB 相切,⊙O 1和⊙O 3都经过点B ,⊙O 3经过点D ,3个圆都经过点C .在这3个圆中,是矩形ABCD 的第Ⅰ类圆的是①,是矩形ABCD 的第Ⅱ类圆的是.【计算求解】(2)已知一个矩形的相邻两边的长分别为4和6,直接写出它的第Ⅰ类圆和第Ⅱ类圆的半径长.【深入研究】(3)如图④,已知矩形ABCD ,用直尺和圆规作图.(保留作图痕迹,并写出必要的文字说明)①作它的1个第Ⅰ类圆;②作它的1个第Ⅱ类圆.【解答】解:(1)由定义可得,①的矩形有一条边AD 与⊙O 1相切,点B 、C 在圆上,∴①是第Ⅰ类圆;②的矩形有两条边AD 、AB 与⊙O 2相切,点C 在圆上,∴②是第Ⅱ类圆;故答案为:①,②;(2)如图1,设AD =6,AB =4,切点为E ,过点O 作EF ⊥BC 交BC 于F ,交AD 于E ,连接BO ,设BO =r ,则OE =r ,OF =4-r ,由垂径定理可得,BF =CF =3,在Rt ΔBOF 中,r 2=(4-r )2+32,解得r =258;如图2,设AD =4,BC =6,切点为E ,过点O 作EF ⊥BC 交BC 于F ,交AD 于E ,连接BO ,设BO =r ,则OE =r ,OF =6-r ,由垂径定理可得,BF =CF =2,在Rt ΔBOF 中,r 2=(6-r )2+22,解得r =103;综上所述:第Ⅰ类圆的半径是258或103;如图3,AD =6,AB =4,过点O 作MN ⊥AD 交于点M ,交BC 于点N ,连接OC ,设AB 边与⊙O 的切点为G ,连接OG ,∴GO ⊥AB ,设OM =r ,则OC =r ,则ON =4-r ,∵OG =r ,∴BN =r ,∴NC =6-r ,在Rt ΔOCN 中,r 2=(4-r )2+(6-r )2,解得r =10-43,∴第Ⅱ类圆的半径是10-43;(3)①如图4,第一步,作线段AD 的垂直平分线交AD 于点E ,第二步,连接EC ,第三步,作EC 的垂直平分线交EF 于点O ,第四步,以O 为圆心,EO 为半径作圆,∴⊙O 即为所求第Ⅰ类圆;②如图5,第一步:作∠BAD 的平分线;第二步:在角平分线上任取点E ,过点E 作EF ⊥AD ,垂足为点F ;第三步:以点E 为圆心,EF 为半径作圆E ,交AC 于点G ,连接FG ;第四步:过点C 作CH ⎳FG ,CH 交AD 于点H ;第五步:过点H 作AD 的垂线,交∠BAD 的平分线于点O ;第六步:以点O 为圆心,OH 为半径的圆,⊙O 即为所求第Ⅱ类圆.13(2021秋•海淀区校级期末)新定义:在平面直角坐标系xOy 中,若几何图形G 与⊙A 有公共点,则称几何图形G 的叫⊙A 的关联图形,特别地,若⊙A 的关联图形G 为直线,则称该直线为⊙A 的关联直线.如图,∠M 为⊙A 的关联图形,直线l 为⊙A 的关联直线.(1)已知⊙O 是以原点为圆心,2为半径的圆,下列图形:①直线y =2x +2;②直线y =-x +3;③双曲线y =2x,是⊙O 的关联图形的是①③(请直接写出正确的序号).(2)如图1,⊙T 的圆心为T (1,0),半径为1,直线l :y =-x +b 与x 轴交于点N ,若直线l 是⊙T 的关联直线,求点N 的横坐标的取值范围.(3)如图2,已知点B (0,2),C (2,0),D (0,-2),⊙I 经过点C ,⊙I 的关联直线HB 经过点B ,与⊙I 的一个交点为P ;⊙I 的关联直线HD 经过点D ,与⊙I 的一个交点为Q ;直线HB ,HD 交于点H ,若线段PQ 在直线x =6上且恰为⊙I 的直径,请直接写出点H 横坐标h 的取值范围.【解答】解:(1)由题意①③是⊙O的关联图形,故答案为①③.(2)如图1中,∵直线l1y=-x+b是⊙T的关联直线,∴直线l的临界状态是和⊙T相切的两条直线l1和l2,当临界状态为l1时,连接TM(M为切点),∴TM=1,TM⊥MB,且∠MNO=45°,∴ΔTMN是等腰直角三角形,∴TN=2,OT=1,∴N(1+2,0),把N(1+2,0)代入y=-x+b中,得到b=1+2,同法可得当直线l2是临界状态时,b=-2+1,∴点N的横坐标的取值范围为-2+1≤N x≤2+1.(3)如图3-1中,当点Q在点P是上方时,连接BQ,PD交于点H,当圆心I在x轴上时,点H与点C重合,此时H(2,0),得到h的最大值为2,如图3-2中,当点P在点Q是上方时,直线PB,QD交于点H,当圆心I在x轴上时,点H(-6,0)得到h的最小值为-6,综上所述,-6≤h<0,0<h≤2.14(2022春•海淀区校级月考)定义:P、Q分别是两条线段a和b上任意一点,线段PQ长度的最小值叫做线段a与线段b的“冰雪距离”.已知O(0,0),A(1,1),B(m,n),C(m,n+2)是平面直角坐标系中四点.(1)根据上述定义,完成下面的问题:①当m=2,n=1时,如图1,线段BC与线段OA的“冰雪距离”是1.②当m=2时,线段BC与线段OA的“冰雪距离”是1,则n的取值范围是.(2)如图2,若点B落在圆心为A,半径为1的圆上,当n≥1时,线段BC与线段OA的“冰雪距离”记为d,结合图象,求d的最小值;(3)当m的值变化时,动线段BC与线段OA的“冰雪距离”始终为1,线段BC的中点为M.求点M随线段BC运动所走过的路径长.【解答】解:(1)①当m=2,n=1时,B(2,1),C(2,3).线段BC与线段OA的冰雪距离为AB=1.故答案为:1.②当m=2时,点A到直线BC的距离为1.若线段BC与线段OA的冰雪距离是1,则点A到BC的垂线的垂足在线段BC上,∴n≤1≤n+2,即-1≤n≤1.故答案为:-1≤n ≤1.(2)如图,B 2(0,1)为圆A 与y 轴的切点,B 11-22,1+22满足∠B 1AO =90°.当B 在B 1右侧时,冰雪距离d ≥B 1A =22.当B 在弧B 1B 2上时,冰雪距离d 为点B 到OA 的距离,结合图象可知,当且仅当B 处在点B 2时,d 取最小值22.(3)如图,当点B 位于图中弧DI 、线段IH 、弧HG 时,线段BC 与线段OA 的“冰雪距离”始终为1.当点C 位于图中弧DE 、线段EF 、弧FG 时,线段BC 与线段OA 的“冰雪距离”始终为1.当线段BC 由图中B 1D 向上平移到DC 3时,或由B 2G 向上平移到GC 4时,线段BC 与线段OA 的“冰雪距离”始终为1.对应中点M 所走过的路线长为:2π+4+22.15(2022•东城区校级开学)对于⊙C 和⊙C 上的一点A ,若平面内的点P 满足:射线AP 与⊙C 交于点Q (点Q 可以与点P 重合),且1≤PAQA ≤2,则点P 称为点A 关于⊙C 的“生长点”.已知点O 为坐标原点,⊙O 的半径为1,点A (-1,0).(1)若点P 是点A 关于⊙O 的“生长点”,且点P 在x 轴上,请写出一个符合条件的点P 的坐标 (2,0)(答案不唯一);(2)若点B 是点A 关于⊙O 的“生长点”,且满足∠BAO =30°,求点B 的纵坐标t 的取值范围;(3)直线y =3x +b 与x 轴交于点M ,且与y 轴交于点N ,若线段MN 上存在点A 关于⊙O 的“生长点”,直接写出b 的取值范围是.【解答】解:(1)根据“生长点”定义,点P 的坐标可以是(2,0),故答案为:(2,0)(答案不唯一);(2)如图,在x 轴上方作射线AM ,与⊙O 交于M ,使得∠OAM =30°,并在射线AM 上取点N ,使AM =MN ,并由对称性,将MN 关于x 轴对称,得M N ,则由题意,线段MN 和M N 上的点是满足条件的点B .作MH ⊥x 轴于H ,连接MC ,∴∠MHA =90°,即∠OAM +∠AMH =90°.∵AC 是⊙O 的直径,∴∠AMC =90°,即∠AMH +∠HMC =90°.∴∠OAM =∠HMC =30°.∴tan30°=MH AH=HC MH =33,设MH=y,则AH=3y,CH=33y,∴AC=AH+CH=433y=2,解得y=32,即点M的纵坐标为32.又由AN=2AM,A为(-1,0),可得点N的纵坐标为3,故在线段MN上,点B的纵坐标t满足:32≤t≤3,由对称性,在线段M N 上,点B的纵坐标t满足:?3≤t≤?3 2,∴点B的纵坐标t的取值范围是:32≤t≤3或?3≤t≤?32.(3)如图,Q是⊙O上异于点A的任意一点,延长AQ到P,使得PA=2AQ,∵Q的轨迹是以O为圆心,1为半径的圆,∴点P的运动轨迹是以K(1,0)为圆心,2为半径的圆,当直线MN与⊙K相切于点R时,连接KR,在RtΔKMR中,∠KRM=90°,∵直线y=3x+b与x轴夹角为60°,∴∠KMR=60°,KR=2,∴KM=2÷sin60°=433,∴OM=1+433,∴ON=3OM=4+3,∴b=-4-3,当直线MN经过G(0,-1)时,满足条件,此时b=-1,观察图象可知:当-4-3≤b≤-1时,线段MN上存在点A关于⊙O的“生长点”,根据对称性,同法可得当1≤b≤4-3时,也满足条件.故答案为:-4-3≤b≤-1或1≤b≤4-3.16(2022•东城区校级开学)在平面直角坐标系xOy中,给出如下定义:若点P在图形M上,点Q在图形N 上,称线段PQ长度的最小值为图形M,N的“近距离”,记为d(M,N).特别地,若图形M,N有公共点,规定d(M,N)=0,如图,点A(-23,0),B(0,2).(1)如果⊙O的半径为2,那么d(A,⊙O)= 23-2 ,d(B,⊙O)=;(2)如果⊙O的半径为r,且d(⊙O,AB)>0,求r的取值范围;(3)如果C(0,m)是y轴上的动点,⊙C的半径为1,使d(⊙C,AB)<1,直接写出m的取值范围为.【解答】解:(1)∵⊙O的半径为2,A(-23,0),B(0,2),∴OB=2,OA=23>2,∴点A在⊙O外,点B在⊙O上,∴d(A,⊙O)=23-2,d(B,⊙O)=0,故答案为:23-2;0;(2)如图1,过点O 作OD ⊥AB 于点D ,在Rt ΔAOB 中,∵tan ∠BAO =OB OA =223=33,∴∠BAO =30°.在Rt ΔADO 中,sin ∠BAO =DO OA =12=DO23,∴DO =3,∵d (⊙O ,AB )=0,∴r 的取值范围是0<r <3或r >23;(3)如图2,过点C 作CN ⊥AB 于点N ,由(2)知,∠BAO =30°.∵C (m ,0),当点C 在点B 的上边时,m >2,此时,d (⊙C ,AB )=BC ,∴BC ≤1,即m -2≤1,解得m ≤3;当点C 与点B 重合时,m =2,此时d (⊙C ,AB )=0,当点C 在点B 的下边时,m <2,∴BC =2-m ,∴CN =BC ⋅sin ∠OBA =32(2-m ).∵d (⊙C ,AB )<1,⊙C 的半径为1,∴0<32(2-m )<1.∴2-233<m <2.综上所述:2-233<m ≤3.故答案为:2-233<m ≤3.17(2021秋•润州区校级月考)在平面直角坐标系xOy 中,⊙C 的半径为r ,P 是与圆心C 不重合的点,点P 关于⊙C 的反称点的定义如下:若在射线CP 上存在一点P ′,满足CP +CP ′=2r ,则称P ′为点P 关于⊙C 的反称点,如图为点P 及其关于⊙C 的反称点P ′的示意图.(1)当⊙O 的半径为1时,①分别判断点M (3,1),N 32,0,T (-1,3)关于⊙O 的反称点是否存在?若存在,直接求其坐标;②将⊙O 沿x 轴水平向右平移1个单位为⊙O ′,点P 在直线y =-x +1上,若点P 关于⊙O ′的反称点P ′存在,且点P ′不在坐标轴上,则点P 的横坐标的取值范围 1-2≤x ≤1+2且x ≠2-2 ;(2)⊙C 的圆心在x 轴上,半径为1,直线y =-x +12与x 轴,y 轴分别交于点A 、B ,点E 与点D 分别在点A 与点B 的右侧2个单位,线段AE 、线段BD 都是水平的,若四边形ABDE 四边上存在点P ,使得点P 关于⊙C 的反称点P ′在⊙C 的内部,直接写出圆心C 的横坐标的取值范围.。
中考数学专题复习新定义问题(一)

中考数学专题复习新定义问题(一)学校:___________姓名:___________班级:___________考号:___________ 评卷人 得分一、解答题1.在平面直角坐标系xOy 中,已知正方形ABCD ,其中2222,0,0,,,0,0,2222A B C D ⎛⎫⎛⎫⎛⎫⎛⎫-- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,M ,N 为该正方形外两点,1MN =.给出如下定义:记线段MN 的中点为P ,平移线段MN 得到线段M N '',使点,M N ''分别落在正方形ABCD 的相邻两边上,或线段M N ''与正方形的边重合(,,M N P '''分别为点M ,N ,P 的对应点),线段PP '长度的最小值称为线段MN 到正方形ABCD 的“平移距离”.(1)如下图,平移线段MN ,得到正方形ABCD 内两条长度为1的线段1122,M N M N ,则这两条线段的位置关系是_______;若12,P P 分别为1122,M N M N 的中点,在点12,P P 中,连接点P 与点_______的线段的长度等于线段MN 到正方形ABCD 的“平移距离”;(2)如图,已知点21,02E ⎛⎫+ ⎪ ⎪⎝⎭,若M ,N 都在直线BE 上,记线段MN 到正方形ABCD 的“平移距离”为1d ,求1d 的最小值;(3)若线段MN 的中点P 的坐标为(2)2,,记线段MN 到正方形ABCD 的“平移距离”为2d ,直接写出2d 的取值范围.2.对于平面直角坐标系xOy 中的线段PQ ,给出如下定义:若存在PQR 使得2PQRSPQ =,则称PQR 为线段PQ 的“等幂三角形”,点R 称为线段PQ 的“等幂点”.(1)已知(3,0)A .①在点1234(1,3),(2,6),(5,1),(3,6)P P P P --中,是线段OA 的“等幂点”的是_____________; ①若存在等腰OAB 是线段OA 的“等幂三角形”,求点B 的坐标;(2)已知点C 的坐标为(2,1)C -,点D 在直线3y x =-上,记图形M 为以点(1,0)T 为圆心,2为半径的T 位于x 轴上方的部分,若图形M 上存在点E ,使得线段CD 的“等幂三角形”CDE △为锐角三角形,直接写出点D 的横坐标D x 的取值范围.3.对于平面直角坐标系xOy 中的图形M 和点P ,给出如下定义:将图形M 绕点P 顺时针旋转90︒得到图形N ,图形N 称为图形M 关于点P 的“垂直图形”.例如,图1中点D 为点C 关于点P 的“垂直图形”.(1)点A 关于原点O 的“垂直图形”为点B . ①若点A 的坐标为(0,2),则点B 的坐标为_______; ①若点B 的坐标为(2,1),则点A 的坐标为_______.(2)(3,3),(2,3),(,0)E F G a --.线段EF 关于点G 的“垂直图形”记为E F '',点E 的对应点为E ',点F 的对应点为F '. ①求点E '的坐标(用含a 的式子表示);①若O 的半径为2,E F ''上任意一点都在O 内部或圆上,直接写出满足条件的EE '的长度的最大值.4.如图,直线l和直线l外一点P,过点P作PH l⊥于点H任取直线l上点Q,点H 关于直线PQ的对称点为点H',标点H'为点P关于直线l的垂对点.在平面直角坐标系xOy中,(1)已知点(0,2)P,则点(0,0),(2,2),(0,4)O A B中是点P关于x轴的垂对点的是_______;(2)已知点(0,)M m,且0m>,直线443y x=-+上存在点M关于x轴的垂对点,求m的取值范围;(3)已知点(,2)N n,若直线y x n=+上存在两个点N关于x轴的垂对点,直接写出n 的取值范围,5.在平面直角坐标系xOy 中,对于点P 和线段ST ,我们定义点P 关于线段ST 的线段比()()PS PS PT ST k PT PS PT ST⎧<⎪⎪=⎨⎪≥⎪⎩(1)已知点(0,1),(1,0)A B .①点(2,0)Q 关于线段AB 的线段比k =__________; ①点(0,)C c 关于线段AB 的线段比2k =,求c 的值.(2)已知点(,0)M m ,点(2,0)N m +,直线2y x =+与坐标轴分别交于,E F 两点,若线段EF 上存在点使得这一点关于线段MN 的线段比14k <,直接写出m 的取值范围.6.在平面直角坐标系xOy 中,对于点A 和线段MN ,如果点A ,O ,M ,N 按逆时针方向排列构成菱形AOMN ,且AOM α∠=,则称线段MN 是点A 的“α-相关线段”.例如,图1中线段MN 是点A 的“30-相关线段”.(1)已知点A 的坐标是(0,2).①在图2中画出点A 的“30-相关线段”MN ,并直接写出点M 和点N 的坐标; ①若点A 的“α-相关线段”经过点(3,1),求α的值;(2)若存在,()αβαβ≠使得点P 的“α-相关线段”和“β-相关线段”都经过点(0,4),记PO t =,直接写出t 的取值范围.7.在平面直角坐标系xOy 中,O 的半径为1,点A 是平面内一点,过点A 的直线交O 于点 B 和点C (ABAC ),01BC ,我们把点 B 称为点A 关于O 的“斜射点”.(1)如图,在点12331(1,1),(0,),(,0)22A A A -中,存在关于 O 的“斜射点”的是_____________.(2)已知若(0,2)A ,点关于O 的“斜射点”为点B ,则点 B 的坐标可以是__________.(写出两个即可)(3)若点A 直线y kx k =+上,点A 关于O 的“斜射点”为(1,0)B -,画出示意图,直接写出 k 的取值范围.8.对于平面内的点P 和图形M ,给出如下定义:以点P 为圆心,r 为半径作圆,若P 与图形M 有交点,且半径r 存在最大值与最小值,则将半径r 的最大值与最小值的差称为点P 视角下图形M 的“宽度M d ”. (1)如图1.点(4,3)A ,(0,3)B .①在点O 视角下,则线段AB 的“宽度AB d ”为_________; ①若B 半径为1.5,在点A 视角下,B 的“宽度Bd”为_________;(2)如图2,O 半径为2,点P 为直线1y x =-+上一点.求点P 视角下O “宽度Od”的取值范围;(3)已知点(,0),1C m CK =,直线333y x =+与x 轴,y 轴分别交于点D ,E .若随着点C 位置的变化,使得在所有点K 的视角下,线段DE 的“宽度”均满足06DE d <<,直接写出m 的取值范围.9.在平面直角坐标系O x y 中,任意两点()11,P x y ,()22,Q x y ,定义线段PQ 的“直角长度”为2121PQ d x x y y =-+-. (1)已知点(3,2)A . ① OA d =________;① 已知点(,0)B m ,若6AB d =,求m 的值;(2)在三角形中,若存在两条边“直角长度”之和等于第三条边的“直角长度”,则称该三角形为“和距三角形”.已知点(3,3)M .① 点(0,)(0)D d d ≠.如果OMD 为“和距三角形”,求d 的取值范围;① 在平面直角坐标系xOy 中,点C 为直线4y x =--上一点,点K 是坐标系中的一点,且满足1CK =,当点C 在直线上运动时,点K 均满足使OMK △为“和距三角形”,请你直接写出点C 的横坐标C x 的取值范围.10.对于平面直角坐标系xOy 中的O 和图形N ,给出如下定义:如果O 平移m 个单位后,图形N 上的所有点在O 内或O 上,则称m 的最小值为O 对图形N 的“覆盖近距”.(1)当O 的半径为1时,①若点()3,0A ,则O 对点A 的“覆盖近距”为_________;①若O 对点B 的“覆盖近距”为1,写出一个满足条件的点B 的坐标_________; ①若直线2y x b =+上存在点C ,使O 对点C 的“覆盖近距”为1,求b 的取值范围; (2)当O 的半径为2时,(3,),(4,1)D t E t +,且12t -≤≤.记O 对以DE 为对角线的正方形的“覆盖近距”为d ,直接写出d 的取值范围.11.在平面直角坐标系xOy 中,对于任意两点()()1122,,,M x y N x y ,若1212x x y y k -+-=(k 为常数且0k ≠),则称点M 为点N 的k 倍直角点.根据以上定义,解决下列问题: (1)已知点(1,1)A①若点(2,3)B -是点A 的k 倍直角点,则k 的值是___________;①在点(2,3),(1,1),(0,2),(0,0)C D E O --中是点A 的2倍直角点的是_______; ①若直线2y x b =-+上存在点A 的2倍直角点,求b 的取值范围;(2)T 的圆心T 的坐标为(1,0),半径为r ,若T 上存在点O 的2倍直角点,直接写出r 的取值范围.12.已知点P 、Q 分别为图形M 和图形N 上的任意点,若存在点P 、Q 使得PQ =1,我们就称图形M 、N 为友好图形,P 、Q 为关于图形M 、N 的一对友好点. (1)已知点 (1,0)A ,1(0,)2B ,C (-1,1)中, 与点O 为一对友好点,(2)已知O 半径r =1,若直线y x b =+与O 有且只有一对友好点,求b 的值;(3)已知点,D(m,2), D 半径r =1,若直线y=x+m 与D 是友好图形,求m 的取值范围.13.规定如下:图形M 与图形N 恰有两个公共点(这两个公共点不重合),则称图形M 与图形N 是和谐图形.(1)在平面直角坐标系xOy 中,已知O 的半径为2,若直线x k =与O 是和谐图形,请你写出一个满足条件的k 值,即k =______; (2)在平面直角坐标系xOy 中,已知点(),0A t ,直线3:33l y x =+与x 轴、y 轴分别交于B ,C 两点(其中点A 不与点B 重合),则线段AB 与直线l 组成的图形我们称为图形V ;①3t =时,以A 为圆心,r 为半径的A 与图形V 是和谐图形,求r 的取值范围;①以点A 为圆心,23为半径的A 与图形V 均组成和谐图形,求t 的取值范围.参考答案:1.(1)平行,P 1;(2)1d 的最小值为24;(3)21332222d -≤≤.【解析】 【分析】(1)根据图形,比较PP 1,PP 2的长度即可求解;(2)根据已知条件求得①P 1BE =45︒,过P 1作P 1Q ①BE 于Q ,则△P 1QB 为等腰直角三角形,利用特殊角三角函数值即可求解;(3)先找到最值点,再利用两点之间的距离公式即可求解. 【详解】(1)解:由图可得MN ①M 1N 1,MN ①M 2N 2, ①M 1N 1①M 2N 2, 而PP 1<PP 2,故线段MN 到正方形ABCD 的“平移距离”为PP 1; 故答案为:平行,P 1; (2)①B (0,22),C (22,0),四边形ABCD 为正方形, ①BC =2222122⎛⎫⎛⎫+=⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,①BCA =45︒, ①E (212+,0), ①CE =221122+-==BC , ①①1=①2,则①1+①2=①BCA =45︒, ①①1=①2=22.5︒,在Rt △BMN 中,BP 1为斜边上的中线, 则BP 1=12MN =12=NP 1,①①P 1BN =①P 1NB , 又MN ①BE , ①①2=①P 1NB ,①①2=①P 1NB =45︒,①P 1BE =①2+①P 1BN =45︒, 过P 1作P 1Q ①BE 于Q ,则△P 1QB 为等腰直角三角形,在Rt△P1QB中,P1Q=P1B sin45︒=122224⨯=,①1d的最小值为24;(3)解:根据题意,P1、P2分别是AB、BC的中点,则线段MN到正方形ABCD的“平移距离”最大为PP1,最小为PP2,此时,P1 (24-,24),P2 (24,24),①PP1=22223322442⎛⎫⎛⎫++-=⎪ ⎪⎪ ⎪⎝⎭⎝⎭,PP2=22222112222224422⎛⎫⎛⎫⎛⎫-+-=-=-⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭,①2d的取值范围是21332222d-≤≤.【点睛】本题考查正方形的性质、等腰直角三角形的判定和性质、坐标与图形的性质、锐角三角函数等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考压轴题.2.(1)①24,P P:①362⎛⎫⎪⎝⎭,或362⎛⎫⎪⎝⎭,-;(2)3212Dx-<<或5232Dx+<<【解析】【分析】(1)①根据定义求出三角形面积与OA 2进行比较即可确定线段OA 的“等幂点”;①如图,由OAB 是线段OA 的“等幂三角形”,可得2OAB S OA =.由点A 的坐标为()3,0A ,若记OAB 中OA 边上的高为h ,可得392OAB S h ==, 求出6h =.由OAB 是等腰三角形,点B 在线段OA 的垂直平分线上即可求点B 的坐标为(32,6)或(32,-6); (2)设半圆与x 轴交于G ,H 两点,过T 作CH 的平行线与半圆交于R ,作CH 的垂线交半圆于Q ,直线y =x -3与y 轴交于N ,设D (x ,x -3),过D 作y 轴平行线,与过C 作x 轴平行线交于F ,求出N (0,-3), H (3,0),可证△ONH 为等腰直角三角形,①OHN =①ONH =45°,点D 运动分两种情况,第一种情况点D 在射线CH ,去掉线段CH 部分运动,在Rt △TCH 中TH =2,TC =CH =TH ×sin45°=22=22⨯,QC=2+2,又因为△ECD 为锐角三角形,点E 在QR 上运动,点E 到CD 的距离h 的范围是222h ≤≤+,可求h =2CD =22(x-2),5232D x +<<; 第二种情况点D 在射线CU 上,去掉线段CU 部分运动,点E 在QG 上运动,求出GU =GH ×cos45°=22,可得2222h ≤≤+,可求()2222222x ≤-≤+,解不等式即可得3212D x -<<. 【详解】(1)①1OP A S=1211933222P OA y OA ⨯⋅=⨯⨯=<,P 1不是线段OA 的“等幂点”. 2OP A S=2211369=22P OA y OA ⨯⋅=⨯⨯=, P 2是线段OA 的“等幂点”. 3OP A S=3211331222P OA y OA ⨯⋅=⨯⨯=<,P 3不是线段OA 的“等幂点”. 4OP AS =421136922P OA y OA ⨯⋅=⨯⨯==, P 4是线段OA 的“等幂点”. 是线段OA 的“等幂点”的是24,P P ,故答案为:24,P P :①如图,①OAB 是线段OA 的“等幂三角形”,①2OAB S OA =.①点A 的坐标为()3,0A ,若记OAB 中OA 边上的高为h ,则有13922OAB S OA h h =⨯⨯==. 解得6h =.①点B 在直线6y =或6y =-上.①OAB 是等腰三角形,①点B 在线段OA 的垂直平分线上.OA 的垂直平分线为x =32,与直线6y =或6y =-的交点为B 1(32,6),B 2(32,-6), 综上所述,点B 的坐标为(32,6)或(32,-6),(2)设半圆与x 轴交于G ,H 两点,过T 作CH 的平行线与半圆交于R ,作CH 的垂线交半圆于Q ,直线y =x -3与y 轴交于N ,设D (x ,x -3),过D 作y 轴平行线,与过C 作x 轴平行线交于F ,当x =0时,y =-3,N (0,-3),当y =0时,x -3=0,x =3,H (3,0),①ON =3=OH ,①ONH 为等腰直角三角形,①OHN =①ONH =45°,点D 运动分两种情况, 第一种情况点D 在射线CH ,去掉线段CH 部分运动,①TC ①NH ,①OHN =45°,①①TCH 为等腰直角三角形,在Rt ①TCH 中TH =2,TC =CH =TH ×sin45°=22=22⨯,QC=2+2, 又因为①ECD 为锐角三角形,点E 在QR 上运动,点E 到CD 的距离h 的范围是222h ≤≤+,CD=CF÷cos45°=2CF=2(x-2),①线段CD 的“等幂三角形”, S △CDE =12h CD ⋅=CD 2, ①h =2CD =22(x -2),①()222222x <-<+,解得55222x+<<,点D在H右侧,x>3,①5232Dx+<<;第二种情况点D在射线CU上,去掉线段CU部分运动,点E在QG上运动,又因为①ECD为锐角三角形,GU=GH×cos45°=22,①2222h≤≤+,①线段CD的“等幂三角形”,S△CDE=12h CD⋅=CD2,①h=2CD=22(2-x),则()2222222x≤-≤+,解得3212Dx-<<,D 的横坐标D x 的取值范围为3212D x -<<或5232D x +<<. 【点睛】 本题考查新定义问题,仔细阅读新定义,抓住三角形的高为底的二倍,涉及三角形面积,等腰三角形,等腰直角三角形,线段垂直平分线,一次函数的性质,圆的性质,直线与圆的位置关系,锐角三角函数,锐角三角形,列双边不等式,解不等式等知识,难度较大,综合较强,熟练掌握多方面知识才是解题关键.3.(1)①()2,0;①()1,2-;(2)①(3,3)+'+E a a ;①22【解析】【分析】(1)①点A 在y 轴上,则点B 在x 轴上,且OB =OA =2,从而易得点B 的坐标;①由OA =OB ,过A 、B 分别作x 轴的垂线于N 、 M ,则可得①ANO ①①OMB ,故有AN =OM =2,ON =BM =1,再由点在第二象限,从而可得点A 的坐标;(2)①分别过点E 、E E '作x 轴的垂线,垂足分别为H 、Q ,则由OE OE '=,可得EHG GQE '△≌△,由此可得E '点的坐标;①由①知,点E '的两个坐标相等,表明E '点在第一、三象限的角平分线上,当E '点位于第一象限的圆上时,EE '最大,此时2OE '=,从而可得E '点坐标为(2,2),这样可求得EE '的最大值.【详解】解:(1)①因点A 在y 轴上,故点B 必在x 轴正半轴上,又OB =OA =2,所以点A 坐标为()2,0;故答案为:()2,0.①如图,过A 、B 分别作x 轴的垂线于N 、 M .则①ANO =①OMB =90,①①AON +①A =90°①①AOB =90°,①①AON +①BOM =90°,①①A =①BOM ,①OA =OB ,①①ANO ①①OMB ,①AN =OM =2,ON =BM =1,根据题意,点A 必在第二象限,①A ()1,2-.故答案为:()1,2-.(2)①如图,过点E 作EH x ⊥轴于点H ,过点E '作'⊥E Q x 轴于点Q .由题意可知,,'90EG E G EGE '=∠=︒.①EHG GQE '△≌△.①,'==EH GQ HG QE .①(3,3),(,0)-E G a ,①()3,0-H .①.|3|3,3HG QE a a EH GQ ==+=+=='①|3|3OQ a a =+=+.①(3,3)+'+E a a .①①EF ①x 轴①E F x ''⊥轴连接OE ',延长E F ''交x 轴于点H ,则E H x '⊥轴;过点E '作x 轴的平行线,过点E 作y 轴的平行线,两线交于点D ,则ED E D '⊥,如图所示;由①知,点E '的两个坐标相等,①|3|OH E H a '==+,表明E '点在第一、三象限的角平分线上,且位于与圆相交的圆内的一条线段上运动,当点E '位于第一象限上的圆上时,即2OE '=时,EE '最大,①①E HO '是等腰直角三角形,①22OH OE '==,①2OH E H '==,①(2,2)E ',①32DE '=+,32DE =-,在Rt EDE '中,由勾股定理得:2222(32)(32)22EE DE DE =+=-++='', 即EE '的最大值为:22.【点睛】本题考查了新定义,对于新定义这类问题,关键是弄清楚新定义的含义,抓住问题的实质,本题新定义的实质是旋转,通过作x 轴的垂线,构造两个全等的直角三角形,问题便容易解决.4.(1)O 和A ;(2)3m 2≥;(3)-2n 1+21<<且n≠2 【解析】【分析】(1)根据垂对点的定义即可得出答案;(2)先得出点M 关于x 轴的垂对点在以M 为圆心MO 即m 为半径的圆上,点(0,2)m 除外,再根据当直线443y x =-+与①M 相切时,m 的值最小,利用相似三角形的判定和性质得出m 的值即可;(3)先得出点N 关于x 轴的垂对点在以N 为圆心2为半径的圆上,点(n,4)除外,再分n =0、n <0 、n >0三种情况进行分类讨论即可.【详解】解:(1)①点(0,2)P ,①根据垂对点的定义可得点P 关于x 轴的垂对点为(0,0),(2,2)O A ; (2)①点(0,)M m ,且0m >,①由垂对点的定义可知,点M 关于x 轴的垂对点在以M 为圆心MO 即m 为半径的圆上,点(0,2)m 除外,则OM =m ;设直线443y x =-+与x 轴和y 轴的交点分别为G 、H ,①G(3,0),H(0,4),①22345GH=+=,①直线443y x=-+上存在点M关于x轴的垂对点,①当直线443y x=-+与①M相切时,m的值最小,此时切点为N,连接MN,则①HOG=①MNH=90°,①①OHG=①NHM①①OHG①①NHM①=MN MHOG GH①m4-m35=①3m=2①m的取值范围是:3m2≥;(3)①(,2)N n,点N关于x轴的垂对点在以N为圆心2为半径的圆上,点(n,4)除外,当n=0时,①N与y=x有两个交点,则直线y x n=+上存在两个点N关于x轴的垂对点,当n>0时,相当于①N向右平移,y=x向上平移,当y=x+n与①N相切于①N左侧时是临界点,设切点为E,连接NE,①DEN=90°,过点E作EF①x轴于F,直线y=x+n与x轴y轴的交点分别为W、K,则W(-n,0),K (0,n),①OK=OW,①①OWK为等腰直角三角形,设过点(,2)N n且平行于x轴的直线与直线y=x+n相交于点D,则①DEN为等腰直角三角形,22DE=,设EF交DN于点I,在直角三角形ENI中,NE=2,①END=45°,①NI=EI=2,①E(n-2,2+2),①点E在y=x+n上,①2+2=n-2+n①n=1+2当n=2时,直线与圆交于点(0,2)、(2,4),此时只有一个垂对点,故n≠2.当n<0时,相当于①N向左平移,y=x向下平移,同理得出n=1-2,①-2n1+21<<且n≠2 .【点睛】本题属于新定义题型,涉及到了三角形的判定和性质、切线的性质,解题的关键在于读懂题目信息,并注意数形结合思想的应用.5.(1)①22;①C点为(0,3)或(0,3)-;(2)92422m-<<-+或52222m-<<-+.【解析】【分析】(1)①利用两点之间的距离公式和线段比k的定义即可得;①分若AC BC<时和AC BC≥时,两种情况讨论,根据线段比k的定义计算即可;(2)分①当点N 在E 点或在其左侧时,①当点N 在E 点右侧,M 点在E 点左侧时,①当M 点在E 点或在E 点右侧时三种情况讨论,结合图形和线段比k 的定义分析即可. 【详解】解:(1)①22112AB =+=,22215AQ =+=,1BQ =, ①BQ AQ <, ①1222BQ k AB ===, 故答案为:22; ①①(0,)C c ,①|1|AC c =-,21BC c =+, 若AC BC <时, |1|22c k -==,解得3c =或1c =-(不满足2|1|1c c -<+舍去); 若AC BC ≥时,2122c k +==,解得3c =(不满足2|1|1c c -≥+舍去)或3c =-;综上所述,C 点为(0,3)或(0,3)-;(2)①直线2y x =+与坐标轴分别交于,E F 两点, ①(2,0)E -,(0,2)F ,①点(,0)M m ,点(2,0)N m +, ①MN =2,①如下图,当点N 在E 点或在其左侧时,22m +≤-,即4m ≤-, M 、N 到线段EF 的最短距离为ME 、NE , 此时ME >NE ,即2(2)124m --+<,解得92m >-,即942m -<≤-;①如下图,当点N在E点右侧,M点在E点左侧时,42m-<<-,M、N到线段EF的最短距离为ME、NG(N到EF的垂线段),()222,422ME m NG EN m=--==+,若2(4)22m m+<--,即22m<-,2(414)22m+<,解得242m<-+,此时2442m-<<-+,若2(4)22m m+>--,即22m>-,4212m--<,解得52m>-,此时522m-<<-;①如下图,当M点在E点,或在E点右侧时,2m≥-M 到线段EF 的距离近,为MG (M 到EF 的垂线段),2(2)1224m +<,解得222m <-+,即2222m -≤<-+ 综上所述,92422m -<<-+或52222m -<<-+. 【点睛】本题是新定义的题目.注意考查一次函数与坐标轴交点问题,两点之间的距离公式.理解题中线段比的定义,能分类讨论结合图形分析是解题关键.6.(1)① 作图见解析;点M 的坐标是(1,3),点N 的坐标是(1,32)+;①α的值为60︒或120︒ ;(2) 224t <≤. 【解析】 【分析】(1)①根据“ α− 相关线段”的定义求解;①由题意点M 必在直线x =3上,记MH ①x 轴于H ,则可得MH =1,①MOH =30°,然后分点M 在x 轴上方和点M 在x 轴下方两种情况分别求出α的值即可; (2)根据题意分0<t ≤22、22<t ≤4、t >4三种情况讨论. 【详解】(1)①如图,MN 即为所求.过点M 作BM ①x 轴于点B , ①四边形AOMN 为菱形, ①AO ①MN ,AO =MO =MN , ①点A 在y 轴上, ①AO ①x 轴,①MN ①x 轴,即N 、M 、B 三点共线, ①①AOM =30°, ①①MOB =90°-30°=60°,在RT ①MOB 中,BO =12MO =1,MB =332MO =, ①点M 的坐标是(1,3),点N 的坐标是(1,32)+. ①解:①点A 的“α-相关线段”MN 经过点(3,1), ①点M 必在直线3x =上.记直线3x =与x 轴交于点(3,0)H , ①2,3OM OA OH ===,①221MH OM OH =-=,30MOH ∠=︒. 分两种情况:a )如图,当点M 在x 轴上方时,点M 恰为(3,1),符合题意,此时60,60AOMα︒∠==︒;b)如图,当点M在x轴下方时,点M为(3,1)-,由2MN=知点N为(3,1),也符合题意,此时120,120AOMα︒∠==︒.综上,α的值为60︒或120︒.(2)当0<t≤22时,任意菱形的边MN都不经过点(0,4);当22<t≤4且N为(0,4)时,点P的“α-相关线段”过(0,4),当22<t≤4且M为(0,4)时,点P的“β-相关线段”过(0,4);当t>4时,只有一种情况使P的“α-相关线段”或“β-相关线段”过(0,4),此时(0,4)在线段OM上,①不符合题意综上所述,224t<≤【点睛】本题考查一次函数的应用,熟练掌握一次函数的图象与性质、菱形的性质是解题关键.7.(1)1A,2A;(2)(32-,12),(35,45);(3)3k>或3k<-.【解析】【分析】(1)过点1(1,1)A -作直线交O 于点1B ,1C ,过点2()30,2A 作22B C y 轴交O 于点2B ,2C ,过点3()1,02A 作33B C x 轴交O 于点3B ,3C ,连接2OB ,3OC ,分别求出22B C ,33B C ,根据“斜射点”的判别条件ABAC ,01BC,分别进行判别即可;(2)过点A 作O 的切线AD ,交O 于点 D ,根据Rt ADO 中,1OD =, 2AO =,可求得点 D 的坐标是(32-,12),可知,满足 AB AC ,01BC,点D 是 O 的“斜射点”;在 OD 上取13=2OD ,并过 1D 作 144OD B C 交O 于点 4B ,4C ,可求得 4C 的坐标是(-1,0),设过A ,4C 两点的直线是 y kx b =+,并交 O 于点5B ,可求出点5B 的坐标是(35, 45),根据(1)中2A 的求法可知,55<1B C ,可得 5B 是O 的“斜射点”; (3)当0k >时,一次函数y kx k =+图像向上,过点B (-1,0)交O 于点5C ,并51BC ,可得5OBC 是等边三角形,根据(1)中 2A 的求法可知,点5C 的坐标是(12-, 32),可求出得: 3k =,则有当满足过点B 并且是O 的“斜射点”时,3k >,同理可得,当 0k >时,点5C 的坐标是(12-, 32-),可得满足过点 B 并且是O 的“斜射点”时,3k <-. 【详解】解:(1)过点1(1,1)A -作直线交O 于点 1B ,1C , 过点2()30,2A 作 22BC y 轴交O 于点2B ,2C , 过点3()1,02A 作33BC x 轴交O 于点3B ,3C ,连接2OB ,3OC ,O 的半径为1,即231OB OC ,①22B C y 轴,2A 的坐标是 3(0,)2①y 轴垂直平分22B C , ①由勾股定理可得:2222222231=11222B C OB OA , ①22=1B C ,满足AB AC ,01BC , ①点2A 是O 的“斜射点”; ①33B C x 轴,3A 的坐标是 1(,0)2①x 轴垂直平分33B C ,①由勾股定理可得:22223323132212=1B C OC OA ,①3331B C ,根据O 中,过点3A 的所有弦中,垂直半径的弦最短可知,过点3A 的所有弦都大于 3,因此点3A 不满足题意, ①点3A 不是是O 的“斜射点”; 由图中图像可知1122B C B C ,即有:1122=1B C B C故满足AB AC ,01BC , ①点1A 是O 的“斜射点”;综上所述,点1A ,2A 是O 的“斜射点”; (2)如图示,过点A 作O 的切线AD ,交O 于点 D ,在Rt ADO 中,1OD =,2AO =, ①2222=213AD AO D O ,设点D 的坐标是(D x ,D y ), 则有:11··22ADOD S OD AD AO x ==, ①11··22ADOD S OD AD AO x == ①32D x (点D 在第二象限,取负值), ①221D D x y ,①12Dy (点D 在第二象限,取正值),①点D 的坐标是(32-,12), 满足AB AC ,01BC ,①点D 是O 的“斜射点”,即点B 的坐标可以是(32-,12);在OD 上取13=2OD ,并过 1D 作144OD B C 交O 于点 4B ,4C ,根据(1)中2A 的求法可知,44=1B C , 4C 的坐标是(-1,0), 设过A ,4C 两点的直线是y kx b =+,并交O 于点5B①20b k b =⎧⎨-+=⎩,解之得 22b k ,①过A ,4C 两点的直线是22y x =+, 设点5B 的坐标是(5B x ,5B y ),则有555522122B B B B x y y x ,解之得5510B Bx y或553545B B x y ,即点5B 的坐标是(35,45), 根据(1)中2A 的求法可知,55<1B C , 即满足AB AC ,01BC ,①点5B 是O 的“斜射点”,即点B 的坐标可以是(35, 45);综上所述,即点B 的坐标可以是(32-,12),( 35,45); (3)如图示,当0k >时,一次函数y kx k =+图像向上,过点B (-1,0)交O 于点 5C ,并51BC ,①51OB OC ,①5OBC 是等边三角形,根据(1)中2A 的求法可知,点5C 的坐标是(12-,32),①1322k k,解之得:3k =,当满足过点B 并且是O 的“斜射点”时,3k >,同理可得,当0k >时,点5C 的坐标是(12-, 32-),①满足过点B 并且是O 的“斜射点”时,3k <-, 【点睛】本题是圆的综合题,主要考查了圆的切线的性质,勾股定理,等边三角形的判定与性质,弦长的性质,点与坐标的关系,方程组的解法,“斜射点”的定义的理解等知识点,熟悉相关性质是解题的关键. 8.(1)①2;①3;(2)24Od ≤≤;(3)332m <--或331m >-+.【解析】 【分析】(1)①根据题意易得当线段AB 与以点O 为圆心的圆相切时半径最小,经过点B 时半径最大,由此问题可得解;①由题意可得当以点A 为圆心的圆与B 外切时半径最小,内切时半径最大,由此问题可得解;(2)设直线1y x =-+与O 的交点分别为M 和N ,与x 轴、y 轴交于点A 、B ,由题意易得点()()1,0,0,1A B ,即OA =1,OB =1,则可分当点P 在点M 上方、点N 下方时和当点P 在线段MN 上时,然后进行分类求解即可; (3)由直线333y x =+可得33,3OD OE ==,则6DE =,30EDO ∠=︒,由(),0,1C m CK =可知点K 在以点C 为圆心,半径为1的圆上,进而可分当C 经过点D 时和当C 与直线DE 相切于点K 时,然后求解即可. 【详解】解:(1)①由题意得:当以点O 为圆心的圆与线段AB 相切于点B 时,半径为最小,经过点A 时半径最大,连接OA ,如图所示:①()4,3A,()0,3B,①3OB=,()()2240305OA=-+-=,①在点O视角下,则线段AB的“宽度ABd”为532-=,故答案为2;①由题意得:以点A为圆心的圆与B外切时半径最小,内切时半径最大,如图所示:①B半径为1.5,①半径最大为1.54 5.5+=,半径最小为4 1.5 2.5-=,①在点A视角下,B的“宽度Bd”为5.5-2.5=3,故答案为3;(2)设直线1y x =-+与O 的交点分别为M 和N ,与x 轴、y 轴交于点A 、B ,如图所示:当点P 在点M 上方时,则以点P 为圆心的圆与O 内切时半径最大,外切时半径最小,如图,设P 的半径最小为r ,由圆与圆的位置关系可得半径最大时为4r +, ①在点P 视角下O “宽度Od”为44r r +-=,同理可得当点P 在点N 下方时,与点P 在点M 外时相同;当点P 在线段MN 上时,则根据点到直线垂线段最短可得当点P 在AB 的中点时,此时在点P 视角下O “宽度Od ”取最小,即:以点P 为圆心的圆与O 内切时半径最大,外切时半径最小,如图所示:①由直线1y x =-+可得点()()1,0,0,1A B ,即OA =1,OB =1, ①①AOB 是等腰直角三角形, ①2AB =, ①点P 是AB 的中点, ①22OP =, ①P 的半径最小为222-,半径最大为222+, ①在点P 视角下O “宽度O d”为2222222⎛⎫+--= ⎪ ⎪⎝⎭, 综上所述:在点P 视角下O “宽度Od ”的取值范围为24Od ≤≤;(3)由题意可得如图所示:由直线333y x =+可得当y =0时,则3033x =+,解得33x =-,当x =0时,则有y =3, ①()()33,0,0,3D E -, ①33,3OD OE ==, ①6DE =, ①30EDO ∠=︒, ①(),0,1C m CK =,①点K 在以点C 为圆心,半径为1的圆上,①由在所有点K 的视角下,线段DE 的“宽度”均满足06DE d <<,则有: 当C 经过点D 时,如图所示:①DC =1, ①331OC =-, ①331m =-+,①当点K 与点D 重合时,以点K 为圆心的圆与线段DE 有交点时,半径最小为0,最大为6,所以在点K 的视角下,线段DE 的“宽度”为6DE d =,而点K 在C 的其他地方时,根据三角形三边关系可知始终满足题意, ①331m >-+;当C 与直线DE 相切于点K 时,如图所示:①CK =1,30EDO ∠=︒,①30CDK ∠=︒, ①22CD CK ==,①332OC =+,即332m =--,此时在点K 的视角下,线段DE 的“宽度”为6DE d =,故不符合题意, ①332m <--,综上所述:当随着点C 位置的变化,使得在所有点K 的视角下,线段DE 的“宽度”均满足06DE d <<,则m 的取值范围为332m <--或331m >-+.【点睛】本题主要考查直线与圆的位置关系、圆与圆的位置关系及一次函数的综合,熟练掌握直线与圆的位置关系、圆与圆的位置关系及一次函数的性质是解题的关键.9.(1)① 5;①1m =-或7;(2)①3d 且0d ≠;①3C x -<222--或2212C x -+<【解析】 【分析】(1)①根据题意把(0,0)O ,(3,2)A 代入2121PQ d x x y y =-+-计算即可;①把(3,2)A ,(,0)B m 代入公式,求得34m -=,去绝对值求得m 的值即可;(2)①据题意,锐角三角形不可能为 “和距三角形”,结合图像求出d 的取值范围;①结合图形画出所有可能情况即可求出C x 的取值范围. 【详解】解:(1)① ①(3,2)A①212130205OA d x x y y =-+-=-+-=; 故答案为:5① 知点(,0)B m ,(3,2)A 若6AB d =, ①21213206AB d x x y y m =-+-=-+-= ①34m -=,34m ∴-=或34,m -=-①1m =-或7;(2)① ()()()0,,0,0,3,3,D d O M,6,33,OD MO MDd d d d d∴===+-∴当d>3时,不存在“和距三角形”,①当3d=时,构成直角三角形如图,符合要求,当3d<时,构成钝角三角形如图,符合要求,①3d且0d≠① 据题意,点K的轨迹是以点C为圆心,半径为1的圆,且锐角三角形不可能为“和距三角形”,如图:①综上所述:3C x -<222--或2212C x -+<【点睛】本题考查了新定义,类比法,点与圆的位置关系,圆的切线等,解题的关键是有较强的理解能力及自学能力等.10.(1) ①2, ①(2,0)(答案不唯一), ①2525b -≤≤ (2) 15432d -≤≤ 【解析】 【分析】(1) ① 根据OA =3,可确定“覆盖近距”为3-1=2;①确定OB =2,写出坐标即可;①确定当OC ①GH 时的“覆盖近距”,以此确定b 的取值范围;(2)确定O 对以DE 为对角线的正方形的“覆盖近距”的最大值和最小值即可. 【详解】解:(1) ①因为OA =3,圆的半径是1,故O 对点A 的“覆盖近距”为3-1=2; 故答案为:2,①O 对点B 的“覆盖近距”为1,圆的半径是1,则OB =2,B 点坐标可以为(2,0)(答案不唯一);故答案为:(2,0)(答案不唯一);①设直线2y x b =+与x 轴、y 轴交于点G 、H ,当x =0时,y =b ,OH =b ;当y =0时,x =2b -,OG =2b ,tan①OHG =12,O 对点C 的“覆盖近距”为1,即OC =2,当OC ①GH 时,刚好存在“覆盖近距”为1,此时,OC =2,CH =4,222425OH =+=,同理,OI =25, 故b 的取值范围为:2525b -≤≤(2)根据题意可知以DE为对角线的正方形边长为1,如图所示,当t=-0.5时,“覆盖近距”最小,此时平移后的F经过E、G两点,EG交x轴于点H,连接FG,221520.52FH=-=,d=4-152;当t=2时,“覆盖近距”最大,如图所示,此时,EH=3,22345OE=+=,d=5-2=3;故d的取值范围为:15432d-≤≤【点睛】本题考查了新定义问题和与圆的位置关系,解题关键是准确理解题意,熟练运用圆的相关知识和解直角三角形,利用数形结合思想,正确推理计算.11.(1)①5;①D 、O ;①b 的取值范围为:17b -≤≤;(2)r 的取值范围为232r ≤≤. 【解析】 【分析】(1)①根据k 倍直角点的定义计算即可求解; ①根据“2倍直角点”的定义分别计算,即可判断;①根据“2倍直角点”的定义得到如图所示有正方形的边界即为点A 的2倍直角点存在的区域,列式计算,即可求解;(2)若T 上存在点O 的2倍直角点,即T 与如图的正方形有交点(正方形的边界为点O 的2倍直角点存在的区域),根据切线的性质以及特殊角的三角函数值即可求解. 【详解】(1)①根据k 倍直角点的定义得:121221315k x x y y =-+-=--+-=,故答案为:5;①点C (2,3),121221313k x x y y =-+-=-+-=, 点D (−1,1),121211112k x x y y =-+-=--+-=, 点E (0,−2),121201214k x x y y =-+-=-+--=, 点O (0,0),121201012k x x y y =-+-=-+-=,①是点A 的2倍直角点的是D (−1,1),O (0,0), 故答案为:D 、O ;①如图,正方形的边界即为点A 的2倍直角点存在的区域,若直线2y x b =-+与其有交点,则过点(-1,1)时,b 值最小, 即()121b =-⨯-+,解得:1b =-, 当过点(3,1)时,b 值最大, 即123b =-⨯+,解得:7b =, ①b 的取值范围为:17b -≤≤;(2)若T 上存在点O 的2倍直角点,即T 与如图的正方形有交点(正方形的边界为点O 的2倍直角点存在的区域),由图可知,当①T 与正方形有交点为H (0,0)时,①T 的半径最大,即3r =; 当①T 与直线MN 相切时,①T 的半径最小, 过T 作TQ ①MN 于Q ,即r TQ =, 根据正方形的性质知①MNO =45︒, ①2sin sin 452TQ QNT TN ∠=︒==, ①1TN =,①22TQ =, ①r 的取值范围为232r ≤≤. 【点睛】本题属于新定义与一次函数相结合的综合压轴题,考查了正方形的性质,特殊角的三角函数值,切线的性质等知识,读懂定义,紧扣定义解题,熟练掌握“k 倍直角点”的定义是解答此题的关键.12.(1)A ;(2)22b =或b=-22;(3)22m -≤≤322. 【解析】 【分析】(1)根据友好点的定义去计算判断,只要满足到原点的距离为1即可;(2)根据直线与圆O 相切时,只有一个公共点,再根据友好点的定义,将直线向外平移1各单位,后确定b 的值即可;(3)确定直线y =x +m 与直线y =2的交点,分交点在点D 左边和右边两种情形求解即可. 【详解】解:(1)①(1,0)A ,1(0,)2B ,C (-1,1),①OA =22(10)(00)-+-=1,OB =221(0)(00)2-+-=12,OC =22(10)(10)--+-=2,①符合新定义的点是(1,0), 故答案为:A ;(2)如图,直线y x b =+与圆O 相切是时,直线与圆有一个公共点,此时OG =OD =1, 根据直线的特点,知道直线与坐标轴构成等腰直角三角形,根据友好点的定义,只需将相切的直线沿着OD 或OG 向外平移一个单位长即可,分别到达E 或H 点,此时OE =2或OH =2,根据平移的性质,OE =EF =2,或OH =HM =2,根据勾股定理,得OM =OF =22, ①b =22或b =-22;。
北京新定义压轴题

1、在北京的公共交通系统中,以下哪种方式不是常用的出行工具?
A. 地铁
B. 公交车
C. 共享单车
D. 私人飞机
(答案)D
2、关于北京的历史文化,以下哪个建筑不是北京的标志性建筑?
A. 故宫
B. 天安门
C. 长城
D. 东方明珠
(答案)D
3、在北京,以下哪种小吃是当地非常有名的传统美食?
A. 烤鸭
B. 火锅
C. 小笼包
D. 臭豆腐
(答案)A
4、关于北京的四季气候,以下哪个描述是不准确的?
A. 春季温暖多风
B. 夏季炎热潮湿
C. 秋季凉爽宜人
D. 冬季温和无雪
(答案)D
5、在北京的购物场所中,以下哪个地方以传统老北京特色商品著称?
A. 王府井步行街
B. 三里屯酒吧街
C. 798艺术区
D. 南锣鼓巷
(答案)D
6、关于北京的公共交通卡,以下哪个描述是错误的?
A. 公交卡可以乘坐地铁
B. 公交卡可以乘坐公交车
C. 公交卡只能在北京使用
D. 公交卡可以充值重复使用
(答案)C
7、在北京,以下哪个景点是古代皇家园林的代表?
A. 颐和园
B. 天坛公园
C. 北海公园
D. 奥林匹克森林公园
(答案)A
8、关于北京的交通规则,以下哪个描述是不正确的?
A. 驾车需遵守右侧通行原则
B. 行人过马路需走人行横道
C. 骑自行车不需佩戴头盔
D. 乘坐公共交通工具需购票
(答案)C。
2022北京中考数学题型专练:新定义压轴题
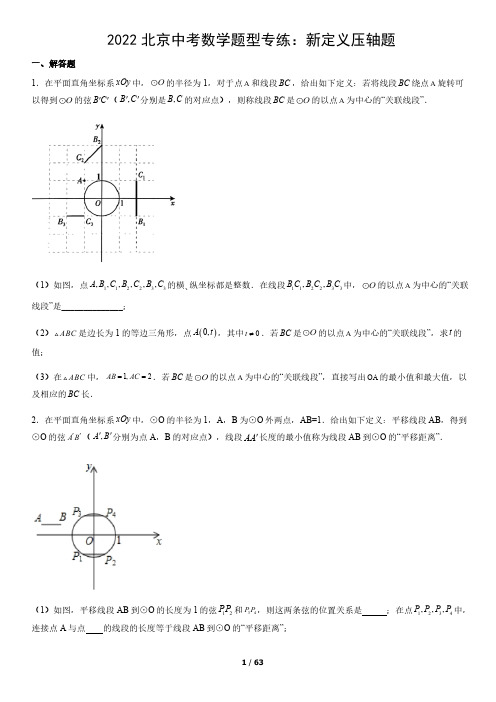
2022北京中考数学题型专练:新定义压轴题一、解答题1.在平面直角坐标系中,的半径为1,对于点和线段,给出如下定义:若将线段绕点旋转可xOy O A BC BC A 以得到的弦(分别是的对应点),则称线段是的以点为中心的“关联线段”.O B C '',B C '',B C BC O A(1)如图,点的横、纵坐标都是整数.在线段中,的以点为中心的“关联112233,,,,,,A B C B C B C 112233,,B C B C B C O A 线段”是______________;(2)是边长为1的等边三角形,点,其中.若是的以点为中心的“关联线段”,求的ABC ()0,A t 0t ≠BC O A t 值;(3)在中,.若是的以点为中心的“关联线段”,直接写出的最小值和最大值,以ABC 1,2AB AC ==BC O A OA 及相应的长.BC 2.在平面直角坐标系中,⊙O 的半径为1,A ,B 为⊙O 外两点,AB=1.给出如下定义:平移线段AB ,得到xOy ⊙O 的弦(分别为点A ,B 的对应点),线段长度的最小值称为线段AB 到⊙O 的“平移距离”.A B '',A B ''AA '(1)如图,平移线段AB 到⊙O 的长度为1的弦和,则这两条弦的位置关系是 ;在点中,12PP 34PP 1234,,,P P P P 连接点A 与点 的线段的长度等于线段AB 到⊙O 的“平移距离”;(2)若点A ,B 都在直线上,记线段AB 到⊙O 的“平移距离”为,求的最小值;y =+1d 1d (3)若点A 的坐标为,记线段AB 到⊙O 的“平移距离”为,直接写出的取值范围. 32,2⎛⎫ ⎪⎝⎭2d 2d 3.在△ABC 中,,分别是两边的中点,如果上的所有点都在△ABC 的内部或边上,则称为△D E ABC DEDE ABC 的中内弧.例如,下图中是△ABC 的一条中内弧. DE(1)如图,在Rt △ABC 中,分别是的中点.画出△ABC 的最长的中内弧AB AC D E ==,AB AC ,,并直接写出此时的长; DEDE(2)在平面直角坐标系中,已知点,在△ABC 中,分别是的()()()()0,20,04,00A B C t t >,,D E ,AB AC ,中点.①若,求△ABC 的中内弧所在圆的圆心的纵坐标的取值范围; 12t = DE P ②若在△ABC 中存在一条中内弧,使得所在圆的圆心P 在△ABC 的内部或边上,直接写出t 的取值范围. DEDE4.对于平面直角坐标系中的图形,,给出如下定义:为图形上任意一点,为图形上任意一xOy M N P M Q N 点,如果,两点间的距离有最小值,那么称这个最小值为图形,间的“闭距离”,记作(,). P Q M N d M N 已知点(,6),(,),(6,).A 2-B 2-2-C 2-(1)求(点,);d O ABC (2)记函数(,)的图象为图形,若(,),直接写出的取值范围; y kx =11x -≤≤0k ≠G d G ABC 1=k (3)的圆心为(t ,0),半径为1.若(,),直接写出t 的取值范围.T T d T ABC 1=5.如图,平面上存在点P 、点M 与线段AB .若线段AB 上存在一点Q ,使得点M 在以PQ 为直径的圆上,则称点M 为点P 与线段AB 的共圆点.已知点P (0,1),点A (﹣2,﹣1),点B (2,﹣1).(1)在点O (0,0),C (﹣2,1),D (3,0)中,可以成为点P 与线段AB 的共圆点的是 ;(2)点K 为x 轴上一点,若点K 为点P 与线段AB 的共圆点,请求出点K 横坐标x K 的取值范围;(3)已知点M (m ,﹣1),若直线y =x +3上存在点P 与线段AM 的共圆点,请直接写出m 的取值范围. 126. A ,B 是⊙C 上的两个点,点P 在⊙C 的内部.若∠APB 为直角,则称∠APB 为AB 关于⊙C 的内直角,特别地,当圆心C 在∠APB 边(含顶点)上时,称∠APB 为AB 关于⊙C 的最佳内直角.如图1,∠AMB 是AB 关于⊙C 的内直角,∠ANB 是AB 关于⊙C 的最佳内直角.在平面直角坐标系xOy 中.(1)如图2,⊙O 的半径为5,A (0,﹣5),B (4,3)是⊙O 上两点.①已知P 1(1,0),P 2(0,3),P 3(﹣2,1),在∠AP 1B ,∠AP 2B ,∠AP 3B ,中,是AB 关于⊙O 的内直角的是 ;②若在直线y =2x +b 上存在一点P ,使得∠APB 是AB 关于⊙O 的内直角,求b 的取值范围.(2)点E 是以T (t ,0)为圆心,4为半径的圆上一个动点,⊙T 与x 轴交于点D (点D 在点T 的右边).现有点M (1,0),N (0,n ),对于线段MN 上每一点H ,都存在点T ,使∠DHE 是DE 关于⊙T 的最佳内直角,请直接写出n 的最大值,以及n 取得最大值时t 的取值范围.7.对于平面直角坐标系xOy中的图形W1和图形W2.给出如下定义:在图形W1上存在两点A,B(点A,B可以重合),在图形W2上存在两点M,N,(点M于点N可以重合)使得AM=2BN,则称图形W1和图形W2满足限距关系(1)如图1,点C(1,0),D(-1,0),E(0,点P在线段DE上运动(点P可以与点D,E重合),连接OP,CP.①线段OP的最小值为_______,最大值为_______;线段CP的取值范直范围是_____;②在点O,点C中,点____________与线段DE满足限距关系;(2)如图2,⊙O的半径为1,直线(b>0)与x轴、y轴分别交于点F,G.若线段FG与⊙O满足限距关y b=+系,求b的取值范围;(3)⊙O 的半径为r(r>0),点H ,K 是⊙O 上的两个点,分别以H ,K 为圆心,1为半径作圆得到⊙H 和 K ,若对于任意点H ,K ,⊙H 和⊙K 都满足限距关系,直接写出r 的取值范围.8.对于平面直角坐标系中的线段,给出如下定义:若存在使得,则称为线段xOy PQ PQR 2PQR S PQ = PQR PQ的“等幂三角形”,点R 称为线段的“等幂点”.PQ (1)已知.(3,0)A ①在点中,是线段的“等幂点”的是_____________;1234(1,3),(2,6),(5,1),(3,6)P P P P --OA ②若存在等腰是线段的“等幂三角形”,求点B 的坐标;OAB OA (2)已知点C 的坐标为,点D 在直线上,记图形M 为以点为圆心,2为半径的位于x (2,1)C -3y x =-(1,0)T T 轴上方的部分,若图形M 上存在点E ,使得线段的“等幂三角形”为锐角三角形,直接写出点D 的横坐标CD CDE △的取值范围.D x9.在平面直角坐标系中,已知正方形,其中,M ,N 为该xOy ABCD ,,,0,A B C D ⎛⎫⎛⎫⎛ ⎪ ⎪ ⎪ ⎪ ⎝⎭⎝⎭⎝正方形外两点,.给出如下定义:记线段MN 的中点为P ,平移线段MN 得到线段,使点分别1MN =M N '',M N ''落在正方形的相邻两边上,或线段与正方形的边重合(分别为点M ,N ,P 的对应点),线段ABCD M N '',,M N P '''长度的最小值称为线段MN 到正方形的“平移距离”.PP 'ABCD (1)如下图,平移线段MN ,得到正方形内两条长度为1的线段,则这两条线段的位置关系是ABCD 1122,M N M N _______;若分别为的中点,在点中,连接点P 与点_______的线段的长度等于线段MN 到正12,P P 1122,M N M N 12,P P 方形的“平移距离”; ABCD(2)如图,已知点,若M ,N 都在直线BE 上,记线段MN 到正方形的“平移距离”为,求1,0E ⎫+⎪⎪⎭ABCD 1d 1d 的最小值;(3)若线段MN 的中点P 的坐标为,记线段MN 到正方形的“平移距离”为,直接写出的取值范(2)2,ABCD 2d 2d 围.10.对于平面直角坐标系中的图形M 和点P ,给出如下定义:将图形M 绕点P 顺时针旋转得到图形N ,图xOy 90︒形N 称为图形M 关于点P 的“垂直图形”.例如,图1中点D 为点C 关于点P 的“垂直图形”.(1)点A 关于原点O 的“垂直图形”为点B .①若点A 的坐标为,则点B 的坐标为_______;(0,2)②若点B 的坐标为,则点A 的坐标为_______.(2,1)(2).线段关于点G 的“垂直图形”记为,点E 的对应点为,点F 的对应点为(3,3),(2,3),(,0)E F G a --EF E F ''E '.F '①求点的坐标(用含a 的式子表示);E '②若的半径为,上任意一点都在内部或圆上,直接写出满足条件的的长度的最大值.O 2E F ''O EE '11.在平面直角坐标系中,对于两个点,和图形,如果在图形上存在点,(,可以重合)xOy P Q W W M N M N 使得,那么称点与点是图形的一对平衡点.PM QN =P Q W (1)如图1,已知点,;(0,3)A ()2,3B ①设点与线段上一点的距离为,则的最小值是 ,最大值是 ;O AB d d ②在,,这三个点中,与点是线段的一对平衡点的是 ; 13,02P ⎛⎫ ⎪⎝⎭2(1,4)P 3(3,0)P -O AB (2)如图2,已知的半径为1,点的坐标为.若点在第一象限,且点与点是的一对平O D (5,0)(,2)E x D E O 衡点,求的取值范围;x (3)如图3,已知点,以点为圆心,长为半径画弧交的正半轴于点.点(其中)是(3,0)H -O OH x K (,)C a b 0b ≥坐标平面内一个动点,且,是以点为圆心,半径为2的圆,若上的任意两个点都是的一对平5OC =C C HK C 衡点,直接写出的取值范围. b12.在△ABM 中,∠ABM =90°,以AB 为一边向△ABM 的异侧作正方形ABCD ,以A 为圆心,AM 为半径作⊙A ,我们称正方形ABCD 为⊙A 的“关于△ABM 的友好正方形”,如果正方形ABCD 恰好落在⊙A 的内部(或圆上),我们称正方形ABCD 为⊙A 的“关于△ABM 的绝对友好正方形”,例如,图1中正方形ABCD 是⊙A 的“关于△ABM 的友好正方形”.(1)图2中,△ABM 中,BA =BM ,∠ABM =90°,在图中画出⊙A 的“关于△ABM 的友好正方形ABCD ”.(2)若点A 在反比例函数y =(k >0,x >0)上,它的横坐标是2,过点A 作AB ⊥y 轴于B ,若正方形ABCD 为k x⊙A 的“关于△ABO 的绝对友好正方形”,求k 的取值范围.(3)若点A 是直线y =﹣x +2上的一个动点,过点A 作AB ⊥y 轴于B ,若正方形ABCD 为⊙A 的“关于△ABO 的绝对友好正方形”,求出点A 的横坐标m 的取值范围.13.在△ABC 中,以AB 边上的中线CD 为直径作圆,如果与边AB 有交点E (不与点D 重合),那么称为△ DEABC 的C ﹣中线弧.例如,如图中是△ABC 的C ﹣中线弧.在平面直角坐标系xOy 中,已知△ABC 存在C ﹣中线 DE弧,其中点A 与坐标原点O 重合,点B 的坐标为(2t ,0)(t >0).(1)当t =2时,①在点C 1(﹣3,2),C 2(0,C 3(2,4),C 4(4,2)中,满足条件的点C 是 ;②若在直线y =kx (k >0)上存在点P 是△ABC 的C ﹣中线弧所在圆的圆心,其中CD =4,求k 的取值范围; DE(2)若△ABC 的C ﹣中线弧所在圆的圆心为定点P (2,2),直接写出t 的取值范围. DE14.在△ABC 中,点P 是∠BAC 的角平分线AD 上的一点,若以点P 为圆心,PA 为半径的⊙P 与△ABC 的交点不少于4个,点P 称为△ABC 关于∠BAC 的“劲度点”,线段 PA 的长度称为△ABC 关于∠BAC 的“劲度距离”. (1)如图,在∠BAC 平分线AD 上的四个点、、、中,连接点A 和点 的线段长度是△ABC 关于∠1P 2P 3P4P BAC 的“劲度距离”.(2)在平面直角坐标系中,已知点M (0,t ),N (4,0).①当t =时,求出△MON 关于∠MON 的“劲度距离”的最大值.51dMON 关于∠MON 的“劲度距离”,请直接写出t 的取值范围.d ≤15.对于平面内的图形G 1和图形G 2,记平面内一点P 到图形G 1上各点的最短距离为d 1,点P 到图形G 2上各点的最短距离为d 2,若d 1=d 2,就称点P 是图形G 1和图形G 2的一个“等距点”.在平面直角坐标系 xOy 中,已知点 A(6,0),B (0,(1)在C (4,0),D (2,0),E (1,3)三点中,点A 和点B 的等距点是 ;(2)已知直线 y =2.①若点A 和直线y =2的等距点在x 轴上,则该等距点的坐标为 ;②若直线y =b 上存在点A 和直线y =2的等距点,求实数b 的取值范围;(3)记直线AB 为直线l 1,直线l 2: ,以原点O 为圆心作半径为r 的⊙O .若⊙O 上有m 个直线l 1和直y =线l 2的等距点,以及n 个直线l 1和y 轴的等距点(m ≠0,n ≠0),当 m ≠n 时,求r 的取值范围.16.对于平面内的点M ,如果点P ,点Q 与点M 所构成的是边长为1的等边三角形,则称点P ,点Q 为点MPQ M 的一对“关联点”,进一步地,在中,若顶点M ,P ,Q 按顺时针排列,则称点P ,点Q 为点M 的一对“顺MPQ 关联点”;若顶点M ,P ,Q 按逆时针排列,则称点P ,点Q 为点M 的一对“逆关联点”.已知,(1,0)A(1)在中,点A 的一对关联点是____,它们为点A 的一对___关联点(填“顺”或3(0,0),(0,1),(2,0),,2O B C D ⎛ ⎝“逆”);(2)以原点O 为圆心作半径为1的圆,已知直线.:l y b =+①若点P 在⊙O 上,点Q 在直线l 上,点P ,点Q 为点A 的一对关联点,求b 的值;②若在⊙O 上存在点R ,在直线l 上存在两点和,其中,且点T ,点S 为点R 的一对顺关联()11,T x y ()22,S x y 12x x >点,求b 的取值范围.17.在平面直角坐标系中,对于任意两点,若(k 为常数且),则xOy ()()1122,,,M x y N x y 1212x x y y k -+-=0k ≠称点M 为点N 的k 倍直角点.根据以上定义,解决下列问题:(1)已知点(1,1)A ①若点是点A 的k 倍直角点,则k 的值是___________;(2,3)B -②在点中是点A 的2倍直角点的是_______;(2,3),(1,1),(0,2),(0,0)C D E O --③若直线上存在点A 的2倍直角点,求b 的取值范围;2y x b =-+(2)的圆心T 的坐标为,半径为r ,若上存在点O 的2倍直角点,直接写出r 的取值范围. T (1,0)T 18.在平面直角坐标系中,任意两点,,定义线段的“直角长度”为O x y ()11,P x y ()22,Q x y PQ .2121PQ d x x y y =-+-(1)已知点.(3,2)A ① ________;OA d =② 已知点,若,求m 的值;(,0)B m 6AB d =(2)在三角形中,若存在两条边“直角长度”之和等于第三条边的“直角长度”,则称该三角形为“和距三角形”.已知点.(3,3)M ① 点.如果为“和距三角形”,求d 的取值范围;(0,)(0)D d d ≠OMD ② 在平面直角坐标系中,点C 为直线上一点,点K 是坐标系中的一点,且满足,当点C 在直xOy 4y x =--1CK =线上运动时,点K 均满足使为“和距三角形”,请你直接写出点C 的横坐标的取值范围.OMK △C x 19.如图,直线l 和直线l 外一点P ,过点P 作于点H 任取直线l 上点Q ,点H 关于直线的对称点为点PH l ⊥PQ ,标点为点P 关于直线l 的垂对点.在平面直角坐标系中,H 'H 'xOy(1)已知点,则点中是点P 关于x 轴的垂对点的是_______;(0,2)P (0,0),(2,2),(0,4)O A B (2)已知点,且,直线上存在点M 关于x 轴的垂对点,求m 的取值范围; (0,)M m 0m >443y x =-+(3)已知点,若直线上存在两个点N 关于x 轴的垂对点,直接写出n 的取值范围,(,2)N n y x n =+20.在平面直角坐标系xOy 中,对于图形Q 和∠P ,给出如下定义:若图形Q 上的所有的点都在∠P 的内部或∠P 的边上,则∠P 的最小值称为点P 对图形Q 的可视度.如图1,∠AOB 的度数为点O 对线段AB 的可视度.(1)已知点N (2,0),在点,,中,对线段ON 的可视度为60º的点是______. 1M 2M 3(2,3)M (2)如图2,已知点A (-2,2),B (-2,-2),C (2,-2),D (2,2),E (0,4).①直接写出点E 对四边形ABCD 的可视度为______°;②已知点F (a ,4),若点F 对四边形ABCD 的可视度为45°,求a 的值.21.在平面直角坐标系中,对于点A 和线段,如果点A ,O ,M ,N 按逆时针方向排列构成菱形,xOy MN AOMN 且,则称线段是点A 的“相关线段”.例如,图1中线段是点A 的“-相关线段”.AOM α∠=MN α-MN 30︒(1)已知点A 的坐标是.(0,2)①在图2中画出点A 的“-相关线段”,并直接写出点M 和点N 的坐标;30︒MN②若点A 的“-相关线段”经过点,求的值; αα(2)若存在使得点P 的“-相关线段”和“-相关线段”都经过点,记,直接写出t 的取值,()αβαβ≠αβ(0,4)PO t =范围.参考答案1.(1);(2)3)当时,此时;当时,此时. 22B C t =min 1OA =BC =max 2OA =BC =【分析】(1)以点A 为圆心,分别以为半径画圆,进而观察是否与有交点即可; 112233,,,,,AB AC AB AC AB AC O (2)由旋转的性质可得是等边三角形,且是的弦,进而画出图象,则根据等边三角形的性质可进AB C ''△B C ''O 行求解;(3)由是的以点为中心的“关联线段”,则可知都在上,且,然后由BC O A ,B C ''O 1,2AB AB AC AC ''====题意可根据图象来进行求解即可.【详解】解:(1)由题意得:通过观察图象可得:线段能绕点A 旋转90°得到的“关联线段”,都不能绕点A 进行旋转得到; 22B C O 1133,B C B C 故答案为;22B C (2)由题意可得:当是的以点为中心的“关联线段”时,则有是等边三角形,且边长也为1,当BC O A AB C ''△点A 在y 轴的正半轴上时,如图所示:设与y 轴的交点为D ,连接,易得轴,B C ''OB 'B C y ''⊥∴, 12B D DC ''==∴ OD ==AD ==∴OA =∴t =当点A 在y 轴的正半轴上时,如图所示:同理可得此时的OA =∴;t =(3)由是的以点为中心的“关联线段”,则可知都在上,且,则有当BC O A ,B C ''O 1,2AB AB AC AC ''====以为圆心,1为半径作圆,然后以点A 为圆心,2为半径作圆,即可得到点A 的运动轨迹,如图所示:B '由运动轨迹可得当点A 也在上时为最小,最小值为1,此时为的直径,O AC 'O ∴,90AB C ''∠=︒∴,30AC B ''∠=︒∴;cos30BC B C AC '''==⋅︒=由以上情况可知当点三点共线时,OA 的值为最大,最大值为2,如图所示:,,A B O '连接,过点作于点P ,,OC B C '''C 'C P OA '⊥∴,1,2OC AC OA ''===设,则有,OP x =2AP x =-∴由勾股定理可得:,即, 22222C P AC AP OC OP '''=-=-()222221x x --=-解得:, 14x =∴ C P '=∴, 34B P OB OP ''=-=在中, Rt B PC '' B C ''=∴ BC =综上所述:当时,此时;当时,此时 min 1OA =BC max 2OA =BC =【点睛】本题主要考查旋转的综合、圆的基本性质、三角函数及等边三角形的性质,熟练掌握旋转的性质、圆的基本性质、三角函数及等边三角形的性质是解题的关键.2.(1)平行,P 3;(23)232d ≤≤【分析】(1)根据圆的性质及“平移距离”的定义填空即可;(2)过点O 作OE ⊥AB 于点E ,交弦CD 于点F ,分别求出OE 、OF 的长,由得到的最小值;1d OE OF =-1d (3)线段AB 的位置变换,可以看作是以点A 为圆心,半径为1的圆,只需在⊙O 内找到与之平行,且长度32,2⎛⎫ ⎪⎝⎭为1的弦即可.平移距离的最大值即点A ,B 点的位置,由此得出的取值范围.2d 2d 【详解】解:(1)平行;P 3;(2)如图,线段AB 在直线上,平移之后与圆相交,得到的弦为CD ,CD ∥AB ,过点O 作OE ⊥AB y =+于点E ,交弦CD 于点F ,OF ⊥CD ,令,直线与x 轴交点为(-2,0),直线与x 轴夹角为60°,∴0y =.2sin 60OE ︒==由垂径定理得: OF ==∴; 1d OE OF =-=(3)线段AB 的位置变换,可以看作是以点A 为圆心,半径为1的圆,只需在⊙O 内找到与之平行,且长度32,2⎛⎫ ⎪⎝⎭为1的弦即可;点A 到O 的距离为. 52AO ==如图,平移距离的最小值即点A 到⊙O 的最小值:; 2d 53122-=平移距离的最大值线段是下图AB 的情况,即当A 1,A 2关于OA 对称,且A 1B 2⊥A 1A 2且A 1B 2=1时.∠2d B 2A 2A 1=60°,则∠OA 2A 1=30°,∵OA 2=1,∴OM=, A 2, 12∴MA=3,AA 2∴的取值范围为: 2d 232d ≤【点睛】本题考查圆的基本性质及与一次函数的综合运用,熟练掌握圆的基本性质、点与圆的位置关系、直线与圆的位置关系是解题的关键.3.(1);(2)①P 的纵坐标或;②π1p y ≥12P y ≤0t <≤【分析】 (1)由三角函数值及等腰直角三角形性质可求得DE=2,最长中内弧即以DE 为直径的半圆,的长即以DE 为 DE直径的圆周长的一半;(2)根据三角形中内弧定义可知,圆心一定在DE 的中垂线上,,①当时,要注意圆心P 在DE 上方的中垂12t =线上均符合要求,在DE 下方时必须AC 与半径PE 的夹角∠AEP 满足90°≤∠AEP <135°;②根据题意,t 的最大值即圆心P 在AC 上时求得的t 值.【详解】解:(1)如图2,以DE 为直径的半圆弧,就是△ABC 的最长的中内弧,连接DE ,∵∠A=90°,D ,E 分别 DEDE是AB ,AC 的中点,, 114,42sin 22∴=====⨯=AC BC DE BC B ∴弧; DE 122ππ=⨯=(2)如图3,由垂径定理可知,圆心一定在线段DE 的垂直平分线上,连接DE ,作DE 垂直平分线FP ,作EG ⊥AC 交FP 于G ,①当时,C (2,0),∴D (0,1),E (1,1),, 12t =1,12⎛⎫ ⎪⎝⎭F 设由三角形中内弧定义可知,圆心线段DE 上方射线FP 上均可,∴m≥1, 1,2P m ⎛⎫ ⎪⎝⎭∵OA=OC ,∠AOC=90°∴∠ACO=45°,∵DE ∥OC∴∠AED=∠ACO=45°作EG ⊥AC 交直线FP 于G ,FG=EF=12根据三角形中内弧的定义可知,圆心在点G 的下方(含点G )直线FP 上时也符合要求;12∴m 综上所述,或m≥1. 12m②图4,设圆心P 在AC 上,∵P 在DE 中垂线上,∴P 为AE 中点,作PM ⊥OC 于M ,则PM= 32, 3,2⎛⎫∴ ⎪⎝⎭P t ∵DE ∥BC∴∠ADE=∠AOB=90°,∴==AE ∵PD=PE ,∴∠AED=∠PDE∵∠AED+∠DAE=∠PDE+∠ADP=90°,∴∠DAE=∠ADP12∴===AP PD PE AE 由三角形中内弧定义知,PD≤PM ,AE≤3,解得:1322∴AE3t0>∴< t t 【点睛】 此题是一道圆的综合题,考查了圆的性质,弧长计算,直角三角形性质等,给出了“三角形中内弧”新定义,要求学生能够正确理解新概念,并应用新概念解题.4.(1)2;(2)或;(3)或10k -≤<01k <≤4t =-04t -≤≤4t =+【详解】分析:(1)画出图形,根据“闭距离”的概念结合图形进行求解即可.(2)分和两种情况,画出示意图,即可解决问题.0k <0k >(3)画出图形,直接写出t 的取值范围.详解:(1)如下图所示:∵(,),(6,)B 2-2-C 2-∴(0,)D 2-∴(,)d O ABC 2OD ==(2)或10k -≤<01k <≤(3)或或 4t =-04t ≤≤-4t =+点睛:属于新定义问题,考查点到直线的距离,圆的切线的性质,认真分析材料,读懂“闭距离”的概念是解题的关键.5.(1)C ;(2)≤x k ﹣1≤x k 3)或【分析】(1)由题意可知当Q 与A 重合时,点C 在以AP 为直径的圆上,所以可以成为点P 与线段AB 的共圆点的是C ;(2)根据题意由两点的距离公式可得,分别画以AP 和BP 为直径的圆交x 轴于4个点:K 1、K 2、K 3、K 4,结合图形2可得4个点的坐标,从而得结论;(3)由题意先根据直线y=x+3,当x=0和y=0计算与x 轴和y 轴的交点坐标,分两种情况:M 在A 的左侧和右12侧,先计算圆E 与直线y=x+3相切时m 的值,从而根据图形可得结论.12【详解】解:(1)如图1,可以成为点P 与线段AB 的共圆点的是C ,故答案为:C ;(2)∵P (0,1),点A (﹣2,﹣1),点B (2,﹣1).∴AP =BP =,如图2,分别以PA 、PB 为直径作圆,交x 轴于点K 1、K 2、K 3、K 4,∵OP =OG =1,OE ∥AB ,∴PE =AE∴OE =AG =1,12∴K 1(0),k 2(,0),k 3﹣1,0),k 4(0),∵点K 为点P 与线段AB 的共圆点,∴≤x k ﹣1≤x k(3)分两种情况:①如图3,当M 在点A 的左侧时,Q 为线段AM 上一动点,以PQ 为直径的圆E 与直线y =x+3相切于点F ,连12接EF ,则EF ⊥FH ,当x =0时,y =3,当y =0时,y =x+3=0,x =﹣6,12∴ON =3,OH =6,∵tan ∠EHF ===, ON EF OH FH 3612设EF =a ,则FH =2a ,EH ,∴OE =,Rt △OEP 中,OP =1,EP =a ,由勾股定理得:EP 2=OP 2+OE 2,∴,2221(6)a =+解得:a ,∴QG =2OE =2()=,∴②如图4,当M 在点A 的右侧时,Q 为线段AM 上一动点,以PQ 为直径的圆E 与直线y =x+3相切于点F ,连12接EF ,则EF ⊥FH ,同理得QG =,∴,综上,m 的取值范围是或.【点睛】本题属于圆和一次函数综合题,考查一次函数的应用,新定义:M 为点P 与线段AB 的共圆点,圆的切线的性质等知识,解题的关键是理解题意,学会利用图象法解决问题,学会利用特殊点解决取值范围问题.6.(1)①∠AP 2B ,∠AP 3B ;②﹣5<b ≤5;(2)n 的最大值为2;t 的取值范围是t <5【分析】(1)判断点P 1,P 2,P 3是否在以AB 为直径的圆弧上即可得出答案;(2)求得直线AB 的解析式,当直线y =2x +b 与弧AB 相切时为临界情况,证明△OAH ∽△BAD ,可求出此时b =5,则答案可求出;(3)可知线段MN 上任意一点(不包含点M )都必须在以TD 为直径的圆上,该圆的半径为2,则当点N 在该圆的最高点时,n 有最大值2,再分点H 不与点M 重合,点M 与点H 重合两种情况求出临界位置时的t 值即可得解.【详解】解:(1)如图1,,,,1(1,0)P (0,5)A -(4,3)B,AB \1P A 1P B 不在以为直径的圆弧上,1P ∴AB 故不是关于的内直角,1APB ∠AB O ,,,2(0,3)P (0,5)A -(4,3)B,,,28P A \=AB =24P B =,22222P A P B AB \+=,290AP B \Ð=°是关于的内直角,2AP B \ÐAB O 同理可得,,22233P B P A AB +=是关于的内直角,3AP B \ÐAB O 故答案为:,;2AP B Ð3AP B Ð(2)是关于的内直角,APB ∠ AB O,且点在的内部,90APB ∴∠=︒P O 满足条件的点形成的图形为如图2中的半圆(点,均不能取到),∴P H A B过点作轴于点,B BD y ⊥D ,,(0,5)A - (4,3)B ,,4BD ∴=8AD =并可求出直线的解析式为,AB 25y x =-当直线过直径时,,∴2y x b =+AB 5b =-连接,作直线交半圆于点,过点作直线,交轴于点,OB OH E E //EF AB y F ,,OA OB = AH BH =,EH AB ∴⊥,EH EF ∴⊥是半圆的切线.EF ∴H ,,OAH OAH Ð=Ð 90OHB BDA Ð=Ð=°,OAH BAD \D D ∽,∴4182OH BD AH AD ===, 1122OH AH EH \==,OH EO \=,,EOF AOH Ð=Ð 90FEO AHO Ð=Ð=°,()EOF HOA ASA \D @D ,5OF OA \==,直线的解析式为,//EF AB AB 25y x =-直线的解析式为,此时,∴EF 25y x =+5b =的取值范围是.b ∴55b -< (3)对于线段上每一个点,都存在点,使是关于的最佳内直角,MN H T DHE ∠DE T 点一定在的边上,∴T DHE ∠,,线段上任意一点(不包含点都必须在以为直径的圆上,该圆的半径为2, 4TD = 90DHT ∠=︒MN )M TD 当点在该圆的最高点时,有最大值,∴N n 即的最大值为2.n 分两种情况:①若点不与点重合,那么点必须在边上,此时,H M T HE 90DHT ∠=︒点在以为直径的圆上,∴H DT 如图3,当与相切时,,G MN GH MN ⊥,,1OM = 2ON =MN \,,,GMH OMN Ð=Ð GHM NOM Ð=Ð2ON GH ==,()GHM NOM ASA \D @DMN GM \==,1OG \=,1OT \=当与重合时,,T M 1t =此时的取值范围是,∴t 11t < ②若点与点重合时,临界位置有两个,一个是当点与重合时,,另一个是当时,, H M T M 1t =4TM =5t =此时的取值范围是,∴t 15t <综合以上可得,的取值范围是.t 15t < 【点睛】本题是圆的综合题,考查了一次函数图象上点的坐标特征,直角三角形的性质,圆周角定理,勾股定理,相似三角形的判定与性质,全等三角形的判定与性质等知识,利用数形结合的思想,正确理解最佳内直角的意义是解本题的关键.7.(1,②O ;(2);(3)0<r≤3. 2CP ≤≤13b ≥【分析】(1)①根据垂线段最短以及已知条件,确定OP ,CP 的最大值,最小值即可解决问题.②根据限距关系的定义判断即可.(2)直线与x 轴、y 轴分别交于点F ,G (0,b ),分三种情形:①线段FG 在⊙O 内部,②线段FG 与y b =+⊙O 有交点,③线段FG 与⊙O 没有交点,分别构建不等式求解即可.(3)如图3中,不妨设⊙K ,⊙H 的圆心在x 轴上位于y 轴的两侧,根据⊙H 和⊙K 都满足限距关系,构建不等式求解即可.【详解】(1)①如图1中,∵D (-1,0),E(0,∴OD=1,OE =∴ OE tan EDO OD∠==∴∠EDO=60°,当OP ⊥DE 时,,此时OP 的值最小, •60OP OD sin =︒=当点P 与E 重合时,OP当CP ⊥DE 时,CP 的值最小,最小值•60CD cos =︒=当点P 与D 或E 重合时,PC 的值最大,最大值为2,. 2CP ≤≤②根据限距关系的定义可知,线段DE 上存在两点M ,N ,满足OM=2ON ,故点O 与线段DE 满足限距关系.故答案为O .(2)直线与x 轴、y 轴分别交于点F ,G (0,b ),y b =+当0<b <1时,线段FG 在⊙O 内部,与⊙O 无公共点,此时⊙O 上的点到线段FG 的最小距离为1-b ,最大距离为1+b ,∵线段FG 与⊙O 满足限距关系,∴1+b≥2(1-b ),解得, 13b ≥∴b 的取值范围为. 131b ≤<当1≤b≤2时,线段FG 与⊙O 有公共点,线段FG 与⊙O 满足限距关系,当b >2时,线段FG 在⊙O 的外部,与⊙O 没有公共点,此时⊙O 上的点到线段FG 的最小距离为,最大距离为b+1, 121b -∵线段FG 与⊙O 满足限距关系,∴, 11212b b ⎛⎫+≥- ⎪⎝⎭而总成立, 11212b b ⎛⎫+≥- ⎪⎝⎭∴b >2时,线段FG 与⊙O 满足限距关系,综上所述,b 的取值范围为. 13b ≥(3)如图3中,不妨设⊙K ,⊙H 的圆心在x 轴上位于y 轴的两侧,两圆的距离的最小值为2r-2,最大值为2r+2,∵⊙H 和⊙K 都满足限距关系,∴2r+2≥2(2r-2),解得r≤3,故r 的取值范围为0<r≤3.【点睛】本题属于圆综合题,考查了解直角三角形,垂线段最短,直线与圆的位置关系,限距关系的定义等知识,解题的关键是理解题意,学会利用参数构建不等式解决问题,属于中考创新题型.8.(1)①:②或;(2或24,P P 362⎛⎫ ⎪⎝⎭,362⎛⎫ ⎪⎝⎭,-1D x <<3D x <<【分析】(1)①根据定义求出三角形面积与OA 2进行比较即可确定线段的“等幂点”;②如图,由是线段OA 的“等OA OAB 幂三角形”,可得.由点A 的坐标为,若记中边上的高为h ,可得, 求出2OAB S OA = ()3,0A OAB OA 392OAB S h == .由是等腰三角形,点B 在线段OA 的垂直平分线上即可求点B 的坐标为(,6)或(,-6); 6h =OAB 3232(2)设半圆与x 轴交于G ,H 两点,过T 作CH 的平行线与半圆交于R ,作CH 的垂线交半圆于Q ,直线y =x -3与y 轴交于N ,设D (x ,x -3),过D 作y 轴平行线,与过C 作x 轴平行线交于F ,求出N (0,-3), H (3,0),可证△ONH 为等腰直角三角形,∠OHN =∠ONH =45°,点D 运动分两种情况,第一种情况点D 在射线CH ,去掉线段CH部分运动,在Rt △TCH 中TH =2,TC =CH =TH ×sin45°=2,QC=2,又因为△ECD 为锐角三角形,点E 在上运动,点E 到CD 的距离h h =2CD , 第二种 QR 2h ≤≤3D x <<情况点D 在射线CU 上,去掉线段CU 部分运动,点E 在上运动,求出GU =GH ×cos45°= QG,可求. 2h ≤≤)22x ≤-≤1D x <<【详解】 (1)①=,P 1不是线段OA 的“等幂点”. 1OP A S 1211933222P OA y OA ⨯⋅=⨯⨯=<=, P 2是线段OA 的“等幂点”. 2OP A S 2211369=22P OA y OA ⨯⋅=⨯⨯==,P 3不是线段OA 的“等幂点”. 3OP A S 3211331222P OA y OA ⨯⋅=⨯⨯=<=, P 4是线段OA 的“等幂点”. 4OP A S 421136922P OA y OA ⨯⋅=⨯⨯==是线段的“等幂点”的是,OA 24,P P 故答案为::24,P P②如图,∵是线段OA 的“等幂三角形”,OAB ∴.2OAB S OA = ∵点A 的坐标为,若记中边上的高为h ,()3,0A OAB OA 则有. 13922OAB S OA h h =⨯⨯== 解得.6h =∴点B 在直线或上.6y =6y =-∵是等腰三角形,OAB ∴点B 在线段OA 的垂直平分线上.OA 的垂直平分线为x =,与直线或的交点为B 1(,6),B 2(,-6), 326y =6y =-3232综上所述,点B 的坐标为(,6)或(,-6), 3232(2)设半圆与x 轴交于G ,H 两点,过T 作CH 的平行线与半圆交于R ,作CH 的垂线交半圆于Q ,直线y =x -3与y 轴交于N ,设D (x ,x -3),过D 作y 轴平行线,与过C 作x 轴平行线交于F ,当x =0时,y =-3,N (0,-3),当y =0时,x -3=0,x =3,H (3,0),∴ON =3=OH ,△ONH 为等腰直角三角形,∠OHN =∠ONH =45°,点D 运动分两种情况,第一种情况点D 在射线CH ,去掉线段CH 部分运动,∵TC ⊥NH ,∠OHN =45°,∴△TCH 为等腰直角三角形,在Rt △TCH 中TH =2,TC =CH =TH ×sin45°=2QC=2 又因为△ECD 为锐角三角形,点E 在上运动, QR点E 到CD 的距离h 2h ≤≤(x-2), ∵线段的“等幂三角形”,CD S △CDE ==CD 2, 12h CD ⋅∴h =2CD (x -2),)22x <-<解得 52x <点D 在H 右侧,x>3,∴ 3D x <<第二种情况点D 在射线CU 上,去掉线段CU 部分运动,点E 在上运动, QG又因为△ECD 为锐角三角形,GU=GH×cos45°=∴2h ≤≤∵线段的“等幂三角形”,CD S △CDE ==CD 2, 12h CD ⋅∴h =2CD (2-x ),则)22x ≤-≤, 1D x <<D 的横坐标或 D x 1D x <<3D x <<【点睛】本题考查新定义问题,仔细阅读新定义,抓住三角形的高为底的二倍,涉及三角形面积,等腰三角形,等腰直角三角形,线段垂直平分线,一次函数的性质,圆的性质,直线与圆的位置关系,锐角三角函数,锐角三角形,列双边不等式,解不等式等知识,难度较大,综合较强,熟练掌握多方面知识才是解题关键.9.(1)平行,P 1;(2)3). 1d 212d -≤【分析】(1)根据图形,比较PP 1,PP 2的长度即可求解;(2)根据已知条件求得∠P 1BE =45,过P 1作P 1Q ⊥BE 于Q ,则△P 1QB 为等腰直角三角形,利用特殊角三角函数︒值即可求解;(3)先找到最值点,再利用两点之间的距离公式即可求解.【详解】(1)解:由图可得MN ∥M 1N 1,MN ∥M 2N 2,∴M 1N 1∥M 2N 2,而PP 1<PP 2,故线段MN 到正方形ABCD 的“平移距离”为PP 1;故答案为:平行,P 1;(2)∵B (0),C ,0),四边形ABCD 为正方形,。
【中考数学压轴题专题突破27】圆中的新定义问题(1)

【中考压轴题专题突破27】圆中的新定义问题(1)1.定义:如果一个三角形中有两个内角α,β满足α+2β=90°,那我们称这个三角形为“近直角三角形”.(1)若△ABC是“近直角三角形”,∠B>90°,∠C=50°,则∠A=度;(2)如图1,在Rt△ABC中,∠BAC=90°,AB=3,AC=4.若BD是∠ABC的平分线,①求证:△BDC是“近直角三角形”;②在边AC上是否存在点E(异于点D),使得△BCE也是“近直角三角形”?若存在,请求出CE的长;若不存在,请说明理由.(3)如图2,在Rt△ABC中,∠BAC=90°,点D为AC边上一点,以BD为直径的圆交BC于点E,连结AE交BD于点F,若△BCD为“近直角三角形”,且AB=5,AF=3,求tan∠C的值.2.定义:如果一个点能与另外两个点构成直角三角形,则称这个点为另外两个点的勾股点.如矩形OBCD中,点C为O,B两点的勾股点,已知OD=4,在DC上取点E,DE=8.(1)如果点E是O,B两点的勾股点(点E不在点C),试求OB的长;(2)如果OB=12,分别以OB,OD为坐标轴建立如图2的直角坐标系,在x轴上取点F(5,0).在线段DC上取点P,过点P的直线l∥y轴,交x轴于点Q.设DP=t.①当点P在DE之间,以EF为直径的圆与直线l相切,试求t的值;②当直线l上恰好有2点是E,F两点的勾股点时,试求相应t的取值范围.3.定义:已知点O是三角形的边上的一点(顶点除外),若它到三角形一条边的距离等于它到三角形的一个顶点的距离,则我们把点O叫做该三角形的等距点.(1)如图1,△ABC中,∠ACB=90°,AC=3,BC=4,O在斜边AB上,且点O是△ABC的等距点,试求BO的长.(2)如图2,△ABC中,∠ACB=90°,点P在边AB上,AP=2BP,D为AC中点,且∠CPD=90°.①求证:△CPD的外接圆圆心是△ABC的等距点;②求tan∠PDC的值.4.定义:如果三角形的两个内角α与β满足α+2β=90°,那么称这样的三角形为“类直角三角形”.尝试运用(1)如图1,在Rt△ABC中,∠C=90°,BC=3,AB=5,BD是∠ABC的平分线.①证明△ABD是“类直角三角形”;②试问在边AC上是否存在点E(异于点D),使得△ABE也是“类直角三角形”?若存在,请求出CE的长;若不存在,请说明理由.类比拓展(2)如图2,△ABD内接于⊙O,直径AB=13,弦AD=5,点E是弧AD上一动点(包括端点A,D),延长BE至点C,连结AC,且∠CAD=∠AOD,当△ABC是“类直角三角形”时,求AC的长.5.我们不妨约定:如图①,若点D在△ABC的边AB上,且满足∠ACD=∠B(或∠BCD =∠A),则称满足这样条件的点为△ABC边AB上的“理想点”.(1)如图①,若点D是△ABC的边AB的中点,AC=2,AB=4.试判断点D是不是△ABC边AB上的“理想点”,并说明理由.(2)如图②,在⊙O中,AB为直径,且AB=5,AC=4.若点D是△ABC边AB上的“理想点”,求CD的长.(3)如图③,已知平面直角坐标系中,点A(0,2),B(0,﹣3),C为x轴正半轴上一点,且满足∠ACB=45°,在y轴上是否存在一点D,使点A是B,C,D三点围成的三角形的“理想点”,若存在,请求出点D的坐标;若不存在,请说明理由.6.定义:有两个相邻内角和等于另两个内角和的一半的四边形称为半四边形,这两个角的夹边称为对半线.(1)如图1,在对半四边形ABCD中,∠A+∠B=(∠C+∠D),求∠A与∠B的度数之和;(2)如图2,O为锐角△ABC的外心,过点O的直线交AC,BC于点D,E,∠OAB=30°,求证:四边形ABED是对半四边形;(3)如图3,在△ABC中,D,E分别是AC,BC上一点,CD=CE=3,CE=3EB,F 为DE的中点,∠AFB=120°,当AB为对半四边形ABED的对半线时,求AC的长.【中考压轴题专题突破27】圆中的新定义问题(1)参考答案与试题解析1.解:(1)∠B不可能是α或β,当∠A=α时,∠C=β=50°,α+2β=90°,不成立;故∠A=β,∠C=α,α+2β=90°,则β=20°,故答案为20;(2)①如图1,设∠=ABD∠DBC=β,∠C=α,则α+2β=90°,故△BDC是“近直角三角形”;②存在,理由:在边AC上是否存在点E(异于点D),使得△BCE是“近直角三角形”,AB=3,AC=4,则BC=5,则∠ABE=∠C,则△ABC∽△AEB,即,即,解得:AE=,则CE=4﹣=;(3)①如图2所示,当∠ABD=∠DBC=β时,则AE⊥BF,则AF=FE=3,则AE=6,AB=BE=5,过点A作AH⊥BC于点H,设BH=x,则HE=5﹣x,则AH2=AE2﹣HE2=AB2﹣HB2,即52﹣x2=62﹣(5﹣x)2,解得:x=;cos∠ABE===cos2β,则tan2β=,则tanα=;②如图3所示,当∠ABD=∠C=β时,过点A作AH⊥BE交BE于点H,交BD于点G,则点G是圆的圆心(BE的中垂线与直径的交点),∵∠AEB=∠DAE+∠C=α+β=∠ABC,故AE=AB=5,则EF=AE﹣AF=5﹣3=2,∵DE⊥BC,AH⊥BC,∴ED∥AH,则AF:EF=AG:GE=2:3,则DE=2k,则AG=3k=R(圆的半径)=BG,点H是BE的中点,则GH=DE=k,在△BGH中,BH==2k,在△ABH中,AB=5,BH=2k,AH=AG+HG=4k,由勾股定理得:25=8k2+16k2,解得:k=;在△ABD中,AB=5,BD=6k=,则cos∠ABD=cosβ===cos C,则tan C=;综上,tan C的值为或.2.解:(1)如图1,连接OE,BE,若点E是O,B两点的勾股点,则∠OEB=90°,∴∠OED+∠CEB=90°,∵∠OED+∠DOE=90°,∴∠DOE=∠CEB,又∵∠C=∠ODE,∴△BCE∽△EDO,∴=,即=,∴CE=2,∴OB=DE=8+2=10;(2)①如图2﹣1,设以EF为直径的圆的圆心为Q,与直线l的切点为M,直线l与OB的交点为H,连接QM,则∠FME=90°,QM⊥PH,∴∠HMF+∠PME=90°,∵∠PME+∠PEM=90°,∴∠HMF=∠PEM,又∵∠MHF=∠EPM=90°,∴△MHF∽△EPM,∴=,∵QM⊥PH,l∥y轴,∴HF∥MQ∥PE,∴=,∵FQ=QE,∴HM=MP=2,又∵DP=OH=t,DE=8,OF=5,∴HF=5﹣t,PE=8﹣t,∴=,解得,t1=4,t2=9(点P在DE之间,舍去),∴t=4;②如图2﹣2,当直线l在⊙Q的右侧与⊙Q相切时,由①知△MHF∽△EPM,∴=,此时,HM=MP=2,HF=t﹣5,PE=t﹣8,∴=,解得,t1=4,t2=9,∴当t=4或9时直线l与⊙Q相切,∵点E,F以及直线l上的点均可为直角三角形的直角顶点,∴当直线l上恰好有2点是E,F两点的勾股点时,相应t的取值范围为0≤t<4或t=5或t=8或9<t≤12.3.解:(1)CB=4,AC=3,则AB=5,①当OH⊥BC时,只有OH=OA一种情况,设OB=x,则OH=OA=5﹣x,则sin B===,解得:x=;②当OH′⊥AC时,同理可得:OH′=OB,解得:x=,综上,OB=或;(2)①设△CPD的外接圆圆心为点O,连接OP、OB,则OD=OP=OC,设圆的半径为R,AP=2BP=2a,则AD=2R,OD=R,则,故PD∥OB,故∠BOP=∠DPO,∠COB=∠ODP,而∠ODP=∠OPD,∴∠POB=∠COB,而BO=BO,OP=OC,∴△BCO≌△BPO(SAS),∴∠BPO=90°,即OP⊥AB,且OP=OC,故:△CPD的外接圆圆心是△ABC的等距点;②∵△BCO≌△BPO(SAS),∴BC=BP=a,而AB=3a,AC=4R,故(3a)2=(4R)2+a2,解得:a=,tan∠PDC=tan∠COB====.4.(1)①证明:如图1中,∵BD是∠ABC的角平分线,∴∠ABC=2∠ABD,∵∠C=90°,∴∠A+∠ABC=90°,∴∠A+2∠ABD=90°,∴△ABD为“类直角三角形”.②如图1中,假设在AC边设上存在点E(异于点D),使得△ABE是“类直角三角形”.在Rt△ABC中,∵AB=5,BC=3,∴AC===4,∵∠AEB=∠C+∠EBC>90°,∴∠ABE+2∠A=90°,∵∠ABE+∠A+∠CBE=90°∴∠A=∠CBE,∴△ABC∽△BEC,∴=,∴CE==,(2)∵AB是直径,∴∠ADB=90°,∵AD=5,AB=13,∴BD===12,①如图2中,当∠ABC+2∠C=90°时,作点D关于直线AB的对称点F,连接F A,FB.则点F在⊙O上,且∠DBF=∠DOA,∵∠DBF+∠DAF=180°,且∠CAD=∠AOD,∴∠CAD+∠DAF=180°,∴C,A,F共线,∵∠C+∠ABC+∠ABF=90°∴∠C=∠ABF,∴△F AB∽△FBC,∴=,即=,∴AC=.②如图3中,由①可知,点C,A,F共线,当点E与D共线时,由对称性可知,BA平分∠FBC,∴∠C+2∠ABC=90°,∵∠CAD=∠CBF,∠C=∠C,∴△DAC∽△FBC,∴=,即=,∴CD=(AC+5),在Rt△ADC中,CD2+AD2=AC2,∴AC=(舍去负值),综上所述,当△ABC是“类直角三角形”时,AC的长为或.5.解:(1)结论:点D是△ABC的“理想点”.理由:如图①中,∵D是AB中点,AB=4,∴AD=DB=2,∵AC2=(2)2=8,AD•AB=8,∴AC2=AD•AB,∴=,∵∠A=∠A,∴△ACD∽△ABC,∴∠ACD=∠B,∴点D是△ABC的“理想点”,(2)如图②中,∵点D是△ABC的“理想点”,∴∠ACD=∠B或∠BCD=∠A,当∠ACD=∠B时,∵∠ACD+∠BCD=90°,∴∠BCD+∠B=90°,∴∠CDB=90°,当∠BCD=∠A时,同法证明:CD⊥AB,∵AB是直径,∴∠ACB=90°,∵AB=5,AC=4,∴BC==3,∵AB•CD=AC•BC,∴CD=.(3)如图③中,存在.有三种情形:过点A作MA⊥AC交CB的延长线于M,作MH⊥y轴于H.∵∠MAC=∠AOC=∠AHM=90°,∠ACM=45°,∴∠AMC=∠ACM=45°,∴AM=AC,∵∠MAH+∠CAO=90°,∠CAO+∠ACO=90°,∴∠MAH=∠ACO,∴△AHM≌△COA(AAS),∴MH=OA,OC=AH,设C(a,0),∵A(0,2),B(0,﹣3),∴OA=MH=2,OB=3.AB=5,OC=AH=a,BH=a﹣5,∵MH∥OC,∴=,∴=,解得a=6或﹣1(舍弃),经检验a=6是分式方程的解,∴C(6,0),OC=6,①当∠D1CA=∠ABC时,点A是△BCD1的“理想点”.设D1(0,m),∵∠D1CA=∠ABC,∠CD1A=∠CD1B,∴△D1AC∽△D1CB,∴CD12=D1A•D1B,∴m2+62=(m﹣2)(m+3),解得m=42,∴D1(0,42).②当∠BCA=∠CD2B时,点A是△BCD2的“理想点”.易知:∠CD2O=45°,∴OD2=OC=6,∴D2(0,6).综上所述,满足条件的点D坐标为(0,42)或(0,6).6.解:(1)由四边形内角和为360°,可得∠A+∠B+∠C+∠D=360°,则∠A+∠B+2(∠A+∠B)=360°,∴∠A+∠B=120°;(2)如图2,连结OC,由三角形外心的性质可得,OA=OB=OC,∴∠OAB=∠OBA=30°,∠OCA=∠OAC,∠OCE=∠OBC,∴∠ACB=(180°﹣30°﹣30°)÷2=60°,则∠CAB+∠CBA=120°,在四边形ABED中,∠CAB+∠CBA=120°,则另两个内角之和为240°,∴四边形ABED为对半四边形;(3)若AB为对半线,则∠CAB+∠CBA=120°,∴∠C=60°,又∵CD=CE,∴△CDE为等边三角形,∵∠CDE=CED=60°,DE=DC=3,∴∠ADF=∠FEB=120°,∵AFB=120°,∴∠DF A+∠EFB=60°,又∵∠DAF+∠DF A=60°,∴∠DAF=∠EFB,∴△ADF∽△FEB,∴=,∵CE=DE=3,CE=3BE,F是DE的中点,∴BE=1,DF=EF=,∴=,∴AD=,∴CA=CD+AD=3+=.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考数学压轴题素材3、10.定义一种运算“*”:对于自然数n 满足以下运算性质:(i )1*1=1,(ii )(n +1)*1=n *1+1,则n *1等于A .nB .n +1C .n -1D .2n 答案:D4、若)(n f 为*)(12N n n ∈+的各位数字之和,如:1971142=+,17791=++,则17)14(=f ;记=∈===+)8(*,)),(()(,)),(()(),()(20081121f N k n f f n f n f f n f n f n f k k 则K ____答案:56、一个计算装置有一个入口A 和一输出运算结果的出口B ,将自然数列{}(1)n n ≥中的各数依次输入A 口,从B 口得到输出的数列{}n a ,结果表明:①从A 口输入1n =时,从B 口得113a =;②当2n ≥时,从A 口输入n ,从B 口得到的结果n a 是将前一结果1n a -先乘以自然数列{}n 中的第1n -个奇数,再除以自然数列{}n a 中的第1n +个奇数。
试问:(1) 从A 口输入2和3时,从B 口分别得到什么数?(2) 从A 口输入100时,从B 口得到什么数?并说明理由。
解(1)2111515a a =⨯÷=3213735a a =⨯÷= (2)先用累乖法得*1()(21)(21)n a n N n n =∈-+得10011(21001)(21001)39999a ==⨯-⨯+7、在△ABC 中,),(),0,2(),0,2(y x A C B -,给出△ABC 满足的条件,就能得到动点A①△ABC 周长为10 1C :252=y②△ABC 面积为102C :)0(422≠=+y y x ③△ABC 中,∠A=90°3C :)0(15922≠=+y y x则满足条件①、②、③的轨迹方程分别为 (用代号1C 、2C 、3C 填入) 答案:213C C C8、已知两个函数)(x f 和)(x g 的定义域和值域都是集合{1,2,3},其定义如下表. 填写下列)]([x f g 的表格,其三个数依次为A. 3,1,2 B . 2,1,3 C. 1,2,3 D. 3,2,1答案:D9、在实数的原有运算法则中,我们补充定义新运算“⊕”如下: 当a b ≥时,a b a ⊕=; 当a b <时,a b b ⊕=2。
则函数[]()f x x x x x ()()()=⊕-⊕∈-1222·,的最大值等于( C ) (“·”和“-”仍为通常的乘法和减法)A. -1B. 1C. 6D. 1210、已知x R ∈,[x ]表示不大于x 的最大整数,如[]π=3,[]-=-121,[]120=,则[]-=3_____________;使[]x -=13成立的x 的取值围是_____________ 答案:213、在算式“2×□+1×□=30”的两个口中,分别填入两个自然数,使它们的倒数之和最小,则这两个数应分别为 和 . 答案:9,12.14、如图为一几何体的的展开图,其中ABCD 是边长 为6的正方形,SD=PD =6,CR=SC ,AQ=AP ,点S,x 1 2 3 f (x )231x 1 2 3 g (x )132x123g (f (x ))D,A,Q 及P,D,C,R 共线,沿图中虚线将它们折叠起来, 使P ,Q ,R ,S 四点重合,则需要 个这样的 几何体,可以拼成一个棱长为6的正方体。
答案:315、用水清洗一堆蔬菜上残留的农药的效果假定如下:用x 单位量的水清洗一次以后,蔬菜上残留的农药量与这次清洗前残留的农药量之比..为21()1f x x=+. (Ⅰ)试解释(0)f 的实际意义;(Ⅱ)现有a (a >0)单位量的水,可以清洗一次,也可以把水平均分成2份后清洗两次.哪种方案清洗后蔬菜上残留的农药比较少?请说明理由. 答案:解:(I )f (0)=1.表示没有用水清洗时,蔬菜上的农药量没有变化.……………2' (Ⅱ)设清洗前蔬菜上的农药量为1,那么用a 单位量的水清洗1次后.残留的农药量为 W 1=1×f (a )=211a +;……………………………………………………………………4' 又如果用2a 单位量的水清洗1次,残留的农药量为1×f (2a )=2)2(11a +,此后再用2a单位量的水清洗1次后,残留的农药量为W 2=2)2(11a +·f (2a )=[2)2(11a +]2=22)4(16a +.……………………………8' 由于W 1-W 2=211a+-22)4(16a +=22222)4)(1()8(a a a a ++-,………………………9' 故当a >22时,W 1>W 2,此时,把a 单位量的水平均分成2份后,清洗两次,残留的农药量较少;当a =22时,W 1=W 2,此时,两种清洗方式效果相同;当a <22时,W 1<W 2,此时,把a 单位量的水清洗一次,残留的农药量较少.…………………………12'16、直角坐标系中横坐标、纵坐标均为整数的点称为格点,如果函数f(x)的图象恰好通过k(k ∈N*)个格点,则称函数f(x)为k 阶格点函数。
下列函数:① f(x)=sinx ; ②f(x)=π(x -1)2+3; ③;)31()(xx f = ④x x f 6.0log )(=,其中是一阶格点函数的有 . 答案:①②④17、一水池有2个进水口,1个出水口,一个口进出水速度如图甲、乙所示.某天0点到6点, 该水池的蓄水量如图丙所示(至少打开一个水口),给出以下3个论断: 进水量 出水量 蓄水量6点不进水不 )。
19、2005年底,某地区经济调查队对本地区居民收入情况进行抽样调查,抽取1000户,按本地区在“十一五”规划中明确提出要缩小贫富差距,到2010年 要实现一个美好的愿景,由右边圆图显示,则中等收入家庭的数 量在原有的基础要增加的百分比和低收入家庭的数量在原有的基础要降低的百分比分别为 ( B )A .25% , 27.5%B .62.5% , 57.9%C .25% , 57.9%D .62.5%,42.1%20、一个三位数abc 称为“凹数”,如果该三位数同时满足a >b 且b <c ,那么所有不同的三位“凹数”的个数是_____________________.答案:三位“凹数”可分两类:一类是aba ,共有210C =45,另一类是abc ,a ≠c ,共有2310C =240,故共有45+240=285个23、定义运算x ※y=⎩⎨⎧>≤)()(y x y y x x ,若|m -1|※m=|m -1|,则m 的取值围是 21≥m26、对任意实数y x ,,定义运算cxy by ax y x ++=*,其中c b a ,,为常数,等号右边的运算是通常意义的加、乘运算。
现已知63*2,42*1==,且有一个非零实数m ,使得对任意实数x ,都有x m x =*,则=m 5 。
28、我国男足运动员转会至海外俱乐部常会成为体育媒体关注的热点新闻。
05年8月,在申花俱乐部队员杜威确认转会至超凯尔特人俱乐部之前,各种媒体就两俱乐部对于杜威的转会费协商过程纷纷“爆料”: 媒体A :“……, 凯尔特人俱乐部出价已从80万英镑提高到了120万欧元。
” 媒体B :“……, 凯尔特人俱乐部出价从120万欧元提高到了100万美元,同时增加了不少附加条件。
”媒体C :“……, 凯尔特人俱乐部出价从130万美元提高到了120万欧元。
”请根据表中提供的汇率信息(由于短时间国际货币的汇率变化不大,我们假定比值为定值),我们可以发现只有媒体 C (填入媒体的字母编号)的报道真实性强一些。
30、在R 上定义运算△:x △y=x(1 -y) 若不等式(x-a)△(x+a)<1,对任意实数x 恒成立,则实数a 的取值围是)23,21(- 。
32、用锤子以均匀的力敲击铁钉入木板。
随着铁钉的深入,铁钉所受的阻力会越来越大,使得每次钉入木板的钉子长度后一次为前一次的()*1N k k∈。
已知一个铁钉受击3次后全部进入木板,且第一次受击后进入木板部分的铁钉长度是钉长的74,请从这个实事中提炼出一个不等式组是 ⎪⎪⎩⎪⎪⎨⎧≥++<+1747474174742k k k。
37、先阅读下列不等式的证法,再解决后面的问题:已知R a a ∈21,,121=+a a ,求证212221≥+a a , 证明:构造函数2221)()()(a x a x x f -+-=22212222121222)(22)(a a x x a a x a a x x f ++-=+++-=因为对一切x ∈R ,恒有)(x f ≥0,所以)(842221a a +-=∆≤0,从而得212221≥+a a ,(1)若R a a a n ∈,,,21Λ,121=+++n a a a Λ,请写出上述结论的推广式; (2)参考上述解法,对你推广的结论加以证明。
解:(1)若R a a a n ∈,,,21Λ,121=+++n a a a Λ,求证:nn a a a 122221≥+++Λ (4')(2)证明:构造函数22221)()()()(n a x a x a x x f -++-+-=Λ (6')22221212)(2n n a a a x a a a nx +++++++-=ΛΛ (9')2222122n a a a x nx ++++-=Λ (11')因为对一切x ∈R ,都有)(x f ≥0,所以△=)(4422221n a a a n +++-Λ≤0,从而证得:nn a a a 122221≥+++Λ. (14')44、已知点列B 1(1,y 1)、B 2(2,y 2)、…、B n (n,y n )(n ∈N ) 顺次为一次函数12141+=x y 图象上的点,点列A 1(x 1,0)、A 2(x 2,0)、…、A n (x n ,0)(n ∈N )顺次为x 轴正半轴上的点,其中x 1=a (0<a <1),对于任意n ∈N ,点A n 、B n 、A n+1构成以 B n 为顶点的等腰三角形。
⑴求{y n }的通项公式,且证明{y n }是等差数列; ⑵试判断x n+2-x n 是否为同一常数(不必证明)⑶在上述等腰三角形A n B n A n+1中,是否存在直角三角形?若有,求出此时a 值;若不存在, 请说明理由。
解:(1)12141n n y +=(n ∈N),y n+1-y n =41,∴{y n }为等差数列 (4')(2)x n+1-x n =2为常数 (6') ∴x 1,x 3,x 5,…,x 2n-1及x 2,x 4,x 6,,…,x 2n 都是公差为2的等差数列,∴x 2n-1=x 1+2(n-1)=2n-2+a ,x 2n =x 2+2(n-1)=2-a+2n-2=2n-a , ∴x n =⎩⎨⎧-+当n为偶数a,-n ,当n为奇数1,a n (10') (3)要使A n B n A n+1为直角三形,则 |A n A n+1|=2n B y =2(1214+n )⇒x n+1-x n =2(1214+n ) 当n 为奇数时,x n+1=n+1-a ,x n =n+a-1,∴x n+1-x n =2(1-a).⇒2(1-a)=2(1214+n ) ⇒a=41211n -(n 为奇数,0<a <1) (*)取n=1,得a=32,取n=3,得a=61,若n ≥5,则(*)无解; (14') 当偶数时,x n+1=n+a ,x n =n-a ,∴x n+1-x n =2a.∴2a=2(1214+n )⇒a=1214+n (n 为偶数,0<a <1) (*'),取n=2,得a=127, 若n ≥4,则(*')无解.综上可知,存在直角三形,此时a 的值为32、61、127. (18')45、⑴证明:当a >1时,不等式23a 12a 13a a +>+成立。
