信号与系统 第二章习题 王老师经典解法(青岛大学)小白发布
信号与系统课后题解第二章

⑺
对⑺式求一阶导,有:
de(t ) d 2 i 2 (t ) di (t ) du (t ) =2 +2 2 + c 2 dt dt dt dt de(t ) d 2 i2 (t ) di (t ) =2 + 2 2 + 2i1 (t ) + 2i 2 (t ) 2 dt dt dt
⑻
将⑸式代入⑻式中,有:
λ 2 + 2λ + 1 = 0
可解得特征根为 微分方程齐次解为
λ1, 2 = −1
y h (t ) = C1e −t + C2 te− t
由初始状态为 y (0 ) = 1, y ' (0 ) = 0 ,则有:
C1 = 1 − C 1 + C 2 = 0
由联立方程可得 故系统的零输入响应为:
由联立方程可得 故系统的零输入响应为:
A1 = 2, A2 = −1
y zi (t ) = 2e − t − e −2 t
(2)由原微分方程可得其特征方程为
λ 2 + 2λ + 2 = 0
可解得特征根为 微分方程齐次解为
λ1, 2 = −1 ± i
y h (t ) = e −t (C1 cos t + C2 sin t )
(− 3C1 + 3C2 )δ (t ) + (C1 + C2 )δ ' (t ) − (− 2C1 + C 2 )δ (t ) = δ (t )
(
(
( + C e )δ (t ) + (C e
2 1
)
−2 t
+ C2 e t δ ' (t )
信号与系统第二章习题

rt et ht
sin tut ut 1ut ut 1
t
0
sin
d
τ
u
t
ut
2
1
t 1
sin
τ
d
τut
u
t
2
1 1 costut ut 2
X
20
第
例2-4 计算卷积 f1(t) f2(t),并画出波形。
页
f1 t
f2 t
2
1
1 e t1u t 1
则得
A1 A2 3 3A1 2A2 2
解得
A1 A2
4 7
代入(1)得
ht 4e2t 7e3t ut X
18
例2-3
第
页
已知线性时不变系统的一对激励和响应波形如下图所示,
求该系统对激励的 et sin tut ut 1零状态响应。
et
r t
1
1
O 12
t
对激励和响应分别微分一次,得
t0
因为特解为3,所以 强迫响应是3,自由响应是 4 et e2t
X
12
方法二
第
页
零状态响应rzs t是方程
d2 r dt
t
2
3
dr d
t
t
2r
t
2
t
6ut
且满足rzs 0 rzs0 0的解
(5)
由于上式等号右边有 t项 ,故rzst应含有冲激函数,
从而rzs t 将发生跳变,即 rzs 0 rzs 0
d2 rt 3 d rt 2rt 0
dt2
dt
信号与系统课后题答案

《信号与系统》课程习题与解答第二章习题(教材上册第二章p81-p87)2-1,2-4~2-10,2-12~2-15,2-17~2-21,2-23,2-24第二章习题解答2-1 对下图所示电路图分别列写求电压的微分方程表示。
图(a):微分方程:11222012()2()1()()()2()()()()2()()()c cc di t i t u t e t dtdi t i t u t dtdi t u t dt du t i t i t dt ⎧+*+=⎪⎪⎪+=⎪⇒⎨⎪=⎪⎪⎪=-⎩图(b ):微分方程:⎪⎪⎪⎩⎪⎪⎪⎨⎧-==+++=+++⎰⎰2021'2'21'2'11)(01)(1Ri t v Ri Mi Li dt i Ct e Ri Mi Li dt i C)()(1)(2)()2()(2)()(33020022203304422t e dtd MR t v C t v dt d C R t v dt d C L R t v dt d RL t v dt d M L =+++++-⇒ 图(c)微分方程:dt i C i L t v ⎰==211'101)(⎪⎪⎪⎩⎪⎪⎪⎨⎧===⇒⎰dt t v L i t v L i dtdt v L i dt d)(1)(1)(10110'1122011∵ )(122111213t i dt d L C i i i i +=+=)(0(1]1[][101011022110331t e dt dR t v RL v dt d RR L C v dt d R C R C v dt d CC μ=+++++⇒图(d)微分方程:⎪⎩⎪⎨⎧+-=++=⎰)()()()()(1)()(11111t e t Ri t v t v dt t i C t Ri t e μRC v dt d 1)1(1+-⇒μ)(11t e V CR = ∵)()(10t v t v μ=)()(1)1(0'0t e R v t v R Cv v =+-⇒2-4 已知系统相应的其次方程及其对应的0+状态条件,求系统的零输入响应。
《信号与系统》课后习题参考答案

《信号与系统》课后习题参考答案第二章 连续信号与系统的时域分析2-9、(1)解:∵系统的微分方程为:)(2)(3)(t e t r t r '=+',∴r(t)的阶数与e(t) 的阶数相等,则h(t)应包含一个)(t δ项。
又∵系统的特征方程为:03=+α,∴特征根3-=α∴)()(2)(3t u Ae t t h t -+=δ∴)]()(3[)(2)(33t e t u e A t t h t t δδ--+-+'=')()(3)(23t A t u Ae t t δδ+-'=-将)(t h 和)(t h '代入微分方程(此时e(t)= )(t δ),得:)()(3)(23t A t u Ae t t δδ+-'-+3)(2)]()(2[3t t u Ae t t δδ'=+-∴A=-6则系统的冲激响应)(6)(2)(3t u et t h t --=δ。
∴⎰⎰∞--∞--==t td ue d h t g τττδτττ)](6)(2[)()(3⎰∞-=t d ττδ)(2⎰∞---t d u e τττ)(63 )()(6)(203t u d e u t t ⎰-∞--=τττ )()3(6)(203t u e t u t --=-τ)()1(2)(23t u e t u t -+=- )(23t u e t -=则系统的阶跃响应)(2)(3t u et g t -=。
2-11、解:①求)(t r zi : ∵系统的特征方程为:0)3)(2(652=++=++αααα,∴特征根:21-=α,32-=α ∴t t zi e C eC t r 3221)(--+= (t ≥0) ②求)(t r zs :t t e A eA t h 3221)(--+= (t ≥0),可求得:11=A ,12-=A (求解过程略) ∴)()()(32t u e e t h t t ---=∴)(*)()(*)()]()[(*)()(*)()(3232t u e t u e t u e t u e t u e e t u e t h t e t r t t t t t t t zs --------=-==)()2121()()(21)()(3232t u e e e t u e e t u e e t t t t t t t -------+-=---= ③求)(t r :)(t r =)(t r zi +)(t r zs ++=--)(3221t te C e C )2121(32t t t e e e ---+- t tt e C e C e 3221)21()1(21---++-+= (t ≥0) ∵)()(t u Ce t r t -=,21=C 21=C ∴ 011=-C , ∴ 11=C0212=+C 212-=C ∴=-)0(r 21211)0(21=-=+=+C C r zi , ='-)0(r 2123232)0(21-=+-=--='+C C r zi 2-12、解:(1)依题意,得:)(2)(*)()(t u e t h t u t r tzi -=+)()()(t t h t r zi δ=+∴)(2)]()([*)()(t u e t r t t u t r t zi zi -=-+δ)(2)()()()1(t u e t r t u t r t zi zi --=-+∴)()12()()()1(t u e t r t r t zi zi -=---,两边求导得:)()12()(2)()(t e t u e t r t r t t zi ziδ-+-=-'-- )(2)()()(t u e t t r t r t zi zi--=-'δ ∴)(11)(112)()()1(t p p t p t t r p zi δδδ+-=+-=- ∴)()(11)(t u e t p t r t zi -=+=δ (2)∵系统的起始状态保持不变,∴)()(t u e t r t zi -=∵)()()(t t h t r zi δ=+,∴)()()(t u e t t h t--=δ∴)]()([*)()()(*)()()(33t u e t t u e t u e t h t e t r t r t t t zi ----+=+=δ )()()(t u te t u e t u e tt t ----+=)()2(t u e t t --= 2-16、证:∑∑∞-∞=--∞-∞=--=-=k k t k t k t u e k t t u e t r )3()3(*)()()3(δ∑∞-∞=--=k k t k t u e e )3(3 ∵当t-3k>0即3t k <时:u(t-3k)为非零值 又∵0≤t ≤3,∴k 取负整数,则:3003311)(---∞=∞=----===∑∑e e e e e et r t k k k t k t 则t Ae t r -=)(,且311--=e A 。
信号与系统第2章作业解答

解:(1) f (t t0 ) (t) f (t0 ) (t)
(2) f (t t0 ) (t t0 )dt f (0)
(3) 2 et (t 3)dt e3 2 (t 3)dt e3
4
4
(4) et sin t (t 1)dt 0 0
第二章 连续时间信号的时域分析
2
n
(4) x1(n) x2 (n) 2n u(n) 3n u(n) 2k 3nk k 0
3n
n
( 2 )k
1 ( 2)n1 3n 3 [3n1 2n1]u(n)
k0 3
1 2
3
(5) x1(n) x2 (n) [(0.5)n u(n 4)][4nu(n 2)]
( 1)k u(k 4) 4nk u(n k 2) 2 k
P59 2.24 解: (2) f1 f3 r(t) r(t 1) r(t 2)
2r(t 1) 2r(t 2) 2r(t 3) r(t 2) r(t 3) r(t 4)
f1 f3
1
0
1
2
34
t
-1
r(t) 3r(t 1) 4r(t 2) 3r(t 3) r(t 4)
4
42
(2) (t 3)etdt e3
(3) (1 t)(t2 4)dt 5
(4) (t) sin 2t dt 2 (t) sin 2t dt 2
t
2t
第二章 连续时间信号的时域分析
6 / 11
P91 3.1 (5) (6) 解: 由题意知 x(n) 的波形如下图示
eatu(t) sin tu(t) a sin t cos t eat u(t) 1 a2
第二章 连续时间信号的时域分析
【VIP专享】信号与系统王明泉第二章习题解答
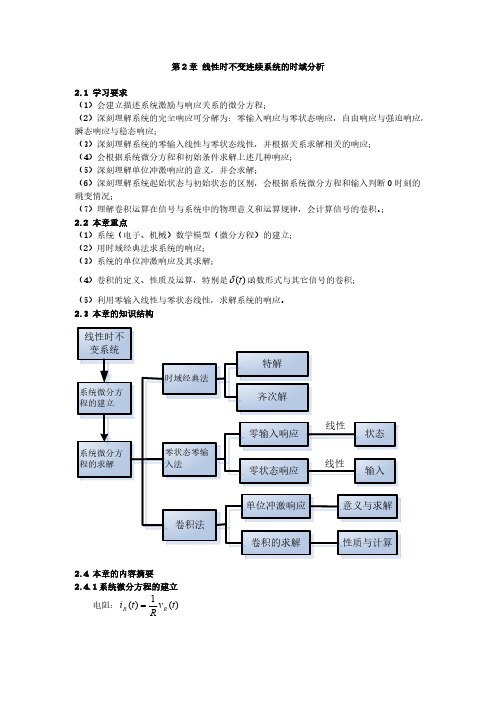
2.1 学习要求 (1)会建立描述系统激励与响应关系的微分方程; (2)深刻理解系统的完全响应可分解为:零输入响应与零状态响应,自由响应与强迫响应, 瞬态响应与稳态响应; (3)深刻理解系统的零输入线性与零状态线性,并根据关系求解相关的响应; (4)会根据系统微分方程和初始条件求解上述几种响应; (5)深刻理解单位冲激响应的意义,并会求解; (6)深刻理解系统起始状态与初始状态的区别,会根据系统微分方程和输入判断 0 时刻的 跳变情况; (7)理解卷积运算在信号与系统中的物理意义和运算规律,会计算信号的卷积。; 2.2 本章重点 (1)系统(电子、机械)数学模型(微分方程)的建立; (2)用时域经典法求系统的响应; (3)系统的单位冲激响应及其求解;
(2)若 x(t) 由几种激励组合而成,则特解也为其相应的组合。 (3)若表中所列特解与齐次解重复,则应在特解中增加一项: t 倍乘表中特解。假
如这种重
复形式有 k 次(特征为 k 次),则依次增加倍乘 t , t 2 ,…, t k 诸项。
2.4.3 起始点的跳变-从 0 到 0 状态的转换
在系统分析中,定义响应区间为确定激励信号 x(t) 加入后系统的状态变化区间。一般
激励 x(t) 都是从 t 0 时刻加入,此时系统的响应区间定义为 0 t 。当系统用微分 方程表示时,系统从 0 到 0 状态有没有跳变取决于微分方程右端自由项是否包含 (t) 及 其各阶导数项。如果包含有 (t) 及其各阶导数项,说明相应的 0 到 0 状态发生了跳变, 即 y(0 ) y(0 ) 或 y'(0 ) y ' (0 ) 等等。这时为确定 y(0 ) 、 y ' (0 ) 等状态,可以用
信号与系统第二章例题

r (0 ) 2 r (0 ) 3 r (0 ) r (0 ) 2
代入r (t ) Ae3t A2et 3e2t 1
A1 A2 3 2 得 3 A1 A2 6 3
r (t ) -4e3t 3et 3e2t
解:1)求自由响应的形式
r '' (t ) 4r ' (t ) 3r (t ) 0
特征方程为: 2 4 3 0 1 3, 2 1
rh (t ) Ae3t A2et 1
2)求强迫响应
利用筛选 特性
e(t ) e2t u(t ) e '(t ) 2e2t u(t ) e2t (t ) 2e2t u(t ) (t )
0 t 0
8
代入方程得
a 2 b 4a 1 c 4b 3a 0
a (t ) b 4a) (t ) (c 4b 3a)u (t ) ( 2 (t ) (t )
a 2 b 7 c 22
4 B 8B 3B 3
rp (t ) 4Be2t
B 3
rp (t ) 3e2t
3)求完全响应
r(t ) rh (t ) rp (t ) Ae3t A2et 3e2t 1
利用冲激函数匹配法求初始条件r (0 )和r(0 )
r '' (t ) 4r ' (t ) 3r (t ) 2 (t ) 3u(t ) r (t ) a (t ) bu (t )
1 3t 5 t (e e )u (t ) 2
注意:1、积分上下限问题; 2、积分结果的始终点问题。
[信号与系统作业解答]第二章
![[信号与系统作业解答]第二章](https://img.taocdn.com/s3/m/90bd92d5240c844769eaeeda.png)
2)
d2 dt 2
r(t)
d r(t) r(t) dt
d e(t) e(t) dt
3)
d dt
r(t)
2r(t)
d2 dt 2
e(t
)
3e(t)
3e(t)
解答:
2)系统的阶跃响应 g(t ) 满足方程
d 2 g(t) d g(t) g(t) (t)
dt 2
dt
其解的形式为
u(t) „„(3)
g(t) e 12t A cos 3 t B sin 3 t
设代入原方程5得从而h0考虑到aabc11代入6式得abte2t1即ht中有t和t因而所求的冲激响应为tut212有一系统对激励为e1tut时的完全响应为r1t2etut对激励为e2tt时的完全响应为r2t1求该系统的零输入响应rzit
第 2 章 连续时间系统的时域分析
2-1 列写电路中电压vo(t)的微分方程表示。
[(t 1)u(t 1) u(t 1) 2u(t 1) u(t 1)]
[u(t) u(t 2) tu(t) u(t 2)]
[(t 1)u(t 1) u(t 2) 2u(t 1) u(t 2)]
[(t 1)u(t 1) 1 (t 1)2u(t 1)] 2
(a)(图略)
解答:符号说明i( 1)(t)
t
i(x )dx
2i1(t) i1(t) i1( 1)(t) i2(t) 2i2(t) i2( 1)(t) vo(t) 2i2(t) (3)
i2( 1)(t) i1( 1)(t)
e(t) (1) 0 (2)
整理得:
2vo(t) 5vo(t) 5vo(t) 3vo(t) 2e (t)
【分析】充分利用冲激函数的卷积性质,卷积的平移性质。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2-16 已知 f1 (t ) =
画出下列各卷积的波形。 (1) s1 (t ) = f1 (t ) ∗ f 2 (t ) ; (2) s2 (t ) = f1 (t ) ∗ f 2 (t ) ∗ f 2 (t ) ; (3) s3 (t ) = f1 (t ) ∗ f 3 (t ) 。
2-17 求题图 2-17 所示电路在 e(t ) = (1 + 2e
第二章
连续时间系统的时域分析
2-1 电路如题图 2-1 所示,列写求 vo (t ) 的微分 方程。
L1 1H R1 2Ω + e(t) i 1 (t )
R2 1Ω + L2 2H 题图 2-1
C
1F
i 2 (t )
vo(t)
2-2 电路如题图 2-2 所示, 列写求 i2 (t ) 的微分方 程。
题图 2-18
−2 t
− 1)U (t ) , 试利用卷积的性质求题
1 0 -1
e2(t)=tU(t) 1 t 0
e3(t)
t 0 1
2-19 一线性时不变的连续时间系统,其初始状态一定,当输入 e1 (t ) = δ (t ) 时,其全响应
r1 (t ) = −3e − tU (t ) ; 当 输 入 e2 (t ) = U (t ) 时 , 其 全 响 应 r2 (t ) = (1 − 5e − t )U (t ) 。 求 当 输 入 e(t ) = tU (t ) 时的全响应。
2-14 计算卷积 f (t ) = f 1 (t ) ∗ f 2 (t ) ,其中 f1 (t ) = sgn(t − 1) , f 2 (t ) = e 2-15 求下列卷积 (1) f1 (t ) = e
−αt
− ( t +1)
U (t + 1) 。
U (t ) ∗ sin(t )U (t ) ;
2-8 电路如题图 2-8 所示, e(t ) 为激励, v(t ) 为响应,求传输算子 H ( p ) ,冲激响应 h(t ) 和
R1
阶跃响应 g (t ) 。
R2 10Ω + v(t) 2H L
+ e(t)
-
20Ω
+
-
0.5v(t)
题图 2-8
2-9 题 图 2-9-1 所 示 电 路 中 , L1 = L2 = M = 1H ,
(2)
(3)
2-4 已知系统的传输算子 H ( p ) 及 0 + 状态条件,求系统的自然频率和零输入响应。 (1) H ( p ) =
p+3 , r (0 + ) = 2 , r ′(0 + ) = 1 ; p + 3p + 2
2
(2) H ( p ) =
p+3 , r (0 + ) = 1 , r ′(0 + ) = 2 。 p + 2p + 2
R1 20Ω + e(t) i 1 (t ) i (t ) L1 0.5H
题图 2-2
R3 10Ω R2 30Ω i 2 (t )
-
+
10i(t)
L2 1H
2-3 已知系统方程及对应的 0 + 状态条件, 求系统 的零输入响应。 (1)
d2 d r (t ) + 3 r (t ) + 2r (t ) = 3e(t ) , r (0 + ) = 4 , r ′(0 + ) = −5 ; 2 dt dt d2 d r (t ) + 2 r (t ) + 5r (t ) = e(t ) , r (0 + ) = 1 , r ′(0 + ) = 1 ; 2 dt dt d3 d2 d d r ( t ) + 2 r (t ) + r (t ) = e(t ) + 3e(t ) , r (0 + ) = r ′(0 + ) = 0 , r ′′(0 + ) = 1 。 3 2 dt dt dt dt
(2)
(3)
(4)
2-11 设 H ( p ) 是线性时不变系统的传输算子,且系统起始状态为零,试证明:
[ H ( p )δ (t )]e − βt = H ( p + β )δ (t )
2-12 求下列函数 f 1 (t ) 与 f 2 (t ) 的卷积 f1 (t ) ∗ f 2 (t ) 。 (1) f1 (t ) = U (t ) , f 2 (t ) = e U (t ) ; (2) f1 (t ) = U (t + 2) , f 2 (t ) = e
e(t ) = x(t )[U (t ) − U (t − 2)] + βδ (t − 2)
式中 x(t ) 为任意 t 函数,若要求系统在 t > 2 的响应为零,试确定 β 值应等于多少。
2-22 设 线 性 时 不 变 系 统 在 零 状 态 条 件 下 , 当 输 入 为 e(t ) 时 , 输 出 为
−2 ( t − 2 ) −2 t
U (t − 2) ;
(3) f1 (t ) = sin(5t +
π
6
) , f 2 (t ) = δ (t − 1) 。
2-13 求下列卷积,并注意相互间的区别。 (1) f a (t ) = A[U (t + 1) − U (t − 1)] ,求 f1 (t ) = f a (t ) ∗ f a (t ) ; (2) f b (t ) = A[U (t ) − U (t − 2)] ,求 f 2 (t ) = f a (t ) ∗ f b (t ) ; (3) f c (t ) = A[U (t ) − U (t − 1)] ,求 f 3 (t ) = f b (t ) ∗ f c (t ) ;
(2) f 2 (t ) = sin( 2πt )[U (t ) − U (t − 1)] ∗ U (t ) ; (3) f 3 (t ) = f a (t ) ∗ f b (t ) ,其中 f a (t ) =
∑ [U (t − 3k ) − U (t − 2 − 3k )] ,
k =0
∞
f b (t ) = sin(πt )U (t ) 。 2− | t | , | t |≤ 2 , f 2 (t ) = δ (t + 5) + δ (t − 5) , f 3 (t ) = δ (t + 1) + δ (t − 1) , , | t |> 2 0
2-24 画出 f (t ) =
∫
t
0−
δ [sin(πt )]dt 的波形图。 π π
2-25 求 f (t ) = [U (t +
) − U (t − )] ∗ {cos(t ) ⋅ δ [sin(t )]} ,并画出结果的波形。 2 2
−3t
)U (t )
+ e(t)
-
R1 1Ω
C
1
R2 2Ω
L
2
+ 1H vo(t)
-
激励下的零状态响应 vo (t ) , 并指出其中的强迫响应 分量与自由响应分量、稳态响应分量与瞬态响应分 量。
2F
0
题图 2-17
2-18 已知某线性时不变系统的单位阶跃响应 g (t ) = ( 2e 图 2-18 所示波形信号激励下的零状态响应。 e1(t) 2 t 1 0 0 2 3 0 1 2
r (t ) = sin(πt )
画出波形图。 2 1 0
,0 ≤ t ≤ 2 ,其波形如题图 2-22-1 所示。试确定该系统的阶跃响应 g (t ) ,并
e(t) 1 t 0 1 2 3
题图 2-22-1
r(t)
0 0 1 2
t
2-23 化简下列两式 (1) δ ( 2t − ) ;
2
1 2
(2) δ [sin(t )] 。
d2 d d (3) 2 r (t ) + 3 r (t ) + 2r (t ) = e(t ) + 3e(t ) ,r (0 − ) = 1 ,r ′(0 − ) = 2 ,e(t ) = e −3tU (t ) 。 dt dt dt
试判断在起始点是否发生跳变,并求 0 + 状态之值。 “1” 且已达稳态,t = 0 时刻开关自 “1” 转至 “2” : 2-6 题图 2-6 所示电路,t < 0 时开关位于 (1)试从物理概念判断 vC (t ) 、 i (t ) 在 t = 0 时刻是否会发生跳变? (2)分别写出 t ≥ 0 + 时间内描述响应 vC (t ) 、 i (t ) 的微 分方程,并求 vC (t ) 、 i (t ) 的完全响应;
d r (t ) + 3r (t ) = e(t ) ; dt d2 r (t ) + 4r (t ) = 2e(t ) ; dt 2 d2 d d3 d2 r t r t r t e t ( ) + 3 ( ) + 2 ( ) = ( ) + 4 e(t ) − 5e(t ) ; dt 2 dt dt 3 dt 2 d2 d d r (t ) + 2 r (t ) + r (t ) = 2 e(t ) + 3e(t ) 。 2 dt dt dt
2 S 1 + +
10V 20V
i (t ) R 2Ω + vC(t) 0.25F C
(3)写出可在 − ∞ < t < ∞ 时间内描述 vC (t ) 、i (t ) 的方 程式,然后利用冲激函数匹配原理判断从 0 − 到 0 + 状态的变化,并与(1)的结果比较。 2-7 系统微分方程、 0 − 状态及激励信号如下:
