青岛大学2020年827信号与系统
青岛大学信号与系统第八章离散时间系统的z域分析
则
Z [an x(n)] X ( z ) a
z , Rx1 a Rx2
特别地 Z [(1)n x(n)] X (z) , Rx1 z Rx2
例：Z
[cos(0n)u(n)]
z(z cos0 ) z2 2z cos0 1
, z 1
Z
[ n cos(0n)u(n)]
z
(z
cos0 )
2
2
nu(n)
z
d dz
z
z 1
(z
z 1)2
n2u(n)
z
d dz
(z
z 1)2
z(z 1) (z 1)3
X (z) 1 [ z z(z 1)] z2 2 (z 1)2 (z 1)3 (z 1)3
, z 1
（四）序列指数加权（ z 域尺度变换）
若 Z [x(n)] X (z) , Rx1 z Rx2
X (z) Z [x(nT )] x(nT )zn n
2T 0 T 3T
t
L [xs (t)] z esT Z [x(nT )]
z
esT
r eT
T 2
s
z re j s j
T—— 抽样间隔，
s
2
T
——
抽样角频率
z平面和 s平面的映射关系：
1. s平面原点 ( 0, 0) j
x(1) (n)
0
n
x(n 1)u(n) x(n 1)u(n 1)
x(0) (n 1)
0
n
x(n 1)u(n) x(n 1)u(n 1) x(1) (n) x(n 1)u(n) x(n 1)u(n 1) x(0) (n 1) x(n 2)u(n) x(n 2)u(n 2) x(2) (n) x(1) (n 1) x(n 2)u(n) x(n 2)u(n 2) x(0) (n 2) x(1) (n 1)
青岛大学考研专业课真题——信号与系统 2009年 (附带答案及评分标准)
科目代码： 827 科目名称： 信号与系统 （共 13 页）请考生写明题号，将答案全部答在答题纸上，答在试卷上无效Ⅰ、填空题（共11题，每空格3分，共33分）1．对冲激偶信号)(t δ'，='⎰∞∞-dt t )(δ ，=-'⎰∞∞-dt t f t t )()(0δ 。
2．时间函数)()(t u e t f t -=的傅里叶变换=)(ωF 。
3．已知()()x n nu n =，()()h n u n =，则卷积和序列)()()(n h n x n y *=在2n =点的取值为(2)y = 。
4．象函数2()221(0)F z z z z -=-++<<∞，则原序列=)(n f 。
5．序列()()x n u n =-的z 变换及其收敛域为 。
6．s 平面的实轴映射到z 平面是 。
7．题图7所示因果周期信号的拉氏变换()F s = 。
8．无失真传输网络的频域系统函数()H j ω= 。
9．某因果LTI （线性时不变）离散时间系统的系统函数3()31z H z z =-，则系统对余弦激励序列()cos()()x n n n π=-∞<<∞的响应()y n = 。
10．写出题图10所示流图描述的连续时间系统的微分方程 。
题图7t题图10科目代码： 827 科目名称： 信号与系统 （共 13 页）请考生写明题号，将答案全部答在答题纸上，答在试卷上无效t题图1322Ⅱ、计算题（共8题，117分）（11分）11．描述某线性时不变因果离散时间系统的差分方程为)1()()1(5.0)(--=-+n x n x n y n y已知当)()(n u n x =时，全响应的1)1(=y ，求零输入响应)(n y zi 。
（12分）12．某因果LTI 连续时间系统，其输入、输出用下列微分—积分方程描述()5()()()()d r t r t e f t d e t dtτττ∞-∞+=--⎰其中()()3()t f t e u t t δ-=+，求该系统的单位冲激响应()h t 。
青岛大学2020年825 自动控制理论
控制科学与工程（0811）/控制工程（085210）
硕士入学考试大纲
考试科目代码及名称：825自动控制理论
一、考试要求
掌握自动控制的基本概念、原理，熟练掌握线性连续系统的时域分析法、根轨迹分析法、频域分析法、状态空间分析法以及系统校正方法，熟练掌握离散系统分析与校正方法、非线性系统特性以及相平面和描述函数分析方法。
二、考试内容
（1）自动控制概念、组成、工作原理
（2）自动控制系统数学模型与结构图化简
（3）典型一阶、二阶线性定常系统分析（输出响应，性能指标分析与计算），稳定性分析与劳斯判据，误差、稳态误差分析与计算（4）根轨迹概念，根轨迹绘制（180度根轨迹、0度根轨迹、参数根轨迹），基于根轨迹的系统性能分析
（5）频率特性概念，频率特性曲线绘制，基于开环频率特性曲线的系统稳定性分析以及稳定程度分析（相角裕度、幅值裕度）（6）基于频率特性的串联校正方法
（7）线性离散系统输出响应、误差响应与稳态误差、稳定性分析
（8）相平面概念、相平面图绘制、相平面分析法，描述函数、
基于描述函数的非线性系统运动分析（周期运动）
（9）线性系统状态空间模型，状态响应与输出响应，能控性与能观性分析，李雅普诺夫稳定性分析。
三、试卷结构（题型分值）
1.本科目满分为150分，考试时间为180分钟。
2.题型结构：计算与分析题。
四、参考书目
《自动控制原理（第六版）》：胡寿松主编，科学出版社，2013年。
青岛大学考研专业课真题——信号与系统 2007年 (附带答案及评分标准)
科目代码： 827 科目名称： 信号与系统 （共 12 页）请考生写明题号，将答案全部答在答题纸上，答在试卷上无效Ⅰ、填空题（共14题，每题3分，共42分）1．积分=-'+⎰∞∞-dt t t )1()2(2δ 。
2．如图1所示，)(t f 为原始信号，)(1t f 为变换信号，则)(1t f 的表达式为 （用)(t f 表示）。
3．若正弦序列0sin()n ω的周期10N =，则0ω的最小取值为0ω= 。
4． 给定微分方程、起始状态、激励信号分别为()2()3()d d r t r t e t dtdt+=、(0)0r -=、()()e t u t =，则(0)r += 。
5．已知)4()()()(--==n u n u n h n x ，则卷积和序列)()()(n h n x n y *=共有 个非零取值。
6．单边拉氏变换21()(2)F s s =+对应的原函数为=)(t f 。
7．图2所示因果周期矩形脉冲的拉氏变换()F s = 。
8．序列||1()2n x n ⎛⎫= ⎪⎝⎭的z 变换及其收敛域为 。
图12 0 )(t f 2t 1 3)(1t f 2t-4 -2图22TT )(t ft1T 2…科目代码： 827 科目名称： 信号与系统 （共 12 页）请考生写明题号，将答案全部答在答题纸上，答在试卷上无效9．若象函数2()(1)z F z z =-，1z <，则原序列=)(n f 。
10．调幅信号26()(100)cos(10)f t Sa t t ππ=⋅的频带宽度为 Hz 。
11．若离散线性时不变系统的单位样值响应()()2(1)3(2)(3)h n n n n n δδδδ=+---+-，则单位阶跃响应()g n 的序列波形为。
12．若某线性时不变离散时间系统的单位样值响应为)(2)1(3)(n u n u n h n n -+--=，则该系统是（因果/非因果、稳定/非稳定）系统。
信号与系统 第二章习题 王老师经典解法(青岛大学)小白发布
2-16 已知 f1 (t ) =
画出下列各卷积的波形。 （1） s1 (t ) = f1 (t ) ∗ f 2 (t ) ； （2） s2 (t ) = f1 (t ) ∗ f 2 (t ) ∗ f 2 (t ) ； （3） s3 (t ) = f1 (t ) ∗ f 3 (t ) 。
2-17 求题图 2-17 所示电路在 e(t ) = (1 + 2e
第二章
连续时间系统的时域分析
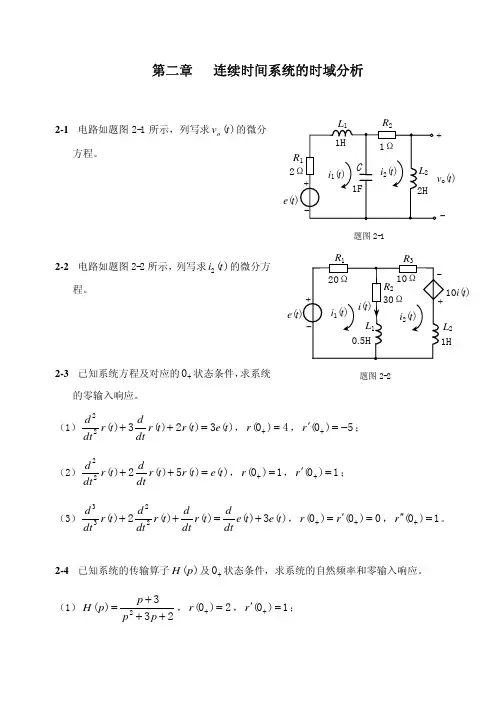
2-1 电路如题图 2-1 所示，列写求 vo (t ) 的微分 方程。
L1 1H R1 2Ω + e(t) i 1 (t )
R2 1Ω + L2 2H 题图 2-1
C
1F
i 2 (t )
vo(t)
2-2 电路如题图 2-2 所示， 列写求 i2 (t ) 的微分方 程。
题图 2-18
−2 t
− 1)U (t ) ， 试利用卷积的性质求题
1 0 -1
e2(t)=tU(t) 1 t 0
e3(t)
t 0 1
2-19 一线性时不变的连续时间系统，其初始状态一定，当输入 e1 (t ) = δ (t ) 时，其全响应
r1 (t ) = −3e − tU (t ) ； 当 输 入 e2 (t ) = U (t ) 时 ， 其 全 响 应 r2 (t ) = (1 − 5e − t )U (t ) 。 求 当 输 入 e(t ) = tU (t ) 时的全响应。
2-14 计算卷积 f (t ) = f 1 (t ) ∗ f 2 (t ) ，其中 f1 (t ) = sgn(t − 1) ， f 2 (t ) = e 2-15 求下列卷积 （1） f1 (t ) = e
信号与系统 第四章习题 王老师经典解法(青岛大学)小白发布
3
E1(s)
∑
1 s
-2 -1
（a）
1 s
2
∑
Y 1( s )
E2(s)
−2 t
Vo ( s ) ； E ( s)
U (t ) ，求零状态响应 vo (t ) ；
（3）若 e(t ) = 10 cos(5t ) ，求正弦稳态响应 voss (t ) 。
0.25F + e(t) -
2:1
1F
2:1
2F +
C1
C2
C3
R
vo(t
-
题图 4-17-1
4-18 题图 4-18-1 所示电路 （1）若初始无储能，信号源为 is (t ) ，为求 i1 (t ) （零状态响应） ，列写转移函数 H ( s ) ，并给 出对应于 is (t ) = 10 cos(2t )U (t ) 的零状态响应 i1 (t ) ； （2）若初始状态以 i1 (0) ， v 2 (0) 表示（都不等于零） ，但
is(t
)
1Ω + 1F
-
1H
i1(t
is (t ) = 0 ，求 i1 (t ) （零输入响应） 。
v 2( t )
1Ω
题图 4-18-1
4-19 求题图 4-19 中电路的电压传输函数，如果要求响应中不出现 强迫响应分量，激励函数应有怎样的模式？
C
R1
+ +
-)
e(t R2
vo(t)
-
题图 4-19
4-11 用拉氏变换分析法，求下列系统的响应。
d 2 r (t ) dr (t ) （1） +3 + 2r (t ) = 0 ， r (0 − ) = 1 ， r ' (0 − ) = 2 2 dt dt
信号与系统(郑君里)ppt
t
f(t)
t/2
f(t/2)
0
1
0
1
T
2
T
2
时间尺度压缩：t t 2 ,波形扩展
求新坐标
t
f(t/2)
0
1
2T
2
f(t)f(2t)
f t
2 1
O
Tt
宗量相同，函数值相同
t
f(t)
2t
f(2t)
0
1
0
1
T
2
T
2
求新坐标
t
f(2t)
0
1
T/2
2
t2t，时间尺度增加，波形压缩。
比较
f t
2 1
O
Tt
•三个波形相似，都是t 的一次 函数。 •但由于自变量t 的系数不同， 则达到同样函数值2的时间不同。 •时间变量乘以一个系数等于改 变观察时间的标度。
a 1 压缩,保持信号的时间缩短 f (t) f (at)0 a 1 扩展,保持信号的时间增长
4．一般情况
f t f at b f at b a 设a 0
f (t) K sin(t )
f
t
T
K
2π
O
2π
衰减正弦信号：
K et sint
f (t) 0
振幅：K 周期：T
2π
1
f
频率：f
角频率： 2 π f t 初相：
t0 0
t0
欧拉(Euler)公式
sin t 1 ejt ejt 2j
cos t 1 ejt ejt 2
t
间为，t0时函数有断点，跳变点
宗量>0 函数值为1 宗量<0 函数值为0
青岛大学825自动控制理论2020年考研专业课初试大纲
青岛大学2020年考研专业课初试大纲
控制科学与工程（0811）/控制工程（085210）
硕士入学考试大纲
考试科目代码及名称：825自动控制理论
一、考试要求
掌握自动控制的基本概念、原理，熟练掌握线性连续系统的时域分析法、根轨迹分析法、频域分析法、状态空间分析法以及系统
校正方法，熟练掌握离散系统分析与校正方法、非线性系统特性以
及相平面和描述函数分析方法。
二、考试内容
（1）自动控制概念、组成、工作原理
（2）自动控制系统数学模型与结构图化简
（3）典型一阶、二阶线性定常系统分析（输出响应，性能指标分析与计算），稳定性分析与劳斯判据，误差、稳态误差分析与计算（4）根轨迹概念，根轨迹绘制（180度根轨迹、0度根轨迹、参数根轨迹），基于根轨迹的系统性能分析
（5）频率特性概念，频率特性曲线绘制，基于开环频率特性曲线的系统稳定性分析以及稳定程度分析（相角裕度、幅值裕度）（6）基于频率特性的串联校正方法
（7）线性离散系统输出响应、误差响应与稳态误差、稳定性分析
（8）相平面概念、相平面图绘制、相平面分析法，描述函数、
精都考研（）——全国100000考研学子的选择。
信号与信息处理专业排名
信号与信息处理(134)1 西安电子科技大学 A+2 北京邮电大学 A+3 电子科技大学 A+4 清华大学 A+5 东南大学 A+6 北京交通大学 A+7 北京理工大学 A8 哈尔滨工业大学 A9 华中科技大学 A10 上海交通大学 A11 北京航空航天大学 A12 北京大学 A13 西北工业大学 A14 大连理工大学 A15 中国科学技术大学 A16 南京大学 A17 四川大学 A18 山东大学 A19 天津大学 A20 浙江大学 A21 西安交通大学 A22 武汉大学 A23 哈尔滨工程大学 A24 南京邮电大学 A25 上海大学 A26 杭州电子科技大学 AB+等(41个):西南交通大学、合肥工业大学、南京理工大学、华南理工大学、苏州大学、吉林大学、深圳大学、大连海事大学、中北大学、重庆邮电大学、南京航空航天大学、重庆大学、武汉理工大学、南开大学、中国海洋大学、成都信息工程学院、上海海事大学、江南大学、安徽大学、北京师范大学、西安理工大学、北京工业大学、同济大学、哈尔滨理工大学、东北大学、湖南大学、长江大学、中国传媒大学、桂林电子科技大学、东华大学、南京信息工程大学、厦门大学、沈阳航空工业学院、济南大学、西安邮电学院、中国民航大学、北方工业大学、长春理工大学、陕西师范大学、浙江工业大学、成都理工大学B等(40个):江苏科技大学、西安科技大学、天津工业大学、长春工业大学、华北电力大学、广东工业大学、中南大学、贵州大学、河海大学、中山大学、暨南大学、西北大学、汕头大学、长安大学、新疆大学、上海理工大学、江西科技师范学院、福州大学、南昌大学、太原理工大学、华东理工大学、山东科技大学、五邑大学、西安工业大学、山西师范大学、西南大学、西华大学、天津理工大学、燕山大学、湘潭大学、兰州理工大学、烟台大学、重庆工学院、北京印刷学院、青岛大学、沈阳工业大学、黑龙江大学、扬州大学、南昌航空工业学院、内蒙古大学C等(25个):名单略电路与系统(91)1 西安电子科技大学 A+2 电子科技大学 A+3 复旦大学 A+4 北京邮电大学 A+5 东南大学 A6 中国科学技术大学 A7 清华大学 A8 上海交通大学 A9 西北工业大学 A10 浙江大学 A11 西安交通大学 A12 南京大学 A13 杭州电子科技大学 A14 华南理工大学 A15 安徽大学 A16 北京工业大学 A17 太原理工大学 A18 重庆大学 AB+等(27个):吉林大学、湖南大学、燕山大学、华中科技大学、厦门大学、上海大学、华南师范大学、同济大学、北京航空航天大学、天津大学、大连理工大学、北京大学、重庆邮电大学、北方工业大学、北京理工大学、武汉理工大学、山东科技大学、宁波大学、南京理工大学、南京邮电大学、华中师范大学、桂林电子科技大学、山东大学、宁夏大学、北京交通大学、兰州大学、广东工业大学B等(27个):东北大学、四川大学、大连海事大学、武汉大学、西安科技大学、东华理工大学、中山大学、南京航空航天大学、安徽理工大学、深圳大学、广西师范大学、兰州交通大学、湖南师范大学、西北师范大学、西安理工大学、东北师范大学、西北大学、郑州大学、中南大学、合肥工业大学、华北电力大学、河北科技大学、长沙理工大学、西南科技大学、贵州大学、河海大学、中国矿业大学C等(19个):名单略通信与信息系统(121)1 北京邮电大学 A+2 西安电子科技大学 A+3 清华大学 A+4 电子科技大学 A+5 东南大学 A+6 上海交通大学 A+7 中国科学技术大学 A8 北京交通大学 A9 北京大学 A10 浙江大学 A11 哈尔滨工业大学 A12 北京理工大学 A13 华南理工大学 A14 华中科技大学 A15 北京航空航天大学 A16 西安交通大学 A17 武汉大学 A18 西南交通大学 A19 哈尔滨工程大学 A20 西北工业大学 A21 南京航空航天大学 A22 南京邮电大学 A23 东北大学 A24 天津大学 AB+等(36个):中山大学、厦门大学、武汉理工大学、山东大学、吉林大学、南京理工大学、北京科技大学、上海大学、中国传媒大学、复旦大学、中国矿业大学、四川大学、重庆邮电大学、重庆大学、华东师范大学、云南大学、中国民航大学、大连海事大学、长春理工大学、郑州大学、福州大学、南开大学、华中师范大学、广东工业大学、湖南大学、中南大学、同济大学、杭州电子科技大学、桂林电子科技大学、华北电力大学、苏州大学、上海海事大学、首都师范大学、北京师范大学、大连理工大学、西安理工大学B等(36个):兰州交通大学、南京大学、中北大学、北京工业大学、长江大学、河北工业大学、太原理工大学、浙江工商大学、深圳大学、河海大学、暨南大学、西安科技大学、辽宁工程技术大学、中国地质大学、中国海洋大学、燕山大学、兰州理工大学、兰州大学、浙江工业大学、南通大学、哈尔滨理工大学、西南科技大学、江苏大学、南昌大学、安徽大学、辽宁工学院、齐齐哈尔大学、宁波大学、贵州大学、上海师范大学、河南理工大学、西安邮电学院、河北大学、海南大学、成都理工大学、长沙理工大学C等(25个):名单略。
【青岛大学2012年考研专业课真题】信号与系统2012
4
科目代码： 827 科目名称： 信号与系统 （共
4
页）
请考生写明题号，将答案全部答在答题纸上，答在试卷上无效
e(t ) e3t u(t ) ，则 r (0 )
。
9 ．若可逆系统的单位冲激响应为 h(t ) ，其逆系统的单位冲激响应为 hI (t ) ，则
h(t ) hI (t )
。
10．图 3 所示以 f (t ) 为输入， g (t ) 为输出的对 调幅波进行相干解调的系统是 （线性/非线性） 、 的。 （时变/时不变）
f (t )
低通滤波
g (t )
cos(0t )
图3
二、 （15 分）计算图 4 所示矩形脉冲信号 h(t ) 和半波正弦脉冲信号 e(t ) 的卷积积 分 r (t ) h(t ) e(t ) ，并画出 r (t ) 的波形。
f e (t ) =
， f o (t ) =
。 。
Hz ，
3．若正弦序列 sin(0 n) 的周期 N 10 ，则 0 的最小取值为 0 4．周期矩形脉冲信号 f (t ) 如图 1 所示，则该信号的谱线间隔为 直流分量为 。
1 … -10 -1 0 1 图1 10
f (t )
…
t
5．频谱函数 F () j sgn() 的傅里叶逆变换 f (t ) 6 ．图 2 所示因果周期信号的拉氏变换 F ( s) 为 。
f (t )
1 0 1 2 3
图2
。 ，对应的收敛域
4
5
6
t
1 7．序列 ( ) n u (n) 的 z 变换 X ( z ) 2
8．给定微分方程、起始状态、激励信号分别为
827信号与系统
C2 v2(t)
V1 ( s)
-
R2
-
H (s) 的零、极点分布图；
图7
（2）在网络参数 R1、 R2 、 C1 、 C2 满足什么条件时可构成全通网络， 给出此条 件下的 H (s) 。
五、（16 分）描述某连续时间系统的微分方程为
d2
d
d
r(t) + 3 r(t) + 2r(t) = e(t) + 3e(t)
R2 两 端 ， 为 使 v2 (t) 较 v1(t) 无 失 真 ， R1 、 R2 、 C1 、 C2 应 满 足 的 关 系
为
。
三、（15 分）计算图 6 所示脉冲函数 f1(t) 和 f2 (t) 的卷积积分 f (t) = f1(t) ∗ f2 (t) ，
并画出 f (t) 的波形。
f1 (t ) 1
ห้องสมุดไป่ตู้
f2 (t) 2
-1 0 1
t 01
图6
t
3
青岛大学 2013 年硕士研究生入学考试试题
科目代码： 827 科目名称： 信号与系统 （共 6 页）
请考生写明题号，将答案全部答在答题纸上，答在试卷上无效
四、（15 分） 格状网络如图 7 所示。
R1
+
+
（1）求电压转移函数 H (s) = V2 (s) ，在 s 平面上绘出 v1(t) C1
6
A. 1 ,σ > 1 B. 1 ,σ < 1 C.
1− s
1− s
1 ,σ < 1 D. 1 ,σ > 1
s −1
s −1
f (t)
g (t )
2
信号与系统 第一章_绪论(青岛大学)小白发布
∫
∞
−∞ ∞
Sa (t )dt = π Sa 2 (t )dt = π
∫
−∞
另外一个类似的函数：
sin π t sinc( t ) = πt
§1.3 信号的运算
（一）对自变量进行的运算： 移位、反褶与尺度 对自变量进行的运算： 移位、 1. 移位： f (t ) → f (t ± t0 ) 移位：
t
t
t
sin (Ωt ) + sin (8 Ωt )
× sin ( Ωt ) sin (8 Ωt )
t
t
反相点
§1.4 阶跃信号与冲激信号 奇异信号： 奇异信号：
（一）单位斜变信号tu(t) （二）单位阶跃信号 u(t) （三）单位冲激信号δ (t) （四）冲激偶信号δ ' (t)
（一）单位斜变信号tu(t)
（3） cos(3n − )
当 当
2π
2π
π
ω0
为有理数时， 为周期序列； 为有理数时，sin(ω0n) 为周期序列； 为无理数时， 为非周期序列。 为无理数时，sin(ω0n) 为非周期序列。
2π 为无理数， 为无理数， 3
非周期序列
4
ω0
4．能量（有限）信号与功率（有限）信号 能量（有限）信号与功率（有限）
2.信号的传输、 2.信号的传输、交换和处理 信号的传输
信号传输（Transmission）
——古代烽火传送边疆警报 ——击鼓、信鸽、旗语等 击鼓、信鸽、 ——电信号传输（19世纪开始）： 电信号传输（ 世纪开始 世纪开始）：
1837年莫尔斯发明了电报 年莫尔斯发明了电报 1876年贝尔发明了电话 年
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
信号与信息处理专业硕士入学考试大纲
考试科目代码及名称：827信号与系统
一、考试要求
掌握连续时间信号与系统分析的基本理论，掌握离散信号分析、离散时间系统设计的基本理论和方法，具备从事实际信号分析与处理工作的基本能力。
二、考试内容
（1）信号的运算和分解
（2）连续线性时不变系统的时域经典分析
（3）系统模型与系统框图
（4）单位冲激响应与卷积
（5）傅里叶变换与采样定理
（6）拉普拉斯变换与连续系统的s域分析
（7）系统函数与频率响应
（8）信号无失真传输、调制与解调
（9）离散时间系统的时域经典分析
（10）序列的z变换与离散傅里叶变换
三、试卷结构（题型分值）
1.本科目满分为150分，考试时间为180分钟。
2.题型结构
（1）选择题：占总分的16%
（2）填空题: 占总分的16%
（3）计算题：占总分的68%
四、参考书目
《信号与系统引论》，郑君里应启珩杨为理，高等教育出版社，出版时间2018-12-10。