上海地区三类主要暴雨天气的云微物理和边界层敏感性模拟研究
WRF模式中微物理和积云参数化方案的对比试验
ａ 以上。 ｒｎ ｉ 本文模拟了５ ４ ０ 月ｌ 日０ 时一 １ 日ｏ 时ｆ ５ ０ 世 界时 ，下同） 发生在广东中部 的强降水过程。
３ 试验 设计 ． ２
一
般 认 为 ，对 于ＷＲＦ 式 ，积 云参 数 适用 于 模
模拟中，究竟采取哪一种方案 的结果会更理想 ，
在 不 同区域 ，仍需 要 深入 研究 ［］ １。 １
目前 ， 对珠 三 角地 区ＷＲ 模 式 的微 物理 过 针 Ｆ
Ｌ ￣＇］ ｉ Ｔ 以及Ｒｌ ｄｅ １的参数化方案的基础 ｎ ２ ｌ ｌｅｇ等［ ｔ １ ３ ］
上得到 ，饱和修正方案采ｍＴ ｏ 的方法 。这 ａ 等【】
收稿 日期 ：２ １—８３；修 订 日期 ：２ １ｄ１１ ０００ —０ Ｏｌ ８
资助项 目：国家自然基金． 广东联合基金重点项 Ｈ（ ８３ ０ ） Ｕ０ ３０ １ 资助 ；中山大学高性能与网格计算中心支持。 通讯 作 者 ：王雪 梅 ，女 ，从 事 环境 科学 研 究工 作 。Ｅ ｉ ｅｓ ｘ ｍａ ：ｅｗ ｍ＠ｍａ． ｓ． ｕｃ ｌ ｉｓ ｕｅ ． ｌｙ ｄ ｎ
量分 离 成格 点单元 的立 体 块 。这种 处理 方法 ，伴
随对快速微物理过程处理方法的一些修改 ，使得 方案在大时间步长时计算结果稳定 。 根据Ｒ ａ的 ｙｎ 观测结果 ，冰的平均半径假定为温度函数。冰水 混合相仅在温度高于一 ℃时考虑 ，而冰面饱和 １ ０ 状态则假定在云体低于－ ０℃。 １
第２卷 第４ ８ 期
２１ ０ ２年 ８月
Ｊ Ｕ Ｎ Ｌ Ｏ 热Ｔ 带 ＰＣ Ｌ ＭＥ Ｅ Ｒ Ｌ Ｇ Ｏ Ｒ Ａ Ｆ Ｒ Ｉ Ａ 象 学 报 Ｏ Ｙ Ｏ 气 ＴＱ Ｏ
bin和bulk微物理方案在我国飑线模拟中的敏感性研究
bin和bulk微物理方案在我国飑线模拟中的敏感性研究殷蕾;平凡【摘要】分别利用weather research and forecasting (WRF)中尺度模式中的bulk和bin微物理参数化方案,对2014年7月12日发生在华东地区的一次飑线过程进行了数值模拟.结果表明:bulk方案基本模拟出了飑线初生、发展、成熟和消亡的生命史,但与实况存在1 ～2h的延迟,且强度偏弱;而bin方案模拟的雷达回波结构松散,组织化程度较低,更类似于现状对流.从模拟的地面降水看,bin方案模拟的雨带偏窄,且强降水区偏北;而bulk方案则基本模拟出了强降水区的位置.在此基础上进一步分析了两种方案模拟的各水凝物的垂直分布,结果表明bulk方案在高层产生了大量云冰,而bin方案中雪和霰粒子数量较多.【期刊名称】《科学技术与工程》【年(卷),期】2016(016)016【总页数】8页(P136-142,148)【关键词】飑线;微物理方案;SBM;bulk;敏感性研究【作者】殷蕾;平凡【作者单位】南京信息工程大学地理与遥感学院,南京210044;南京信息工程大学地理与遥感学院,南京210044;中国科学院大气物理研究所云降水物理与强风暴重点实验室,北京100029【正文语种】中文【中图分类】P457.9飑线是由许多活跃的雷暴单体排列成线状的中尺度对流系统，其过境处常伴有雷暴、大风、冰雹、龙卷等剧烈天气现象。
目前我国对这类强对流天气的预报能力还十分有限，一个重要原因是数值模式对云微物理过程的描述还有待完善。
目前模式中的云微物理参数化方案大致可分为两类：一类是传统的谱函数(bulk)方法，如Lin方案[1]；另一种是分档法(bin方法)，如Hebrew大学发展的微物理过程分档云模式(SBM Hebrew University cloud model, HUCM)。
简单说来谱函数参数化法是用一个经验函数(如gamma函数)来描述云中水凝物粒子的总体分布特征；而分档法则是根据水成物的相态、粒子大小、形状、密度等微物理特征将其分为几十或几百档，给出各个档粒子的预报方程及它们之间的相互转化关系[2]。
降雨数据时空精度对城市暴雨变异性及频率分析的影响
第34卷第3期2023年5月㊀㊀水科学进展ADVANCES IN WATER SCIENCE Vol.34,No.3May 2023DOI:10.14042/ki.32.1309.2023.03.007降雨数据时空精度对城市暴雨变异性及频率分析的影响庄㊀琦1,刘曙光1,2,周正正1,2(1.同济大学土木工程学院,上海㊀200092;2.中国气象局上海城市气候变化应对重点开放实验室,上海㊀200030)摘要:提升城市暴雨内涝防治精细化水平是解决城市洪涝问题的关键㊂采用16种不同时空分辨率的降雨产品,利用暴雨时空异质性评估指标和随机暴雨移置法,在上海地区定量评估降雨数据精度对暴雨事件时空变异性诊断和频率分析的影响㊂研究发现利用低精度降雨数据得到的年最大暴雨序列发生时间延迟㊁降水量低估,暴雨过程不均匀性提升㊁空间不均匀性降低;在不同重现期下,降雨数据精度对频率分析结果影响有显著差异,重现期越大,低精度数据带来的低估程度越大;时间精度的影响占主导地位,可达空间精度的5倍㊂在城市暴雨洪涝研究中有必要采用更高精度的降雨数据,建议与研究区域类似的小型城市地区在防洪设计中使用精度达(12h㊁0.05ʎ)或以上的降雨数据㊂关键词:城市极端降雨;时空分辨率;不确定性;频率分析;IDF 曲线;上海中图分类号:TV122㊀㊀㊀文献标志码:A㊀㊀㊀文章编号:1001-6791(2023)03-0398-11收稿日期:2023-01-29;网络出版日期:2023-04-19网络出版地址:https :ʊ /kcms /detail /32.1309.P.20230418.1444.002.html基金项目:国家自然科学基金资助项目(42271031;51909191)作者简介:庄琦(1997 ),女,江苏徐州人,博士研究生,主要从事城市水文㊁极端水文气象事件等方面的研究㊂E-mail:2110026@ 通信作者:周正正,E-mail:19058@ 在气候变暖及快速城市化的双重影响下,近年来中国地区性暴雨落区多与城市密集区重叠,城市防洪形势复杂严峻㊂极端暴雨事件在时间和空间尺度上的变异性[1]及频率变化显著[2],加之城市化流域面积相对较小㊁水文响应时间较快,城市洪涝管理精细化程度不高㊁设计标准不足等问题日益突显[3-5]㊂2019年发表在Water Resources Research 上的研究强调了城市水文学面临数据精度不足带来的挑战[6]㊂为匹配城市社会经济发展的需求㊁满足新阶段水利高质量发展要求,在城市地区亟待使用时空精度与发展目标相适配的观测数据来提升精细化城市水灾防御能力㊂降雨数据的时空精度(时空分辨率)很大程度上决定了对一场暴雨时空变异性的表达程度及频率分析的可靠程度[6]㊂国内外研究普遍发现使用精细时间分辨率的降雨数据能显著提高洪水模拟效果[7-8],而粗糙时间分辨率的降雨数据会造成暴雨量级(如最大雨强㊁累积雨量等)被低估,且暴雨过程(雨型)不准确,从而带来洪涝风险评估的偏差[9-10]㊂刘业森等[11]发现随着降雨数据空间分辨率降低,暴雨空间分布被坦化㊁洪峰计算误差随之增加;而Ochoa-rodriguez 等[12]发现降雨时间分辨率对洪水模拟结果的影响要超过空间分辨率,同时,随着流域面积的增加,降雨时空分辨率对计算结果的影响减弱;此外,Li 等[13]发现受多重水文气候因子的影响,不同时空分辨率下的暴雨洪水模拟精度会呈现出复杂的非线性特征㊂可见,降雨数据分辨率对暴雨以及洪水特征的刻画有重要影响,但是两者作用并非简单的线性关系,不同地区的结论尚不统一㊂系统化㊁定量化分析不同精度降雨数据对暴雨时空变异性及设计暴雨的影响仍是亟待深入探讨的重要问题㊂上海作为长三角一体化的核心城市,易受台风㊁暴雨㊁潮汐㊁洪水等多种灾害影响,是中国31个重点防洪城市之一㊂近年来,基于站点数据或单一精度卫星数据的研究已表明上海市极端暴雨事件的时空㊀第3期庄琦,等:降雨数据时空精度对城市暴雨变异性及频率分析的影响399㊀异质性变化及暴雨频率变化显著㊁城市洪涝灾害风险加剧[2,14-15],但未见该地区针对降雨数据精度的影响问题进行定量化探讨㊂基于此,本文在上海市区,构建16种不同时空分辨率组合的降雨数据,对比分析数据精度对暴雨时空变异性特征刻画能力㊁暴雨强度-历时-频率(IDF,Intensity-Duration-Frequency)曲线计算的影响,以期对降雨数据精度在城市暴雨 时-空-频 多维结构中的作用形成更为客观㊁定量的认识,并提出与研究地区最适宜的降雨数据分辨率范围,为提升城市水旱灾害防御能力㊁也为提升城市气象 三精 能力提供科学依据㊂1 研究区域及数据资料为研究小型城市区域降雨数据精度的适用性,本文选取上海市行政面积最小的黄浦区为研究区域,面积约为20.52km 2㊂利用美国国家航空航天局开发的GPM-IMERG 卫星降雨数据(Early V06B 版本,时间分辨率为1h,空间分辨率为0.1ʎ,https:ʊgpm.nasa.goc /data /directory)和47个上海市翻斗雨量计收集的逐时实测降雨数据,基于空间降尺度矫正技术获得2008 2017年上海市时空精度更高的格点降雨数据集(IMERG_CorSH,空间分辨率为0.01ʎ,时间分辨率为1h)作为本文的输入数据㊂图1㊀不同数据集降水空间分布及IMERG_CorSH 精度评估Fig.1Spatial distribution of different rainfall products and accuracy assessment of the IMERG_CorSH 原IMERG 数据(图1(a))与其他卫星降雨产品相比,在空间覆盖㊁捕获微雨和固态降水的性能上都有较大的优势,能更好地描绘降水量的空间分布,在缺资料及无资料地区具有明显优势[16],但与实测值相比,该数据集在中国不同地区仍存在异质性的观测误差[17-18]㊂从雨量站点获得的实测降雨数据(站点位置见图1(b))被认为是最准确的数据源,但受限于站点数量有限且位置固定,空间分辨率的精细程度不如IMERG 数据㊂为了融合两数据源的优势,应用经典的一元线性回归降尺度方法建立年尺度㊁0.1ʎ精度下归一化植被指数(NDVI)数据和卫星降雨的线性关系,基于此关系和0.01ʎ的NDVI 数据估计年尺度㊁0.01ʎ精度上降雨,采用时间分解方法分解得到小时尺度上的降雨数据,再基于地理偏差矫正技术(GDA)在小时尺度上进行降雨量级的修正,最终得到2008 2017年IMERG_CorSH 数据集(图1(c))㊂本文所用的空间降尺度矫正详细400㊀水科学进展第34卷㊀步骤及结果合理性见文献[19]㊂该数据集覆盖上海市,经验证,IMERG_CorSH与站点实测降水在年㊁月㊁日尺度上Pearson相关系数(C c)均超过0.85(图1(d) 图1(f),E MA为平均绝对误差,E RMS为均方根误差),小时尺度上Pearson相关系数也高达0.74(图1(g))㊂相比于IMERG数据,IMERG_CorSH数据大大减少了统计误差,且提供了0.01ʎ尺度上丰富的降雨信息㊁远高于雨量站的空间观测精度,可作为探究数据时空分辨率对城市极端暴雨的不确定性影响的重要数据基础㊂2㊀研究方法2.1㊀时空精度重构与极端暴雨事件提取以0.01ʎ㊁1h原始精度为参考,对IMERG_CorSH降雨数据进行时间(6h㊁12h㊁24h)㊁空间(0.02ʎ㊁0.05ʎ㊁0.1ʎ)尺度上的分辨率重构,最终获得16种具有不同时空分辨率组合的降雨产品㊂时间尺度上(图2(a)),利用一维滚动窗口求和方法[20]将原始逐一小时降雨序列重采样至6h㊁12h及24h㊂一维滚动窗口向前滚动的距离等于窗口长度,分别为6㊁12和24,相邻时刻滚动窗口不交叉,且时序重构过程保留原始降雨空间信息㊂同理,空间尺度上(图2(b)),利用二维滚动窗口求平均方法[12]将原始0.1ʎ数据重采样至0.02ʎ㊁0.05ʎ和0.1ʎ㊂二维滚动窗口向右㊁向下滚动距离等于滚动窗口边长,分别为2㊁5和10,相邻空间位置滚动窗口不交叉,空间重采样过程不改变时序信息㊂由于滚动窗口在时序上累加㊁空间上求平均此类采样过程并不损失或增加降雨信息,故时空分辨率重构过程不改变同场降雨的累积总雨量㊁面平均雨量,以此消除数据处理中的不确定性㊂本文使用的16种不同时空分辨率的组合见图2(c)㊂基于不同时空分辨率的降雨数据提取年最大24h降雨事件(2008 2017年)作为极端暴雨进行分析㊂目前针对年最大值序列的采样方法仍存在较大差异,国内一般采用正点统计法,选取当日08:00至次日08:00为1d降雨的起止时间㊂而实际上,自然降雨事件中强降水过程存在跨时㊁跨日的现象,正点统计采样可能导致完整的强降水过程被分割㊁降雨累积量被低估[21]㊂因此,本文利用自然降水过程统计方法对年最大24h事件进行采样,即基于24h为滑动窗口大小㊁数据时间分辨率大小为滑动步长,以保留更贴近真实的降雨起止过程,并讨论时空分辨率在极端暴雨分析计算中的不确定性影响㊂注:R(t)为时序t时刻降水量/mm;R(s)为空间上s格点处降水量/mm;ρ(s)为区域名为A的流域占s网格的面积权重;S4,A 为4号网格内流域A所占的面积;S4为4号网格面积;T为时序上滚动窗口长度;N为空间上滚动窗口包含的网格总数㊂图2㊀降雨数据时空分辨率重构方法示意Fig.2Schematic diagram of spatiotemporal resolution reconstruction of rainfall inputs㊀第3期庄琦,等:降雨数据时空精度对城市暴雨变异性及频率分析的影响401㊀2.2㊀暴雨时空变异性特征分析本文选取了一系列暴雨特征指标来表征暴雨事件的时空结构,包括累积暴雨量(R )㊁暴雨量极值(M )㊁暴雨变异系数(C v)㊁暴雨覆盖率(F )㊂其中,暴雨总量是计算研究区域内t h 降雨累积量,暴雨量极值㊁暴雨变异系数㊁暴雨覆盖率分别可以在时间㊁空间2个尺度上进行计算,计算公式见表1㊂表1㊀暴雨时空特征指标计算公式Table 1Formula of temporal and spatial characteristics of storms指标时间尺度空间尺度累积暴雨量/mmR =ðT 1ʏS A R (t ,s )d s 暴雨量极值/mm M t =max{R (t );t ɪ[0,T ]}M s =max{R (s );s ɪ[0,N ]}暴雨变异系数C v t =ðT t =1[R (t )-R (t )]2/(T -1)R (t )C v s =ðN s =1[R (s )-R (s )]2/(N -1)R (s )暴雨覆盖率F t =1TʏT (t |R (t ,s )>x )d t F s =1S A ʏS A (s |R (t ,s )>x )d s注:S A 为目标流域面积,km 2;R (t )为[0,T ]时刻内平均降水量,mm;R (s )为空间[0,N ]格点内平均降水量,mm;x 为暴雨阈值,mm,用来研究暴雨事件中大于某一阈值的降雨时长占比或降雨空间范围占比,本文中设1d 累积雨量达50mm 为阈值,为方便对比,在逐小时计算时累积雨量达(50/24)mm 计为x 值㊂2.3㊀暴雨频率分析及其不确定性随机暴雨移置(Stochastic Storm Transposition,SST)法是一种基于区域性概率重采样与地理移置相结合的地区性降雨频率分析方法㊂该方法利用与目标区域气候特征相同㊁降雨过程相似的邻域暴雨模拟延长本地样本序列,仅10a 历史数据即可获得可靠的频率分析结果[22]㊂SST 方法结合不同分辨率降雨数据能够提供考虑降雨时空结构㊁数据分辨率不确定性区间的暴雨频率分析结果㊂此处对基于SST 法的暴雨频率分析及其结果的不确定性量化作简要概括:(1)首先确定一个包括研究地区A 流域在内㊁与研究区域具有相似气候特征的暴雨移置区Aᶄ㊂本文所选取的研究地区㊁移置区范围与文献[15]一致,研究地区A 与移置区Aᶄ位置可参照该文献中的图1,移置区选择及结果合理性见文献[14-15]㊂(2)从n 年(如本文n =10,2008 2017年)降雨序列中筛选出发生在移置区Aᶄ内㊁历时为T r (本文取1㊁6㊁12㊁24h)的最大的m 场(本文m =200)暴雨,作为暴雨目录㊂(3)从暴雨目录中随机选择k 场暴雨事件,即假设一年内发生的暴雨事件数量为k ㊂k 服从泊松分布,分布的平均发生率为λ=m /n ㊂(4)对选定的k 个暴雨事件进行整体移动,计算目标流域A 内降雨历时为T r 的降雨累积量,并保留其中的最大值作为该年的年最大降水量㊂不同于传统方法,由于移置过程保留整个降雨场的时空信息,故该方法计算过程中考虑了尺度相关的暴雨时空分布结构对暴雨频率分析的影响㊂重复该过程N 次,即可构建长为N 年㊁历时为T r 的年最大序列㊂(5)对N 年㊁历时为T r 的年最大暴雨从大到小排序,进行频率分析,得到IDF 曲线㊂(6)本文以输入1h㊁0.01ʎ分辨率数据的频率分析结果为参考,选取相对误差(E )和时空不确定性系数(U )2个指标量化数据分辨率对频率分析结果的不确定性影响:E p ,st =(q p ,st -q p ,ref )q p ,ref ˑ100%(1)402㊀水科学进展第34卷㊀U p,st=q p,st_0.95-q p,st_0.05q p,ref_0.95-q p,ref_0.05(2)式中:q p,ref和q p,st分别为重现期p下利用分辨率为(1h㊁0.01ʎ)和(t h㊁sʎ)的数据所计算的IDF结果; q p,ref_0.95㊁q p,st_0.95,q p,ref_0.05㊁q p,st_0.05分别为各自对应IDF曲线上95%与5%分位数处的值,mm㊂3㊀结果与分析3.1㊀基于不同时空精度的暴雨事件提取基于16种不同时空精度数据所提取的年最大24h暴雨序列在发生时间和量级上存在较为显著的差异㊂在本节暴雨事件对比过程中,根据不同精度暴雨事件与(1h㊁0.01ʎ)事件的发生时间差异划分3种情况:若两者时间差为0h则视作无相位差的同场暴雨事件;若两者存在时间差且时间差<24h视作有相位差的同场暴雨事件;若两者存在时间差且时间差>24h则视为非同场暴雨事件㊂首先在发生时间上,其余15种分辨率的暴雨序列与(1h㊁0.01ʎ)结果相比,同场暴雨事件㊁有相位差的同场暴雨事件和非同场暴雨事件3种情况占比约为17%㊁70%和13%㊂各精度下暴雨事件的划分结果列于表2(因以(1h㊁0.01ʎ)精度为参考,故表中仅列出15种精度结果)㊂如(1h㊁0.02ʎ)精度下所提取的事件与(1h㊁0.01ʎ)精度下无差异;(6h㊁0.01ʎ)与(6h㊁0.02ʎ)精度下10a均为同场暴雨但普遍存在1~5h 相位差;12h精度下相位差进一步增加到1~17h,并伴随1~2a非同场暴雨;至(24h㊁0.01ʎ)~(24h㊁0.05ʎ)精度下10a间有20%场非同场暴雨,(24h㊁0.1ʎ)精度下则有30%非同场暴雨㊂由表2可见,随着降雨时空精度降低,同场暴雨事件发生起止时间差异越大,且非同场暴雨事件出现的概率越大㊂此外,表2中69.5%的有相位差暴雨事件起始时间后置于(1h㊁0.01ʎ)暴雨㊂尽管各精度下暴雨发生概率最大的时间均集中在7月中下旬(峰值位置发生时间标注于图3(a)),但随着时空分辨率的降低,暴雨发生最大概率时间后移4~19d左右,说明低分辨率捕捉的暴雨发生时间有日尺度上的滞后㊂表2㊀不同时空精度降雨数据提取的暴雨事件对比Table2Rainstorm events extracted from rainfall data with different spatiotemporal resolutions㊀㊀降雨量级分布上(图3(b)),随着时空分辨率的降低,雨量概率密度曲线尾部变薄㊁变短,而峰值处概率变高㊁分布更为集中,尾部风险被低估㊂图3(b)中,随着时空分辨率变低,雨量概率密度曲线的峰现位置前移,即年最大24h量级被低估2.9%~9.5%;同时峰值处概率密度提高5.5%~65%,即最大24h雨量分布更为 尖瘦 ㊂峰值处概率变高伴随着尾部变短㊁极值雨量漏估,尤其是累积雨量超过130mm的暴雨事件在粗糙分辨率下被严重低估,累积雨量超过180mm的暴雨在不同分辨率组合下被低估4%(出现在㊀第3期庄琦,等:降雨数据时空精度对城市暴雨变异性及频率分析的影响403㊀(6h㊁0.01ʎ)处)~60%(出现在(24h㊁0.05ʎ)及(24h㊁0.1ʎ)处),累积雨量220mm以上的暴雨在(24h㊁0.1ʎ)精度下完全被忽略㊂与(1h㊁0.01ʎ)相比,低分辨率数据提取的非同场暴雨事件占比变多㊁相位差变大造成了年最大24h累积雨量的低估甚至漏估㊂非同场暴雨事件显然会在降水量计算中带来显著差异,而即便是存在相位差的同场暴雨事件,降雨过程被粗糙分辨率分割带来的影响也不容忽视㊂如2013年,时间分辨率为24h时,与1h精度下事件相位差仅差15h,降水量级差异为72.4mm;2017年时间相位差仅差7h,降水量级差异为47.5mm,说明暴雨事件在此时极可能存在跨时㊁跨日的情况㊂使用粗糙的数据采样会将一个真实的强降水过程分割成2个(或多个)时间步长,导致低分辨率条件下提取的暴雨事件出现时间偏移㊁降水量被低估的情况㊂图3㊀不同时空分辨率的暴雨事件年内概率密度分布Fig.3Annual density distribution of extreme rainfall events with different spatiotemporal resolutions3.2㊀时空精度对刻画暴雨时空变异性特征的影响图4展示了基于16种不同时空精度数据所提取的年最大24h暴雨事件的时空特征变化㊂本节采用相对误差(见式(1),原公式中q p,ref为参照值,q p,st为其他精度条件下的输入值)评估不同精度条件下暴雨事件时空特征指标结果的差异:如图4中以(1h㊁0.01ʎ)精度暴雨事件计算得到的时空特征指标值作为参照值,再输入其他精度下暴雨时空特征指标值计算得到量化时空精度影响的相对误差(E st);以(1h㊁sʎ)(s取值分别为0.01㊁0.02㊁0.05㊁0.1)精度下的结果作为参照值计算不同空间尺度下量化时间精度影响的相对误差(E s);同理以(t h㊁0.01ʎ)(t取值分别为1㊁6㊁12㊁24)精度下的结果作为参照值计算不同时间尺度下量化空间精度影响的相对误差(E t)㊂从降水总量上看,随着时空精度的降低,降水总量也随之降低,如图4(a),在空间上,精度从0.01ʎ到0.1ʎ,相对误差E s为-2.2%;在时间上,从1h到24h,相对误差E t为-14.8%;最大误差出现在(24h㊁0.1ʎ)精度下,时空相对误差E st为-16%㊂暴雨量级的低估性在粗糙分辨率下(0.05~0.1ʎ,12~24h)更为显著㊂在其他时空特征上,不同特征指标受时间㊁空间精度的影响存在差异㊂如图4(b)㊁图4(d)和图4(g)所示,随时空精度降低,暴雨量的空间极值(M s)㊁空间变异系数(C v s)和暴雨时间覆盖率(F t)呈现单调递减趋势㊂数据精度由(0.01ʎ㊁1h)到(0.1ʎ㊁24h),M s㊁C v s㊁F t相对误差E st分别为-29.6%㊁-9.1%㊁-24.4%,即低时空分辨率将造成M s㊁C v s㊁F t的严重低估㊂从空间精度变化上看,精度从0.01ʎ到0.02ʎ,各项指标未受空间分辨率影响,M s㊁C v s㊁F t在0.01ʎ~0.02ʎ处E s值相同㊂而空间精度从0.02ʎ到0.05ʎ,下降梯度最大,M s㊁C v s㊁F t在0.02ʎ~0.05ʎ处E s分别下降14.3%㊁9%㊁4%㊂从时间精度变化上看,精度从6h到12h,变化梯度最大,M s㊁C v s㊁F t在6h~12h处E t分别下降15.2%㊁9.1%㊁7.5%㊂可见,时间精404㊀水科学进展第34卷㊀图4㊀基于不同时空分辨率降雨数据提取的暴雨事件时空结构诊断Fig.4Spatiotemporal structure diagnosis of extreme rainfall events based on rainfall data extraction withdifferent spatiotemporal resolutions度降低同样会影响对空间特征指标M s㊁C v s的描述,粗糙的时间分辨率亦无法合理刻画空间极值和空间不均匀性㊂与M s㊁C v s恰恰相反,随着时空精度降低,暴雨量时序极值(M t)㊁时间变异系数(C v t)呈现单调递增趋势㊂如图4(c)和图4(e),数据时空精度由(0.01ʎ㊁1h)降低到(0.1ʎ㊁24h)将造成M t㊁C v t分别被高估22%㊁24.4%㊂空间精度从0.01ʎ到0.02ʎ,M t㊁C v t在各时间分辨率下相对误差值E s不变;空间精度从0.02ʎ到0.1ʎ,M t㊁C v t指标随着时间分辨率降低而增加㊂与M s㊁C v s相同,M t㊁C v t指标亦在0.02ʎ~ 0.05ʎ㊁6~12h处变化梯度最为显著,M t㊁C v t在0.02ʎ~0.05ʎ处相对误差E s升高17.7%㊁14%,在6~12h处相对误差E t升高17.6%㊁12.1%㊂可见,粗糙精度的降雨数据会导致瞬时㊁局地暴雨极值量级被错误估计甚至遗漏㊂粗糙的时间分辨率影响空间局地暴雨极值量级,同样的,粗糙的空间分辨率也会影响短历时暴雨极值量级的估计㊂降雨数据时空精度对暴雨空间覆盖率(F s)的影响更为复杂,表现为F s随时空精度降低呈小幅波动下降趋势(E st=-2.5%,见图4(f))㊂F s指标在1~6h㊁12~24h时间精度下随空间分辨率降低分别下降0.9%㊁0.5%,在6~12h分辨率下又随空间分辨率降低小幅上升3.9%㊂空间分辨率对F s指标的影响表现为随空间分辨率降低波动上升1.4%,但在0.01ʎ~0.02ʎ处E s值未见变化㊂说明时空精度对暴雨空间覆盖率的影响呈现复杂的非线性关系㊂从影响程度上看,时间精度对暴雨时空变异性的影响强于空间精度㊂如对时序特征指标降雨总量(R)和F t,时间精度约为空间精度影响的6倍;而对空间极值指标M s,影响差异为2倍;对M t㊁F s㊁C v s指标,时间㊁空间精度影响作用相当;对于C v t而言,则以空间精度影响为主导㊂可见,时间和空间精度变化均对捕捉暴雨时空结构特征有不可忽视的影响㊂从指标类型上看,时间精度会影响空间指标,而空间指标也受时间精度的影响,尤其是在精细分辨率下影响更为显著㊂综上,粗糙时空精度的降雨数据会低估降水总量,倾向于捕捉时序不均匀性高㊁空间不均匀性低的暴雨事件㊂采用0.02ʎ㊁6h精度以内的数据对暴雨时空特征的刻画结果较为可靠㊂由于实际降雨过程具有随机㊀第3期庄琦,等:降雨数据时空精度对城市暴雨变异性及频率分析的影响405㊀性,不同降雨的雨型㊁时段雨强㊁持续时间等不同,因此,用精度粗糙的数据在描述降雨时空变化特征中不充分性㊁不确定性应被重视㊂同时,降水量级㊁时空结构特征在数据时空精度影响下的变化及其变化程度各有不同,采用不同分辨率计算的设计暴雨不确定性有待进一步研究㊂3.3㊀时空精度对暴雨频率的不确定性影响将16种具有不同时空分辨率的降雨数据输入SST模型,计算得到2~200a重现期下历时为24h的IDF 曲线,并将结果与(1h㊁0.01ʎ)分辨率下求得的IDF结果对比(图5(a))㊂相较于更精细的降雨数据,不同分辨率组合下的IDF结果具有不同程度的低估(E,见式(1))㊂6h㊁12h㊁24h数据对IDF的低估率平均值分别为3%㊁7%和14%,0.02ʎ㊁0.05ʎ㊁0.1ʎ对IDF的低估率分别为0.4%㊁4%和10%㊂时间尺度上,24h分辨率数据最大会造成设计值低估36%,使用6h以内分辨率的数据可以将误差控制在-0.4%~-4%之间㊂空间尺度上,0.1ʎ分辨率的数据相较于0.01ʎ的数据而言,误差在-31%~2%;使用0.05ʎ精度内的数据进行频率分析,所得结果误差范围为-0.3%~-17%;0.02ʎ与0.01ʎ数据所得的暴雨事件本身差异较小,故此处设计暴雨随机误差仅有-1%~1%㊂图5(a)中所展示的设计暴雨量级差异存在2个来源,一为数据时空精度误差,二为SST模拟不同降雨过程本身带来的随机误差(由于随机降雨场时空结构的变化),故图5(c)进一步剥离了不同重现期下降雨数据时空精度对IDF的影响,可见时空分辨率对IDF造成的不确定性占比接近50%,随着重现期增大(2~ 50a),时空分辨率造成的低估程度增加㊂50~200a重现期,受限于时序短(10a)㊁以及降雨事件本身的随机成分大,随机不确定性比重亦增大,分辨率不确定性占比略降低㊂可见,使用粗糙的降雨数据进行频率计算会造成设计暴雨量级的低估,且数据分辨率越低,量级低估程度越严重,随着重现期增大,时空分辨率导致的IDF不确定性亦增大㊂其中,时间分辨率的影响大约是空间分辨率的5倍左右(图5(b)和图5(d)),即时间分辨率的影响在该地区的极端暴雨时-空-频特征分析中占主导地位㊂图5㊀数据时空分辨率对IDF曲线的影响Fig.5Influence of rainfall spatial and temporal resolution on IDF curves图6为不同重现期下使用不同时空分辨率降雨数据进行计算的设计暴雨值与(1h㊁0.01ʎ)计算结果的相对误差散点图㊂时间㊁空间分辨率均粗糙的情况下(24h㊁0.1ʎ),结果误差最大,如T=200a时,误差达到-30%㊂而时间㊁空间分辨率中有一者较为精细时可降低结果的误差程度,如(1h㊁0.1ʎ)的数据所得结406㊀水科学进展第34卷㊀果的相对误差为-5%㊁(24h㊁0.01ʎ)结果的相对误差为-20%㊂图6中,精度在(12h㊁0.05ʎ)以内所得结果的相对误差存在一个较为平稳的平台面(Tɤ2a除外),可以认为该精度内设计结果差异不显著㊂尽管采用(0.02ʎ㊁6h)精度以内的数据对暴雨时空特征的刻画更为准确,但频率分析时,降雨量级㊁时空结构特征在数据时空精度变化下的影响相互交错且复杂,最终导致精度在(12h㊁0.05ʎ)以内的频率分析结果相对误差均较小㊂综上,以面积为20.52km2的典型城市地区黄浦区为例,建议水利工程设计中(Tȡ2a)使用精度在(12h㊁0.05ʎ)以内的降雨数据进行极端暴雨事件的频率计算,排水工程设计中(Tɤ2a)应使用精度更高的数据为宜㊂图6㊀不同重现期下降雨数据时空分辨率对暴雨设计值影响的3-D散点图Fig.63-D scatter plot of influence of spatial and temporal resolution of rainfall inputs on design storms under different return periods 4㊀结㊀㊀论本文基于16种不同时空分辨率的降雨数据,利用暴雨时空异质性评估指标和随机暴雨移置法在上海市黄浦区分析了降雨数据精度对城市暴雨时空变异性特征刻画㊁暴雨IDF曲线计算的影响㊂主要结论如下: (1)粗糙分辨率降雨数据会造成年最大暴雨序列的抽样存在误差,主要体现在暴雨发生时间出现误差(延迟)㊁降水量低估㊁暴雨过程在时序上的不均匀性增大㊁空间上的不均匀程度减小㊂在研究区域采用(0.02ʎ㊁6h)精度及以上的数据对暴雨时空变异性的刻画结果较为可靠㊂(2)降雨数据时间和空间分辨率的影响差异较大,时间分辨率对暴雨时空变异性刻画能力的影响强于空间分辨率㊂数据的时间分辨率不仅会影响暴雨的时序特征,也会影响暴雨事件的空间变化特征,同理数据空间分辨率亦会对暴雨事件的时序变化特征带来影响㊂(3)降雨数据分辨率越低㊁重现期越大,暴雨频率结果的低估程度越大㊂时间分辨率影响占主导作用,大约是空间分辨率的5倍㊂建议小型城市地区在水利工程设计中使用时间分辨率为12h㊁空间分辨率为0.05ʎ或更高精度的输入数据㊂。
上海地区暴雨预警评估及不同天气型暴雨预警差异分析
周伟东,韩宁,戴建华,等.2022.上海地区暴雨预警评估及不同天气型暴雨预警差异分析[J].暴雨灾害，41(4):405-412ZHOU Weidong,HAN Ning,DAI Jianhua,et al.2022.Investigation of rainstorm warning and its difference under different synoptic condi-tions in Shanghai [J].Torrential Rain and Disasters,41(4):405-412上海地区暴雨预警评估及不同天气型暴雨预警差异分析周伟东1，韩宁1，戴建华2，陈浩1，岳彩军3，张瑞怡1(1.上海市气象服务中心，上海200030；2.上海中心气象台，上海200030；3.上海海洋中心气象台，上海200030)摘要：利用2010—2020年上海地区79个自动气象观测站逐小时观测资料和2016—2020年上海中心气象台和上海各区气象台发布的暴雨预警信号资料，采用趋势分析、累积频率等统计方法，分析了上海地区暴雨的时空分布特征，并且在对不同级别暴雨预警信号发布频次、预警时效进行统计分析的基础上，对不同天气形势下暴雨预警时效的差异进行了研究。
结果表明:上海地区6h 雨量标准的暴雨呈现显著上升趋势，其中暴雨蓝色预警上升趋势最为明显；7月6h 雨量标准的暴雨出现了明显的低谷，而1h 雨量标准的暴雨较6月仍然有所增加，显示出7月副高控制下上海地区多短时暴雨的特征。
上海午后暴雨一般持续时间相对较短，而持续时间较长的暴雨多出现在上午。
暴雨频次在中心城区和浦东靠近黄浦江地区存在大值中心，这可能与城市热岛效应有关。
上海地区暴雨预警信号发布时间呈现双峰型变化特征，第一峰值出现在中午12∶00，12∶00—17∶00预警信号发布相对集中，第二峰值出现在早晨06∶00，各级别预警信号持续时间平均为5.9h。
一次江淮暴雨高分辨率数值预报中云微物理方案敏感性分析
& 南京信息工程大学 气象灾害教育部重点实验室江苏 南京 !(""%%
' 上海市生态气象与卫星遥感中心上海 !"""#"
( 中国民用航空青岛空中交通管理站山东 青岛 !&&("*
联系人
.!M?H@ 6=@H:M?, :=HA08D3= 89:
联系人
.!M?H@Y7L(!#'+,(!&89<M
理方案对模式空间分辨率具有较强的敏感性"合理
的微物理方案也可相应提高细网格嵌套区的暴雨模
拟效果% 李 安 泰 和 何 宏 让" !"((! 马 严 枝 等" !"(! & "
不同云微物理方案对降水落区影响明显"但强降水
中心强 度 对 云 微 物 理 方 案 却 不 敏 感 % 段 海 霞 等"
!"(#&' 廖镜彪等%!"(!&针对一次华南暴雨过程开
3D3)=:H0!("3' A3( & !% ?& (!"" ^"'<: 0/D-0/)% 7& (*"" ^"'<: 0/D-0/)% 9& """" ^"'<: 0/D("0/)% 3& "&"" ^"'
<: 0/D("0/
+&&
孟泽华"等!一次江淮暴雨高分辨率数值预报中云微物理方案敏感性分析
WRF模式模拟某新区风场及温度场
WRF模式模拟某新区风场及温度场利用NCEP再分析资料，选取YSU、MYJ、ACM2 3种不同的边界层参数化方案，通过WRF模式模拟某新区2014年1月8日-11日的温度场及风场的特征，与测风塔和自动站的实测数据对比，结果表明：WRF模式提供的3种边界层参数化方案都能较好地模拟出某新区冬季的地面温度场和流场特征，某新区西北部及东部的山丘环绕形成的夹山地貌导致城市夜间地面流场多为辐合，河谷地区风向为偏北风；白天流场多为辐散，谷地风向为偏南风。
这三种边界层参数化方案均能较好地模拟出某新区冬季温度场日变化特征，但对夜间地面温度的模拟结果均偏高。
关键词：边界层参数化方案，WRF模式，某新区，风场，温度场第一章引言中纬度行星边界层的厚度约为1~1.5km，是靠近地球表面的，受地面摩擦力影响较大的一层大气。
在大气边界层中，气体的垂直运动速度比其水平运动速度小好几个量级，然而就速度梯度而言，垂直方向上却比水平方向上要大得多。
大气边界层内气体运动的主要特点就是湍流性，在这一层大气中，强烈的风切变以及下垫面非均匀加热的作用，常会引起湍流的发生发展，而边界层内湍流的发生发展有利于污染物在该层内的扩散，近几年来，随着城市化的全面推进，大气污染等环境问题不断加剧，因此，对于大气边界层的研究是大气污染研究中的重要一环。
大气边界层的另一个特征是由热力作用导致的明显的日变化，白天和夜间的大气边界层结构有着显著的区别。
白天，太阳辐射到达地表后将其加热，地表温度上升，而边界层内的湍流运动使热量向上传递，大气层结处于不稳定状态，此时的边界层为对流边界层，边界层顶可到达几百米甚至几千米；而夜间正好相反，地面因长波辐射冷却后，热通量向下，大气层结处于十分稳定的状态，此时的边界层称为稳定边界层，边界层顶相对较低，约为二三百米的高度。
夜间的稳定边界层结构与白天的对流边界层结构相比有着显著的不同，值得一提的是，夜间大气经常在较低的高度上出现逆温层，该逆温层严重阻碍了物质和能量的扩散，是导致大气污染的一大原因。
上海暴雨强度公式与设计雨型标准
【上海暴雨强度公式与设计雨型标准探析】在城市规划与设计中，暴雨强度公式和设计雨型标准是至关重要的参数。
特别是在像上海这样的我国地区，由于地理环境和气候特点的影响，暴雨频发，因此对暴雨强度公式和设计雨型标准的研究显得尤为重要。
一、上海暴雨强度公式1. 暴雨强度的概念暴雨强度是指在一定时间内，降雨量达到或超过一定数值的暴雨过程的平均降雨强度。
在城市防洪、排涝、建筑排水等工程设计中，暴雨强度是一个重要的设计参数。
2. 上海暴雨特点上海地处长江三角洲地区，属于亚热带季风气候，夏季多雷雨，降雨集中，强度大，且瞬时雨强大。
上海暴雨强度公式的研究对城市建设和生活具有重要意义。
3. 上海暴雨强度公式上海市的暴雨强度公式一直是工程设计中研究的重点。
根据上海气象资料，经过多次实测与数据分析，上海市编制了适合本地气候特点的暴雨强度公式，从而为城市防洪排涝工程提供了科学的依据。
二、设计雨型标准1. 设计雨型的概念设计雨型是指为城市防洪、排涝等水利工程建设而预先确定的一种代表性的降雨过程。
通过设计雨型，可以科学合理地预测暴雨时的径流量，从而为工程设计提供依据。
2. 上海设计雨型标准根据上海暴雨的实际情况和历史气象资料，上海制定了适合本地气候特点的设计雨型标准。
这一设计雨型标准不仅考虑了降雨量的大小，还兼顾了暴雨的时间分布、降雨过程的强度等多个因素，从而为城市防洪排涝工程的设计提供了科学依据。
三、个人观点与理解在城市建设中，暴雨是一个不容忽视的自然灾害因素，尤其对于像上海这样的城市而言，暴雨频发，防洪排涝工程的设计显得尤为重要。
暴雨强度公式和设计雨型标准的制定，不仅需要充分考虑本地的气候特点，还需要结合工程实际情况，以科学合理的方式来预测暴雨对城市的影响，从而保障城市的安全和稳定发展。
上海暴雨强度公式与设计雨型标准的研究，对于上海城市的规划与建设具有重要意义。
通过科学的研究与制定，可以为城市的防洪排涝工程提供可靠的依据，保障城市的安全和稳定发展。
【国家自然科学基金】_wrf数值模拟_基金支持热词逐年推荐_【万方软件创新助手】_20140802
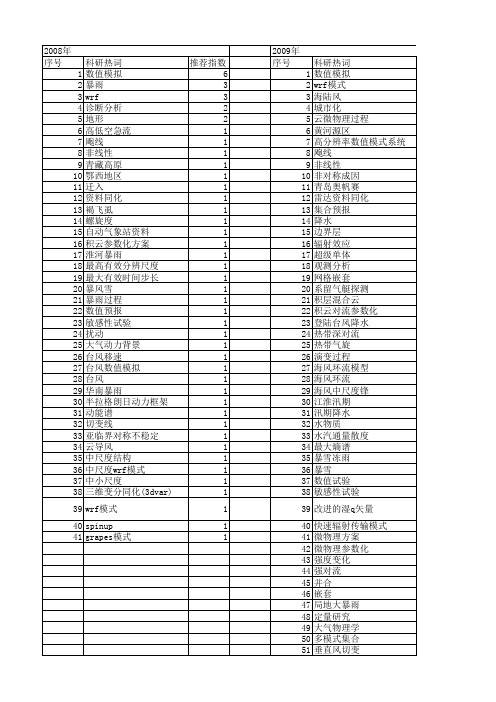
推荐指数 27 10 9 7 7 3 3 3 3 3 3 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 48 49 50 51 52
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41
科研热词 数值模拟 暴雨 wrf 诊断分析 地形 高低空急流 飑线 非线性 青藏高原 鄂西地区 迁入 资料同化 褐飞虱 螺旋度 自动气象站资料 积云参数化方案 淮河暴雨 最高有效分辨尺度 最大有效时间步长 暴风雪 暴雨过程 数值预报 敏感性试验 扰动 大气动力背景 台风移速 台风数值模拟 台风 华南暴雨 半拉格朗日动力框架 动能谱 切变线 亚临界对称不稳定 云导风 中尺度结构 中尺度wrf模式 中小尺度 三维变分同化(3dvar) wrf模式 spinup grapes模式
WRF模式不同微物理过程对东北降水相态预报的影响
WRF模式不同微物理过程对东北降水相态预报的影响崔锦;周晓珊;阎琦;张爱忠;李得勤;宋国云;陈雨【摘要】In order to study the impact of different microphysical processes of WRF model on precipitation phase forecasting,1 1 precipitation processes with precipitation phase change in the Northeast China from 2006 to 2008 were simulated based on WRF V3.1 and NCEP reanalysis data.Studies were carried out by three microphysical schemes,i.e.a WSM 6 scheme,a Goddard scheme and a New Thompson scheme.According to analysis of precip-itation phase and cloud microphysical characteristics,forecast differences existed in the different schemes were ob-tained.The results show that effects of different microphysical schemes on precipitation falling area and precipitati-on intensity are not significant,while precipitation phase is sensitive to microphysical schemes,especially for fore-casting of falling area of rain and sleet.The Goddard scheme is the best among all schemes according to results of overall forecast.The simulated cloud microphysical features of atmosphere in the bottom layer have significant differences among three schemes,which lead directly to the difference of precipitation phase forecast.%为了研究不同微物理过程对中尺度模式降水相态预报的影响，利用中尺度模式WRF（V3.1）和NCEP再分析资料，采用WSM 6方案、Goddard方案和New Thompson方案等3种不同微物理过程参数化方案，对2006-2008年东北地区存在降水相变的11次降水过程进行敏感性试验。
2种边界层参数化方案对1013号超强台风“鲇鱼”数值模拟的敏感性研究
2种边界层参数化方案对1013号超强台风“鲇鱼”数值模拟的敏感性研究利用中国台湾地区“侵台台风之飞机侦察及投落送观测实验（DOTSTAR）”探空数据与WRF模式（3.8版本），针对1013号超强台风“鲇鱼”开展了边界层参数化方案的数值模拟敏感性研究。
结果表明，非局地YSU方案在台风强度、路径、螺旋雨带、内核尺度以及台风外围位温、水汽混合比、风向这些方面的模拟效果优于局地MYNN2方案；但在风速的模拟上，YSU方案与MYNN2方案没有明显的优劣之分。
由于大气运动学方程中存在着湍流通量项，使得方程组无法闭合，为了解决方程组的闭合问题，就需要引入边界层参数化方案[1]。
WRF模式作为一种主流的中尺度数值模式，其中一共引入了13种边界层参数化方案。
前人对于边界层参数化方案在降水[2-4]、边界层结构[5-8]、污染扩散[9-10]、台风[11-12]等方面的适用开展了大量的模拟研究。
笔者选取非局地YSU方案与局地MYNN2方案这2种常用的边界层参数化方案对1013号超强台风“鲇鱼”进行模拟与分析，以期为台风周边区域边界层热力与动力结构的数值模拟研究提供参考。
1 资料与方法1.1 DOTSTAR计划观测情况中国台湾地区“侵台台风之飞机侦察及投落送观测实验（DOTSTAR，Dropwindsonde Observations for Typhoon Surveillance near the TAiwan Region）”计划于2010年10月17日05∶40—09∶46共释放了16个探空仪对台风“鲇鱼”进行观测（图1）。
根据探空位置和台风中心之间的关系DOTSTAR观测航程大致可以分为3段：首先，第1个至第3个探空仪自西向东在台风西侧外围释放进行观测；接着，环绕台风中心外围释放了第4个至第13个探空仪；最后，在台风北侧释放了第14个至第16个探空仪。
于是大致上台风西侧有3个探空仪进行观测，环绕台风中心外围有10个探空仪进行观测，在台风北侧有3个探空仪进行观测。
上海地区 暴雨强度公式与设计雨型标准
上海地区暴雨强度公式与设计雨型标准上海地区是中国东部的一个重要城市，位于长江口的黄浦江畔。
虽然上海地区四季分明，降雨比较均匀，但暴雨天气时常会给城市带来严重的水灾。
为了有效预防和应对暴雨天气，设计有效的暴雨强度公式和适宜的设计雨型标准非常重要。
暴雨强度公式是指通过分析历史气象数据和实测数据建立的一种数学模型，用于预测和计算暴雨的强度。
对于上海地区而言，制定合适的暴雨强度公式尤为重要。
这需要考虑上海地区的地理特征、气候条件以及降雨历史数据等方面的因素。
在上海地区，地理条件复杂，地势较为平坦，存在一些低洼地带。
这些地形特点使得上海在暴雨天气下更容易发生内涝现象。
因此，暴雨强度公式的制定需要考虑到上海的地势特点，以确保在短时间内尽可能准确地预测到暴雨的强度。
此外，上海地区的气候条件也是制定暴雨强度公式的重要依据。
上海地区属于亚热带季风气候，冬季寒冷，夏季炎热潮湿，降雨相对较多。
暴雨强度公式需要充分考虑此类气候特点，准确反映上海地区暴雨发生的可能性和强度，以便制定有效的防范措施。
另外，暴雨强度公式的制定还需要基于上海地区的降雨历史数据进行分析。
通过对历史降雨数据的统计和分析，我们可以了解上海地区不同等级的暴雨发生频率和持续时间。
这些数据可以为制定暴雨强度公式提供重要依据，使公式更接近实际情况。
在制定暴雨强度公式的过程中，还需要考虑到暴雨对城市的影响。
上海作为中国经济和金融中心，人口众多，城市建设密集，水资源和排水系统等基础设施需要承受大量降雨的冲击。
因此，暴雨强度公式的制定还需要充分考虑到城市建设的风险和需求，确保公式对城市建设起到有效的指导作用。
设计雨型标准是指根据暴雨的实际情况和影响范围，确定合理的设计雨型。
设计雨型标准的制定需要综合考虑上海地区的气候、地理条件、降雨历史数据等因素。
对于上海地区而言，设计雨型标准的制定应该考虑到城市建设的需求和防洪排水设施的能力。
上海地区的基础设施较为发达，但仍需进一步完善城市的防洪排水系统，以应对暴雨等极端天气事件。
云凝结核浓度对一次梅雨锋降水影响的数值模拟
云凝结核浓度对一次梅雨锋降水影响的数值模拟鹿翔;王春明;陈浩伟【摘要】利用WRF模式(V3.6),采用WDM6双参数微物理方案对2012年7月2～3日江淮地区的一次持续性梅雨锋暴雨过程进行数值模拟,对不同初始云凝结核(CCN)浓度背景下的地面累积降水量和云中微物理过程进行对比分析.结果表明,初始CCN浓度在一定程度上影响了降水的微物理过程,进而影响降水量;当背景CCN 浓度增加时,在降水前期引起云滴半径减小,云滴转化效率变低,抑制暖云降水,后期冷云过程得到加强,大量冰相粒子生成,最终导致降水增加.%By using the WDM6 two-moment microphysics scheme of WRF v3.6 (Weather Research & Forecasting version 3.6),the continuous Meiyu front rainfall event during July 2-3 in 2012 in Jianghuai Region was simulated.The surface accumulated precipitations and the cloud mi crophysics processes under different initial CCN concentration were analyzed.The results showed that the initial CCN concentration to some extent impacts on the processes of precipitation,thus further influences the amount of precipitation.When increasing background CCN concentration,in earlier stage of precipitations the radius of cloud droplet and its conversion efficiency decrease,inhibiting the precipitations from warm clouds,while in the later stage the processes of cold clouds are enhanced,forming a large number of ice particles and thus leading to the increasing rain falls.【期刊名称】《安徽农业科学》【年(卷),期】2016(000)002【总页数】6页(P219-223,228)【关键词】云凝结核;微物理方案;梅雨锋;降水;数值模拟【作者】鹿翔;王春明;陈浩伟【作者单位】解放军理工大学气象海洋学院,江苏南京211101;解放军理工大学气象海洋学院,江苏南京211101;解放军理工大学气象海洋学院,江苏南京211101【正文语种】中文【中图分类】S161.6大气中的某些气溶胶粒子可在大气过饱和或接近饱和的情况下作为云凝结核(CCN)形成云滴的核心，气溶胶浓度的变化对于云的性质和降水的形成有重要影响。
台风“莫拉菲”对不同边界层方案的敏感性数值模拟
表 述 这 ３个 区域 。其 中 Ｄ １区域 是 网格 距 为 １ ｍ 粗 网 ０ ８ｋ
格 区域 ， 点 数 为 ２０×２５ 用 于 模 拟 大 尺 度 的环 境 格 ４ ０， 条件 ， 区域中 心 为 １９０ Ｅ，９ ０ Ｎ， 围是 （ ． ７ Ｎ～ １． 。 １ ． 。 范 １５ 。 ３ ．９ Ｎ，８ １ 。 ４ ７ 。 ９ ． ５ Ｅ～１９ ８ 。 ） 中 网格 区域 Ｄ ２格点 数 ３．５Ｅ ； Ｏ 为 ２ ８×１９， ９ ９ 格距为 ６ｋ 区域 中心 为 １５ ３ 。 ２ ． ８ ｍ， １ ．２ Ｅ，０ ９ 。
第３ ２卷第 ６期
２１ ０ ０年 ｌ ２月
ｄ ｉ１ ．９ ９ｊｉ ｎ １０ ｏ：０ ３ ６ ／．ｓ ．０ ７—６９ ．０ ０ ０ ．０ ｓ １０ ２ １ ．６０ ３
广 东 气 象
Ｇｕ ｎ ｄ ｎ ｅ ｅ ｒ ｌ ｇ ａ ｇ ｏ ｇ Ｍ ｔｏ ｏｏ ｙ
Ｖ０ ． １３２ Ｄｅ ｅ ｅ ｃ ｍｂ ｒ
３ 不 同边 界层 方案模 拟 结果 比较
３ １ “ 拉菲” ． 奠 的大 尺 度 环境 场
取 Ｂ ｔ —Ｍｉｅ —Ｊ ｉ 流参 数 化方案 ， ０ ｅｔ ｓ ｌ ｒ ａ ｃ对 ｌ Ｉ ３不采 用对 ） 流参数化方案 。云微物理方案为 ＷＳ ６含霰复杂云微物 Ｍ 理方案 。长波辐射方 案使用 Ｒ Ｔ Ｒ Ｍ方 案 ， 波辐 射方案 短 使用 Ｄ ｄ ｉ ｕｈ ａ方案 。利用 ４次／ ｄ水平分 辨率 为 １ ×１ 的 。 。
要过程进行了数值模拟 ， 分析 了边 界层参数化 方案 对台风 的大环境 场 、 路径 、 度和 累积降水 的影 ｕ 。 强 向 并通过对边界层 过程 中的感热通量和潜热通量 进行分析 ， 明台风 强度和 累积 降水主要是 由水汽凝结 表
《WRF-Chem模式不同参数化方案对呼和浩特大气污染的数值模拟研究》范文
《WRF-Chem模式不同参数化方案对呼和浩特大气污染的数值模拟研究》篇一一、引言随着工业化进程的加快和城市化水平的提升，大气污染问题逐渐凸显，对人们的健康和生活质量产生了严重影响。
呼和浩特作为内蒙古自治区的省会城市，其大气污染问题也日益受到关注。
为了更好地理解和预测大气污染状况，本文采用WRF-Chem模式，对呼和浩特地区的大气污染进行数值模拟研究，并探讨不同参数化方案对模拟结果的影响。
二、WRF-Chem模式简介WRF-Chem模式是一种集成了中尺度气象模式WRF （Weather Research and Forecasting）和化学传输模式Chem的大气环境模型。
该模式可以模拟大气中的气态污染物、颗粒物等污染物的传输、扩散、转化和沉降等过程，为大气污染研究和防控提供有力支持。
三、研究方法本研究以呼和浩特市为研究区域，采用WRF-Chem模式进行数值模拟。
在模拟过程中，我们设置了多种不同的参数化方案，包括边界层参数化方案、云微物理参数化方案、积云参数化方案等。
通过对这些不同参数化方案的模拟结果进行比较和分析，评估各方案对呼和浩特大气污染数值模拟的影响。
四、不同参数化方案对模拟结果的影响1. 边界层参数化方案的影响：边界层参数化方案主要影响近地层的气象条件和污染物的扩散过程。
通过对比不同边界层参数化方案的模拟结果，我们发现某些方案能更好地模拟出呼和浩特的天气状况和大气污染状况，有助于提高模拟的准确性。
2. 云微物理参数化方案的影响：云微物理参数化方案主要影响云的形成和演变过程，进而影响云与大气污染物的相互作用。
我们发现，在某些云微物理参数化方案下，呼和浩特的污染物浓度得到更好的模拟效果，说明适当的云微物理参数化方案有助于提高大气污染的模拟精度。
3. 积云参数化方案的影响：积云参数化方案主要影响地表能量平衡和地表热通量的分配，从而影响大气的垂直运动和污染物的扩散过程。
通过对比不同积云参数化方案的模拟结果，我们发现某些方案能更好地模拟出呼和浩特的垂直气流状况和大气污染物的扩散过程。
物理方案不同组合对双台风影响的数值试验
!"#!$%&$'(')*+&,-./&$01$21(3$&)%))%)%)0物理方案不同组合对双台风影响的数值试验张晓慧$4朱名名)4郑莹$#&空军航空大学航空作战勤务学院航空气象教研室!吉林长春!#&%%%%"&解放军@$#"@部队!河南开封!"###%#44摘4要 本文采用中尺度5J W 模式对)%$(年双台风+W /N P \,和+!F -F D ,进行了不同参数化方案敏感性试验!研究结果表明b K D D M K L 微物理方案和b F /-2W L /N D ,6积云参数化方案的组合对台风路径模拟效果最好$e Bj 边界层方案与b F /-2W L /N D ,6积云参数化方案的组合对台风强度模拟效果最好$综合分析物理过程中的b K D D M K L 方案"b F /-2W L /N D ,6方案和e Bj 方案是最佳的组合!主要是对直接影响双台风路径"强度的西太平洋副热带高压和西风带槽脊的位置和强度模拟效果好#关键词 数值模拟$5J W 模式$双台风$物理方案#概述两个台风靠近时它们的路径$强度等都会受到彼此的影响"早在$')(年W [+/6F L F M ($)就通过一系列的涡旋实验及观测发现两个接近的水旋涡绕着两者连线的中心互相旋转#$'1'年曾庆存())则从大气动力学理论上研究了两个大气涡旋的相互作用以及其移动方式#王玉清等(()采用正压无辐散模式模拟发现两个同等强度的涡旋-合并.后体现了西北向的平移"而不同强度的两个涡旋-合并.后体现了陀螺运动和平移相叠加的形态"这与实际中双台风的相互作用表现类似#张晓慧等(329)采用集合变分混合同化的方法研究了台风W /N P \%$()3&登陆前$后的强度变化与台风!F -F D %$()(&相连的水汽输送通道的变化$相互作用等直接相关#陈德辉等(0)研究发现对模式物理过程参数化方案改进后能明显提高台风路径和强度的预报效果#Y /等(1)发现边界层参数化方案对飓风的早期发展非常敏感#所以有必要进行单独个例分析和研究"这样有助于改进双台风的天气预报水平"对具有自身明显特点和造成较大灾害的"更是如此#本文采用中尺度数值模式5J W o (&("物理过程则使用三种微物理方案"三种边界层方案和三种积云对流参数化方案的不同组合配置"来讨论对双台风-菲特.%W /N P \&和-丹娜丝.%!F -F D &的路径$强度和降水模拟的影响"以揭示5J W 模式中物理过程的组合配置方案在该双台风模拟中的作用"也为集合预报中各物理集合成员的选取打下基础#"本文双台风简介双台风中的$()(号台风-W /N P \.于)%$(年'月(%日$)时开始编号%热带风暴级&后"路径沿西北偏北方向移动"$%月%3日%<时-W /N P \.%强台风级&转向西北偏西方向移动%此时-!F -F D .编号后)6&"$%月0日$9时强台风-W /N P \.登陆福建福鼎市沙埕镇"登陆后路径稍向南折#-!F -F D .生成编号到$%月0日$9时-W /N P \.登陆时"-!F -2F D .一直在-W /N P \.东南侧且沿西北方向移动"且两个台风的距离越来越近#$%月1日$<时转折北上"$%月<日%%时由向北运动转为向东北方向移动#&所用资料和数值模拟方案设计本文采用的数值模拟模式为非静力的中尺度数值模式5J W #为揭示不同参数化方案对双台风模拟的影响"利用5J W 模式中自带的三种微物理参数化方案$三种边界层参数化方案以及三种积云对流参数化方案(在下表和下文中分别简称为微物理%方案&$边界层%方案&$积云%方案&)的不同的组合"设计了)1组试验"具体见下表#模拟初始场和侧边界条件采用$p V $p 的W g Y %W /-F M I M P ^F M !F N F X D D /U /M F N /P -B]D N K U &再分析资料"时间间隔为06"垂直方向)0层"模式水平格距为(%.U "格点数为)%%V $)%"垂直方向分为)<层"模式层顶为9%6=F "时间步长为$)%D "模拟时段为!)%$(年$%月%3日%%时%世界时"以下同&至)%$(年$%月%1日%%时#不同物理参数化方案组合试验表序号微物理边界层积云序号微物理边界层积云%$b K D D M K L e Bj b W $9W K L L /K L ?J W b W%)b K D D M K L ?J W b W $0Y /-?J W b W%(b K D D M K L ?e g g )&9b W $1W K L L /K L ?J W b W%3Y /-e Bj b W $<Y /-e Bj b W'环境科学科技风"#""年$月. All Rights Reserved.续表序号微物理边界层积云序号微物理边界层积云%9Y /-?e g g )&9b W $'Y /-?e g g )&9b W %0W K L L /K L e Bj b W )%W K L L /K L e Bj b W %1W K L L /K L ?e g g )&9b W )$W K L L /K L ?e g g )&9b W %<b K D D M K L e Bj @?H ))Y /-?J W @?H %'b K D D M K L ?J W @?H )(Y /-e Bj @?H $%b K D D M K L ?e g g )&9@?H )3Y /-?e g g )&9@?H $$b K D D M K L ?J W I !)9W K L L /K L e Bj I !$)Y /-?J W b W )0W K L L /K L ?J W b W $(b K D D M K L e Bj I !)1W K L L /K L ?e g g )&9I !$3b K D D M K L ?e g g )&9I !44注 b W 为b F /-2W L /N D ,6方案 @?H 为@K N N D 2?/M M K L 2H F -+/,方案 I !为I L K M M 2!K Q K -]/方案(数值模拟结果分析3&$对台风路径的影响为揭示微物理过程对双台风路径模拟的影响"采取相同的边界层方案和积云方案模拟了台风-W /N P \.和-!F -F D .的路径"模拟结果与实况资料对比分析后可见"对台风-W /N P \.$b K D D M K L 方案模拟的台风路径较Y /-方案$W K L L /K L 方案效果好'在模拟开始)36后"%9日%%时Y /-方案和W K L L /K L 方案均未模拟出-W /N P \.路径由西北偏北转为西北偏西方向移动的变化"即对台风路径的模拟"在边界层和积云方案固定的情况下"微物理过程选用b K D D M K L 方案要较Y /-和W K L L /K L 方案的模拟误差小#对于台风-!F -F D c 路径的模拟"在固定边界层和积云方案后"对微物理过程也是选用b K D D M K L 方案较Y /-方案和W K L L /K L 方案模拟的误差小#b K D D M K L 微物理方案是暖云方案"主要考虑雨水的产生$降落以及蒸发"云水的凝结等过程"而Y /-*W K L L /K L 方案部分的考虑了云冰等冷云过程#此次数值模拟过程中b K D D M K L 优于Y /-*W K L L /K L 方案"这说明对低纬台风(%b U 分辨率的模拟"考虑冷云过程并不一定能提高预报效果#为揭示积云方案对台风路径模拟效果的影响"各敏感性试验采用相同的微物理$边界层方案"不同的积云方案来模拟台风-W /N P \.和-!F -F D .的路径"模拟结果与实况对比后发现b F /-2W L /N D ,6方案模拟的路径较@K N N D 2?/M M K L 2H F -+/,方案$I L K M M 2!K Q K -]/方案的效果好"在模拟开始)36后"@K N N D 2?/M M K L 2H F -+/,和I L K M M 2!K Q K -]/方案模拟的-W /N P \.路径较实况偏南#固定微物理方案和边界层方案"积云方案选用b F /-2W L /N D ,6则要较@K N N D 2?/M M K L 2H F -+/,以及I L K M M 2!K Q K -]/方案模拟的台风路径误差小"对于台风-!F -FD .路径的模拟"几种方案差异不大"但总体来讲选用有利于热对流混合层高度升高"使边界层结构更接近中性的b F /-2W L /N D ,6方案效果最好#为揭示边界层方案对台风路径模拟效果的影响"采用相同的微物理方案和积云物理方案"不同的边界层方案来模拟双台风路径并与实况资料作对比分析发现在微物理过程和积云方案固定的情况下"边界层方案无论采用何种方案"对台风移动路径影响都不大'但对台风!F -F D 的模拟"?J W 方案模拟结果与实况更要接近些"总体来看?J W 方案模拟效果更好些#对比试验%$%b F /-2W L /N D ,6&和试验$(%@K N N D 2?/M M K L 2H F -+/&发现"在积分1)6时%%1日%%时&模拟的台风路径差异最显著"此时试验%$%b F /-2W L /N D ,6&方案模拟的副高中心位置$强度与实况较接近"受副高外围引导气流影响"模拟的-W /N P \.移动路径较实况偏北#而台风-!F -F D .在%3日*%1日期间基本位于副高南侧"故副高位置和强度对其影响不大#试验$(方案模拟的副高脊线呈西北偏西向"故-E /N P \.和-!F -F D .受副高南侧引导气流的影响"移动路径较实况偏南#由于双台风的副高引导气流都较实况偏弱"所以模拟的双台风移速都较实况偏慢#总体对比分析可见"副高中心位置"副高西伸脊点位置和副高强度都影响到双台风的移动方向和移动速度#3&)对台风强度的影响以台风中心海平面气压作为衡量台风强度的标准"选用相同的边界层方案和积云方案"不同的微物理方案组合对双台风强度模拟研究发现不同的微物理方案模拟台风-W /N P \.的强度差别不大"且都较实况强度偏弱#但对-!F -F D .强度的模拟差别较大#总体来看3<6内微物理过程选用b K D D M K L 方案较Y /-方案和W K L L /K L 方案模拟的台风强度误差要小#选用相同的边界层方案和微物理方案"不同的积云方案对双台风强度的模拟研究发现不同的微物理方案模拟-W /N P \.的强度"b F /-2W L /N D ,6方案模拟的台风强度相比于实况偏弱的程度要较@K N N D 2?/M M K L 2H F -+/,$I L K M M 2!K Q K -]/方案小"且都较实况强度偏弱#但对-!F -F D .强度的模拟差别较大"在模拟之初台风强度较实况偏强"但模拟$)6以后"@!科技风"#""年$月环境科学. All Rights Reserved.-!F -F D .的加强程度较实况偏小#但总体来看"b F /-2W L /N D ,6方案模拟的台风强度"无论是台风强度的大小"还是减弱$增强趋势都较@K N N D 2?/M M K L 2H F -+/,方案$I L K M M 2!K Q K -]/方案的模拟效果要好"即在固定微物理方案和边界层方案后"积云方案采用b F /-2W L /N D ,6方案要比@K N N D 2/M M K L 2H F -+/,$I L K M M 2!K Q K -]/方案模拟的台风强度误差小#敏感性试验选用相同的微物理方案和积云方案"不同的边界层方案组合对双台风强度的模拟结果显示所有方案模拟的-W /N P \.台风强度都较实况偏弱"e Bj 方案较J W 方案$?e g g )&9方案方案模拟的效果要好#对-!F -F D .强度的模拟"?J W 方案模拟的台风强度无论是大小还是台风减弱$增强的趋势"都比e Bj $?e g g )&9方案的效果要好#故而在微物理方案和边界层方案固定的情况下"边界层方案选用e Bj 还是?J W 方案"则要要依据不同的台风情况来确定#积云方案对台风强度的模拟也较敏感#试验%$方案模拟的副高和中纬度西风带槽脊的强度较试验$(强"而模拟的双台风强度也较试验$(强见下图#总体对比分析可见"副高$西风带槽脊位置和强度变化对双台风的强度也有影响#4%F )试验%$!方案)b K D D M K L q e Bj q b F /-2W L /N D ,6$^)试验$()b K D D M K L q e Bj q I L K M M 2!K Q K -]/&%0日%%时不同物理方案9%%6=F 环流形势场图结语通过)1种不同参数化方案组合对)%$(年双台风-W /N P \.和-!F -F D .进行了数值模拟"得到以下主要结论!%$&微物理方案的不同和积云方案的不同对台风路径的影响明显"其中b K D D M K L 微物理方案和b F /-2W L /N D ,6积云方案的组合"模拟的台风路径与实况的平均偏差最小#%)&边界层方案与积云方案都对台风强度模拟效果影响明显"e Bj 边界层方案与b F /-2W L /N D ,6积云方案的组合模拟的台风强度变化与实况更接近#%(&模式中不同物理过程的组合对模拟台风的路径$强度等影响较大"物理过程中的b K D D M K L 方案$b F /-2W L /N D ,6方案和e Bj 方案是对双台风-W /N P \.和-!F -F D .模拟的最佳的组合方案#%3&西太副高和西风带槽脊的位置和强度变化直接影响了双台风-W /N P \.和-!F -F D .的移动路径及强度#参考文献 '$(W [+/\6F L F M B !$')(&A 6K U [N [F M N K -OK -,]N P \F L OD D ]U 2U K N L ]P E U P N /P -F -O /N D F ZZM /,F N /P -F D F ZL /-,/ZM K /-U K N K P L P M P 7]'H (&r [F L N H J P ]?K N K P L BP ,!$')(!3'%$)&))<12'(&')(曾庆存&数值天气预报的数学物理基础%第一卷&'?(&北京)科学出版社!$'1')3)$233%&'((王玉清!朱永?&正压无辐散模式中双涡的相互作用'H (&热带气象!$'<'!9%)&)$%92$$9&'3(王玉清!朱永?&双涡藤原效应的数值模拟研究'H (&应用气象学报!$'<'%$&)$(2)%&'9(张晓慧!张立凤!周海申!魏通峰&双台风相互作用及其影响'H (&应用气象学报!)%$'!(%%%3&)3902300&'0(张晓慧!张立凤!熊春晖!彭军&基于集合变分混合同化方法的双台风数值模拟'H (&热带气象学报!)%$9!($%%3&)9%929$0&'1(Y /e !C M M /-7\P P O @J &a [L L /,F -K OF U F 7K N P L K D /OK -N /F M ,P -D N L [,N /P -/-N 6K j B )#U ZP L N F -,K P E [-,K L N F /-N ]U P OK M /-7/-L /D .F D D K D D U K -N 'H (&C -7/-K K L /-7BN L [,N [L K D !)%%0!)<%1&)$%%'2$%$<&基金项目 +双重,兵种作战0基于大数据的航空兵作战指挥气象辅助决策系统1!课题号)Bi %0(2@i $92H e %(作者简介 张晓慧%$'<'*4&!女!甘肃天水人!大气科学硕士!讲师!研究方向)数值天气预报与航空危险天气预报#%'环境科学科技风"#""年$月. All Rights Reserved.。
GRAPES_GFS不同湿物理过程对云降水预报性能的诊断与评估
GRAPES_GFS不同湿物理过程对云降水预报性能的诊断与评估马占山;刘奇俊;秦琰琰【期刊名称】《高原气象》【年(卷),期】2016(35)4【摘要】积云对流和云微物理是数值天气预报模式中最为重要的两类湿物理过程,它们共同影响云和降水的预报性能。
通过采用CMAP降水资料和MODIS、MLS 及Cloud Sat卫星云观测资料对全球中期数值预报模式GRAPES_GFS中这两类湿物理过程参数化方案的不同组合所预报的降水场和云宏微观场进行诊断和评估,以揭示其对云和降水的预报性能。
结果表明:(1)云微物理方案是中高纬度地区总降水预报差异的主因,三种云微物理方案预报的降水强度为SI>NCEP3>NCEP5。
赤道及低纬地区降水差异主要是由积云对流方案引起的,KF_SI组合与CMAP降水最为一致。
(2)SI方案和NCEP3方案在中纬度地区格点降水要显著多于混合相云NCEP5方案;与SAS方案和KF方案相比,BM方案使与其组合的云方案产生的格点降水明显偏少。
(3)BM方案产生的对流降水要明显多于SAS方案和KF方案,中高纬地区SAS方案和KF方案预报的对流降水基本一致,在低纬地区SAS方案对流降水最少。
(4)NCEP5方案预报的云顶温度与MODIS观测吻合较好,NCEP3方案和SI方案预报的云顶温度要较实况偏暖。
三种对流方案预报的云顶温度冷暖关系为SAS<BM<KF,BM和KF预报的云顶温度与实况较为接近。
(5)NCEP5方案预报的积分云水与卫星观测最为接近,两种简冰方案显著偏少,尤以SI方案偏少最多。
SAS 和KF方案能较好的预报积分云水的空间分布,但其量值较观测偏大,BM方案预报的积分云水在低纬度地区偏少明显。
(6)所有方案组合预报的卷云较MLS卫星观测显著偏少,混合相云方案对卷云预报较简冰方案具有一定优势,BM方案偏少最显著。
(7)全球平均而言,KF对流方案和NCEP5云微物理方案对GRAPES_GFS的云和降水预报性能较其他降水物理方案具有一定优势。
基于WRF模式的暴雨天气过程的数值模拟及诊断分析
基于WRF模式的暴雨天气过程的数值模拟及诊断分析袁成松;王秋云;包云轩;严明良【摘要】A heavy rainstorm occurring in the southern part of Jiangsu Province including Shanghai-Nanjing Expressway on September 17th,2009 is simulated by using WRF2.2（Weather Research and Forecasting Model for version 2.2） and NCEP（National Center of Environment Predicting）reanalyzed meteorological data with 1°×1° grid.The verification of the observed data from the Automatic Weather Monitoring System on the Shanghai-Nanjing Expressway displays that the results of the simulation on the rainstorm process are satisfactory and the simulations coincide with the observed values.Diagnoses are made based on the output data from the model.The results are shown as follows：（1）The development and movement of a meso-β-scale low vortex in the middle and lower reaches of the Yangtze River play an important role in the enhancement and maintenance of the rainfall in the process;（2）The moisture convergence zone below 500 hPa is significant and it provides important vapor conditions for the unstable growth of convection and the maintaining of rainstorm by the forming of the deep and humid environment in the rainfall area;（3）There is strong vertical motion in the rainfall area and the vertical structure configuration of the vorticity field is consistent with that of the divergence field.As a result,the unstable energy in the atmosphere release and the strong convective weather forms;（4）The atmospheric stratification is neutral in the middle and upper of troposphere butpotential instable in the lower atmosphere.So there is convection development in the whole layer of the atmosphere,which is conducive to the formation of the rainstorm.%利用新一代中尺度数值预报模式WRF2.2和1°×1°的NCEP气象再分析资料,对2009年9月17日发生在江苏南部地区覆盖沪宁高速公路的一次大暴雨天气过程进行了数值模拟。
WRF模式中不同边界层及云微物理方案对两次黄海海雾个例数值模拟的影响
WRF模式中不同边界层及云微物理方案对两次黄海海雾个例数值模拟的影响饶莉娟; 高山红; 张恺【期刊名称】《《气象科技进展》》【年(卷),期】2019(009)006【总页数】8页(P12-19)【关键词】黄海海雾; WRF模式; 数值模拟; 边界层方案; 云微物理方案【作者】饶莉娟; 高山红; 张恺【作者单位】青岛市黄岛区气象局青岛 266400; 中国海洋大学青岛 266100【正文语种】中文0 引言海雾是海洋上低层大气中的一种水汽凝结现象，由于水滴或冰晶的大量聚积，使能见度低于1 km[1]，给海上交通运输、沿岸的生产与生活造成严重影响。
黄海是我国近海发生海雾最为频繁的海区[2]。
近年来我国从多方面对海雾进行了研究：海雾天气气候学研究[3-7]、海雾遥感探测和观测分析[8-11]、海雾微物理研究[12-15]和海雾数值模拟研究[16-18]等。
其中，海雾的数值模拟研究蓬勃发展，已成为研究海雾的不可缺少的主要方法[19-20]。
但边界层方案和云微物理方案直接影响海雾的数值模拟质量。
WRF（Weather Research and Forecasting）模式有多个边界层方案和云微物理方案可供选择，这些方案都有各自的特点、适用条件及优势。
研究表明，选取不同边界层方案和云微物理方案对降水、气温、风速、台风等模拟效果均存在显著差异[21-25]，对雾的模拟也是如此。
陈阳权等[26]对乌鲁木齐机场一次冻雾天气过程进行数值模拟研究，发现此次冻雾过程对边界层方案较为敏感；黄政等[27]对江苏省高速公路网2011—2013年发生的21场大雾过程进行研究，表明云微物理方案选用WDM6，边界层方案选用QNSE雾的数值模拟效果最优；王佳等[28]对2006年沪宁高速公路的一次持续性大雾的模拟中，发现对相对湿度等常规气象要素的模拟，各个参数化方案的模拟效果都较好，对直接表征能见度的液态水含量的模拟，云微物理过程采用Lin方案模拟效果最好；陆雪等[29]利用2005—2011年11次春季黄海海雾个例开展WRF模式参数化方案敏感性研究，发现边界层与云微物理方案的最佳组合为YSU与Lin方案，最差为Mellor Yamada与WSM5方案；而Steeneveld等[30]在对英国的一次强浓雾过程的研究中，则发现云微物理方案WDM6要优于WSM5和WSM6。
区域洪水灾害风险快速评估研究——以上海市为例
李文彬 ， 覃东华 。 ， 翟高鹏。
（ １ ． 石 家庄 经济 学院勘 查技 术 学院 ， 河北 石 家庄 ０ ５ ０ ０ ３ １ ； ２ ． ｑ － 国地质 大 学信 息工程 学院 ， 武汉 ４ ３ ０ ０ ７ ４ ； ３ ． 武汉 大 学测绘 学院 ， 武汉 ４ ３ ０ ０ ７ ９ ）
摘 要 ：根 据 洪 水 灾 害形 成 机 理 ， 本 文 构 建 了一 种 快 速 评 估 区 域 洪 水 灾 害 风 险 的 方 法 ， 即 用 致 灾 因 子 危 险 性 和 承 灾 体 脆 弱 性 且 辅 以 地 形 因 子 来 反 映 区域 洪 水 灾 害 风 险 ， 并 以 上海 市 为 例 ， 对 该 区域 洪 水 灾 害 风 险 进 行 了快 速 评 估 ：
Ａｂ ｓ ｔ ｒ ａ ｃ ｔ ：Ａ ｃ ｃ ｏ ｒ ｄｉ ｎｇ ｔ ｏ ｔ ｈ ｅ ｆ ｏ ｒ ｍａ ｔ ｉ ｏ ｎ ｍｅ ｃ ｈ ａ ｎｉ ｓ ｍ ｏ ｆ ｆ ｌ ｏ ｏ ｄ ｄｉ ｓ ａ ｓ ｔ ｅ ｒ ， ａ ｒ ａ ｐｉ ｄ ａ ｓ ｓ ｅ ｓ ｓ ｍｅ ｎｔ ｍｅ ｔ ｈ ｏｄ ｏｆ ｆ ｌ ｏｏ ｄ ｒ ｉ ｓ ｋ ｉ ｓ ｂｕｉ ｌ ｔ， ａ ｎｄ ｒ ｅ ｇ ｉ ｏ ｎａ ｌ ｆ ｌ ｏｏ ｄ ｒ ｉ ｓ ｋ ｉ ｓ ｒ ｅ ｆ ｌ ｅ ｃ ｔ ｅ ｄ ｂｙ ｔ ｈｅ ｒ ｉ ｓ ｋ ｏｆ ｄｉ ｓ ａ ｓ ｔ ｅ ｒ — ｃ ａ ｕ ｓ ｉ ｎｇ ｆ ａ ｃ ｔ ｏ ｒ，ｔ ｈｅ ｖ ｕ ｌ ｎ ｅ ｒ ａ ｂ ｉ ｌ ｉ ｔ ｙ ｏ ｆ ｈ ａ ｚ ａ ｒ ｄ ｂｅ ａ ｒ ｉ ｎｇ ｂｏ ｄ ｙ ａ ｎｄ ｔ ｅ ｒ ｒ ａ ｉ ｎ ｆ ａ ｃ ｔ ｏｒ ｓ ． Ｔｈｉ ｓ ｐａ ｐ ｅ ｒ ｔ ａ ｋｅ ｓ Ｓｈ ａ ｎｇ ｈａ ｉ Ｃｉ ｔ ｙ ａ ｓ ａ ｎ ｅ ｘ ａ ｍｐ ｌ ｅ ．Ｆｉ ｒ ｓ ｔ ｔ ｈｅ ｒ ｉ ｓ ｋ ｏ ｆ ｄ ｉ ｓ ａ ｓ ｔ ｅ ｒ — ｃ ａ ｕｓ ｉ ｎｇ ｆ ａ ｃ ｔ ｏ ｒ ｉ ｓ ａ ｎ ａ ｌ ｙｚ ｅ ｄ ｂｙ ｒ ａ ｉ ｎｆ ａ ｌ ｌ ｄ ａ ｔ ａ， ａ ｎ ｄ ｔ ｈ ｅ ｎ ｄ ｉ ｓ ａ ｓ ｔ ｅ ｒ ｌ ｏ ｓ ｓ ａ ｎ ｄ ｄ ｉ ｓ ａ ｓ ｔ ｅ ｒ — ｃ ａ ｕｓ ｉ ｎ ｇ ｆ ａ ｃ ｔ ｏｒ ａ ｒ ｅ ｃ ｏ ｍｐｒ ｅ ｈ ｅ ｎ
层状云降水微物理特征及降水机制研究概述
层状云降水微物理特征及降水机制研究概述第33卷第2期2005年4月气象科技METEOROLOGICALSCIENCEANDTECHNOLOGYVO1.33.NO.2ADr.2005引言层状云降水微物理特征及降水机制研究概述石爱丽(中国气象科学研究院,北京100081)摘要层状云是中国北方大部分地区降水的主要云系,采用综合观测资料的分析研究并结合最新的数值模式对层状云特征和降水机制进行深入研究很有必要,也是含后工作的方向.描述了层状云的种类,特点,通过分析机载PMS(粒子测量系统)资料和地面雨滴谱资料介绍了国内外在层状云云滴谱,冰晶谱,雪质粒谱,雨滴谱,云中质粒总谱等微物理特征方面的研究方法及成果,还介绍了国内外在层状云降水机制方面的研究方法及成果,包括层状云降水数值模拟以及暖云降水机制和冷云降水机制研究.关键词层状云微物理特征降水机制层状云是水平范围很广阔的云系,广义地说,包括卷云(Ci),高层云(),高积云(Ac),层积云(Sc),层云(St),雨层云(s).从出现的天气条件来说,基本上有两种:一种是与锋面气旋相联系的,主要是由a,Sc,As,Ns,St,Fs云系组成的层状云;另一种是气团平流变性或地形影响形成的层状云,以St,Sc,为主.层状云的水平尺度一般为l0～10km,垂直尺度为l0～100km(约100m至5km)….20世纪70年代以来,国内外对层状云进行了大量的外场探测和数值模拟研究,主要有苏联对冬季层状云的探测和人工影响试验,美国对温带气旋云系和地形云的探测和数值模拟以及我国北方层状云人工降水试验研究,取得了许多研究成果.层状云系,尤其是层状冷云,是我国北方冬半年的主要降水云系,是缓解北方春季干旱开展人工增雨的主要作业对象,是我国雨季从南向北推进的主要降水云系.本文旨在对层状云系降水微物理特征及降水机制研究已有成果进行概括总结.1层状云的一般特征层状云的含水量一般在0.01--0.1g/m,在我国北方较薄的层状云含水量更小,常为0.01g/m3,在南方及低纬度地区,层状云中含水量较大,特别是在雨层云和层积云的对流泡中含水量可高达2～3g/m_】一.层状云的总含水量不大,一般为0.0l～0.1mm.层状云的含水量的垂直分布常见的有两种,对于非降水性的St,Sc,含水量的极大值在云的中上部位(3/4高度).对于降水性层状云,如,s系统,含水量的极大值一般在云的下部(1/6高度),H.R, Byers曾在s中进行飞机观测,发现含水量最大值一般在云底附近,为1.5g/m左右.层状云水平方向的含水量也有起伏,平均起伏强度是25.5%,且起伏和平均风速关系不大,对于锋面云系,许多观测说明在锋区里含水量最大,为0.32～0,92g/m,锋区两边含水量较小,通常为0.1～0.3g/m3l2一.层状云中温度层结特点:①云内层结接近湿绝热梯度,最大可能值不超过一0.75～0.79℃/hm;②在云的上部或顶部有逆温层,大多数情况在云顶以下0.1～0.2km内有逆温.层状云中上升气流相对较小,一般在0.1～0.2cm/s,对于大范围的槽前滑升运动一般比较缓慢,每秒一般不超过几厘米,但在气旋辐合上升运动时,升速可达5～30cm/s.层状云中大范围无规则扰动形成的湍流场是其流场的一个重要物理性质.通过大量观测事实和计算表明,层状云云下的里查逊数(R)最低,湍流最强,云内稍微减弱,云上的(R)比云内要大20～40科技部"十五"科技攻关项目"人工增雨技术研究及示范"(2001BA610A一06)资助作者简介:石爱丽,女,1974年生,硕士,从事人工影响天气研究,Email:*******************收稿日期:2003年8月19日;定稿日期:2003年12月16日第2期石爱丽:层状云降水微物理特征及降水机制研究概述l05倍,是云中湍流最弱的地方.层状云就是在湍流发展区的顶部和湍流衰减区的底部之间发展起来的.层状云降水持续时间较长,可从几小时到几天.雨强不大,一般为0.1～1mm/h.但在锋面层状云和层积云降水过程常观测到阵性降水,雨强随时间的变化不比积云小.2层状云微物理特征研究方法及成果2.1研究方法云的微物理特征主要是通过云中各种粒子的谱分布来研究的.云中粒子谱分布是通过对机载PMS(粒子测量系统)资料和地面雨滴谱(GBPP一100,滤纸色斑法)资料进行指数式拟合分析得到的.2.2研究成果2.2.1云滴谱南岳的长期观测表明_2J:不同类型的层状云滴谱不同,一般以层云(St)滴谱最窄,雨层云(Ns)的滴谱最宽.层状云不同层次的滴谱不同,底部的谱要窄一些,中部滴谱比下部要宽.层状云滴谱的演变与天气过程密切相关.层状云不仅在一次天气过程中滴谱有着明显的规律变化,而且在1年中存在着季节变化.春秋季最宽,最大直径达70m,冬夏季最窄,最大直径为50m.在北方层状云的研究中_3,据17次飞机观测的云滴谱资料,厂分布拟合式中,n>5的个例约占总数的40%,而且发现n值的大小与所处云中部位有关,从云底向上,n值逐渐增大.Korolev_4从PMS的FSSP一100探头获取的资料分析得出,在层状云中粒子谱普遍呈双峰分布,这种现象与云中扰动密切相关,与云滴浓度,云的温度,高度及冰晶没有很大关系.2.2.2冰晶谱(d<300m)表1给出的是北方层状云研究中得到的云中质粒特征.表1北方层状云的质粒特征注:为谱斜率参数,Nn为粒子数密度.叶家东等_5用PMS资料,雷达资料和其他实时观测资料对层状云中的冰粒子和中尺度辐合系统中的冰水转化区进行分析,发现这两者的冰粒子特征很不相同,冰水转化区中冰粒子的浓度是层状云区里的冰粒子浓度的4～6倍,而层状云区里的冰粒子的大小却是冰水转化区中冰粒子直径的2倍左右.2.2.3雪质粒谱据北方层状云探测资料统计_3一,有关雪质粒谱的垂直演变可区分为饱和型和非饱和型两类,饱和型对应于枝星状雪晶或雪团,非饱和型则对应于空间状雪质粒.枝星状雪质粒具有更强的攀附过程,在一12～17℃温度层有一迅速增长区,说明雪质粒的增长既与环境条件有关也与其自身的形态特征有关.云中雪质粒谱的垂直演变具有"消耗型"和"补给型"两种类型.2.2.4雪质粒谱的融滴谱据北方层状云探测资料统计_3一,随降水强度增加,雪质粒谱变宽,雪质粒的总个数也相应增多,这与许多观测事实一致.与Gunn和Marshall(1958)拟合的雪质粒谱结论相反,可能是他们未按晶形区分而取总体拟合引起的.2.2.5融化层中的质粒谱对北方层状云的研究表明3一,在一5～一15℃层内,降水粒子谱经历迅速变宽(0℃层向上)和迅速变窄(0℃层向下)的过程.LiuChungming等C6用PMS资料对中尺度对流系统中的层状云降水区的融化层及暖雨区的微物理过程分析得出:融化层在5km以下厚度几百米,温度一直到2～3℃,随着冰粒子下落速度的加大,雪在融化层融化成雨滴,冰粒子数浓度剧减,同时融化层上的大粒子数量出现稳定的增加.2.2.6雨滴谱在北方层状云的研究中_3一认为,雨滴在下落过程中其谱斜率基本维持不变,其降水强度的增大主要是由于截距参数的增加,这反映出雨滴谱的基本谱型的斜率主要是由负温层中冷雨过程确定的.降水过程前期具有宽谱特征,对应于高空暖雪带(温度高于～20℃),雪晶形态为枝星状;降水后期对应于高空冷雪带(温度接近一30℃),雪晶形态为空间状.宫福久等和陈宝君等7对沈阳的降水雨滴谱106气象科技第33卷进行了分类研究,层状云雨滴谱分布窄,最大雨滴直径约3mm,呈指数分布,雨滴浓度量级为100/m. M—P分布和r分布和实测谱偏差都较小,两种拟合谱也比较接近.RolandListE发现:在稳定的层状暖云降水中,雨滴谱仪资料分析得出直径在1～2m问的粒子浓度出现峰值,而由PMS资料分析得出,在0.3m 时出现峰值浓度.2.2.7云中质粒总谱(2～6400m)在北方层状云的研究中3,在催化云作用下的供水云中,降水粒子谱常为具有第二锋值的宽谱,其峰值直径随高度下降而明显增大.冷锋窄降雪带为宽谱,类似于供水云中粒子谱;冷锋宽降雪带的降雪粒子谱则类似于催化云粒子谱.纯暖云过程作用下的雨滴谱为指数式谱,有高空冷云带作用下的雨滴谱为宽谱,且有明显的第二峰值.3层状云降水机制研究3.1数值模拟用模式来研究层状云降水国内外都做了一些工作.相对来说,层状云云物理模式国外研究较少,为深入了解层状云中各物理过程间的相互制约关系及模拟人工催化效果,国内先后研制了一维,二维层状云微物理模式.1981年建立了层状冷云和层状暖云模式.1985年建立了包括有18种微物理过程的冷暖云模式,1985年建立了包括有微物理过程的边界层低云模式,1986年建立了二维层状云模式.并用冷暖云模式对中纬度气旋云系的微物理过程进行了模拟,得出了与实际比较一致的结果.刘公波在硕士论文中完成了中尺度模式与层状云微物理模式的耦合,王成恕在研究生论文中用该模式模拟了一次华北地区锋面云系的降水过程,汪晓滨在论文中加入了催化的模拟."九五"期间,在国家科技攻关的支持下,已研制出大气静力平衡中尺度云系人工增雨模式."十五"期间,已完成大气非静力平衡中尺度模式MM5与云物理模式的耦合.1981年Matveev建立了定常锋面模式.1984年HsieEirh—Yu和Anthes等发展了维非定常锋面云系降水模式,比较了干模式和湿模式的计算结果, 讨论了水汽凝结和蒸发等对中尺度锋面环流的影响.1983年S.Rutledge和P.V.Hobbs6+对层状云降水中的播种云一供应云降水机制进行了模拟,他们采用二维时变层状冷云模式,微物理过程参数化, 考虑5种水成物,数值模拟结果表明,播种云和供应云的组合,有利于降水的产生和加大.T.Traumann (1996)用一维热力流体动力模式以求解水平风分量,位温和比湿的预报方程,同时应用湍流闭合二维半模式求解湍流动能预报方程研究了层状云中毛毛雨的形成.近年来,乌克兰水文气象研究所一直开展冬季锋面云系的理论及外场研究,发展了层状锋面云系和降水形成的基本理论.同时,已发展并使用了一维,二维和三维定常及时变模式,以便对外场试验和基本研究作理论解释.雷达,卫星,PMS,双通道地基微波辐射计等多种探测仪器的综合使用,为验证数值模拟结果以及综合分析降水云的结构特征,进而研究其降水机制提供了依据.3.2研究成果3.2.1层状暖云降水机制Berry和Reinhardt(1974)对暖云随机碰并的数值积分进行了综合分析,认为对于云滴尺度谱符合r分布,平均直径大于24m,含水量达1g/m,在10～20min出现少量达毛毛雨尺度(200m)的雨滴.Johnson(1982)认为大气中的超巨核尺度大至足以在云底发动碰冰增长,应是大气气溶胶谱的常规成分,同时计算得出在具有明显上升气流条件下, 无论海洋云滴谱或大陆云滴谱,超巨核均为雨的发动源.Hobbs等(1985)测量美国高海拔地区可达1000个/m,但在近地面层巨核和超巨核的数浓度的变化可高达几个量级.Ochs和Johnson通过模式研究证实,暖雨可由出现于云凝结核中的超巨核发动,并表明更多的雨可由相继的云水碰并产生.周秀骥9J对暖云降水机制进行过深入研究,讨论了云滴增长的随机过程,凝结作用下云滴的增长,碰并作用下的云滴增长以及重力电和湍流电碰并对云滴电化的影响.南开大学温景嵩教授等把微尺度大气运动的研究从湍流区间,开拓到微米,亚微米粘性流区间,突破了原有理论的限制,建立了重力和布朗耦合碰并与对流碰并以及多分散悬浮粒子沉降的统计理论;在湍流区问研究中,建立了大云滴随机增长的马尔柯夫过程理论,并发现了湍流的不连续性.胡志晋(1987)用模式计算和实测均得出厚度为2km的层状暖云可以通过云水一雨水自动转化产生0.4～0.8mm/h的降水.LiuChungming等J用PMS资第2期石爱丽:层状云降水微物理特征及降水机制研究概述107 料对中尺度对流系统中的层状云降水区的融化层及暖雨区的微物理过程分析得出雪花在融化层能更多的聚合其他粒子产生大粒子,在到达融化层底以前,因为随着粒子增大破碎效率增大,碰并一破碎和自发破碎过程导致大粒子数的急剧减少.3.2.2层状冷云降水机制早在1920年前后,以Bjerkness为代表的挪威学派在提出着名的极锋学说时也总结出了锋面气旋的天气模式.1940年初,Petterson和Bergeron等就建立了云系模型,提出冷锋,暖锋锋面云系的宏观特征及其与锋面部位的对应关系.50年代和60年代初,Newton,Kessler和Wexler等人发现,在大片冷锋回波中,有一强度极大的条状回波带,产生比周围更大的降水,他们指出这是由对流云组成的飑线.1970年前后,Browning等根据雷达和雨量自计网的观测,除了进一步肯定冷锋雨带之外,提出了暖锋雨带和暖区雨带,并对它的形成以及结构特征进行了分析.1973年华盛顿大学的云物理小组在沿太平洋的美国西海岸开始研究中纬度气旋云中云与降水的中尺度和微物理结构,称为温带气旋雨系计划l10.Hobbs等_10l根据一系列探空观测到的冷锋结构,结合大尺度天气形势,用雷达资料分析降水的大的中尺度和小的中尺度结构,定量估计了气旋云系不同部位降水的生长机制.同时,归纳出温带气旋的6种雨带,即暖锋雨带,锋区雨带,冷锋雨带,锢囚锋前的冷波雨带,锋后雨带,类波状雨带,以及它们的动力特征和微观特征.在降水机制的研究中,宽冷锋雨带与部分暖区雨带中形成降水的主要过程符合"播种一供应"机制.在宽冷锋雨带中,播种区的降水粒子含水量占雨带的20%左右,其余80%的降水含水量是在供水区形成的.在供水区中,随着高度的下降,降水含量急剧增大是由两种过程造成的,一种是在"供水区"的水汽凝华增长;另一种是当雨带赶上在低层的云和弱的降水区时,会有降水粒子平流入"供水区".在窄冷锋雨带中,雨核中的淞附过程可能是其降水增长的主要机制,另一种可能机制是重力流.在暖锋雨带中,降水的形成具有"播种一供应"机制的特征.在低层,增强的中尺度抬升的动力作用促使低空水汽的凝结,产生浓密的层状云,成为含水量较高的供水带.锋前冷涌雨带的降水主要通过冰质粒的聚合增长形成,来自低层由普遍的稳定空气运动产生的层状云的水汽和水凝物的向上通量是水分的主要来源.由此可见,Bergeron 的"播种一供应"理论已得到了发展.在我国对北方层状云的研究成果中,通过个例分析得出,我国北方的降水微物理过程基本符合Bergeron提出的催化云一供水云相互作用导致降水的总体概念.对催化云与供水云温度特征的综合分析表明,冬季催化云的云顶温度常低于一20℃(新疆),春夏季则低于一l5℃(陕西,吉林).冬季供水云温度高于一l5℃,春夏季高于一l0℃,有时甚至是高于0℃的纯暖云.催化云与供水云在垂直方向上是分离的,中间常夹有无云区(常与冷锋锋区对应).催化云常为对流层中,高层的高空云带(与冷涌对应的位势不稳定区中的对流泡区或带).供水云常为锋下层积云或锋面上稳定抬升的高层云下部云水区.当层状云中内嵌有对流体并具有一定伸展厚度时,则可在其单一云体内完成云水向降水的转化过程.降水的垂直向增长表明,冰晶在高层催化云中形成后下落,主要增长于低层的冷云或暖云中,催化云中的降水质量增长常低于总降水量的30%,供水云中的增长量常大于70%.供水云中的云水向降水转化有赖于催化云的降水强度,催化作用的持续时间;并与催化云的降水微结构特征有关.许梓秀,王鹏云_1通过对移经京,津,冀地区的33次冷锋前部雨带的雷达观测分析,归纳出3种不同类型的暖区中尺度雨带:平行类,交角类和垂直类.讨论了各类雨带的宏观特征,发生源地,传播方式以及与强对流天气的关系.并用对称不稳定,开尔文一赫姆霍兹型不稳定,切变不稳定等理论对各类雨带发生发展的可能机制作了初步分析探讨.叶家东等_5J用PMS资料,雷达资料和其他实时观测资料对层状云中的冰粒子和中尺度辐合系统中的冰水转化区进行分析,认为层状云中主要降水粒子的增长机制是聚合增长,聚合增长开始于较高,较冷的层次,在下落接近融化层时聚合增长越来越明显.致谢:写作过程中得到郑国光老师的指导,在此表示感谢参考文献1黄美元,徐华英.云和降水物理.北京:科学出版社,19992顾震潮.云雾降水物理基础北京:科学出版社,19803游来光,马培民,胡志晋.北方层状云人工降水试验研究.气象科技,2002,30(增刊):19—5O4KorolevA V.Astudyofbimodaldropletsizedistributioninstrati—108气象科技第33卷56formclouds.AtmosphericResearch,1994,32(1—4):143—170Y eJiadong,FanBeifen,CottonWR,etaJ.ObservatJonaJstudvof microphysicsinthestratiformregionandtransitionregionofamid—latitudemesoscaleconvectivecomplex. ActaMeteorologicaSinica.1991,5(5):527—540LiuChungming,Lo,K.K.ThemicrophysicsofaMei—yucase:da—taanalysis.In:ShamP,ChangCP(eds.).InternationalConfer_ enceonEastAsiaandWesternPacificMeteorologyandClimate, HongKong,6～8July1989,Teaneck(NJ):WorldScienti[icPub—IishingCO,1990.304—3127李大山.人工影响天气现状与展望北京:气象出版社,20028ListRResultsfrom14rarmrainstudiesinPenang,Majaysia.Al几. nalenderMeteorologie,1988,2(25):446—4489周秀骥.暖云降水微物理机制的研究北京:科学出版社,1964 10内蒙古自治区气象局科技情报中心(编译).中纬度气旋云和降水的中微尺度组织结构呼和浩特:内蒙古自治区气象局,198511许梓秀,王鹏云.冷锋前部中尺度雨带特征及其机制分析气象,1989,47(2):198—206 ProgressinResearchesonMicrophysicalCharacteristicsand PrecipitationMechanismsofStratiformCloudPrecipitationShiAiIi(ChineseAcademyofMeteorologicalSciences,Beijing100081)Abstract:StratiformcloudsarethemainprecipitationsysteminmostpartsofNorthChina.Itisnecessarvto combmetheanalysisofcompositeobservationdatawiththenewnumericalmodelstostudyfu rtherthecharacte卜lStlCSandpreclpltatlonmechanismsofstratiformclouds. Thecategoriesandcharacteristicsofstratiformcloudsaredescribed?Theresearchmethodsandmainfindingsinresearchesonmicrophysica1characteristicsathome andabroadnsuchareasasclouddropspectrum,icecrystalspectrum,snowparticlespectrum,r aindropspec—trumandtotalpartic1espectrumarediscussedthroughanalyzingairbornePMSdataandsurfa ceraindroDdata.Inaddition,theresearchesmethodsandmainachievementsinstratiformcloudprecipitation mechanismresearch—esareaIS()mtroduced,includingstratiformcloudprecipitationsimulationandcoldandwar mc1oudDrecipitationmechanismresearchPsKeywords:stratiformcloud,microphysicalcharacteristics,precipitationmecbanisms。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
上海地区三类主要暴雨天气的云微物理和边界层敏感性
模拟探究
暴雨天气是上海地区常见的极端天气事件之一，给城市生活和交通带来诸多困扰和风险。
为了更好地理解和猜测暴雨天气的形成机制，保障城市的防灾减灾工作，科学家们对上海地区三种主要暴雨天气的云微物理和边界层敏感性进行了模拟探究。
起首，我们来看一下三种主要暴雨天气类型。
第一类是锋面型暴雨，主要受到冷锋、暖锋和浓雾锋的影响。
冷锋暴雨常见于冬季，气温骤降，大规模的云团融合产生持续降水；暖锋暴雨则多出此刻春季，冷暖交汇的地方容易形成云团，产生短时强降水；浓雾锋暴雨则多在夏季，锋面激活了潜在不稳定的大气层，导致一系列的云团形成，从而引发强降水。
第二类是台风暴雨，上海地区近海屡屡有台风影响，产生大范围的暴雨。
台风中心引导着强大的水蒸气输送，与地形碰撞产生降水。
在靠拢台风中心的地方，云层高云顶温度低，垂直云结构明显，导致大范围的暴雨。
第三类是对流暴雨，多发生在夏季热带气旋或对流天气的影响下。
强热浮力和较强的垂直风切变，以及地形对气流的影响，导致对流性云团的形成和进步，出现强降水。
对流暴雨的特点是短时间强降水、局地性和不规则分布。
为了模拟上述三类主要暴雨天气的云微物理和边界层敏感性，科学家接受了先进的数值模式和模拟技术，并对上海地区的地形、大气环流、水汽输送等因素进行了详尽的观测和分析。
在锋面型暴雨的模拟探究中，科学家们发现冷锋、暖锋和
浓雾锋对上海暴雨的影响有所不同。
冷锋暴雨主要受到锋面周边冷空气的影响，冷空气的抬升作用使云团形成和降水增强；暖锋暴雨则主要受到暖锋带动的地面湿空气的影响，暖湿空气的上升使云层逐渐增厚；浓雾锋暴雨则主要受到湿空气和冷空气的互相作用，湿空气的饱和和冷空气的降温共同促使云团的进步和增强。
在台风暴雨的模拟探究中，科学家们发现台风的路径、强度和移速都是影响暴雨分布的重要因素。
台风中心周边水汽释放量大，湿度高，大范围的云团形成，产生暴雨。
而在台风的东南象限和西南象限，由于受到台风强风的影响，湿空气被压缩，降水相对较少。
在对流暴雨的模拟探究中，科学家们发现对流云团在不同地形条件下有着不同的进步过程。
地形对气流的阻挡和加速作用，使对流云团的形成和演化具有一定的规律。
例如，山脉的阻挡作用使得上层湿空气不能继续向上挪动，导致雨带出此刻山脉背风侧；而海洋和湖泊对气流的储存和输送作用，使得一些对流云团在海陆之间不息形成和进步，产生强降水。
总结起来，通过对，我们可以更加深度地了解其形成机制，并能够从模拟结果中提取有关降水分布、云团进步等信息，为城市的防灾减灾工作提供科学依据和预警指导。
这对于提高上海城市的抗洪能力和缩减暴雨带来的灾难具有重要意义。
综上所述，湿空气对天气现象的形成和进步具有重要影响。
暖湿空气的上升会增厚云层并导致降水，而湿空气和冷空气的互相作用则可能引发浓雾、锋面暴雨等极端天气。
在台风暴雨和对流暴雨的模拟探究中，科学家们发现了影响暴雨分布的重要因素，如台风路径、强度和移速，以及地形对对流云团进步
过程的影响。
通过对这些天气现象的探究，我们可以更好地理解其形成机制，提供科学依据和预警指导，以提高城市的防灾减灾能力。
因此，对湿空气和暴雨天气的探究对于缩减灾难和提高城市的抗洪能力具有重要意义。