初中数学九年级上册正方形的性质专项练习题
北师大版九年级数学上册《1.3正方形的性质与判定》同步测试题带答案

北师大版九年级数学上册《1.3正方形的性质与判定》同步测试题带答案·知识点1正方形的性质1.正方形具有而矩形不具有的性质是( )A.对边相等B.对角相等C.对角线相等D.对角线互相垂直2.如图,正方形ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=8√2cm,则EF的长度为( )A.1 cmB.2 cmC.2√2cmD.4 cm3.(2023·青岛中考)如图,O为正方形ABCD对角线AC的中点,△ACE为等边三角形.若AB=2,则OE的长度为√6.4.如图,在正方形ABCD中,对角线BD所在的直线上有两点E,F,满足BE=DF,连接AE,AF,CE,CF,求证:△ABE≌△ADF.·知识点2利用正方形的性质求面积5.为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为( )A.2a2B.3a2C.4a2D.5a26.将三个大小不同的正方形如图放置,顶点处两两相接,若正方形A的边长为4,正方形C的边长为3,则正方形B的面积为( )A.25B.5C.16D.127.(2023·重庆中考)如图,在正方形ABCD中,AE平分∠BAC交BC于点E,点F是边AB上一点,连接DF,若BE=AF,则∠CDF的度数为( )A.45°B.60°C.67.5°D.77.5°8.(2023·黄石中考)如图,正方形OABC的边长为√2,将正方形OABC绕原点O顺时针旋转45°,则点B的对应点B1的坐标为( )A.(-√2,0)B.(√2,0)C.(0,√2)D.(0,2)9.(2023·黔东南州中考)如图,在边长为2的等边△ABC的外侧作正方形ABED,过点D作DF⊥BC,垂足为F,则DF的长为√3.10.如图,在正方形ABCD中,对角线AC与BD相交于点O,点P为AD边上的一点,过点P分别作PE⊥AC于点E,作PF⊥BD于点F.若PE+PF=5,则正方形ABCD 的面积为.【素养提升】11.(2023·贵阳中考)如图,在正方形ABCD中,E为AD上一点,连接BE,BE的垂直平分线交AB于点M,交CD于点N,垂足为O,点F在DC上,且MF∥AD.(1)求证:△ABE≌△FMN;(2)若AB=8,AE=6,求ON的长.【解题模型】·模型:正方形内两条直线与对边相交所成线段若垂直则必相等(若相等则必垂直)模型.如图1,在正方形ABCD中,点E,F分别在BC,CD上,AE,BF相交于点O,若AE⊥BF,则AE=BF.如图2,点E,F,G,H分别在边BC,CD,DA,AB上,EG,FH相交于点O,若GE=HF,则GE⊥HF.参考答案·知识点1正方形的性质1.正方形具有而矩形不具有的性质是(D)A.对边相等B.对角相等C.对角线相等D.对角线互相垂直2.如图,正方形ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=8√2cm,则EF的长度为(B)A.1 cmB.2 cmC.2√2cmD.4 cm3.(2023·青岛中考)如图,O为正方形ABCD对角线AC的中点,△ACE为等边三角形.若AB=2,则OE的长度为√6.4.如图,在正方形ABCD中,对角线BD所在的直线上有两点E,F,满足BE=DF,连接AE,AF,CE,CF,求证:△ABE≌△ADF.【证明】∵四边形ABCD是正方形,∴AB=AD,∠BAD=90°∴∠ABD=∠ADB,∴∠ABE=∠ADF在△ABE与△ADF中{AB=AD∠ABE=∠ADFBE=DF,∴△ABE≌△ADF(SAS).·知识点2利用正方形的性质求面积5.为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为(A)A.2a2B.3a2C.4a2D.5a26.将三个大小不同的正方形如图放置,顶点处两两相接,若正方形A的边长为4,正方形C的边长为3,则正方形B的面积为(A)A.25B.5C.16D.127.(2023·重庆中考)如图,在正方形ABCD中,AE平分∠BAC交BC于点E,点F是边AB上一点,连接DF,若BE=AF,则∠CDF的度数为(C)A.45°B.60°C.67.5°D.77.5°8.(2023·黄石中考)如图,正方形OABC的边长为√2,将正方形OABC绕原点O顺时针旋转45°,则点B的对应点B1的坐标为(D)A.(-√2,0)B.(√2,0)C.(0,√2)D.(0,2)9.(2023·黔东南州中考)如图,在边长为2的等边△ABC的外侧作正方形ABED,过点D作DF⊥BC,垂足为F,则DF的长为√3+1.10.如图,在正方形ABCD中,对角线AC与BD相交于点O,点P为AD边上的一点,过点P分别作PE⊥AC于点E,作PF⊥BD于点F.若PE+PF=5,则正方形ABCD的面积为50.【素养提升】11.(2023·贵阳中考)如图,在正方形ABCD中,E为AD上一点,连接BE,BE的垂直平分线交AB于点M,交CD于点N,垂足为O,点F在DC上,且MF∥AD.(1)求证:△ABE≌△FMN;(2)若AB=8,AE=6,求ON的长.【解析】略【解题模型】·模型:正方形内两条直线与对边相交所成线段若垂直则必相等(若相等则必垂直)模型.如图1,在正方形ABCD中,点E,F分别在BC,CD上,AE,BF相交于点O,若AE⊥BF,则AE=BF.如图2,点E,F,G,H分别在边BC,CD,DA,AB上,EG,FH相交于点O,若GE=HF,则GE⊥HF.。
北师版九年级上册正方形的性质与判定综合练习题
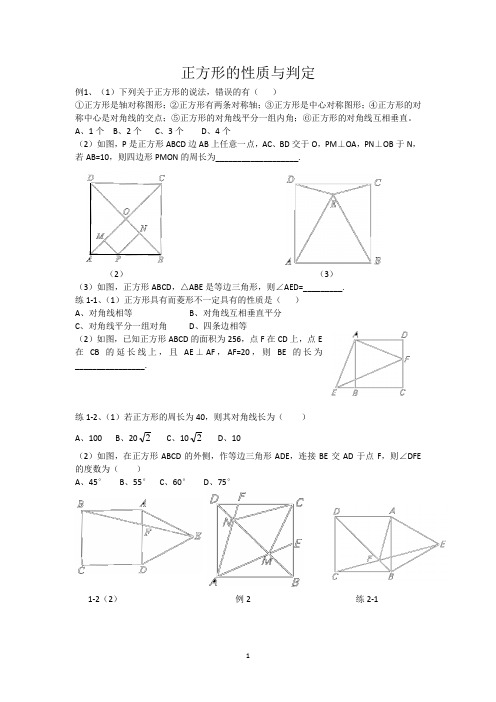
正方形的性质与判定例1、(1)下列关于正方形的说法,错误的有()①正方形是轴对称图形;②正方形有两条对称轴;③正方形是中心对称图形;④正方形的对称中心是对角线的交点;⑤正方形的对角线平分一组内角;⑥正方形的对角线互相垂直。
A、1个B、2个C、3个D、4个(2)如图,P是正方形ABCD边AB上任意一点,AC、BD交于O,PM⊥OA,PN⊥OB于N,若AB=10,则四边形PMON的周长为___________________.(2)(3)(3)如图,正方形ABCD,△ABE是等边三角形,则∠AED=_________.练1-1、(1)正方形具有而菱形不一定具有的性质是()A、对角线相等B、对角线互相垂直平分C、对角线平分一组对角D、四条边相等(2)如图,已知正方形ABCD的面积为256,点F在CD上,点E在CB的延长线上,且AE⊥AF,AF=20,则BE的长为________________.练1-2、(1)若正方形的周长为40,则其对角线长为()A、100B、202C、102D、10(2)如图,在正方形ABCD的外侧,作等边三角形ADE,连接BE交AD于点F,则∠DFE 的度数为()A、45°B、55°C、60°D、75°1-2(2)例2 练2-1例2、如图,已知E、F分别是正方形ABCD的边BC、CD上的点,AE、AF分别与对角线BD 相交于M、N,若∠EAF=50°,则∠CME+∠CNF=_______。
练2-1、如图,四边形ABCD为正方形,以AB为边向正方形外作正△ABE,CE与BD相交于点F,则∠AFD的度数为_________.练2-2、如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F。
求证:(1)AP=EF;(2)AP⊥EF。
例3、如图,在正方形ABCD中,对角线AC、BD交于点O,E是BD延长线上的点,且EA=EC。
2022-2023学年北师大版九年级数学上册《1-3正方形的性质与判定》同步练习题(附答案)

2022-2023学年北师大版九年级数学上册《1.3正方形的性质与判定》同步练习题(附答案)一.选择题1.正方形具有而矩形不一定具有的性质是()A.对角线相等B.四个角都是直角C.对角线互相垂直D.两组对边分别平行2.下列说法正确的是()A.正方形既是矩形,又是菱形B.有一个内角是直角的四边形是矩形C.两条对角线互相垂直平分的四边形是正方形D.对角线互相垂直的四边形是菱形3.如图,已知四边形ABCD是平行四边形,下列结论正确的是()A.当AB=BC时,四边形ABCD是矩形B.当AC⊥BD时,四边形ABCD是矩形C.当AC⊥BD时,四边形ABCD是菱形D.当∠ABC=90°时,四边形ABCD是正方形4.在正方形ABCD中,BF平分∠DBC交CD于F点,则∠DBF的度数是()A.15°B.22.5°C.30°D.45°5.如图,点E、F分别是正方形ABCD的边CD、BC上的点,且CE=BF,AF、BE相交于点G,下列结论不正确的是()A.AF=BE B.AF⊥BEC.AG=GE D.S△ABG=S四边形CEGF6.如图,点E,F,P,Q分别是正方形ABCD的四条边上的点,并且AF=BP=CQ=DE,则下列结论不一定正确的是()A.∠AFP=∠BPQB.EF∥QPC.四边形EFPQ是正方形D.四边形PQEF的面积是四边形ABCD面积的一半7.如图1是由一根细铁丝围成的正方形,其边长为1.现将该细铁丝围成一个三角形(如图2所示),则AB的长可能为()A.3.0B.2.5C.2.0D.1.58.如图,已知正方形ABCD的边长为4,P是对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接AP,EF.给出下列结论:①PD=EC;②四边形PECF的周长为8;③AP=EF;④EF的最小值为2.其中正确结论有几个()A.1B.2C.3D.49.如图,在平面直角坐标系xOy中,P(4,4),A、B分别是x轴正半轴、y轴正半轴上的动点,且△ABO的周长是8,则P到直线AB的距离是()A.4B.3C.2.5D.210.如图四块同样大小的正方形纸片,围出一个菱形ABCD,一个小孩顺次在这四块纸片上轮流走动,每一步都踩在一块纸片的中心,则这个小孩走的路线所围成的图形是()A.平行四边形B.矩形C.菱形D.正方形二.填空题11.如图,已知阴影部分是一个正方形,AB=4,∠B=45°,则此正方形的面积为.12.添加一个条件,使矩形ABCD是正方形,这个条件可能是.13.如图,平行四边形ABCD的对角线互相垂直,要使ABCD成为正方形,还需添加的一个条件是(只需添加一个即可)14.边长为4的一个正方形和一个等边三角形如图摆放,则△ABC的面积为.15.如图,正方形ABCD内部有一个等边△ABE,则∠DAE=°.16.如图,正方形ABCD的顶点B、C都在直角坐标系的x轴上,点D的坐标是(2,3),则点B的坐标是.17.如图,点D,E,F分别是△ABC三边的中点,连接AD,DE,DF,有下列结论:①四边形AEDF一定是平行四边形;②若∠BAC=90°,则四边形AEDF是矩形;③若AD平分∠BAC,则四边形AEDF是正方形;④若AD⊥BC,则四边形AEDF是菱形.其中正确的有.(填序号)三.解答题18.如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且AB=4,CF=1.(1)求AE,EF,AF的长;(2)求证:∠AEF=90°.19.如图,在正方形ABCD中,PD=QC,求证:PB=AQ,BP⊥AQ.20.四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交线段BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.(1)如图,求证:矩形DEFG是正方形;(2)若AB=2,CE=2,求CG的长.参考答案一.选择题1.解:∵正方形的性质为:对边平行且相等,四条边相等,四个角为直角,对角线互相垂直平分,相等,且每条对角线平分一组对角,矩形的性质为:对边平行且相等,四个角为直角,对角线互相平分,相等,∴正方形具有而矩形不一定具有的性质是:对角线互相垂直,故选:C.2.解:A.正方形既是矩形,又是菱形,正确,符合题意;B.有一个内角是直角的四边形是矩形,错误,不符合题意;C.两条对角线互相垂直平分的四边形是正方形,错误,不符合题意;D.对角线互相垂直的四边形是菱形,错误,不符合题意.故选:A.3.解:A、∵四边形ABCD是平行四边形,又∵AB=BC,∴四边形ABCD是菱形,故本选项不符合题意;B、∵四边形ABCD是平行四边形,又∵AC⊥BD,∴四边形ABCD是菱形,故本选项不符合题意;C、∵四边形ABCD是平行四边形,又∵AC⊥BD,∴四边形ABCD是菱形,故本选项符合题意;D、∵四边形ABCD是平行四边形,又∵∠ABC=90°,∴四边形ABCD是矩形,故本选项不符合题意;故选:C.4.解:∵BD是正方形ABCD的对角线,∴∠DBC=45°.∵BF平分∠DBC,∴∠DBF=∠DBC=22.5°.故选:B.5.解:∵四边形ABCD是正方形,∴AB=BC,∠ABC=∠C=90°,∵BF=CE,∴△ABF≌△BCE(SAS),∴AF=BE,∠BAG=∠CBE,∴选项A不符合题意;∵∠ABG+∠CBE=∠ABC=90°,∴∠BAG+∠ABG=90°,∴∠AGB=90°,∴AF⊥BE,∴选项B不符合题意;∵△ABF≌△BCE,∴S△ABF=S△BCE,∴S△ABF﹣S△BFG=S△BCE﹣S△BFG,∴S△ABG=S四边形CEGF,∴选项D不符合题意;∵无法证明AG=GE,∴选项C符合题意;故选:C.6.解:∵四边形ABCD是正方形,∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=AD,∵AF=BP=CQ=DE,∴DF=CE=BQ=AP,∴△APF≌△DFE≌△CEQ≌△BQP(SAS),∴EF=FP=PQ=QE,∠AFP=∠BPQ,故A选项正确,不符合题意;∵EF=FP=PQ=QE,∴四边形EFPQ是菱形,∴EF∥PQ,故B选项正确,不符合题意;∵△APF≌△BQP,∴∠AFP=∠BPQ,∵∠AFP+∠APF=90°,∴∠APF+∠BPQ=90°,∴∠FPQ=90°,∴四边形EFPQ是正方形.故C选项正确,不符合题意;∵四边形PQEF的面积=EF2,四边形ABCD面积=AB2,若四边形PQEF的面积是四边形ABCD面积的一半,则EF2=AB2,即EF=AB.若EF≠AB,则四边形PQEF的面积不是四边形ABCD面积的一半,故D选项不一定正确,符合题意.故选:D.7.解:∵由一根细铁丝围成的正方形,其边长为1,∴该细铁丝的长度为4.∴AC+BC+AB=4,∴AC+BC=4﹣AB.∵AC+BC>AB,∴4﹣AB>AB,∴AB<2.∴AB的长可能为1.5,故选:D.8.解:如图,连接PC,①∵正方形ABCD的边长为4,P是对角线BD上一点,∴∠ABC=∠ADC=∠BCD=90°,∠PDC=∠DBC=45°,AB=BC=CD=AD=4,又∵PE⊥BC,PF⊥CD,∴∠PEC=∠PEB=∠PFC=∠PFD=90°=∠BCD,∴∠DPF=∠PDF=∠BPE=∠DBC=45°,∴PF=DF,PE=BE,即△PDF和△BPE均为等腰直角三角形,∴PD=PF,∵∠PEC=∠PFC=∠BCD=90°,∴四边形PECF是矩形,∴CE=PF=DF,PE=FC,∴PD=CE,故①正确;②由①知:PE=BE,且四边形PECF为矩形,∴四边形PECF的周长=2CE+2PE=2CE+2BE=2(CE+BE)=2BC=2×4=8,故②正确;③∵四边形PECF为矩形,∴PC=EF,∵四边形ABCD为正方形,∴AD=CD,∠ADP=∠CDP,在△ADP和△CDP中,,∴△ADP≌△CDP(SAS),∴AP=PC,∴AP=EF,故③正确;④由③得:EF=PC=AP,∴当AP最小时,EF最小,∴当AP⊥BD时,垂线段最短,即AP=BD=2时,EF的最小值等于2;故④错误;综上,①②③正确.故选:C.9.解:方法一:如图,过点P作PC⊥x轴,PD⊥y轴,垂直分别为C,D,设OB=a,OA=b,AB=c,P到直线AB的距离是h,∵△ABO的周长是8,∴a+b+c=8,∴a+b=8﹣c,∴a2+2ab+b2=64﹣16c+c2根据勾股定理得:a2+b2=c2,∴ab=32﹣8c,∵S△P AB=4×4﹣ab﹣4(4﹣b)﹣4(4﹣a)=2(a+b)﹣ab=2(8﹣c)﹣(32﹣8c)=16﹣2c﹣16+4c=2c,∵S△P AB=×c•h,∴2c=×c•h,∴h=4.∴P到直线AB的距离为4.方法二:如图,过点P作PC⊥x轴,PD⊥y轴,垂直分别为C,D,∵P(4,4),∴四边形CODP是边长为4的正方形,∴PC=PD=OC=OD=4,∵A、B分别是x轴正半轴、y轴正半轴上的动点,∴将△P A′D沿P A′折叠得到△P A′E,延长A′E交y轴于点B,∴∠P A′D=∠P A′E,PE=PD,A′D=A′E,∠PDA′=∠PEA′=90°,∴PE=PC,在Rt△PEB和Rt△PCB中,,∴Rt△PEB≌Rt△PCB(HL),∴BE=BC,∵△A′BO的周长是8,∴A′O+BO+A′B=A′O+BO+BE+A′E=A′O+BO+BC+A′D=CO+DO=8,∴△A′BO符合题意中的△ABO,∴P到直线AB的距离PE=4,故选:A.10.解:如图,根据题意,顺次连接四个正方形的中心,所构成的图形是正方形,所以这个小孩走的路线所围成的图形是正方形.故选:D.二.填空题11.解:∵阴影部分是一个正方形,∴∠ACB=90°,∵∠B=45°,∴△ABC是等腰直角三角形,∴AC===2,∴正方形的面积为(2)2=8,故答案为:8.12.解:AB=AD(或AC⊥BD答案不唯一).理由:∵四边形ABCD是矩形,又∵AB=AD,∴四边形ABCD是正方形.或∵四边形ABCD是矩形,又∵AC⊥BD,∴四边形ABCD是正方形,故答案为:AB=AD(或AC⊥BD答案不唯一).13.解:条件为∠ABC=90°或AC=BD,理由是:∵平行四边形ABCD的对角线互相垂直,∴四边形ABCD是菱形,∵∠ABC=90°或AC=BD,∴四边形ABCD是正方形,故答案为:∠ABC=90°或AC=BD.14.解:过C作CD⊥AB交AB延长线与D,如图:∵∠CBD=180﹣90°﹣60°=30°,∠D=90°,∴CD=BC=×4=2,∴△ABC的面积为AB•CD=×4×2=4,故答案为:4.15.解:∵四边形ABCD是正方形,∴∠DAB=90°,∵△ABE是等边三角形,∴∠DAE=∠DAB﹣∠EAB=90°﹣60°=30°,故答案为:30.16.解:∵四边形ABCD为正方形,∴AD=CD=BC=AB,∵点D的坐标是(2,3),∴AD=CD=BC=3,OC=2,∴OB=1,∴点B的坐标是(﹣1,0).故答案为:(﹣1,0).17.解:①∵点D、E、F分别是△ABC三边的中点,∴DE、DF为△ABC的中位线,∴ED∥AC,且ED=AC=AF;DF∥AB,且DF=AB=AE,∴四边形AEDF一定是平行四边形,故正确;②若∠BAC=90°,则平行四边形AEDF是矩形,故正确;③若AD平分∠BAC,则∠BAD=∠CAD,∵DE∥AC,∴∠CAD=∠ADE,∴∠BAD=∠ADE,∴AE=DE,又∵四边形AEDF是平行四边形,∴四边形AEDF是菱形,∴不能判定四边形AEDF是正方形,故错误;④若AD⊥BC,则AD垂直平分BC,∴AB=AC,∵AB=AC,AD⊥BC,∴AD平分∠BAC,即∠BAD=∠CAD,∵DE∥AC,∴∠CAD=∠ADE,∴AE=DE,又∵四边形AEDF是平行四边形,∴四边形AEDF是菱形,故正确.故答案为:①②④.三.解答题18.(1)解:∵四边形ABCD是正方形,∴∠B=∠C=∠D=90°,∵E为AB的中点,∴BE=CE=2,∴AE===2,EF===,AF===5;(2)证明:∵AE2+EF2=20+5=25,AF2=52=25,∴AE2+EF2=AF2,∴∠AEF=90°.19.证明:由题意可得:AD=AB=BC=DC,∠BAD=∠ADC=∠ABC=∠C=90°,∵PD=QC,∴AP=DQ,在△ADQ和△BAP中,,∴△ADQ≌△BAP(SAS),∴BP=AQ,∠APB=∠AQD,∵∠DAQ+∠AQD=90°,∴∠DAQ+∠APB=90°,∴BP⊥AQ,∴BP=AQ,BP⊥AQ.20.(1)证明:如图1,作EP⊥CD于P,EQ⊥BC于Q,∵∠DCA=∠BCA,∴EQ=EP,∵∠QEF+∠FEC=45°,∠PED+∠FEC=45°,∴∠QEF=∠PED,在Rt△EQF和Rt△EPD中,,∴Rt△EQF≌Rt△EPD(ASA),∴EF=ED,∴矩形DEFG是正方形;(2)解:如图2,在Rt△ABC中,AB=2,∴AC=AB=4,∵CE=2,∴AE=4﹣2=2,∴AE=CE,∴点F与C重合,此时△DCG是等腰直角三角形,∴CG=CE=2.。
北师大版九级数学上正方形的性质与判定正方形的判定专题练习题及答案

北师大版九年级数学上册第一章特殊平行四边形3.正方形的性质与判定正方形的判定专题练习题1.下列说法不正确的是()A.一组邻边相等的矩形是正方形B.对角线相等的菱形是正方形C.对角线互相垂直的矩形是正方形D.有一个角是直角的平行四边形是正方形2.在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的条件是() A.AC=BD,AB∥CD,AB=CD B.AD∥BC,∠A=∠CC.AO=BO=CO=DO,AC⊥BD D.AO=CO,BO=DO,AB=BC3. 已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC ⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是()A.选①②B.选②③C.选①③D.选②④4.如图,只要把一张矩形纸片的一个角沿折痕AE翻折上去,使AB和AD边上的AF重合,则四边形ABEF就是一个正方形,判断的依据是____________________________.5.如图,在四边形ABCD中,AB=BC=CD=DA,对角线AC与BD相交于点O,若不增加任何字母与辅助线,要使得四边形ABCD是正方形,则还需增加的一个条件是__________________.6.黑板上画有一个图形,学生甲说它是多边形,学生乙说它是平行四边形,学生丙说它是菱形,学生丁说它是矩形,老师说这四位同学的答案都正确,则黑板上画的图形是__________.7.对角线________的菱形是正方形,对角线________的矩形是正方形,对角线________________的平行四边形是正方形,对角线的四边形是正方形.8.已知:如图,△ABC中,∠ABC=90°,BD是∠ABC的平分线,DE⊥AB于点E,DF ⊥BC于点F.求证:四边形DEBF是正方形.9.如图,在△ABC中,点D,E分别是边AB,AC的中点,将△ADE绕点E旋转180°得到△CFE.(1)求证:四边形ADCF是平行四边形;(2)当△ABC满足什么条件时,四边形ADCF是正方形?请说明理由.10.四边形ABCD的对角线AC=BD,AC⊥BD,分别过点A,B,C,D作对角线的平行线,所成的四边形EFMN是()A.正方形B.菱形C.矩形D.任意四边形11.如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,添加一个条件,仍不能证明四边形BECF为正方形的是()A.BC=AC B.CF⊥BF C.BD=DF D.AC=BF12.如图,将一张长方形纸片对折两次,然后剪下一个角,打开.如果要剪出一个正方形,那么剪口线与折痕成________度角.13.如图,以边长为1的正方形的四边中点为顶点作四边形,再以所得四边形的四边中点为顶点作四边形,…依次作下去,图中所作的第三个四边形的周长为________;所作的第n 个四边形的周长为________.14.如图,正方形ABCD的边长为6,菱形EFGH的三个顶点E,G,H分别在正方形ABCD 的边AB,CD,DA上,且AH=2,连接CF.若DG=2,求证:菱形EFGH为正方形.15.如图,正方形CEFG的边GC在正方形ABCD的边CD上,延长CD到H,使DH=CE,K在BC边上,且BK=CE,求证:四边形AKFH为正方形.答案:1---3 DCB4. 有一组邻边相等的矩形是正方形5. AC=BD6. 正方形7. 相等互相垂直互相垂直且相等互相垂直平分且相等8.证明:∵DE⊥AB,DF⊥BC,∴∠DEB=∠DFB=90°.又∵∠ABC=90°,∴四边形BEDF为矩形.∵BD是∠ABC的平分线,且DE⊥AB,DF⊥BC,∴DE=DF,∴矩形BEDF为正方形.9. (1)证明:∵△CFE是由△ADE绕点E旋转180°得到的,∴A,E,C三点共线,D,E,F三点共线,且AE=CE,DE=FE,故四边形ADCF是平行四边形;(2)解:当∠ACB=90°,AC=BC时,四边形ADCF是正方形.理由如下:在△ABC中,∵AC=BC,AD=BD,∴CD⊥AB,即∠ADC=90°.由(1)知,四边形ADCF是平行四边形,∴四边形ADCF是矩形.又∵∠ACB=90°,∴CD=12AB=AD,故四边形ADCF是正方形10. A11. D12. 4513. 2 4(2 2)n14.证明:∵四边形ABCD是正方形,∴∠D=∠A=90°.∵四边形EFGH是菱形,∴HG =HE.∵DG=AH=2,∴Rt△HDG≌Rt△EAH,∴∠DHG=∠AEH.又∵∠AEH+∠AHE=90°,∴∠DHG+∠AHE=90°,∴∠GHE=90°,∴菱形EFGH为正方形.15.证明:∵四边形ABCD和四边形CEFG是正方形,∴AB=BC=CD=AD,∠BAD=∠DCB=∠B=∠ADC=90°,∠GCE=∠E=∠GFE=∠CGF=90°,∴∠ADH=∠HGF=∠E=∠B=90°.又∵DH=CE,BK=CE,∴BK=GF=DH=EF,KE=GH=AB=AD,∴△ABK ≌△KEF≌△HGF≌△ADH,∴AK=KF=HF=AH,∠BAK=∠DAH.∵∠BAD=90°,∴∠HAK=∠HAD+∠DAK=∠BAK+∠DAK=∠BAD=90°,∴四边形AKFH为正方形.。
2021-2022学年北师大版九年级数学上册正方形的性质习题含答案

北师版九年级数学上册1.3.1正方形的性质一、选择题(共10小题,3*10=30)1.已知在四边形ABCD中,∠A=∠B=∠C=90°,如果添加一个条件,即可推出该四边形是正方形,那么这个条件可以是()A.∠D=90°B.AB=CD C.AD=BC D.BC=CD2.正方形具有而菱形不一定具有的性质是( )A.四条边都相等B.对角线互相垂直平分C.对角线相等D.对角线平分一组对角3.如图,在正方形ABCD的外侧,作等边△ABE,则∠BED的度数为( )A.15° B.35° C.45° D.55°4.如图,在菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为( )A.14 B.15 C.16 D.175.如图,已知P是正方形ABCD对角线BD上一点,且BP=BC,则∠ACP的度数是( )A.45° B.22.5° C.67.5° D.75°6. 如图,在正方形ABCD中,点E,F分别在BC,CD上,BE=CF,则图中与∠AEB相等的角的个数是()A.1 B.2 C.3 D.47.如图,在正方形ABCD中,AB=2,P是AD边上的动点,PE⊥AC于点E,PF⊥BD于点F,则PE +PF 的值为( )A .4B .2 2C . 2D .28.四边形具有不稳定性,对于四条边长确定的四边形,当内角度数发生变化时,其形状也会随之改变.如图,改变正方形ABCD 的内角,正方形ABCD 变为菱形ABC′D′.若∠D′AB =30°,则菱形ABC′D′的面积与正方形ABCD 的面积之比是( )A .1B .12C .22D .329.如图,正方形ABCD 的边长为1,点E ,F 分别是对角线AC 上的两点,EG ⊥AB.EI ⊥AD ,FH ⊥AB ,FJ ⊥AD ,垂足分别为G ,I ,H ,J.则图中阴影部分的面积等于 ( )A .1B .12C .13D .1410.如图,正方形ABCD 的边AB 上有一动点E ,以EC 为边作矩形ECFG ,且边FG 过点D.在点E 从点A 移动到点B 的过程中,矩形ECFG 的面积( )A .先变大后变小B .先变小后变大C .一直变大D .保持不变 二.填空题(共8小题,3*8=24)11.如图,在正方形ABCD 中,E 是对角线BD 上一点,AE 的延长线交CD 于点F ,连接CE.若∠BAE =56°,则∠CEF =________.12. 如图,在正方形ABCD中,对角线AC,BD相交于点O,则图中的等腰直角三角形有_______个13.如图,在正方形ABCD中,点E在边DC上,DE=4,EC=2,则AE的长为_______.14.如图,已知P是正方形ABCD对角线BD上的一点,且BP=BC,则∠ACP的度数是_______.15.如图,将正方形纸片按如图折叠,AM为折痕,点B落在对角线AC上的点E处,则∠CME=.16.如图,正方形ABCD的边长为1,点E在边DC上,AE平分∠DAC,EF⊥AC,F为垂足,那么FC=__________.17.如图,点P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为______.18.如图,已知点E在正方形ABCD的边AB上,以BE为边向正方形ABCD外部作正方形BEFG,连接DF,M,N分别是DC,DF的中点,连接MN.若AB=7,BE=5,则MN=__ __.三.解答题(共6小题,46分)19.(6分) 如图,在正方形ABCD中,点E在BC边的延长线上,点F在CD边的延长线上,且CE =DF,连接AE和BF相交于点M. 求证:AE=BF.20.(7分) 如图,在正方形ABCD中,E,F分别为边AD和CD上的点,且AE=CF,连接AF,CE 交于点G.求证:AG=CG.21.(7分) 如图,在正方形ABCD中,点E是BC上的一点,点F是CD延长线上的一点,且BE=DF,连接AE,AF,EF.(1)求证:△ABE≌△ADF;(2)若AE=5,请求出EF的长.22.(8分) 如图,在正方形ABCD的外侧,作等边三角形ADE,连接BE,CE.(1)求证:△BAE≌△CDE;(2)求∠AEB的度数.23.(8分) 如图,在正方形ABCD中,点E,F分别在边CD,AD上,且AF=CE.(1)求证:△ABF≌△CBE;(2)若AB=4,AF=1,求四边形BEDF的面积.24.(10分) 如图,E,F是正方形ABCD的对角线AC上的两点,且AE=CF.(1)求证:四边形BEDF是菱形;(2)若正方形边长为4,AE=2,求菱形BEDF的面积.参考答案1-5 DCCCB 6-10CCBBD11. 22° 12. 8 13. 213 14. 22.5° 15. 45° 16. 2 -1 17. 135° 18. 13 219. 解:在正方形ABCD 中,AB =BC =CD =AD ,∵CE =DF ,∴BE =CF ,在△AEB 和△BFC 中, ⎩⎪⎨⎪⎧AB =BC ,∠ABE =∠BCF ,BE =CF ,∴△AEB ≌△BFC(SAS),∴AE =BF 20. 证明:易证△ADF ≌△CDE(SAS),∴∠DAF =∠DCE ,在△AGE 和△CGF 中,⎩⎪⎨⎪⎧∠GAE =∠GCF ,∠AGE =∠CGF ,AE =CF ,∴△AGE ≌△CGF(AAS),∴AG =CG21. 解:(1)证明:∵四边形ABCD 是正方形,∴AB =AD ,∠ABC =∠ADC =∠ADF =90°.又∵BE =DF ,∴△ABE ≌△ADF(SAS)(2)由(1)知△ABE ≌△ADF ,∴AE =AF ,∠BAE =∠DAF ,∴∠EAF =∠DAF +∠EAD =∠BAE +∠EAD =90°,∴EF = 2 AE =5 222. 解:(1)∵△ADE 为等边三角形,∴AD =AE =DE ,∠EAD =∠EDA =60°,∵四边形ABCD 为正方形,∴AB =AD =CD ,∠BAD =∠CDA =90°,∴∠EAB =∠EDC =150°,在△BAE 和△CDE 中,⎩⎪⎨⎪⎧AB =DC ,∠EAB =∠EDC ,AE =DE ,∴△BAE ≌△CDE(SAS) (2)∵AB =AD ,AD =AE ,∴AB =AE ,∴∠ABE =∠AEB ,∵∠EAB =150°,∴∠AEB =12 (180°-150°)=15°23. 解:(1)∵四边形ABCD 是正方形,∴AB =CB ,∠A =∠C =90°.在△ABF 和△CBE 中, ⎩⎪⎨⎪⎧AB =CB ,∠A =∠C =90,AF =CE ,∴△ABF ≌△CBE(SAS) (2)由已知可得S 正方形ABCD =16,S △ABF =S △CBE =12×4×1=2.所以S 四边形BEDF =16-2×2=1224. 解:(1)连接BD 交AC 于点O ,∵四边形ABCD 为正方形,∴BD ⊥AC ,OD =OB =OA =OC ,∵AE =CF ,∴OA -AE =OC -CF ,即OE =OF ,∴四边形BEDF 为平行四边形,又∵BD ⊥EF ,∴▱BEDF 为菱形(2)∵正方形边长为4,∴BD =AC =42,∵AE =CF =2,∴EF =AC -22=22,∴S 菱形BEDF=12BD·EF =12×42×22=8。
初三上册正方形判定练习题

初三上册正方形判定练习题1. 介绍正方形正方形是一种特殊的四边形,它的四条边长度相等且四个内角均为直角。
正方形具有很多特性,比如对角线相等、对边平行等。
接下来,我们将通过练习题来测试你对正方形的判定能力。
2. 练习题一请判定下面的图形是否为正方形。
如果是,请说明理由;如果不是,请说明是什么图形。
a)AB = BC = CD = DAAD ⊥ ABb)PQ = QR = RS = SPPQ ⊥ PSc)EF = FG = GH = HEEG ⊥ EH3. 解析练习题一并且角BAD为90度。
b) 这个图形不是正方形。
虽然四条边PQ、QR、RS、SP的长度相等,但是角PSQ不是直角,而是锐角。
c) 这个图形不是正方形。
虽然四条边EF、FG、GH、HE的长度相等,但是角EGH不是直角,而是钝角。
4. 练习题二请判定下面的图形是否为正方形。
如果是,请说明理由;如果不是,请说明是什么图形。
a)MN = NO = OP = MP∠MNO = 90°b)QR = RS = ST = TQQS ⊥ QTc)UV = VW = WX = XUUY ⊥ UY5. 解析练习题二并且角MNO为90度。
b) 这个图形不是正方形。
虽然四条边QR、RS、ST、TQ的长度相等,但是角QST不是直角,而是钝角。
c) 这个图形不是正方形。
虽然四条边UV、VW、WX、XU的长度相等,但是角UYU不是直角,而是钝角。
6. 总结通过以上练习题,我们可以得出以下结论:- 要判断一个图形是不是正方形,需要满足四个内角均为直角且四条边长度相等。
- 如果只有四条边长度相等,而角不是直角,则图形不是正方形。
- 如果只有四个内角为直角,而边的长度不相等,则图形也不是正方形。
希望通过这些练习题,你能对正方形的判定有更进一步的理解和掌握。
继续努力,加油!。
北师大版九年级上册数学 正方形 专项训练
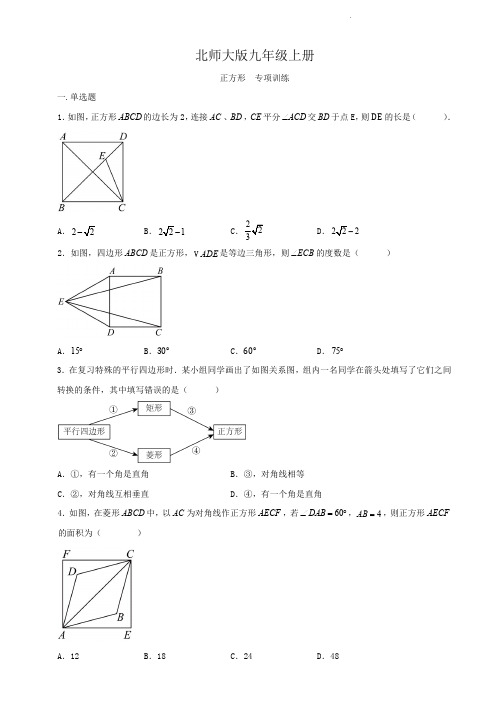
北师大版九年级上册正方形专项训练一.单选题1.如图,正方形ABCD 的边长为2,连接AC 、BD ,CE 平分ACD ∠交BD 于点E,则DE 的长是().A.22B.221223D.2222.如图,四边形ABCD 是正方形,ADE V 是等边三角形,则ECB ∠的度数是()A.15︒B.30°C.60°D.75︒3.在复习特殊的平行四边形时.某小组同学画出了如图关系图,组内一名同学在箭头处填写了它们之间转换的条件,其中填写错误的是()A.①,有一个角是直角B.③,对角线相等C.②,对角线互相垂直D.④,有一个角是直角4.如图,在菱形ABCD 中,以AC 为对角线作正方形AECF ,若60DAB ∠=︒,4AB =,则正方形AECF 的面积为()A.12B.18C.24D.485.如图,点E 是正方形ABCD 的对角线AC 上的一点,连接BE ,过点E 作EF CD ⊥,垂足为F ,若8=CF ,10EB =,则正方形ABCD 的面积为()A.196B.256C.144D.1006.如图所示摆放的5个正方形,面积分别为1S ,2S ,3S ,4S ,5S ,其中11S =,22S =,33S =,则45S S +=()A.6B.7C.8D.97.如图,在正方形ABCD 中,将边BC 绕点B 逆时针旋转至BE ,若90CED ∠=︒,1ED =,则线段BE 的长度为()A.2C.38.如图,E ,F 分别是正方形ABCD 的边CD ,AD 上的点,且CE DF =,AE 与BF 相交于O .下列结论:①AE BF =;②AE BF ⊥;③AO OE =;④AOB DEOF S S =四边形△.其中错误的有()A.1个B.2个C.3个D.4个9.如图,将正方形纸片ABCD 折叠,使点D 落在边AB 上的点D ¢处,点C 落在点C '处,若60AD M ∠='︒,则MNB ∠的度数为()A.65︒B.70︒C.75︒D.80︒二.填空题10.如图,点E 是正方形ABCD 内一点,ADE 是等边三角形,连接CE 并延长交AB 边于点F ,则CFB ∠=11.如图,正方形ABCD 的边长为5,对角线AC BD ,交于点E,线段FG 的长为2,FG 在边BC 上移动,连接FE GE ,,则EF EG +的最小值是.12.如图,在菱形ABCD 中,对角线AC ,BD 交于点O,要使菱形ABCD 成为正方形,应添加的一个条件是.13.如图,在正方形ABCD 中,1AD =,将ABD △绕点B 顺时针旋转45︒得到A BD '' ,此时A D ''与CD 交于点E,则DE 的长为.14.如图,E、F 分别是边长为2的正方形ABCD 边BC 、CD 上的两个动点,连接AE 、AF 、EF ,若EAF∠的大小始终保持45︒不变,则CEF △的周长为.15.如图,将正方形ABCD绕点C顺时针旋转30︒得到正方形CGEF,AD与EF相交于H,若3AB=,则AH=.三.解答题16.如图,在正方形ABCD中,E,F是对角线BD上的两点,且45绕点A顺时针∠=︒,将ADFEAF,连接EQ.旋转90°得到ABQ=.(1)求证:EQ EF∠的度数.(2)求QBEAD=,点P从点A出发,17.在正方形ABCD中,对角线AC,BD相交于点O,点E是OA的中点,4cm沿着AD DC-向点C运动,速度为每秒1cm,连结OP,做点E关于OP的对称点F,连结OF,CF.设点P的运动时间为t秒.(1)线段OE的长为______.(2)当点F落在线段OC上时,求t的值.(3)当点P在边AD上运动,且线段OP最短时,求OCF△的面积.(4)当OCF△是锐角三角形时,直接写出t的取值范围.18.如图,在ABC V 中,过BC 边上的点D 作∥DE AC ,交AB 于点E ,DF AB 交AC 于F ,连接AD .(1)若AD 平分BAC ∠,则四边形AEFD 是什么四边形?并说明理由.(2)若90BCA ∠=︒,则四边形AEFD 是什么四边形?并说明理由.(3)在(2)的条件下,给ABC V 添加一个条件___________使四边形AEDF 是正方形,并说明理由.。
北师大版九年级数学上同步练习1:正方形的性质 (含答案)

正方形的性质
1、下列说法中错误的是()
A、一组对边平行且一组对角相等的四边形是平行四边形
B、每组邻边都相等的四边形是菱形
C、四个角相等的四边形是矩形
D、对角线互相垂直的平行四边形是正方形
2、下列结论:(1)正方形具有平行四边形的一切性质;(2)正方形具有矩形的一切性质;(3)正方形具有菱形的一切性质;(4)正方形具有四边形的一切性质。
其中正确的结论有()
A、1个
B、2个
C、3个
D、4个
3、如图,已知正方形ABCD,E为BC上任意点,延长AB至F,使BF = BE,AE的延长线交CF于G,求证:AG⊥CF
4、如图,已知正方形ABCD,BE∥AC,AE=AC,求证:CF=CE
补:1、已知如图,矩形ABCD的两条对角线相交于点O,∠AOD = 120°,且对角线长为10cm,求AB的长
2、如图,将矩形纸片ABCD沿对角线AC折叠,使点B落在点E处,
试说明EF与DF相等
3、如图,矩形ABCD中,DF平分∠ADC,交AC于E,交BC于F,
∠BDF = 15°,求∠DOC和∠COF的度数
4、如图,矩形ABCD中,点H在对角线BD上,HC⊥BD,HC的延长线
交∠BAD的平分线于点E,试说明CE与BD的数量关系
参考答案1、D 2、D
3、略
4、略
补:
1、AB = 5cm
2、略
3、60度和75度
4、CE = BD
5、。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.3 正方形的性质与判定
第1课时 正方形的性质
一、填空题
1、如图,E 是正方形ABCD 的对角线BD 上一点,且BE =BC ,则∠ACE = °.
2、如图,四边形ABDC 是正方形,延长CD 到点E ,使CE=CB ,则∠AEC = °.
3、如图,正方形ABCD 中,点E 在BC 的延长线上,AE 平分∠DAC,则下列结论:①∠E=
22.5°; ②∠AFC=112.5°; ③∠ACE=135°;④AC=CE ;⑤AD ∶CE=1∶ 2. 其中正确的有 个.
4、如图,等边△EDC 在正方形ABCD 内,连结EA 、EB ,则∠AEB = °;∠ACE = °.
5、已知正方形ABCD ,以CD 为边作等边△CDE ,则∠AED 的度数是 °.
6、如图,四边形ABCD 是正方形,E 是边CD 上一点,若△AFB 经过逆时针旋转角θ(0°<θ<180°)后,与△AED 重合,则θ值为 °
第6题图 第7题图 第8题图 第9题图
7、已知正方形ABCD 中,点E 在边DC 上,DE = 2,EC = 1,把线段AE 绕点A 旋转,使点E 落在直线BC 上的点F 处,则F 、C 两点的距离为___________.
8、如图,正方形ABCD 的面积为12,△ABE 是等边三角形,点E 在正方形ABCD 内,在对角线AC 上有一点P ,使PD +PE 的和最小,则这个最小值为 .
9、如图,四边形ABCD 是边长为9的正方形纸片,将其沿MN 折叠,使点B 落在CD 边上的B '处,点A 对应点为A ',且C B '=3,则CN= ;AM 的长是 .
10、正方形的面积是3
1,则其对角线长是________.
11、如图,三个边长均为2的正方形重叠在一起,O 1、O 2是其中两个正方形的中心,则阴影部分的面积是 .
第1题图 第2题图 第3题图 第4题
O 2O 1 第11题图 第12题图 第13题图 第14题图
12、如图,将n个边长都为1cm的正方形按如图所示摆放,点A1、A2、…、A n分别是正方形的中心,则n
个这样的正方形重叠部分的面积和为 .
13、边长为1的正方形ABCD绕点A逆时针旋转30°得到正方形AB′C′D′,两图叠成一个“蝶形风筝”
(如图所示重叠部分),则这个风筝的面积是 .
14、如图,边长为1的正方形ABCD绕点A逆时针旋转45度后得到正方形
AB′C′D′,边B′C′与DC交于点O,则四边形AB′OD的周长是 .
15、如右图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.
将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.
下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.
其中正确的结论是 .(填序号)
16、如右图,四边形ABCD为正方形,以AB为边向正方形
外作等边△ABE,CE与DB相交于点F,则= 。
二、解答题
17、如图,正方形ABCD中,E、F、G分别是AD、AB、BC上的点,且AE=FB=GC.
试判断△EFG的形状,并说明理由.
18、E为正方形ABCD内一点,且△EBC是等边三角形,求∠EAD的度数.
19、如图,在正方形ABCD中,F是CD的中点,E是BC边上一点,且AF平分∠DAE,求证:AE=EC+CD.。
