广义对称正则长波方程的拟紧致守恒差分逼近

合集下载

【国家自然科学基金】_精确孤波解_基金支持热词逐年推荐_【万方软件创新助手】_20140731

2014年科研热词推荐指数非线性发展方程 1 薛定谔系统 1 精确行波解 1 渐近解 1 推广的简单方程方法 1 扭结波(反扭结波)解 1 孤波解 1 孤波 1 周期波解 1 同(异)宿轨 1 分岔 1 whitham-broer-kaup-like方程组 1
2012年序号 1 2 3 4 5
科研热词耦合kdv波动方程定性分析孤波解周期波解全局相图
推荐指数 1 1 1 1 1
2013年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
科研热词齐次平衡原理行波解推广的g'/g展开方法孤波解
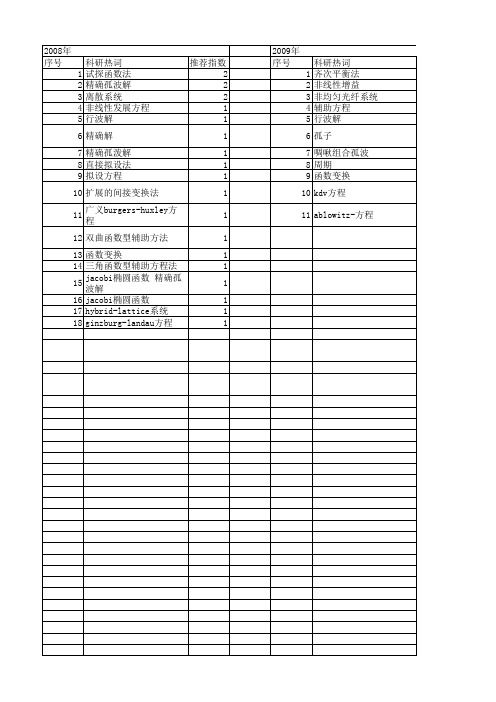
2008年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
科研热词推荐指数试探函数法 2 精确孤波解 2 离散系统 2 非线性发展方程 1 行波解 1 精确解 1 精确孤泼解 1 直接拟设法 1 拟设方程 1 扩展的间接变换法 1 广义burgers-huxley方程 1 双曲函数型辅助方法 1 函数变换 1 三角函数型辅助方程法 1 jacobi椭圆函数精确孤波解 1 jacobi椭圆函数 1 hybrid-lattice系统 1 ginzburg-landau方程 1
科研热词推荐指数孤波解 4 精确解 2 周期解 2 周期波解 2 非线性 1 辅助常微分方程 1 试探函数法 1 血管 1 约化摄动法 1 扩展的jacobi椭圆函数展开法 1 孤渡解 1 变量分离 1 双曲函数正切法 1 动脉 1 sine-gordon方程 1 mkdv差分微分方程 1 klein-gordon方程 1 kdv方程 1 hirota方法 1 ablowitz-ladik-lattice系统 1 (3+1)维k-p方程 1 (2+1)维hybrid-lattice系统 1

AXB_CXD_F的中心对称解及其最佳逼近的迭代算法_刘大瑾

记 Rm×n表示 m× n 阶实矩阵集合 , En 表示 n阶反序单位阵 , CSRn× n和 CA SRn×n分别表示 Rn× n中
实中心对称矩阵和实中心反对称矩阵集合 . 定义〈A, B〉= t r( BT A) , 则由它诱导的范数为 Frobenius 范数 . 对矩阵 A= ( a1 , a2 ,… , an )∈ Rm× n , 其中 ai∈ Rm , i= 1, 2,… , n, 记 v ec A= ( a1T , aT2 ,… , anT ) T , A B表示矩阵 A与 B的 Kronecker内积 . 本文主要考虑下面两个问题 .
( 5)
证明用数学归纳法即可证得 .
定理 1 假定问题Ⅰ 相容 ,那么对任意的初始矩阵 X1∈ CSRn×n , 问题 I的解可以通过有限步迭
代得到 .
证明若 Qi≠ 0, i= 1, 2,… , mp , 则由引理 4有 Qi≠ 0, i= 1, 2,… , mp , 于是由算法 1可以计算出 Xmp+ 1 , Rmp+ 1 . 由引理 3, 有 tr ( RmTp+ 1 Ri ) = 0和 t r( RiTRj ) = 0, i= 1, 2,… , m p; i≠ j . 因此 , R1 , R2 , … , Rmp是矩阵空间 Rm× p的一组正交基 ,从而 Rmp+ 1 = 0, 即 Xmp+ 1是问题Ⅰ 的一个解 . 当问题Ⅰ 相容时 ,可以证明问题Ⅰ 的解通过最多不超过 t0 ( t 0= min( m p, n2 ) )步得到 . 事实上 ,若 n2≤m p , Ri≠ 0, i= 1, 2,… , n2 , 则由迭代算法 1, Qi≠ 0, i= 1, 2,… , n2 , 且可以计算 Xn2+ 1 , Rn 2+ 1 , Qn 2+ 1 . 与前面的证明相似 ,得到 Qn2+ 1≠ 0以及 Rn 2+ 1= 0, 从而 Xn2+ 1就是问题Ⅰ 的一个解 .

紧致差分法研究概况

紧致差分法研究概况伴随计算物理的发展，为了能更加方便研究与剖析差分问题，人们对于数值结果的精度要求越来越高，而普通的有限差分格式在很大步长下的精度偏低，为了提高精度不得不缩小步长，增加更多的网格点数量，这肯定增加了计算机的计算量，使得计算速度变慢，计算时间拉长。

为了克服这一计算难题，人们开始寻找计算少精度高的差分方法。

紧致差分方法正是在这种情形下应运而生。

在1991年，lelei总结好了对称型紧致差分格式。

相比于传统的差分格式，在相同的计算网格中，紧致差分格式有着更高的精度和分辨率。

1993年傅德薰在紧致差分格式中引入迎风机制，1997年提出了五格点五阶精度的迎风紧致格式。

紧致差分格式中迎风机制的引入能够有效抑制非物理振荡，更适合于多尺度复杂流场的计算。

以上的对称型紧致差分格式和迎风型紧致差分格式是建立在均匀网格的基础上的。

1抛物线方程偏微分方程可用于描述出现在工程问题中的许多数学模型。

抛物线问题作为偏微分方程中的一种频繁处理，在诸如扩散，渗流和热传导等问题中具有大量应用。

因此，在很多情况下，偏微分方程找不到精确解，只能通过求解其数值解来研究问题。

因此，找到高精度，小计算，稳定性好的数值计算方法具有重要意义。

对于抛物问题，有限差分法经常用于解决数值问题。

有限差分方法的基本思想是将连续解区域分离为有限点网格，然后使用网格上定义的离散变量差。

该方程近似于连续解区域上的连续变量微分方程。

最后，原始微分方程可以转换为代数方程组。

求解方程可以得到离散点处原始微分方程的数值解。

在众多差分方法中，紧凑差分格式使用较少的网格基点，但计算格式精度很高。

因此，与传统的髙精度格式相比，紧凑的差分格式具有许多优点，例如计算量。

小，对单元敏感，易于处理边界条件等。

.因此，紧凑差分格式的研究是高精度格式研究的主要方向之一。

目前，关于抛物问题的高精度紧致差分方法的研究就显而易见，由于稳定条件的过度限制，显式紧致差分方法难以被广泛使用。

【国家自然科学基金】_二阶收敛性_基金支持热词逐年推荐_【万方软件创新助手】_20140802

2008年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
107 108 109 110 111 112 113 114 115 116 117 118 119 120 121
二阶常微分方程组二阶常微分方程二阶双曲方程二阶runge-kutta方案乘子映射不适定问题 yosida逼近 shepard形函数 scm parseval等式 p-稳定性 newton法 laplace变换 lagrange乘子 asselin-robert滤波
科研热词推荐指数收敛性 20 稳定性 16 差分格式 12 有限差分格式 4 广义对称正则长波方程 4 守恒 4 bbm方程 4 迭代算法 3 非协调有限元 2 蛙跳格式 2 等参变换 2 离散能量分析 2 最大模误差估计 2 数值积分 2 可解性 2 stokes问题 2 sonnier-christov格式 2 rosenau-burgers方程 2 du fort-frankel格式 2 高阶微商余项 1 非齐次稳态热问题 1 非高斯噪声 1 非线性耦合schr(o)dinger方程 1 非线性耦合 1 非线性算子方程 1 非线性最小二乘 1 非线性fir 1 隐式差分格式 1 间断有限元方法 1 锥 1 重要性采样 1 误差估计 1 试探函数空间 1 蒙特卡罗 1 自适应计算 1 网格质量 1 网格拓扑 1 线性重构方法 1 精度 1 粒子滤波 1 类似burgers方程 1 稳定性和收敛性 1 离散能量估计 1 离散化 1 电容层析成像(ect) 1 电子枪 1 电子光学系统 1 特征值 1 湍流统计场 1 测量精度 1 欧拉算符 1 欧拉法 1

广义正则长波方程的一个新的守恒差分逼近

ｑａｉＧＬｕｔｎ（ＲＷ）ｉｃｎｉｒｄｎｔｄｆｒｎｅｓｈｍｆｈｅｖｌｉｐｏｏｅ．Ｔｉｓｈｍｉｕａｓｈｏｓｏｓｅｅ．Ａｆｉｉｅｅｃｃｅｅｏｒｅｌｅｒｐｓｄｈｃｅｅｓｌｔｅｄｉｅｆｔｅｓｓｓｍｅｔ
ｓａｌｔｔｂｉｙｉ
其中Ｃ为一般正常数（文中，本Ｃ在不同的地方有
１问题的提出
本文考虑如下一类广义正则长波（ＲＷ）ＧＬ方程的初边值问题：
不同的取值）方程（）．Ｉ最早由Ｐｒｇｉｅ在文［ｅｅｒｎ１— ２中提出，］由于它所描述的运动有与ＫＶ方程相同Ｄ的逼近阶，能很好地模拟ＫＶ方程的几乎所有而且Ｄ应用．以备受关注 … 所．
ＨＵＪｎｓｎｉ— ｇｏ
（ｃｏｌｆｔｅａｉｎｏｐｔｎｉｅｒｇｉｕｎｖｒｔ，Ｃｅｇｕ６￣３，ＣｉａＳｈｏｈｍｔｓａｄＣｍｕｅＥｇｎｅｉ，ＸｈａＵｉｓｙｈｎｄ１９ｈｎ）ｏＭａｃｒｎｅｉ
Ａｂｔａｃ：ｅｎｍｅｃｌｓｌｔｏｏａｎｔａ — ｏｎａｙｖｌｅｐｏｌｍｆｇｎｒｌｚｄｒｇａｚｄｌｎｖ — ｓｒｔＴｈｕｒａｏｕｉｎｔｎｉｉｉｌｂｕｄｒａｕｒｂｅｏｅｅａｉｅｅｕｌｒｅｏｇｗａｅｅｉｉ
广义正则长波方程的一个新的守恒差分逼近
胡劲松

第七章正则方程

H px x py y pzz L
1 2m
( px2
p
2 y
pz2 )
k 2
(x2
y2
z2)
将H代入正则方程中,得到质点的动力学方程:
x
H px
px m
,
y
H py
py , m
z
H
pz
,
pz m
p x
H x
kx
p y
H y
ky
p z
H z
kz
m x kx 得到质点的运动微分方程 m y ky
1
L dt t
由于 q , p , t 相互独立的, 所以
q
p
H p H
q
( 1,2,, s)
——- 哈密顿正则方程 ,它是一阶微分方程,且形式对称.
和 H L 不是动力学方程 t t
说明如果L不显含时间, H也不显含时间.
q
H p
p
H q
( 1,2,, s)
结合初始条件,得到描述力学系统运动状态的运动方程:
2s个广义坐标 q , 1,2,s 和广义动量 p , 1,2,s，
统称为正则变量。
由2s个 q , p 组成的2s维空间称为相空间。相空间中的一个点（相点）代表系统在某时刻的运动状态.在相空间中, 利用正则方程可对力学系统进行定性的几何研究,尤其是对非线性系统在解析求解困难时.
正则方程的意义:它结构简单对称,为后续的力学发展 (如泊松括号、正则变换、哈密顿-雅可比方程等理论) 奠定基础；在数学上，正则方程是一阶微分方程，有利用计算机数学软件对非线性系统的运动作数值计算。
T2
V

利用FEXP方法求对称正则长波方程的精确解毕业论文

2010年度本科生毕业论文（设计）利用F-EXP方法求对称正则长波方程的精确解院－系：数学学院专业：数学与应用数学年级： 2006级学生：段雪妮学号： 7导师与职称：丁玉敏（教授）2010年5月2010 Annual Graduation Thesis (Project) of the College UndergraduateF-Exp Method for Solving Exact Solutions of Symmetric Regularized Long WaveEquationDepartment:College of MathematicsMajor:Mathematics and Applied of MathematicsGrade: 2006Student’s Name:Duan XueniStudent No.:7Tutor: Ding Yumin （Professor）May, 2010毕业论文（设计）原创性声明本人所呈交的毕业论文（设计）是我在导师的指导下进行的研究工作与取得的研究成果。

据我所知，除文中已经注明引用的容外，本论文（设计）不包含其他个人已经发表或撰写过的研究成果。

对本论文（设计）的研究做出重要贡献的个人和集体，均已在文中作了明确说明并表示意。

作者签名：日期：毕业论文（设计）授权使用说明本论文（设计）作者完全了解红河学院有关保留、使用毕业论文（设计）的规定，学校有权保留论文（设计）并向相关部门送交论文（设计）的电子版和纸质版。

有权将论文（设计）用于非赢利目的的少量复制并允许论文（设计）进入学校图书馆被查阅。

学校可以公布论文（设计）的全部或部分容。

的论文（设计）在解密后适用本规定。

作者签名：指导教师签名：日期：日期：段雪妮毕业论文（设计）答辩委员会(答辩小组)成员摘要利用F Exp-方法并借助Maple数学软件,获得了对称正则长波方程的许多行波解, 包括孤立波解与三角函数周期解.并用Maple软件获得几种典型的波形图.本文用的方法还可以用到其他的非线性发展方程中去.关键词: 对称正则长波方程; F-展开法; Exp-函数法;F Exp-方法; 行波解;齐次平衡原则ABSTRACTIn this paper, with the aids of the symbolic mathematical software-Maple, we obtained traveling wave solutions of symmetric regularized long wave equation. These traveling wave solutions include solitary wave solutions and trigonometric functions periodic solution. Some typical waveforms of these traveling wave solutions are obtained by Maple software. Obviously, the method which has been used in this paper is also can be used to other nonlinear evolution equations.Keywords: Symmetric regularized long wave equation; F- expansion method;The exp-function method; F-Exp method;Traveling wave solution;Homogeneous balance principle目录第一章引言11.1方程介绍11.2方法简述2第二章对称正则长波方程的精确解3 2.1对称正则长波方程的一般解32.2利用E XP-方法求方程R ICCATI方程的精确解42.3对称正则长波方程的精确解142.4几种典型的波形图18第三章结论20参考文献22致24第一章引言随着科学技术的飞速发展,现代科学研究的核心已经逐步从线性转向非线性,而且许多非线性科学问题的研究,最终可用非线性常微分方程或非线性偏微分方程来描述.非线性方程的发展被广泛应用于物理、工程技术和数学的众多分支当中,如非线性光学、量子论、流体力学、弹性理论和凝聚态物理等.由于非线性科学的飞速发展,对非线性方程求解方法的研究,在数学、物理、化学、生物等众多领域发挥着越来越重要的作用,因此如何求解这些非线性方程成为广大数学和物理工作者致力于研究的重要课题.因为只有首先求得了描述系统的解,才能谈得上对系统的性态和行为进行比较具体的分析,也才能谈得上对系统有了比较准确的了解和把握.1.1 方程介绍对称正则长波方程0xxt t x xtx u u uu u ρρ-=+⎧⎨-=⎩ （1-1-1）出自文献[1~3], 在文献[4]中数值考察表明其孤立波的相互作用是非弹性的; 文献[5]研究了广义对称正则长波方程孤立波解的轨道稳定性与不稳定性; 文献[6]研究了一类广义对称正则长波方程整体解的存在性, 唯一性与正则性, 并得到了谱近似解的误差估计; 程洁在文献[7]中考虑了带有耗散项的广义对称正则长波方程, 用谱分解方法证明了指数吸引子的存在性, 并得到指数吸引子的分形维数的上界估计; 文献[8]考虑了带有非齐次边值的对称正则长波方程的初边值问题; 文献[9]运用常微分方程定性理论中的相平面分析方法讨论了带有耗散项的广义对称正则长波方程, 与文献[6]不同的是, 它不但得到了有界行波解的存在性, 同时也得到了它的单调性与震荡性的若干结果, 并求出了一类扭状精确孤波解和震荡解的近似解.在本文中, 所研究的对称正则长波方程[10~11]如下:2()0tt xx xt xxtt u u u u αβγ+++= (1-1-2)对此方程, 黄正洪在文献[12]中利用齐次平衡原则[13~14]导出了该方程的一个非线性函数变换, 利用这个变换求得了该方程精确孤立波解.1.2 方法简述F Exp -方法[15]是把F -展开法[16~17]和Exp -函数法[18~19]有机结合起来.即: 考虑非线性偏微分方程(,,,,,,,,)0x y t xx xy xt yy p u u u u u u u u ⋅⋅⋅= （1-2-1）（1）令(,,)(),u x y t u ax cy bt ξξ==++ （1-2-2）其中,a b 为待定常数, 将（1-2-2）代入到（1-2-1）中, 可将其化为()u ξ的常微分方程:(,,,,)0p u u u u ''''''⋅⋅⋅= （1-2-3）其中,,u u u ''''''⋅⋅⋅分别表示u 对ξ求一阶，二阶，三阶⋅⋅⋅导数.（2）设01()()ni i i u A A F ξξ==+∑ （1-2-4）其中01,,,n A A A ⋅⋅⋅为待定常数, 非负整数n 由（1-2-3）式中具有支配地位的非线性项与最高阶导数项之间通过齐次平衡原则来确定, 且0n A ≠, ()F ξ满足下列Riccati 方程:224024F h h F h F '=++ （3242F h F h F ''=+） (1-2-5) 其中024,,h h h 为待定常数. 将（1-2-4）代入（1-2-3）并利用（1-2-5）可将（1-2-5）的左边化为关于()F ξ的多项式. 令()F ξ的各次幂的系数为零, 得到关于01,,,n A A A ⋅⋅⋅,,a b ,024,,h h h 的代数方程组, 解此代数方程组, 并将结果代入（1-2-4）式中, 就得到方程（1-1-2）的用()F ξ表示的行波解的一般形式.（3）用Exp -函数法求出方程（1-2-5）的指数函数解, 代入第（2）步中所得到的一般解中，从而得到方程（1-1-2）的指数函数解或孤立波解.第二章对称正则长波方程的精确解2.1 对称正则长波方程的一般解将(1-2-2)代入方程(1-1-2)得到关于()u ξ的常微分方程:22(4)222(2)2()0a b u a b ab u u ab u γαββ'''++++= （2-1-1）其中 (4),,u u u '''分别表示u 对ξ求一阶、二阶、四阶导数. 由方程（2-1-1）中uu ''和(4)u 齐次平衡, 得2n =. 由此()u ξ可表示为2012()()()u A A F A F ξξξ=++, ax bt ξ=+ （2-1-2）其中012,,A A A 为待定常数, 且20A ≠, ()F ξ满足方程（1-2-5）.将（2-1-2）代入（2-1-1）中并利用（1-2-5）可将(2-1-1) 的左边化为关于()F ξ的多项式, 令()F ξ的各次幂的系数为零, 得到关于012,,A A A ,,a b 的代数方程组:6()F ξ: 22222424201200ab A h a b A h βγ+=;5()F ξ: 2221241424240ab A A h a b Ah βγ+=;4()F ξ: 222222242422141206166a b A h h a A h ab A h ab A h γαββ+++02412ab AA h β+ 22460b A h β+=;3()F ξ: 2222141412412201422201840a Ah b Ah a b Ah h ab A A h ab A Ah αγββ++++=;2()F ξ: 22222222040222222227284164a b A h h ab A A h a A h a b A h b A h γβαγ++++2220121240ab A h ab A h ββ++=;1()F ξ: 2222222104120121212122a b Ah h b Ah ab A Ah a Ah a b Ah γβαγ++++120120ab A A h β+=;0()F ξ: 22222202002020210224820a A h b A h ab A A h a b A h h ab A h αβγβ++++=.解上述代数方程组得到:222242120640,,2abh a b a b h A A A ab γαγββ++==-=-(0)ab ≠ （2-1-3）将（2-1-3）代入（2-1-2）中得到:2222224446()()(0)2a b a b h abh F u abh ab αγγξξββ++=--≠ （2-1-4）2.2 利用Exp-方法求方程Riccati 方程的精确解根据Exp -函数法，设4322344321012344341013a e a e a e a e a a e a e a e a e F b e b e b b e b e ξξξξξξξξξξξξ------------++++++++=++++ （2-2-1）其中,i i a b 为待定常数, 将（2-2-1）代入（1-2-5）中, 有161610.j jj c e Aξ=-=∑ （2-2-2）其中443(),j j j j A b e c ξ=-=∑为各次项系数,令（2-2-2）中j e ξ的系数为零,有 123160123160,0,0,,0,0,0,0,0,,0.c c c c cd d d d ====⎧⎪=⎨⎪====⎩ （2-2-3）解关于,,i j k a b h 的代数方程组（2-2-3）得到如下多组参数值, 相应就得到方程（1-2-5）的多组解如下（表一）:（表一）:广义Riccati 方程的解2.3 对称正则长波方程的精确解2.3.1对称正则长波方程的第一组精确解将表一中的j F 代入（2-1-2）式中, 得到方程（1-1）的二十八个精确解:(1)012()()(),,(0,1,2,3,50)j j j u A A F AF ax bt A j ξξξξ=++=+≠=⋅⋅⋅.例如：(1)2100())18A u A h ξ=-; 2(1)1323502112cosh(2)4cosh(2)()A a A a u A b b ξξξ=++, 22(1)112180211(cosh()sinh())(2cosh ()2sinh()cosh()1)()A a A a u A b b ξξξξξξ-----=++, 2221020(1)100211(sinh())cosh ())2(sinh()cosh ())2222()cosh()cosh()22A a A a u A b b ξξξξξξξ--++=++, (1)24221101122222011()sinh cosh(2)2u A Ab a A a A a h b ξξξ-----=-+-, 2(1)1222150200(cosh(2)sinh(2))(cosh(2)sinh(2))(),A a A a u A b b ξξξξξ----=++2(1)1424180233(sinh(7)cosh(7))(sinh(14)cosh(14))()A a A a u A b b ξξξξξ--++=++, 22(1)14242602002sinh(4)4(cosh (4)1)()A a A a u A b b ξξξ-=++, 2(1)14224270223432sinh()2cosh(2)2()A a A A a u A b a b ξξξ-----=-+-, (其中240234a h b --=), 2(1)1020330244(cosh(4)sinh(4))(cosh(8)sinh(8))()A a A a u A b b ξξξξξ--=++, 2(1)10203902211()2cosh()4cosh ()A a A a u A b b ξξξ=++,2(1)112144022332cosh(2)4cosh (2)A a A a u A b b ξξ--=++, 22(1)1020460204tanh(/2)tanh (/2)()A a A a u A b b ξξξ=++, 2(1)21424500244()tanh(2)tanh (2)A a A a u A b b ξξξ=-+.令12,,a k i b k i i ===,且 2120A k k ≠, 上述孤立波解分别成为如下的三角函数周期解:(2)2100())18A u A h ξ=--, 2(2)13122312502112cos(22)4cos(22)()A a kx k t A a kx k t u A b b ξ++=++, (2)111212801(cos()sin())()A a kx k t i kx k t u A b ξ-+-+=+222112121221(2cos ())2sin()cos()1),A a kx k t i kx k t kx k t b -+-++-+2121210(2)100121(sin())cos ())22()cos()2kx k t kx k t A a i u A kx k t b ξ-+++=++2212122021212(sin())cos ())22cos()2kx k t kx k tA a i kx k t b -+++++, (2)242211011212221222011()sin()cos(22)2u A Ab a i k x k t A a k x k t A a h b ξ-----=-+++-, (2)1212121500(cos(22)sin(22))()A a kx k t i kx k t u A b ξ-+-+=+22212122(cos22)sin(22))A a kx k t i kx k t b -+-++, 22(2)141224122602002sin(44)4(cos (44)1)()A a i k x k t A a k x k t u A b b ξ++-=++,2(2)141221224270223432sin()2cos(22)2()A a i k x k t A k x k t A a u A b a b ξ-----++=-+-, (2)1012123304(cos(44)sin(44))()A a k x k t i k x k t u A b ξ+-+=+220121224(cos(88)sin(88))A a k x k t i k x k t b +-++,2(2)102039022112112()2cos()4cos ()A a A a u A b k x k t b k x k t ξ=++++, 2(2)112144022312312()2cos(22)4cos (22)A a A a u A b kx k t b kx k t ξ--=++++, 2(2)210204601212204()tan(/2/2)tan (/2/2))A a A a u A i k x k t k x k t b b ξ=++-+,2(2)214245001212244()tan(22)tan (22)A a A a u A i k x k t k x k t b b ξ=-+-+.2.3.2 对称正则长波方程的第二组精确解将表一中的j F 代入（2-1-4）式中, 得到方程（1-1）的二十二个精确解:22222(3)2446()()2i a b a b h abh F u ab αγγξξββ++=--, 4,(0,1,2,,)ax bt abh i ξ=+≠=⋅⋅⋅ 如下所示:222(3)440112241(36(cosh(3)sinh(3))(cosh(3)sinh(3)))()216abh a h b u a b γξξξξξβ-++-=-222224,2a b a b h ab αγβ++-22(3)4352124cosh(2)()abh a u b γξξβ=-222224,2a b a b h ab αγβ++- 222222(3)4128216(2cosh ()2cosh()sinh()1)4()2abh a a b a b h u b ab γξξξαγξββ---++=--, 2(3)4215206(cosh(4)sinh(4))()abh a u b γξξξβ--=-2222242a b a b h ab αγβ++-, 2(3)4016236(cosh(6)sinh(6))()abh a u b γξξξβ-+=-2222242a b a b h ab αγβ++-,22(3)44262024sinh (4)()abh a u b γξξβ=-2222242a b a b h ab αγβ++-, 222222(3)440322722343((cosh(2)sinh(2)))(cosh(2)sinh(2))4(),82abh a h b a b a b h u b a ab γξξξξαγξββ-------++=--2(3)40392213()2cosh ()abh a u b γξξβ=-2222242a b a b h ab αγβ++-, 2(3)424223()2cosh (2)abh a u γξξβ=-2222242a b a b h ab αγβ++-, 2(3)24450246()tanh (2)abh a u b γξξβ=-2222242a b a b h ab αγβ++-, 22(3)4054206tanh (3/2)()abh a u b γξξβ=-2222242a b a b h ab αγβ++-, (3)24156216()tanh (2)abh a u b γξξβ=-2222242a b a b h ab αγβ++-. .令12,,a k i b k i i ===且 40abh ≠则上述孤立波解分别成为如下的三角函数周期解:2(4)1244121212241(36(cos(33)sin(33))()216k k h a k x k t i k x k t ua b γξβ-+++=220112122241(cos(33)sin(33))216h b k x k t k x k t a b β+++-2222121221242k k k k h k k αγβ+--, 22(4)12431252124cos (22)()k k h a k x k t u b γξβ+=2222121221242k k k k h k k αγβ+--, 222222(3)124112*********821126(2cos ()2cos()sin()1)4(),2k k h a k x k t i k x k t k x k t k k k k h u b k k γαγξββ-+-++-+-=-2(4)1242121215206(cos(44)sin(44))()k k h a k x k t i k x k t u b γξβ-+-+=2222121221242k k k k h k k αγβ+--, 2(4)1240121216236(cos(66)sin(66))()k k h a k x k t i k x k t u b γξβ-+++=2222121221242k k k k h k k αγβ+--,22(4)124412262024sin (44)()k k h a k x k t u b γξβ+=-2222121221242k k k k h k k αγβ+--, 22(4)12441212032722343(cos(22)sin(22))()8k k h a k x k t i k x k t h b u b a γξβ----+-+-=- 12122234(cos(22)sin(22))8k x k t i k x k t b a β--+-+⋅2222121221242k k k k h k k αγβ+--, 2(4)124039221123()2cos ()k k h a u b k x k t γξβ=+2222121221242k k k k h k k αγβ+--,2(4)1242422123()2cos (22)k k h a u k x k t γξβ=+2222121221242k k k k h k k αγβ+--, 2(4)212445012246()tan (22)k k h a u k x k t b γξβ=-+2222121221242k k k k h k k αγβ+--, 2(4)212405412206()tan ((33)/2)k k h a u k x k t b γξβ=-+2222121221242k k k k h k k αγβ+--, 2(4)212415612216()tan (22)k k h a u k x k t b γξβ=-+2222121221242k k k k h k k αγβ+--. 2.4 几种典型的波形图利用Maple 软件, 我们绘出了几种孤立子解和周期波解的三维空间波形图, 如图所示:(a) 奇异周期波 (b)孤立波 (c) 周期波(d) 光滑孤立波 (e) 扭子波 (f)周期波(a) 奇异周期波(4)39402112:3,2,1010,u h a h b k k x αγβ=========-≤≤04;t ≤≤(b) 孤立波(1)39:u 01201122,3,1010,12;A A A a b k k x t =======-≤≤-≤≤(c) 周期波 (2)10u 0120112:2,3,66,22;A A A a b k k x t -=======-≤≤-≤≤(d) 光滑孤立波(1)46:u 01201201,2,3,1212,88;A k k b A A a x t =======-≤≤-≤≤ (e) 扭子波(1)10u : 1022012,3,7,1,1212,88k A k A a b x t -======-≤≤-≤≤; (f) 周期波(4)56u :1241123,,2,1212,88;a h h b k k x t αβγ=========-≤≤-≤≤第三章结论本文利用一种新的求解精确解的方法:F Exp-方法, 即将F-展开法和Exp-函数法有机结合, 并用此方法求得了对称正则长波方程的许多行波解, 包括孤立波解与三角函数周期解. 所得的这些解都是不同于文献[12]的新解, 值得一提的是此方法同样可用到求其他的一些非线性偏微分方程的精确解行波解中去.参考文献[1] SEYL ER E C,FANSTERMACL ER D C. A symmetricregularized long wave equation[J] .Phys Fluids.1984,27(1):4 -7.[2] ALBERT J. On the decay of solutions of the generalizedBBM equation[J]. J MathAnalAppl.1989,141:527-537.[3] AMICK C J ,BONA J L , SCHONBEK M E. Decay ofsolutions ofsome nonlinear waveequations[J].J DiffEqn,1989,81:1-49.[4] BOGOLUBSKYJ L. Some examples of inelastic solutioninteraction[J]. ComputePhysComm,1977,13:149-155.[5] Lin Chen. Stability and instability of solitary wave forgeneralized symmetricregularizedlong wave equations.[J ] . Physical D ,1998 ,118 (1-2) :53-68.[6] Boling Guo. The spectral method for symmetric regularized wave equations[J] .JComp Math ,1987, 5 (4) :297-306.[7] 程洁,戴正德.耗散广义对称正则长波方程的指数吸引子[J]. 大学学报(自然科学版). 2004, 26(1): 15-19.[8] Chenxia Miao. The initial boundary value problem forsymmetric long waveequationswith non-homogeneousboundary value[J]. Northeastern Math J,1994,10(4):463-472.[9] 卫国,任迎春,刚. 具有散项的对称正则长波方程的定性分析与显式解[J].理工大学学报. 2008,30(1),1-6.[10] C E Seyler. Phys Fluids[J].1984(27):4.[11] 恩贵.可积系统与计算机代数[M]. 科学. 2004. 144-145.[12] 黄正洪. 对称正则长波方程的非线性函数变换和孤立波解[J].西南师大学学报(自然科学版). 2000, 25(6) ,633-636.[13] Mingliang Wang. Solitary Wave Solutions for Variant Boussinesq Equations[J].Physics Letters A .1995, 199: 167-172.[14] Mingliang Wang. Exact Solutions for a Compound Kdv - Burgers Equation[J].Physics Letters A, 1996, 213: 279-287.[15] Yumin Ding .Exp-function Method Combined with F-expansion Method for obtaininNewExactSolutionsof2+1-Dimen-sionalBoussinesqEquation[J]. Math.Sci. Res.J.2009, 13(6).[16] Wu X.-H.,He J.-H. Solitary solution, periodic solutions and compacton-likesolutionsusingthe Exp-function method[J].Appl.Math put 2007,54:966-986.[17] He J.-H., Wu X.-H. Exp-function method for nonlinear wave equations[J]. Chaos,Solitons & Fractals 2006, 30:700-708.[18] 丁玉敏、冀小明.利用EXP-函数展开法求解Modified Equal Width的精确解[J]. 西南民族大学学报, 2008,34(1): 20-26.[19] 云梅、芮伟国. 用EXP函数法求Equal Width波方程的精确解[J]. 科技大学报.2008,29(2):94-98.致经过半年忙碌的学习和工作, 本次毕业设计已经接近尾声, 作为一个本科生的毕业设计, 由于经验的匮乏, 难免有许多考虑不周全的地方, 如果没有导师的督促指导, 一起工作的同学们的支持和帮助, 要完成这个毕业设计是完全不可能的.在这里首先要感我的父母, 是他们不辞劳苦的给我们创造这样读书的机会, 衷心的希望他们身体健康. 其次我要感我的导师丁老师. 丁老师平日里工作繁忙, 但在我做毕业设计的每个阶段, 从查阅资料, 到设计草案的确定和修改, 中期检查, 后期详细设计, 装配草图等整个过程中都给予了我悉心的指导. 我的设计较为复杂烦琐, 但是丁老师仍然细心地纠正论文中的错误. 除了敬佩丁老师的专业水平外, 他的治学严谨和科学研究的精神也是我永远学习的榜样, 并将积极影响我今后的学习和工作.再次还要感大学四年来所有的老师, 为我们打下数学专业知识的基础; 同时还要感所有的同学们, 正是因为有了你们的支持和鼓励., 此次毕业设计才会顺利完成.最后由衷的感数学学院和我的母校—红河学院四年来对我的大力栽培.。

正则长波方程的拟紧致守恒C-N差分格式

正则长波方程的拟紧致守恒C-N差分格式郑茂波【摘要】对正则长波方程的初边值问题进行了数值研究,提出了一个两层隐式拟紧致Crank Nicolson差分格式,该格式很好地模拟了问题的守恒性质,证明了差分解的存在唯一性,利用能量方法分析了该格式的二阶收敛性与稳定性并利用数值算例进行了验证.%In this paper, a pseudo-compact conservative difference scheme for regularized long wave( RLW) equation is proposedo Existence and uniqueness of numerical solutions are derived. By method of discrete energy, second order convergence and stability are discussed. Numerical examples show the availability of the scheme.【期刊名称】《西华大学学报（自然科学版）》【年(卷),期】2012(031)001【总页数】4页(P87-90)【关键词】正则长波方程;差分格式;守恒;收敛性【作者】郑茂波【作者单位】成都电子机械高等专科学校,四川成都610031【正文语种】中文【中图分类】O241.82正则长波方程(RLW)是非线性长波方程的一种表述形式，在进行非线性扩散波的研究时,正则长波方程因其能描述大量的物理现象而占有重要的地位,特别是它所描述的运动有与KDV方程相同的逼近界，而且能很好地模拟KDV方程的几乎所有应用,因此备受关注。

但是RLW方程少有解析解,所以讨论方程的数值解法就显得很有意义 [1-10],文献[1-4]从能量守恒的角度分别提出了三层和两层的差分格式,文献[5]提出了三层拟紧致差分格式。

本文考虑如下RLW方程的初边值问题：ut+ux+uux-uxxt=0，x∈[xL,xR]，t∈[0,T](1)u(xL,t)=u(xR,t)=0，t∈[0,T](2)u(x,0)=u0(x)，x∈[xL,xR](3)不难证明此问题具有如下守恒律：E(t)=+=C(4)其中C为一般正常数(本文中，C在不同的地方有不同的取值)。

【国家自然科学基金】_jacobi椭圆函数解_基金支持热词逐年推荐_【万方软件创新助手】_20140729

2011年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
2011年科研热词推荐指数辅助方程 2 解的非线性叠加公式 2 精确解 2 三角函数解 2 非线性演化方程 1 非线性发展方程 1 雅可比函数解 1 辅助方程法 1 白噪声泛函分析 1 无穷序列解 1 无穷序列精确解 1 改进的jacobi椭圆函数展开法 1 孤立波解 1 孤立子 1 吴消元法 1 变系数组合kdv方程 1 变形浅水波方程组 1 代数方法 1 wick型随机广义sinh(sine)-gordon方程 1 sine-gordon型方程 1 jacobi椭圆函数解 1 hermite变换 1 f扩张法 1 f扩展方法 1 fan子方程法 1
2010年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
科研热词推荐指数精确解 3 jacobi椭圆函数 3 非线性叠加公式 2 辅助方程法 2 孤波解 2 周期解 2 非线性方程 1 辅助方程 1 解的叠加公式 1 无穷序列精确解 1 新的形式解 1 扩展的jacobi椭圆函数展开法 1 函数变换 1 三角函数型辅助方程 1 klein-gordon方程 1 klein-gordon-zakharov方程 1 f-展开法 1 (n+1)维双sine-gordon方程 1 (2+1)维davey-stewartson方程 1
2009年序号 1 2 3 4 5 6 7 8 9 10 11 12
科研热词辅助方程精确解孤波解复mkdv方程周期解变系数非线性发展方程分解和相容解函数变换 nls方程 f-展开法 2+1维 (2+1)维nizhnik-novikov-veselov方程组

Rosenau-RLW方程的加权守恒差分格式

Rosenau-RLW方程的加权守恒差分格式张曦;胡兵;胡劲松【摘要】In this paper,a numerical method for an initial-boundary problem of the Rosenau-RLW equation is considered.A three-layer weighted conservative difference scheme is proposed.The scheme simulates the conservation property of the equations.The existence of discrete solution is discussed.The priori and error estimates of the discrete solution are derived,the second order convergence and unconditional stability of the discrete solution are analyzed by the discrete energy method.Numerical examples verify the reliability of the scheme and that the accuracy of the calculation can be improved by adjusting weighted coefficient properly.%本文对Rosenau-RLW方程初边值问题的数值解法进行了研究,提出了一个三层的加权差分格式,该格式较好地模拟了方程的守恒性质.然后本文讨论了差分解的存在唯一性,给出了差分解的先验估计和误差估计,并利用能量方法分析了该格式的二阶收敛性、无条件稳定性.数值算例验证了格式的可靠性,并且适当调整加权系数还可以提高计算精度.【期刊名称】《四川大学学报（自然科学版）》【年(卷),期】2017(054)001【总页数】6页(P1-6)【关键词】Rosenau-RLW方程;加权系数;守恒格式;存在唯一性【作者】张曦;胡兵;胡劲松【作者单位】四川大学数学学院,成都610064;四川大学数学学院,成都610064;西华大学理学院,成都610039【正文语种】中文【中图分类】O241.82(2010 MSC 65M60)RLW方程(正则长波方程)ut-uxxt+ux+uux=0,x∈R,t≥0由Peregrine[1,2]首先提出，通常用于模拟非线性发散介质中的长波，可以描述如浅水波等诸多物理现象.它所描述的现象几乎涵盖了Kdv方程的所有应用[2].文献[3]等研究了广义正则长波方程孤波解的一些性质.由于解析解许多形式目前无法得到，对其数值解的研究就显得非常重要.文献[4,5]从能量守恒的角度分别对RLW方程的初边值问题提出了两层和三层的差分格式.文献[6] 对RLW方程提出了一个三层的拟紧致差分格式，进一步提高了计算的精度.但是，在离散动力系统的研究中，对于波与波以及波与墙相互作用，不能用Kdv方程来描述.于是Rosenau[7]提出了Rosenau方程ut+uxxxxt+ux+uux=0,x∈R,t≥0Rosenau方程可以看作RLW方程的一种变形.另一方面，在处理非线性波时需要引入粘性项-uxxt，因此需要考虑如下一类Rosenau-RLW方程：ut-uxxt+uxxxxt+ux+uux=0,x∈[xl,xr],t∈[0,T]文献[8,9]对Rosenau-RLW方程进行了数值研究.其中，文献[8]提出了具有二阶精度的三层线性守恒差分格式，但三层格式不是自启动的，需要先用两层的格式计算出第一时间层的数值解才能计算出其他层;文献[9]提出了具有二阶精度的两层非线性C-N守恒差分格式，对比文献[8]的结果可以看出两层格式的精度要优于三层格式.本文参照文献[10,11]的加权思想和处理非线性项的方法，对Rosenau-RLW方程的粘性项引入加权系数，提出了一个新的二阶精度三层线性守恒差分格式.数值算例表明当加权系数较小时，加权格式对比未加权格式，精度有所提高.对方程(3)给出如下出边值条件:初值条件u(x,0)=u0(x),x∈[xl,xr]边值条件u(xl,t)=u(xr,t)=0,uxx(xl,t)=uxx(xr,t)=0,t∈[0,T]问题(3)～(5)满足如下守恒律：文献[12]中指出，守恒的差分格式可以更好模拟本身具有的守恒律，而且避免了其他非守恒差分格式的非线性“爆炸”.对区域[xl,xr]×[0,T]进行网格剖分.空间≤j≤J,时间τ,tn=nτ,0≤n≤,差分求解空间,.引入如下标记,,,,.对于初边值问题(3)～(5),我们提出以下三层差分格式：对于边界条件(10)，增加一排虚拟点u-1uJ+1,可得u-1+u1=0,uJ+1+uJ-1=0. 引理2.1[13] 对于网格函数,有如下差分分部求和公式与差分格林公式成立：且由v0=vJ=0可得进一步有引理2.2 设[xl,xr].那么差分格式(8)对于以下离散能量是守恒的，即En-1=…=E0,n=1,2,…,N证明将式(8)两端乘以h以后对j求和，利用引理2.1和边界条件(10)有.根据Qn的定义可得(18)式成立.将式(8)与n作内积，利用引理2.1和引理2.2并结合边界条件(10)有其中，并且有又注意到将式(20)～(22)带入式(19)可得由En定义可知式(18)成立.定理3.1 差分格式(8)～(10)是唯一可解的.证明数学归纳法.初值u0是由初条件(9)式唯一确定的，适当选择一个二阶方法计算u1(即u0和u1是被唯一确定的).假设u0,u1,…,un是唯一可解的，现在来考虑方程(8)中的un+1：将(24)式两端与un+1作内积，又有.从而可得又由Schwarz不等式得≥代入式(25)得≤0.当a>1/2时，>0.则方程(8)仅有零解.因此，式(8)中的是唯一可解的.证毕. 将精确解代入差分格式(8)，并记=v(xj,tn),可得截断误差由Taylor展开可知，当h,τ→0时，).引理4.1(离散的Sobolev不等式)[11] 存在常数C1,C2使得‖un‖∞≤C1‖un‖+C2‖‖引理4.2(离散的Gronwall不等式)[11] 设网格函数非负递减，满足≤,则有≤定理4.3 设.则差分格式 (8)～(10)的解满足‖un‖≤C,‖‖≤C,‖‖≤C,‖un‖∞≤≤C证明由能量守恒等式(18)可得En≤≤.又≤，≤C当,即时,有‖‖≤C,‖‖≤C,‖‖≤C.再由引理4.1可得‖u‖∞≤C,‖ux‖∞≤C.定理4.4 设.则差分格式(8)～(10)的解收敛，且收敛阶为. 证明令则其中.将rn与n作内积可得利用定理4.3与柯西不等式，可得≤≤≤又由≤及将式(34)～(36)代入式(33)可得≤令).由式(37)可得Bn-Bn-1≤Cτ·O(h2+τ2)2+两端叠加可得.又Bn≥由,则,以及≤可得≤‖en‖2)+B0+C·O(h2+τ2)2先由两层格式[16]计算出具有二阶精度的u1,使得B0≤O(h2+τ2)2,再利用引理4.2可得≤O(h2+τ2)2.从而有‖en‖≤O(h2+τ2),‖‖≤O(h2+τ2).从而‖‖≤O(h2+τ2),再由引理4.1可得‖en‖∞≤O(h2+τ2).证毕定理4.5 设.差分格式(8)～(10)的解un以‖·‖∞稳定.证明令初值μ0=u0+ε0.设μn为初值增加一个扰动ε0后差分格式差分格式(8)～(10)的解，误差为εn=μn-un.类似于定理4.2的证明过程可得‖εn‖∞≤‖ε0‖∞.对问题(3)～(5)取初值.用本文的差分格式计算数值解，与该问题如下的孤波解来作比较:.令xl=-20,xr=40,T=20.由于该格式是个三层的，不能自启动，因此首先采用文献[9]的两层格式算出具有二阶精度的u1.表1是当加权参数θ取不同值时数值解的误差情况，表2是差分解的收敛性验证和收敛阶，表3是差分解的离散能量，图1是波的传播情况.通过对比表1中在不同θ取值下数据结果可知，当加权系数θ增大时，误差也将增大，所以θ较小时，加权格式比未加权格式误差要小，本文格式是可行的.表2表明本文格式数值解满足二阶收敛性.表3和图1表明，本文格式较好地拟合了原方程的守恒性，适合长时间计算.另外，经过几个参数值的尝试，可以看出适当调整参数θ可以有所提高计算精度.【相关文献】[1] Peregrine D H.Calculations of the development of an Undular Bore[J]. J Fluid Mech, 1966, 25: 321.[2] Peregrine D H. Long waves on a beach [J]. J Fluid Mech, 1967, 27: 815.[3] Zhang W, Chen X, Li Z,etal. Orbital stability of solitary waves for generalized symmetric regularized-long-wave equations with two nonlinear Terms[J]. J Appl Math, 2014, 2014: 688.[4] Li S, Wang J,Luo Y. A fourth-order conservative compact finite difference scheme forthe generalized RLW equation[J]. Math Probl Eng, 2015, 2015: 1.[5] Hu J, Wang Y. A high-accuracy linear conservative difference scheme for rosenau-RLW equation[J]. Math Probl Eng, 2013, 2013: 841.[6] 胡劲松,胡朝浪,郑茂波. 广义对称正则长波方程的一个拟紧致守恒差分算法[J]. 四川大学学报:自然科学版,2010, 47: 221.[7] Rosenau P. Dynamics of dense discrete systems-high order effects[J]. Prog Theor Phys, 1988, 79: 1028.[8] Pan X,Zhang L. On the convergence of a conservative numerical scheme for the usual Rosenau-RLW equation [J].Appl Math Model,2012, 36: 3371.[9] 何挺，胡兵，徐友才. 广义Rosenau方程的有限元方法[J]. 四川大学学报：自然科学版， 2016, 53: 1.[10] 陈涛，卓茹，胡劲松. 广义Rosenau-Kawahara方程的一个非线性守恒差分逼近[J]. 四川大学学报：自然科学版， 2016, 53: 265.[11] 冯博,闵心畅,余跃玉,胡兵. Rosenau方程的一个新的三层守恒差分格式[J]. 四川大学学报:自然科学版,2011, 48: 7.[12] Zhou Y,Zhou Y. Application of discrete functional analysis to the finite difference method [J]. Fourier, 1990, 8: 49.[13] 胡建伟, 汤怀民. 微分方程数值解法[M]. 北京: 科学出版社, 1999.。

紧束缚近似

1
N
e u ik (r Rm ) k
(r
Rm
)
k
1 N
nk
(r
Rm )
k
an (r Rm )
2.万尼尔(Wannier)函数的重要特征 (1) 此函数是以格点 Rm 为中心的波包，因而具有定域的特性；
6.适用性
(1).上面讨论的是最简单的情况，只适用于s态电子，一
个原子能级 at对应一个能带； i (2).若考虑p态电子，d态电子，这些状态是简并的，N个
原子组成的晶体形成能带比较复杂，一个能带不一定同孤立原子的某个能级对应，可能出现能带交叠.
(3).本节只讨论简单格子，对于复式格子必须对每个子晶格写出布洛赫波函数，再把这些函数组合成整个晶体中适用的布洛赫函数.
第三节紧束缚近似 (tight binding approximation)
本节主要内容: 一、模型及计算
二、万尼尔函数(Wannier function)
§5.3 紧束缚近似
一、模型及计算
紧束缚模型是1928年布洛赫提出的第一个能带计算方法。
在固体当中，束缚电子或称局域电子(localized electrons) 是占多数的，而巡游电子或称非局域电子(nde- localized electrons)是少数。紧束缚近似得到的结果除了使布洛赫电子的波函数和能带进一步具体化以外，还能初步解释半导体和绝缘体中所有电子的能带，尤其对过渡族金属中的3d电子的能带比较适用。
4).能带宽度取决于交叠积分的大小，J越大能带越宽；
5). 原子能级简并时(如：p态为三重简并,d态为五重简并等),非简并情形的紧束缚波函数要作修改，应计入各简并轨道的线性

对称正则长波方程的行波解分岔(英文)

对称正则长波方程的行波解分岔(英文)
钟吉玉;谷秀川
【期刊名称】《应用数学》
【年(卷),期】2011(24)3
【摘要】通过平面动力系统的方法讨论了对称正则长波方程的分岔问题.得到了该方程的分岔条件,在一些参数的具体值的情况下给出相图并通过微分方程的数值模拟方法模拟出了该方程的周期行波解、孤立行波解及无界行波解.
【总页数】5页(P488-492)
【关键词】分岔;行波解;相图;数值模拟
【作者】钟吉玉;谷秀川
【作者单位】湛江师范学院数学系
【正文语种】中文
【中图分类】O175.2
【相关文献】
1.利用试探方程法求对称正则长波方程的精确行波解 [J], 李文赫;张春辉
2.对称正则长波方程的精确行波解 [J], 程源泉;冯大河;余晶晶;贾荣
3.具有任意阶非线性项的广义对称正则长波方程的显式行波解 [J], 姬天富
4.广义对称正则长波方程的孤波解和周期波解及它们与Hamilton能量的关系 [J], 凌兴乾;张卫国
5.对称正则长波方程组的对称,精确解和守恒律 [J], 陈美;刘希强;王猛
因版权原因，仅展示原文概要，查看原文内容请购买。

紧束缚近似法 - 扬州大学物理实验教学示范中心!

J 为交迭积分对
晶格常数为 a 的简立方结构晶体
原点原子有六个最近邻
坐标
r Rn
分别为
( a,0,0) (0, a,0) (0,0, a) 故
E = E (0) + C − J (eikxa + e−ikxa + eikya + e−ikya + eikza + e−ikza )
= E (0) + C − 2J [cos(kxa) + cos(k ya) + cos(kza)]
4.证明应用紧束缚方法于一维单原子链如只计及最近邻原子间的相互作用
其 s 态的能带为
E(k)
=
Emin
+
4J
sin 2
ka 2
式中 Emin 为带底能量 J 为交迭积分 a 为原子间距并且求能带的宽度和带底
带顶附近电子的有效质量
544
固体物理讲稿
附由 Bloch 定理
∑ ψ r (rr) = eikr⋅rr k
称
波函数为
φ(rr
−
r Rn
)
能量为 E (0)
在晶体中
该电子的势能函数为V (rr)
电
子态是 N 度简并的考虑微扰后的零级近似波函数为
∑ ψ r (rr) = k
C
r nk
φ(rr
−
r Rn
)
n
其中 C
r
与
r n, k
有关
不是 rr 的函数
根据 Bloch 定理
nk
波函数可以写成[注]
∑ ∑ ψ r (rr) = eikr⋅rr k
e C −i kr⋅rr

多孔介质方程的广义条件对称和精确解

多孔介质方程的广义条件对称和精确解随着科学技术的发展，多孔介质方程（Porous Media Equation，PME）在数学物理模拟中被越来越广泛的应用。

PME描述的是流体流动和物质混合在多孔介质中的过程，它是一个二维非线性物理系统方程，具有未知参数，动态系统和非结构性表征。

由于PME在数学物理模拟中的重要性，人们试图研究PME的解析解。

在这方面，广义条件对称（GCS）和精确解（Exact Solutions）是两个重要的研究领域。

首先，研究GCS可以帮助我们了解PME的对称结构，以及它如何在PME上产生新的解。

其次，运用GCS，我们可以得到精确的PME解，这些解可以用来衡量近似解的质量，以及识别存在系统偏差的偏移。

最后，在那些没有被广义条件对称所包括的情况下，我们可以使用精确解讨论PME的特殊情况，包括分析奇异解，对称和对称构造解，以及无穷多解等。

为了探索多孔介质方程的GCS和精确解，本文将重点介绍GCS和精确解的特性，以及它们在PME上的应用。

首先，本文将介绍GCS的定义以及它如何在PME上产生新的解。

广义条件对称是指一个方程的一组解析解，它们满足某种符合特定对称性的条件。

例如，如果一个方程具有旋转对称性，那么它的GCS应满足有关旋转操作的相关约束。

在PME中，GCS主要由流速，压力，物质质量和物质质量约束构成。

在基于GCS的解中，流速和压力呈现出对称性，物质质量和物质质量也有各自的对称性，从而有助于构建出新的对称解。

接下来，本文将探讨PME的精确解。

精确解给出了PME的所有解，包括奇异解，对称解，对称构造解，以及受制于边界条件的非无穷多解等。

例如，在PME中，解析解可以被用来分析源以外的解的演化，这可以帮助我们了解系统的行为。

此外，精确解也可以用来衡量近似解的精度，从而帮助我们检验和校核近似算法。

最后，本文将介绍PME的GCS和精确解在现实问题中的应用。

它们可以用来模拟多种实际问题，如流体运动，物质混合，传输，反应和振动等。

广义对称正则长波方程的孤立波解

广义对称正则长波方程的孤立波解以《广义对称正则长波方程的孤立波解》为标题，本文主要探讨对称正则长波方程的孤立波解及其在天文学中的应用。

现代物理学中有许多不同的方程，其中一类是长波方程，它是一类受到重力作用的重要的非线性波方程。

这类方程在描述深海的潮汐预报，总水位的变化，地壳和大气中的波动与其他流体动力学现象中发挥着重要作用。

其中最著名的对称正则长波方程，就是以求解风暴中心位置及其机制所必须采用的方法之一。

该方程实质上是一维的、不可约、非线性的、拉普拉斯微分方程：$$U+U^{n+1}=0$$其中，U为木棒函数，n为正整数。

该方程中的孤立波解则是指方程的定性总路径，具体来说，就是将$$U+U^{n+1}=0$$对U的导数积分，得到的表达式的等价的表达形式。

孤立波解可以用于模拟风暴中心的运动，并可以用来预测风暴中心的位置。

在天文学上，孤立波解可以用于研究太阳的外层的极端运动，以及太阳系的惯性引力波传播，从而提出新的观点，用来解释太阳系的结构。

对称正则长波方程的孤立波解可以以多种形式描述，其中最常见的形式是双曲线形式：$$U(x,t)=(x^2-t^2)^{-1/2}$$其中，U(x,t)表示波的幅度，x表示空间变量，t表示时间变量，这种形式的孤立波解是最常用的形式。

另外，还有其他形式的孤立波解，例如，“指数波解”：$$U(x,t)=e^{-t/sqrt{x}}$$这种孤立波解可以用来模拟布朗运动中超声波的行为，在应用到声子发射和太阳风体形成等方面具有广泛的应用。

总之，以《广义对称正则长波方程的孤立波解》为标题，本文主要介绍了对称正则长波方程的孤立波解及其在天文学中的应用，对称正则长波方程的孤立波解有多种表示形式，可以用来模拟风暴中心的运动，预测风暴中心的位置，以及描述太阳系的结构。

正则长波方程的新的守恒差分方法

作者简介：潘新田（９５）男，东潍坊人，１７一，山潍坊学院数学与信息科学学院助教，士。硕
一
７６一
第４期
潘新田：则长波方程的新的守恒差分方法正
一
号１＋Ｕ）ｈ（＋一）ｌ＋（Ｉｗ塞ＩＪ＋ｒ（（｝ｌｎ孚ＪＩＩ
ｕ一ｕ（ｊ，一０，，，一１ … Ｎ。ｏＸ）ｊ … Ｊｎ，
（）７
差分格式（）于（）５对１的数值模拟为：
定理１差分格式（）满足如下的离散守恒律，：５即
Ｅ（１计ｌ＋Ｍ ”一Ｉｌ “
从而由（）式就可以得到（）９８。２差分格式的收敛性与稳定性下面我们分析差分格式（）（）的截断误差。设差分格式（）５一７５的截断误差，ｕｙ记：（，）在ｔ，点（，），ｔｙｏｔ处作ａｌｒ展开，得
ｕ＋［）（］ｗｕ＋［（ｒ：（ｉ（（（ｕ）＋（）告ｕ（＋ｕ）ｕｕ）ｕ＋ｉ一ｕ））＋＋
（）５
（）６
ｕ）ｉ一７（一０）］ｕ）。
ｕ — ｕ＝０，＝０１ … Ｎ，ｎ＝ｎ＝，，＝＝
ｃ一， ≤ ＡｃｃＪｒ１ｒ＋Ｂｏ呦１＋ｒＡ，Ｃ（一１ …Ｎ）是非负常数，，Ｂ，，
比较。数值结果表明，文格式不仅保持了计算量小的特点，本而且数值精度有着显著的提高。

多孔介质方程的广义条件对称和精确解

多孔介质方程的广义条件对称和精确解多孔介质理论是流体力学领域中一个重要的分支，由英国物理学家伊曼纽尔库伦发现，并在20世纪50年代得到广泛的应用。

以前的研究只考虑了多孔介质中的流体间的相互作用，忽略了它们具有的自身静力学性质，因而无法解释一些重要的实际现象。

这就促使物理学家们对多孔介质方程进行了进一步的研究，设计出了与原方程有区别的广义多孔介质方程。

广义多孔介质方程能描述多孔介质流体及多孔介质自身静力学性质，更能够更有效地求解多孔介质流体间的相互作用。

本文的目的是探讨这种方程的广义及其对称性，以及更加精确的解，以期更准确地模拟多孔介质的实际现象。

广义多孔介质方程广义多孔介质方程是一种考虑多孔介质自身静力学性质而设计的多孔介质方程，主要用来求解多孔介质流体间的相互作用。

广义多孔介质方程的形式如下：$frac{partial u}{partial t}+div (frac{1}{rho}abla p-uabla^2 u ) + alphaabla cdot (u cdotabla u) = 0$其中，$u$是流动场物理量，$u$是粘性参数，$alpha$是网格系数，$p$是动压，$rho$是流体的密度。

从上式可以看出，广义多孔介质方程多了一项非陡峭系数项，即$alphaabla cdot (u cdotabla u)$，它能够反映出多孔介质自身具有的静力学性质，因此更能够准确模拟出多孔介质流体间的相互作用；此外，在多孔介质中，$u$和$alpha$两个参数同时存在，会对多孔介质的流动特性产生较大的影响，例如它们会影响多孔介质的扩散效率和流动速度等等。

广义多孔介质方程的广义及其对称性在作用准确描述多孔介质流体间相互作用时，广义多孔介质方程需要非陡峭系数项$alphaabla cdot (u cdotabla u)$配合，它能体现出多孔介质自身静力学性质，但有时由于多孔介质流体中涉及到的局部系统可能具有后继性或者旋转性，这就对广义多孔介质方程的形式提出了新的要求。

【国家自然科学基金】_广义条件对称_基金支持热词逐年推荐_【万方软件创新助手】_20140802

科研热词鞍点问题非线性反应扩散方程非圆信号线性流形精确解波达方向估计最佳逼近无穷多对称收敛域截断对称广义自回归条件异方差广义相位平滑广义条件对称对称约化对称的广义中心对称矩阵对称正定矩阵声矢量阵列反对称矩阵利率期限结构上海银行间同业拆放利率 gsaor迭代法 gcbs方程 frobenius范数
2014年序号 1 2 3 4
2014年科研热词相位解缠广义最小余量法干涉合成孔径雷达对称超松弛预条件 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
科研热词精确解非李拟设闭性距离几何秩最小二乘解最佳逼近抽象距离空间强鞍点广义条件对称(clbs) 广义度量方程广义中心对称矩阵广义ky fan不等式问题对称强向量拟均衡问题对称弱向量拟均衡问题判别式几何约束 hamilton-jacobi方程 burgers-fisher方程
2012年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47
科研热词推荐指数精确解 2 等价关系 2 强对称关系 2 广义条件对称 2 预处理子 1 非线性扩散方程 1 非理性泡沫 1 进化博弈链 1 近似泛函分离变量法 1 近似广义条件对称 1 谱分析 1 解析层元 1 股票市场 1 经典粗糙集 1 线性方程组 1 约束力学系统 1 精确集 1 粗糙集 1 等几何分析 1 等价性变换 1 特征值法 1 波动方程 1 李代数 1 机械应变能释放率 1 最小多项式 1 新守恒量 1 弱施加法 1 广义精确集 1 广义粗糙集 1 广义极小残量法 1 广义保角映射 1 广义tzénoff方程 1 平面应变biot固结 1 对称分类 1 多孔介质方程 1 噪声交易 1 变系数非线性扩散方程 1 压电复合材料 1 具有不对称共线裂纹的圆形孔口 1 公理特征 1 公理化特征 1 位移边界条件 1 不变解 1 nitsche方法 1 mei对称 1 laplace-fourier变换 1 dirichlet边界 1

一类四阶发展方程的拟局部对称分类问题

一类四阶发展方程的拟局部对称分类问题黄晴;王丽真;左苏丽【摘要】目的研究一类四阶发展方程的拟局部对称分类问题.方法利用群分类方法.结果给出了容许拟局部对称的四阶发展方程及其所容许的对称.结论完成了四阶发展方程的拟局部对称分类问题.【期刊名称】《西北大学学报（自然科学版）》【年(卷),期】2010(040)002【总页数】3页(P207-209)【关键词】四阶发展方程;拟局部对称;对称分类【作者】黄晴;王丽真;左苏丽【作者单位】西北大学,数学系;西北大学,数学系;西北大学,数学与科学史研究中心,陕西,西安,710127;西北大学,数学系【正文语种】中文【中图分类】O175.2本文研究四阶抛物方程的拟局部对称群分类问题,其中F为光滑函数,u=方程(1)是许多重要的数学物理方程的推广,如Kuramoto-Sivashinsky方程[1-2] 广义的Fishier-Kolmogorov方程[3]和Swift-Hohenberg方程[4]等。

近年来方程(1)已经引起了数学物理学家广泛的关注和浓厚的研究兴趣。

李对称在微分方程的现代理论中起着重要的作用,将方程(1)进行群分类是很自然的想法,文献[5]对式(1)做了李群分类,给出了所有可能使得方程容许直到四维的可解李群和使得方程Galilei不变的F的形式。

由于李对称并不能回答非线性微分方程现代理论中的所有问题,人们对其进行了推广,如允许无穷小依赖于因变量的全局行为,这样非局部对称的概念应运而生。

迄今为止,线性偏微分方程的非局部对称已得到了较为广泛深入的研究,而对非线性偏微分方程的非局部对称知之甚少。

Bluman 通过研究方程的辅助系统所容许的局部对称来研究方程的势对称[6]。

非局部对称构造的另一种方式是对容许非平凡李对称的方程作非局部变换,若原方程的李对称在变换的作用下变为新方程的非局部对称,则称为拟局部对称。

最近,Zhdanov和Lahno得到了一些容许拟局部对称的二阶发展方程[7]。