Keller-Segel趋化模型的高精度紧致差分方法
一类趋化-流体耦合方程组的能量不等式

一类趋化-流体耦合方程组的能量不等式何璞;林静秋【摘要】能量不等式的建立对于偏微分方程解的整体存在性、有界性的研究具有重要意义.本文结合精细的积分估计与不等式估计技巧,推导一类耗氧的趋化-流体耦合方程组的能量不等式.【期刊名称】《西华大学学报(自然科学版)》【年(卷),期】2018(037)005【总页数】5页(P108-112)【关键词】趋化-流体耦合方程组;能量不等式;分部积分【作者】何璞;林静秋【作者单位】西华大学理学院,四川成都 610039;西华大学理学院,四川成都610039【正文语种】中文【中图分类】O175.291 预备知识趋化方程是一类刻画细胞自我组织和趋化运动规律的数学模型,这类问题经典的研究模型是标准Keller-Segel模型[1],标准Keller-Segel模型的解的整体存在性和有限时刻爆破等问题已经被大量数学工作者研究(参考综述[2-4]及其中的参考文献)。
然而,在实际生物学背景中,细胞所处流体环境对于细胞趋化运动行为同样有着不可忽视的影响。
因而,文献[5]的作者经过实验观察,提出了如下趋化-流体(chemotaxis-fluid)耦合模型:此处的未知函数n=n(x,t)表示细胞密度、c=c(x,t)代表化学物质、信号的浓度,u=u(x,t)和P分别表示流体速度场和相应的压力;参数κ∈R与非线性流体对流项的强度有关;φ表示重力势,是已知函数。
本文将考虑这类方程组的如下初边值问题:(1)其中,Ω⊂RN为具有光滑边界的有界凸区域。
这类方程组研究的一个基本问题是解的整体存在性和有界性,而能量不等式估计的方法是研究方程(组)解的整体存在性与有界性的一个重要方法。
一旦建立了方程组的能量不等式,我们就可结合Lp-Lq估计、Neaumann热半群、Stokes半群的衰减性质等建立方程组解的相应先验估计;从而最终建立方程组解的整体存在性或有界性。
本文将主要建立方程组(1)的一个能量不等式。
一维时间分数阶Keller-Segel模型的解析解

一维时间分数阶Keller-Segel模型的解析解侯婕;王丽真【摘要】在这篇文章中,用广义分离变量法、齐次平衡法和不变子空间方法研究了含有分数阶导数的广义Burgers方程.借助一维抛物-椭圆型Keller-Segel模型与Burgers方程之间的关系,建立了一维分数阶Keller-Segel模型的几类精确解.【期刊名称】《纯粹数学与应用数学》【年(卷),期】2019(035)003【总页数】11页(P276-286)【关键词】广义分离变量法;齐次平衡法;不变子空间方法;广义Burgers方程;Keller-Segel模型【作者】侯婕;王丽真【作者单位】西北大学数学学院, 陕西西安 710127;西北大学数学学院, 陕西西安710127【正文语种】中文【中图分类】O175.21 IntroductionFractional partial differential equations(PDEs)appear more and more frequently in different research fields and engineering applications,such as biology,physics,rheology,control theory,signal processing andelectrochemistry[1-2].There are many methods introduced to discuss the construction of solutions to fractional PDEs,such as Lie symmetry method[3-4],generalized differential transform method[5],Adomian decomposition[6],homotopy perturbation[7],which have achieved significant progress for some fractional PDEs.The generalized separation variable method can split the original equation into several ordinary differential equations(ODEs)[8].The time-fractional heat conduction equation[9],fractional Korteweg-de Vries equation[10],two and three-dimensional timefractional telegraph equations[11]and nonlinear time fractional biological population model[12]were discussed by separation variable method.And the function expansion method of separation variable type based on the homogenous balanced principle was introduced in reference[13].And Rui[14]has studied the exact solutions of nonlinear fractional PDEs.The invariant subspace method is another method for finding the analytical exact solution of the fractional PDEs.This method was initially proposed by reference[15].General fractionalODEs[16],Burgers equation under the Caputo derivative[17]and time fractional coupled nonlinear PDEs[18]were investigated by the invariant subspace method.And the homogenous balanced principle and the invariant subspace method are both special cases of the generalized separation variable method.In this paper,we consider the following time fractional one-dimensional Keller-Segel(KS)modelwhere 0<α<1.Equation(1)is the generalization of a class of parabolic-elliptic equations called KS model that characterizes the chemotaxis phenomenon in biology.The KS model was proposed byreference[19],while the parabolic-elliptic model was introduced due to the fact that the diffusion coefficient of the chemical substance is verylarge[20].Cauchy problems for Keller-Segel type time-space fractional diffusion was studied in reference[21].The main discussion of this paper is as follows.In section 2,we begin with some basic definitions and remarks of time fractional PDEs with Riemann-Liouville derivative and Caputo derivative.In section 3,we use three methods to solve the generalized Burgers equation.And in Section 4,with the help of the relation between the generalized Burgers equation and KS equations,the solutions of the KS equations are constructed.2 PreliminaryIn this section,we introduce some definitions and properties of the Riemann-Liouville derivative and Caputo derivative which will be used later. Definition 2.1 Let α>0,the Riemann-Liouville fractional integral operator of order α of the function f(t)∈ L1([a,b],R+)is defined byis the Euler gamma function.Definition 2.2 The Riemann-Liouville fractional derivative is defined byhere and hereafteris the usual partial derivative of integer order n. Definition 2.3 The Caputo fractional derivative is given byAnd the following two properties of fractional derivatives and integrals are useful for our discussion.For γ >0,0< δ<1,t>0,one hasThe result related to the solution of the special type fractional ODE is listed as follows.Lemma 2.1[22] Let α >0,λ,β ∈ R,λ 0.If α + β <1,t>a,then the α-th order fractional ODE3 The exact solutions of the generalized Burgers equationIn this section,we consider the following generalized Burgers equationwhere h(t)is an arbitrary function of t.We will use the generalized separation variable method,homogenous balanced principle and invariant subspace method to solve equation(4)separately.3.1 Generalized separation variable methodFor generalized Burgers equation(4)with Riemann-Liouville fractional derivative defined by Definition 2.2,we use generalized separation variable method introduced in reference[8]to seek exact solutions of equation(4). Case 3.1SetSubstituting the ansaze into(4),we can obtainUsing splitting method mentioned in reference[8],we obtain the determining equationsSolving(7)and(8)with the help of Maple yieldsC1is an arbitrary constant,and G=LambertW is the inverse of f(w)=wewin which w is an arbitrary complex number.The combination(5)with(6)gives,In particular,when A2=0,solving(10)with the formula given in Lemma2.1,we find thatThus,we obtain the following observation on the solution of the Burgers equation.Theorem 3.1 Generalized Burgers equation(4)has solutions of the formwhere f(x)satisfies(9)and g(t)satisfies(10).Especially,when A2=0,g(t)is given by(11).Case 3.2Let (x,t)=xg1(t)+f(x)g2(t).Substituting it into(4),we haveDifferentiating(12)with respect to x twice,and using the splitting method,we obtain the determining equationsC1,C2,Z are arbitrary constants,and L=RootOf is a placeholder for representing all the roots of an equation in one variable.Thus we have the following result on the solution of(4).Theorem 3.2 Generalized Burgers equation(4)has solutions of the formwhere g1(t),g2(t),f(x)satisfy(17),(18),(21),separately.Particularly,we obtain the exact solution g1(t),g2(t)which satisfy(20)and(19),respectively.3.2 Homogenous balanced principleIn this subsection,we will investigate the exact solution of(4)in Caputo sense,that is,using homogeneous balanced principle given in reference[14].Supposewhere ak,γkare constants to be determined later.The highest order of x in the te rm is m.And the highest order of x in the nonlinearis 2m−1.Thus we obtain m=1 using the homogenous balancedmethod.Therefore,equation(22)has the following type exact solutionwhere γ0,γ1,a0and a1are determined constants.We balance the order of t and the coefficients of every terms in(24)to obtainwhere a0is an arbitrary nonzero constant,γ0+1>0 and γ0+1 − α >0.So,we have the following result.Theorem 3.3 Let a0 0,γ0> −1+ α,the generalized Burgers equation(22)with Caputo fractional derivative has the solution of the form3.3 Invariant subspace methodIn this section,we use invariant subspace method to solve the generalizedBurgers equation(22).First,we use the invariant subspace method to solveSet (x,t)=∂x(x,t).The equation(25)is equivalent to(22).If h(t)=0,the solution of the equation is given in reference[17].When h(t)0,it is possible to find an exact solution to(22)by using invariant subspace method.First,we consider a scalar evolution equation.For(22),we haveThen we obtain the invariant subspace W3=<1,x,x2>under the given operator F[].Thus,the solution has the following formwhere a(t),b(t)and c(t)will be determinedlater.Substitution(26)into(25)yieldsSince equation(27)holds for all x∈R.Therefore,vanishing the constant and the coefficients of x and x2,we obtain a simple system of fractional ODEs4 The establishment of the solutions of KS equationsDue to the special structure of the parabolic-elliptic KS equations(1),we can transform it into the generalized Burgers equation.In this part,we apply the results of the solutions of generalized Burgers equation to the KS equations to establish the expression of solutions of the KS equations(1).Integrating(33)with respect to x,we obtain the equation with Riemann-Liouville derivative(4).Using the same method we can findIntegrating(34)with respect to x,we obtain the equation with Caputo derivative(22).Therefore,we get the connection between the generalized Burgers equation and the KS equations(1).With the help of these relations,we can deduce the formulas of the solutions to KSequations(1)with the formExplicitly,applying Theorem 3.1,we get the expression of the solution to the KS equations(1)where f(x)satisfies(9)and g(t)satisfies(10).Especially,the exact solutiong(t)satisfies(11).And using Theorem 3.2,the solution of the KSequations(1)takes the formwhere g1(t),g2(t),f(x)satisfy(17),(18)and(21),separately.Particularly,we obtain the exact solution g1(t),g2(t)satisfy(20),(19),respectively.Exploiting Theorem 3.3,that is,using homogenous balanced principle,we arrive at the solution of the KS equations(1)Due to Theorem 3.4,the solution of the KS equations(1)can be expressedTherefore,we can obtain that equation(35),(36),(37),(38)are the solutions to the fractional one-dimensional parabolic-elliptic Keller-Segel model(1).Reference【相关文献】[1]Oldham K B,Spanier J.The Fractional Calculus[M].London:Academic Press,1974.[2]Podlubny I.Fractional Differential Equations[M].San Diego:Academic Press,1999.[3]Huang Q,Zhdanov R.Symmetries and exact solutions of the time fractional Harry-Dym equation with Riemann-Liouville derivative[J].Physica.A,2014,409:110-118.[4]Wang L Z,Wang D J,Shen S F,et al.Lie point symmetry analysis of the Harry-Dym Type equation with Riemann-Liouville fractional derivative[J].Acta.Math.Appl.Sin-E.,2018,34(3):469-477.[5]Odibat Z,Momani S.A generalized differential transform method for linear partial differential equations of fractional order[J].Appl.Math.Lett.,2008,(21):194-199.[6]Momani S,Odibat Z.Analytical solution of a time fractional Navier-Stokes equation by Adomian decompostion method[J]put.,2006,177:488-494.[7]He J H.Approximate analytical solution for seepage flow with fractional derivatives in porous media[J].Comput.Methods Appl.Mech.Eng.,1998,167:57-68.[8]Polyanin A D,Zaitsev V F.Handbook of Nonlinear Partial Differential Equations[M].Boca Raton:Chapman Hall/CRC Press,2003.[9]Ning T H,Jiang X Y.Analytical solution for the time-fractional heat conduction equation in spherical coordinate system by the method of variableseparation[J].Acta.Mech.Sin.,2011,27(6):994-1000.[10]Zhuang J Y,Qiao P,Li Z M.The method of separation of variables for local fractional Korteweg-de Vries equation[J].Therm.Sci.,2016,20:859-862.[11]Wang X B,Liu F W.Analytical solutions for the two and three-dimensional time-fractional telegraph equations by the method of separating variables:proceedings of the Fifth Symposium on Fractional Differentiation and Its Application,Nanjing[C].New York:Springer-Verlag,2012.[12]Zhang S,Cai B.Variable separation method for nonlinear time fractional biological population model[J].Int.J.Numer.Method.H.,2015,25:1531-1541.[13]Wu C,Rui W G.Method of separation variables combined with homogenous balanced principle for searching exact solutions of nonlinear time-fractional biological population model[J].Commun.Nonlinear.Sci.Numer.Simulat.,2018,63:88-100.[14]Rui W G.Applications of homogenous balanced principle on investigating exactsolutions to a series of time fractional nonlinearPDEs[J].Commun.Nonlinear.Sci.Numer.Simulat.,2017,47:253-266.[15]Galaktionov V,Svirshchevskii S.Exact Solutions and Invariant Subspaces of Nonlinear Partial Differential Equations in Mechanics and Physics[M].Boca Raton:Chapman Hall/CRC Press,2007.[16]Gazizov R K,Kasatkin A A.Construction of exact solutions for fractional order differential equations by the invariant subspacemethod[J].Comput.Math.Appl.,2013,66:576-584.[17]Harris P A,Garra R.Analytic solution of nonlinear fractional Burgers-type equation by invariant subspace method[J].Nonlinear Studies,2013,20(4):247-268.[18]Sahadevan R,Prakash P.Exact solution of certain time fractional nonlinear partial differential equations[J].Commun.Nonlinear.Sci.Numer.Simulat.,2017,42:158-177. [19]Keller E F,Segel L A.Initiation of slime mold aggregation viewed as aninstability[J].J.Theoret.Biol.,1970,26(3):399-415.[20]Jäger W,Luckhaus S.On explosions of solutions to a system of partial differential equations modelling chemotaxis[J].Trans.Amer.Math.Soc.,1992,329(2):819-824.[21]Li L,Liu J G,Wang L Z.Cauchy problems for Keller-Segel type time-space fractional diffusion equation[J].J.Differential Equations.,2018,265:1044-1096.[22] Kilbas A A,Srivastava H M,Trujilo J J.Theory and Application of Fractional Differential Equations[M].Amsterdam:Elsevier Science B.V.,2006.。
基于高精度加权紧致非线性格式的γ-Reθ转捩模型标定与应用

基于高精度加权紧致非线性格式的γ-Reθ转捩模型标定与应用王圣业;王光学;董义道;邓小刚【摘要】为准确模拟航空工程中的转捩问题,在高精度数值风洞平台上采用低速平板试验数据对基于高精度加权紧致非线性格式的γ-Reθ转捩模型进行了标定,并在二维低速问题中进行了应用。
计算结果与试验的对比表明:基于高精度加权紧致非线性格式的γ-Reθ转捩模型可准确模拟自然转捩、旁路转捩及分离转捩的位置,并且具有较低的网格敏感性;在中等雷诺数范围,层流区域和湍流区域有相同量级时,计算必须采用转捩模型才能准确模拟阻力系数。
%In order to accurately simulate the transition in aeronautical engineering,the low speed flat plate data was adopted for the calibration of γ-Reθtransition model based on high-order WCNS (weighted compact nonlinear scheme)on the platform of high-order numerical wind tunnel.Based on the calibrated transition model,the flow over the low speed airfoil was parison between the calculated results and the experiment data indicates that the γ-Reθtransition model based on WCNS can predict the location of nature transition,bypass transition or separation transition very well and has low mesh sensitivity;only the transition model can calculate the drag coefficient accurately within a moderate Reynolds number range where the length of the laminar flow region is comparable to that of the turbulent flow region.【期刊名称】《国防科技大学学报》【年(卷),期】2016(038)004【总页数】7页(P14-20)【关键词】转捩模型;高精度格式;加权紧致非线性格式;湍流模型【作者】王圣业;王光学;董义道;邓小刚【作者单位】国防科技大学航天科学与工程学院,湖南长沙 410073;国防科技大学航天科学与工程学院,湖南长沙 410073; 中山大学物理学院,广东广州510006;国防科技大学航天科学与工程学院,湖南长沙 410073;国防科技大学航天科学与工程学院,湖南长沙 410073【正文语种】中文【中图分类】TN95转捩机理非常复杂,包含了自然转捩、旁路转捩、分离诱导转捩以及湍流边界层在顺压梯度下可能再层流化等[1],故而对转捩的模拟十分困难。
求解对流方程的高精度紧致差分格式及软件实现

Key Words: Convection equation; High-order; Compact difference scheme; LOD method; Finite difference method
II
目录
第一章 绪论...................................................................................................................... 1
Finally, these schemes deduced in this paper are integrated into the software of "PHOEBESolver", which makes it easier for scholars in numerical solutions of partial differential equations to use these schemes in this paper.
【国家自然科学基金】_高精度紧致差分格式_基金支持热词逐年推荐_【万方软件创新助手】_20140801
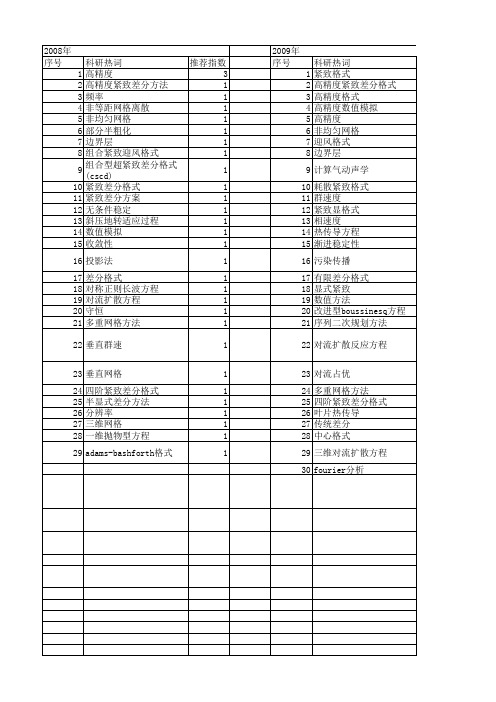
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35
科研热词 推荐指数 高精度 6 richardson外推法 4 高阶紧致格式 3 非均匀网格 2 边界层 2 对流扩散方程 2 高精度紧致差分格式 1 高精度紧致差分方法 1 隐式紧致格式 1 隐式差分 1 调制对传波 1 行进波 1 紧致格式 1 紧致差分格式 1 稳定性 1 泊松方程 1 有限差分法 1 对传波 1 定常行进波 1 定常对流扩散方程 1 交替方向隐式格式 1 二维波动方程 1 stationary traveling wave 1 soret效应 1 soret effect 1 1 schrsoinger equation 1 schrodinger方程 1 richardson extrapolation method 1 poiseuille流动 1 modulated eounterpropagating wave 1 high-order compact scheme 1 high order compact scheme 1 high accuracy 1 counterpropagating wave 1
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
科研热词 推荐指数 非均匀网格 3 高阶紧致差分格式 2 高精度紧致格式 2 预报校正 2 非线性对流扩散方程 2 紧致差分格式 2 二维热传导方程 2 高精度紧致差分格式 1 高精度 1 预条件技术 1 非定常对流扩散方程 1 边界层问题 1 边界层 1 自然对流 1 线性多步法 1 涡量-流函数方法 1 扩散反应方程 1 多重网格方法 1 四阶紧致格式 1 加权隐式差分格式 1 二维对流扩散方程 1 不可压navier-stokes/boussinesq方程组 1 一维定常对流扩散方程 1 richardson外推法 1 richardson 外推法 1 maccormack方法 1 fgmres迭代法 1 adi方法 1 adi 方法 1
一维非定常对流扩散方程非均匀网格上的高精度紧致差分格式

一维非定常对流扩散方程非均匀网格上的高精度紧致差分格式黄雪芳;郭锐;葛永斌【摘要】A high accuracy compact finite difference scheme with non-uniform grids is pro-posed to solve unsteady convection diffusion equations, which are used to describe boundary layer problems or locally large gradient problems, etc. The new method starts from the dis-cretization of the steady convection diffusion equation. Firstly, the spatial derivatives are discretized by using the Taylor series expansion on non-uniform grids. Then, the second order backward Eulerian difference formula is used to discretize the temporal derivative term. The three-level full implicit compact difference scheme on non-uniform grids for solving the one-dimensional unsteady convection diffusion equation is derived. The new scheme has the second order accuracy in time and the third to fourth order accuracy in space and is unconditionally stable. Finally, some numerical experiments are conducted to demonstrate the high accuracy and the advantages in solving boundary layer problems or locally large gradient problems.%本文在非均匀网格上给出了求解非定常对流扩散方程的一种高精度紧致差分格式,特别适合边界层和大梯度等问题的求解。
二维波动方程的一种高精度紧致差分方法

(一 ) —2) = ) A ( , ( ; T2 + ×
e
,
J
+R
0≤ , ≤ 一1, O≤ n≤ Ⅳ 一 1
用 r表示时 间步 长 , h表 示空 间步 长 , 1给 出 了 当 7= 表 -
() 8
e =o
h [ ( L 曰
A
(
3 数值 验 证
对于式 ( )一( ) 令 ( y  ̄ , i( )i(r) ( 1 4, , )= 2 rn s T , , r s n y
Y )=0g , ,) , 问题 的精确解 为 / , ,)= i( 订 ) ,( Y t =0 则 2 Y t s t ( n s (T)i(r) i ' s 叮 。数值 实验计算是用 F  ̄a 7语言进行编程 nI n y X o rn7
h) 。 阶精度的数值 解。孙 志 忠 提 出 了求 解二 维波 动方 程 的 高精度交替方 向隐式 方法 , 并且是无条件稳定 的。有关这方 面 最新 的一 些 工作 可参 见 文献 [ 6—8 。本文 在 此工 作基 础 之 ]
上, 利用 Rc a sn外推法进 一步 提 高计 算精 度 , i ro hd 最终 可得 到
o≤ √≤ 一1
4 t h ,=1时刻 , 本文格 式在不 同网格步 长下误 差 的 、 、
范数 , 以及与四阶 A I D 格式 计 算结 果 的 比较 。L 范 数定 义 2
厂]i 面=广——一 『
d] = o 。 e
\ e =0
。 ≤ M
一
1
层的。即每一次时间推进都需要知道前 两个 时间步 的值 , 0 第
求解该 问题 精度为 O( + 。 的数值解 。 h)
趋化-流体耦合模型研究进展

趋化-流体耦合模型研究进展王玉兰【摘要】从经典的Keller-Segel模型出发,简述趋化方程组的生物学背景、一般研究方法和最新研究进展.特别对趋化-流体耦合模型的起源、研究进展、研究困难进行详细的分析,并指出此类方程组研究中一些尚待解决的问题.【期刊名称】《西华大学学报(自然科学版)》【年(卷),期】2016(035)004【总页数】6页(P30-34,38)【关键词】趋化;趋化-流体耦合模型;趋化灵敏度;整体存在;有界性【作者】王玉兰【作者单位】西华大学理学院,四川成都610039【正文语种】中文【中图分类】O175.29趋化性(也被称为化学趋向性)是趋向性的一种,指身体细胞、细菌及其他单细胞、多细胞生物依据环境中某些化学物质的分布而趋向的运动。
这种趋向性的运动对细菌寻找食物(如葡萄糖)十分重要,细菌以此趋进有较高食物分子浓度的地方,或远离有毒(如苯酚)的地方。
在多细胞生物中,趋化性对其生存和发展不可或缺。
另外,已证实趋化性不仅对研究生物运动具有很重要的作用,而且在生物除污、生物膜的形成、感染的发病机制(如癌细胞的转移)、生物固氮、微生物在地下环境和土壤中的迁移以及微生物采油等领域的研究中也具有重要意义。
事实表明,对趋化性现象的研究不仅具有理论意义,而且有很强的现实意义。
趋化方程(chemotaxis equation)就是从生物趋化性现象研究中抽象出的一类用于刻画细胞趋化运动规律的反应扩散方程。
为了描述细胞种群的动力学行为,在过去的几十年中,最典型的趋化模型-Keller-Segel趋化模型被广泛关注和研究 [1]。
此处的n表示细胞密度,c代表化学物质、信号的浓度,而S则是趋化灵敏度函数,根据不同的生物具体背景,它可能依赖于细胞密度n、化学物质浓度c及环境位置变量x。
当(1.1)中的灵敏度函数S恒为常值函数1时,便得到标准的Keller-Segel模型。
这个模型具有很多丰富而有趣的性质,包括解的整体存在、有限时刻爆破及空间模式形成等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Keller-Segel趋化模型的高精度紧
致差分方法
专业品质权威
编制人:______________
审核人:______________
审批人:______________
编制单位:____________
编制时间:____________
序言
下载提示:该文档是本团队精心编制而成,期望大家下载或复制使用后,能够解决实际问题。
文档全文可编辑,以便您下载后可定制修改,请依据实际需要进行调整和使用,感谢!
同时,本团队为大家提供各种类型的经典资料,如办公资料、职场资料、生活资料、进修资料、教室资料、阅读资料、知识资料、党建资料、教育资料、其他资料等等,想进修、参考、使用不同格式和写法的资料,敬请关注!
Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!
And, this store provides various types of classic materials for everyone, such as office materials, workplace materials, lifestyle materials, learning materials, classroom materials, reading materials, knowledge materials, party building materials, educational materials, other materials, etc. If you want to learn about different data formats and writing methods, please pay attention!
Keller-Segel趋化模型的高精度紧致差分方法
Keller-Segel趋化模型的高精度紧致差分方法
引言
Keller-Segel模型是一种用于描述生物群体中化学物质扩散和
趋化运动的数学模型。
它最初由Ernst Keller和Ludwig Segel在1970年提出,被广泛应用于许多领域,如癌症探究、群体行为模
拟等。
为了更准确地解决Keller-Segel模型,许多数值方法被提出。
本文将介绍一种高精度紧致差分方法,用于解决Keller-Segel趋化模型问题。
Keller-Segel模型的描述
Keller-Segel模型描述了生物群体中的细胞扩散和趋化运动。
模型基于两个方程:一个控制化学物质浓度的扩散方程,另一个
控制细胞的趋化运动。
这两个方程可以写为:
∂c/∂t = D∇²c - χ∇·(c∇u)
∂u/∂t = Δu - κc
其中,c是化学物质的浓度,u是细胞的趋化物质浓度,D是
扩散系数,χ是趋化敏感度,κ是趋化速度。
高精度紧致差分方法的原理
高精度紧致差分方法是一种数值解法,通过将偏微分方程离
散化为差分方程并利用紧致差分格式来近似求解。
它在较少的网
格节点上获得了高精度的数值解。
详尽地说,对于Keller-Segel模型的扩散方程,可以利用标准的中心差分格式来进行离散化,得到如下差分方程:
(c_i,j)_t = D((c_i+1,j - 2c_i,j + c_i-1,j)/(Δx^2) + (c_i,j+1 - 2c_i,j + c_i,j-1)/(Δy^2))
其中,(c_i,j)_t是化学物质浓度在时刻t的离散值,(c_i+1,j, c_i,j+1, c_i-1,j, c_i,j-1)是相邻节点上的浓度值,Δx和Δy是网格的空间步长。
类似地,对于趋化方程,可以使用类似的差分格式:
(u_i,j)_t = ((u_i+1,j - 2u_i,j + u_i-1,j)/(Δx^2) + (u_i,j+1 - 2u_i,j + u_i,j-1)/(Δy^2)) - κc_i,j
高精度紧致差分方法的优势
高精度紧致差分方法相较于其他数值方法具有以下优势:
1. 高精度:该方法使用紧致差分格式,通过减小网格尺寸来提供更高的数值精度。
2. 空间效率:由于紧致差分格式只使用少许的邻近节点,该方法可以在较少的网格节点上获得精确的数值解,从而提高空间效率。
3. 稳定性:高精度紧致差分方法结合了适应性网格技术,可以有效地处理数值解中的不稳定性。
4. 并行计算:紧致差分方法适合于并行计算,可以通过将计算任务分配给多个处理器来加速计算速度。
结论
高精度紧致差分方法是解决Keller-Segel趋化模型的一种有效数值方法。
该方法利用紧致差分格式对偏微分方程进行离散化,并通过适应性网格技术和并行计算来提高计算效率和精度。
在实际应用中,可以依据详尽问题的要求选择不同的空间步长和时间步长,进一步优化数值解的准确性和计算效率
综上所述,高精度紧致差分方法是一种在解决Keller-Segel趋化模型中具有优势的数值方法。
通过减小网格尺寸和使用紧致差分格式,该方法能够提供更高的数值精度,并且在较少的网格节点上获得精确的数值解,提高空间效率。
此外,结合适应性网格技术和并行计算,该方法能够处理数值解中的不稳定性,并加速计算速度。
因此,高精度紧致差分方法在解决Keller-Segel趋化模型中具有较高的计算效率和精度。
