新人教版初中七年级数学下册《8.4 三元一次方程组的解法 阅读与思考 一次方程组的古今表示及解法》优质课
人教版数学七年级下册 8.4 三元一次方程组的解法 课件(共21张PPT)
3x＋4z=7
11x＋10z=35
解这个方程组，得
x= 5
z=−2
把x=5、z=-2代入②，得2×5+3y-2=9，解得y=
所以
=
=
= −
是这个三元一次方程组的解.
x y 3
y z 5
z x 4
小试牛刀
解方程组
解:
③ - ②，得
三元一次方程组的解法
学习目标
1．熟练掌握解三元一次方程组的方法与步骤，会
解简单的三元一次方程组．
2．会用三元一次方程组的解法解决实际问题．
新课导入
x 2y 3 ①
解方程组：
2 x y 1 ②
（1）这是几元几次方程组？
二元一次方程组
（2）求解的思想是什么？
消元
（3）用什么方法消元可以解这个方程？
时,y=3;当x=5时,y=60. 求a,b,c的值.
解:根据题意，得三元一次方程组
a－b＋c= 0，
①
4a＋2b＋c=3， ②
25a＋5b＋c=60. ③
②－①， 得 a＋b=1 ④
③－①，得 4a＋b=10 ⑤
④与⑤组成二元一次方程组
a＋b=1，
4a＋b=10.
问题1：题中有哪些未知量？你能找出哪些等量关系？
④与⑤组成二元一次方程组
a＋b=1，
4a＋b=10.
利用三元一次方程组解决实际问题-提高
x y 8
如果方程组 y z 6 的解使代数式kx+2y﹣3z的值为8，则k＝（
z x 4
人教版七年级数学下册8.4_三元一次方程组的解法课件ppt精品课件
你能根据等量关系列出方程吗?
设1元、2元、5元的纸币分别为x张、y张、z张.
根据题意，可以得到下面三个方程：
x+y+z=12
①
x=4y
②
x+2y+5z=22
③
x+y+z=12
①
x=4y
②
x+2y+5z=22
③
观察方程①、③你能得出什么？
都含有三个未知数，并且含有未知数的项的次数都是1，像这样 的方程叫做三元一次方程.
z＋x－y＝1.
③
y＝______，z＝_______. 【解析】通过观察未知数的系数，可采取① +②求出y， ②+ ③求出z，最后再将y与z的值代入任何一个方程求出x即可.
【答案】6 8 3
3.若x＋2y＋3z＝10，4x＋3y＋2z＝15，则x＋y＋z的值为（ ）
A.2
B.3
C.4
D.5
【解析】选D.通过观察未知数的系数，可采取两个方程相加得， 5x+5y+5z=25，所以x+y+z=5.
5x－9y＋7z=8. ③
解：②×3＋③ ，得 11x＋10z=35 ④
①与④组成方程组
3x＋4z=7， 11x＋10z=35.
解这个方程组，得
x=5， z=-2.
把x＝5，z＝-2代入②，得y=
1,
3
因此，这个三元一次方程组的解为
x=5， y= 1 ,
3
z=-2.
x＋y－z＝6，
①
解三元一次方程组
*8.4 三元一次方程组的解法
1.经历探索三元一次方程组的解法的过程; 2.会解三元一次方程组; 3.能利用三元一次方程组解决简单的实际问题.
人教版初一数学 8.8.4 三元一次方程组的解法PPT课件
探究新知
用代入消元法解
+ + = ，
将③代入①，②，得ቊ
+ + = .
+ = ，
= ，
即ቊ
解得ቊ
代入①得出x＝8.
+ = ，
ቐ = ，
探究新知
消元思想
解三元一次方程组的基本思路：
2.七彩作业.
例3：若|a－b－1|＋(－2＋) ＋2|c－b|＝0，求a，b，
c的值.
解析：本题考查非负数性质的综合应用，要使等式成立必须
使每个非负数都为0.
探究新知
解：因为三个非负数的和等于0，所以每个非负数都为0.
− − = ，
= −，
可得方程组ቐ − + = ，解得ቐ = −，
求1元、2元和5元的纸币各多少张？
设1元、2元、5元的纸币分别
为x张、y张、z张
x＋y＋z＝12
x＋2 y＋5 z＝22
x＝4 y
这样的方程组我们叫它什么呢，该怎样解呢？
探究新知
学生活动一【一起探究】
+ + = ，
三元一次方程组ቐ + + = ，
= .
3.在知识的学习过程中，感受事物之间的相互联系.
学习重难点
学习重点：解三元一次方程组的基本思路，会解
三元一次方程组.
学习难点：会选择适当的方法消元并熟练解三元
一次方程组.
回顾复习
问题1：二元一次方程组的概念？
方程组中含有两个未知数，含有每个未知数的项
的次数都是1，并且一共有两个方程，像这样的方程
人教版七年级数学下册8.4 三元一次方程组的解法
（2）解该三元一次方程组，求出满足要求的A、B、C的份数.
解：(1)由该食谱中包含35单位的铁、70单位的钙和35单位 的维生素，得方程组
类似二元一次方程组的解，三元一次方程组中各个方程 的公共解，叫做这个三元一次方程组的解.
怎样解三元一次方程组呢？
x y z 23, ①
x
y
1,
②
2x y z 20.③
能不能像以前一样“消元”， 把“三元”化成“二元”呢？
探究新知
考点 1 三元一次方程组的解法
解三元一次方程组
3x 4z 7， ① 2x 3y z 9， ② 5x 9 y 7z 8．③
y=8,z=6. 把y=8代入④，得x=9.
x=9, 所以原方程组的解是 y=8,
z=6.
探究新知
考点 2 三元一次方程组求字母的值 在等式 y=ax2＋bx＋c中,当x=－1时,y=0;当x=2时,y=3;当
x=5时,y=60. 求a,b,c的值.
解:根据题意，得三元一次方程组 a－b＋c= 0， ① 4a＋2b＋c=3， ② 25a＋5b＋c=60. ③
巩固练习
x 1
已知
y
2
z 3
是方程组
ax by 2 by cz 3 cx az 7
的解,则a+b+c的值是___3_________.
探究新知
考点 3 利用三元一次方程组解答实际问题 幼儿营养标准中要求每一个幼儿每天所需的营养量中应包含35 单位的铁、70单位的钙和35单位的维生素.现有一批营养师根
探究新知 知识点 1 三元一次方程组的概念
小明手头有12张面额分别是1元、2元、5元的纸币，共 计22元，其中1元纸币的数量是2元纸币数量的4倍．求1元、 2元、5元的纸币各多少张？
新人教版数学七下《8.4三元一次方程组解法》视频课堂实录+课件+教案+练习+反思+建议+整体规划+评
新世纪教育网版权所有 单位租用个人充值 QQ:448966300
新世纪教育网版权所有 单位租用个人充值 QQ:448966300 教学规划
菊城中学 陈南球
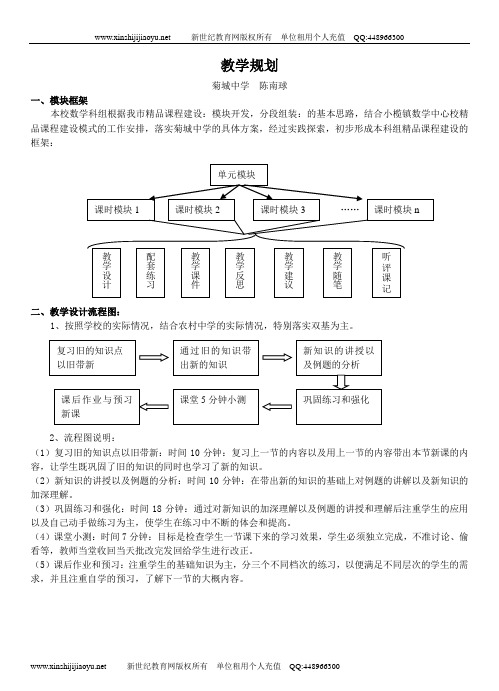
一、模块框架
本校数学科组根据我市精品课程建设：模块开发，分段组装：的基本思路，结合小榄镇数学中心校精品课程建设模式的工作安排，落实菊城中学的具体方案，经过实践探索，初步形成本科组精品课程建设的框架：
二、教学设计流程图：
1、按照学校的实际情况，结合农村中学的实际情况，特别落实双基为主。
2、流程图说明：
（1）复习旧的知识点以旧带新：时间10分钟：复习上一节的内容以及用上一节的内容带出本节新课的内容，让学生既巩固了旧的知识的同时也学习了新的知识。
（2）新知识的讲授以及例题的分析：时间10分钟：在带出新的知识的基础上对例题的讲解以及新知识的加深理解。
（3）巩固练习和强化：时间18分钟：通过对新知识的加深理解以及例题的讲授和理解后注重学生的应用以及自己动手做练习为主，使学生在练习中不断的体会和提高。
（4）课堂小测：时间7分钟：目标是检查学生一节课下来的学习效果，学生必须独立完成，不准讨论、偷看等，教师当堂收回当天批改完发回给学生进行改正。
（5）课后作业和预习：注重学生的基础知识为主，分三个不同档次的练习，以便满足不同层次的学生的需求，并且注重自学的预习，了解下一节的大概内容。
单元模块
课时模块1 课时模块2 课时模块3 …… 课时模块n 教学设计 教学课件 教学随笔
教学反思 配套练习 复习旧的知识点
以旧带新
通过旧的知识带出新的知识 新知识的讲授以及例题的分析 巩固练习和强化
课堂5分钟小测 课后作业与预习新课
教学建议 听
评课记录。
人教版数学七年级下册8.4 三元一次方程组的解法(教案与反思)
*8.4 三元一次方程组的解法灵师不挂怀,冒涉道转延。
——韩愈《送灵师》汪村学校 钱少华【知识与技能】1.理解三元一次方程组的定义；2.掌握三元一次方程组的解法；3.会解简单的三元一次方程组应用题.【过程与方法】先运用实际问题引入三元一次方程组的概念，再类比解二元一次方程组的思想方法，学习三元一次方程组的解法，最后学习三元一次方程组应用题.【情感态度】让学生学会“举一反三”的学习方法，体会数学的魅力.【教学重点】1.三元一次方程组的解法；2.三元一次方程组的应用.【教学难点】三元一次方程组的应用.一、情境导入，初步认识问题1 小明手头有12张面额分别为1元、2元、5元的纸币，共计22元，其中1元纸币的数量是2元纸币数量的4倍.求1元、2元、5元纸币各多少张.解：设1元、2元、5元的纸币分别为x 张、y 张、z 张，根据题意，得方程组__________________________________⎧⎪⎨⎪⎩，①，②_________________. ③请观察上面方程组的特点，归纳三元一次方程组的定义.问题2 上例中，③分别代入①②,得只含_____、_____的二元一次方程组______________.______________.⎧⎨⎩再消元，转化为____________方程.从而得到解三元一次方程组的思想方法是：问题3 解三元一次方程组3472395978.x z x y z x y z +=⎧⎪++=⎨⎪-+=⎩，①，②③解：方程①只含_____、______，因此，可由②③消去，得到一个只含x ，y的方程_____________，与①组成一个二元一次方程组______________.______________.⎧⎨⎩解这个方程组得__________.x y =⎧⎨=⎩，进而求得z=_____.因此，原方程组的解为__________,_____.x y z =⎧⎪=⎨⎪=⎩，【教学说明】以上三个问题以填空题形式出现，大大降低了学生自主学习的难度，所以鼓励学生先独立完成，再交流成果.二、思考探究，获取新知思考 1.什么叫三元一次方程组？2.解三元一次方程组的思想方法是什么？【归纳结论】1.三元一次方程组：含有三个不相同的未知数，每个方程中含有未知数的项的次数都是1，并且一共有三个方程，这样的方程组叫做三元一次方程组.2.解三元一次方程组的想方法：三、运用新知，深化理解1.解方程组：2.已知方程关于x、y的y=ax2+bx+c 的三个解为求出此方程（即求出a、b、c，再将a、b、c代入原方程即可）3.扬子江药业集团生产的某种药品包装盒的侧面展开图如图所示.如果长方体盒子的长比宽多4cm，求这种药品包装盒的体积.4.已知有理数x、y、z满足条件|x-z-2|+|3x-6y-7|+（3y+3z-4）2=0，求xyz的值.5.某区中学足球赛共赛8轮，胜一场得3分，平一场得1分，负一场得0分，在这次足球联赛中，猛足球队平的场数是所负场数的2倍，共得17分，试问该队胜了几场？6.若x+2y+3z=10，4x+3y+2z=15，则x+y+z=_______.（提示：可将z当成已知数，将已知变为210343152 .x y zx y z+=-⎧⎨+=-⎩，求出x，y，再求x+y+z .还有一种简便的方法，即把x+2y+3z=10和4x+3y+2z=15相加除以5便可得x+y+z=5.）【教学说明】让学生主完成.也可合作完成，在练习中加深理解.教师巡视指导，及时点拨.【答案】1.解：（1）34145217 223x y zx y zx y z++=⎧⎪++=⎨⎪+-=⎩，①，②；③由①+③，②+2×③消去z得5617 5923. x yx y+=⎧⎨+=⎩，解得12xy=⎧⎨=⎩代入①得z=3.即原方程组的解为12,3.x y z =⎧⎪=⎨⎪=⎩，2)原式可化为错误!未找到引用源。
人教版初中数学七年级数学下册《8.4阅读与思考一次方程组的古今表示及解法》
古
今
3 2 1 39 2 3 1 34 1 2 3 26
世界领先 发展进步 一脉相承
七、巩固知识 小组竞赛
随机抽组 每组先完成一个《九章算术》方程 一章中利用一次方程组解决实际问题的 原题，再试着完成另一个.比一比！
七、巩固知识 小组竞赛
【题1】7.方程:今有牛五、羊二，直金十两. 牛二、羊五直金八两.问牛羊各直金 几何？
第三站：一次方程组在古代数学中 的发展和繁荣时期
宋元时期，中国数学家创立了“天元 术”，用天元表示未知数进而建立方程，这 种方法的代表作是数学家李治写的《测圆海 镜》（1248）书中所说的“立天元一”相当 于现在的“设未知数x”.
第四站： 一次方程组的中西方融合时期
第四站：一次方程组的中西方融合时期
第一站： 中国古代数学的萌芽时期
第一站：中国古代数学的萌芽时期
1.原始公社末期，用文字符号取代结绳记事； 2.夏禹治水时使用了规、矩、准、绳等作图与测 量工具； 3.商代中期产生了十进制数字和计数法； 4.周代在八卦的基础上发展为六十四卦； 5.公元前一世纪的《周髀算经》举出勾三、股四、 弦五的例子； 6.西周贵族子弟从九岁要受礼、乐、射、驭、书、 数的“六艺”训练，“数”成为了专门的课程； 7.春秋战国时期，筹算已得到普遍的应用.
第二站：中国古代数学体系的形成时期 操作算筹 筹算方程
6.你能用这个方法操作算筹将第三个 方程中中等谷的系数筹算为0吗？试 一试吧！
第二站：中国古代数学体系的形成时期
古今两种一次方程组的表示及解 法，你选择哪一种？为什么？
第二站：中国古代数学体系的形成时期
外国人眼中的《九章算术》
第三站： 一次方程组在古代数学中的 发展和繁荣时期
最新人教版七下数学 8.4 三元一次方程组的解法
x+z-y=1
____________
z=3
____________.
2. 今年小新一家三口的岁数总和是80岁，爸爸比妈 妈大3岁，妈妈的岁数恰好是小新岁数的5倍.问：今 年爸爸、妈妈和小新分别几岁？
等量关系: (1) 爸爸年龄 + 妈妈年龄 + 小新年龄 = 80； (2) 爸爸年龄 = 妈妈年龄 + 3； (3) 妈妈年龄 = 小新年龄×5.
“加减”
“加减”
一元一次 方程组
3x+4z=7 ①
例1 解三元一次方程组 解：②×3+③，得11x+10z=35.④
2x+3y+z=9 ② 5x-9y+7z=8 ③
①与④组成方程组 还3x有+4其z=他7 解法解这吗个？方程组，得
11x+10z=35
把x=5，z=
-2代入②，得2×5+3y-2=9，所以
将 a，b，c 将 x、y 看作未知数 代入原式
a-b+c=0
①
4a+2b+c=3 ②
25a+5b+c=60 ③
a-b+c=0
①
解：根据题意，得三元一次方程组 4a+2b+c=3 ②
25a+5b+c=60 ③
②-①，得a+b=1，④ ③-①，得4a+b=10，⑤
a+b=1 ④ ④与⑤组成二元一次方程组
y
=
1 3
因此，这个三元一次方程组的解为
x=5
z= -2
x=5
y=1 3
z= -2
解：由①，得
x
最新人教版七年级数学下册第八章三元一次方程组的解法1
).
关闭
D
答案
8
快乐预习感知
核心知识概览
1
互动课堂理解
2 3 4
轻松尝试应用
5
������ + ������ = 1, 4.三元一次方程组 ������ + ������ = 5,的解是 ������ + ������ = 6
.
关闭
������ = 1, ������ = 0, ������ = 5
5
快乐预习感知
核心知识概览
1
互动课堂理解
2 3 4
轻松尝试应用
5
1.下列方程组中为三元一次方程组的是( ������ = 1, ������ + ������ = 2, A. ������ = 2, B. ������ + ������ = 1, ������-������ = 3 ������ + ������ = 3 4������-3������ = 7, ������������ + ������ = 3, C. 5������-2������ = 14, D. ������ + ������������ = 5, ������������ + ������ = 7 2������-������ = 4
4
快乐预习感知
核心知识概览
互动课堂理解
轻松尝试应用
解:设篮球有 x 个,排球有 y 个,足球有 z 个, ������ = 2������-3, ① 根据题意得 ② 2������ = 3������, ������ + ������ + ������ = 41. ③ 把①代入③,得 3y+z=44,④ 由④得 z=44-3y,⑤ 把⑤代入②,得 y=12.把 y=12 分别代入①,⑤,得 x=21,z=8. ������ = 21, 所以这个方程组的解为 ������ = 12, ������ = 8. 答:篮球有 21 个,排球有 12 个,足球有 8 个.
人教版七年级数学下册8.4 三元一次方程组的解法1
*8.4 三元一次方程组的解法【学习目标】1、知道解三元一次方程组的基本思想方法是消元，即化“三元”为“二元”。
2、会用加减法和代入法解简单的三元一次方程组。
【学习重点与难点】1.学习重点：掌握三元一次方程组的解法。
2.学习难点：三元一次方程组如何化归到二元一次方程组。
【学习过程】一、自主学习（一）预习自我检测（阅读课本，完成下列各题）1、温故而知新：解下列方程组：⎩⎨⎧+=-=-536553)1(x y y x （2）2、阅读课本：了解三元一次方程组的概念。
3、在下列方程中，是三元一次方程的在括号内打“√”，否则打“×”。
（1）2x+3y=12－z ( ) (2) xy －z=14 （ ）（3）13361-=+-z y x ( ) (4)4243+=-z y x ( )4、在等式中c bx ax y ++=2中，当x=-1，y=0时; 当x=2，y=3时; 当x=5，y=60时;求a 、b 、c 的值二、合作探究1、三元一次方程组的解法：二元一次方程组解法思路是先用加减法或代入法消去一个未知数，化____元为_____元，那么，三元一次方程组的解法是否类似地将“三元”化为“二元”呢？⎩⎨⎧=--=-+07650132y x y x解方程组⎪⎩⎪⎨⎧=+-=-=++③②①182126z y x y x z y x解法一：（消x ）由②得 x=___________ ④ 把④代入①，得：___________________ 用④代入③消去x 得：__________________整理得 解以上二元一次方程组得:把 代入④得x=解法二:(观察②缺z,考虑消z)⎪⎩⎪⎨⎧=+-=-=++③②①182126z y x y x z y x ③－①得：__________ ④ 解方程组⎩⎨⎧④②_____________________________得x= ________y= __________ 把x= ______y= ________ 代入 ①, 得z= ⎪⎩⎪⎨⎧===∴z y x解法三：（先消去y 行吗？） ①+②，得：_____________④ ③－②，得：_____________⑤解方程组⎩⎨⎧⑤④____________________________ 得x=_______z= ______ 把x 的值代入 ②得y=_________⎪⎩⎪⎨⎧===∴z y x由上可知，三元一次方程组的思路也是先消元，但方法灵活，应选择简便方法。
七年级数学下册 8.4 三元一次方程组的解法1 新人教版
;
⑶若先消去 z，可得含 x、y 的方程组是
练习
1．下列方程组中是三元一次方程组的是（ ）
x 2 y 3,
A. x2y4,
2x y7
x 2 y 5,
B. 3x z7,
2y3z 6
x y2,
C. yz1,
z t 3
x2 y z5,
D. x y6,
y xy 7
2．解下列三元一次方程组：
x 2 y 9, ⑴ y x 3,
2z x 47;
x y 7, ⑵ y z 8,
z x 1 3;
x: y 3:2, ⑶ y :z 5:4,
x y z 66.
问题9：解含有一个二元一次方程的三元 一次方程组时应该怎样选择方法？
消元时，大多数用加减消元法比代入法简单.
通过本节课的学习，你有什么新的收获？ 还有什么疑惑？
含有三个方程； 含有三个不同的未知数； 含未知数的项的次数都是1.
问题4：你能类比二元一次方程组给三元 一次方程组下一个定义吗？
问题5：怎样解这个方程组？ 你能否类比解二元一次方程组的思路 和方法解决三元一次方程组呢？
问题6：比较代入消元法与加减消元 法
哪种方法比较简单？
问题7：归纳解三元一次方程组的 基本思路是什么？
问题1：二元一次方程组是怎样定义的？ 解二元一次方程组的基本思路是什么？ 基本方法有哪些？
问题2：小明手头有12张面额分别1元、2元、 5元的纸币，共计22元，其中1元纸币的数量是2 元纸币数量的4倍．求1元、2元、5元纸币各多 少张.
思考：上面的问题中，你可以设几个 未知数，怎样列出方程组？
问题3：请你观察这个方程组， 它有什么特征？
典例分析
人教版七年级数学下册课件：8.4三元一次方程组的解法(共12张PPT)
3.某牧场用卖2头牛、5只羊的钱买13头猪,还剩下1 000元; 用卖3头牛、3头猪的钱买9只羊,钱正好花完;用卖6只羊、8头猪 的钱买5头牛,还差600元.求牛、羊、猪的价钱各是多少.
解:设每头牛的价格是 x 元,每只羊的价格是 y 元,每 头猪的价格是 z 元,根据题意得 ������������ + ������������-������������������ = ������ ������������������, ������������ + ������������-������������ = ������, ������������ + ������������-������������ = -������������������. ������ = ������ ������������������ 解得 ������ = ������������������, ������ = ������������������. 答:每头牛的价格是 1 200 元,每只羊的价格是 500 元,每头猪的价格是 300 元.
������������ + ������������-������ = ������, 1.解方程组 ������������-������������ + ������ = ������������,时,宜先消去 z ,得 ������ + ������ + ������ = ������������
解法 1:由②+③,得 x+y=3. ④ ������������-������������ = ������, ①与④组成方程组,得 ������ + ������ = ������. 解这个方程组,得 ������ = ������, ������ = ������.
人教版七年级数学下册8.4三元一次方程组的解法 (1)ppt精品课件
把x＝ 1, 0y＝ 代入 得：
解得：z＝___ 7 ∴三元一次方程组的解为：
_x _－_y＝_1_________ _x－_2_y_＝_－_8 _______
解这个方程组得：
x _1_0___
y
_9____
x __1_0__
y
__9___
举一反三
明确概念： 含有三个未知数，并且含有未知数的项的次数都
1次的整式方程，叫做三元一次方程. 含有三个未知数，并且每个方程中含未知数的项
次数都是1次，这样的方程组叫三元一次方程组.
举一反三
探究:解方程组：
x y z 12 (1)
x
2
y
5z
22
(2)
x 4 y
(3)
解：把(3)分别代入(1)、(2)得： 4y+y+z=12 (4) 4y+2y+5z=22(5)
把y=____2代入（3）， 得x=____8
把方程(4)、(5)组成方程组
_5_y+_z=_12_________
_6_y+_5z_=2_2 ________
解这个方程组，得
y _2____ z __2___
得：
解得：c＝____ 3
∴三元一次方程组的解为：
a ___13 __
b
___2__
c
1
___3__
举一反三
老师今天来的时候给大家带了漫画、作文、英语读物三种 26本，漫画书比作文书多1本，漫画书的两倍与英语读物的 作文书多18本，问老师每种书各带了多少本?
新人教版初中七年级数学下册《8.4三元一次方程组的解法 阅读与思考 一次方程组的古今表示及解法》课件
重点、难点知识★▲
练习：如图，点C在线段AB上，AC=6 cm，MB=10 cm，点M、N分别
为AC、BC的中点．
（1）求线段BC、MN的长；
（2）若C在线段AB的延长线上，且满足AC-BC=a cm ，M、N分别是
线段AC、BC的中点，请画出图形，并用a的式子表示MN的长度．
解：（2）如图：
∵M是AC的中点，∴ CM 1 AC
A.3 cm或13 cm B.3 cm C.13 cm
D.18 cm
解：∵在直线AB上画线段BC，∴CB的长度有两种可能： ①当C在AB之间，此时AC=AB﹣BC=8-5=3 cm； ②当C在线段AB的延长线上，此时AC=AB+BC=8+5=13 cm．故选A．
【思路点拨】由于在直线AB上画线段BC，那么CB的长度有两种可能： ①当C在AB之间，此时AC=AB﹣BC；②当C在线段AB的延长线上，此 时AC=AB+BC． 然后代入已知数据即可求出线段AC的长度．
点C在直线AB上”. （1）题的结果会变化吗？如果不会，请说明 理由；如果会，请求出结果．
解： （2）分两种情况：
当点C在线段AB上，由（1）得MN=5 cm，
当C在线段AB的延长线上时， ∵AC=6 cm，且M是AC的中点 同理：CN=2 cm，
∴ MC 1 AC 1 6 3cm
2
探究二：探索线段大小的比较方法
活动1 你能比较两名同学的身高吗？
重点知识★
现在我们抽3名同学到讲台上来，一名同学为示范，比较另两人的身 高，观察思考，从中寻找比较线段大小的方法.
从刚才同学们比较身高的方法中，你能想到比较线段的方法吗？ 叠合法
叠合法的注意事项有哪些？ 总结：（1）一个端点对齐；（2）另一个端点落在同一侧；
七年级数学下册8.4三元一次方程组的解法阅读与思考一次方程组的古今表示及解法分享
七年级数学下册8.4三元一次方程组的解法阅读与思考一次方程组的古今表示及解法分享1、如图，绕点逆时针旋转到的位置，已知，则等于答案D 解析2、解方程的结果是（）A．B．C．D 答案D 解析3、据《北京日报》报道，去年北京批准约209亿元公积金贷款投入保障房建设，数字209用科学记数法可表示为A．B．C．答案B 解析4、已知，化简二次根式的正确结果是答案A 解析5、如图，已知正方形ABCD的边长为4 ，E是BC边上的一个动点，AE⊥EF， EF交DC于F, 设BE=，FC=，答案A 解析6、下列图案中是轴对称图形的是（）答案D 解析7、经过直线外一点，有几条直线和已知直线平行n 答案B 解析8、、若，则二次函数的图象的顶点在答案D 解析9、计算【小题1】【小题2】化简：（1－）÷答案解析10、二次函数的图象如图所示，则一次函数的图象不经过()A．第一象限B．第二象限C．第三象限D．第四象限答案D 解析11、矩形纸片ABCD的边长AB=4，AD=2．将矩形纸片沿EF折叠，使点A与点C重合，折叠后在其一面着色(如图)，则答案B 解析12、如图，正方形的边长为2，反比例函数图像过点，则k的值是A．B．C．D．答案D解析13、下列运算正确的是（）A．B．C．D．答案B 解析14、下列图案是轴对称图形的有（m 答案B 解析15、-3的倒数为（）A．B．C．D．答案D 解析16、已知抛物线C：，将抛物线C平移得到抛物线C，若两条抛物线C、C关于直线x=1对称，则下列平移方法中，正确的是（答案C 解析17、．在这四个数中，最小的数是（;）A．B．C．D．答案A 解析18、（2013?盐城）如图①是3×3正方形方格，将其中两个方格涂黑，并且使涂黑后的整个图案是轴对称图形，约定绕正方形答案C 解析试题分析：根据轴对称的定义，及题意要求画出所有图案后即可得出答案．解：得到的不同图案有：，共6种．故选C．点评：本题考查了学生实际操作能力，用到了图形的旋转及轴对称的知识，需要灵活掌握．19、化简的结果是（;）．A．B．C．D．答案B 解析20、下列说法错误的是答案C 解析21、把分式方程，的两边同时乘以x-2，约去分母，得（; 答案D 解析22、已知方程的两个解分别为、，则的值为（）A．-7B．-3C．7D．3 答案D 解析23、下列图形是中心对称图形的是答案D 解析24、（2014?海拉尔区模拟）用长8米的铝材制成一个矩形窗框，使它的面积为5平方米．若设它的一边长为x米，根据题意列答案C 解析试题分析：一边长为x米，则另外一边长为：4﹣x，根据它的面积为5平方米，即可列出方程式．解：一边长为x米，则另外一边长为：4﹣x，由题意得：x（4﹣x）=5，故选：C．点评：本题考查了由实际问题抽相出一元二次方程，难度适中，解答本题的关键读懂题意列出方程式．25、如图是一个圆锥的主视图，则这个圆锥的全面积是shyshy;A．B．C．D．答案D 解析26、表示一次函数y＝mx+n与正比例函数y＝mnx(m、n是常数且mn≠0)图象是（n 答案A解析27、有一种记分方法：以80分为基准，85分记为＋5分，某同学得77分，则应记为（）A．＋3分B．－3分C．＋7分答案B 解析考点：正数和负数．分析：首先审清题意，明确“正”和“负”所表示的意义；再根据题意作答．解答：解：∵以80分为基准，85分记为+5分，∴得77分记为-3分．故选B．点评：此题主要考查了正负数的意义，解题关键是理解“正”和“负”的相对性，明确什么是一对具有相反意义的量．在一对具有相反意义的量中，先规定其中一个为正，则另一个就用负表示．28、如图，把Rt△ABC放在直角坐标系内，其中∠CAB=90°，BC=5，点A、B的坐标分别为（1，0）、（4，0）答案C 解析29、下列图案中是轴对称图形的有（答案A 解析30、如图是正方体的展开图，则正方体相对两个面上的数字之和的最小值是 ( ). 答案B解析31、一队师生共328人，乘车外出旅行，已有校车可乘64人，如果租用客车，每辆可乘44人，那么还要租用多少辆客车？在这答案C 解析32、一个平行四边形绕着对角线的交点旋转90°能够与本身重合，则该平行四边形为（;答案C 解析考点：旋转的性质；正方形的判定．分析：根据题意，该四边形的对角线互相垂直平分且相等．解答：解：因为平行四边形对角线互相平分，绕着它的对角线的交点旋转90°，能够与它本身重合，说明对角线互相垂直平分且相等，所以该四边形是正方形．故选C．点评：此题考查了平行四边形的性质及与特殊四边形的关系，属基础题．解题时要根据旋转的性质解答．33、（2011?舟山）如图，点A、B、C、D、O都在方格纸的格点上，若△COD是由△AOB绕点O按逆时针方向旋转而得答案C 解析. （2011湖北宜昌，17，7分）解方程组答案解：①+②，得3x＝3，∴x＝1．将x＝1代入①，得1－y＝1，∴y＝0．∴原方程组的解是x=1,y=0.（7分）解析既是轴对称，又是中心对称图形的是;（答案A 解析34、。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
上等谷2束，中等谷3束，下等谷1束，可得粮食34斗;
上等谷1束，中等谷2束，下等谷3束，可得粮食26斗。
求上、中、下三等谷每束各可得粮食几斗?
同学们，你们能否用所学的知识来解决这个个问题?
师：我们通过什么方法解三元一次方程组的?
教师通过ppt展示消元解题的过程。
情感态度和价值观目标：
培养学生，在遇到知识难点时，自己寻求书籍或网络，解决问题的水平。提升学生的自学水平。了解中国古人在解一次方程组的方法早于世界其他国家，对世界自然科学做出的巨大贡献。激发学生的民族自豪感。
学情分析
因为学校所在区内的大量优质生源被民办学校招收。近几年招收的学生文化素质明显下滑。所教学生的文化素质处在区域中等。
教学重点
1、了解算筹所表示的意思
2、了解算筹作为计算工具，解一次方程组的过程
3、现代数学中的矩阵与算筹图的联系
教学难点
如何理解使用算筹解一次方程组的解题过程。
教学工具
ppt
教学内容分析
学生通过阅读本节内容，了解我国古代对一次方程组的解法。古代的解法与本章内容所学的一次方程组的知识有何异同?让同学们对我国古代数学史有一定的了解。算筹作为古代的计算工具，了解它所表示的意思以及算筹解一次方程组的过程。算筹解一次方程组的过程与现代高等代数的矩阵解法是一致的。这个成就要比西方早1000多年，这是我国古代数学的一个光辉成就。
从算筹的演变图中我们能够找到课本中算筹图，和汉代的图是一致的。
在算筹计数法中，以纵横两种排列方式来表示单位数目的，表示多位数时，个位用纵式，十位用横式，百位用纵式，千位用横式，以此类推，遇零则置空。
从这个图，同学们现在明白算筹图第一行第四个图为什么是表示39。
通过ppt演示，使用算筹作为计算工具解一次方程组的过程
这种由数排成的表叫做矩阵。容易看出，这个矩阵与上面的算筹图是一致的，利用矩阵解一次方程组的方法，与前面说的算筹方法也是一致的。我们祖先掌握上述解法，比起欧洲人来，要早1000多年。这是我国古代数学的一个光辉成就。
小结
1，我们了解算筹的表示方法以及如何用算筹作为计算工具解一次方程组。
2，体会古代解一次方程组与本章8.4三元一次方程组解法的不同。
教学设计
章节名称
第八章阅读与标
知识和技能目标：
了解中国古代在解一次方程组的方法，了解算筹表示的意思，理解算筹作为计算工具用于解一次方程组的过程。让学生了解古代中国在解一次方程组的方法对全世界的贡献。
过程和方法目标：
引导学生在课外有目的的学习，在遇到知识难点时，自己或与同学寻求书籍或网络解决问题。尽可能的理解相关的课本阅读内容。从而提升学生的自学水平。在课堂上与老师共同完成导学题，了解和掌握相关知识。
3。矩阵与算筹图的解法是一致的，比起欧洲人来，要早1000多年。这是我国古代数学的一个光辉成就。
学生设每束上等谷、中等谷、中等谷，各可得粮食x斗、y斗、z斗。列三元一次方程组
学生：消元法
将三元一次方程组通过消元得到二元一次方程组，再经过消元得到一元一次方程
学生：32139
23 1 34
1 2 3 26
原文：今有上禾三秉,中禾二秉，
下禾一秉,实三十九斗;
上禾二秉,中禾三秉,下禾一秉,实三十四斗;
上禾一秉,中禾二秉,下禾三秉,实二十六斗。
问上、中、下禾实一秉各几何?
师：这个问题摘自《九章算术》卷第八“方程”第一个问题。《九章算术》是汉代丞相张苍等辑撰。总结了战国、秦、汉时期的数学成就。用现代白话文翻译如下：
预习《阅读与思考：一次方程组的古今表示及解法》并通过网络或书籍，如《九章算术》了解相关内容。思考算筹图所表示的意思，及算筹作为计算工具解一次方程组的过程。
在这个过程中，与同学相互探讨问题，查找资料。
培养学生的阅读，和思考的水平。
引入新课
通过ppt展示《九章算术》卷第八方程第一个问题的原文。
摘自《九章算术》卷第八方程
学生跟着老师的引导共同解一次方程组
学生：算筹图，它相较于我们所列出的方程组，省略了各未知数，只用算筹表示出未知数的系数和常数项。它与减法消元的过程是一样的。
学生回顾所学的内容。
。
让学生用所学的知识解这个个问题
培养学生探索和思考的水平。
使学生能充分的理解算筹图表示的意思，以及对算筹的演变历史有所了解。
以右行上禾“3”乘中行每一项
以中行减去右行对应项的2倍。使得中行上禾为零
以右行上禾“3”乘左行每一项
,再以左行减去右行对应项的1倍。使得左行上禾为零。
以中行中禾“5”乘左行每一项
以左行减去中行对应项的4倍。使得左行中禾为零
师：现在，同学们知道古代的解法与本章内容所学的一次方程组的知识有何异同吗?
用现代高等代数的符号能够将前面的方程组的系数排成一个表
让学生能够直观生动的体会，算筹解一次方程组的运算过程。
教学评价
本节课教学效果良好。内容结合我国古代数学史使数学知识生动有趣。通过本节课的学习，同学们了解中国古代在解一次方程组的方法，了解算筹表示的意思，理解算筹作为计算工具用于解一次方程组的过程。让学生了解古代中国在解一次方程组的方法对全世界的贡献。培养学生，在遇到知识难点时，自己寻求书籍或网络，解决问题的水平。提升学生的自学水平。了解中国古人在解一次方程组的方法早于世界其他国家，对世界自然科学做出的巨大贡献。激发学生的民族自豪感。
教学过程的设计
教学环节
教师活动
学生活动
设计意图
课前活动
同学们在第八章我们学习了二元一次方程组和三元一次方程组的解法和应用。在古代的人们生活中是否也会遇到一次方程组的问题?如果他们遇到这个类问题，又是如何解决的呢？带着这些问题，同学们在我们下节课上课前。先预习《阅读与思考：一次方程组的古今表示及解法》并通过网络或书籍，如《九章算术》了解相关内容。思考算筹图所表示的意思，及算筹作为计算工具解一次方程组的过程。
师：下面的算筹图代表了古代解决这个问题的方法，它是什么意思？
师：古人书写都是竖排，。《九章算术》的算筹图是竖排的为了看图方便上图改为横排，三个横行表示三句话的含义。
公元前13世纪，算筹就已经出现。开始是作为祭祀和占卜。到了汉代出现了用算筹做计算工具，它是世界上最早使用“十进制”的数码体系。到了宋代用“0”表示零，最终形成完整的积数法。接下来我们来看一下算筹的演变过程。