6 均匀设计
均匀设计法

第六章 均匀设计法
▪例如用U11(1110)的1,7 和1,2列分别画图,得到下面的图 (a)和图 (b)。我们看到,(a)的点散布比较均匀,而(b)的点散 布并不均匀。均匀设计表的这一性质和正交表有很大的不同, 因此,每个均匀设计表必须有一个附加的使用表。
11 10
9 8 7 6 5 4 3 2 1
第六章 均匀设计法
▪1978年,七机部由于导弹设计的要求,提出了一个 五因素的试验,希望每个因素的水平数要多于10, 而试验总数又不超过50,显然优选法和正交设计都 不能用,方开泰与王元经过几个月的共同研究,提 出了一个新的试验设计,即所谓“均匀设计”,将 这一方法用于导弹设计,取得了成效。
▪均匀设计法与正交设计法的不同:
两种设计的均匀性比较
很难找到正交设计和均匀设计具有相同的试验数和相同的水平数。我们从 如下三个角度来比较:
v 1.试验数相同时的偏差的比较
v 当因素s=2时,若用L8(27)安排试验,其偏差为0.4375;
若用均匀设计表
U
* 8
(88
)
,则偏差最好时要达0.1445。
显然试验数相同时均匀设计的均匀性要好得多。值得
U6(64)的使用表
s列
号
213
312 3
412 3 4
偏差值越小,表示均匀度越好
D
0.1875 0.2656 0.2990
第六章 均匀设计法
均匀设计和正交设计的比较
将目前最常用正交设计和均匀设计作一下比较,讨论两种试验设计方法的特 点。
➢1.试验次数的比较 ➢正交设计用于水平数不高的试验,因为它的试验数至少为 水平数的平方。例如一项试验,有五个因素,每个因素取31 水平,若用正交设计,至少需要做961次试验,而用均匀设 计只需31次,所以均匀设计适合于多因素多水平试验。
均匀设计
•均匀设计方法•一、均匀试验设计•均匀设计是在正交试验设计的基础上,创造出的一种新适用于多因素、多水平试验的试验设计方法。
•均匀设计特别适合需要考察因素因素变化范围较大,且每个因素有较多水平的试验设计问题。
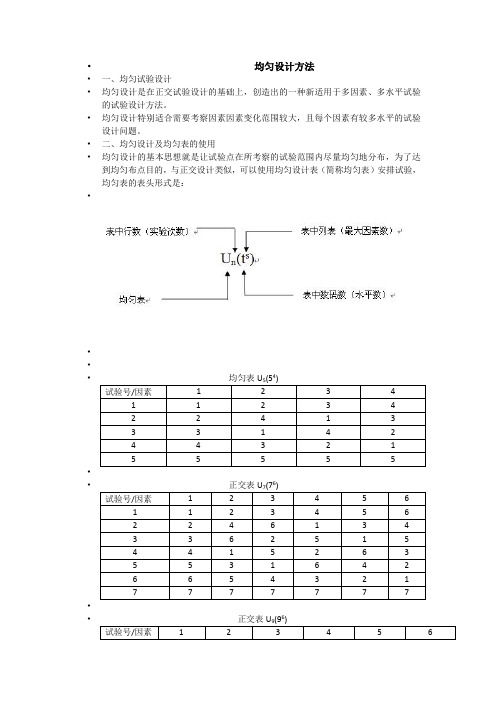
•二、均匀设计及均匀表的使用•均匀设计的基本思想就是让试验点在所考察的试验范围内尽量均匀地分布,为了达到均匀布点目的,与正交设计类似,可以使用均匀设计表(简称均匀表)安排试验,均匀表的表头形式是:••••4••正交表U6••正交表U6•••三、均匀表的特点• 1.任何一列,各水平仅出现一次;• 2.任何两列同行数码构成的有序数对仅出现一次;• 3.均匀表中任两列组成的试验方案不等价; 因此,每个均匀表都附加了使用表,告诉我们如何挑选相应的列按排试验。
• 4.当因素的水平数增加时,试验次数按水平数增加;• 5.使用表最多可安排的因素数都比均匀表列数少。
只能安排(s/2+1)个因素•四、用均匀表安排试验的步骤• 1.根据试验的目的,确定考察的指标;• 2.选择合适的因素和因素的考察范围;• 3.选择合适该项试验的均匀表,然后根据该表的使用表从中选出列号,将因素分别安排到相应的列号上;• 4.确定各因素的水平,并将这些因素的水平按所在列的指示分别对号号入座。
最后进行试验。
• 5.对实验结果进行分析,确定最佳的试验方案。
•例1.在阿魏酸的合成工艺考察中,选取原料配比,吡啶量,反应时间三个因素进行考察,试验的考察指标是阿魏酸的收率。
因素的变化范围如下:•原料配比A:1.0~3.4•吡啶量B:10~28(ml)•反应时间C:0.5~3.5(hr)•试用均匀设计安排试验。
•解:对于三个因素,s/2+1=3,求出s=4或5,考虑试验的承受程度,选用U7(76)均匀表安排试验,根据各因素的变化范围,划分因素水平表如下:••由U7(76)均匀表的配套使用表可知,应选1,2,3列,因而得下面的试验设计表:••将各因素所对应的水平值填入表中,得试验表如下,按试验表中每个试验的条件安排试验,将所得结果填入表最右列。
均匀设计法的基本原理和应用范围

农业试验设计
总结词
在农业研究中,均匀设计法可用于优化种植密度、施肥量等农业措施,提高作物产量和 品质。
详细描述
在农业试验中,需要研究多种因素对作物生长的影响,如种植密度、施肥量、灌溉方式 等。通过均匀设计法,可以有效地安排试验条件,以最少的试验次数获得最佳的试验效
果。
产品制造工艺优化
总结词
在产品制造过程中,均匀设计法可用于优化工艺参数,提高产品质量和生产效率。
均匀设计法的基本原理和应用范围
目录
• 均匀设计法的基本概念 • 均匀设计法的基本原理 • 均匀设计法的应用范围 • 均匀设计法的优势与局限性 • 均匀设计法的实际应用案例
01 均匀设计法的基本概念
定义与特点
定义
均匀设计法是一种实验设计方法,旨在通 过合理地选择实验点和实验次数,最大限 度地获取所需的信息,并减少实验误差。
确定试验点数量
根据试验因素和水平,确定试 验点数量,以确保试验结果的 准确性和可靠性。
进行试验
按照生成的试验点进行试验, 收集数据。
确定试验因素和水平
根据研究目的和问题,确定试 验因素和水平,为后续的试验 设计提供基础。
生成试验点
根据均匀性准则和试验点分布 方法,生成试验点,确保每个 试验点具有代表性。
有限制条件
在满足一定限制条件下选择实验点。
均匀分散
在实验范围内,实验点均匀分散,避免集 中在某些区域。
高效性
通过合理设计,用较少的实验次数获取更 多信息。
与其他设计方法的比较
与正交设计法比较
均匀设计法的实验点分布更均匀,适 用于探索性实验和多因素多水平实验 。
与拉丁方设计法比较
拉丁方设计法适用于两因素实验,而 均匀设计法可应用于多因素实验。
第6讲 均匀设计

x1 2.2 L11 4.48
_
x2 19 L12 16.8
_
x3 2.0 L12 1.4 L33 7.0
_
y 0.3683 L1 y 0.2404 L2 y 0.5640 L3 y 0.5245
_
L22 252.0 L23 10.5
由于Lij L ji,故不必全部列出,将它们代入方程组中 可以解得 b1 0.037, b2 0.00343, b3 0.077 从而 a 0.3683 0.037 2.2 0.00343 19 0.077 2.0 0.201
将一个新变量引进回归模型,这时相应的F统计量必须大 于Fin 将一个变量从回归模型中剔除,这时相应的F统计量必须 小于Fout 将回归模型内的一个变量和回归模型外的一个变量交换位 置。
设先用后退法来选变量.所谓后退法,就是开始将 所有的变量全部采用,然后逐步剔除对方程没有 显著贡献的变量,直到方程中所有的变量都有显 著贡献为止。 仍考虑线性模型,开始三个因素全部进入方程, 得(6.12).统计软件包通常还会提供每个变量的t值, t值越大(按绝对值计)表示该因素越重要.对本 例有
第 6章
均匀设计
均匀设计(uniform design) : 一种只考虑试验点在试验范围内均匀散布的试验设 计方法 通过均匀表来安排试验 应用:试验因素变化范围较大,需要取较多水平时 例如:5因素31水平的试验: 正交设计试验次数≥312=961
均匀设计试验次数:31
6.1 均匀设计表
U7(76)使用表
因素数 2 3 4 5 6 1 1 1 1 1 3 2 2 2 2 3 3 3 3
均匀设计

7.1 均匀设计表
7.1.1 等水平均匀设计表
(1)记号: )记号: Un(rl)或 Un*(rl) 或 U——均匀表代号; 均匀表代号; 均匀表代号 n——均匀表横行数(需要做的试验次数); 均匀表横行数(需要做的试验次数); 均匀表横行数 r——因素水平数,与n相等; 因素水平数, 相等; 因素水平数 相等 l——均匀表纵列数; 均匀表纵列数; 均匀表纵列数 *——均匀性更好的表,优先选用Un*表 均匀性更好的表,优先选用 均匀性更好的表 表
试验号 1 2 3 4 5 6 7 8 9 10
A (1)1 (2)1 (3)2 (4)2 (5)3 (6)3 (7)4 (8)4 (9)5 (10)5
B (2)1 (4)2 (6)3 (8)4 (10)5 (1)1 (3)2 (5)3 (7)4 (9)5
C (5)1 (10)2 (4)1 (9)2 (3)1 (8)2 (2)1 (7)2 (1)1 (6)2
均匀设计( design) 均匀设计(uniform design) : 一种只考虑试验点在试验范围内均匀散布的 试验设计方法 通过均匀表来安排试验 应用:试验因素变化范围较大,需要取较多 应用:试验因素变化范围较大, 水平时 例如: 因素31水平的试验: 31水平的试验 例如:5因素31水平的试验: 正交设计试验次数≥ 正交设计试验次数≥312=961 均匀设计试验次数: 均匀设计试验次数:31
7.2 均匀Biblioteka 计基本步骤(1)明确试验目的,确定试验指标 )明确试验目的, (2)选因素 ) (3)确定因素的水平 ) 可以随机排列因素的水平序号 (4)选择均匀设计表 ) 根据试验的因素数和水平数来选择 参考使用表 首选U 表 首选 n*表
7.2
均匀设计基本步骤
均匀设计法

2
1.4(2) 19(4) 3.0(6) 0.336
3பைடு நூலகம்
1.8(3) 25(6) 1.0(2) 0.294
4
2.2(4) 10(1) 2.5(5) 0.476
5
2.6(5) 16(3) 0.5(1) 0.209
6
3.0(6) 22(5) 2.0(4) 0.451
7
3.4(7) 28(7) 3.5(7) 0.482
xik
_
xi
xik
_
xj
Liy
N K 1
xik
_
xi
yk
_
y
Lyy
N i1
yk
_
y
2
_
N
xi xi
i1
i 1, 2, m
i, j 1, 2, , m i 1, 2, , m
(8 2) (8 3) (8 4) (8 5)
_ 1 N
y N i1 yk 回归方程组系数由下列正规方程组决定:
^
2mT
方程(8 9)化为 y b0 bl xl (T Cm2 ) (8 11)
l 1
在这种情况下,为了求得二次项和交互作用项,就不能
选用试验次数等于因素数的均匀设计表,二必须选用试
验次数大于或等于回归方程系数总数的U表了
§9-2 应用举例
▪ 利用均匀设计表来安排试验的步骤:
• (1)根据试验的目的,选择合适的因素和相应的水平。 • (2)选择适合该试验的均匀设计表,然后根据该表的使
§6-1 基本原理
• 一、引言
• 正交试验设计利用:
▪ 均衡分散:试验点在试验范围内排列规律整齐
▪ 整齐可比:试验点在试验范围内散布均匀
均匀设计的基本步骤

均匀设计的基本步骤
均匀设计是一种实验设计方法,用于在有限次试验中寻找最佳的试验条件。
以下是均匀设计的基本步骤:
1.确定实验目的和响应变量:首先需要明确实验的目的,确定要研究的响应变量,以便于确定实验的主要内容和目标。
2.确定实验因素和水平:根据专业知识和实际经验,选择对响应变量影响较大的因素作为实验因素。
根据实际情况和历史数据,为每个实验因素选择适当的水平。
3.制定均匀设计表:根据实验因素和水平的数量,选择合适的均匀设计表进行实验。
均匀设计表是一种特殊的矩阵,用于安排实验并确保各因素水平在实验中均匀分布。
4.安排实验:根据均匀设计表,安排实验的具体实施方案。
确保每个实验条件只被试验一次或多次,以确保结果的准确性。
5.收集数据:按照实验方案进行实验,并记录各实验条件下的响应变量值。
6.分析数据:对收集到的数据进行分析,探索各因素与响应变量之间的关系。
可以采用回归分析、方差分析等方法进行数据分析。
7.优化条件:根据数据分析结果,选择最优的实验条件进行进一步优化。
这可能涉及对实验方案进行调整或重复试验。
8.验证和确认:对优化后的条件进行验证和确认,以证明其在实践中具有可行性和有效性。
9.总结和报告:整理实验过程和结果,编写详细的实验报告,总
结实验的经验和教训,并提出改进意见和建议。
以上步骤是一个典型的均匀设计过程的基本流程。
具体的实施过程中,可以根据实际需求和条件进行调整和优化。
单因素6水平均匀设计

单因素6水平均匀设计
单因素6水平均匀设计是一种实验设计方法,用于研究一个因素对结果变量的影响。
在该设计中,将一个因素分为6个水平,每个水平都有相同数量的观测值。
以下是单因素6水平均匀设计的步骤:
确定因素和水平:首先确定要研究的因素,并将其分为6个水平。
确保每个水平的差异程度相对均匀,并且能够涵盖因素的全部范围。
确定观测值数量:确定每个水平的观测值数量,这些观测值数量应该相等。
通常情况下,观测值的数量越多,实验结果的可靠性越高。
随机化实验次序:为了消除实验中其他可能的干扰因素,需要随机化实验次序。
这样可以减小实验结果的偏差,并增加实验结果的可靠性。
进行实验并记录数据:按照随机化的实验次序,进行实验并记录结果变量的数据。
确保在每个水平上的观测值都得到准确记录。
数据分析:
对实验结果进行数据分析,可以使用统计方法,如方差分析。
通过分析结果,可以确定因素对结果变量的影响是否显著。
结果解释和推论:
根据数据分析的结果,解释因素对结果变量的影响,并进行推论。
根据推论,可以对因素的不同水平进行比较,并得出结论。
单因素6水平均匀设计的优点是简单易行,容易分析和解释结果。
然而,它也
有一些限制,如无法分析因素与其他因素的交互作用。
因此,在实际应用中,需要根据具体的研究目的和需求来选择合适的实验设计方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(4) 用试验的指标值和取得该指标值的 各因素水平值,建立试验指标与各因素 水平关系的回归模型;
(5) 利用回归模型寻找最佳的各因素水 平组合,并进行该组合的验证试验; (6) 从步骤2开始重复进行各因素水平 范围缩小试验,进一步寻找最优试验条 件组合。
均匀设计表任两列组成的试验方案一般并不 等价。
如用U6(64)的1,3 和1,4列分别画图,得到下面 的图(a)和图(b)。可以看到(a)的点散布比较均匀, 而(b)的点散布并不均匀。 均匀设计表的这一性质和正交表有很大的不同. 因此,每个均匀设计表必须有一个附加的使用表, 根据U6(64)的使用表,2因素的试验应排1,3 列。
1.2 均匀设计的特点
1)均匀设计具有试验设计方法的共性及本质
内容,从少量试验结果中获取带规律性的结 果,也可进行回归分析。
2)试验点具有充分均衡分散的特点 正交设计是根据正交性来挑选代表点的, 为了估计各因素的主效应和部分交互效应, 试验点的数目较多。
如用正交表安排每因素为q个水平数的多因素 试验,试验的次数为rq2,r为自然数。
15
2.3 混合型水平的均匀设计
• 试验中各因素的水平数不同,
• 比如,其水平数分别为q1,…,qk。这时 应使用混合型的均匀设计表。
“方开泰,均匀设计与均匀设计表,科学出版(1994).”
16
混合水平表的代号,含义为:
均匀设计
定量因素 的最大数
Un(q ×
1
… × q )
k
试验次数
各定量因素 之水平数
U11(116)的使用表
6
S 列 号 D
2
2 4 6 8 10 1 3 5 7 9 11
3
3 6 9 1 4 7 10 2 5 8 11
4
5 10 4 9 3 8 2 7 1 6 11
5
7 3 10 6 2 9 5 1 8 4 11
10 9 8 7 6 5 4 3 2 1 11
2
3 4 5 6
1
1 1 1 1
用方程的离回归标准误判断模型的好坏,另外, 还要根据专业知识判断。
以上是对均匀设计原理和应用方法等 的简单介绍,只要按着这样的一条线索记 忆就可以了:表的含义→安排试验→回归 建模→参数寻优→继续试验→最优条件。 利用均匀设计方法进行回归模型建立 及其参数寻优还需要专门的计算机软件支 持,有关的内容不作介绍了。
下表是一个混合水平均匀设计表:
17
它的试验数 n为 12。
可以安排水 平数为6、 4、3的因 素各一个。
U12(624)
它的试验数 n为 12。 可以安排一 个6水平因素 和二个4水平 因素的设计。
18
3 均匀设计的基本步骤
均匀设计一般分以下6个步骤:
(1) 确定试验指标、因素、水平数和水平范围;
U6(64)
试验号 1 2 3 4 5 6
列号 1 1 2 3 4 5 6 2 2 4 6 1 3 5 3 3 6 2 5 1 4 4 6 5 4 3 2 1
每个均匀设计表都附有一个使用表,指 示我们如何从设计表中选用适当的列。 下表是U6(64)的使用表。它告诉我们, 若有两个因素,应选用1,3两列来安 排试验。
2 均匀设计表
2.1 均匀设计表和使用表各部分的含义 2.2 等水平均匀设计表 2.3 混合水平均匀设计表
2.1 均匀设计表及各部分含义
均匀设计是通过均匀设计表来进行设计的。其表的含义:
均匀设计
因素的最大数(列数)
Un
试验次数
s) (q
水平数
7
如U6(64)表示要做6次试验,每个因素有6个 水平,该表有4列。
4.2 模型好坏的判断标准问题
F检验给出的显著性与否是判断回归模型是否有 效的重要依据,如在复相关系数或相关系数上,R2 数 值越大越好, 但模型的好坏,在数理统计中还有误差自由度 和离回归标准误进行判断。 模型一般应保持误差自由度≥5,前面有 “试 验次数选为因素数的3倍左右为宜” 观点就在于此。
5
4 3 2 2 5 4 3 3 5 4 4 5 5 6
0.16942
2.2 等水平均匀设计表
均匀设计有其独特的试验布点方式:
每个因素的每个水平做一次且仅做一次试验 任两个因素的试验点在平面的格子点上,每 行每列有且仅有一个试验点
以上两个性质反映了均匀设计试验安排的“均 衡性”,即对各因素的每个水平一视同仁。
s
U9*(94)的使用表
列 号 D
2
3
1
2
2
3 4
0.1574
0.1980
• 有时出现加“*”与不加 “*”的同类型均匀设计表, 通常优先使用加“*”的均 匀设计表。
均匀设计表U11(116)和它的使用表
均匀设计表 U11(116)
1
1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9 10 10 11 11
第六章 均匀设计
Uniform Design
1 均匀设计的概念与特点 2 均匀设计表 3 均匀设计的基本步骤
4 均匀设计应注意的问题
1 均匀设计的概念和特点
1.1 均匀设计的概念
均匀设计是由中国数学家方开泰教授和王元教授 在1978年共同提出,是数论方法中的“维蒙特卡罗 方法”的一个应用,已得到国际上广泛承认。 只考虑试验点在试验范围内均匀分布的一种试验 设计方法。 它适用于多因素、多水平的试验设计,是部分实 施的试验设计。 试验次数等于因素的水平数,比正交设计更能减少 试验次数。
3)只考虑试验点在试验范围内充分 “均匀分布”,而不考虑“均衡可比” 或“正交性”。
其试验点的均匀性比正交设计的均匀 性更好,更具有代表性。 由于该法不再考虑 “均衡可比”而设 置处理,因而大大减少了试验次数。 这是它与正交试验设计法的最大不同
4)每个因素的各个水平仅做一次试验。
当水平数增加时,试验数随水平数增加而 增加。若采用正交设计,试验数则随水平数的 平方数而增加。 如5因素31水平的试验,用正交设计需做 961次,采用均匀设计只需做31次试验。 均匀设计也可采用线性回归或多项式回归 分析。根据因素偏回归平方和的大小确定该因 素对回归的重要性。
• 思考题:
• 正交设计和均匀设计各有什么特点?正 交试验设计的基本步骤有哪些?
• 有一组实验数据,用最小二乘法原理可 配置成一元线性回归方程和一元指数回 归方程,如何判断哪个方程更拟合实验 数据?
4 需要注意的问题
• • • • • 试验次数问题 设计表的选择 回归模型建立 回归模型优化 试验参数优化
4.1 试验次数问题
均匀设计的最大特点是试验次数等于 因素的最大水平数 试验次数与被考察的因素的个数有关, 建议试验次数选为因素数的3倍左右为 宜, 这样选择的均匀设计表的均匀性好, 也有利于以后的建模和优化。
最后1列D 表示刻划均匀度的偏差 (discrepancy),偏差值越小,表示均 匀度越好。
U6(64)的使用表
因素数 2 3 4 1 1 1 列 3 2 2 号 3 3 D 0.1875 0.2656 0.2990
4
均匀设计表U9*(94)和它的使用表
均匀设计表U9*(94)
1 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 2 3 4 9 2 5 8 1 4 7 3 7 6 1 8 5 2 9 6 3 4 9 8 7 6 5 4 3 2 1
