按应力求解平面问题
合集下载
平面应力问题
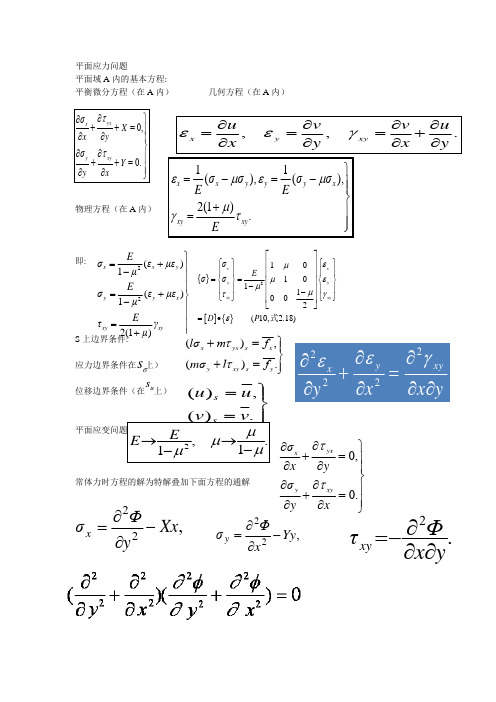
平面应力问题平面域A 内的基本方程:平衡微分方程（在A 内） 几何方程（在A 内）物理方程（在A 内）即: S 上边界条件:应力边界条件在 上）位移边界条件（在 上） 平面应变问题常体力时方程的解为特解叠加下面方程的通解0,0.yx x y xyσX x y σY y x ∂⎫∂++=⎪∂∂⎪⎬∂∂⎪++=⎪∂∂⎭ττ, , .x y xy u v v ux y x yεεγ∂∂∂∂===+∂∂∂∂11(),(),2(1).x x y y y x xy xy σσσσE E Eεμεμμγτ⎫=-=-⎪⎪⎬+⎪=⎪⎭22()1()(a)12(1)x x y y y x xy xyE σεμεμE σεμεμE τγμ⎫=+⎪-⎪⎪=+⎬-⎪⎪=⎪+⎭{}[]{}2101011002(10, 2.18)x x y y xy xy σE σσD P ⎡⎤⎧⎫⎧⎫⎢⎥⎪⎪⎪⎪⎢⎥==⎨⎬⎨⎬⎢⎥-⎪⎪⎪⎪⎢⎥-⎩⎭⎩⎭⎢⎥⎣⎦=•εμμεμμτγε式(),().x yx s x y xy s y l σm f m σl f ττ⎫+=⎪⎬+=⎪⎭σs(),().s s u u v v ⎫=⎪⎬=⎪⎭us 2222y xy x y x x yεγε∂∂∂+=∂∂∂∂.1 ,12μμμμ-→-→E E 0,0.yx x y xyσx y σy x ∂⎫∂+=⎪∂∂⎪⎬∂∂⎪+=⎪∂∂⎭ττ22,y ΦσYy x∂=-∂.2yx Φτxy ∂∂∂-=22,x ΦσXx y∂=-∂二、基本假设 1、连续性假定假定物体是连续的。
因此，各物理量可用连续函数表示。
2、完全弹性假定a.完全弹性—外力取消，变形恢复，无残余变形。
b.线性弹性—应力与应变成正比。
即应力与应变关系可用胡克定律表示（物理线性）。
3、均匀性假定假定物体由同种材料组成,因此， E 、 μ等与位置 无关。
4、各向同性假定假定物体各向同性。
E 、μ与方向无关。
平面问题的基本理论
平⾯问题的基本理论弹性⼒学⽹上辅导3平⾯问题的基本理论⼀、两类平⾯问题1.平⾯应⼒问题。
这类问题的条件是：弹性体是多厚度的薄板,体⼒、⾯⼒和约束都只有xy 平⾯内的量，都不沿Z向变化；并且⾯⼒和约束只作⽤于板边，在板⾯上没有任何⾯⼒和约束的作⽤。
平⾯应⼒问题特征是：⑴由于板⾯上⽆⾯⼒和约束作⽤，以及薄板很薄，可以得出（σz，τzx和τxy）=0（在平⾯域A内）。
因此，只有σx，σy，τxy三个平⾯内的应⼒分量。
⑵由于物体形状和外⼒、约束沿z向均不变化，因此应⼒分量只是X，y两变量的函数。
以后还可从物理⽅程得出，应变分量也只是X，y的函数；⽽从⼏何⽅程积分求位移可见，位移与Z有关。
归纳起来讲，所谓平⾯应⼒问题，就是只有平⾯应⼒分量（σx，σy和τxy）存在，且仅为X，y的函数的弹性⼒学问题。
例如，厚度较薄的浅梁和深梁，受上部荷载及⾃重的墙，以及有分缝的重⼒坝等，都属于平⾯应⼒问题，凡是符合上述这两点的问题，均属于平⾯应⼒问题。
2.平⾯应变问题这类问题的条件是：弹性体为常截⾯的很长柱体，体⼒、⾯⼒和约束条件与平⾯应⼒问题相似，只有xy平⾯内的体⼒、⾯⼒和约束的作⽤，且都不沿z向变化。
这个问题可以简化为平⾯应变问题。
平⾯应变问题特征是：⑴假想柱体为⽆限长时，则任⼀截⾯（z⾯）都是对称⾯，于是ω=0，只有平⾯位移分量u和v存在，因此，此问题可称为平⾯位移问题；同样由于对称性，εz =0和γzx，γzy=0（相应的τzx，和τzy=0），只有平⾯应变分量εx ，εy, τxy存在，所以此问题⼜称为平⾯应变问题。
⑵由于截⾯形状、体⼒、⾯⼒及约束沿z向均不变，因此，它们只是X，y 的函数。
由此可见，所谓平⾯应变问题，就是只有平⾯应变分量（εz ，εy和τxy，）存在，且仅为x，y的函数的弹性⼒学问题。
进⽽可认为，凡是符合这两点的问题，也都属于平⾯应变问题。
⼆、平衡微分⽅程平衡微分⽅程表⽰区域内任⼀点（x，y）的微分体的平衡条件。
第三章弹性力学平面问题的解析解法资料
ql z y l y l
ql x
xy y
—— 主要由剪力引起；
——由 q 引起（挤压应力）。
又∵ q =常数，图示坐标系和几何对称，∴ y 不随 x 变化。 推得：
y f ( y)
(2) 由应力分量表达式确定应力函数 ( x, y ) 的形式：
xf ( y ) f1 ( y ) (a) 2 x y 2 f ( y ) 积分得： x2 x f ( y ) xf1 ( y ) f 2 ( y ) (b) 2
x , y , xy
的某种函数形式 ； ，求 4 0
（3）最后利用式（2-26）计算出 x , y , xy 并让其满足边界条件和 位移单值条件。 —— 半逆解法的数学基础：数理方程中分离变量法。
位移分量求解：
（1） 将已求得的应力分量 x , y , xy 代入物理方程，求得应变分量
x , y , xy（具有待
（3）再利用应力边界条件式（2-18），来考察这些应力函数φ(x,y) 对 应什么样的边界面力问题，从而得知所设应力函数φ(x,y) 可以求 解什么问题。
半逆解法 （1）根据问题的条件（几何形状、受力特点、边界条件等）， （2）根据 x , y , xy 与应力函数φ(x,y)的关系及 出φ(x,y) 的形式； 假设部分应力分量
(e)
式中含有9个待定常数。
x2 ( Ay 3 By 2 Cy D) x( Ey 3 Fy 2 Gy) 2
A 5 B 4 ( y y Hy 3 Ky 2 ) 10 6
（ 2）
x , y , xy 将应变分量 x , y , xy 代入几何方程，并积分求得位移分量
弹性力学A-06温度应力的平面问题
第六章 温度应力的平面问题
力学与土木工程学院力学系弹性力学电子教案
CHINA UNIVERSITY OF MINING AND TECHNOLOGY
（5） 热传导微分方程
由热平衡原理，可知
（温度升高积蓄的热量）= （热流传入的热量）＋（热源供给的热量）
cdxdydz T dt 2Tdxdydzdt Wdxdydzdt
—— 热传导微分方程。
y
qx
dy
qx
qx x
dx
其中：
a c
O zx
y
zx dz dx
a —— 称为导温系数(又称为热扩散率)。单位：米2/时。
混凝土的导温系数 a = 0.003 ~ 0.005。
说明：
式中系数： , c, , a 均可近似地当作常数，但热源强度 W 一般不能
当作常量，而必须是 W W (t )
（1） 热平衡原理
在任意一段时间内，物体的任一微小部分所积蓄的热量（亦即温度升高 所需的热量），等于传入该微小部分的热量加上内部热源所供给的热量。
（2） 温度升高积蓄的热量
取如图微元体 dxdydz ，设微元体 在dt时间内，温度由 T 升高到：
—— 热平衡原理 y
dy
T T dt
t
微元体积蓄的热量为：cdxdydz T dt
2T
2T x 2
2T y 2
2T z 2
0
此时，热传导微分方程成为：
( C)
T a 2T W （b）
t
c
T W （c）
t c
而此时的 T 就是绝热温升率 。 因此有 W
t
t
c t
有：
T a 2T —— 混凝土硬化发热期热传导微分方程
弹性力学：平面问题02 应力函数解答
总结：（多项式应力函数 的性质）
（1） 多项式次数 n < 4 时，则系数可以任意选取，总可满足4 0 。 多项式次数 n ≥ 4 时，则系数须满足一定条件，才能满足 4 0。
多项式次数 n 越高，则系数间需满足的条件越多。
（2） 一次多项式，对应于无体力和无应力状态；任意应力函数φ(x,y)上加
横截面保持平面 —— 材力中“平面保持平面”的假设成立。
（2） 将下式中的第二式对 x 求二阶导数：
u
M EI
xy y
u0
v
M
2EI
y2
M 2EI
x2
x v0
1 2v M 常数 说明：在微小位移下，梁纵向纤维的曲
x2 EI
率相同。即
1
2v x2
M EI
—— 材料力学中挠曲线微分方程
EI 2
(3-3)
v M (l x)x M y2
2EI
2EI
梁的挠曲线方程：
v M (l x)x y0 2EI
—— 与材力中结果相同
（2）悬臂梁
边界条件
u 0 xl
h y h
v 0 2
2
xl
由式（f）可知，此边界条件无法满足。
u
M EI
xy y
u0
(f)
v
M
2EI
y2
M 2EI
要使上式成立，须有
f1( y)
M EI
x
f 2( x)
(e)
式中：ω为常数。 积分上式，得
f1( y) y u0
f2 ( x)
M EI
x2
x
v0
将上式代入式（d），得
u
M EI
5第三章弹性力学平面问题的解析解法讲解
2 X Y 2 x y y 2 x 2 ( x y ) (1 )
（平面应力情形）
（3）边界条件：
l ( x ) s m( xy ) s X m( y ) s l ( xy ) s Y
x 2 y
2
y 2 x
2
xy
2 xy
(2-28)
（无体力情形）
（3） 再让 x , y , xy满足应力边界条件和位移单值条件 （多连体问题）。
第三章 弹性力学平面问题的 解析解法
第四节 第五节 逆解法与半逆解法—多项式解答 矩形梁的纯弯曲
（2）边界条件： 位移边界条件： 应力边界条件：
（1 ）
u s u , vs v
（2）
E u v 1 u v l m X 2 y s 2 y x s 1 x （3 ） v u 1 v u E m l Y 2 1 y x s 2 x y s
4.
按应力求解平面问题的基本方程 说明：
（1）对位移边界问题，不易按应力 求解。
（1）平衡方程
x xy X 0 x y yx y Y 0 x y
（2）相容方程（形变协调方程）
（2）对应力边界问题，且为单连通 问题，满足上述方程的解是唯 一正确解。
（3）对多连通问题，满足上述方程 外，还需满足位移单值条件， 才是唯一正确解。
按应力求解平面问题（X = 常量、Y = 常量）的归结为： （1） 先由方程（2-27）求出应力函数： ( x ,7) 0 4 2 2 4 x x y y x , y , xy （2） 然后将 ( x , y ) 代入式（2-26）求出应力分量：
弹性力学第3章(徐芝纶第五版)
最主要量级q( l )2 h
,和次要量级 q l h
, 在材力
中均已反映,且与弹力相同。
最小量级 ~ q, 在材力中没有:
当lh
时,
仅占主项
M I
y
的1/15
( 6 %) ,
当 l 时h , 量级q 的值很小,可以不计。
弹力与材力的解法比较:
应力比较
弹力严格考虑并满足了A内的平衡微分 方程 ,几何方程和微分方程,以及S上的所有 边界条件(在小边界上尽管应用了圣维南 原理,但只影响小边界附近的局部区域)。
4 楔形体受重力和液体压力 问题
设有楔形体， 左面垂直，顶角为α， 下端无限长，受重 力及齐顶液体压力,
fx 0, f y 1g.
o
α 2g
y
x
n
α
2
1g
用半逆解法求解。
（1）用量纲分析法假设应力: （2）由应力~Φ关系式，Φ应为x,y的三次式，
（3）Φ 满足相容方程 4Φ 0.
（4）由 Φ求应力， （5）考察边界条件——本题只有两个大边 界，均应严格满足应力边界条件:
o
M
y
h/2
h/2
x
M
l
( l >>h)
半逆解法
3.半逆解法 步骤：
⑴ 假设应力的函数形式 （根据受力情况， 边界条件等）；
⑵ 由应力(d)式，推测 的Φ 函数形式；
⑶ 代入 4Φ，解0 出 ； Φ
半逆解法
⑷ 由式（d），求出应力；
⑸ 校核全部应力边界条件（对于多连体， 还须满足位移单值条件）. 如能满足，则为正确解答；否则修改假 设，重新求解。
为b,如图,水的密
度为 2 ，试求
平面问题中一点的应力状态
已知X=q， y=0， xy = -2q， 求： 1 ， 2 ，α1 1=2.562q 2=-1.562q tgα1=-0.781 α1=-37.99o=-37o59`
问题：
平面问题中，
(a)已知一点的应力为 方向的正应力n为 （b）已知 那么
，那么任一 1 2 n 为 ; a , b x y ? 1 2
⑶ 它是在边界上物体保持连续性的条 件，或位移保持连续性的条件。
应力边界条件－－设在 s 上给定了面力分 量
fx (s), f y (s).
通过三角形微分体的平衡条件，导出坐标面应力 与斜面应力的关系式，
p l σ m , p m σ l , x x y x y y x y
A
N
B
N
1 1 2 l ( ) N 2 1 4 2
2
s
N
1 显然，当 1l2 0 (l ) 时，τN为最大、最小值： 2 2
max 1 2 min 2
由 l
1 得， τmax、 τmin 的方向与σ1 2
（ σ2 ）成45°。
⑹ 所有边界均应满足，无面力的边界
（自由边） fx f也必须满足。 , y 0
坐标面
当边界面为坐标面时， 若x=a为正x 面，l = 1, m = 0, 则式(d)成为
() σ f ,() f . x x a x x y y x a
b a x
( e )
fx
xy
σ
x
σ
x
fx
n
B
py
xy
2
x
xy
y
σ2－(σx+σy)σ+(σxσy－τ2xy)=0
问题：
平面问题中，
(a)已知一点的应力为 方向的正应力n为 （b）已知 那么
，那么任一 1 2 n 为 ; a , b x y ? 1 2
⑶ 它是在边界上物体保持连续性的条 件，或位移保持连续性的条件。
应力边界条件－－设在 s 上给定了面力分 量
fx (s), f y (s).
通过三角形微分体的平衡条件，导出坐标面应力 与斜面应力的关系式，
p l σ m , p m σ l , x x y x y y x y
A
N
B
N
1 1 2 l ( ) N 2 1 4 2
2
s
N
1 显然，当 1l2 0 (l ) 时，τN为最大、最小值： 2 2
max 1 2 min 2
由 l
1 得， τmax、 τmin 的方向与σ1 2
（ σ2 ）成45°。
⑹ 所有边界均应满足，无面力的边界
（自由边） fx f也必须满足。 , y 0
坐标面
当边界面为坐标面时， 若x=a为正x 面，l = 1, m = 0, 则式(d)成为
() σ f ,() f . x x a x x y y x a
b a x
( e )
fx
xy
σ
x
σ
x
fx
n
B
py
xy
2
x
xy
y
σ2－(σx+σy)σ+(σxσy－τ2xy)=0
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2 xy
式（b）满足相容方程，∴（b）为可能的应变分量。
例题
已知薄板有下列形变关系：
x Axy, y By3 , xy C Dy2
式中A,B,C,D皆为常数，试检查在形变过程中是否符合连续条 件，若满足并列出应力分量表达式。 解答： （1）相容条件
x 将形变分量代入应变协调条件（相容方程） 2 2 y x xy
位移用变形─应力表示，须通过积分，
不仅表达式较复杂，而且包含积分带来的未
知项，因此位移边界条件用应力分量来表示
时既复杂又难以求解。故在按应力求解时，
只考虑全部为应力边界条件的问题,
即 (s sσ , su 0) 。
⑶ 在A内求解应力的方程 平衡微分方程 （2个）。 (a)
补充方程─从几何方程，物理方程中 消去位移和形变得出 : 从几何方程中消去位移 u ， v ，得相容方 程（形变协调条件）：
EA y 2GDy f x 0 2 1 若满足平衡微分方程，必须有 E ( Ax 3By3 ) f 0 y 2 1
例
图示矩形截面悬臂梁，在自由端受集中力P作用，不计体力。试根据 材料力学公式，写出弯曲应力 x 和剪应力 xy 的表达式，并取挤 压应力 y =0，然后说明这些表达式是否代表正确解。
而不能满足这个方程, 那么, 由三个几何方程中的任何两个 求出的位移分量, 将与第三个几何方程不能相容。这就表示, 变形以后的物体就不再是连续的, 而将发生某些部分互相脱 离或互相侵入的情况。
相容方程几何意义
不相容举例
例： x
0 y 0 xy Cxy
u v 0, 0 x y
1.按应力求解平面应力问题
（1）取 σ x , σ y , xy 为基本未知函数；
（2）其他未知函数用应力来表示:
平面应力问题的基本方程
平衡微分方程
x yx fx 0 x y y xy f y 0 y x
物理方程
几何方程
将 上式整理得：
2 f x f y 2 x y y 2 x 2 ( x y ) (1 ) （2）平面应变情形 将 上式中的泊松比μ代为： 1 ， 得
（2-23）
应力表示的相容方程 （平面应力情形）
2
2 y
2 xy
其中
x 0, 2 y
2
2 y x
2
0
2 xy xy
0
所以满足相容方程 ，符合连续条件。
解答：
（2）在平面应力问题中，用形变分量表示的应力分量为
E E 3 x ( ) ( Axy By ) x y 2 2 1 1 E E 3 y ( ) ( Axy By ) y x 2 2 1 1
§2-8 按应力求解平面问题
弹性力学里求解问题,有三种基本方法——按位移求 解,按应力求解和混合求解。
按应力求解平面问题——平衡微分方程本来就不包 含应变分量和位移分量,应当保留。于是,只须由三个
几何方程中消去位移分量,得出三个应变分量之间的
一个关系式, 再将三个物理方程代入这个关系式,使 它只包含应力分量。
Байду номын сангаас
+ -
b
c
-
+ d
对于多连通物体：我们总可以作适当的截面使它变成单连通物体，则上 述的结论也完全适用。具体地说，如果应变分量满足应变协调方程，则 在此被割开以后的区域里，一定能求得单值连续的函数。但对求得的位 移分量，当x，y点分别从截面两侧趋向于截面上某一点时，一般说它们 将趋向于不同的值。为使所考察的多连通物体在变形以后仍保持为连续 体，则必须加上补充条件。
（2-18）
例 下面给出平面应力问题（单连通域）的应力场和应变场，试分别判断它
们是否为可能的应力场与应变场（不计体力）。
3 2 2 1 4 （ a） x y , y y , xy xy3 ; 22 4 2 2 （2） x C ( x y ), y Cy , xy 2Cxy; （ b） 解 （1） 将式（a）代入平衡方程： x xy 3 2 2 1 4 fx 0 ( x y y ) x y x y 2 4 （2-2） yx y fy 0 2 2 x y 2 2 ( y y )
2 2 1 f x f y x y x 2 y 2 ( x y ) 1
2 2 x 2 y 2 ( x y ) 0
（2-24） 应力表示的相容方程 （平面应变情形）
注意： 当体力 为常数时，两种平面问题的相容方程相同，即
（2-25）
用应力表示的相容方程 ：
f x f y (σ x σ y ) (1 )( ), x y
2
(c)
其中
2 2 2 2. x y 2
(4) 应力边界条件－－假定全部边界上均 为应力边界条件 ( s sσ ,su 0) 。
x 2 2 y x
2
2 y
2 xy . xy
(b)
平面应力问题
变形协调方程或相容方程
u x x
v y y
v u xy x y
要使得满足几何方程的位移存在且是单
值的,应变分量之间必须满足一定的条件
平面应力问题
变形协调方程或相容方程
（1） x
3xy 3xy 0
2 2
x
y
y y 0
3 3
2 2
—— 满足
3 y 2 3x 2 3 y 2 0
∴ 式（a）不是一组可能 的应力场。
将式（a）代入相容方程：
x 2 y 2 ( x y ) 0
D
D
F
3.按应力求解平面问题的基本方程
（1）平衡方程
x xy X 0 x y yx y Y 0 x y
说明：
（2-2）
（2）相容方程（形变协调方程）
2 X Y 2 x y y 2 x 2 ( x y ) (1 )
u x x
将
v y y
v u xy x y
x对y偏导数两次， 将 y 对x偏导数两次， 将 xy 分别对x和y偏导数两次
x 3u 3v 3u u v 2 2 2 2 y x xy yx xy y x
归纳：
按应力求解平面应力问题 ，应力 σ x , σ y , xy 必须满足下列条件： （1）A内的平衡微分方程； （2）A内的相容方程； （3）边界 s sσ上的应力边界条件； （4）对于多连体，还须满足位移的单值条 件.
（1）-（4）也是校核应力分量是否正确的全部条件。
例 三连杆系统，由于物体是连续的，变 形前三连杆在 D 点共点（连续）， 变形后三连杆在 D ② ③ ① 点共点，则三连杆 的应变必须满足一 定的协调条件。
（2-22）
x fx y x 2 xy 2 x f x 2 yx x x
将上述两边相加：
xy
2 xy
x
fy
xy
2 y y
f y y
（2-2） 2 x 2 y f x f y 2 2 （b ） 2 xy y x y x
1 x y E 1 y y x E 21 xy xy E u x x v y y v u xy x y
x
变形用应力表示（物理方程）。
（1） x
（ a） （ b）
x 2 2 y x xy 2 x 2 xy 2 y 2C 2C 0 2 2 y xy x
2
2 y
2 xy
x 2 2C 2C 0 2 y x xy
2
2 y
因此，对于多连通物体，应变分量满足应变协调方程，只 是物体连续的必要条件,只有加上补充条件,条件才是充分的。
2. 变形协调方程的应力表示
（1）平面应力情形 将物理方程代入相容方程，得：
2 2 ( x y ) 2 ( y x ) 2 y x 2(1 )
2 xy
x xy fx 0 x y yx y fy 0 x y
2 2 y f x f y x ( x y ) 2 ( y x ) (1 ) 2 2 2 y x y x y x 2 2
xy G xyG (C Dy 2 )
（3）平衡微分方程
解答：
（3）平衡微分方程
其中
x EA y, 2 x 1 xy yx 0, 2GDy x y
x yx fx 0 x y y xy fy 0 y x y E 3 ( Ax 3 By ) 2 y 1
（平面应力情形） （2-23） （3）边界条件：
（1）对位移边界问题，不易按应 力求解。 （2）对应力边界问题，且为单连 通问题，满足上述方程的解 是唯一正确解。 （3）对多连通问题，满足上述方 程外，还需满足位移单值条 件，才是唯一正确解。
l ( x ) s m( xy ) s X m( y ) s l ( xy ) s Y
例 下面给出平面应力问题（单连通域）的应力场和应变场，试分别判断它